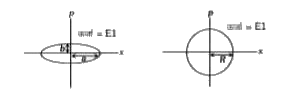ERRORLESS PHYSICS (HINDI) सरल आवर्त गति की JEE Section (Comprehension Type Questions) कक्षा 12 के लिए
| कक्षा 12 | भौतिकी |
| Chapter | सरल आवर्त गति |
| ERRORLESS PHYSICS (HINDI) | JEE Section (Comprehension Type Questions) |
| माध्यम | हिंदी |
| शैक्षणिक वर्ष | 2023-2024 |
Question 3
द्रव्यमान m की एक वस्तु स्प्रिंग स्थिरांक k के द्रव्यमान रहित स्प्रिंग के एक सिरे से जुड़ी होती है। स्प्रिंग का दूसरा सिरा एक दीवार से सटा हुआ है। ब्लॉक एक क्षैतिज खुरदरी सतह पर चल सकता है। ब्लॉक और सतह के बीच घर्षण का गुणांक है μ । तब स्प्रिंग का संपीड़न जिसके लिए स्प्रिंग का अधिकतम विस्तार अधिकतम संपीड़न का आधा हो जाता है:हल देखेंQuestion 4
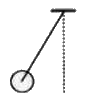
लम्बाई 'L' व् द्रव्यमान 'm' की एक धातु चढ़ अपने एक सिरे पर कीलित है। 'R'(<L) त्रिज्या 'M' द्रव्यमान की एक डिस्क छड़ के मुक्त सिरे पर अपने केंद्र से दो तरह से कीलित की जाती है। (स्थिति A ) डिस्क अपने केंद्र पर नहीं घूम सकती और ( स्थिति B ) डिस्क अपने केंद्र पर घूमने को स्वतंत्र है। एक ही विस्थापन अवस्था से छोड़ने पर यह छड़ डिस्क निकाय ऊर्ध्वाधर तल में सरल आवर्त दोलन (SHM ) करता है |तब
 हल देखें
हल देखेंQuestion 5
यदि बल नियतांक क्रमशा k1 एवं k2 वाली दो कमानियां, S1 एवं S2 एक समान बल से तानित की जाए, तब यह पाया जाता है, की कमानी S1 पर कमानी S2 के मुकाबले अधिक कार्य किया जाता है।
कथन-I : यदि कमानियां एकसमान मात्रा से तनित की जाती है , तब S1 पर किया गया कार्य S2 पर किये गए कार्य से अधिक है
कथन-2 : k1<k2 हल देखेंQuestion 7
जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = kx2', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल √mk के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ kx2 से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = ax4, (a>0) है तथा |x|>X0 के लिए स्थितिज ऊर्जा V(x) = V0, है (चित्र देखें) .
Q |x|> X0 के लिए कण का त्वरण-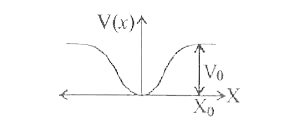 हल देखें
हल देखेंQuestion 8
जब m द्रव्यमान का एक कण x अक्ष पर V(x)=kx2 , स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवृतकाल √mk के समानुपाती होता है , जो की विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालांकि, यदि किसी एक कण की स्थितिज ऊर्जा x =0 के दोनों तरफ kx2 से भिन्न तरफ से बढे तथा कण की कुल ऊर्जा इतनी हो की वह अनंत तक पलायन न कर सकें, तब भी कण की गति आवृति हो सकती है। m द्रव्यमान का एक कण x -अक्ष पर गति करता है जहाँ |x| के केंद्र के पास होने पर स्थितिज ऊर्जा V(x)=ax4,(a>0) है तथा |x|≥X0 के लिए स्थितिज ऊर्जा V(x)=V0 है (चित्र देखें)
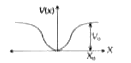
कम आयाम A के दोलन के लिए , कण का आवर्तकाल T निम्न में से किसके समानुपाती है हल देखेंQuestion 9
जब m द्रव्यमान का एक कण x अक्ष पर V(x)=kx2 , स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवृतकाल √mk के समानुपाती होता है , जो की विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालांकि, यदि किसी एक कण की स्थितिज ऊर्जा x =0 के दोनों तरफ kx2 से भिन्न तरफ से बढे तथा कण की कुल ऊर्जा इतनी हो की वह अनंत तक पलायन न कर सकें, तब भी कण की गति आवृति हो सकती है। m द्रव्यमान का एक कण x -अक्ष पर गति करता है जहाँ |x| के केंद्र के पास होने पर स्थितिज ऊर्जा V(x)=ax4,(a>0) है तथा |x|≥X0 के लिए स्थितिज ऊर्जा V(x)=V0 है (चित्र देखें)
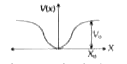
|x|>X0 के लिए कण का त्वरण हल देखेंQuestion 10
हर प्रकार की गतिकीय समस्याओं के विश्लेषण के लिए फेज समष्टि चित्रम ( Phase space diagrams ) का उपयोग किया जाता है। प्रारंभिक दशा, स्थिति व् सवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझाने में बहुत उपयोगी है। यहाँ हम एक विमीय सरल गतिकीय निकायों की बात करते है । इनके संवेग Y - अक्ष पर रखते है। तब फेज समष्टि चित्राम इस समतल में एक x(t)vs.p(t) (i ) वक्र होता। वक्र पर तीर समय बढ़ाने की दिशा दर्शाता है। उदाहरण के लिए, स्थिर वेग से चल रहें कण के लिए फेज समष्टि चित्राम सरल रेखा है जिसे चित्र में दिखाया गया है। चिन्ह परिपाटी में स्थित या संवेग को ऊपर (या दाहिने ) और धनात्मक तथा निचे (या बायीं) और ऋणात्मक मान जाता है
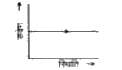
जमीन से ऊपर की और फेंकी गई गेंद का फेज समष्टि चित्राम है। हल देखेंQuestion 11
हर प्रकार की गतिकीय समस्याओं के विश्लेषण के लिए फेज समष्टि चित्रम ( Phase space diagrams ) का उपयोग किया जाता है। प्रारंभिक दशा, स्थिति व् सवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझाने में बहुत उपयोगी है। यहाँ हम एक विमीय सरल गतिकीय निकायों की बात करते है । इनके संवेग Y - अक्ष पर रखते है। तब फेज समष्टि चित्राम इस समतल में एक x(t)vs.p(t) (i ) वक्र होता। वक्र पर तीर समय बढ़ाने की दिशा दर्शाता है। उदाहरण के लिए, स्थिर वेग से चल रहें कण के लिए फेज समष्टि चित्राम सरल रेखा है जिसे चित्र में दिखाया गया है। चिन्ह परिपाटी में स्थित या संवेग को ऊपर (या दाहिने ) और धनात्मक तथा निचे (या बायीं) और ऋणात्मक मान जाता है
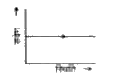
सरल आवर्त दोलन (SHM ) का फेज समष्टि चित्राम उदगम पर केंद्रित वृत है। चित्र में दर्शया गए दो वृत, एक ही दोलक के लिए है, जब उसकी आरंभिक अवस्थाएं भिन्न है ,तथा E1 व् E2 क्रमशः दोलक की कुल यांत्रिक ऊर्जाएं है। तब
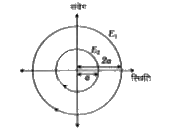 हल देखें
हल देखेंQuestion 13
द्रव्यमान M तथा त्रिज्या R की एक समान पतली बेलनाकार चक्ति को स्प्रिंग नियतांक k की दो समान द्रव्यमान रहित स्प्रिंग से जोधा जाता गया है जो दीवार पर लगी है ( चित्रानुसार) चकती के एक्सेल से सम्मित रूप में स्प्रिंग चक्ति के केंद्र से दोनों और d दुरी पर जुड़ी है। एक्सेल द्रव्यमान रहित है तथा दोनों स्प्रिंग और एक्सेल क्षैतिज तल में है। प्रत्येक स्प्रिंग की सामान्य स्थिति में लम्बाई L है। प्रारम्भ में चकती दीवार से उसके द्रव्यमान केंद्र (CM ) की दुरी L पर साम्य स्थिति में है। चकती बिना फिसले वेग V0=V0ˆi से लुढ़कती है। घर्षण गुणांक μ है।
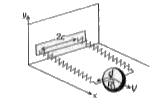
जब चकती का द्रव्यमान केंद्र साम्य स्थिति से x विस्थापन पर होता है, तब इस पर क्रियाशील कुल बाह्य बल होगा। हल देखेंQuestion 14
द्रव्यमान M तथा त्रिज्या R की एक समान पतली बेलनाकार चक्ति को स्प्रिंग नियतांक k की दो समान द्रव्यमान रहित स्प्रिंग से जोधा जाता गया है जो दीवार पर लगी है ( चित्रानुसार) चकती के एक्सेल से सम्मित रूप में स्प्रिंग चक्ति के केंद्र से दोनों और d दुरी पर जुड़ी है। एक्सेल द्रव्यमान रहित है तथा दोनों स्प्रिंग और एक्सेल क्षैतिज तल में है। प्रत्येक स्प्रिंग की सामान्य स्थिति में लम्बाई L है। प्रारम्भ में चकती दीवार से उसके द्रव्यमान केंद्र (CM ) की दुरी L पर साम्य स्थिति में है। चकती बिना फिसले वेग V0=V0ˆi से लुढ़कती है। घर्षण गुणांक μ है।
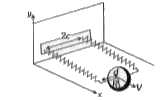
चकती का द्रव्यमान केंद्र, कोणीय आवर्ती ω से सरल आवर्त गति करता है , जो बराबर है हल देखेंQuestion 15
द्रव्यमान M तथा त्रिज्या R की एक समान पतली बेलनाकार चक्ति को स्प्रिंग नियतांक k की दो समान द्रव्यमान रहित स्प्रिंग से जोधा जाता गया है जो दीवार पर लगी है ( चित्रानुसार) चकती के एक्सेल से सम्मित रूप में स्प्रिंग चक्ति के केंद्र से दोनों और d दुरी पर जुड़ी है। एक्सेल द्रव्यमान रहित है तथा दोनों स्प्रिंग और एक्सेल क्षैतिज तल में है। प्रत्येक स्प्रिंग की सामान्य स्थिति में लम्बाई L है। प्रारम्भ में चकती दीवार से उसके द्रव्यमान केंद्र (CM ) की दुरी L पर साम्य स्थिति में है। चकती बिना फिसले वेग V0=V0ˆi से लुढ़कती है। घर्षण गुणांक μ है।
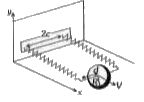
चकती के बिना फिसले लोटनिक गति करने के लिए V0 का अधिकतम मान है। हल देखें
ERRORLESS PHYSICS (HINDI) सरल आवर्त गति की सभी प्रश्नावली कक्षा 12 के लिए
- ORDINARY THINKING ( OBJECTIVE QUESTION) (आवर्तकाल एवं आवृति )
- ORDINARY THINKING ( OBJECTIVE QUESTION) (सरल आवर्त गति में ऊर्जा )
- ORDINARY THINKING ( OBJECTIVE QUESTION) (सरल आवर्त गति में कला एवं विस्थापन)
- ORDINARY THINKING ( OBJECTIVE QUESTION) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
- ORDINARY THINKING ( OBJECTIVE QUESTION) (सरल आवृत गति में त्वरण )
- ORDINARY THINKING ( OBJECTIVE QUESTION) (सरल आवृत गति में वेग )
- ORDINARY THINKING ( OBJECTIVE QUESTION) (सरल लोलक )
- ORDINARY THINKING ( OBJECTIVE QUESTION) (स्प्रिंग लोलक )
- CRITICAL THINKING (OBJECTIVE QUESTION)
- GRAPHICAL QUESTION (OBJECTIVE QUESTIONS )
- JEE SECTION (COMPREHENSION TYPE QUESTIONS)
- JEE SECTION (INTEGER TYPE QUESTIONS)
- JEE SECTION (JEE (ADVANCED )2018)
- JEE SECTION (MATRIX MATCH TYPE QUESTIONS)
- JEE SECTION (MORE THAN ONE CORRECT ANSWER)
- JEE SECTION (REASONING TYPE QUESTIONS)
- ASSERTION & REASON
- SELF EVALUATION TEST (सरल आवर्त गति )