दो स्वतंत्र समान द्रव्यमान के आवर्त दोलन मूल बिंदु के परितः कोणीय आवर्तियों ω1एवं ω2 तथा कुल ऊर्जाओं क्रमशा E1 तथा E2 से दोलन कर रहे है। उनके संवेगों (p ) का स्थिति x के साथ परिवर्तन सम्बन्ध चित्रों में दर्शाया गया है। यदि ab=n2 तथा aR=n, है , तब सही कथन है ( है)
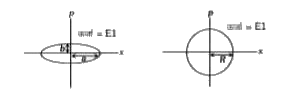
E1ω1=E2ω2
ω2ω1=n2
ω1ω2=n2
E1ω1=E2ω2
The correct Answer is:B, D
प्रथम दोलित्र के लिए
b=maω1
ab=1mω1=n2
द्वितीय दोलित्र के लिए
1mω2=1
E1=12m ω21 a2
E2=12mω22R2
E1E2=ω21ω22×n2=ω21ω22×ω2ω1
E1E2=ω1ω2⇒E1ω1=E2ω2
Topper's Solved these Questions
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - JEE Section (Reasoning Type Questions)
2 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - JEE Section (Comprehension Type Questions)
12 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Graphical Question (Objective Questions )
14 Videos
- विधुत चुम्बकीय प्रेरण BOOK - ERRORLESS HINDICHAPTER - विधुत चुम्बकीय प्रेरण EXERCISE - Self Evaluation Test विधुत चुम्बकीय प्रेरण
17 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Self Evaluation Test
8 Videos
Similar Questions
यदि बल नियतांक क्रमशा k1 एवं k2 वाली दो कमानियां, S1 एवं S2 एक समान बल से तानित की जाए, तब यह पाया जाता है, की कमानी S1 पर कमानी S2 के मुकाबले अधिक कार्य किया जाता है।
कथन-I : यदि कमानियां एकसमान मात्रा से तनित की जाती है , तब S1 पर किया गया कार्य S2 पर किये गए कार्य से अधिक है
कथन-2 : k1<k2
View Solutionजब m द्रव्यमान का एक कण :-अक्ष पर V(x) = kx2', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल √mk के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ kx2 से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = ax4, (a>0) है तथा |x|>X0 के लिए स्थितिज ऊर्जा V(x) = V0, है (चित्र देखें) .
Q |x|> X0 के लिए कण का त्वरण-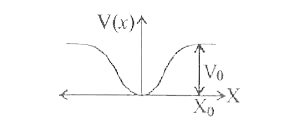
View Solutionएक कण स. आ. गति कर रहा है। इस कण के विस्थापन तथा त्वरण के बीच खींचे गए ग्राफ की प्रकृति होगी
View Solutionचित्र में चार तार लूपो को दिखाया गया है। जिनकी भुजाओ की लम्बाई L या 2L है सभी चारो एकसमान वेग से एक समरूप चुम्बकीय क्षेत्र →B (कागज़ तल के लम्बवत बाहर की ओर) से गुजरते है। जब ये चुम्बकीय क्षेत्र से गुजरते है तब इनमे उत्पन्न वि. वा. बल. के परिमाण के आधार पर इसका क्रम क्या होगा
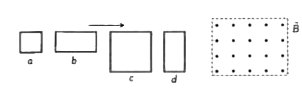
View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
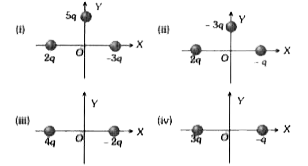
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
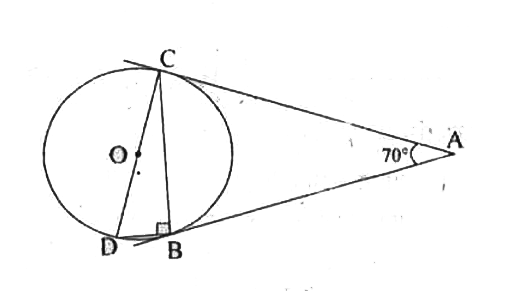
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionबिंदु P समिष्ट में इस प्रकार है की OP=6 तथा ¯¯¯¯op,OX तथा OY-अक्षो के साथ क्रमश: 45∘ व 60∘ के कोण बनता है तो का स्थिति सदिश होगा -
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionयदि पिता एवं पुत्र की आयु का योग (वर्षो में) 65 है तथा उनकी आयु के अन्तर का दुगुना 50 वर्ष है तब पिता की आयु होगी -
View Solutionभाषायी कौशलों के सम्बन्ध में कौन-सा कथन सही है?
View Solution
