चुम्बकत्व तथा द्रव्य कक्षा 12 भौतिकी
भूमिका
पिछले कुछ अध्यायों में हमने सीखा कि गतिशील आवेश या विद्युत धारा चुंबकीय क्षेत्र उत्पन्न करती है। यह खोज जो उन्नीसवीं शताब्दी के पूर्वार्द्ध में की गई थी, इसका श्रेय आर्स्टेड, ऐम्पियर, बायो-सावर्ट तथा अन्य कुछ लोगों को दिया जाता है। प्रस्तुत अध्याय में हम चुंबकत्व पर एक स्वतंत्र विषय के रूप में अध्ययन करेंगे।
भौतिकी में चुम्बकत्व वह प्रक्रिया है, जिसमें एक वस्तु दूसरी वस्तु पर आकर्षण या प्रतिकर्षण बल लगाती है। जो वस्तुएँ यह गुण प्रदर्शित करती हैं, उन्हें चुम्बक कहते हैं। निकल, लोहा, कोबाल्ट एवं उनके मिश्रण आदि सरलता से पहचाने जाने योग्य चुम्बकीय गुण रखते हैं। तो आइये हम चुम्बकत्व के बारे में विस्तार से अध्ययन करते है।
चुम्बक तथा इसके गुण
- वह पदार्थ जो चुम्बकीय वस्तुओं (जैसे-लोहा, कोबाल्ट तथा निकिल) को आकर्षित करता है, चुम्बक कहलाता है तथा चुम्बक द्वारा चुम्बकीय वस्तुओं को आकर्षित करने के गुण को चुम्बकत्व कहते हैं।
चुम्बक के प्रकार (Types of Magnet):
चुम्बक दो प्रकार के होते हैं:- (1) प्राकृतिक चुम्बक (Natural Magnet)
(2) कृत्रिम चुम्बक (Artificial Magnet)
(1) प्राकृतिक चुम्बक:
- प्रकृति से प्राप्त चुम्बक को प्राकृतिक चुम्बक कहते हैं ।

ये अनिश्चित आकार के तथा कम शक्तिशाली होते हैं । इन्हें इच्छानुसार आकृति नहीं दी जा सकती है ।
(2) कृत्रिम चुम्बक:
- मानव द्वारा निर्मित चुम्बक को कृत्रिम चुम्बक कहते हैं।
कृत्रिम चुम्बक दो प्रकार के होते हैं-
- (i) अस्थायी चुम्बक या विद्युत् चुम्बक, तथा
(ii) स्थायी चुम्बक।
(i) अस्थायी चुम्बक-
- वह चुम्बक जिसका चुम्बकत्व शीघ्र नष्ट हो जाता है, अस्थायी चुम्बक कहलाता है।
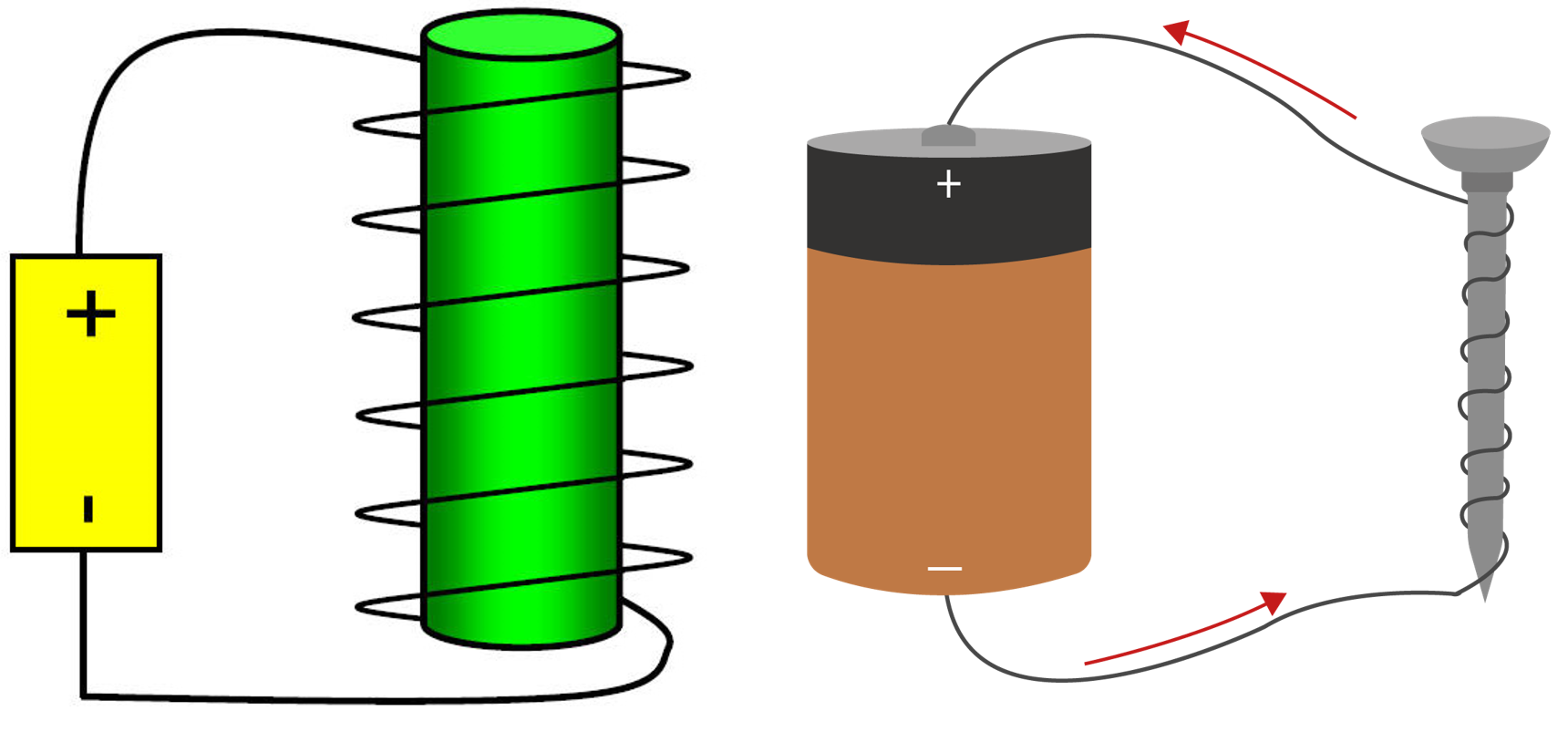
यह मुलायम लोहे का बनाया जाता है। मुलायम लोहे पर धात्विक तार की कुण्डली लपेटकर कुण्डली में धारा प्रवाहित कराने पर लोहा, चुम्बक बन जाता है। इसका चुम्बकत्व केवल तभी तक रहता है जब तक कि कुण्डली में धारा बहती है। कुण्डली में धारा प्रवाह बन्द करने पर लोहे का चुम्बकत्व समाप्त हो जाता है।
(ii) स्थायी चुम्बक-
- वह चुम्बक जिसका चुम्बकत्व शीघ्र नष्ट नहीं होता है, अपितु स्थायी होता है, स्थायी चुम्बक कहलाता है।

यह स्टील, निकिल, कोबाल्ट आदि का बनाया जाता है।
चुम्बक के सामान्य गुण (General properties of a magnet)-
चुम्बक के सामान्य गुण निम्नलिखित हैं :- यह चुम्बकीय पदार्थों को आकर्षित करता है (आकर्षण गुण)।
- चुम्बक के सिरों के जिन बिन्दुओं पर आकर्षण शक्ति (अर्थात् चुम्बकत्व) सबसे अधिक होती है, उन्हें चुम्बक के ध्रुव (poles) कहते हैं।
- स्वतन्त्रतापूर्वक लटका हुआ चुम्बक सदैव उत्तर-दक्षिण दिशा में ठहरता है (दैशिक गुण)।
- वह सिरा जो सदैव भौगोलिक उत्तर-दिशा की ओर ठहरता है, उत्तरी ध्रुव (north pole) कहलाता है तथा वह सिरा जो सदैव भौगोलिक दक्षिण-दिशा की ओर ठहरता है, दक्षिणी ध्रुव (south pole) कहलाता है।
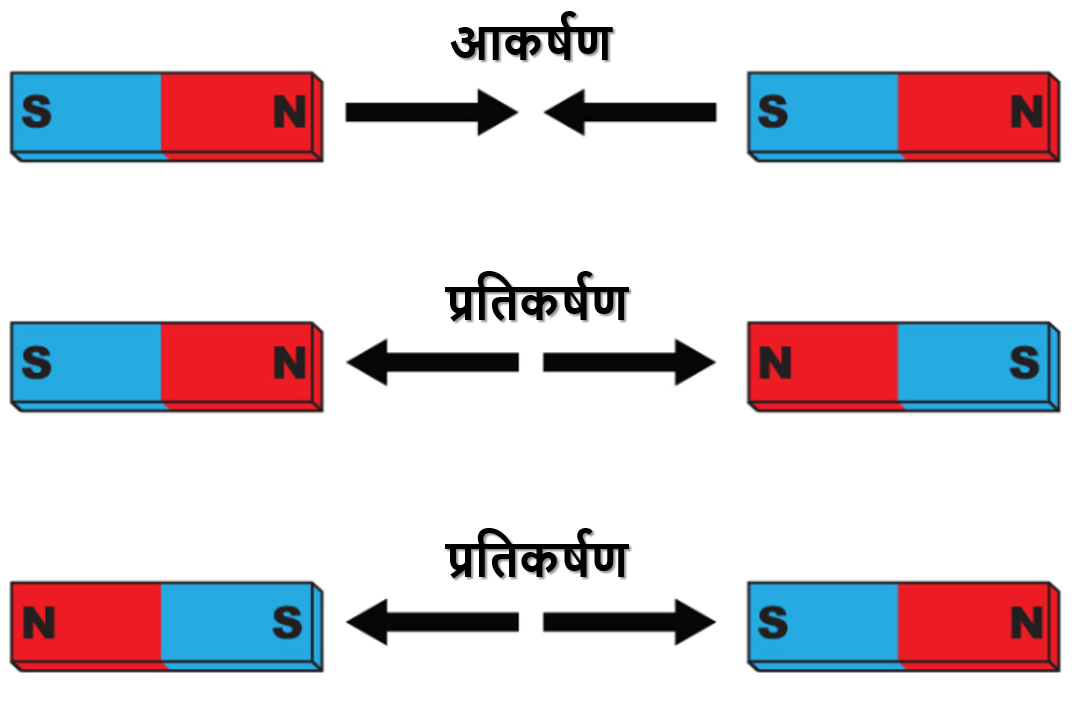
- चुम्बक के सजातीय ध्रुवों में परस्पर प्रतिकर्षण तथा विजातीय ध्रुवों में परस्पर आकर्षण होता है।
- चुम्बक के सजातीय ध्रुवों (उत्तरी-उत्तरी या दक्षिणी-दक्षिणी) में परस्पर प्रतिकर्षण होता है तथा विजातीय ध्रुवों (उत्तरी-दक्षिणी) में परस्पर आकर्षण होता है।
- चुम्बक, चुम्बकीय पदार्थों में प्रेरण द्वारा चुम्बकत्व उत्पन्न कर देता है।
- चुम्बक की उपस्थिति में किसी चुम्बकीय पदार्थ में अस्थायी चुम्बकत्व उत्पन्न होने की घटना को चुम्बकीय प्रेरण कहते हैं।
- एक अकेले चुम्बकीय ध्रुव का कोई अस्तित्व नहीं होता है।


चुम्बकीय द्विध्रुव तथा द्विध्रुव आघूर्ण
प्रत्येक चुम्बक के दो ध्रुव होते हैं- उत्तरी ध्रुव तथा दक्षिणी ध्रुव ।
दोनों ध्रुवों की ध्रुव प्रबलता (pole strength) समान होती है। ये ध्रुव एक-दूसरे के विपरीत ध्रुव कहलाते हैं। एक चुम्बक के चाहे जितने छोटे टुकड़े किये जाएँ, प्रत्येक छोटे चुम्बक में दोनों ध्रुव होते हैं। एक अकेले ध्रुव का अस्तित्व असम्भव है।
- परस्पर कुछ दूरी पर रखे दो बराबर व विपरीत ध्रुव प्रबलता के दो ध्रुवों का निकाय एक चुम्बकीय द्विधुव कहलाता है।

चित्र में ध्रुव प्रबलता m तथा −m के दो ध्रुव A व B एक-दूसरे से दूरी 2l पर स्थित हैं। ये एक चुम्बकीय द्विध्रुव बनाते हैं।
- चुम्बकीय द्विध्रुव का द्विध्रुव आघूर्ण, एक ध्रुव की ध्रुव प्रबलता तथा दोनों ध्रुवों के बीच की दूरी के गुणनफल के बराबर होता है।
M=m×2l
ध्रुव सामर्थ्य (या ध्रुव प्रबलता) का S. I. मात्रक ऐम्पियर x मीटर है,
- अतः द्विध्रुव आघूर्ण M का S. I. मात्रक ऐम्पियर x मीटर2 है।
- द्विध्रुव आघूर्ण M का विमीय सूत्र [M°L2A] है।
महत्वपूर्ण तथ्य
- चुम्बक, वास्तव में चुम्बकीय द्विध्रुव है जिसके उत्तरी ध्रुव की ध्रुव प्रबलता धनात्मक तथा दक्षिणी ध्रुव की ध्रुव प्रबलता ऋणात्मक मानते हैं।
- चुम्बकीय आघूर्ण की दिशा, चुम्बक के दक्षिणी ध्रुव से उत्तरी ध्रुव की ओर होती है।
परिक्रमण करते इलेक्ट्रॉन का चुम्बकीय द्विध्रुव आघूर्ण
प्रत्येक पदार्थ परमाणुओं से मिलकर बना है। प्रत्येक परमाणु के केन्द्र पर एक नाभिक होता है जिसमें परमाणु का लगभग समस्त द्रव्यमान तथा धन आवेश केन्द्रित रहता है,
नाभिक के चारों ओर विभिन्न निश्चित कक्षाओं में इलेक्ट्रॉन परिक्रमण करते हैं। इसे इलेक्ट्रॉन की कक्षीय गति (orbital motion) कहते हैं। इस गति के साथ-साथ इलेक्ट्रॉन अपनी धुरी पर भी घूमता है। इसे इलेक्ट्रॉन की चक्रण गति (spin motion) कहते हैं।
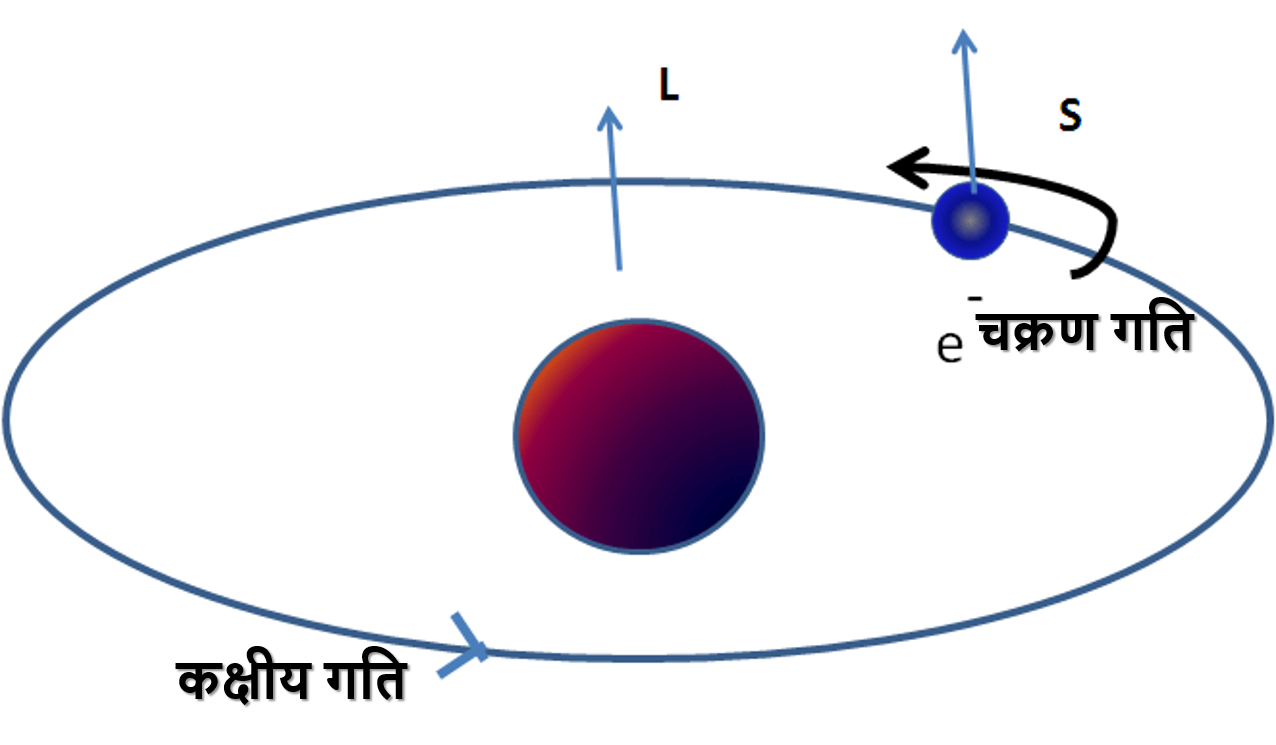
इलेक्ट्रॉन की इन्हीं गतियों के कारण परमाणु में चुम्बकत्व उत्पन्न होता है, परन्तु परमाणु के चुम्बकीय आघूर्ण का अधिकांश भाग इलेक्ट्रॉन की चक्रण गति के कारण उत्पन्न होता है, परिक्रमण गति का चुम्बकीय आघूर्ण में योगदान बहुत कम होता है।
- परिक्रमण अथवा चक्रण करता हुआ इलेक्ट्रॉन एक धारा लूप की भाँति व्यवहार करता है जिससे चुम्बकीय क्षेत्र सम्बद्ध होता है।
- प्रत्येक धारा लूप को एक चुम्बकीय द्विध्रुव के तुल्य माना जा सकता है।
M=NIA ....(1)
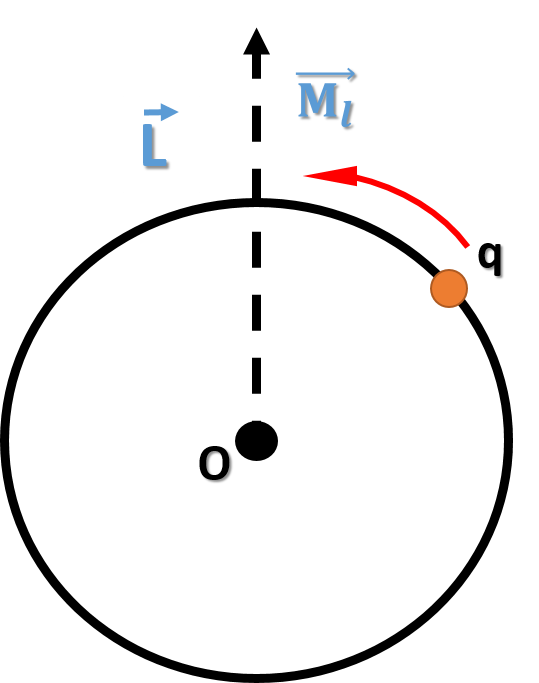
माना दिए हुए चित्र में आवेश q एकसमान कोणीय वेग ω (या रेखीय चाल v) से त्रिज्या r के वृत्तीय मार्ग में परिक्रमण (अथवा घूर्णन) कर रहा है। यदि आवेश एक चक्कर पूर्ण करने में T समय लेता है तो आवेश की गति से उत्पन्न धारा
I=qT
- लेकिन T=2πω तथा ω=vr, अतः T=2πrv तब,
I=q2πrv=qv2πr .....(2)
इस प्रकार, परिक्रमण (अथवा घूर्णन) करता हुआ आवेश, एक धारा लूप की भाँति व्यवहार करता है जिसका क्षेत्रफल A=πr2 (= आवेश की कक्षा का क्षेत्रफल) है। इस धारा लूप को एक चुम्बकीय द्विध्रुव के तुल्य माना जा सकता है जिसका द्विध्रुव आघूर्ण, ऐम्पियर के नियमानुसार, लूप में धारा तथा लूप के प्रभावी क्षेत्रफल के गुणनफल के बराबर होता है, अर्थात्- धारा लूप के तुल्य चुम्बकीय द्विध्रुव का द्विध्रुव आघूर्ण M = (लूप में धारा) x (लूप का प्रभावी क्षेत्रफल )
M=I×A
M=qv2πr×πr2=qvr2 ....(3)
चित्र में चूँकि आवेश q की गति वामावर्त है, अतः धारा लूप का ऊपरी सिरा उत्तरी ध्रुव व निचला सिरा दक्षिणी ध्रुव की भाँति व्यवहार करेगा जिसके फलस्वरूप द्विध्रुव आघूर्ण M की दिशा, लूप की अक्ष के अनुदिश बाहर की ओर (चित्र में कागज के तल के लम्बवत् बाहर की ओर) होगी।M=qv2πr×πr2=qvr2 ....(3)
- यदि आवेश (या आवेशित कण) का द्रव्यमान m है तो आवेश का घूर्णन (या परिक्रमण) अक्ष के परितः कोणीय संवेग
→L=m→r×→v
या∣∣→L∣∣=mvr .....(4)
स्पष्टतः चित्र में कोणीय संवेग की दिशा कागज के तल के लम्बवत् बाहर की ओर होगी। समीकरण (3) तथा (4) से, M=qvr2×mm=q×mvr2m=q2mL
वेक्टर रूप में,→M=q2m→L .....(5)
चुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता
- किसी चुम्बक के चारों ओर का वह क्षेत्र जिसमें इस चुम्बक के प्रभाव का अनुभव किया जा सकता है, चुम्बकीय क्षेत्र कहलाता है।
- किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता, उस बिन्दु पर रखे एक काल्पनिक एकांक उत्तरी ध्रुव पर लगने वाले बल के बराबर होती है।
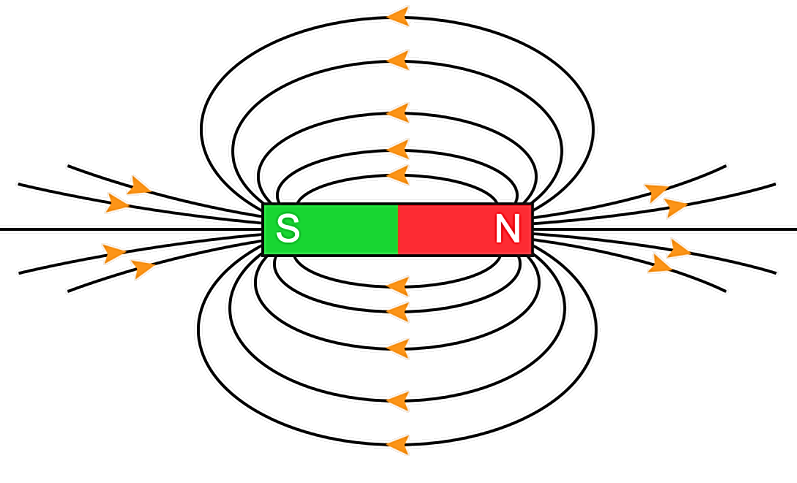
चित्रानुसार चुम्बकीय क्षेत्र के किसी बिन्दु पर चुम्बकीय क्षेत्र की दिशा उत्तरी से ध्रुव दक्षिणी ध्रुव की ओर होती है दूसरे शब्दों में, किसी बिन्दु पर चुम्बकीय क्षेत्र की दिशा, उस बिन्दु पर रखे काल्पनिक उत्तरी ध्रुव पर लगने वाले बल की दिशा होती है।
यह अध्ययन किया जा चुका है कि चुम्बक के दो सजातीय ध्रुवों के बीच परस्पर प्रतिकर्षण होता है तथा दो विजातीय ध्रुवों के मध्य परस्पर आकर्षण होता है। दो चुम्बकीय ध्रुवों के बीच लगने वाले बल का परिमाण ज्ञात करने के लिए वैज्ञानिक कूलॉम ने एक नियम प्रतिपादित किया जिसे कूलाम का व्युत्क्रम वर्ग का नियम कहते हैं। कूलॉम के नियमानुसार,
- दो चुम्बकीय ध्रुवों के बीच लगने वाला बल, उनकी ध्रुव प्रबलताओं के गुणनफल के अनुक्रमानुपाती तथा ध्रुवों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
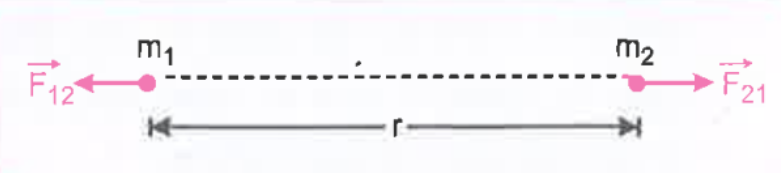
चित्र में यदि ध्रुव प्रबलता m1 व m2 के दो चुम्बकीय ध्रुवों के बीच की दूरी r है तो उनके बीच लगने वाला बल,
F∝m1m2
तथाF∝1r2
उपर्युक्त दोनों समीकरणों से,F∝m1m2r2
याF=μ4π×m1m2r2 .....(1)
यदि वायु (या निर्वात्) की चुम्बकशीलता μ0 है तथा माध्यम की आपेक्षिक चुम्बकशीलता μr तो
μ=μ0μr
- यहाँ μr विमाहीन नियतांक है।
तब समीकरण (1) से,
F=μ0μr4π×m1m2r2
वायु (या निर्वात) में μr=1, तबF=μ04π×m1m2r2
चुम्बकीय क्षेत्र की तीव्रता :-

चित्रानुसार यदि ध्रुव सामर्थ्य m1 तथा ध्रुव सामर्थ्य m2 पर क्रमशः चुम्बकीय क्षेत्र की तीव्रता B1 तथा B2 है, तो ध्रुव सामर्थ्य m1 पर बल m2B1, लगेगा तथा ध्रुव सामर्थ्य m2 पर बल m1B2, लगेगा। तब
- ध्रुव सामर्थ्य m1 के कारण दुरी r पर ध्रुव सामर्थ्य m2 पर चुम्बकीय बल होगा,
F21=m1B2
m1B2=μ4π×m1m2r2
याB2=μ4π×m2r2 ......(2)
F12=m2B1
m2B1=μ4π×m1m2r2
याB1=μ4π×m1r2 ......(3)
एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
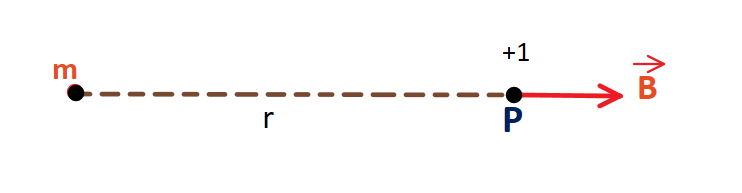
माना चित्र में ध्रुव प्रबलता m का एक अकेला काल्पनिक चुम्बकीय ध्रुव है जिसके कारण r दूरी पर स्थित किसी बिन्दु P पर हमें चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है। इसके लिए बिन्दु P पर हम एकांक काल्पनिक ध्रुव की कल्पना करते हैं। तब बिंदु P पर चुम्बकीय बल की प्रबलता +1 है तब
बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता B = काल्पनिक एकांक उत्तरी ध्रुव पर लगने वाला बल
अर्थातB=μ04π×m×1r2
याB=μ04πmr2 .....(1)
अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
चित्र में एक चुम्बकीय द्विध्रुव NS है जिसकी ध्रुव प्रबलता m, प्रभावकारी लम्बाई 2l तथा चुम्बकीय आघूर्ण M=m×2l है। इसकी अक्ष पर एक बिंदु P, मध्य बिन्दु O से दूरी x पर स्थित है, जहाँ हमें चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है। चित्र से स्पष्ट है कि NP=x−l तथा SP=x+l
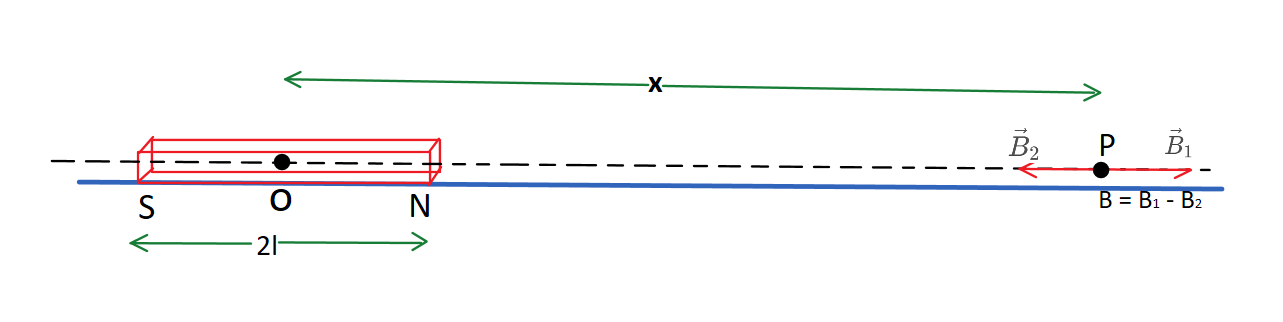
- माना बिन्दु P पर काल्पनिक एकांक उत्तरी ध्रुव रखा है। द्विध्रुव के उत्तरी ध्रुव N के कारण बिन्दु P पर रखे एकांक उत्तरी ध्रुव पर लगने वाला बल (अर्थात् चुम्बकीय क्षेत्र की तीव्रता)
→B1=μ04πm(NP)2
→B1=μ04πm(x−l)2 ......(दिशा NP में)
तथा द्विध्रुव के दक्षिणी ध्रुव S के कारण बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता→B1=μ04πm(x−l)2 ......(दिशा NP में)
→B2=μ04πm(SP)2
→B2=μ04πm(x+l)2 ......(दिशा PS में)
→B2=μ04πm(x+l)2 ......(दिशा PS में)
→B=∣∣→B1∣∣−∣∣→B2∣∣
→B=μ04π×[m(x−l)2−m(x+l)2]
→B=μ04π×4mlx(x2−l2)2
परन्तु 2ml=M (चुम्बक का चुम्बकीय आघूर्ण) अत:→B=μ04π×[m(x−l)2−m(x+l)2]
→B=μ04π×4mlx(x2−l2)2
B=μ04π2Mx(x2−l2)2 .......(1)
चुम्बकीय क्षेत्र B की दिशा, चुम्बक की अक्ष के समान्तर चुम्बक के दक्षिणी ध्रुव S की ओर अथवा चुम्बक के उत्तरी ध्रुव N से दूर की ओर होता है।- यदि छड़ चुम्बक NS अत्यन्त छोटा है तथा बिन्दु P, चुम्बक की अक्ष पर बहुत अधिक दूर स्थित है (अर्थात् x के सापेक्ष l बहुत कम है, x⟩>l), तो समीकरण (1) से,
B=μ04π2Mxx4
B=μ04π2Mx3 न्यूटन/ऐम्पियर-मीटर .....(2)
निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
चित्र में एक चुम्बकीय द्विध्रुव NS है जिसकी ध्रुव प्रबलता m, प्रभावकारी लम्बाई 2l तथा चुम्बकीय आघूर्ण M=m×2l है। चुम्बकीय अक्ष NS का लम्ब सम-द्विभाजक, चुम्बकीय अक्ष के मध्य बिन्दु O पर अभिलम्ब OP है। रेखा OP को चुम्बक का निरक्षीय अथवा अनुप्रस्थ रेखा कहते हैं। माना इस निरक्षीय रेखा पर कोई बिन्दु P, चुम्बक के मध्य बिन्दु O से दूरी x पर स्थित है जहाँ हमें चुम्बकीय क्षेत्र की तीव्रता ज्ञात करती है। माना बिन्दु P पर काल्पनिक एकांक उत्तरी ध्रुव रखा है।
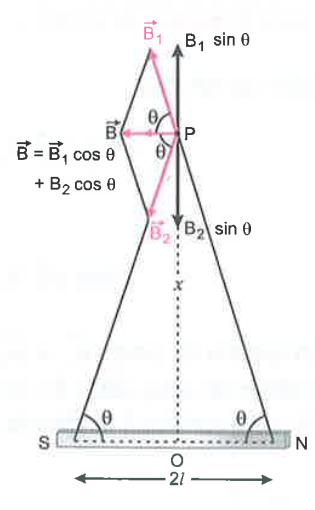
- चुम्बक के उत्तरी ध्रुव N के कारण बिन्दु P पर रखे एकांक उत्तरी ध्रुव पर लगने वाला बल (अर्थात् चुम्बकीय क्षेत्र की तीव्रता)
B1=μ04πm(NP)2....(दिशा →PS में)
- तथा चुम्बक के दक्षिणी ध्रुव S के कारण बिन्दु P पर एकांक दक्षिणी ध्रुव पर लगने वाला बल (अर्थात् चुम्बकीय क्षेत्र की तीव्रता)
B2=μ04πm(SP)2 .....(दिशा →PS में)
चित्र से स्पष्ट है कि NP=SP, अत: इन दोनों चुम्बकीय क्षेत्रों के परिमाण बराबर हैं, (अर्थात् B1=B2) तथा दिशाएँ क्रमशः NP (या PB) तथा PS हैं। यदि ∠PNS=θ, तब∠PSN=∠BPB1=∠BPS=θ
- चूंकि B1sinθ=B2sinθ, अत: ऊर्ध्वाधर घटक एक-दूसरे की विपरीत दिशा में होने से एक-दूसरे के परिमाण को निष्फल कर देते हैं तथा क्षैतिज घटक B1cosθ और B2cosθ एक ही दिशा (PB दिशा) में होने से परस्पर जुड़ जाते हैं। अत: बिन्दु P पर परिणामी चुम्बकीय क्षेत्र की तीव्रता
B=B1cosθ+B2cosθ
याB=μ04π×[m(NP)2cosθ+m(SP)2cosθ]
- लेकिन चित्र से स्पष्ट है कि समकोण त्रिभुज PON व POS में,
NP=SP=√x2+l2
- तथा
cosθ=ONNP=l√x2+l2
- अत:
B=μ04π×m(NP)2cosθ
B=2×μ04πmx2+l2×l√x2+l2
B=2×μ04πmx2+l2×l√x2+l2
- या
B=μ04π×2ml(x2+l2)32
लेकिन 2ml=M (चुम्बक का चुम्बकीय आघूर्ण)B=μ04π×M(x2+l2)32 न्यूटन/ऐम्पियर-मीटर .....(1)
इस चुम्बकीय क्षेत्र की दिशा, चुम्बकीय अक्ष के समान्तर उत्तरी ध्रुव N से दक्षिण ध्रुव S की ओर है।- यदि चुम्बक के मध्य बिन्दु O से बिन्दु P की दूरी x के सापेक्ष, चुम्बक की लम्बाई l नगण्य (अर्थात x>>>l), तो समीकरण (1) से,
B=μ04π×Mx3 न्यूटन/ऐम्पियर-मीटर .....(2)
एकसमान चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव पर बल आघूर्ण
माना किसी दण्ड चुम्बक NS को स्वतन्त्रतापूर्वक किसी एकसमान चुम्बकीय क्षेत्र B में लटका दिया जाता है। माना चुम्बक की ध्रुव प्रबलता m एवं प्रभावकारी लम्बाई 2l है तथा चुम्बक की अक्ष, चुम्बकीय क्षेत्र B की दिशा के साथ कोण θ बनाती है।
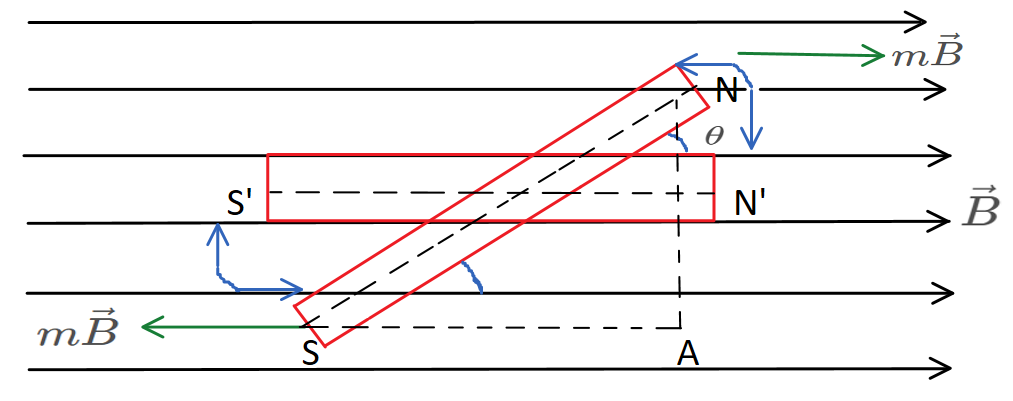
स्पष्ट है कि चुम्बकीय क्षेत्र B के कारण चुम्बक के उत्तरी ध्रुव N पर लगने वाला बल mB, चुम्बकीय क्षेत्र की दिशा में होगा तथा दक्षिणी ध्रुव पर लगाने वाला बल mB, चुम्बकीय क्षेत्र के विपरीत दिशा में होगा, अत: चुम्बक पर परिणामी बल शून्य होगा।
- चुम्बक के ध्रुवों पर लगने वाले बराबर तथा विपरीत बल, एक बलयुग्म (couple) बनाते है जो चुम्बक को चुम्बकीय क्षेत्र की दिशा के समान्तर N'S' स्थिति में लाने का प्रयत्न करता है। इसे चित्र में बिन्दु मे रेखाओं द्वारा दिखाया गया है। इस बलयुग्म के आघूर्ण को प्रत्यानयन बल आघूर्ण कहते हैं।
- प्रत्यानयन बल आघूर्ण τ = बल x बलों के बीच की लम्बवत् दूरी
τ=mB×NA
- लेकिन समकोण त्रिभुज NAS में, NA=SNsinθ=2lsinθ
अतः
τ=mB×2lsinθ
- या
τ=MBsinθ .....(1)
- सदिश रूप में, बल आघूर्ण
→τ=→M×→B .......(2)
- यदि चुम्बक की अक्ष, चुम्बकीय क्षेत्र B के लम्बवत् है (अर्थात् θ=90° या sinθ=1), तो चुम्बक पर लगने वाला बल आघूर्ण अधिकतम होगा अत: समीकरण (1) से अधिकतम बल आघूर्ण
τmax=MB
M=τmaxB
यदि B=1 तो,M=τmaxB
M=τmax ......(3)
चुम्बकीय आघूर्ण का मात्रक तथा विमीय सूत्र-
समीकरण (3) से,- M का मात्रक = τmax का मात्रक/ B का मात्रक = (न्यूटन × मीटर)/(न्यूटन/ऐम्पियर × मीटर)
M का मात्रक = ऐम्पियर × मीटर2
M का विमीय सूत्र = [MLT−2]×[L]MLT−2AL=[M0L2T0A]
उदाहरण 1
चित्र में, चुंबकीय सुई का चुंबकीय आघूर्ण 6.7×10−2Am2 और जड़त्व आघूर्ण I=7.5×10−6kgm2 है। यह 6.70s में 10 पूरे दोलन करती है। चुंबकीय क्षेत्र का परिमाण क्या है?
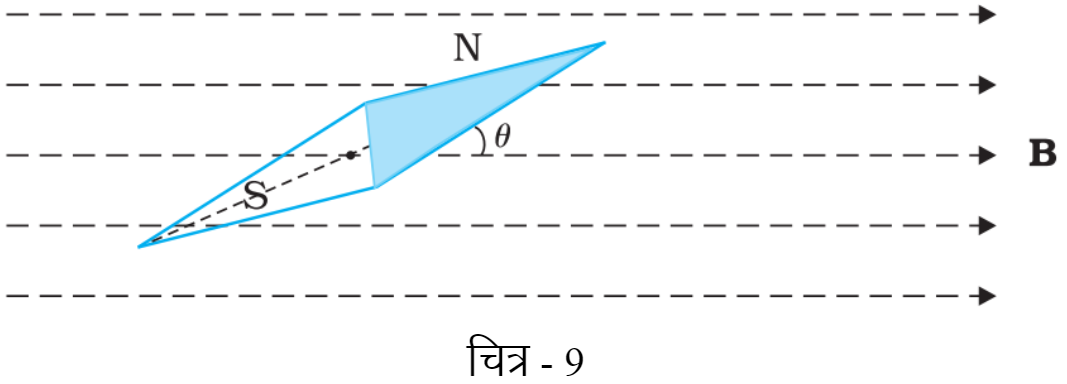
दोलनकाल
समिकरण B=4π2ImT2 से,
B=4×(3.14)2×7.5×10−66.7×10−2×(0.67)2
B=0.01T
उदाहरण 2
एक छोटे छड़ चुंबक को जब 800 G के बाह्य चुंबकीय क्षेत्र में इस तरह रखा जाता है कि इसकी अक्ष क्षेत्र से 30° का कोण बनाए, तो यह 0.016 N m का बलआघूर्ण अनुभव करता है।
(a) चुंबक का चुंबकीय आघूर्ण कितना है?
(b) सर्वाधिक स्थायी स्थिति से सर्वाधिक अस्थायी स्थिति तक इसको घुमाने में कितना कार्य करना पड़ेगा?
(c) छड़ चुंबक को यदि एक परिनालिका से प्रतिस्थापित कर दें जिसमें 1000 फेरे हों, जिसके अनुप्रस्थ काट का क्षेत्रफल 2×10−4m2 हो और जिसका चुंबकीय आघूर्ण उतना ही हो जितना छड़ चुंबक का है, तो परिनालिका में प्रवाहित होने वाली धारा ज्ञात कीजिए।
(a) समीकरण τ=mBsinθके अनुसार, θ=30°, इसलिये sinθ=1/2
अतः,
m=160×2/800
m=0.40Am2
(b) समीकरण (6) के अनुसार सर्वाधिक स्थायी स्थिति तब है जब θ=0° एवं सर्वाधिक अस्थायी स्थिति तब है जब θ=180°
W=2mB
W=2×0.40×800×10−4
W=0.064J
(c) चूँकि ms=NIA
भाग (a) से,
मान रखने पर
I=0.40×104/(1000×2)
I=2A
उदाहरण 3
(a) क्या होता है जबकि एक चुंबक को दो खंडों में विभाजित करते हैं (i) इसकी लंबाई के लंबवत (ii) लंबाई के अनुदिश?
(b) एकसमान चुंबकीय क्षेत्र में रखी गई किसी चुंबकीय सुई पर बल आघूर्ण तो प्रभावी होता है पर इस पर कोई परिणामी बल नहीं लगता। तथापि, एक छड़ चुंबक के पास रखी लोहे की कील पर बल आघूर्ण के साथ-साथ परिणामी बल भी लगता है। क्यों?
(c) क्या प्रत्येक चुंबकीय विन्यास का एक उत्तरी और एक दक्षिणी ध्रुव होना आवश्यक है? एक टोरॉयड के चुंबकीय क्षेत्र के संबंध में इस विषय में अपनी टिप्पणी दीजिए।
(d) दो एक जैसी दिखाई पड़ने वाली छड़ें A एवं B दी गई हैं जिनमें कोई एक निश्चित रूप से चुंबकीय है, यह ज्ञात है (पर कौन सी यह ज्ञात नहीं है)। आप यह कैसे सुनिश्चित करेंगे कि दोनों छड़ें चुंबकीय हैं या केवल एक? और यदि केवल एक छड़ चुंबकित है तो यह कैसे पता लगाएँगे कि वह कौन सी है। [आपको छड़ों A एवं B के अतिरिक्त अन्य कोई चीज प्रयोग नहीं करनी है।]
(a) दोनों ही प्रकरणों में आपको दो चुंबक प्राप्त होते हैं जिनमें से प्रत्येक में एक उत्तरी और एक दक्षिणी ध्रुव होता है।
(b) यदि क्षेत्र एकसमान हों केवल तभी चुंबक पर कोई बल नहीं लगता। परंतु छड़ चुंबक के कारण कील पर आसमान क्षेत्र आरोपित होता है जिसके कारण कील में चुंबकीय आघूर्ण प्रेरित होता है। अतः इस पर परिणामी बल भी लगता है और बल आघूर्ण भी। परिणामी बल आकर्षण बल होता है, क्योंकि कील में प्रेरित दक्षिण ध्रुव (माना) इसमें प्रेरित उत्तरी ध्रुव की अपेक्षा चुंबक के अधिक निकट होता है।
(c) आवश्यक नहीं है। यह तभी सत्य होगा जब चुंबकीय क्षेत्र के स्रोत का परिणामी चुंबकीय आघूर्ण शून्य नहीं होगा। टोराइड या अनंत लंबाई की परिनालिका के लिए ऐसा नहीं होता।
(d) चुंबकों के अलग-अलग सिरों को एक-दूसरे के पास लाने की कोशिश कीजिए। यदि किसी स्थिति में प्रतिकर्षण बल का अनुभव हो तो दोनों छड़ें चुंबकित हैं। यदि हमेशा आकर्षण बल ही लगे तो उनमें से एक छड़ चुंबक नहीं है। यह देखने के लिए कि कौन-सी छड़ चुंबकित है, एक छड़ A मान लीजिए और इसका एक सिरा नीचे कीजिए; पहले दूसरी छड़ B के सिरे के पास लाए और फिर बीच में। अगर आप पाएँ कि B के बीच में छड़ A आकर्षण बल अनुभव नहीं करती तो B चुंबकीय है। और यदि आप पाएँ कि सिरे पर और बीच में आकर्षण बल बराबर है, तो छड़ A चुंबकीत है।
चुम्बकीय क्षेत्र में चुम्बक घुमाने में कार्य, चुम्बक की स्थितिज ऊर्जा
चुम्बक को घुमाने में किया गया कार्य -
माना चित्र में एक दण्ड चुम्बक NS है जिसका चुम्बकीय आघूर्ण M है, तथा यह एक एकसमान चुम्बकीय क्षेत्र B में चुम्बकीय क्षेत्र की दिशा से कोण θ बनाता हुआ रखा है। चुम्बक के उत्तरी व दक्षिणी ध्रुवों पर लगने वाले बराबर व विपरीत बलों के कारण उस पर लगने वाला प्रत्यानयन बलयुग्म आघूर्णτ=MBsinθ
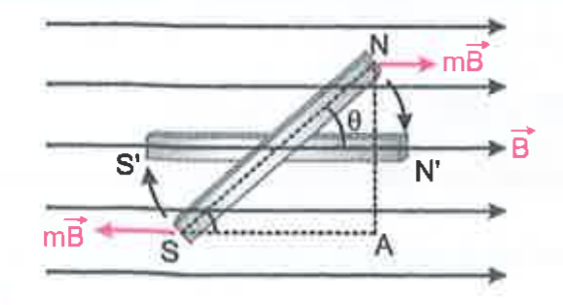
हमें चुम्बक को चुम्बकीय क्षेत्र की दिशा से कोण θ घुमाने में किये गये कार्य की गणना करनी है।
- यदि चुम्बक को अल्प कोण dθ से घुमाया जाए, तो किया गया कार्य
dW=τdθ=MBsinθdθ
- ∵ चुम्बक को चुम्बकीय क्षेत्र की दिशा (θ=0°) से कोण θ घुमाने में किया गया कार्य
W=∫θ0MBsinθdθ
W=MB(−cosθ)θ0
W=MB[−cosθ−(−cos0°)]
W=MB[−cosθ+1]
W=MB(−cosθ)θ0
W=MB[−cosθ−(−cos0°)]
W=MB[−cosθ+1]
- या
W=MB(1−cosθ) .....(1)
स्थितिज ऊर्जा-
जब चुम्बक, चुम्बकीय क्षेत्र की दिशा के लम्बवत् होता है (अर्थात् θ=π2 ), तो इसे चुम्बक की मानक स्थिति मानते हैं। किसी अन्य स्थिति में चुम्बक की स्थितिज ऊर्जा उस किये गये कार्य के बराबर होती है, जो इसे मानक स्थिति से वर्तमान स्थिति तक लाने के लिए करना पड़ता है।- माना चित्र में एक दण्ड चुम्बक NS है जिसका चुम्बकीय आघूर्ण M है तथा यह एकसमान चुम्बकीय क्षेत्र B में क्षेत्र की दिशा से कोण θ बनाता हुआ रखा है। चुम्बक के उत्तरी व दक्षिणी ध्रुवों पर लगने वाले बराबर व विपरीत बलों के कारण उस पर लगने वाला प्रत्यानयन बलयुग्म आघूर्ण τ=MBsinθ
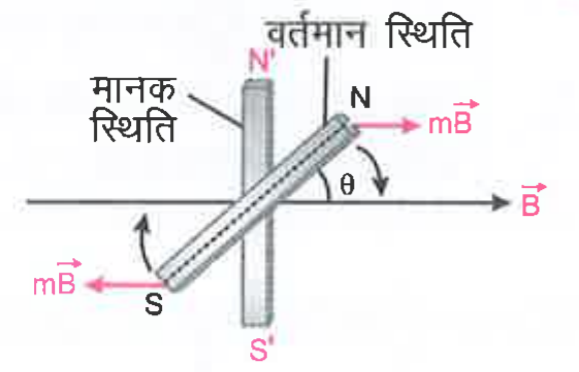
- अब यदि चुम्बक को अल्प कोण dθ से घुमाया जाए तो किया गया कार्य
dW=τdθ=MBsinθdθ
- अतः चुम्बकीय क्षेत्र की दिशा से कोण θ पर चुम्बक की स्थितिज ऊर्जा U = चुम्बक को मानक स्थिति (θ=π2) से कोण θ की स्थिति तक लाने में किया गया कार्य
U=∫θπ2MBsinθdθ
U=MB(−cosθ)θπ2
U=MB[−cosθ−(−cosπ2)]
याU=MB(−cosθ)θπ2
U=MB[−cosθ−(−cosπ2)]
U=−MBcosθ ......(2)
U=−→M.→B
पृथ्वी का चुम्बकीय क्षेत्र तथा अवयव
हमारी पृथ्वी का स्वयं चुम्बकीय क्षेत्र होता है तथा वह एक चुम्बक की भाँति व्यवहार करती है पृथ्वी के चुम्बकीय क्षेत्र (अर्थात् भू-चुम्बकीय क्षेत्र) की पुष्टि निम्नलिखित तथ्यों से होती है :
- स्वतन्त्रतापूर्वक लटकी चुम्बकीय सुई सदैव भौगोलिक उत्तर-दक्षिण दिशा में ठहरती है।
- पृथ्वी में लोहे की छड़ को उत्तर-दक्षिण दिशा में गाड़ने पर वह चुम्बक बन जाती है।
- किसी चुम्बक की क्षेत्र रेखाएँ खींचने पर उदासीन बिन्दु प्राप्त होते हैं।
- यदि एक चुम्बकीय सुई को इस प्रकार लटकाकर कि वह ऊर्ध्वाधर तल में स्वतन्त्रतापूर्वक घूम सके, पृथ्वी के भौगोलिक ध्रुवों से होते हुए एक पूर्ण चक्कर लगाएँ तो हम पाते हैं कि चुम्बकीय सुई दो स्थानों पर पृथ्वी की सतह के लम्बवत् (अर्थात् ऊर्ध्वाधर) हो जाती है तथा दो स्थानों पर पृथ्वी की सतह के समान्तर (अर्थात् क्षैतिज) हो जाती है। अन्य स्थानों पर यह क्षैतिज से भिन्न-भिन्न कोण बनाती हुई ठहरती है। इसका तात्पर्य यह है कि पृथ्वी का स्वयं का चुम्बकीय क्षेत्र होता है।
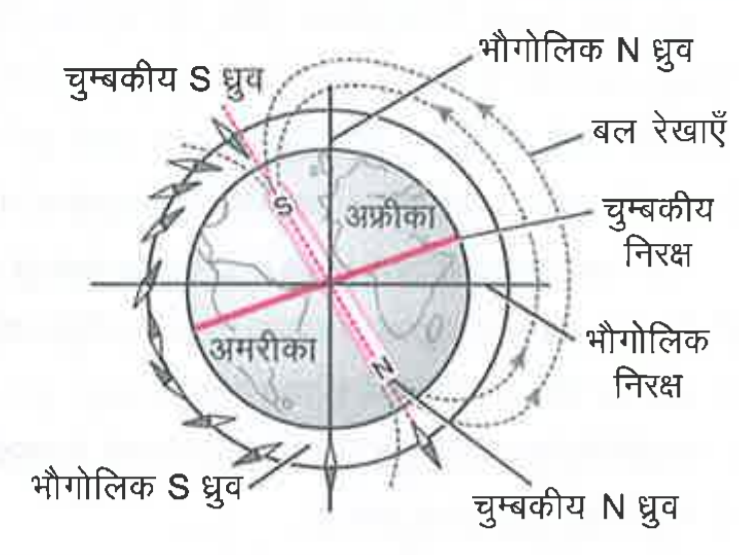
वे स्थान जहाँ चुम्बकीय सुई ऊर्ध्वाधर हो जाती है, चुम्बकीय ध्रुव (magnetic poles) कहलाते हैं तथा वे स्थान जहाँ चुम्बकीय सुई क्षैतिज हो जाती है, उनसे गुजरने वाली रेखा चुम्बकीय निरक्ष (magnetic equator) कहलाती है।
- पृथ्वी के चुम्बकीय क्षेत्र की क्षेत्र रेखाएँ, पृथ्वी के चुम्बकीय ध्रुवों के समीप पृथ्वी की सतह के लम्बवत् तथा चुम्बकीय निरक्ष के समीप पृथ्वी की सतह के समान्तर होंगी, लेकिन किसी छोटे स्थान में पृथ्वी के चुम्बकीय क्षेत्र की क्षेत्र रेखाएँ परस्पर समान्तर तथा समदूरस्थ प्राप्त होती हैं जो सदैव भौगोलिक दक्षिण से भौगोलिक उत्तर की ओर दिष्ट होती हैं। अत: सीमित प्रायोगिक स्थान में पृथ्वी का चुम्बकीय क्षेत्र एकसमान माना जा सकता है तथा चुम्बकीय क्षेत्र रेखाएँ परस्पर समदूरस्थ तथा समान्तर मानी जा सकती हैं।
चुम्बकीय याम्योत्तर (Magnetic meridian)-
- पृथ्वी के चुम्बकीय ध्रुवों को मिलाने वाली रेखा को चुम्बकीय अक्ष कहते हैं तथा इससे होकर गुजरने वाले ऊर्ध्वाधर तल को चुम्बकीय याम्योत्तर कहते हैं।
भौगोलिक याम्योत्तर (Geographical meridian)-
- भौगोलिक उत्तर-दक्षिणी ध्रुवों को मिलाने वाली रेखा को भौगोलिक अक्ष कहते हैं तथा इससे होकर गुजरने वाले ऊर्ध्वाधर तल को भौगोलिक याम्योत्तर कहते हैं।
पृथ्वी के चुम्बकत्व के चुम्बकीय अवयव :-
किसी स्थान पर पृथ्वी के चुम्बकत्व की पूर्णरूप से जानकारी प्राप्त करने के लिए निम्नलिखित तीन तत्त्वों का ज्ञान होना आवश्यक है- दिक्पात का कोण,
- नमन (या नति) कोण, तथा
- पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक।
(1) दिक्पात का कोण (Angle of declination)
- किसी स्थान पर चुम्बकीय याम्योत्तर एवं भौगोलिक याम्योत्तर दो अलग-अलग तल होते हैं जो परस्पर कुछ कोण पर झुके होते हैं। किसी स्थान पर भौगोलिक याम्योत्तर और चुम्बकीय याम्योत्तर के बीच के न्यूनकोण को उस स्थान का दिक्पात का कोण (या दिक्पात) कहते हैं।

चित्र में OPQR चुम्बकीय याम्योत्तर है और OLMR भौगोलिक याम्योत्तर है। कोण LOP(=α) दिक्पात का कोण है।
(2) नमन या नति कोण (Angle of dip or Inclination)-
यदि किसी चुम्बकीय सुई को उसके गुरुत्व केन्द्र से उस प्रकार लटकाया जाए कि वह उर्ध्व तल में स्वतंत्रता पूर्वक घूम सके तो उत्तर-दक्षिण दिशा में स्थिर होने पर सुई क्षैतिज न ठहरकर, क्षैतिज तल के साथ कुछ कोण बनाती हुई ठहरती है।- किसी स्थान पर स्वतन्त्रतापूर्वक लटकी हुई चुम्बकीय सुई की अक्ष, चुम्बकीय याम्योत्तर में क्षैतिज रेखा के साथ जिस कोण पर झुकी ठहरती है, उसे उस स्थान का नति कोण कहते हैं।
- किसी स्थान पर पृथ्वी के परिणामी चुम्बकीय क्षेत्र की दिशा तथा क्षैतिज के मध्य बने कोण को उस स्थान का नमन कोण कहते हैं।
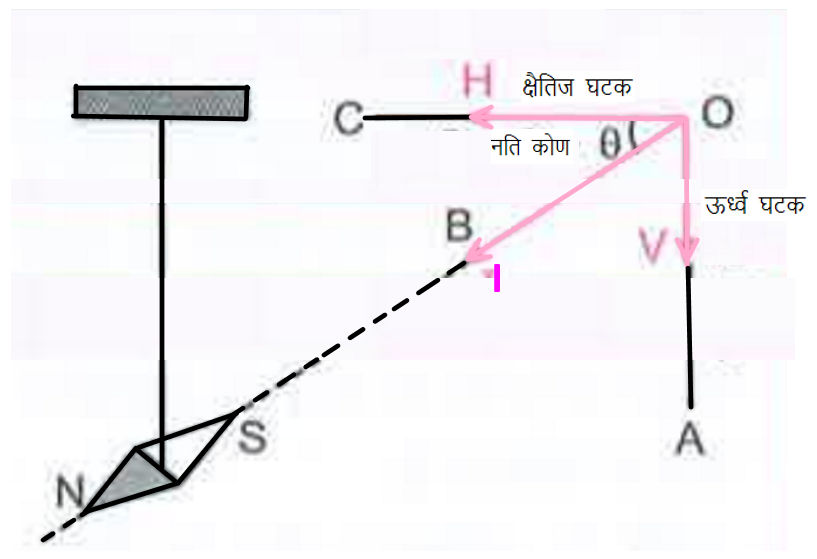
दोनों चित्रों में, पृथ्वी के परिणामी चुम्बकीय क्षेत्र की दिशा OB है (अर्थात् स्वतन्त्रतापूर्वक लटकी चुम्बकीय सुई की अक्ष की दिशा OB है)। OB व क्षैतिज दिशा OC के बीच का कोण COB(=θ) नमन कोण है।
(3) पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक (Horizontal component of earth's magnetic field)-
पृथ्वी के चुम्बकीय क्षेत्र की दिशा, पृथ्वी के चुम्बकीय ध्रुवों पर पृथ्वी तल के लम्बवत् (अर्थात् ऊर्ध्वाधर दिशा में) तथा चुम्बकीय निरक्ष पर पृथ्वी तल के समान्तर (अर्थात् क्षैतिज दिशा में) होती है। अतः किसी स्थान पर पृथ्वी के परिणामी चुम्बकीय क्षेत्र I को दुसरे चित्र की भाँति दो घटकों में विभाजित किया जा सकता है :- क्षैतिज घटक H, दिशा OC में, तथा
- ऊर्ध्वाधर घटक V, दिशा OA में।
- क्षैतिज घटक H की दिशा भौगालिक दक्षिण से भौगोलिक उत्तर की ओर क्षैतिज तल में होती है, जबकि ऊर्ध्वाधर घटक V की दिशा ऊपर से नीचे की ओर ऊर्ध्वाधर तल में होती है।
पृथ्वी के चुम्बकत्व के अवयवों `V, H, B` और `V, H, theta` में सम्बन्ध
ऊपर दिए हुए चित्र में पृथ्वी के परिणामी चुम्बकीय क्षेत्र B की दिशा OB है तथा नमन कोण θ है। इसे दो घटकों में वियोजित किया क्या है :
- दिशा OC में क्षैतिज घटक H, तथा
- दिशा OA में ऊर्ध्वाधर घटक V
- क्षैतिज घटक
तथा ऊर्ध्वाधर घटक
VH=BsinθBcosθ=tanθ
याV=Htanθ .....(3)
- समीकरण (1) तथा (2) का वर्ग करके जोड़ने पर,
H2+V2=B2cos2θ+B2sin2θ
याH2+V2=B2 .....(4)
- उपर्युक्त समीकरण (4) V,H तथा B में सम्बन्ध बताता है।
नोट-
यहाँ पर हम कई पुस्तकों के हिसाब से V तथा H को क्रमशः BV तथा BH भी लिख सकते है।उदाहरण 4
पृथ्वी के चुंबकत्व संबंधी निम्नलिखित प्रश्नों के उत्तर दीजिए : (a) दक्षिण भारत में किसी स्थान पर नति कोण का मान लगभग 18° है करेगें या कम की ?
(b) यदि आप ऑस्ट्रेलिया के मेल्बोर्न शहर में चुंबकीय क्षेत्र रेखाओं का नक्शा बनाएँ तो ये रेखाएँ पृथ्वी के अंदर जाएँगी या इससे बाहर आएँगी ?
( c) एक सुई जो क्षैतिज तल में घूमने के लिये स्वतंत्र है, यदि यह भू-चुंबकीय उत्तर या दक्षिण ध्रुव पर रखी हो तो यह किस दिशा में संकेत करेगी ?
( d) एक जगह से दूसरी जगह जाने पर पृथ्वी का चुंबकीय क्षेत्र बदलता है। क्या यह समय के साथ भी बदलता है? यदि हाँ, तो कितने समय अंतराल पर इसमें पर्याप्त परिवर्तन होते है?
( e) अपने 4-5 अरब वर्षों के इतिहास में पृथ्वी अपने चुंबकीय क्षेत्र की दिशा कई बार उलट चुकी होगी। भूगर्भशास्त्री, इतने सुदूर अतीत के पृथ्वी के चुंबकीय क्षेत्र के बारे में कैसे जान पाते है?
(a) ब्रिटेन में अधिक है (लगभग 70°), क्योंकि ब्रिटेन चुंबकीय दक्षिण ध्रुव के निकट है
(b) पृथ्वी की चुंबकीय क्षेत्र रेखाएँ B सतह से बाहर आती हुई प्रतीत होंगी।
(c) सुई क्षैतिज तल में किसी भी दिशा में संकेत कर सकती है।
( d) हाँ, यह समय के साथ बदलता है। स्पष्ट दिखाई पढ़ने वाले अंतर के लिए समय-अंतराल कुछ सौ वर्ष है। लेकिन कुछ वर्षों के छोटे पैमाने पर भी इसमें होने वाले परिवर्तन पूर्णतः उपेक्षणीय नहीं हैं।
(e) कुछ चट्टानें जब ठोस रूप ग्रहण करती हैं तो पृथ्वी के चुंबकीय क्षेत्र का एक धुंधला-सा अभिलेखन उनमें हो जाता है। चट्टानों में निहित इन चुंबकन अभिलेखों के विश्लेषण से हमें भू-चुंबकीय इतिहास संबंधी निष्कर्ष प्राप्त होते हैं।
उदाहरण 5
किसी स्थान पर पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक 3×10−5 T है भौगोलिक उत्तर की ओर है। एक बहुत लम्बे सीधे चालक में नियत धारा 1 A प्रवाहित हो रही है। जब इसे एक क्षैतिज टेबल पर रखा जाता है तो इस पर प्रति इकाई लम्बाई पर बल क्या होगा जब धारा की दिशा (a) पूर्व से पश्चिम तथा (b) दक्षिण से उत्तर की ओर है ?
→F=I→l×→B or F=IlBsinθ
जब धारा पूर्व से पश्चिम दिशा की ओर प्रवाहित है तो, 0 = 90°
अत: F=IlB=(1A)(1m)(3×10−5T) बल की दिशा नीचे की ओर है। इस दिशा को फ्लेमिंग के बांये हाथ के नियम अथवा सदिशों के वज्र गुणनफल के दिशात्मक गुण के द्वारा ज्ञात किया जा सकता है। (b) जब धारा दक्षिण से उत्तर की ओर प्रवाहित है तो, 0 = 0° = F = 0
अतः चालक की प्रति इकाई लम्बाई पर कोई बल नहीं लगेगा।
उदाहरण 6
एक चुम्बकीय सुई को क्षैतिज अक्ष के सापेक्ष कीलकीत किया जाता है और वह चुम्बकीय याम्योत्तर मे घूमने के लिये स्वतन्त्र है जिसे निम्न बिन्दुओं के अनुदिश देखा जाता है
(a) स्थान A पर ऊर्ध्वाधर दिशा में
(b) स्थान B पर क्षैतिज दिशा में इन दोनो स्थानो पर नति कोण के मान बताइये।
(a) A पर नति कोण का मान 90° है
(b) B पर नति कोण का मान 0° है
उदाहरण 7
एक स्पर्शज्या धारामापी मे फेरो की संख्या 50 तथा त्रिज्या 20 सेमी है एवं पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक का मान BH=3×10−5T है। धारामापी में 45∘ का विक्षेप उत्पन्न करने के लिए आवश्यक धारा होगी
हम जानते है कि I=Ktanθ=2RBHμ0Ntanθ=2×(0.20m)×3×10−5T4π×10−2TmA−1×50tan45∘=0.19A
उदाहरण 8
विषुवत-रेखा पर पृथ्वी के चुंबकीय क्षेत्र का परिणाम लगभग 0.4 G है। पृथ्वी के चुम्बक के द्विध्रुव आघूर्ण की गणना करें। (पृथ्वी की त्रिज्या=6.4×106m)
विषुवत रेखीय चुम्बकीय क्षेत्र B=E=μ0M4πr3
चम्बकीय आघूर्ण M=(BE4πr3μ0), जहाँ BE=0.4G=4×10−5T,r=6.4×106m
=4×10−5×(6.4×106)3μ0/4π=4×102×(6.4×106)3=1.04×1023A−m2
महत्वपूर्ण परिभाषाएं
(1) चुम्बकन क्षेत्र -
- किसी चुम्बकीय क्षेत्र में चुम्बकीय पदार्थ को रखने पर उसे चुम्बकित करने वाले क्षेत्र को चुम्बकन क्षेत्र कहते हैं। इसे अक्षर H द्वारा प्रदर्शित करते है।
उदहारण के लिए, यदि n फेरे प्रति मीटर तथा धारा I वाले टोरोइड (या-परिनालिका) के अन्दर किसी चुम्बकीय पदार्थ को रखकर चुम्बकित किया जाता है तो चुम्बकन क्षेत्र H=nI होता है। यहाँ राशि nI को ऐम्पियर × फैरों की संख्या (number of ampere turns) भी कहते हैं। चुम्बकन क्षेत्र का S. I. मात्रक ऐम्पियर/मीटर (Am−1) है।
(2) चुम्बकीय फ्लक्स घनत्व या चुम्बकीय प्रेरण -
- जब किसी चुम्बकीय पदार्थ को चुम्बकीय क्षेत्र B में रखा जाता है तो वह पदार्थ चुम्बकित हो जाता है। इस स्थिति में पदार्थ के अन्दर निम्नलिखित दो कारणों से चुम्बकीय क्षेत्र रेखाएँ उपस्थित होती हैं-
- पदार्थ के चुम्बकित हो जाने से उसमें उत्पन्न चुम्बकीय क्षेत्र B के कारण,
- चुम्बकन क्षेत्र H द्वारा निर्वात् या वायु में उत्पन्न चुम्बकीय क्षेत्र Bo(=μoH) के कारण।
इस प्रकार, पदार्थ के अन्दर प्रत्येक बिन्दु पर परिणामी चुम्बकीय क्षेत्र B, पदार्थ के चुम्बकत्व के कारण चुम्बकीय क्षेत्र Bm तथा चुम्बकीय क्षेत्र Bo के सदिश योग के बराबर होता है, अर्थात् →B=→Bm+→Bo । इस परिणामी चुम्बकीय क्षेत्र B को चुम्बकीय फ्लक्स घनत्व या चुम्बकीय प्रेरण कहते हैं। इसका S.I. मात्रक न्यूटन/(ऐम्पियर मीटर) (NAm) है यदि चुम्बकीय पदार्थ की निरपेक्ष चुम्बकनशीलता μ है तो B=μH होगा।
(3) चुम्बकन तीव्रता -
- चुम्बकन क्षेत्र में स्थित किसी चुम्बकीय पदार्थ के एकांक आयतन में प्रेरित चुम्बकीय आघूर्ण को चुम्बकन तीव्रता कहते हैं तथा इसे अक्षर I से प्रदर्शित करते हैं। इसका S.I. मात्रक ऐम्पियर/मीटर (Am−l) है।
- स्पष्टत: यदि पदार्थ का आयतन V है तथा उसमें प्रेरित चुम्बकीय आघूर्ण M है, तो चुम्बकन तीव्रता
I=MV .....(1)
- अब यदि पदार्थ की लम्बाई L, अनुप्रस्थ काट का क्षेत्रफल A तथा ध्रुव प्रबलता m है तो
I=MV=m×lA×L=mA
- या
I=mA ....(2)
- अर्थात् चुम्बकन क्षेत्र में स्थित पदार्थ के प्रति एकांक क्षेत्रफल प्रेरित ध्रुव प्रबलता को भी चुम्बकन तीव्रता कहते हैं।
(4) चुम्बकीय प्रवृत्ति -
- किसी पदार्थ में उत्पन्न चुम्बकन तीव्रता । तथा चुम्बकन क्षेत्र H के अनुपात को उस पदार्थ की चुम्बकीय प्रवृत्ति कहते हैं। इसे अक्षर χ (काई) से प्रदर्शित कहते हैं। अतः
χ=IH .....(3)
- इसका कोई मात्रक नहीं होता है।
(5) B, H तथा । में सम्बन्ध -
- किसी चुम्बकीय पदार्थ की निरपेक्ष चुम्बकनशीलता, उस पदार्थ के अन्दर चुम्बकीय क्षेत्र B तथा उसे चुम्बकित करने वाले चुम्बकन क्षेत्र की निष्पत्ति के बराबर होती है अर्थात्
μ=BH .....(4)
- स्पष्टतः निरपेक्ष चुम्बकनशीलता का मात्रक न्यूटन/ऐम्पियर (NA−2) है। अब यदि पदार्थ की आपेक्षिक चुम्बकनशीलता μr है तो
μ=μ0μr .....(5)
- जहाँ आपेक्षिक चुम्बकनशीलता μr विमाहीन राशि है। अत: B,H तथा I में सम्बन्ध है :
B=μ0(I+H) ......(6)
(6) धारावाही परिनालिका :-
- धारावाही परिनालिका का व्यवहार ठीक दण्ड चुम्बक के समान होता है।
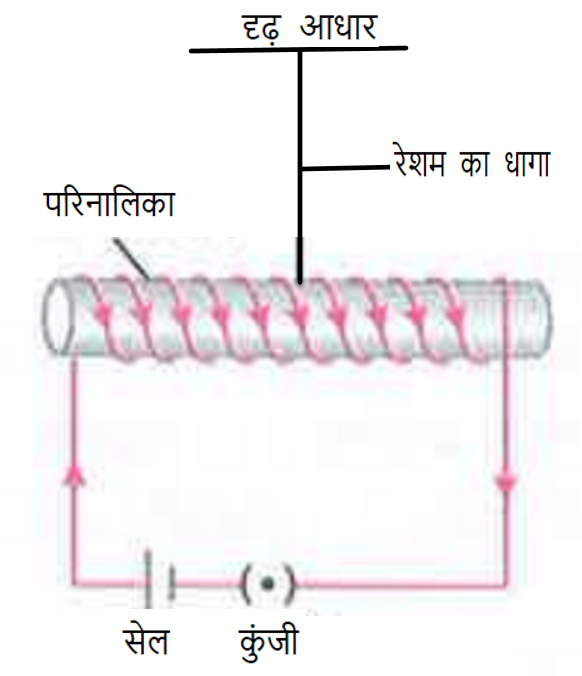
इसके दोनों सिरों के बीच एक सेल व कुंजी जोड़ लेते हैं तथा परिनालिका को सीधे ही रेशम के धागे की सहायता से बाँधकर दृढ़ आधार से इस प्रकार लटकाते हैं कि वह क्षैतिज तल में स्वतन्त्रतापूर्वक घूम सके। हम देखते है की
- जब परिनालिका में धारा प्रवाहित नहीं की जाती है (अर्थात् कुंजी खुली होती है), तो यह किसी भी स्थिति में ठहर जाती है।
- जैसे ही कुंजी बन्द करके परिनालिका में धारा बहाते हैं, यह अपनी अक्ष को एक निश्चित दिशा, भौगोलिक उत्तर-दक्षिण में लाकर ठहरती है। अब यदि इसे इस स्थिति से थोड़ा-सा घुमाया जाता है, तब भी यह पुनः उसी दिशा में आकर ठहरती है।
- यदि सेल के सिरों को उलटकर परिनालिका में प्रवाहित धारा की दिशा उलट दी जाती है, तो हम देखते है कि परिनालिका भी 180° घूम जाती है। परिनालिका में प्रवाहित धारा की दिशा उलटने से इसके सिरों की ध्रुवता उलट जाती है।
- अब यदि दो धारावाही परिनालिकाओं को स्वतन्त्रतापूर्वक लटकाकर एक परिनालिका के किसी सिरे के पास दूसरी परिनालिका के सिरों को बारी-बारी से लाते हैं, दोनों परिनालिकाओं के विजातीय ध्रुव एक-दूसरे को आकर्षित करते हैं तथा सजातीय ध्रुव एक-दूसरे को प्रतिकर्षित करते हैं।
- परिनालिका में चुम्बकत्व का गुण तभी तक रहता है जब तक कि उसमें धारा बहती है। जैसे ही परिनालिका में धारा का प्रवाह बन्द होता है, इसका चुम्बकत्व भी समाप्त हो जाता है।
- एक धारावाही परिनालिका एवं एक दण्ड चुम्बक की चुम्बकीय क्षेत्र रेखाएँ प्रदर्शित करता है।
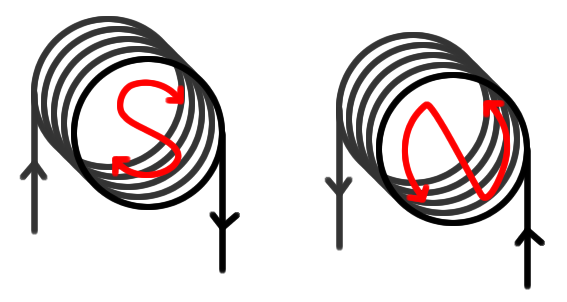
यदि परिनालिका के किसी सिरे को सामने से देखने पर परिनालिका पर लिपटी कुण्डली में धारा की दिशा वामावर्त (अर्थात् घड़ी की सुई के चलने की विपरीत दिशा में) है, तो वह सिरा उत्तरी ध्रुव N होगा तथा दूसरा सिरा दक्षिणी ध्रुव S होगा। इसके विपरीत, यदि धारा की दिशा दक्षिणावर्त (अर्थात् घड़ी की सुई के चलने की दिशा में) है, तो सामने वाला सिरा दक्षिणी ध्रुव S होगा तथा दूसरा उत्तरी ध्रुव N होगा।
चुम्बकीय पदार्थ
प्रत्येक पदार्थ परमाणुओं से मिलकर बना है तथा प्रत्येक परमाणु, एक चुम्बकीय द्विध्रुव की भाँति व्यवहार करता है, क्योंकि इसमें प्रत्येक इलेक्ट्रॉन, नाभिक के चारों ओर परिक्रमण करता है तथा अपनी अक्ष के परितः चक्रण गति करता है। प्रयोगों द्वारा यह पाया जाता है कि सभी पदार्थों में चुम्बकत्व के गुण होते हैं। पदार्थों को उनके चुम्बकीय व्यवहार के आधार पर निम्नलिखित तीन वर्गों में बाँटा जा सकता है :
- प्रतिचुम्बकीय पदार्थ,
- अनुचुम्बकीय पदार्थ, तथा
- लौहचुम्बकीय पदार्थ ।
(1) प्रतिचुम्बकीय पदार्थ (Dinmagnetic substance)
- वे पदार्थ जो किसी प्रबल चुम्बक के सिरों के पास लाने पर हल्का-सा प्रतिकर्षण बल अनुभव करते हैं, प्रतिचुम्बकीय पदार्थ कहलाते हैं।
- पदार्थ द्वारा बाह्य चुम्बकीय क्षेत्र में क्षेत्र की विपरीत दिशा में अल्प चुम्बकत्व प्राप्त करने के गुण को प्रतिचुम्बकत्व कहते हैं।
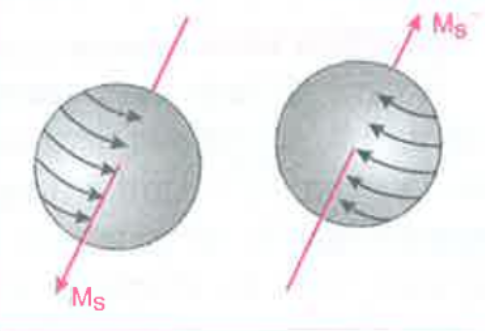
- इस प्रकार, प्रतिचुम्बकीय पदार्थ में प्रत्येक परमाणु का कुल चुम्बकीय आघूर्ण शून्य होता है।
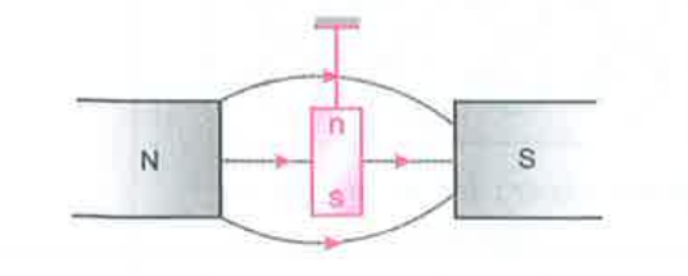
- यदि किसी प्रतिचुम्बकीय पदार्थ की छड़ को चुम्बकीय ध्रुवों के बीच में स्वतन्त्रतापूर्वक लटकाते हैं तो चित्र की भाँति छड़ घूमकर अपनी अक्ष को चुम्बकीय क्षेत्र के लम्बवत् कर लेती है।
- असमान चुम्बकीय क्षेत्र में ये पदार्थ, क्षेत्र के कम तीव्रता वाले भाग की ओर आकर्षित होते हैं।
- इन पदार्थों के चुम्बकीय गुणों पर ताप का कोई प्रभाव नहीं पड़ता है।
- इन पदार्थों की आपेक्षिक चुम्बकनशीलता μr का मान 1 से थोड़ा कम होता है।
- प्रतिचुम्बकीय पदार्थ की चुम्बकीय प्रवृत्ति, उसके ताप तथा चुम्बकन क्षेत्र पर निर्भर नहीं करती है (विशेषत: कम ताप पर केवल बिस्मथ को छोड़कर) ।
- इन पदार्थों की चुम्बकीय प्रवृत्ति ऋणात्मक तथा बहुत कम होती है।
प्रतिचुम्बकीय पदार्थों के गुण ⇒
(2) अनुचुम्बकीय पदार्थ (Paramagnetic substance)
- वे पदार्थ जो किसी प्रबल चुम्बक के समीप लाये जाने पर हल्का सा आकर्षण अनुभव करते हैं, अनुचुम्बकीय पदार्थ कहलाते हैं।
- पदार्थ द्वारा बाह्य चुम्बकीय क्षेत्र में, बाह्य क्षेत्र की दिशा में क्षीण चुम्बकत्व ग्रहण करने के गुण को अनुचुम्बकत्व कहते हैं।
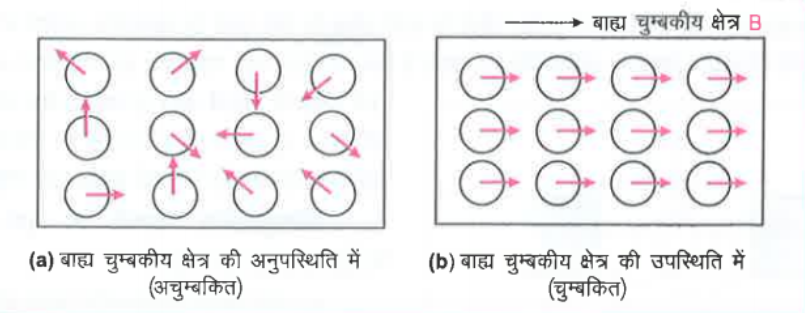
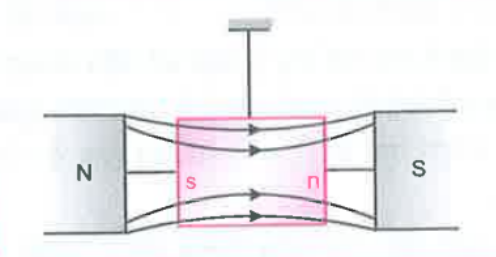
- यदि किसी अनुचम्बकीय पदार्थ की छड़ को चुम्बकीय शुर्यों के बीच में स्वत्त्रतापूर्वक भाँति छड़ घूमकर अपनी अक्ष चुम्बकीय क्षेत्र के समान्तर कर लेती है।
- असमान चुम्बकीय क्षेत्र में ये पदार्थ, क्षेत्र के अधिक तीव्रता वाले भाग की ओर आकर्षित होते हैं।
- ये पदार्थ किसी शक्तिशाली चुम्बक के सिरे के समीप लाये जाने पर आकर्षित हो जाते हैं।
- ताप बढ़ने पर अनुचुम्बकत्व का गुण घट जाता है।
- इन पदार्थों की आपेक्षिक चुम्बकनशीलता μr का मान 1 से थोड़ा अधिक होता है।
- इन पदार्थों की चुम्बकीय प्रवृत्ति धनात्मक, लेकिन बहुत कम होती है।
अनुचुम्बकीय पदार्थ के गुण ⇒
(3) लौहचुम्बकीय पदार्थ (Ferromagnetic substance)
- वे पदार्थ जो क्षीण चुम्बक के समीप लाये जाने पर भी आकर्षण अनुभव करते हैं, लौहचुम्बकीय पदार्थ कहलाते हैं।
- पदार्थ द्वारा बाह्य चुम्बकीय क्षेत्र में रखे जाने पर बाह्य क्षेत्र की दिशा में प्रबल चुम्बकत्व ग्रहण करने के गुण को लौहचुम्बकत्व-कहते हैं।
जब लौहचुम्बकीय पदार्थ को बाह्य चुम्बकीय क्षेत्र में रखते है , तो इस पर निम्नलिखित दो प्रभाव होते है:
- डोमेन इस प्रकार घूमने लगती हैं जिससे कि उनके चुम्बकीय आघूर्णों की दिशाएँ बाह्य क्षेत्र की दिशा में हो जाएँ जैसे-जैसे बाह्य चुम्बकीय क्षेत्र की तीव्रता बढ़ाते हैं, अधिकाधिक डोमेन, बाह्य चुम्बकीय क्षेत्र की दिशा में संरेखित होने लगती हैं। जब सभी डोमेन बाह्य क्षेत्र की दिशा में संरेखित हो जाती हैं [चित्र(b)] तो पदार्थ का चुम्बकत्व संतृप्त हो जाता है।
- डोमेनों की परिसीमाएँ खिसकने लगती हैं। वे डोमेन जिनके चुम्बकीय आघूर्ण की दिशा, बाह्य चुम्बकीय क्षेत्र की दिशा में होती है, आकार में बढ़ जाती हैं तथा वे डोमेन जिनके चुम्बकीय आघूर्ण की दिशा, बाह्य चुम्बकीय क्षेत्र की दिशा से भिन्न होती है, आकार में घट जाती हैं [चित्र(c)]। इस प्रकार पदार्थ बाह्य चुम्बकीय क्षेत्र की दिशा में नैट चुम्बकीय आघूर्ण प्राप्त कर लेता है अर्थात् वह चुम्बकित हो जाता है।
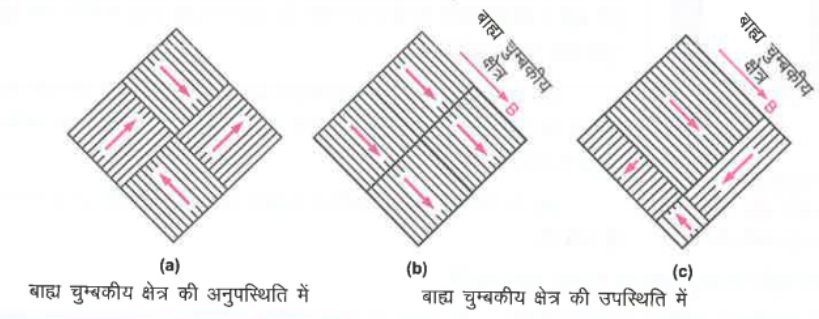
- ये पदार्थ चुम्बक द्वारा तेजी से आकर्षित होते हैं।
- ये पदार्थ आसानी से अल्प चुम्बकीय क्षेत्र द्वारा चुम्बकित किये जा सकते हैं।
- इन पदार्थों में अनुचुम्बकीय पदार्थों के सभी गुण अधिक प्रबलता से पाये जाते हैं।
- लौहचुम्बकीय पदार्थ का ताप बढ़ाने पर लौहचुम्बकत्व का गुण घट जाता है तथा अन्ततः एक ऐसा ताप प्राप्त होता है जिस पर पदार्थ का लौहचुम्बकत्व का गुण समाप्त हो जाता है और पदार्थ अनुचुम्बकीय हो जाता है। इस निश्चित ताप को पदार्थ का क्यूरी ताप (Curie temperature) कहते हैं।
- इन पदार्थों की आपेक्षिक चुम्बकनशीलता, का मान बहुत अधिक होता है।
- लौहचुम्बकीय पदार्थों की चुम्बकीय प्रवृत्ति धनात्मक तथा बहुत अधिक होती है।
लौहचुम्बकीय पदार्थों के गुण ⇒
विद्युत् चुम्बक (Electromagnets)
विद्युत् चुम्बक एक अस्थायी चुम्बक होता है। वास्तव में, इसे एक नर्म लोहे के टुकड़े पर ताँबे के अवरुद्ध तार की कुण्डली लपेट कर बनाया जाता है जो चुम्बक की भाँति केवल तभी व्यवहार करता है जबकि कुण्डली में धारा प्रवाहित की जाती है। जैसे ही कुण्डली में धारा का प्रवाह बन्द किया जाता है, नर्म लोहे के टुकड़े का चुम्बकत्व समाप्त हो जाता है तथा यह चुम्बकीय व्यवहार नहीं दर्शाता है।
I आकृति का दण्ड विद्युत् चुम्बक बनाना-
इसके लिए नर्म लोहे की छड़ PQ पर पतले पृथक्कृत ताँबे के तार की कुण्डली परिनालिका के रूप में लपेट ली जाती है तथा चित्र की भाँति कुण्डली के सिरों के बीच श्रेणीक्रम में अमीटर A, परिवर्ती प्रतिरोध Rh, बैटरी B तथा कुंजी K जोड़ देते हैं।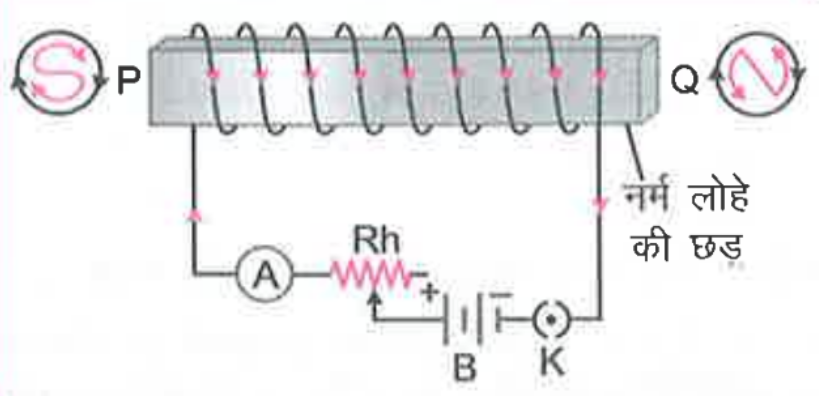
- विद्युत् चुम्बक द्वारा उत्पन्न चुम्बकीय क्षेत्र की तीव्रता जितनी अधिक होती है, वह विद्युत् चुंबक उतना ही प्रबल कहलाता है।
- फेरों की संख्या पर
- परिनालिका में प्रवाहित धारा पर
विद्युत् चुम्बक के उपयोग (Uses of electromagnet)
- भारी लोहे के सामान (जैसे-गर्डर, प्लेट, आदि) को उठाने तथा दूर किसी स्थान पर पहुँचाने में (जहाँ मजदूर द्वारा पहुँचाना सम्भव न हो)।
- लोहे की भट्टियों को लोहे से भरने में।
- विद्युत् संयन्त्रों (जैसे-विद्युत् घण्टी, विद्युत् गाड़ी, विद्युत् मोटर, रिले, माइक्रोफोन, लाउडस्पीकर आदि) में।
- वैज्ञानिक शोध कार्य में (चुम्बकीय क्षेत्र में किसी पदार्थ के चुम्बकीय गुणों का अध्ययन करने के लिए) ।
उदाहरण 9
500 फेरे/मीटर की परिनालिका में 3A धारा प्रवाहित हो रही है | इसका कोर लोहे का बना हुआ है जिसकी आपेक्षिक पारगम्यता 5000 है | चुंबकन क्षेत्र, चुंबकन तीव्रता तथा चुंबकीय क्षेत्र का परिमाण क्रोड के अंदर ज्ञात कीजिए |
चुम्बकन क्षेत्र H=ni
=500m−1×3A=1500Am−1
दिया गया है कि μr=5000
μr=1+λ, i.e., λ=5000−1=4999=5000
μ=5000μ0
अतः चुम्बकन तीव्रता I=γH=7.5×106Am−1
चुम्बकीय क्षेत्र B=5000μ0H=5000×4π×10−7×1500=9.4T
उदाहरण 10
लौहे के एक नमूने की पारगम्यता μ एवं चुम्बकन क्षेत्र H में निम्न सम्बन्ध है μ=(0.4H+12×10−4) henery/meter. जहाँ H का मात्रक A/m है। H का वह मान ज्ञात करो जो कि 1.0Wb/m2 का चुम्बकीय प्रेरण उत्पन करे।
चुम्बकीय प्रेरण B=μH (माध्यम के लिए)
1=(0.4H+12×10−4)H
1=0.4+12×10−4H⇒H=1−0.412×10−4
H = 500 A/m
उदाहरण 11
यदि 10 cm x 0.5 cm x 0.2 cm की लौह चुम्बकीय पदार्थ की छड़ को 0.5×104 A/m के चुम्बकीय क्षेत्र में रखने पर 5A−m2 का चुम्बकीय आघूर्ण उत्पन्न होता है, तो छड़ में चुम्बकीय प्रेरण की गणना करो।
छड़ में कुल चुम्बकीय प्रेरण B=μ0(I+H)
=(μ0)(MV+H)(∴I=MV)=4π×10−7(510−6+0.5×104)=6.28Wb/m2
उदाहरण 12
एक चुम्बकीय पदार्थ की छड़ को जिसका अनुप्रस्थ काट क्षेत्रफल 0.25cm2 है, 4000 A/m तीव्रता वाले चुम्बकन क्षेत्र में रखा जाता है। छड़ में से गुजरने वाले चुम्बकीय फ्लक्स का मान 25×10−6 Wb है। पारगम्यता
(i) चुम्बकीय फ्लक्स ϕ=BA⇒B=ϕ/a=25×10−60.25×10−4=1Wb/m2
लेकिनB=μH⇒μ=BH=14000=2.5×10−4Wb/A−m
(ii) μr=1+χm=μr−1(∴μr=μμ0)
χm=μμ0−1=25×10−44π×10−7−1=199−1=198
(iii) ) चुम्बकन I=χmH=198×4000=7.92×105A/m
उदाहरण 13
पृथ्वी के केन्द्र (Core) में लोहा (IRON) विद्यमान है परन्तु भूगर्भशास्त्री इसे पृथ्वी के चुम्बकत्व का कारण नहीं मानते है क्यों ?
चूँकि पृथ्वी के केन्द्र (Core) में बहुत उच्च तापमान विद्यमान है जिसके कारण Nire लावा के रूप में उपस्थित होता है। इस कारण इसमें चुम्बकीय गुण अनुपस्थित होता है।
उदाहरण 14
पृथ्वी की चुम्बकन तीव्रता ज्ञात करो। कल्पना करिए की पृथ्वी का चुम्बकीय क्षेत्र 8.0×1021Am2 चुम्बकीय आघूर्ण वाली विशाल छड़ चुम्बक के तुल्य है। पृथ्वी की त्रिज्या 6400 km है।
पृथ्वी की त्रिज्या R=6400km=6.4×106m
चुम्बकन तीव्रता एकांक आयतन में चुम्बकीय आघूर्ण है अतः
I=M43πR3=8.0×1022×34×π×(6.4×106)3=24.0×1044×262.1=72.9Am−1