गतिमान आवेश और चुंबकत्व कक्षा 12 भौतिकी
भूमिका
इस अध्याय में यह अध्ययन करेंगे कि चुंबकीय क्षेत्र किस प्रकार आवेशित कणों; जैसे-इलेक्ट्रॉन, प्रोटॉन तथा विद्युत धारावाही तारों पर बल आरोपित करते हैं। यह भी जानेंगे कि विद्युत धाराएँ किस प्रकार चुंबकीय क्षेत्र उत्पन्न करती हैं। साइक्लोट्रॉन में कणों को अति उच्च ऊर्जाओं तक त्वरित करने की प्रक्रिया का भी अध्ययन होगा। गैल्वेनोमीटर द्वारा विद्युतधाराओं एवं वोल्टताओं के संसूचन के विषय में भी अध्ययन करेंगे।
इस अध्याय तथा आगे आने वाले चुंबकत्व के अध्यायों में निम्नलिखित परिपाटी को अपनाया जायेगा। कागज़ के तल से बाहर की ओर निर्गत विद्युत धारा अथवा क्षेत्र (विद्युत अथवा चुंबकीय) को एक बिंदु (⊙) द्वारा व्यक्त किया जाता है। कागज़ के तल में भीतर की ओर जाती विद्युत धारा अथवा विद्युत क्षेत्र को एक क्रॉस (⊗) द्वारा व्यक्त किया जाता है।
चुंबकीय क्षेत्र की अवधारणा
अध्याय 1 (विद्युत आवेश तथा क्षेत्र) में यह अध्ययन किया जा चूका हैं कि एक स्थिर आवेश अपने चारों ओर एक विद्युत् क्षेत्र उत्पन्न करता है। किसी स्थिर आवेश के चारों ओर का वह क्षेत्र (region या space) जहाँ विद्युत् प्रभाव अनुभव किया जा सकता है, विद्युत् क्षेत्र कहलाता है। किसी एक बिन्दु पर विद्युत् क्षेत्र, एक अकेले आवेश अथवा अनेक आवेशों के कारण हो सकता है। यदि अनेक आवेश विद्युत् क्षेत्र उत्पन्न करते हैं तो किसी बिन्दु पर परिणामी विद्युत् क्षेत्र, अध्यारोपण के सिद्धान्त के अनुसार अलग-अलग प्रत्येक आवेश के कारण उत्पन्न विद्युत् क्षेत्रों का सदिश योग होता है। यदि किसी बिन्दु पर विद्युत् क्षेत्र →E है तो उस बिन्दु पर रखा परीक्षण आवेश q0 एक बल →F=q0→E अनुभव करता है।
ठीक इसी प्रकार, एक गतिमान आवेश या धारावाही चालक अपने चारों ओर एक चुम्बकीय क्षेत्र उत्पन्न करता है, जो ठीक एक चुम्बक के चारों ओर उत्पन्न चुम्बकीय क्षेत्र के समान होता है इसका प्रायोगिक अध्ययन सन् 1820 में वैज्ञानिक ओर्स्टेड (Oersted) द्वारा किया जा चुका है।
- किसी धारावाही चालक अथवा चुम्बक के चारों ओर का वह क्षेत्र जिसमें चुम्बकीय प्रभाव अनुभव किया जा सकता है, चुम्बकीय क्षेत्र कहलाता है।
- जैसे ही चालक में धारा का प्रवाह बन्द किया जाता है अथवा आवेश गति करना बन्द करता है, चुम्बकीय क्षेत्र समाप्त हो जाता है। चुम्बकीय क्षेत्र को सदिश →B द्वारा व्यक्त करते हैं। किसी बिन्दु पर उत्पन्न कुल चुम्बकीय क्षेत्र, अध्यारोपण के सिद्धान्त के अनुसार उस बिन्दु पर अलग-अलग धारावाही चालकों (अथवा चुम्बकों) से उत्पन्न चुम्बकीय क्षेत्रों के सदिश योग के बराबर होता है।
लारेन्ज़ बल
यदि एक आवेश q, वेग →v से किसी बाह्य चुम्बकीय क्षेत्र →B में प्रवेश करता है तो उस पर गति की दिशा तथा चुम्बकीय क्षेत्र की दिशा दोनों के लम्बवत् एक बल लगता है जिसे लॉरेन्ज बल (Lorentz force) कहते हैं, तथा इसे सदिश रूप में →F निरूपित किया जाता है।
- लॉरेन्ज बल का सूत्र -
→F=q→v×→B
F=qvBsinθ
Fmax=qvB
- इस प्रकार, B का S.I. मात्रक न्यूटन/ऐम्पियर × मीटर (संकेत NA−m ) है जिसे टेसला (संकेत T) अथवा वेबर/मीटर−2 (संकेत : Wbm−2) भी कहा जाता है।
F=B
- किसी स्थान पर एक मीटर प्रति सेकंड से (एकांक) गतिमान एक कूलॉम (एकांक) आवेशित कण पर लगने वाले बल के परिमाण को चुंबकीय क्षेत्र कहते है जबकि आवेश चुंबकीय क्षेत्र के लंबवत गतिशील है।
B का विमीय सूत्र = [MLT−2][A][L]=[ML0T−2A−1]
महत्वपूर्ण बिंदु
- एक स्थिर आवेश से केवल विद्युत् क्षेत्र उत्पन्न होता है।
- एक गतिमान आवेश विद्युत् क्षेत्र तथा चुम्बकीय क्षेत्र दोनों उत्पन्न करता है, लेकिन चुम्बकीय क्षेत्र केवल तभी तक रहता है जब तक कि आवेश गतिमान रहता है। आवेश के स्थिर होते ही, चुम्बकीय क्षेत्र शून्य हो जाता है।
- एक धारावाही चालक केवल चुम्बकीय क्षेत्र उत्पन्न करता है। यह चुम्बकीय क्षेत्र तभी तक रहता है जब तक कि चालक में धारा बहती है। एक धारावाही चालक का कुल आवेश शून्य होता है, अत: यह विद्युत् क्षेत्र उत्पन्न नहीं करता है।
- चुम्बकीय क्षेत्र को चुम्बकीय प्रेरण (magnetic induction) अथवा चुम्बकीय फ्लक्स घनत्व (magnetic flux density) भी कहते हैं तथा इसे अक्षर B द्वारा निरूपित करते हैं।
आर्स्टेड का प्रयोग
आर्स्टेड ने सन 1820 में एक प्रयोग किया, यह प्रयोग उन्होंने चालक तार में धारा प्रवाहित होने पर घटित घटनाओ के अध्ययन करने के उद्देश्य से किया था। आर्स्टेड ने अपने प्रयोग से यह स्पष्ट सिद्ध किया की
- जब किसी चालक में विद्युत धारा प्रवाहित की जाती है तो चालक के चारों ओर चुंबकीय क्षेत्र उत्पन्न हो जाता है अर्थात गतिमान आवेश के कारण उसके चारो ओर चुंबकीय क्षेत्र उत्पन्न होता है।
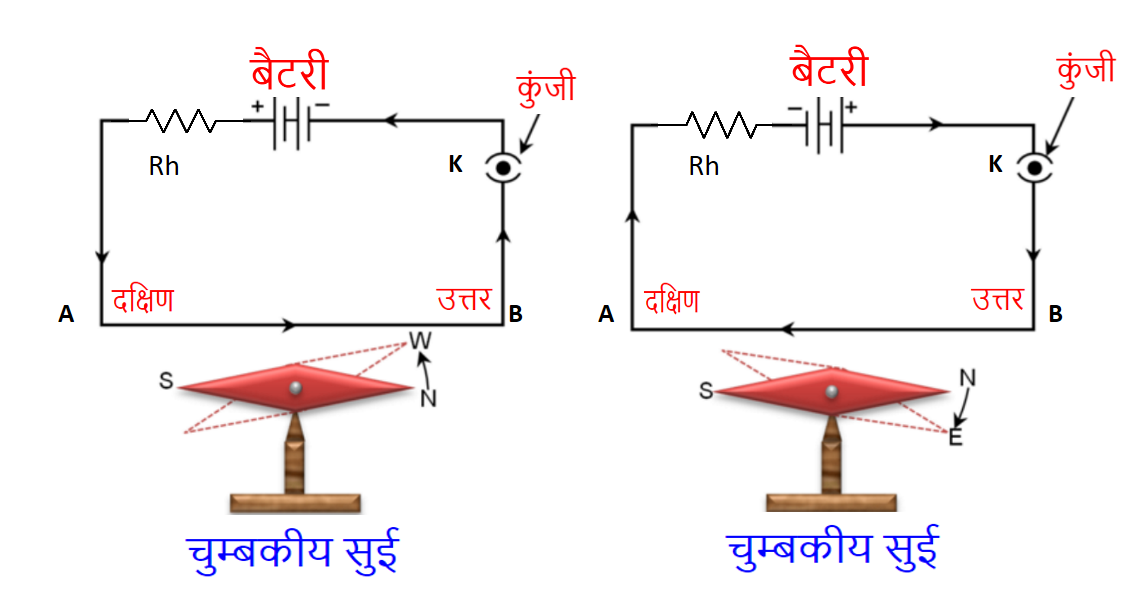
चालक तार AB के नीचे समान्तर में एक चुंबकीय सुई (कम्पास) को उत्तर-दक्षिण में रखा गया जैसा चित्र में दिखाया गया है। इस प्रकार परिपथ पूर्ण करने के बाद आर्स्टेड ने विभिन्न स्थितियों का अध्ययन किया।
- जब कुंजी K को खुला रखा जाता है अर्थात परिपथ में कोई धारा प्रवाहित न होने की स्थिति में कम्पास या चुंबकीय सुई स्थिर बनी रहती है।
- जब कुंजी ऑन की जाती है तो परिपथ में धारा प्रवाहित होने लगती है और इस स्थिति में कम्पास में विक्षेप उत्पन्न हो जाता है।
- जब तार AB में प्रवाहित धारा का मान बढ़ाया जाता है तो चुंबकीय सुई (कम्पास) में विक्षेप भी अधिक होता है।
- यदि चालक तार AB में प्रवाहित धारा की दिशा बदल दी जाए अर्थात बैटरी के टर्मिनल विपरीत करने पर चुंबकीय सुई (कम्पास) में विक्षेप भी विपरीत दिशा में होता है अर्थात विक्षेप की दिशा बदल जाती है।
आर्स्टेड के प्रयोग के निष्कर्ष :-
आर्स्टेड द्वारा किये गए निम्न प्रयोग से उन्होंने निष्कर्ष निकाले वे निम्न है -- चालक तार में विद्युत धारा प्रवाहित करने पर इसके चारों ओर चुंबकीय क्षेत्र उत्पन्न हो जाता है।
- चालक के चारों ओर उत्पन्न चुंबकीय क्षेत्र का परिमाण तार में प्रवाहित धारा के परिमाण पर निर्भर करता है अर्थात विद्युत धारा का मान बढ़ाने पर चुंबकीय क्षेत्र भी बढ़ता है।
- कम्पास को तार से दूर ले जाने पर चुंबकीय क्षेत्र कम होता जाता है।
- जब चालक तार में प्रवाहित धारा दक्षिण-उत्तर दिशा में होती है तो चुंबकीय सुई (कम्पास ) का उत्तरी ध्रुव पश्चिम दिशा में विक्षेपित हो जाता है।
- जब चालक तार में प्रवाहित धारा उत्तर-दक्षिण दिशा में होती है तो चुंबकीय सुई (कम्पास) का उत्तरी ध्रुव पूर्व दिशा में विक्षेपित हो जाता है।
- चालक तार में धारा प्रवाह के कारण चालक के ऊपर तथा नीचे चुंबकीय क्षेत्र उत्पन्न होता है, उत्पन्न ऊपर व नीचे चुंबकीय क्षेत्र की दिशा परस्पर विपरीत होती है।
एम्पियर का तैरने का नियम
एम्पियर का तैरने का नियम के अनुसार -
- मान लो एक व्यक्ति विद्युत धारा की दिशा में तैर रहा है। विद्युत धारा उसके पांव से प्रविष्ट होकर सिर से निकल रही हो और उसका चेहरा चुंबकीय सूई की तरफ हो तो उत्तरी ध्रुव में विक्षेपण उसकी बायें हाथ की दिशा में होगा।
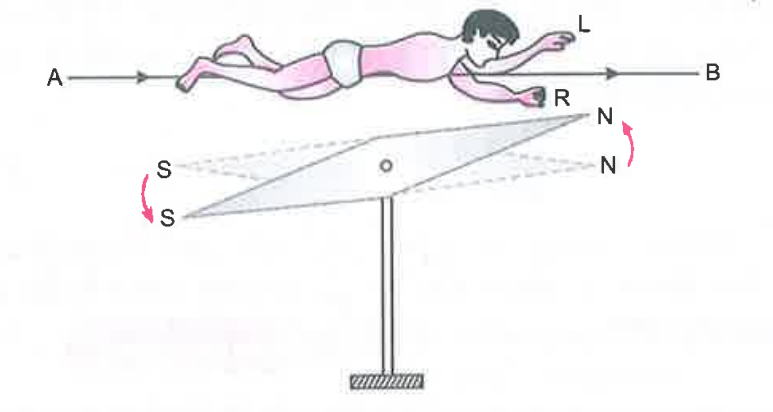
चित्र में तार AB में धारा की दिशा A से B की ओर है तथा L व R, तार के ऊपर तैरते मनुष्य के क्रमश: बायाँ व दायाँ हाथ प्रदर्शित करते हैं। तार में धारा A से B की ओर बहने से तार के नीचे रखी चुम्बकीय सुई का उत्तरी सिरा N, मनुष्य के बायें हाथ L की ओर विक्षेपित हुआ है।
दक्षिण हस्त का नियम तथा मैक्सवेल का कार्क दक्षिणावर्त पेंच नियम
दक्षिण हस्त का नियम ⇒
इस नियम के अनुसार,- यदि हम अपने दायें हाथ की हथेली खुली रखकर अंगूठे तथा अंगुलियों को परस्पर लम्बवत् इस प्रकार फैलाएँ कि अँगूठा, चालक में बहने वाली धारा की दिशा की ओर तथा अँगुलियाँ, उस बिन्दु की ओर संकेत करें जहाँ चुम्बकीय क्षेत्र की दिशा ज्ञात करनी है, तो चुम्बकीय क्षेत्र की दिशा, खुली हथेली के लम्बवत् तथा हथेली के बाहर की ओर होगी।

चित्र में धारावाही चालक कागज के तल में है। बिन्दु P पर चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत् बाहर की ओर है जिसे चित्र में ⊙ द्वारा दर्शाया गया है।
मैक्सवेल का कार्क दक्षिणावर्त पेंच नियम ⇒
इस नियम के अनुसार,- यदि चित्र की भाँति किसी पेच को दायें हाथ द्वारा इस प्रकार घुमाया जाए कि पेच की नोंक विद्युत् धारा की दिशा में आगे बढ़े, तो पेच को घुमाने के लिए जिस दिशा में अँगूठा घूमता है, वह चुम्बकीय क्षेत्र रेखाओं की दिशा प्रदर्शित करेगा।
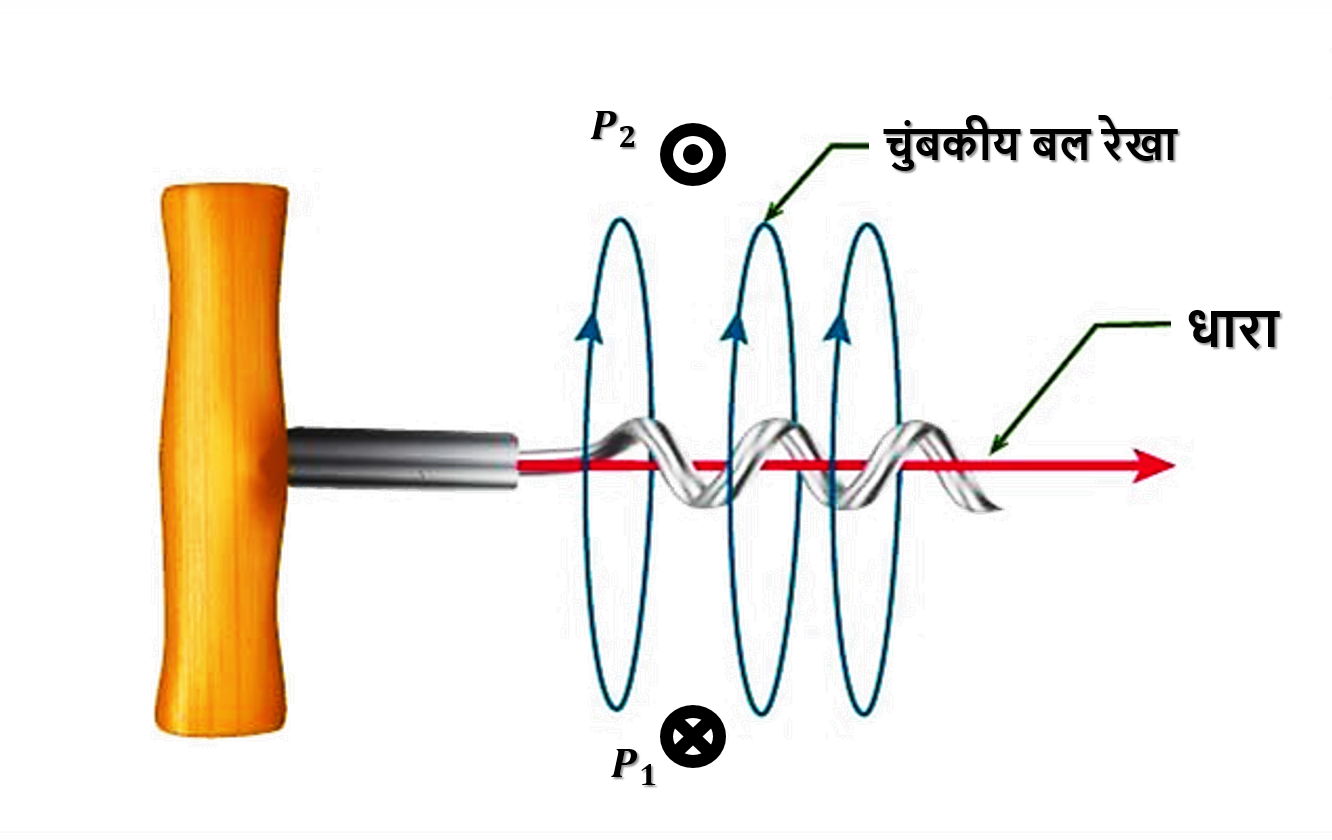
चित्र में धारावाही चालक कागज के तल में है। कागज के तल में स्थित बिन्दु P1 पर चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत् अन्दर की ओर है तथा बिन्दु P2 पर कागज के तल के लम्बवत् बाहर की ओर है। चित्र में इन्हें क्रमश: ⊗ तथा ⊙ द्वारा दर्शाया गया है।
बायो सावर्ट का नियम
बायो-सावर्ट (Biot-Savart) ने 1820 में चालक के विभिन्न अल्पांश के कारण किसी बिंदु पर उत्पन्न चुंबकीय क्षेत्र का अध्ययन किया और अध्ययन से प्राप्त निष्कर्षों को एक नियम के रूप में प्रस्तुत किया इस नियम को ही बायो सावर्ट का नियम कहते है।
- माना एक चालक तार है जिसमे I धारा प्रवाहित हो रही है, चालक के अल्पांश dL से r दूरी पर एक बिंदु P स्थित है जिस पर हमें चुंबकीय क्षेत्र की गणना करनी है, माना P बिंदु पर चुंबकीय क्षेत्र dB है। हम यहाँ अल्पांश dL की दिशा धारा की दिशा में मान रहे है।
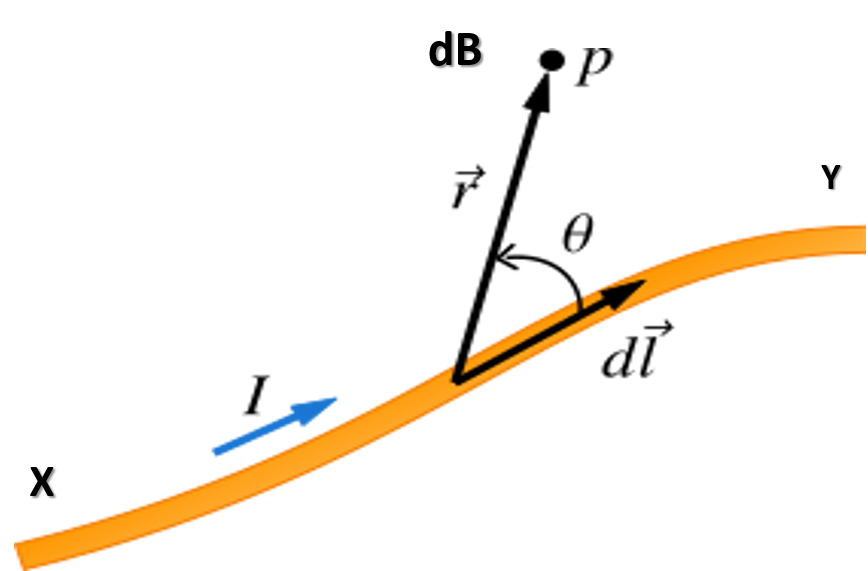
बायो सावर्ट ने अल्पांश dL के कारण उत्पन्न चुंबकीय क्षेत्र dB का मान ज्ञात करने के लिए बताया की -
- dB का मान चालक में प्रवाहित विद्युत धारा के समानुपाती होता है -
dB∝I - चुंबकीय क्षेत्र की तीव्रता dB का मान अल्पांश dL के समानुपाती होता है
dB∝dL - तथा अल्पांश dL के मध्य बने कोण के समानुपाती होता है
dB∝sinθ - अल्पांश dL तथा बिन्दु P के मध्य की दुरी (r) के वर्ग के व्युत्क्रमानुपाती होता है।
dB∝1r2
dB∝Idlsinθr2
याdB=μ0Idlsinθ4πr2
μ0 को निर्वात की चुंबकशीलता या चुंबकीय पारगम्यता कहते है।
उदाहरण 1
कोई विद्युत धारा अवयव Δl=Δ׈i जिससे एक उच्च धारा I=10A प्रवाहित हो रही है, मूल बिंदु पर स्थित है (चित्र 18), y-अक्ष पर 0.5 m दूरी पर स्थित किसी बिंदु पर इसके कारण चुंबकीय क्षेत्र का क्या मान है। Δx=1cm
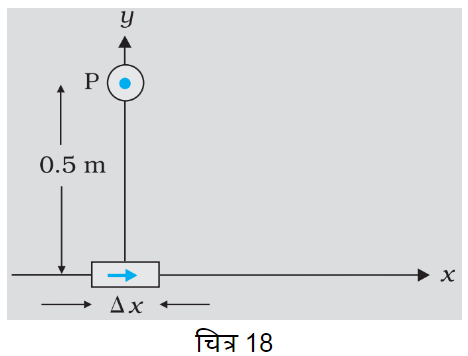
dl=Δx=10−2m,
I=10A, r=0.5m=y
μ04π=10−7Tm/A
θ=90° ; sinθ=1
|dB|=4×10–8T
इस चुंबकीय क्षेत्र की दिशा +z दिशा में है। इसका कारण यह है कि
सदिश गुणनफलो के चक्रीय गुण से -
ˆj׈k=ˆi;
ˆk׈i=ˆj
ध्यान देने वाली बात यह है कि इस क्षेत्र का परिमाण लघु है।
सीधे धारावाही तार द्वारा उत्पन्न चुम्बकीय क्षेत्र
यदि एक क्षैतिज तल में रखे गत्ते के ठीक बीचों-बीच छेद करके उसमें होकर ताँबे का तार गुजारें जिससे कि तार ऊर्ध्वाधर हो तथा तार में धारा प्रवाहित करके गत्ते पर कम्पास सुई द्वारा चुम्बकीय क्षेत्र रेखाएँ खींचें तो हम पाते हैं कि ये क्षेत्र रेखाएँ तार के चारों ओर समकेन्द्रिक वृत्ताकार होती हैं। जिनके केन्द्र, तार की अक्ष पर स्थित होते हैं। ये क्षेत्र रेखाएँ तार के समीप पास-पास होती हैं तथा जैसे-जैसे तार से दूरी बढ़ती है, ये क्षेत्र रेखाएँ दूर-दूर होती जाती हैं। तार में धारा की दिशा विपरीत करने पर चुम्बकीय क्षेत्र रेखाओं की दिशा विपरीत हो जाती है।
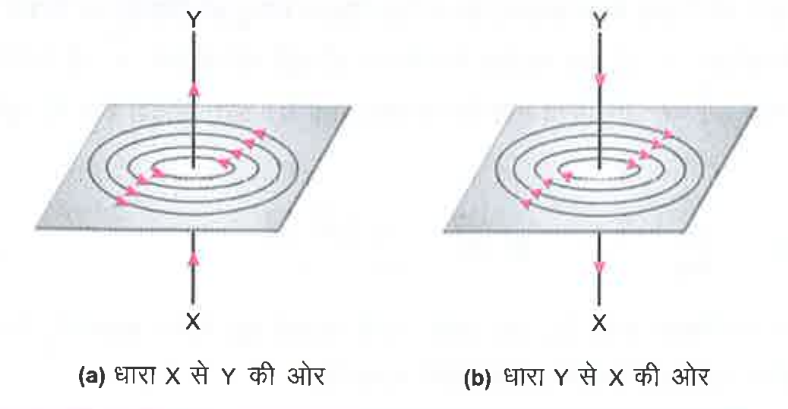
चित्र (a) में तार में धारा की दिशा ऊर्ध्वाधर ऊपर की ओर (X से Y की ओर) है, अत: चुम्बकीय क्षेत्र रेखाएँ वामावर्त हैं। चित्र (b) में तार में धारा की दिशा ऊर्ध्वाधर नीचे की ओर (Y से X की ओर) है, अत: चुम्बकीय क्षेत्र रेखाएँ दक्षिणावर्त हैं।
सीधे धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र की तीव्रता को प्रभावित करने वाले कारक-
सीधे धारावाही तार के समीप किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता- तार में प्रवाहित धारा I के अनुक्रमानुपाती होती है, तथा
- तार से उस बिन्दु की दूरी r के व्युत्क्रमानुपाती होती है।
B=μ04π2Ir
विद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र
जब हम किसी वृत्ताकार कुंडली में धारा प्रवाहित करते है तो इसके चारो ओर एक चुंबकीय क्षेत्र उत्पन्न हो जाता है, यदि यह वृत्ताकार कुण्डली कागज के तल में रखी हो तो इसके चारों ओर उत्पन्न चुम्बकीय क्षेत्र कागज के तल के लंबवत होगा। वृताकार कुंडली के कारण उत्पन्न चुंबकीय क्षेत्र की दिशा वृतीय धाराओं के लिए दायीं हथेली का नियम से ज्ञात कर सकते है। इसके अनुसार
- जब कुण्डली में धारा दक्षिणावर्त दिशा में बह रही हो तो चुंबकीय क्षेत्र कागज के तल के लंबवत नीचे की तरफ होगा। तथा जब धारा वामावर्त दिशा में बह रही हो तो चुम्बकीय क्षेत्र कागज के तल के लंबवत दिशा में ऊपर की ओर होगा।
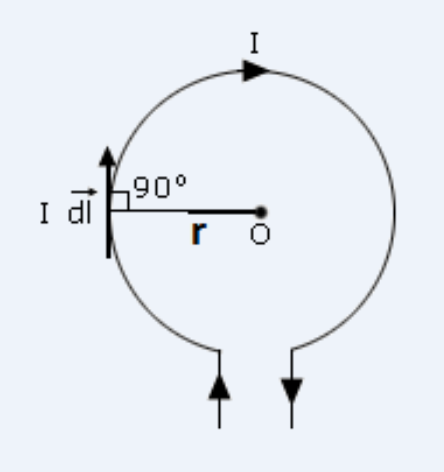
माना एक कुण्डली में धारा I प्रवाहित हो रही है इसकी त्रिज्या r है।
हम कुंडली के केंद्र पर चुम्बकीय क्षेत्र की गणना करने के लिए कुण्डली की परिधि को अल्पांश में बाँट लेते है तथा सभी अल्पांश के कारण केंद्र पर चुंबकीय क्षेत्र की गणना करके सबको जोड़कर केंद्र पर कुल चुम्बकीय क्षेत्र की गणना करते है।
- dl अल्पांश के कारण केंद्र पर चुम्बकीय क्षेत्र dB है तो
dB=μ04πIdlsinθr2 ....(1)
चूँकि dl तथा r के मध्य 90° का कोण है अतः θ=90° अतः सूत्र में मान रखने पर sin90°=1 अतःdB=μ04πIdlr2
अतः पूरे अल्पाँशो के कारण केंद्र पर उत्पन्न कुल चुम्बकीय क्षेत्रB=∫2πr0dB
B=∫2πr0μ04πIdlr2
B=∫2πr0μ04πIr2∫2πr0dl
B=μ04πIr2[l]2πr0
B=μ04πIr22πr
याB=∫2πr0μ04πIdlr2
B=∫2πr0μ04πIr2∫2πr0dl
B=μ04πIr2[l]2πr0
B=μ04πIr22πr
B=μo2lr
B=μo2lnr
विद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
माना किसी r त्रिज्या वाली वृताकार कुंडली में i विद्युत धारा प्रवाहित हो रही है, इस कुण्डली के कारण x दूरी पर स्थित किसी बिन्दु P पर हमें चुम्बकीय क्षेत्र ज्ञात करना है। कुण्डली द्वारा P बिंदु बनाया गया अंतरित अर्द्ध शीर्ष कोण θ है। कुण्डली की व्यास AB की लम्बाई L है। सम्पूर्ण वृत्ताकार कुंडली के कारण P पर चुंबकीय क्षेत्र का मान ज्ञात करने के लिए कुण्डली को अल्पांश में विभाजित कर सभी अल्पांश के कारण P पर चुंबकीय क्षेत्र की गणना कर सबको आपस में जोड़ने से P पर सम्पूर्ण कुंडली के कारण कुल चुंबकीय क्षेत्र का मान प्राप्त हो जायेगा।
यहां चित्रानुसार बिंदु A तथा B पर दो अल्पांश dl लिया गया है, तथा बिंदु A तथा B की P तक की दुरी y है। बायो सावर्ट का नियम प्रयोग करके इन अल्पाँशो के कारण P पर चुंबकीय क्षेत्र की गणना करेंगे तत्पश्चात कुल चुम्बकीय क्षेत्र का मान ज्ञात करेंगे।
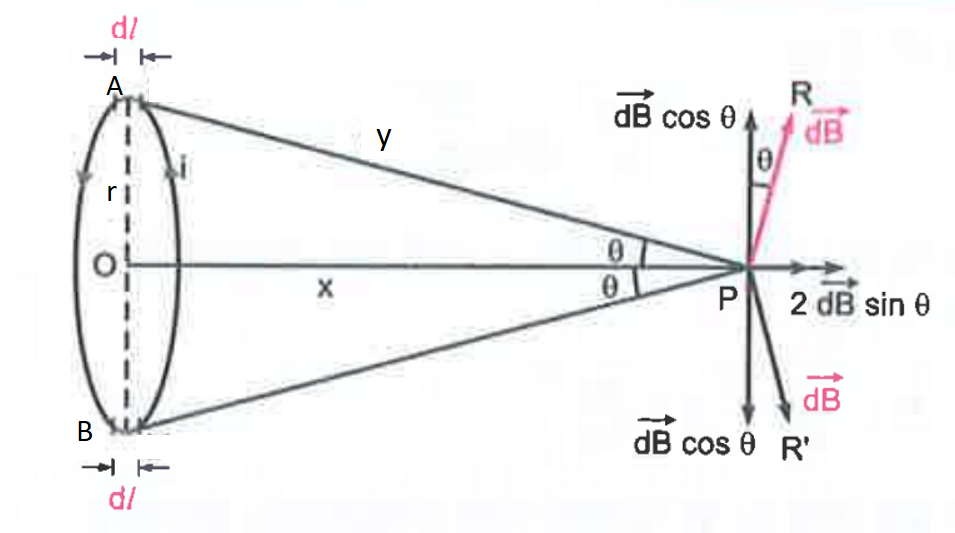
दोनों अल्पाँशो के कारण P पर चुंबकीय क्षेत्र
dB=μ04πIdlsinθy2
dB=μ04πIdlsin90°y2
dB=μ04πIdly2
चूँकि यहाँ cosθ वाले घटक परिमाण में समान तथा दिशा में विपरीत है अतः ये एक दूसरे को निरस्त कर देते है। अतः बायो सावर्ट का नियम से सम्पूर्ण कुण्डली के कारण बिन्दु P पर चुम्बकीय क्षेत्र का मान ज्ञात करने के लिए अल्पांश वाले मान को θ से 2πr तक समाकलन कर देते है क्योंकि कुंडली की परीधि 2πr है। अंतः P पर कुल चुम्बकीय क्षेत्रdB=μ04πIdlsin90°y2
dB=μ04πIdly2
B=∫2πr0dBsinθ
B=∫2πr0μ04πIdly2ry ....(∴sinθ=ry)
B=∫2πr0μ04πIdl(x2+r2)r(x2+r2)12
B=μo4πIr(x2+r2)322πr
याB=∫2πr0μ04πIdly2ry ....(∴sinθ=ry)
B=∫2πr0μ04πIdl(x2+r2)r(x2+r2)12
B=μo4πIr(x2+r2)322πr
B=μo4π2πIr2(x2+r2)32 Tesla
B=μo4π2πInr2(x2+r2)32 Tesla
उदाहरण 2
चित्र 19 में दर्शाए अनुसार किसी सीधे तार जिसमें 12A विद्युत धारा प्रवाहित हो रही है, को 2.0 cm त्रिज्या के अर्धवृत्ताकार चाप में मोड़ा गया है। इस चाप के केंद्र पर चुंबकीय क्षेत्र →B को मानें।
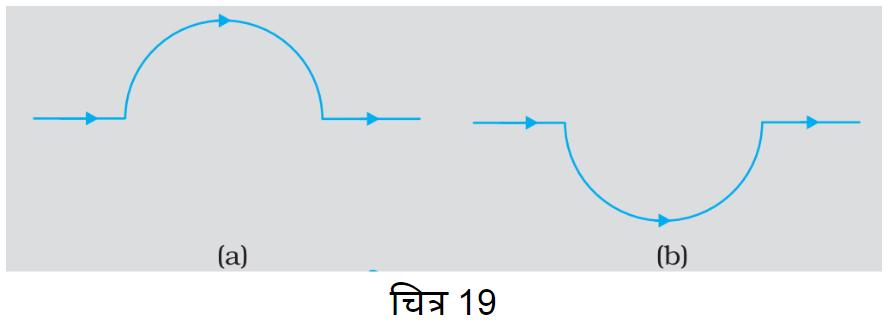
(a) सीधे खंडों के कारण चुंबकीय क्षेत्र कितना है?
(b) किस रूप में अर्धवृत्त द्वारा →B को दिया गया योगदान वृत्ताकार पाश के योगदान से भिन्न है और किस रूप में ये एक दूसरे के समान हैं।
(c) क्या आपके उत्तर में कोई परिवर्तन होगा यदि तार को उसी त्रिज्या के अर्धवृत्त में पहले की तुलना में चित्र 19 (b) में दर्शाए अनुसार उलटी दिशा में मोड़ दें।
(a) सीधे खंडों के प्रत्येक अवयव के लिए d→I तथा r समांतर हैं। अत: d→l×→r=0 । इस प्रकार सीधे खंड |B| को कोई योगदान नहीं देते।
(b) अर्धवृत्ताकार चाप के सभी खंडों के लिए, d→l×→r सभी एक दूसरे के समांतर हैं (तल में भीतर को जाते हुए)। इस प्रकार के सभी योगदान परिमाण में संयोजित हो जाते हैं । अत: अर्धवृत्ताकार चाप के लिए →B की दिशा दक्षिण हस्त नियम द्वारा प्राप्त होती है। इसका परिमाण वृत्ताकार पाश के लिए →B का आधा होता है। इस प्रकार →B का मान 1.9×10−4T है तथा दिशा तल के अभिलंबवत उसके भीतर जाते हुए है।
(c) →B का परिणाम तो वही है जो (b) में है पर दिशा विपरीत है।
उदाहरण 3
10 cm त्रिज्या की 100 कसकर लपेटे गए फेरों की किसी ऐसी कुंडली पर विचार कीजिए जिससे 1 A विद्युत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है?
चूँकि कुंडली कसकर लपेटी गई है अत: प्रत्येक वृत्ताकार अवयव की त्रिज्या R = 10 cm = 0.1 m मान सकते हैं। फेरों की संख्या N = 100 है, अत: चुंबकीय क्षेत्र का परिमाण
B=4π×10−7×102×12×10−1
B=2π×10−4
B=6.28×10−4T
ऐम्पियर का परिपथीय नियम
यह अध्ययन किया जा चुका है कि गतिमान आवेश (अथवा धारा) के कारण चुम्बकीय क्षेत्र उत्पन्न होता है। ऐम्पियर का नियम चुम्बकीय क्षेत्र →B तथा धारा I में परिमाणात्मक सम्बन्ध व्यक्त करता है। ऐम्पियर के नियमानुसार,
- किसी बन्द वक्र C के अनुदिश चुम्बकीय क्षेत्र →B का रेखीय समाकलन, उस वक्र C के अन्दर निहित धाराओं के बीजीय योग का μ0 गुना होता है
∮→B→dl=μ0I ....(1)
यहाँ μ0 निर्वात् (अथवा वायु) की चुम्बकनशीलता है।यदि बन्द वक्र में निहित कुल धारा शून्य होती है तो उस वक्र के अनुदिश घुम्बकीय क्षेत्र B का रेखीय समाकलन शून्य होता है। ऐम्पियर के नियम का उपयोग सममित धारा वितरण के लिए चुम्बकीय क्षेत्र की गणना में सुविधाजनक रहता है।
उत्पत्ति :-
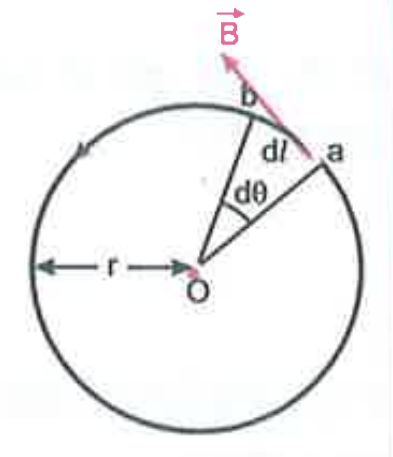
चित्र में माना कि कागज के तल के लम्बवत् बिन्दु O से गुजरता अनन्त लम्बाई का एक चालक तार है जिससे होकर धारा I ऊपर की ओर प्रवाहित हो रही है। यदि बिन्दु O को केन्द्र मानकर त्रिज्या r का वृत्तीय मार्ग लें तो बायो-सावर्ट नियम से, वृत्तीय मार्ग के किसी भी बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता →B=μ0I2πr होगी जिसकी दिशा वृत्तीय मार्ग की स्पर्श रेखा के अनुदिश होगी।
- अत: वृत्तीय मार्ग के अनुदिश चुम्बकीय क्षेत्र →B का रेखीय समाकलन
∮→B.→dl=∮Bdl
=∮μ0I2πr×rdθ ...(∴ab=dl=rdθ)
या=∮μ0I2πr×rdθ ...(∴ab=dl=rdθ)
∮→B.→dl=μ0I2π∮dθ=μ0I2π×2π
या∮→B.→dl=μ0I
उदाहरण 4
चित्र 20 में एक लंबा सीधा वृत्ताकार अनुप्रस्थ काट का (जिसकी त्रिज्या a है) विद्युत धारावाही तार जिससे स्थायी विद्युत धारा I प्रवाहित हो रही हो, दर्शाया गया है। स्थायी विद्युत धारा इस अनुप्रस्थ काट पर एकसमान रूप से वितरित है। क्षेत्रों r<a तथा r>a में चुंबकीय क्षेत्र परिकलित कीजिए
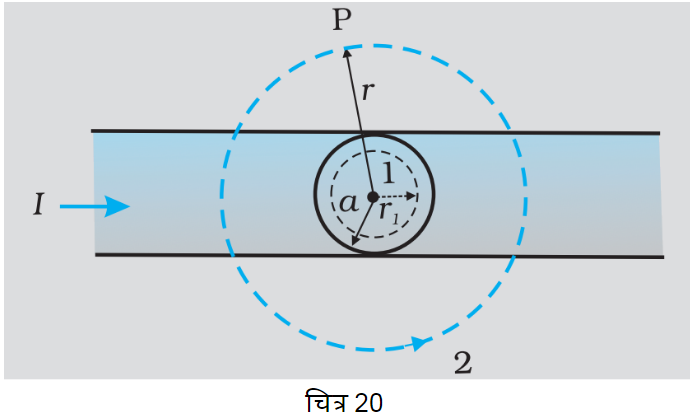
(a) प्रकरण r>a पर विचार कीजिए। जिस पाश पर 2 अंकित है वह अनुप्रस्थ काट के साथ संकेंद्री वृत्त के रूप में एम्पियर पाश है। इस पाश के लिए
Ie= पाश द्वारा परिबद्ध विद्युत धारा = I
यह परिणाम किसी सीधे लंबे तार के लिए सुपरिचित व्यंजक है।
B=μ0I2πr
B∝1r (r>a)
(b) प्रकरण r<a पर विचार कीजिए। इसके लिए ऐम्पियर पाश वह वृत्त है जिस पर 1 अंकित है।
इस पाश के लिए वृत्त की त्रिज्या r लेने पर,
अब यहाँ परिबद्ध विद्युत धारा Ie का मान I नहीं है परतु यह इस मान से कम है। चूँकि विद्युत धारा का विवरण एकसमान है, परिबद्ध विद्युत धारा के अंश का मान
ऐम्पियर के नियम का उपयोग करने पर
B=(μ0I2πa2)r
B∝r(r<a)
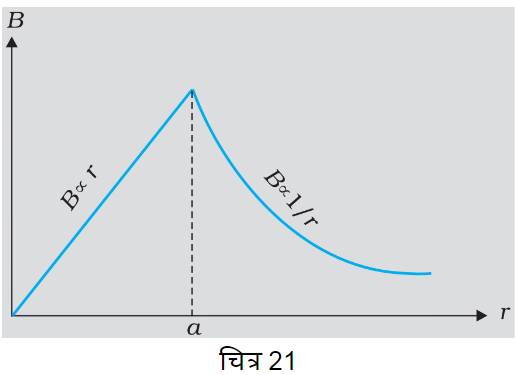
चित्र (21) में →B के परिमाण तथा तार के केंद्र से दूरी r के बीच ग्राफ दर्शाया गया है। चुंबकीय क्षेत्र की दिशा अपने अपने वृत्ताकार पाशों (1 अथवा 2) के स्पर्शरेखीय है तथा यह दक्षिण हस्त नियम से निर्धारित की गई है। इस उदाहरण में आवश्यक सममिति विद्यमान है इसलिए इसी पर ऐम्पियर का नियम आसानी से लागू किया जा सकता है।
परिनालिका
- जब किसी चीनी मिट्टी से बनी बेलनाकार नलिका जिसकी लम्बाई अधिक हो तथा त्रिज्या बहुत कम हो, पर ताँबे का तार लपेटा जाता है इस व्यवस्था को परिनालिका कहते है।

ऊपर प्रदर्शित चित्र परिनालिका का है, इसमें दर्शाया गया है कि एक चीनी मिट्टी की बनी हुई बेलनाकार आकृति पर तांबे का तार लम्बाई के अनुदिश लपेटा गया है।
जब किसी परिनालिका में विद्युत धारा प्रवाहित की जाती है तो चुम्बकीय क्षेत्र उत्पन्न हो जाता है।
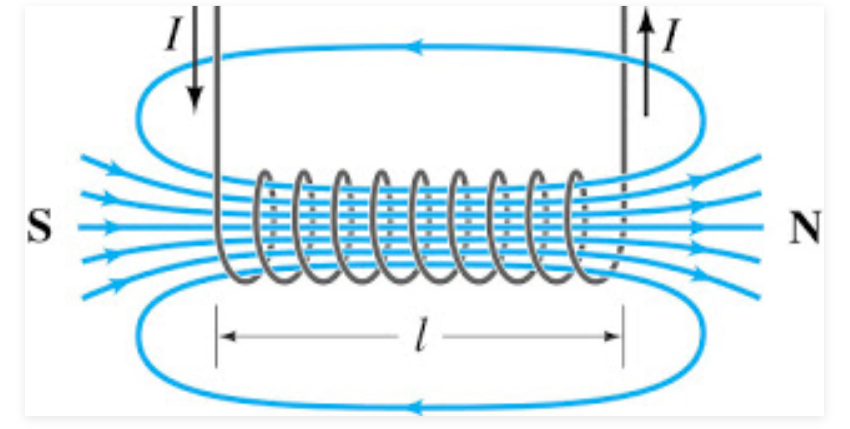
जब किसी परिनालिका अथवा सोलेनोइड में धारा i प्रवाहित की जाती है तो चित्रानुसार इसमें चुम्बकीय क्षेत्र उत्पन्न हो जाता है। इस चुंबकीय क्षेत्र की दिशा समान होती है तथा बाहर के बिन्दुओ पर चुंबकीय क्षेत्र एक दूसरे का विरोध करते है यही कारण है की बाहरी बिंदुओं पर चुम्बकीय क्षेत्र का मान तुलनात्मक कम होता है। ताम्बे के फेरे जितने ज्यादा पास पास होते है चुम्बकीय क्षेत्र बढ़ता जाता है,
- किसी भी आदर्श परिनालिका के अंदर चुम्बकीय सभी जगह समान माना जाता है तथा परिनालिका के बाहर शून्य माना जाता है।
लम्बी धारावाही परिनालिका के कारण चुम्बकीय क्षेत्र
माना एक लम्बी परिनालिका (जिसकी लम्बाई l, उसकी त्रिज्या r की तुलना में बहुत अधिक है) में प्रति एकांक लम्बाई में n फेरे हैं तथा इसमें धारा I प्रवाहित हो रही है। परिनालिका के अन्दर चुम्बकीय प्रेरण रेखाएँ चित्र की भाँति परस्पर समान्तर तथा समदूरस्थ इसकी अक्ष के समान्तर होंगी, क्योंकि परिनालिका के अन्दर प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र लगभग एकसमान रहेगा।
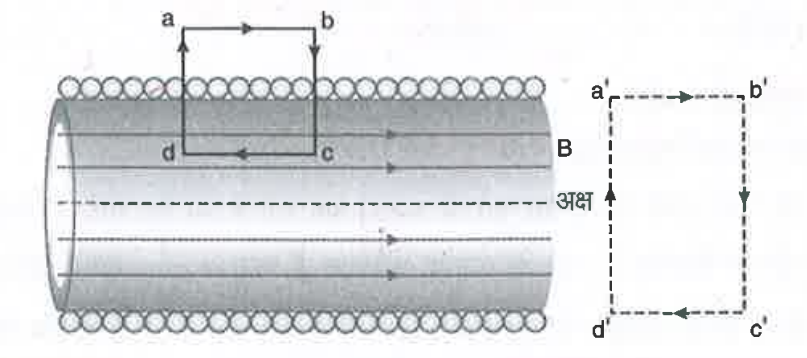
(i) परिनालिका के बाहर चुम्बकीय क्षेत्र ⇒
परिनालिका के बाहर चुम्बकीय क्षेत्र की गणना करने के लिए एक बन्द पथ a'b'c'd' लेते हैं। ऐम्पियर के परिपथीय नियम से,∮→B.→dl=μ0×I
बंद पथ a'b'c'd' में निहित धारा = μ0×0
(क्योंकि परिनालिका के बाहर बन्द पथ a'b'c'd' में निहित धारा शून्य है)बंद पथ a'b'c'd' में निहित धारा = μ0×0
∵B=0 (शून्य)।
- अत: परिनालिका के बाहर चुम्बकीय क्षेत्र शून्य होता है।
(ii) परिनालिका के अन्दर चुम्बकीय क्षेत्र ⇒
परिनालिका के अन्दर चुम्बकीय क्षेत्र की गणना करने के लिए एक बन्द पथ abcd लेते हैं।- यदि ab=cd=1 है तो बन्द पथ abcd में निहित धारा =nIl (क्योंकि l लम्बाई में फेरों की संख्या nl होगी) । तथा
∮→B.→dl=∫ba→B.→dl
+∫c'b→B.→dl
+∫dc→B.→dl+∫ad→B.→dl
जहाँ ∫ba→B.→dl=0 (क्योंकि परिनालिका के बाहर चुम्बकीय क्षेत्र →B=0), ∫c'b→B.→dl=0 क्योंकि चुम्बकीय क्षेत्र →B की दिशा लम्बाई bc के लम्बवत् है, ∫dc→B.→dl=Bl तथा ∫ad→B.→dl=0 क्योंकि चुम्बकीय क्षेत्र →B की दिशा लम्बाई da के लम्बवत् है, अतः +∫c'b→B.→dl
+∫dc→B.→dl+∫ad→B.→dl
∮→B.→dl=Bl
- अब ऐम्पियर के परिपथीय नियम से,
∮→B.→dl=μo× बंद पथ abcd में निहित धारा
याBl=μ0nIl
याB=μ0nI
टोरॉइड
यह एक वृताकार खोखला छल्ला होता है जिस पर किसी तार के अत्यधिक फेरे पास-पास सटाकर लपेटे जाते हैं। इसे एक ऐसी परिनालिका के रूप में भी देखा जा सकता है जिसे बंद करके एक वृताकार मोड़ दिया गया है।

मान लीजिए टोरॉइड पर लगते हुए तार से I विद्युत धारा प्रवाहित हो रही है। हम यह देखेंगे कि टोरॉइड के भीतर खुले स्थान में तथा टोरॉइड कि बाहर चुंबकीय क्षेत्र शून्य है।
- किसी आदर्श टोरॉइड जिसके फेरे सटाकर लिपटे होते हैं , के लिए टोरॉइड के भीतर चुंबकीय क्षेत्र B नियत रहता है।
टोरोइड के कारण चुम्बकीय क्षेत्र
माना चित्र में टोरोइड की आन्तरिक व बाह्य त्रिज्याएँ क्रमशः r1 व r2 हैं । इसमें कुल फेरों की संख्या N है तथा इसमें धारा I प्रवाहित हो रही है। हमें इसके केन्द्र से दूरी x पर स्थित किसी बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है जबकि बिन्दु P
- आन्तरिक पृष्ठ पर,
- बाह्य पृष्ठ पर, तथा
- बाह्य पृष्ठ के बाहर स्थित है।
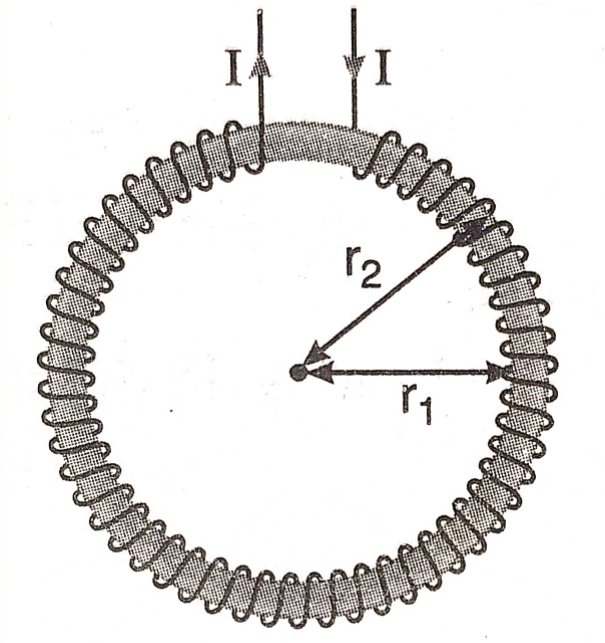
इसके लिए त्रिज्या x के समकेन्द्रिक वृत्तीय मार्ग की कल्पना करते हैं। तब ऐम्पियर के नियम से,
∮→B.→dl=μo× अन्दर निहित धारा
(i) आन्तरिक पृष्ठ पर (अर्थात् x=r1 पर)
B×2πr1=μ0×NI
B=μ0NI2πr1 ....(1)
(ii) बाहा पृष्ठ पर (अर्थात् x=r2 पर),
B×2πr2=μ0×NI
B=μ0NI2πr2 ....(2)
(iii) बाह्य पृष्ठ के बाहर (अर्थात् x>r2 पर ),
B×2πx=μ0×0
B=0 (शून्य)। ....(3)
उदाहरण 5
कोई परिनालिका जिसकी लंबाई 0.5 m तथा त्रिज्या 1 cm है, में 500 फेरे हैं। इसमें 5A विद्युत धारा प्रवाहित हो रही है। परिनालिका के भीतर चुंबकीय क्षेत्र का परिमाण क्या है?
प्रति एकांक लंबाई फेरों की संख्या
लंबाई l=0.5m तथा त्रिज्या r=0.01m
इस प्रकार, l/a=50 अर्थात l>>a अत: हम लंबी परिनालिका का सूत्र का उपयोग कर सकते हैं
B=4π×10–7×103×5
B=6.28×10–3T
एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
प्रयोगों द्वारा पाया जाता है कि
- यदि कोई आवेशित कण किसी बाह्य चुम्बकीय क्षेत्र में गति करता है, तो उस कण पर चुम्बकीय क्षेत्र के कारण एक बल लगता है जिसे लॉरेन्ज बल कहते हैं।
- कण के आवेश पर,
- कण के वेग पर,
- चुम्बकीय क्षेत्र की दिशा के सापेक्ष कण की गति की दिशा पर तथा
- चुम्बकीय क्षेत्र के परिमाण पर।
लॉरेंज बल का परिमाण-
यदि एक आवेशित कण (आवेश q) एकसमान वेग v से किसी चुम्बकीय क्षेत्र B में गतिमान है, तो आवेशित कण पर लगने वाले लॉरिन्ज बल का परिमाण निम्नलिखित सूत्र द्वारा दिया जाता है :-F=qvBsinθ ....(1)
लॉरेन्ज बल की दिशा-
लॉरेन्ज बल की दिशा आवेशित कण के वेग v तथा चुम्बकीय क्षेत्र B के सम्मिलित तल के लम्बवत् होती है। इसे चित्र में समझाया गया है।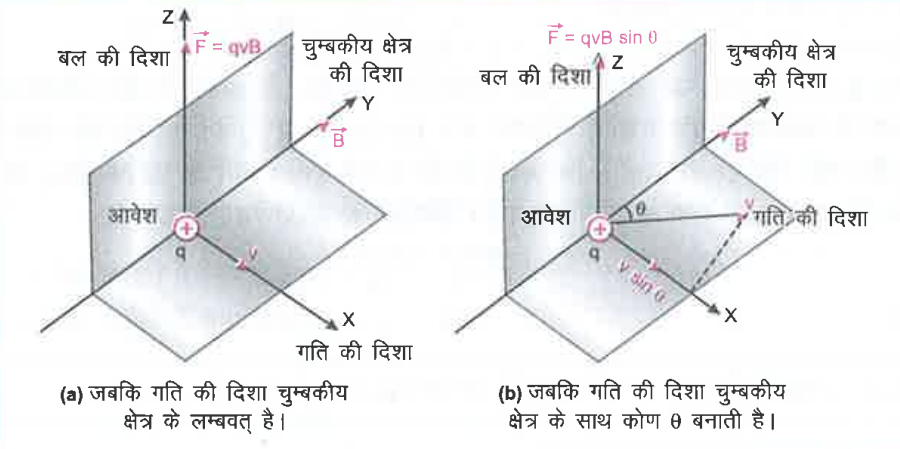
ध्यान रहे कि चित्र में यदि कण पर आवेश ऋणात्मक है, तो बल F की दिशा चित्र में प्रदर्शित दिशा के विपरीत होगी लेकिन बल का परिमाण समान होगा|
- यदि सीधे हाथ में एक पेच लेकर पेच को कण के वेग →v की दिशा से चुम्बकीय क्षेत्र →B की दिशा की ओर उनके बीच न्यूनतम कोण से घुमाया जाये तो लारेन्ज़ बल →F की दिशा, पेंच के आगे बढ़ने की दिशा में होती है| अतः समीकरण (1) से लरिन्ज बल को सदिश रूप में निम्नलिखित समीकरण द्वारा व्यक्त कर सकते हैं :-
→F=q→v×→B
लॉरेन्ज बल की दिशा ज्ञात करने के नियम
चुम्बकीय क्षेत्र में गतिमान आवेशित कण पर लगने वाले बल की दिशा हम निम्नांकित दो नियमों में से किसी भी एक नियम द्वारा ज्ञात कर सकते हैं :
- दायें हाथ की हथेली का नियम,
- फ्लेमिंग का बायें हाथ का नियम।
दायें हाथ की हथेली का नियम ⇒
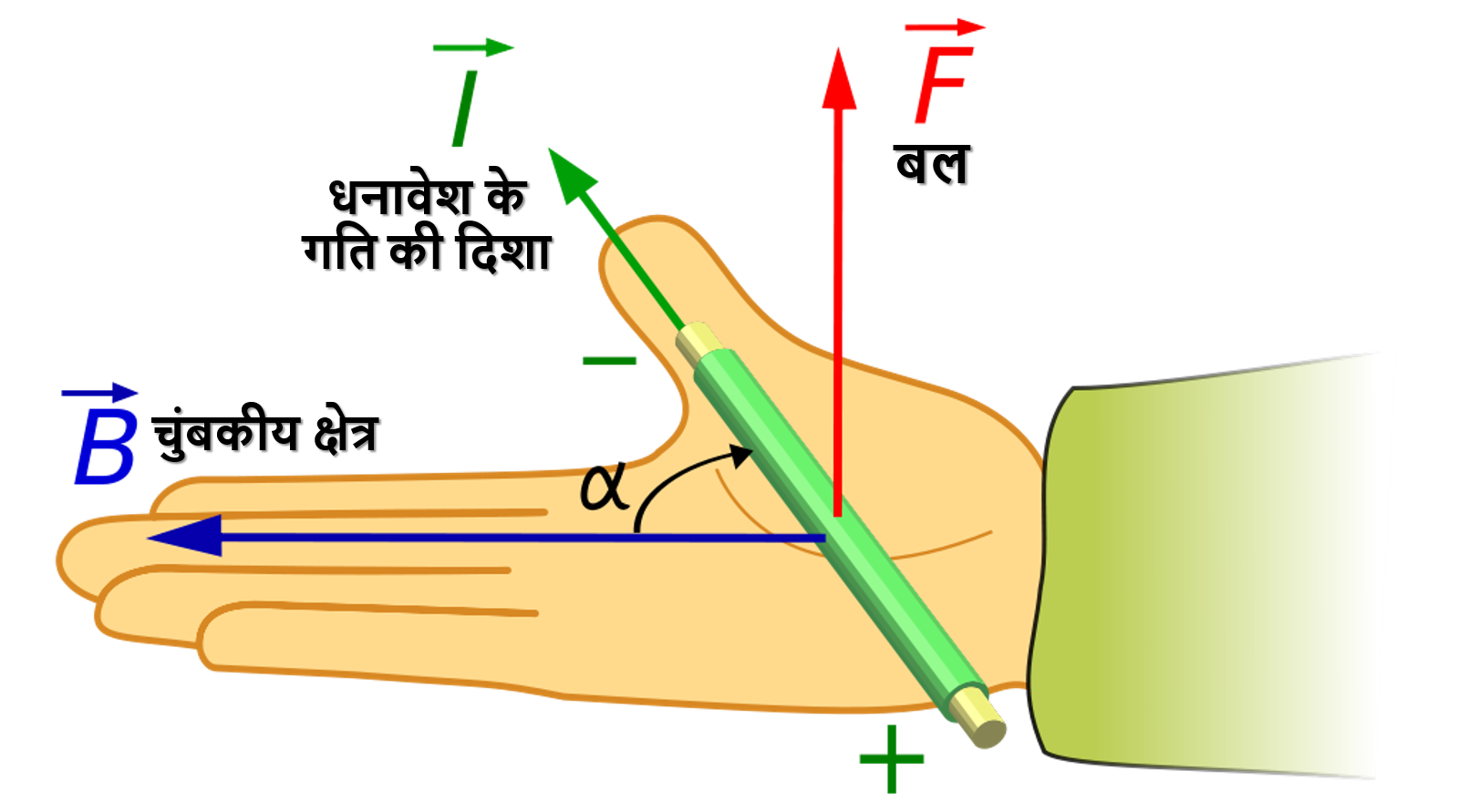
यदि हम चित्र की भाँति अपने दायें हाथ की हथेली खुली रखकर अंगुलियों तथा अँगूठे को लम्बवत् इस प्रकार फैलाएँ कि अँगुलियाँ, चुम्बकीय क्षेत्र B की दिशा में तथा अँगूठा, धनात्मक आवेशित कण की गति की दिशा में (अर्थात् वेग v की दिशा में) संकेत करे, तो आवेशित कण पर लगने वाले बल F की दिशा खुली हथेली के लम्बवत् तथा हथेली से बाहर की ओर होगी।
फ्लेमिंग का बायें हाथ का नियम ⇒
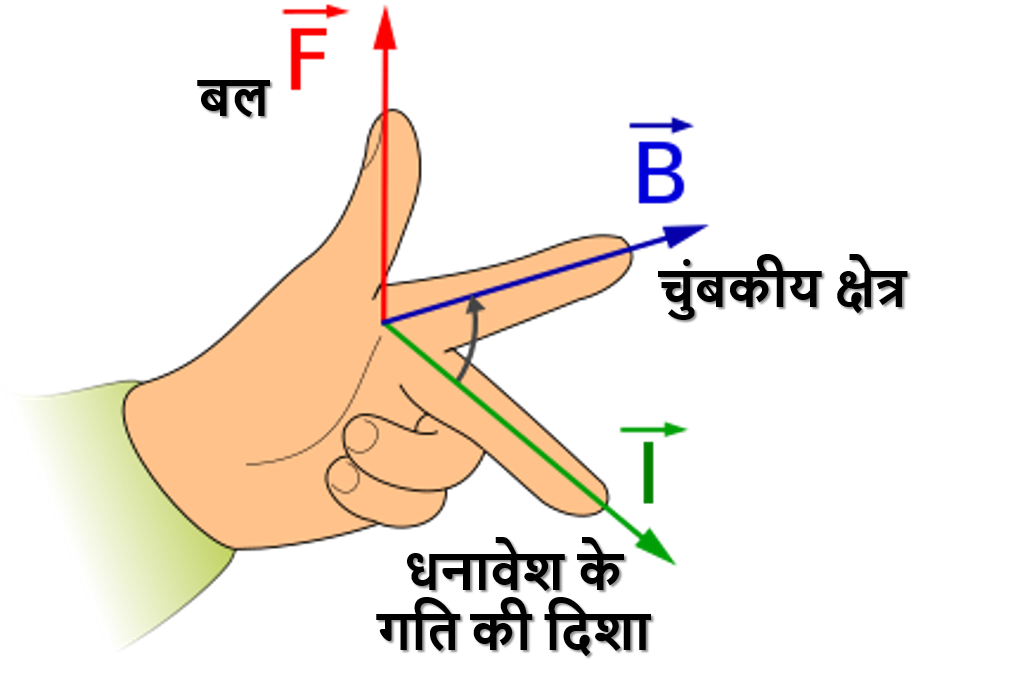
यदि हम चित्र की भाँति बायें हाथ का अँगूठा , तर्जनी अँगुली तथा बीच की अंगुली तीनों को एक-दूसरे के लम्बवत् फैलाएँ तथा तर्जनी अँगुली चुम्बकीय क्षेत्र B की दिशा तथा बीच वाली अँगुली धनात्मक आवेशित कण की गति की दिशा (अर्थात् वेग v की दिशा) इंगित करे, तो अँगूठा आवेशित कण पर लगने वाले बल F की दिशा बताएगा।
उदाहरण 6
यदि चुंबकीय क्षेत्र धनात्मक y-अक्ष के समान्तर है तथा आवेशित कण धनात्मक x-अक्ष के अनुदिश गतिमान है (चित्र 7), तो लोरेंज बल किस ओर लगेगा जबकि गतिमान कण (a) इलेक्ट्रॉन (ऋण आवेश) (b) प्रोटॉन (धन आवेश) है।
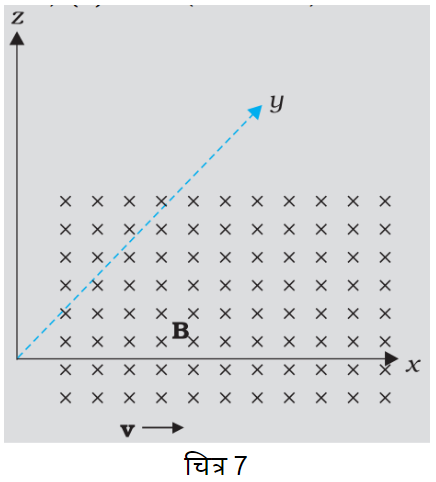
कण के वेग →v की दिशा x-अक्ष के अनुदिश है जबकि चुंबकीय क्षेत्र →B की दिशा y-अक्ष के अनुदिश है, अत: लोरेंज बल →v×→B की दिशा z-अक्ष के अनुदिश (पेंच नियम अथवा दक्षिण हस्त अंगुष्ठ नियम) है। अतः
- (a) इलेक्ट्रॉन के लिए यह बल -z अक्ष के अनुदिश तथा
(b) धनावेश (प्रोटॉन) के लिए यह +z अक्ष के अनुदिश है।
संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
जब कोई गतिशील आवेश q किसी चुम्बकीय क्षेत्र B तथा विद्युत क्षेत्र E में v वेग से प्रवेश या गति करता है तो आवेश q पर दो प्रकार के बल कार्य करते है।
- चुम्बकीय बल =qvB
- विद्युत बल =qE
F=qvB+qE
इस बल के बारे में सबसे पहले एच.ए.लोरेन्ज (H. A. Lorentz) ने बताया था इसलिए इसे लॉरेंज बल भी कहते है।चूंकि इस अध्याय में केवल चुम्बकीय बल का अध्ययन किया जा रहा है अतः आवेश पर लगने वाले चुंबकीय बल के बारे में विशेष ध्यान दिया जायेगा।
- यदि v तथा B के मध्य कोण θ है तो आवेश पर लगने वाला लॉरेंज बल
F=qvBsinθ
चुंबकीय क्षेत्र की दिशा ज्ञात करने हेतु पहले कई नियम पढ़ा जा चुका है जैसे दक्षिण हस्त पेच का नियम इत्यादि। यदि आवेश विराम अवस्था में हैं, अर्थात v=0 तब बल F=0 अतः केवल गतिशील आवेश ही चुंबकीय क्षेत्र उत्पन्न करता है।- अधिक विस्तार से अध्ययन के लिए कुछ विशेष स्थितियों का अवलोकन किया जा सकता है -
(1) जब आवेशित कण चुम्बकीय क्षेत्र की दिशा में प्रवेश करता है ⇒
किसी आवेशित कण पर लगने वाला बलF=qvBsinθ
यदि आवेशित कण की गति चुंबकीय क्षेत्र की दिशा में हो रही है तो v तथा B के मध्य कोण शून्य होगा अर्थात θ=0 अतः sinθ=0 तबF=0
(2) जब आवेशित कण चुम्बकीय क्षेत्र की दिशा के लम्बवत प्रवेश करता है ⇒
इस स्थिति में आवेशित कण चुंबकीय क्षेत्र के लंबवत प्रवेश करता है अर्थात इस स्थिति में v तथा B के मध्य 90° का कोण बनता है। अर्थात θ=90° अतः sin90°=1 तबF=qvB
चूँकि यह बल आवेशित कण के वेग की दिशा के लम्बवत कार्य करता है अतः इस स्थिति में कण इस बल के कारण वृत्ताकार गति करता है , वृत्ताकार गति के लिए इस कण पर आवश्यक अभिकेंद्रीय बल चुंबकीय बल (लोरेंज बल) द्वारा प्रदत्त होता है। - अतः वृताकार मार्ग में गति करवाने के लिए यह आवश्यक है की कण पर अभिकेंद्रिय बल तथा चुम्बकीय बल (लॉरेन्ज बल) का मान समान होना चाहिए।
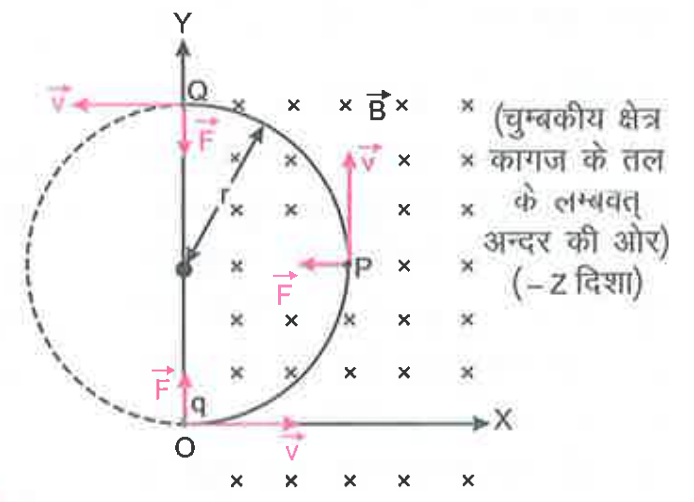
चूँकि इस स्थिति में आवेशित कण वृत्ताकार गति कर रहा है अतः यहाँ
अभिकेंद्रिय बल =mv2r
चुम्बकीय बल (लॉरेन्ज बल) =qvB
अतः
mv2r=qvB
r=mvqB
- चूँकि यहाँ आवेशित कण वृतीय गति कर रहा है अतः कण की कोणीय आवृति (ω) को निम्न प्रकार दर्शाया जाता है, चूँकि
तथा कोणीय आवृति
ω=2πν=qBm
आवेशित कण को वृत्तीय पथ का एक चक्कर पूरा करने में लगा समय -T=2πω=1ν=2πmqB
(3) जब आवेशित कण चुम्बकीय क्षेत्र से किसी कोण पर गति करता है ⇒
यहाँ किसी कोण पर गति करने का तात्पर्य है की आवेशित कण चुंबकीय क्षेत्र से θ,90° या 180° के अतिरिक्त अन्य किसी θ कोण पर गति करता है।- इस स्थिति में आवेशित कण कुण्डलिनी मार्ग में गति करता है।
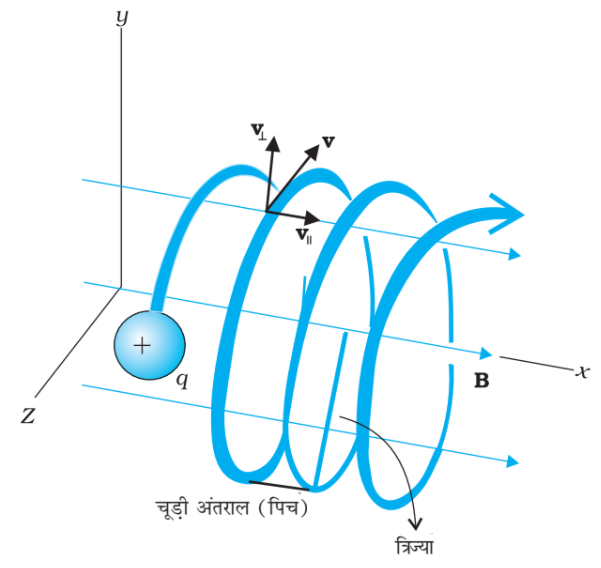
इस स्थिति में कुण्डलिनी मार्ग में गति कर रहे कुण्डलिनी की त्रिज्या -
r=mvsinθqB
उदाहरण 7
6×10−4T के चुंबकीय क्षेत्र के लंबवत 3×107ms की चाल से गतिमान किसी इलेक्ट्रॉन (द्रव्यमान 9×10−31kg तथा आवेश 1.6×10−19C) के पथ की त्रिज्या क्या है? इसकी क्या आवृत्ति होगी? इसकी ऊर्जा KeV में परिकलित कीजिए। ( 1eV=1.6×10−19J)
r=9×10–31kg×3×107ms–11.6×10–19C×6×10–4T
r=26×10–2m
r=26cm
ν=v2πr
ν=2×106s–1
ν=2×106Hz
ν=2MHz
E=(12)mv2
E=(12)9×10–31kg×9×1014m2/s2
E=40.5×10–17J
E≈4×10–16J=2.5keV
वेग वर्णक तथा साइक्लोट्रॉन
वेग वर्णक ⇒
- प्राय: आवेशित कणों के स्रोत से आवेशित कण एक निश्चित दिशा में, परन्तु विभिन्न चालों से उत्सर्जित होते हैं तथा हमें उस दिशा में केवल एक निश्चित चाल से आने वाले आवेशित कणों का चयन करना होता है। इसके लिए वेग वरणक (velocity selector) उपयोग में लाया जाता है।
सिद्धान्त ⇒
वेग वरणक में स्रोत में आने वाले आवेशित कणों को एक ऐसे क्षेत्र से होकर गुजारा जाता है, जहाँ परस्पर लम्बवत् दिशाओं में तथा आपतित कणों के वेग की दिशा के लम्बवत् विद्युत् क्षेत्र व चुम्बकीय क्षेत्र दोनों उपस्थित होते हैं। विद्युत् क्षेत्र व चुम्बकीय क्षेत्र की तीव्राताओं को इस प्रकार समंजित किया जाता है कि विद्युत् क्षेत्र की तीव्रता तथा चुम्बकीय क्षेत्र की तीव्रता का अनुपात, उस वेग के बराबर हो जिस वेग के कणों का हमें चयन करना है। इस स्थिति में, इस नियत वेग के आवेशित कणों पर विद्युत् क्षेत्र के कारण लगने वाला बल तथा चुम्बकीय क्षेत्र के कारण लगने वाला बल परस्पर बराबर व विपरीत होते हैं, अर्थात् आवेशित कण पर पणिामी बल शून्य होता है, अतः ये कण अविक्षेपित उसी मार्ग पर चलते रहते हैं।- माना आवेशित कणों का एक पुंज (आवेश q, द्रव्यमान m) x - दिशा में गतिमान है। यदि इस पुंज को एक ऐसे क्षेत्र से होकर गुजारा जाता है, जहाँ विद्युत् क्षेत्र E तथा चुम्बकीय क्षेत्र B परस्पर लम्बवत् दिशाओं में क्रमश: Y तथा Z-अक्ष के अनुदिश हैं तो विद्युत् क्षेत्र E के कारण आवेश q पर विद्युत् बल qE (Y-दिशा में) लगता है तथा चुम्बकीय क्षेत्र B के कारण आवेश q पर लॉरेन्ज बल qvB फ्लेमिंग के बायें हाथ के नियमानुसार ऋणात्मक Y-दिशा में लगता है।
qE=qvB
v=EB
साइक्लोट्रॉन ⇒
साइक्लोट्रोन एक ऐसी युक्ति है जिसका उपयोग आवेशित कणो या आयनों को उच्च वेगों में त्वरित करने में किया जाता है या आवेशित कणो को उच्च ऊर्जा तक त्वरित करने करने के लिए प्रयोग किया जाता है। इसकी खोज सन 1934 में ई. ओ.लॉरेन्ज व एम.एस.लिविंस्टन ने की थी, ई.ओ.लॉरेन्ज व एम.एस.लिविंस्टन को नाभिकीय संरचना पर रोध करते हुए आवश्यक ऊर्जा के आवेशित कण की आवश्यकता पड़ी और उन्होंने अपनी इस आवश्यक ऊर्जा के आवेशित कण की आवश्यकता को पूरा करने के लिए साइक्लोट्रॉन का निजात किया।सिद्धांत ⇒
साइक्लोट्रॉन इस सिद्धांत कर कार्य करता है की जब किसी धनावेशित कण को उच्च आवृति वाले विद्युत क्षेत्र में प्रबल चुम्बकीय क्षेत्र का उपयोग करते हुए बार बार गति करवाई जाए तो आवेशित कण त्वरित हो जाता है तथा इसकी ऊर्जा बहुत अधिक बढ़ जाती है।रचना (Construction) ⇒
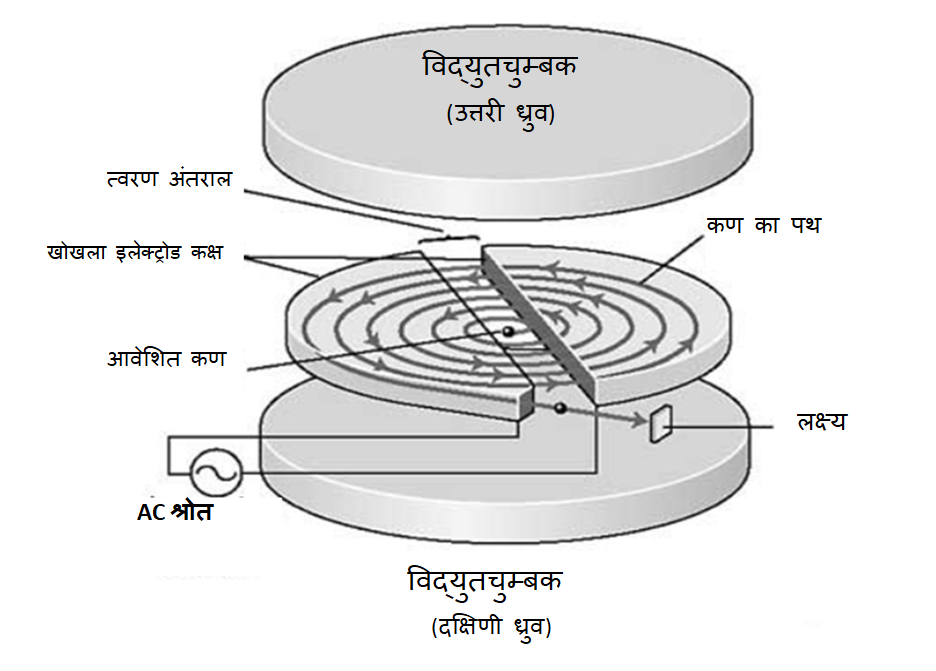
साइक्लोट्रॉन में दो D आकृति के खोखले धातु के पात्र लगे होते है इन्हे डीज (dees) कहते है, नीचे दिए गए चित्र में इन्हे D1 तथा D2 नाम से दर्शाया गया है। दोनों डीज एक दूसरे के अल्प दुरी पर स्थित होती है, दोनों डीज के मध्य उच्च आवृत्ति का प्रत्यावर्ती विभवांतर उत्पन्न करने के दोनों को A.C स्रोत से जोड़ा जाता है इससे दोनों डीज के मध्य उच्च आवृति का विद्युत क्षेत्र उत्पन्न हो जाता है। धनावेशित कण को दोनों डीज के मध्य में अल्प स्थान में रखा जाता है जहां उच्च आवृत्ति का विद्युत क्षेत्र उत्पन्न किया गया है तथा इस सम्पूर्ण व्यवस्था को दो प्रबल चुम्बकों के मध्य में रखा जाता है जैसा चित्र में दर्शाया गया है।
कार्यप्रणाली (Working) ⇒
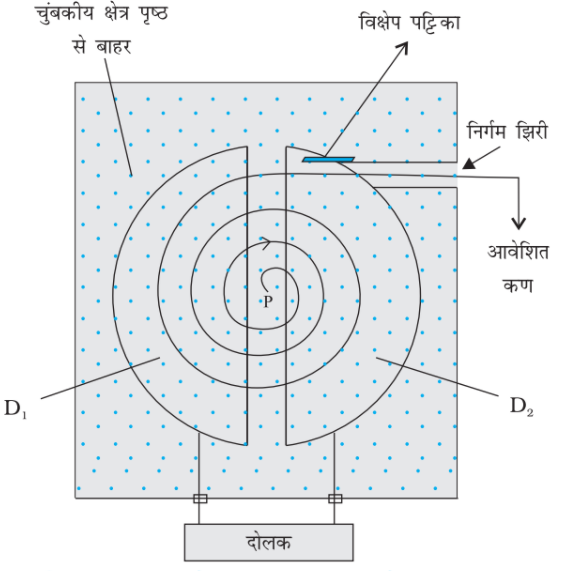
चूँकि दोनों डीज के मध्य प्रत्यावर्ती विभवान्तर उत्पन्न करने के लिए AC स्रोत लगाया गया है अतः हर आधे चक्कर के बाद डीज की ध्रुवता आपस में बदल जाती है।
- माना s पर धनावेशित कण रखा हुआ है, माना प्रारम्भ में डीज D1 धनावेशित है और D2 ऋणावेशित। अतः s पर रखा धनावेशित कण D2 की तरफ आकर्षित होगा और चूँकि चुम्बकीय क्षेत्र लंबवत लग रहा है अतः यह कण वृत्तीय पथ पर गति करता है।
अतः धनावेशित कण को पूरे 1 चक्कर में T समय लगता है तथा धनावेशित कण की ऊर्जा में 2qV वृद्धि हो जाती है। यह घटना बार बार दोहराई जाती है जिससे कण की ऊर्जा के साथ वेग बढ़ता जाता है तथा वेग में वृद्धि के कारण उसके वृतीय पथ की त्रिज्या भी बढ़ती जाती है जैसा चित्र में दिखाया गया है। जब वृत्तीय पथ की त्रिज्या डीज की त्रिज्या के बराबर हो जाती है तो धनावेशित कण साइक्लोट्रॉन में बने द्वार से बाहर निकल जाता है।
- प्रत्यावर्ती विभवांतर की आवृत्ति, डीज के अंदर आवेशित कण की परिक्रमा आवृत्ति के बराबर होनी चाहिए इसे साइक्लोट्रॉन अनुनादी स्थिति कहते है।
अनुनादी प्रतिबन्ध (resonance condition in cyclotron) ⇒
- साइक्लोट्रॉन के कार्य करने का प्रतिबन्ध यह है कि रेडियो आवृत्ति प्रत्यावती विभवान्तर की आवृति, डीज के अन्दर आवेशित कण की परिक्रमण आवृत्ति के बराबर होनी चाहिए। इस प्रतिबन्ध को अनुनादी प्रतिबन्ध कहते है।
F=qvBsin90°=qvB
यहाँ q आवेशित कण का आवेश है।यही बल r त्रिज्या के वृत्तीय पथ के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है। अतः
qvB=mv2r
या r=mvqB ....(A)
अर्ध चन्द्र में कण द्वारा अर्द्धवृत पूर्ण करने में लगा समयT=πrv=πv×mvqB
याT=πmqB ....(B)
(1) आवर्तकाल (time period) ⇒
माना प्रत्यावर्ती विद्युत क्षेत्र का आवर्तकाल T है तो अद्द्धचन्द्रों की ध्रुवता T2 समय के पश्चात् परिवर्तित होगी। यदि कण द्वारा अर्द्धवृत्त पूर्ण करने में लगा समय T2 के बराबर होगा तो कण त्वरित होगा अर्थातT2=nmqB
T=2nmqB ....(1)
(2) साइक्लोट्रॉन आवृत्ति (cyclotron frequency) ⇒
साइक्लोट्रॉन की आवृति यदि ν है तोν=1T
याν=qB2nm ....(2)
ω=2πν=2π×qB2nm=πqBnm ....(3)
(3) प्राप्त ऊर्जा (energy gained by cyclotron) ⇒
धनावेशित कण द्वारा प्राप्त ऊर्जाE=12mv2
समीकरण (A) सेv=qBrm
अत: E=12m×q2B2r2m2
E=12m×q2B2r2m ....(4)
अत: धनावेशित कण द्वारा प्राप्त की गयी अधिकतम ऊर्जाE=12m×q2B2r2m ....(4)
Emax=q2B2mr2max
उदाहरण 8
साइक्लोट्रॉन की दोलित्र आवृत्ति 10 MHz है। प्रोटॉनों को त्वरित करने के लिए प्रचालन चुंबकीय क्षेत्र का मान कितना होना चाहिए। यदि डीज़ की त्रिज्या 60 cm है तो त्वरक द्वारा उत्पन्न प्रोटॉन पुंज की गतिज ऊर्जा MeV में परिकलित कीजिए।
(e=1.60×10–19C, mp=1.67×10–27kg, 1MeV=1.6×10–13J).
दोलित्र आवृत्ति प्रोटॉन के साइक्लोट्रॉन के बराबर होनी चाहिए।
B=6.3×1.67×10–27×1071.6×10–19
B=0.66T
प्रोटॉन का अंतिम वेग
v=0.6m×6.3×107
v=3.78×107m/s
E=12mv2
E=1.67×10–27×14.3×10142×1.6×10–13
E=7MeV
विद्युत धारावाही चालक पर चुंबकीय बल
चालक तार में मुक्त इलेक्ट्रॉन बहुतायत से पाए जाते है अतः जब किसी चालक तार को किसी चुम्बकीय क्षेत्र में रखा जाता है तो तार में उपस्थित मुक्त इलेक्ट्रॉनो पर लॉरेन्ज बल कार्य करता है और इस लॉरेंज बल (चुम्बकीय बल) के कारण तार में उपस्थित मुक्त इलेक्ट्रॉन चालक में अपवहन चाल (वेग) से प्रवाहित होना शुरू हो जाते है। अतः किसी धारावाही चालक को चुम्बकीय क्षेत्र में रखने पर यह चालक एक बल का अनुभव करता है।

यहाँ चित्र में दर्शाया गया है की एक छड़ को चुम्बकीय क्षेत्र में रखा गया है, यहाँ धारावाही चालक तार की लम्बाई L है, तार का अनुप्रस्थ काट का क्षेत्रफल A है, तथा चालक तार के इकाई आयतन में इलेक्ट्रोनो की संख्या n है तो
- चालक तार पर कुल आवेश का मान q=neAL होगा।
F=qvBsinθ
यहाँ सूत्र में कुल आवेश का मान रखने पर, चूँकि q=neAL अतःF=neALvBsinθ
चूंकि I=neAv अतःF=ILBsinθ
F=ILBsin0°=0
यदि चालक तार व चुम्बकीय क्षेत्र के मध्य 90∘ का कोण हो अर्थात दोनों एक दूसरे के लंबवत स्थित हो तो इस स्थिति में θ=90°
F=ILBsin90°=ILB
उदाहरण 9
200 g द्रव्यमान तथा 1.5 m लंबाई के किसी सीधे तार से 2A विद्युत धारा प्रवाहित हो रही है। यह किसी एकसमान क्षैतिज →B चुंबकीय क्षेत्र द्वारा वायु के बीच में निलंबित है (चित्र 6)। चुंबकीय क्षेत्र का परिमाण ज्ञात कीजिए।
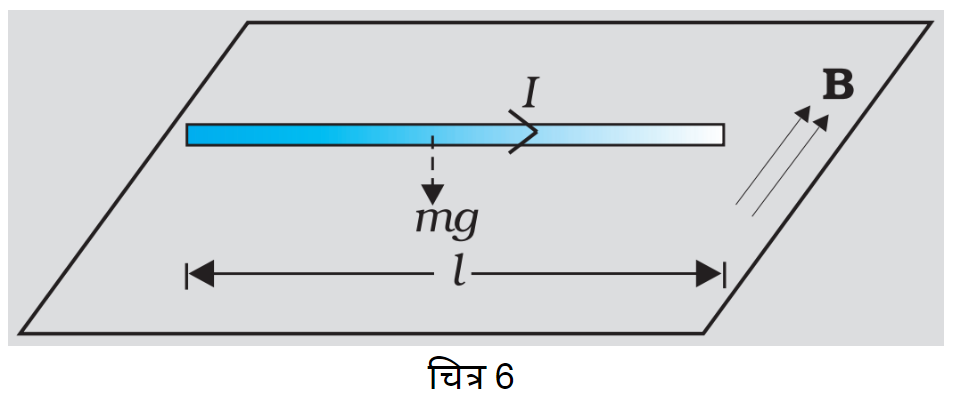
तार बीच वायु में निलंबित है इसके निलंबित रहने के लिए इस पर एक उपरिमुखी बल F जिसका परिणाम IlB लगना चाहिए जो इसके भार mg को संतुलित कर सके। अत:
B=mgIl
B=0.2×9.82×1.5=0.65T
यहाँ पर m/l अर्थात तार का प्रति एकांक लंबाई द्रव्यमान बताना पर्याप्त है। पृथ्वी के चुंबकीय क्षेत्र का मान लगभग 4×10−5T है जिसकी यहाँ उपेक्षा की गई है।
दो समांतर विद्युत धाराओं के बीच बल
यह अध्ययन किया जा चुका हैं कि किसी चालक में धारा प्रवाहित कराने पर चालक के चारों ओर चुम्बकीय क्षेत्र उत्पन्न हो जाता है। अब यदि इस चालक के पास एक अन्य धारावाही चालक रखा जाए, तो इस चालक पर, पहले वाले धारावाही चालक से उत्पन्न चुम्बकीय क्षेत्र के कारण एक बल लगता है।
बल का परिमाण-
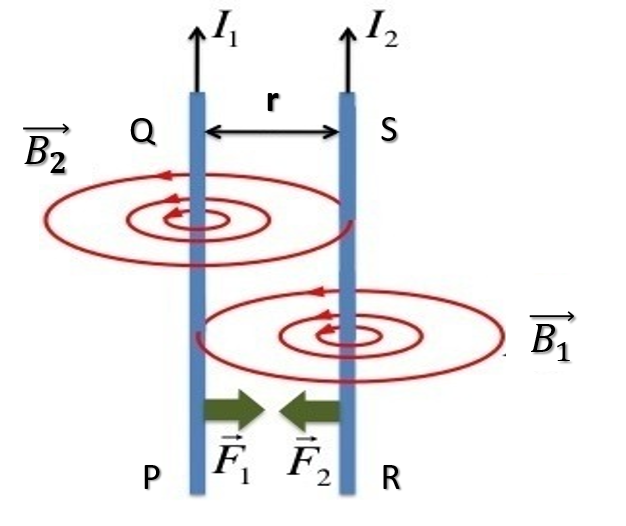
चित्र में दो ऋजु धारावाही चालक PQ तथा RS कागज के तल में परस्पर समान्तर रखे हैं। माना इनमें धारा क्रमशः I1 व I2 ऐम्पियर एक ही दिशा में बह रही हैं तथा इनके बीच की दूरी r मीटर है।
- अनन्त लम्बाई के धारावाही चालक PQ के कारण चालक RS के किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता
B1=μ04π2I1r न्यूटन/(ऐम्पियर मीटर)...(1)
इस चुम्बकीय क्षेत्र B1 की दिशा दायें हाथ की हथेली के नियम से कागज के तल के लम्बवत् अन्दर की और होगी।- चालक RS (जिसमें धारा I2 ऐम्पियर बह रही है) इस चुम्बकीय क्षेत्र B1 में क्षेत्र के लम्बवत् रखा है, अत: इस पर धारा की दिशा तथा चुम्बकीय क्षेत्र की दिशा, दोनों के लम्बवत् एक बल (लॉरेन्ज बल) लगता है। चालक RS की लम्बाई l पर लगने वाला लरिन्ज बल का परिमाण
F=I2B1lsin90°=I2×μ04π)×2I1r×l×1
याF=μ04π×2I1I2lr न्यूटन ....(2)
Fl=μ04π×2I1I2r न्यूटन/मीटर ....(3)
उदाहरण 10
किसी निर्धारित स्थान पर पृथ्वी के चुंबकीय क्षेत्र का क्षैतिज घटक 3.0×10−5T है, तथा इस क्षेत्र की दिशा भौगोलिक दक्षिण से भौगोलिक उत्तर की ओर है। किसी अत्यधिक लंबे सीधे चालक से 1A की अपरिवर्ती धारा प्रवाहित हो रही है। जब यह तार किसी क्षैतिज मेज़ पर रखा है तथा विद्युत धारा के प्रवाह की दिशाएँ (a) पूर्व से पश्चिम की ओर; (b) दक्षिण से उत्तर की ओर हैं तो तार की प्रत्येक एकांक लबाई पर बल कितना है?
F=IlBsinθ
(a) जब विद्युत धारा पूर्व से पश्चिम की ओर प्रवाहित होती है, तब यह एम्पियर की परिभाषा में वर्णित बल के मान 2×10−7Nm−1 से बड़ा है। अतः ऐम्पियर का मानकीकरण करने के लिए पृथ्वी के चुंबकीय क्षेत्र तथा अन्य भूले भटके क्षेत्रों के प्रभावों को समाप्त करना महत्वपूर्ण है। बल की दिशा अधोमुखी है। इस दिशा को 'सदिशों के सदिश गुणनफल' के दैशिक गुण के द्वारा प्राप्त किया जा सकता है।
(b) जब विद्युत धारा के प्रवाह की दिशा दक्षिण से उत्तर की ओर है, तो
f=0
एकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
जब किसी एकसमान चुम्बकीय क्षेत्र में स्वतन्त्रतापूर्वक लटकी किसी कुण्डली में धारा प्रवाहित की जाती है, तो कुण्डली पर एक बलयुग्म लगता है, जो कुण्डली को घुमाकर उसके तल को चुम्बकीय क्षेत्र के लम्बवत् करने का प्रयास करता है (अर्थात् कुण्डली की अक्ष को चुम्बकीय क्षेत्र के समान्तर करने का प्रयास करता है)।
माना चित्र (a) में एक आयताकार कुण्डली abcd है जिसे एकसमान चुम्बकीय क्षेत्र B में इस प्रकार लटकाया गया है कि कुण्डली का तल, चुम्बकीय क्षेत्र के समान्तर है। माना कुण्डली की एक भुजा ab=cd=l तथा दूसरी भुजा ad=bc=b है।
- अब यदि कुण्डली में abcd दिशा में धारा I प्रवाहित करते हैं, तो चूँकि कुण्डली की भुजाएँ ab व cd चुम्बकीय क्षेत्र के लम्बवत् हैं, अत: भुजा ab पर लॉरेन्ज बल F1=IlB लगता है जिसकी दिशा फ्लेमिंग के बायें हाथ के नियमानुसार कागज के तल के लम्बवत् बाहर की ओर होती है तथा भुजा cd पर लॉरेन्ज बल F2=IlB कागज के तल के लम्बवत् अन्दर की ओर लगता है।
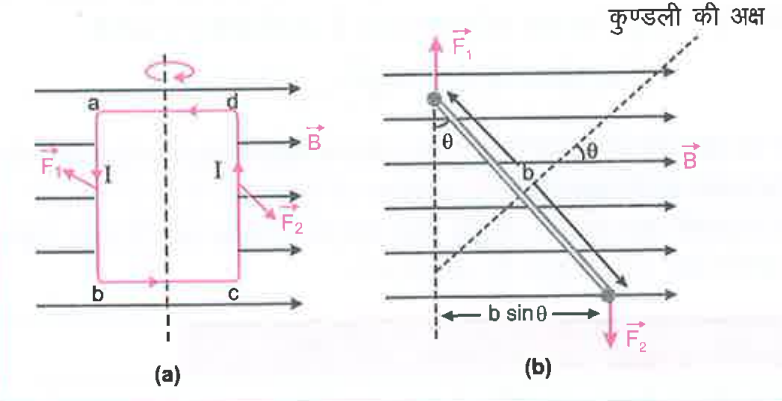
स्पष्टत: कुण्डली की भुजाओं ab व cd पर लगने वाले बराबर तथा विपरीत बलों F1 व F2 के कारण कुण्डली पर बलयुग्म कार्य करता है जिससे कुंडली अपनी अक्ष से दक्षिणावर्त घूम जाती है। इम बलयुग्म केे आघूर्ण को विक्षेपक बल आघूर्ण (deflecting torque)कहते हैं।
- यदि किसी क्षण चित्र (b) की भाँति कुण्डली की अक्ष ( अर्थात् कुण्डली के तल पर खींचा गया अभिलम्ब) चुम्बकीय क्षेत्र B की दिशा से कोण θ बनाती है, तो दोनों बलों F1 व F2 के बीच की लम्बवत दुरी bsinθ तथा उस क्षण
τ=IlB×bsinθ=IABsinθ
जहाँ A=lb = कुंडली का क्षेत्रफल - यदि कुंडली में n फेरे है तो कुल विक्षेपक बल आघूर्ण
τ=nIABsinθ
उदाहरण 11
10 cm त्रिज्या की किसी कुंडली जिसमें पास पास सटे 100 फेरे हैं, में 3.2A विद्युत धारा प्रवाहित हो रही है। (a) कुंडली के केंद्र पर चुंबकीय क्षेत्र कितना है? (b) इस कुंडली का चुंबकीय आघूर्ण क्या है?
यह कुंडली ऊर्ध्वाधर तल में रखी है तथा किसी क्षैतिज अक्ष जो उसके व्यास से सरेखित है, के परितः घूर्णन करने के लिए स्वतंत्र है। एक 2T का एकसमान चुंबकीय क्षेत्र क्षैतिज दिशा में है जो इस प्रकार है कि आरंभ में कुंडली का अक्ष चुंबकीय क्षेत्र की दिशा में है। चुंबकीय क्षेत्र के प्रभाव में कुंडली 90∘ के कोण पर घूर्णन कर जाती है। (c) आरभिक तथा अंतिम स्थिति में कुंडली पर बल आघूर्ण परिमाण क्या हैं? (d) 90∘ पर घूर्णन करने के पश्चात कुंडली द्वारा अर्जित कोणीय चाल कितनी है? कुंडली का जड़त्व आघूर्ण 0.1kgm2 है।
(a) समीकरण B=μ0NI2R से
N=100; I=3.2A, तथा R=0.1m
अतः,
B=4×10−5×102×10−1
(π×3.2=10 रखने पर)
B=2×10–3T
B की दिशा दक्षिण हस्त अंगुष्ठ नियम द्वारा प्राप्त होती है।
(b) चुम्बकीय आघूर्ण,
m=NIπr2
m=100×3.2×3.14×10–2
m=10Am2
एक बार फिर दिशा दक्षिण हस्त अंगुष्ठ नियम द्वारा प्राप्त होती है।
(c)
τ=mBsinθ
आरंभ में, θ=0.
इस प्रकार आरंभिक बल आघूर्ण τi=0
अंत में, θ=π2 (90∘). इस प्रकार, अंतिम बल आघूर्ण
(d) न्यूटन के द्वितीय नियम से,
यहां I कुंडली का जड़त्व आघूर्ण है। श्रृंखला नियम के अनुसार,
इसका उपयोग करने पर,
θ=0 से θ=π2 तक समाकलन करने पर,
Iω2f2=−mB[cosθ]π20=mB
ωf=(2mBI)12
ωf=(2×2010−1)12
ωf=20s−1
उदाहरण 12
(a) किसी चिकने क्षैतिज तल पर कोई विद्युत धारावाही वृत्ताकार पाश रखा है। क्या इस पाश के चारों ओर ऐसा चुंबकीय क्षेत्र स्थापित किया जा सकता है कि यह पाश अपने अक्ष के चारों ओर स्वयं चक्कर लगाए (अर्थात ऊर्ध्वाधर अक्ष के चारों ओर)। (b) कोई विद्युत वाही वृत्ताकार पाश किसी एकसमान बाह्य चुंबकीय क्षेत्र में स्थित है। यदि यह पाश घूमने के लिए स्वतंत्र है, तो इसके स्थायी संतुलन का दिविन्यास क्या होगा। यह दर्शाइए कि इसमें कुल क्षेत्र (बाह्य क्षेत्र + पाश द्वारा उत्पन्न क्षेत्र) का फ्लक्स अधिकतम होगा। (c) अनियमित आकृति का कोई विद्युत धारावाही पाश किसी बाह्य चुंबकीय क्षेत्र में स्थित है। यदि तार लचीला है तो यह वृत्ताकार आकृति क्यों ग्रहण कर लेता है?
(a) नहीं, क्योंकि इसके लिए ऊर्ध्वाधर दिशा में बल आघूर्ण τ की आवश्यकता होगी। परंतु τ=I→A×→B, और चूँकि क्षैतिज पाश का क्षेत्रफल सदिश →A ऊर्ध्वाधर दिशा में है, τ को →B के किसी मान के लिए पाश के तल में होना चाहिए।
(b) स्थायी संतुलन वाला दिक् विन्यास वह है जिसमें पाश का क्षेत्रफल सदिश →A बाह्य चुंबकीय क्षेत्र की दिशा में होता है। इसे विन्यास में पाश द्वारा उत्पन्न चुंबकीय क्षेत्र बाह्य क्षेत्र की दिशा में ही है। इस प्रकार, दोनों क्षेत्र पाश के तल के लंबवत होने के कारण कुल क्षेत्र का अधिकतम फ्लक्स प्रदान करते हैं।
(c) यह क्षेत्र के लंबवत तल में वृत्ताकार पाश का रूप इसलिए ग्रहण कर लेता है ताकि इससे होकर अधिकतम फ्लक्स प्रवाहित हो सके। क्योंकि किसी दी गई परिमिति के लिए वृत्त का क्षेत्रफल किसी भी अन्य आकृति की तुलना में अधिकतम होता है।
चल कुंडली धारामापी
किसी विद्युत परिपथ में अल्प विद्युत धारा के मापन के लिए जिस युक्ति का उपयोग किया जाता है उसे धारामापी या गैल्वेनोमीटर कहते है। यह युक्ति इस सिद्धांत पर कार्य करती है की
- यदि किसी समान या नियत चुम्बकीय क्षेत्र में एक कुण्डली रखी जाए और इसमें धारा प्रवाहित की जाए तो कुंडली पर एक बल आघूर्ण कार्य करता है तथा इस बलाघूर्ण का मान कुण्डली में प्रवाहित धारा के परिमाण पर निर्भर करता है। अर्थात जितनी ज्यादा धारा प्रवाहित होती है उतना ही अधिक कुंडली पर बलाघूर्ण का मान होता है
- चल कुण्डली धारामापी
- चल चुम्बक धारामापी
- निलम्बित कुण्डली धारामापी
- कीलकित कुण्डली धारामापी
निलम्बित कुण्डली :-
संरचना (Construction) ⇒
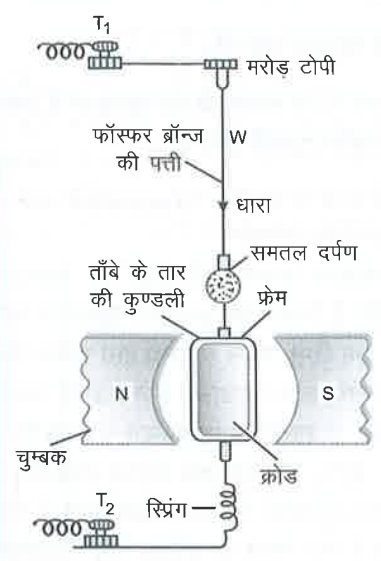
निलम्बित कुण्डली धारामापी की संरचना चित्र में दिखाई गयी है, इसमें एक अनुचुम्बकीय धातु (एल्युमिनियम) पर विद्युत रोधी तथा ताँबे के तार को लपेटकर कुण्डली बनाई जाती है।
इस कुण्डली को फॉस्फर ब्रॉन्ज (phosphor bronze) के तार की सहायता से दो प्रबल चुम्बकों के मध्य लटकाया जाता है। कुण्डली के भीतर एक नरम लोहे की क्रोड़ रखी रहती है। कुंडली का एक सिरा मरोड़ कुंजी (Torsion hand) से होता हुआ संयोजक पेच T1 से जुड़ा रहता है , यहाँ मरोड़ कुंजी (Torsion hand) कुण्डली को आवश्यकता पड़ने पर घूमने के लिए स्वतंत्र रखता है। मरोड़ कुंजी तथा कुण्डली के मध्य फॉस्फर ब्रॉन्ज तार पर एक समतल दर्पण लगा रहता है जो तार के साथ आसानी से घूम सकता है। कुण्डली का नीचे वाला सिरा एक प्रत्यास्थ स्प्रिंग से जुड़ा रहता है तथा यह स्प्रिंग T2 से जुडी रहती है।
निलंबित कुण्डली धारामापी का सिद्धान्त ⇒
यह युक्ति इस सिद्धांत पर कार्य करती है कि -- जब किसी धारावाही कुण्डली को किसी समान या समरूप चुम्बकीय क्षेत्र में रखा जाए और इसमें धारा प्रवाहित की जाये तो कुंडली पर एक एक बल आघूर्ण कार्य करता है जो कुण्डली को घुमाता है तथा यह घूर्णन विक्षेप (बल आघूर्ण) कुण्डली में प्रवाहित धारा के मान पर निर्भर करता है।
τ=nIABsinθ
यदि चुम्बकीय क्षेत्र त्रिज्य है तो θ=90° अतःτ=nIAB
इस बल आघूर्ण के कारण कुण्डली घूमने लगेगी फलस्वरूप फॉस्फर ब्रॉन्ज़ तार में ऐंठन आने लगेगी।- माना फॉस्फर ब्रॉन्ज़ (phosphor bronze) तार में ऐंठन कोण ϕ हे तो
ऐंठन बल युग्म =Cϕ
यहाँ ध्यान दे की यह ऐंठन बल युग्म, बल आघूर्ण के विपरीत लगता हैऐंठन बल युग्म = बल आघूर्ण
Cϕ=nIAB
अतःCϕ=nIAB
I=CϕnAB
यहाँ CnAB एक नियतांक है जिसे धारामापी का दक्षता नियतांक (figure of merit) या धारामापी नियतांक K कहते हैं। अतःI=Kϕ ....(1)
- समीकरण (1) से स्पष्ट है कि धारामापी की कुण्डली में प्रवाहित धारा, कुण्डली के विक्षेप के अनुक्रमानुपाती होती है।
कीलकित कुण्डली धारामापी ⇒
संरचना ⇒
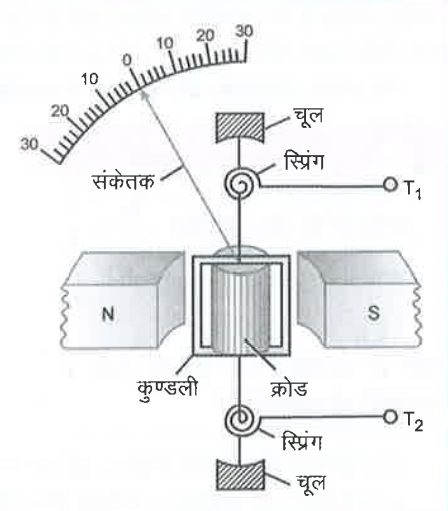
चित्र में कीलकित कुण्डली धारामापी प्रदर्शित है। इसमें ऐलुमिनियम के आयताकार अथवा वृत्ताकार फ्रेम पर ताँबे के पतले व पृथक्कृत तार के अनेक फेरे लपेटकर एक कुण्डली बनायी जाती है। कुण्डली के फ्रेम को एक धुरी पर लगाकर धुरी के सिरे दो चूलों (pivots) में इस प्रकार बनाये जाते हैं कि कुण्डली, धुरी के परितः आसानी से घूम सकती है। कुण्डली के दोनों सिरों पर चूलों के पास दो स्प्रिंग लगी रहती हैं जिनका सम्बन्ध संयोजक पेचों T1 व T2 से होता है। यह कुण्डली एक प्रबल नाल चुम्बक के ध्रुव खण्डों N व S के बीच के स्थान में घूमती है। चुम्बक के ध्रुव अवतल बेलनाकार कटे होते हैं। कुण्डली के अन्दर मुलायम लोहे का एक क्रोड लगा रहता है, जो कुण्डली को कहीं भी स्पर्श नहीं करता है। क्रोड होने से चुम्बकीय क्षेत्र प्रबल एवं त्रिज्यीय हो जाता है अर्थात् कुण्डली का तल सदैव चुम्बकीय क्षेत्र के समान्तर रहता है। कुण्डली के साथ एक संकेतक लगा रहता है जो कुण्डली के घूमने पर उसके साथ एक वृत्ताकार स्केल पर घूमता है। वृत्ताकार स्केल पर शून्य चिह्न बीच में अंकित होता है तथा इसके दोनों ओर बराबर-बराबर दूरी पर अन्य चिह्न अंकित रहते हैं
सिद्धान्त ⇒
- जब एक धारावाही कुण्डली किसी एकसमान चुम्बकीय क्षेत्र में स्वतन्त्रतापूर्वक इस प्रकार लटकायी जाती है कि इसका तल, चुम्बकीय क्षेत्र के समान्तर रहे, तो कुण्डली पर एक विक्षेपक बल आघूर्ण लगता है, जो इसे घुमाकर इसके तल को चुम्बकीय क्षेत्र के लम्बवत् करने का प्रयास करता है।
τ=nIAB
इस विक्षेपक बल आघूर्ण के कारण जब कुण्डली घूमती है, तो नियन्त्रक स्प्रिगों में ऐंठन उत्पन्न हो जाती है जिसके कारण कुण्डली पर ऐंठन बल आघूर्ण लगने लगता है। यह बल आघूर्ण कुण्डली के घूमने का विरोध करता है। इस ऐंठन बल आघूर्ण का मान कुण्डली के विक्षेप के अनुक्रमानुपाती होता है। जब ऐंठन बल आघूर्ण, विक्षेपक बल आघूर्ण के बराबर हो जाता है, तो कुण्डली सन्तुलन की स्थिति में ठहर जाती है। यदि सन्तुलन की स्थिति में कुण्डली का विक्षेप रेडियन होता है, तोऐंठन बल आघूर्ण =Cϕ
जहाँ C, नियन्त्रक स्प्रिंगों की ऐंठन दृढ़ता है।- कुण्डली की सन्तुलन अवस्था में
विक्षेपक वल आघूर्ण = ऐंठन बल आघूर्ण
अर्थात्nIAB=Cϕ
याI=CϕnAB
याI=Kϕ
I∝ϕ
- स्पष्ट है कि धारामापी की कुण्डली में प्रवाहित धारा, कुण्डली के विक्षेप के अनुक्रमानुपाती होता है, इसालए इसके स्केल पर चिह्न बराबर-बराबर दूरी पर अंकित होते हैं।
धारामापी को अमीटर में बदलना
अमीटर वह यन्त्र है, जो किसी विद्युत् परिपथ में बहने वाली धारा को सीधे ऐम्पियर (या मिली ऐम्पियर अथवा माइक्रो ऐम्पियर) में नापता है।
अतः इसे परिपथ के श्रेणीक्रम में लगाते हैं जिससे कि नापी जाने वाली सम्पूर्ण धारा इसमें से होकर प्रवाहित हो जाए। स्पष्टत: इसे परिपथ में श्रेणीक्रम में जोड़ने पर परिपथ का प्रतिरोध अप्रभावित रहना चाहिए, अन्यथा परिपथ में धारा का मान बदल जाएगा। अत: यह आवश्यक है कि अमीटर का अपना प्रतिरोध नगण्य होना चाहिए जिससे कि इसे परिपथ में जोड़ने पर परिपथ की मुख्य धारा अप्रभावित रहे, अर्थात् आदर्श अमीटर का अपना प्रतिरोध शून्य होना चाहिए ।
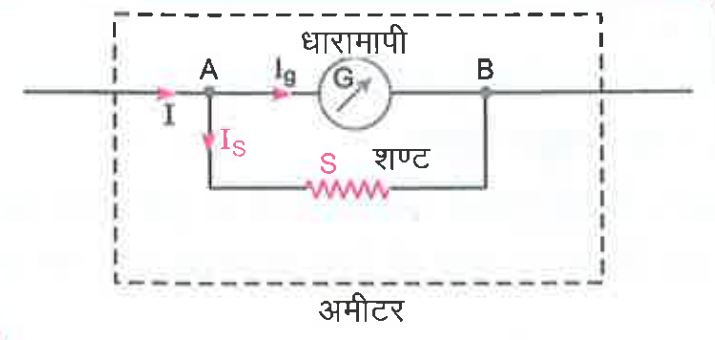
चूँकि धारामापी की कुण्डली का अपना कुछ प्रतिरोध होता है, अतः धारामापी को अमीटर में बदलने के लिए इसके प्रतिरोध को कम करना होता है। इसके लिए चित्र की भाँति धारामापी की कुण्डली के समान्तर क्रम में एक उचित (कम) प्रतिरोध का तार लगा दिया जाता है जिसे शण्ट कहते हैं। शण्ट के प्रतिरोध का मान अमीटर की परास पर निर्भर करता है। शण्ट लगाने से अमीटर का प्रभावी प्रतिरोध, शण्ट के प्रतिरोध से भी कम हो जाता है, फलतः इसे परिपथ में श्रेणीक्रम में जोड़ने से परिपथ का प्रतिरोध लगभग अपरिवर्तित रहता है। इसके अतिरिक्त, परिपथ की धारा का केवल कुछ भाग ही इसकी कुण्डली से होकर जाता है, शेष अधिकाँश भाग शण्ट से होकर जाता है जिससे कुण्डली का विक्षेप काफी कम हो जाता है तथा इसकी परास बढ़ जाती है (यद्यपि इसकी सुग्राहिता घट जाती है) ।
- चित्र में परिपथ में प्रवाहित धारा I नापने के लिए बिन्दु A व B के बीच शण्टित धारामापी जोड़ा गया है।
I=Ig+Is तथा IgG=IsS
इन्हें हल करने पर,I=Ig+Ig(GS)
याIg=ISS+G ....(1)
शण्ट से प्रवाहित धारा Is=(IG).(S+G) ....(2)
तथा शण्ट का प्रतिरोधS=IgGI−Ig ....(3)
अमीटर का प्रभावी प्रतिरोधRAm=SGS+G
धारामापी को वोल्टमीटर में बदलना
वोल्टमीटर वह यन्त्र है जो विद्युत् परिपथ में किन्हीं दो बिन्दुओं के मध्य विभवान्तर को सीधे वोल्ट (या मिली वोल्ट अथवा माइक्रो वोल्ट) में नापता है, अतः इसे परिपथ के उन दो बिन्दुओं के समान्तर क्रम में जोड़ते हैं, जिनके बीच विभवान्तर नापना होता है।
स्पष्टतः इसे परिपथ में उन बिन्दुओं के मध्य समान्तर क्रम में जोड़ने पर परिपथ का प्रतिरोध अप्रभावित रहना चाहिए, अन्यथा उन बिन्दुओं के बीच जुड़े चालक में प्रवाहित होने वाली धारा का मान बदल जाएगा जिससे उसके सिरों के बीच विभवान्तर भी बदल जाएगा। अतः यह आवश्यक है कि वोल्टमीटर का स्वयं का प्रतिरोध अधिक से अधिक होना चाहिए जिससे कि उन बिन्दुओं के बीच (जहाँ विभवान्तर नापना है) इसे जोड़ने पर इससे होकर अधिक धारा न बहे, अर्थात् परिपथ की मुख्य धारा अप्रभावित रहे, अत: आदर्श वोल्टमीटर का अपना प्रतिरोध अनन्त होना चाहिए।
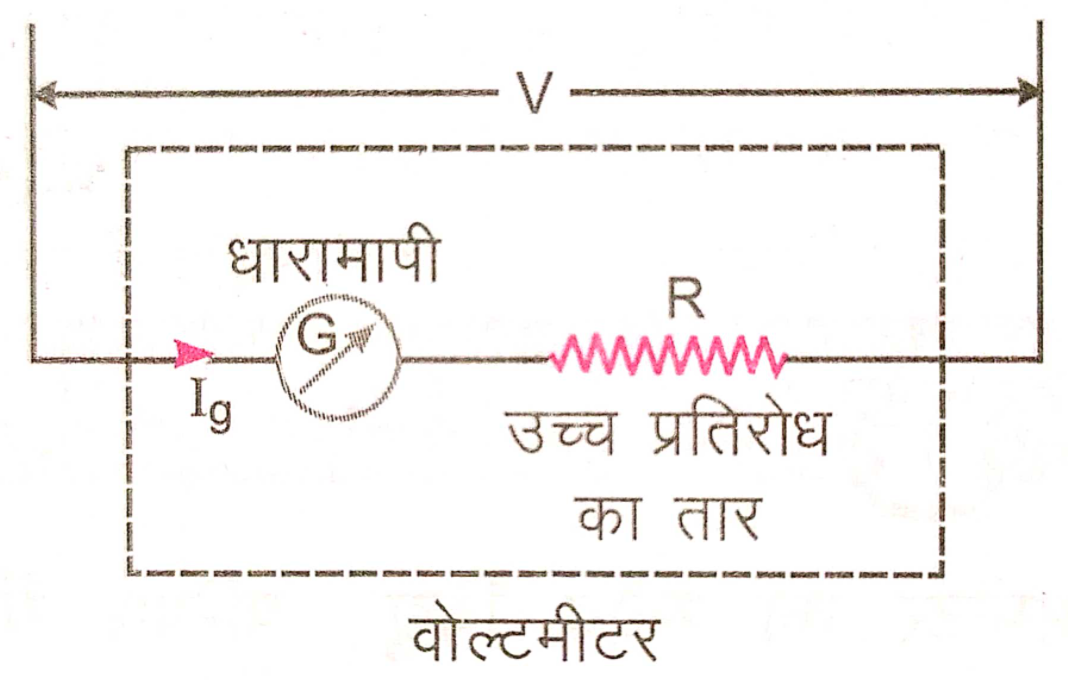
वोल्टमीटर, वास्तव में कीलकित कुण्डली धारामापी का ही संशोधित रूप है। चूँकि धारामापी की कुण्डली का अपना प्रतिरोध कम होता है, अत: धारामापी को वोल्टमीटर में बदलने के लिए इसके प्रतिरोध को बढ़ाना होता है। इसके लिए चित्र की भाँति धारामापी की कुण्डली के साथ श्रेणीक्रम में एक उचित (उच्च) प्रतिरोध लगा दिया जाता है। इस प्रतिरोध का मान वोल्टमीटर की परास पर निर्भर करता है।
यदि चित्र में धारामापी में पूर्ण विक्षेप के लिए धारा का मान Ig है, धारामापी की कुण्डली का प्रतिरोध G है तथा इसे विभवान्तर V वोल्ट नापने के लिए वोल्टमीटर में बदलना है। इसके लिए यदि धारामापी के साथ श्रेणीक्रम में प्रतिरोध R जोड़ा गया
V=Ig(R+G)
या धारामापी के साथ श्रेणीक्रम में आवश्यक प्रतिरोधR=VIg−G ....(1)
तथा तब वोल्टमीटर का प्रभावी प्रतिरोध Rvm=R+G ....(2)
उदाहरण 13
नीचे दिखाए गए परिपथ में धारा का मान क्या है यदि दिखाया गया ऐमीटर, (a) RG=60.00ω प्रतिरोध का गैल्वेनोमीटर है। (b) भाग (a) में बताया गया गैल्वेनोमीटर ही है परंतु इसको rs=0.02ω का शंट प्रतिरोध लगाकर ऐमीटर में परिवर्तित किया गया है। (c) शून्य प्रतिरोध का एक आदर्श ऐमीटर है।
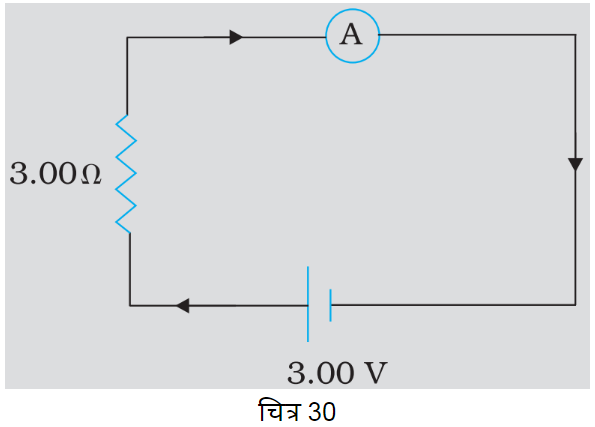
(a) परिपथ में कुल प्रतिरोध है
इसलिए I=363=0.048A
(b) ऐमीटर में रूपांतरित गैल्वेनोमीटर का प्रतिरोध
परिपथ में कुल प्रतिरोध = 0.02+3=3.02Ω
अतः,
(c) शून्य प्रतिरोध के आदर्श ऐमीटर के लिए