30 from CHETANA PUBLICATION Rational Dynamics for Class 12
| Class 12 | PHYSICS |
| Chapter | Rational Dynamics |
| CHETANA PUBLICATION | 30 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 14
Somehow, an ant is stuck to the rim of a bicycle wheel of diameter 1m . While the bicycle is on a central stand. The wheel is set into rotation and attains the frequency of2revs in 10 seconds, with uniform angular acceleration. Calculate number of revolutions completed by the ant in these 10 seconds.View SolutionQuestion 15
Somehow, an ant is stuck to the rim of a bicycle wheel of diameter 1m . While the bicycle is on a central stand. The wheel is set into rotation and attains the frequency of2revs in 10 seconds, with uniform angular acceleration. Calculate number of revolutions completed by the ant in these 10 seconds.View SolutionQuestion 16
Coefficient of static friction between a coin and gramophone disc is 0.5. Radius of the disc is 8cm . Initially the centre of the coin is πcm cm away from the centre of the disc. At what minimum frequency will it start slipping from there? By what factor will the answer change if the coin is almost at the rim?(Useg=π2ms−2).View SolutionQuestion 50
A merry-go-round usually consists of a central vertical pillar. At the top of it there are horizontal rods which can rotate about vertical axis. At the end of this horizontal rod there is a vertical rod fitted like an elbow joint . At lower end of each vertical rod, There is a horse on which the rider can sit. As the merry-go-round is set into rotation, these vertical rods move away from the axis by making some angle with the vertical. The figure above shows vertical section of a merry go round in which the 'initially vertical ' rods are inclined with the vertical at 37∘,during rotation. Calculate the frequency of revolution of merry go round.(Useg=π2ms−2andsin37∘=0.6)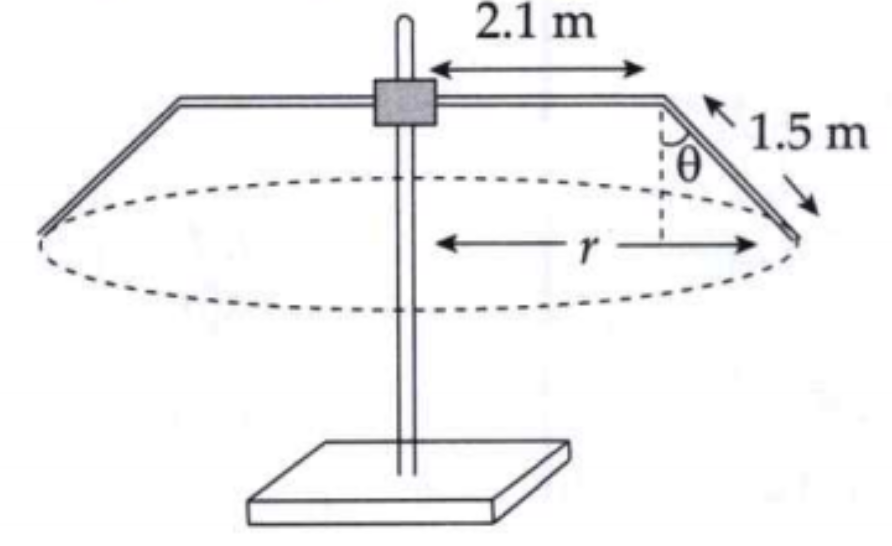
View SolutionQuestion 51
Semi - vertical angle of the conical section of a funnel is 37∘. There is a small ball kept inside the funnel. On rotating the funnel, the maximum speed that the ball can have in order to remain in the funnel is 2 m/s. Calculate inner radius of the brim of the funnel . Is there any limit upon the frequency of rotation ? How much is it ? Is it lower or upper limit ? Given a logical reasoning. (Use g = 10 m/s^2 and sin 37∘ =0.6)View SolutionQuestion 59
During a stunt a cyclist ( considered to be a particle is undertaking horizontal circles inside a cylindrical well of radius 6.05m. If the necessary friction coefficient is 0.5, how much minimum speed should the stunt artist maintain? Mass of the artist is 50kg. If she / he increases the speed by 20% how much will the force of friction be?(Useg=10ms2)View SolutionQuestion 63
Using the energy conservation, derive the expression for the minimum speeds at different locations along a vertical circular motion controlled by gravity. Also prove that the difference between the extreme tensions (or normal forces) depends only upon the weight of the object.View SolutionQuestion 66
A tiny stone of mass 20g is tied to a practically massless, inextensible, flexible string and whirled along vertical circles. Speed of the stone is 8m/s when the centripetal force is exactly equal to the force due to the tension. Calculate minimum and maximum kinetic energies of the stone during the entire circle. Let θ=00 be the angular position of the string, when the stone is at the lowermost position. Determine the angular position of the string when the force due to tension is numerically equal to weight of the stone. Take g = 10m/s2 and Length string = 1.8 mView SolutionQuestion 93
A fly wheel is a mechanical device specifically designed to efficiently store rotational energy. For a particular machine it is in the form of a uniform 20 kg disc of diameters 50 cm, able to rotate about its own axis. Calculate its kinetic energy when rotating at 1200 rpm. Use n =10.Calculate its moment of inertia, in case it is rotated about a tangent in its plane.View SolutionQuestion 97
A big dumb-bell is prepared by using a uniform rod of mass 60 g and length 20 cm. Two identical solid spheres of mass 50 g and radius 10 cm each are at the two ends of the rod. Calculate moment of inertia of the dumb-bell when rotated about an axis passing through its centre and perpendicular to the length.View SolutionQuestion 109
Two wheels of moment of inertia 4kgm2 rotate side by side of the rate of 120 r.p.m. and 240 r.p.m. respectively in the opposite direction. If now both the wheels are coupled by means of weightless shaft so that both the wheels now rotate with a common angular speed, find the new speed of rotation.View SolutionQuestion 110
A flywheel used to prepare earthenware pots is set into rotation at 100 rpm. It is in the form of a disc of mass 10 kg and radius 0.4 m. A lump of clay (to be taken equivalent to a particle) of mass 1.6 kg falls on it and adheres to it at a certain distance X from the centre. Calculate X if the wheel now rotates at 80rpm.View SolutionQuestion 111
A homogeneous rod XY of length 'L' and mass 'M' pivoted at the centre C such that it can rotate freely in vertical plane. Initially the rod is in the horizontal position .A blob of wax of same mass M as that of the rod falls vertically with the speed 'V' and the sticks to the rod midway between points 'C' and 'Y'. If the rod rotates with angular speed ω what will be angular speed in terms of V and L?View Solution