Illustrative Example from GK PUBLICATIONS PHYSICS (HINGLISH) WAVE OPTICS for Class 12
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| GK PUBLICATIONS PHYSICS (HINGLISH) | Illustrative Example |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
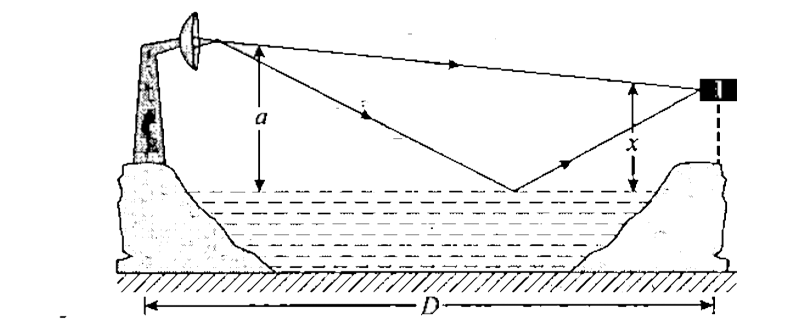
In figure-6.9, a microwave transmitter a height a above the water level of a wide lake transmits microwaves of wavelength λ towards a receiver on the opposite shore, a distance x above the water level. The microwaves reflecting from the water interface with the microwaves arriving directly from the transmitter. Assuming that the lake width D is much greater than a and x, that λ>>a, at what values of x is the signal at the receiver maximum?
 View Solution
View SolutionQuestion 8
In a YDSE setup sodium light of wavelength 5893Å is being used. The interference pattern is obtained on a screen which is located at a distance 1 m from the slit plane. In the interference pattern it is observed that 10th bright fringe is located at a distance of 12mm from the central maximum. Find the slit separation.View SolutionQuestion 10
In Young's experiment, interference bands are produced on the screen placed at 1.5 m from the two slits 0.15 mm apart and illuminated by light of wavelength 6599Å. Find (a) the fringe width and (b) the change in the fringe width if the screen is taken away from the slit by 50 cm.View SolutionQuestion 11
In Young's double slit experiment the slits are 0.5 mm apart and interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 8.835 mm from the second dark fringe from the centre of the fringe pattern. Find the wavelength of light used. View SolutionQuestion 14
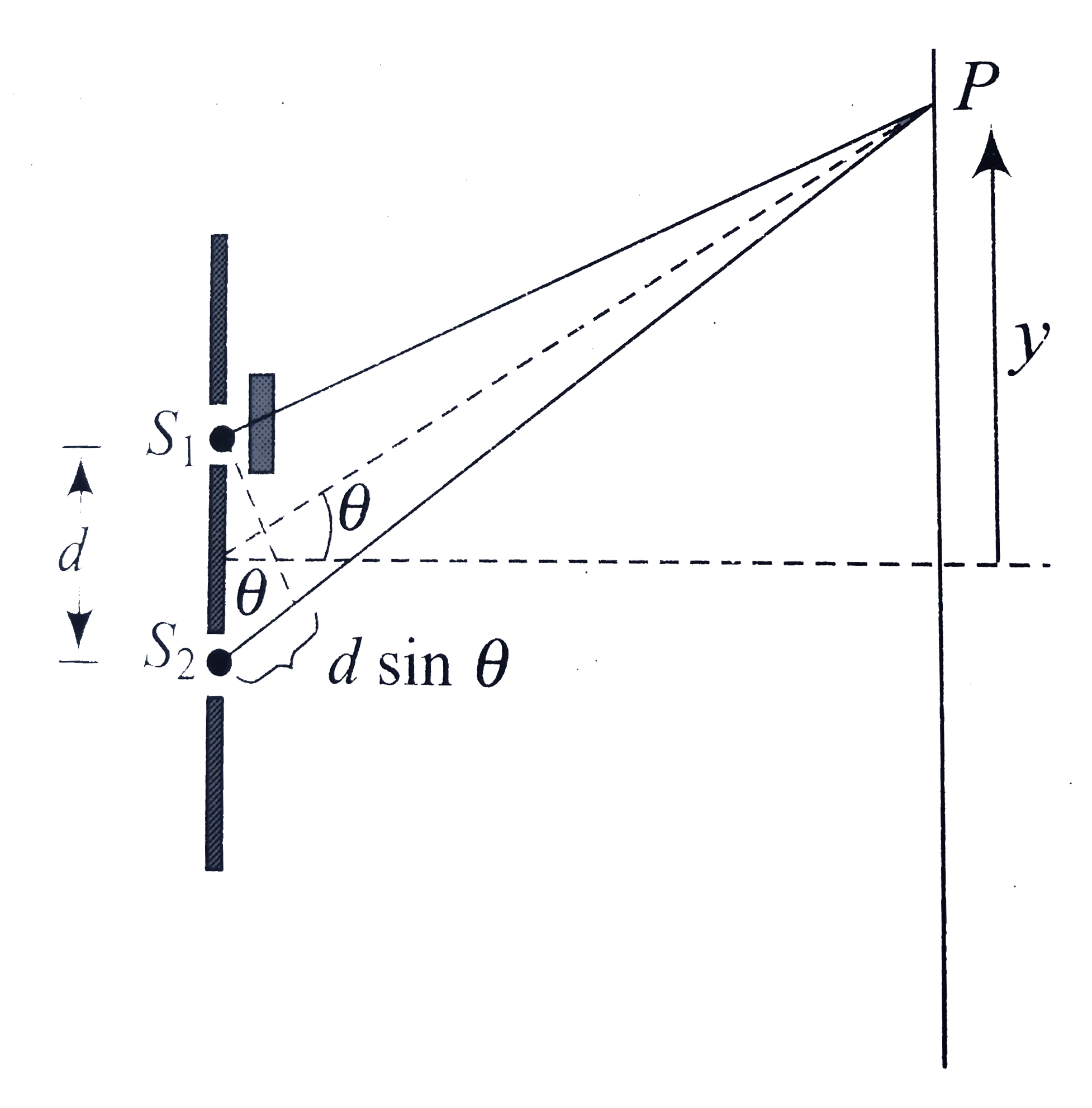
There are two coherent sources S1 and S2 which produce waves in same phase placed on Y axis at points (0, 2d) and (0, d) as shown in figure-6.23. A detector D is placed at origin which moves along X direction, find the number of maxima recorded by detector excluding points x = 0 and x=∞. Given that wavelength of light produced is 6200Å and separation between sources is 0.34 mm.
 View Solution
View SolutionQuestion 16
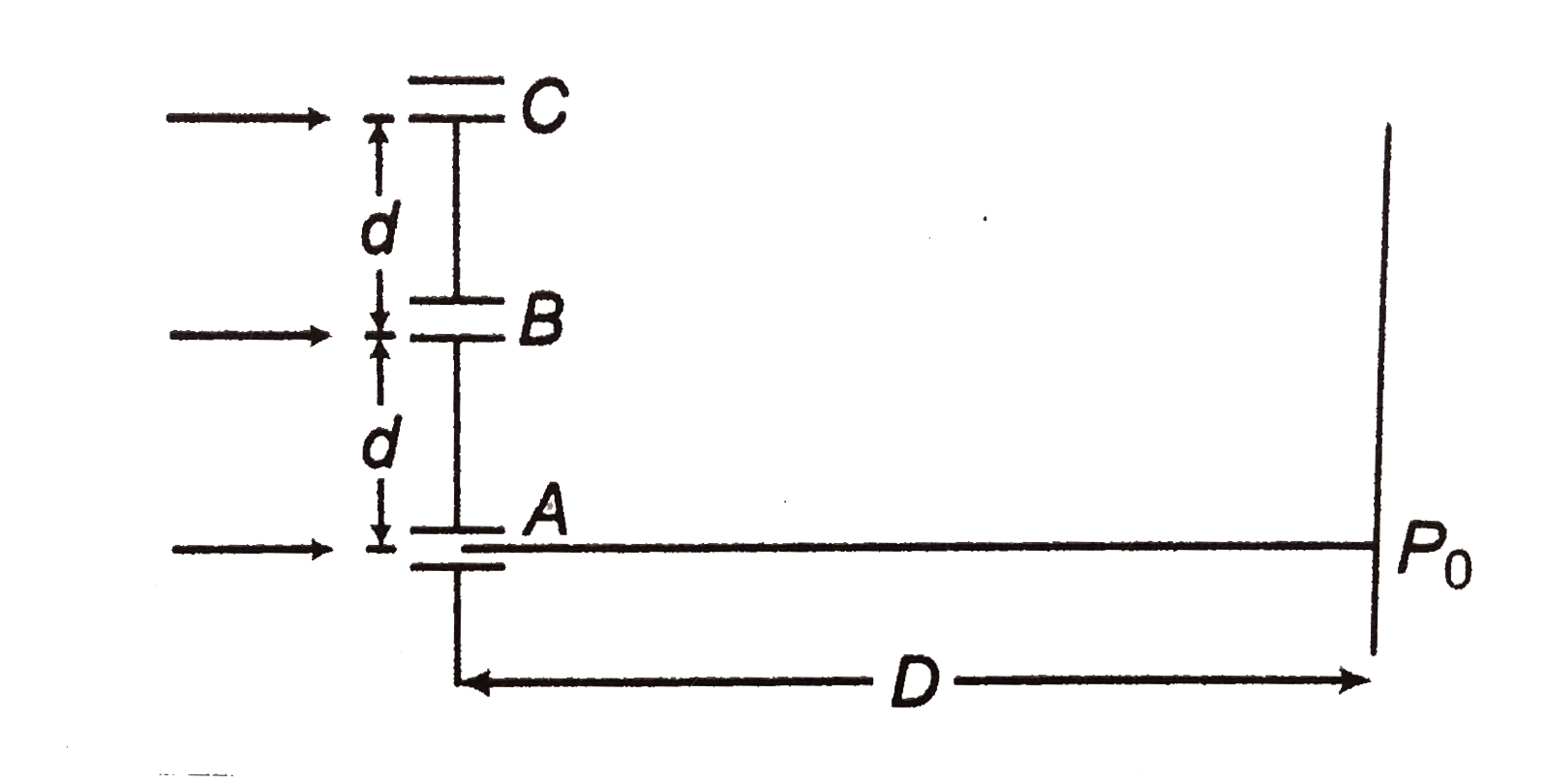
In YDSE, light of wavelength λ=5000Å is used, which emerges in phase from two slits distance d=3×10−7m apart. A transparent sheet of thickness t=1.5×10−7m, refractive index n=1.17, is placed over one of the slits. Where does the central maxima of the interference now appear from the center of the screen? (Find the value of y?)
 View Solution
View SolutionQuestion 18
Consider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
 View Solution
View SolutionQuestion 19
The two coherent sources of monochromatic light of wavelength λ are located at a separation λ. The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources. View SolutionQuestion 20
In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
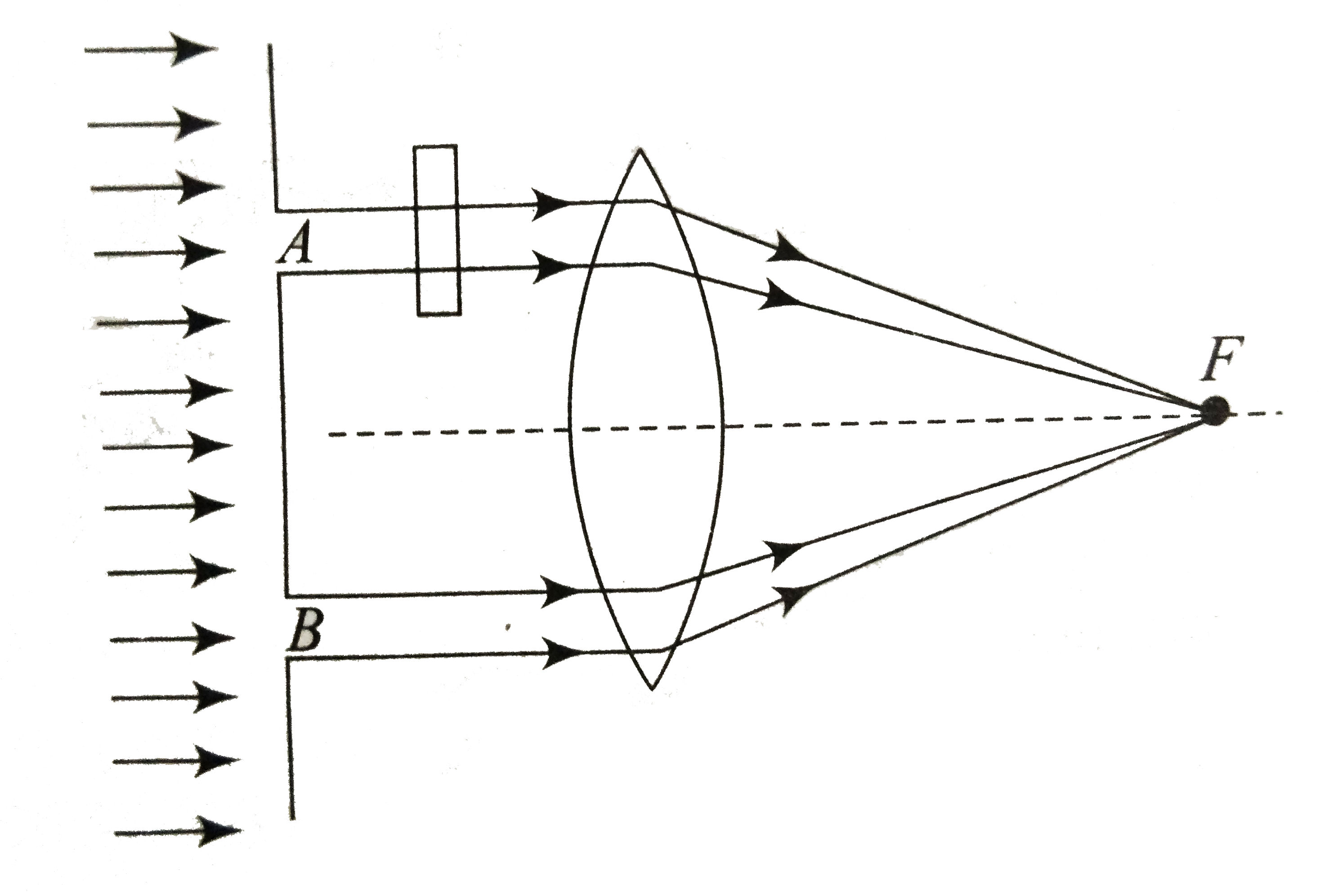 View Solution
View SolutionQuestion 21
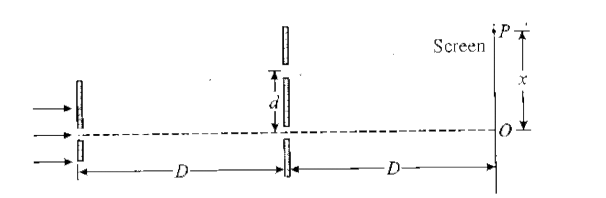
Consider the arrangement shown in figure-6.38. The distance D is large compared to the separation d between the slits.
(a) Find the minimum value of d so that there is a dark fringe at O.
(b) Suppose d has this value. Find the distance x at which the next bright fringe is formed.
(c ) Find the fringe width.
 View Solution
View SolutionQuestion 22
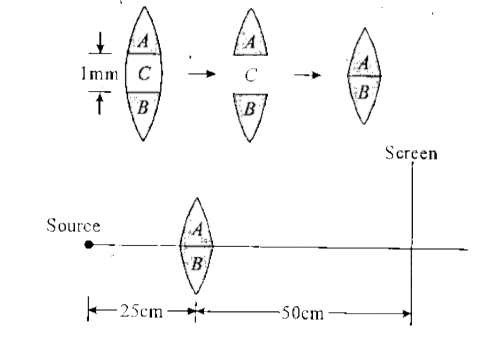
In Billet's Lens Arrangement, a convex lens of focal length 50 cm is cut along the diameter into two indentical halves Å and B and in the process a layer C of the lens thickness 1 mm is lost. Then the two halves A and B are put together to form a composite lens. Now, infront of this composite lens a source of light emitting wavelength λ=6000Å is placed at a distance of 25 cm as shown in the figure. Behind the lens there is a screen at a distance 50 cm from it. Find the fringe width fo the interference pattern obtained on the screen.
 View Solution
View SolutionQuestion 24
A glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
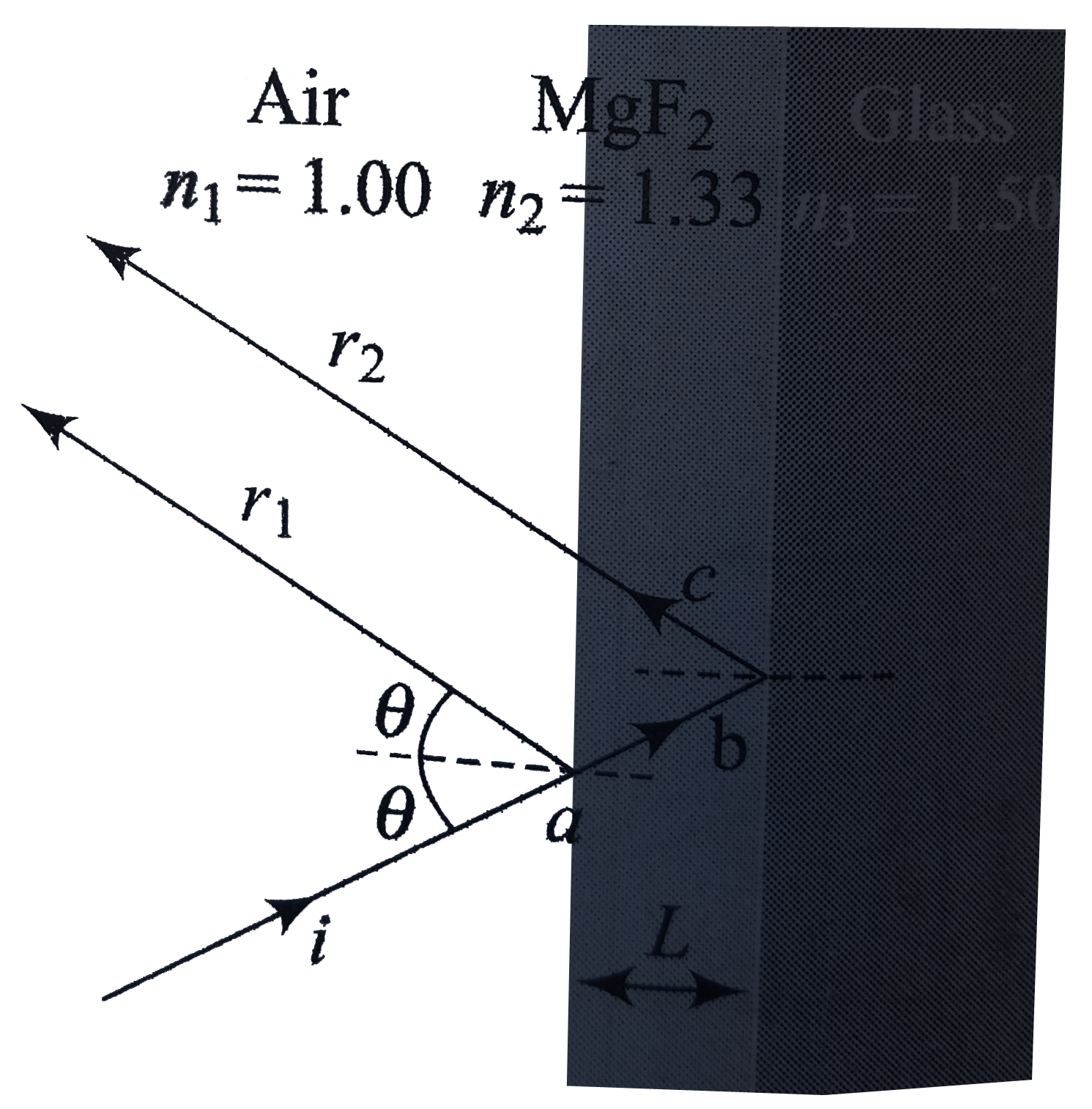 View Solution
View SolutionQuestion 29
Angular width of central maximum in the Fraunhoffer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength 6000Å. When the slit is illuminated by light of another wavelength, the angular width decreases by 30%. Calculate the wavelength of this light. The same decrease in the angular width of central maximum is obtained when the original apparatus is immersed in a liquid. Find the refractive index of the liquid.View SolutionQuestion 31
The axes of a polarizer and an analyzer are oriented at 30∘ to each other.
(a) If unpolarized light of intensity I0 is incident on them, what is the intensity of the transmitted light?
(b) Polarized light of intensity I0 is incident on this polarizer-analyzer system. If the amplitude of the light makes an angle of 30∘ with the axis of the polarizer, what is the intensity of the transmitted light? View SolutionQuestion 32
A beam of plane polarised light falls normally on a polariser (cross sectional area 3×10−4m2) which rotates about the axis of the ray with an angular velocity of 31.4rad/s. Find the energy of light passing through polariser per revolution and the intensity of emergent beam, if flux of energy of the incident ray is 10−3W.View SolutionQuestion 33
The axes of a polarizer and an analyzer are oriented at right angles to each other. A third Polaroid sheet is placed between them with its axis at 45∘ to the axes of the polarizer and analyzer.
(a) If unpolarized light of intensity I0 is incident on this system, what is the intensity of the transmitted light?
(b) What is the intensity of the transmitted light when the middle Polaroid sheet is removed? View Solution
 .
. .
.