MCQ (Level -I) from MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) Chapter 66 ATOMS, MOLECULES AND NUCLEI for Class 12
| Class 12 | PHYSICS |
| Chapter | ATOMS, MOLECULES AND NUCLEI |
| MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) | MCQ (Level -I) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 20
Electron in a hydrogen atom makes a transition from n1 to n2, where n1andn2 are principal quantum numbers of two states. Assuming Bohr's model to be valid, time period of clectron in the n1 state is found to be eight times the time period in the final state. Then possible values of principal quantum numbers n1andn2 are:View SolutionQuestion 61
Statement I: In a hydrogen atom, if the difference in the energy of the electron between the second orbit and third orbit is E, then the ionisation potential of hydrogen atom will be 3.2 E.
Statement II: The minimum energy (in eV) electrons must have for all the lines of all the series of H2 spectrum to appear when the H2 atoms are excited is 10.2 eV.View SolutionQuestion 66
When sunlight shines on the atmosphere, mass of CO2 at an altitude of 75 km undergo natural laser action. The energy levels involved in the action are shown in fig Population inversion occurs between levels E2andE1.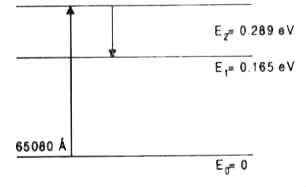
66. The wavelength of sunlight exciting the molecules in laser action isView SolutionQuestion 74
A nuclear reactor generates power at 50% efficiency, by fusion 92U235 into two canal fragments of 6Pd116 with the emission of two gamma rays and three neutrons. The average B.E. per particle of U235andPd116 is 7.2 MeV and 8.2 MeV respectively.
The energy released in one fission event isView SolutionQuestion 75
A nuclear reactor generates power at 50% efficiency, by fusion 92U235 into two canal fragments of 6Pd116 with the emission of two gamma rays and three neutrons. The average B.E. per particle of U235andPd116 is 7.2 MeV and 8.2 MeV respectively.
75. Amount of U235 consumed per hour to produce 1600 mega watt power isView SolutionQuestion 79
A high powered laser beam (λ=630nm) with a beam diameter of 0.1 m is aimed at the Moon, 3.8×108m distant. The beam spreads only because of diffraction, The angular location of the edge of the central diffraction disc is given by sinθ=1.22λd
where d is the diameter of the beam aperture. What is the diameter of the central diffraction disc on the Moon's surface ?View SolutionQuestion 98
He+ ions are excited to respective first excited states. Subsequently, H-atoms transfer their total excitation Energy to Het jons collisions). Assume that the Bohr model of atom is exactly valid.
The wavelength of light emitted in the visible region by He+ ions after collisions with H atoms isView SolutionQuestion 99
He+ ions are excited to respective first excited states. Subsequently, H-atoms transfer their total excitation Energy to Het jons collisions). Assume that the Bohr model of atom is exactly valid.
The ratio of the kinetic energy of the n= 2 electron for the H atom to that of He+ ion isView SolutionQuestion 100
When a particle is restricted to move along x-axis between x = 0 and x = 4, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends r = 0 and x= a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de-Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p2/2m. Thus, the energy of the particle can be denoted by a quantum number 'r' taking values 1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving in the line x=0 to x=a. Take h=6.6×10−34Jsande=1.6×10−19C.
The allowed energy for the particle for a particular value of n is proportional toView SolutionQuestion 101
When a particle is restricted to move along x-axis between x = 0 and x = 4, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends r = 0 and x= a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de-Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p2/2m. Thus, the energy of the particle can be denoted by a quantum number 'r' taking values 1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving in the line x=0 to x=a. Take h=6.6×10−34Jsande=1.6×10−19C.
If the mass of the particle is m=1.0×10−30 kg and a= 6.6 nm, the energy of the particle in its ground state is close toView SolutionQuestion 102
When a particle is restricted to move along x-axis between x = 0 and x = 4, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends r = 0 and x= a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de-Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p2/2m. Thus, the energy of the particle can be denoted by a quantum number 'r' taking values 1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving in the line x=0 to x=a. Take h=6.6×10−34Jsande=1.6×10−19C.
The speed of the particle that can take discrete values is proportional toView Solution


