Revision Test from MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) UNIFORM CIRCULAR MOTION for Class 12
| Class 12 | PHYSICS |
| Chapter | UNIFORM CIRCULAR MOTION |
| MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) | Revision Test |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
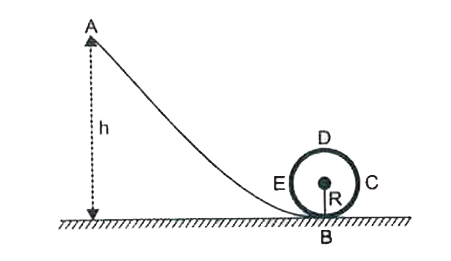
A particle Pis sliding down a frictionless hemispherical bowl. It passes the point at t=0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at i = 0 along the horizontal string AB with the speed y. Ift, tp and tq to be the respective time taken by P and to reach the point B.Then
Length of are ACBLength of chord AOBis equal to : View Solution
View SolutionQuestion 46
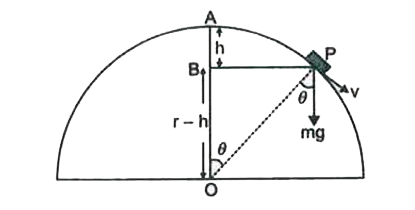
An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle a with the vertical, the maximum possible value of cis given by :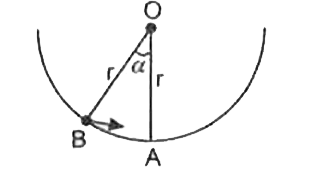 View Solution
View SolutionQuestion 47
A small body is placed on the top of smooth sphere of radius R. The sphere is imparted a constant acceleration a0 = ng in the horizontal direction. The body begins sliding down. Find the velocity of body relative to the sphere at the moment it just leaves the surface of sphere:View SolutionQuestion 48
A sleeve A can slide freely along a smooth rod bent to from a semi-circle of radius R. The system is rotated about the vertical diameter with a constant angular velocity . The value of angle which the radius vector R makes at the centre corresponding to steady position of the sleeve is :View SolutionQuestion 49
A small object of mass m = 0.3 kg starts sliding down from the top of a smooth sphere of radius R = Im. The sphere rotates with a constant angular velocity w = 6.0 rad.s- about the vertical axis passing through the centre. The centripetal force which tries to keep the body in contact at the point breaking off the surface of the sphereView SolutionQuestion 52
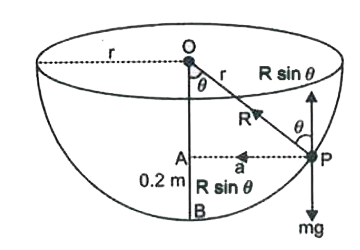
A smooth wire is bent into a vertical circle of radius a'. A bead of mass 'm' can slide smoothly on this circle. The loop is rotated about the vertical diameter with a constant angular speed of 'ω' rad. s−1. Bead is at rest with respect to the circular ring at a position Pas shown. the position is such that the radius of horizontal circle passing through P is half the radius of the loop. The value of ω is :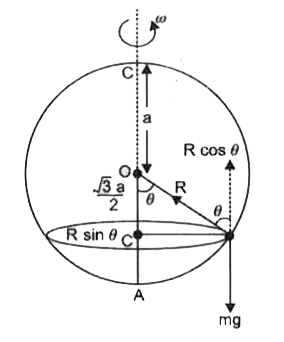 View Solution
View Solution