PRACTICE QUESTIONS (Single Correct Choice Type) from RESNICK AND HALLIDAY PHYSICS (HINGLISH) INTERFERENCE AND DIFFRACTION for Class 12
| Class 12 | PHYSICS |
| Chapter | INTERFERENCE AND DIFFRACTION |
| RESNICK AND HALLIDAY PHYSICS (HINGLISH) | PRACTICE QUESTIONS (Single Correct Choice Type) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
A parallel beam of light of intensity I is incident on a glass plate. 25% of light is reflected in any reflection by upper surface and 50% of light is reflected by any reflection from lower surface. Rest is refracted The ratio of maximum to minimum intensity in interference region of reflected rays is
View SolutionQuestion 8
Light passes successively through two polarimeters tubes each of length 0.29m. The first tube contains dextro rotatory solution of concentration 60kgm−3 and specific rotation 0.01radm2kg−1. The second tube contains laevo rotatory solution of concentration 30kg/m3 and specific rotation 0.02radm2kg−1. The net rotation produced is View SolutionQuestion 14
In Young's double-slit interference experiment a first screen with a single narrow slit is used in addition to the double-slit screen. An interference pattern is observed on the screen. What happens if the first screen is removed and light from an extended but monochromatic source, e.g.,yellow light from large sodium vapor lamp, is allowed to illuminate the double-slit screen directly?View SolutionQuestion 15
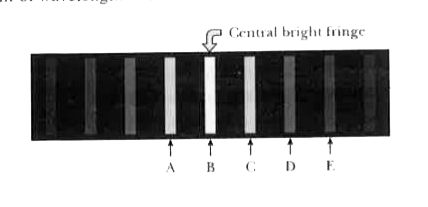
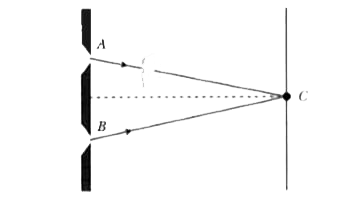
Two sources, in phase and a distance d apart, each emit a wave of wavelength l (as shown in the following figure). Which of the choices for the path difference Delta L = Delta P = S_(2)P - S_(1)P Delta L = L_(1)-L_(2) will always produce constructive interference at point P?
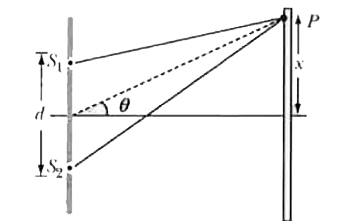View SolutionQuestion 17
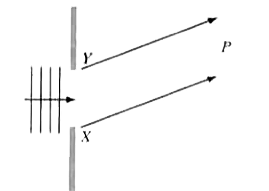
Light shining through two very narrow slits produces an interference maximum at point P when the entire apparatus is in air as shown in the following figure. For the interference maximum represented, light through the bottom slit travels one wavelength further than light through the top slit before reaching point P. If the entire apparatus is immersed in water, the angle θ to the interference maximum
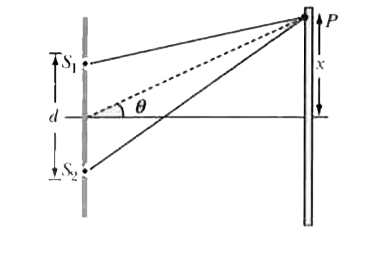View SolutionQuestion 21
In a Young's double-slit experiment, if the incident light consists of two wavelengths λ1 and λ2, the slit separation is d, and the distance between the slit and the screen is D, the maxima due to each wavelength will coincide at a distance from the central maxima, given byView SolutionQuestion 24
An interference pattern is formed on a screen by shining a planar wave on a double-slit arrangement. If we cover one slit with a glass plate, the phases of the two emerging waves will be different because the wavelength is shorter in glass than in air. If the phase difference is 180∘, how is the interference pattern altered?View SolutionQuestion 26
On introducing a thin sheet of mica (thickness 12×10−7 cm) in path of one of the interfering beams (λvacuum=600nm) in Young's double-slit experiment, the central fringe is shifted through a distance equal to the spacing between successive bright fringes. Calculate the refractive index of mica.View SolutionQuestion 27
A Young's double-slit experiment is conducted in water (n1) as shown in the following figure, and a glass plate of thickness t and refractive index n2 is placed in the path of S2. Wavelength of light in water is λ. Find the magnitude of the phase difference between waves coming from S1 and S2 at O.
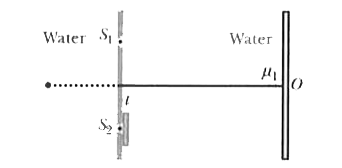View SolutionQuestion 31
Three coherent, equal intensity light rays arrive at a point Pon a screen to produce an interference minimum of zero intensity. If any two of the rays are blocked, the intensity of the light at P is I1. What is the intensity of the light at P if only one of the rays is blocked?View SolutionQuestion 36
_E01_026_Q01.png)
As shown in the right figure, a point light source is placed at distance 2f from a lens with focus length f. and a screen is placed at 4f from the lens. The lens is then cut at the middle into two equal portions: upper half and lower half. the upper half is moved upwards by a small distance d comparable to the light wavelength and the lower half is moved downwards by the same distance d. What is the light pattern on the screen?View SolutionQuestion 37
A fresnel biprism is used to form the inerference fringes. The distance between the source and the biprisim is 20 cm and that between the biprism and the screen is 80 cm. If A= 6563 A and the separation between the virtual sources is 3.6 mm, then the fringes width (in mm) is.View SolutionQuestion 39
Two radio station that are 250 m apart emit radio waveslength 100m. Point A is 400m from both station.Point B is 450m from both station. Point C is 400m from one station and 450 m from the other.The radio station emit radio waves in phase. Which of the following statement is true ?View SolutionQuestion 41
A thin oil film of refracting index 1.2 floats on the surface of water (μ=43). When a light of wavelength λ=9.6×10−7m falls normally on the film air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is Z×10−7m. Then find Z.View SolutionQuestion 61
_E01_041_Q01.png)
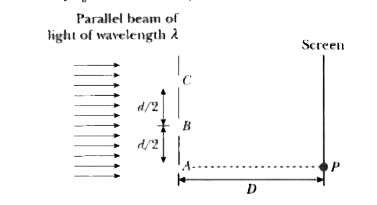
Light wavelength 650 nm is incident normally upon a glass plate the glass plate rests on top of second plate so that hey touch at one end and are separated by 0.0325 mm at the other end as shown in the figure. Which range of values contains the horizontal separation between adjacent bright fringes?View SolutionQuestion 62
Two glass plates, each with an index of refraction of 1.55, are separated by a small distance D. The space between the plates is filled with water (n = 1.33) as shown. For which one of the following conditions will the reflected light appear green?
Note: The wavelength of green light is 460 nm in vacuum.
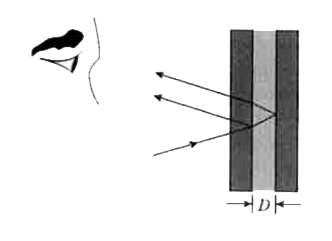View SolutionQuestion 63
Light of 600.0 nm is incident upon a single slit. The resulting diffraction pattern is observed on a screen that is 0.50 m from the slit. The distance between the first and third minima of the diffraction pattern is 0.80 mm. Which range of values listed below contains the width of the slit?View SolutionQuestion 64
A spy satellite is in orbit at a distance of 1.0×106 m above the ground. It carries a telescope that can resolve the two rails of a railroad track that are 1.4 m apart using light of wavelength 600 nm. Which one of the following statements best describes the diameter of the lens in the telescope?View SolutionQuestion 71
White light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(gtb) from the slits. At a point on the screen directly in front of one of the slits, certain wavelength are missing. Some of these missing wavelength areView SolutionQuestion 94
Angular width of central maxima in the Fraunhofer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength 6000Å. When the slit is illuminated by light of another wavelength, the angular width decreases by 30%. The wavelength of this light will beView SolutionQuestion 95
Angular width of central maximum in the Fraunhoffer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength 6000Å. When the slit is illuminated by light of another wavelength, the angular width decreases by 30%. Calculate the wavelength of this light. The same decrease in the angular width of central maximum is obtained when the original apparatus is immersed in a liquid. Find the refractive index of the liquid.View SolutionQuestion 96
An initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
31. The initial shape of the wavefront of the beam is View SolutionQuestion 97
An intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The speed of light in the medium is View SolutionQuestion 98
An initially parallel cylindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
30 . At the beam enters the medium, it willView SolutionQuestion 99
When waves from two herent sources, having amplitudes a and b superimpose, the amplitude R of the resultant wave is given by R=√a2+b2+2abcosϕ where ϕ is the constant phase angle between the two waves. The resultant intensity I is directly proportional to the square of the amplitude of the resultant wave, i.e., I∝R2,
i.e., I∝(a2+b2+2abcosϕ)
For constructive interference, ϕ=2nπ,
Imax=(a+b)2
For destructive interference, ϕ=(2n−1)π
Imin=(a−b)2
If I1,I2 are intensities of light from two slits of widths ω1 and ω2, then I1I2=ω1ω2=a2b2
Light waves from two coherent sources of intensity ratio 81:1 produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of amplitude of two sources is View SolutionQuestion 100
When waves from two herent sources, having amplitudes a and b superimpose, the amplitude R of the resultant wave is given by R=√a2+b2+2abcosϕ where ϕ is the constant phase angle between the two waves. The resultant intensity I is directly proportional to the square of the amplitude of the resultant wave, i.e., I∝R2,
i.e., I∝(a2+b2+2abcosϕ)
For constructive interference, ϕ=2nπ,
Imax=(a+b)2
For destructive interference, ϕ=(2n−1)π
Imin=(a−b)2
If I1,I2 are intensities of light from two slits of widths ω1 and ω2, then I1I2=ω1ω2=a2b2
Light waves from two coherent sources of intensity ratio 81:1 produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of slit widths of the two sources is View SolutionQuestion 101
When waves from two herent sources, having amplitudes a and b superimpose, the amplitude R of the resultant wave is given by R=√a2+b2+2abcosϕ where ϕ is the constant phase angle between the two waves. The resultant intensity I is directly proportional to the square of the amplitude of the resultant wave, i.e., I∝R2,
i.e., I∝(a2+b2+2abcosϕ)
For constructive interference, ϕ=2nπ,
Imax=(a+b)2
For destructive interference, ϕ=(2n−1)π
Imin=(a−b)2
If I1,I2 are intensities of light from two slits of widths ω1 and ω2, then I1I2=ω1ω2=a2b2
Light waves from two coherent sources of intensity ratio 81:1 produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of amplitude of two sources is View SolutionQuestion 102
When waves from two coherent source of amplitudes a and b superimpose , the amplitude R of the resultant wave is given by R = √a2+b2+2abcosϕ.
where ϕ is the constant phase angle between the two waves. The resultant intensity I is directly proportional to the square of the amplitude of the resultant wave i.e I∝R2 i.e,
I∝(a2+b2+2abcosϕ)
For constructive interference ,
ϕ=2nπ and Imax=(a+b)2
For destructive interference ,
ϕ=(2n−1)πandImin=(a−b)2
If I1I2 are intensities from two slits of width w1andw2 then
I1I2=w1w2=a2b2
Light waves from two coherent sources of intensity ratio 81 : 1 produce interference. With the help of the passage choose the most appropriate alternative for each of the following questions
If two slits in Young's experiment have width ratio 1:4 the ratio of maximum and minimum intensity in the interference pattern would be View SolutionQuestion 103
When waves from two herent sources, having amplitudes a and b superimpose, the amplitude R of the resultant wave is given by R=√a2+b2+2abcosϕ where ϕ is the constant phase angle between the two waves. The resultant intensity I is directly proportional to the square of the amplitude of the resultant wave, i.e., I∝R2,
i.e., I∝(a2+b2+2abcosϕ)
For constructive interference, ϕ=2nπ,
Imax=(a+b)2
For destructive interference, ϕ=(2n−1)π
Imin=(a−b)2
If I1,I2 are intensities of light from two slits of widths ω1 and ω2, then I1I2=ω1ω2=a2b2
Light waves from two coherent sources of intensity ratio 81:1 produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of amplitude of two sources is View SolutionQuestion 104
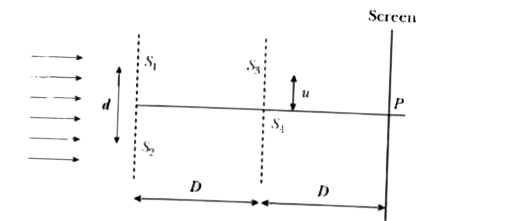
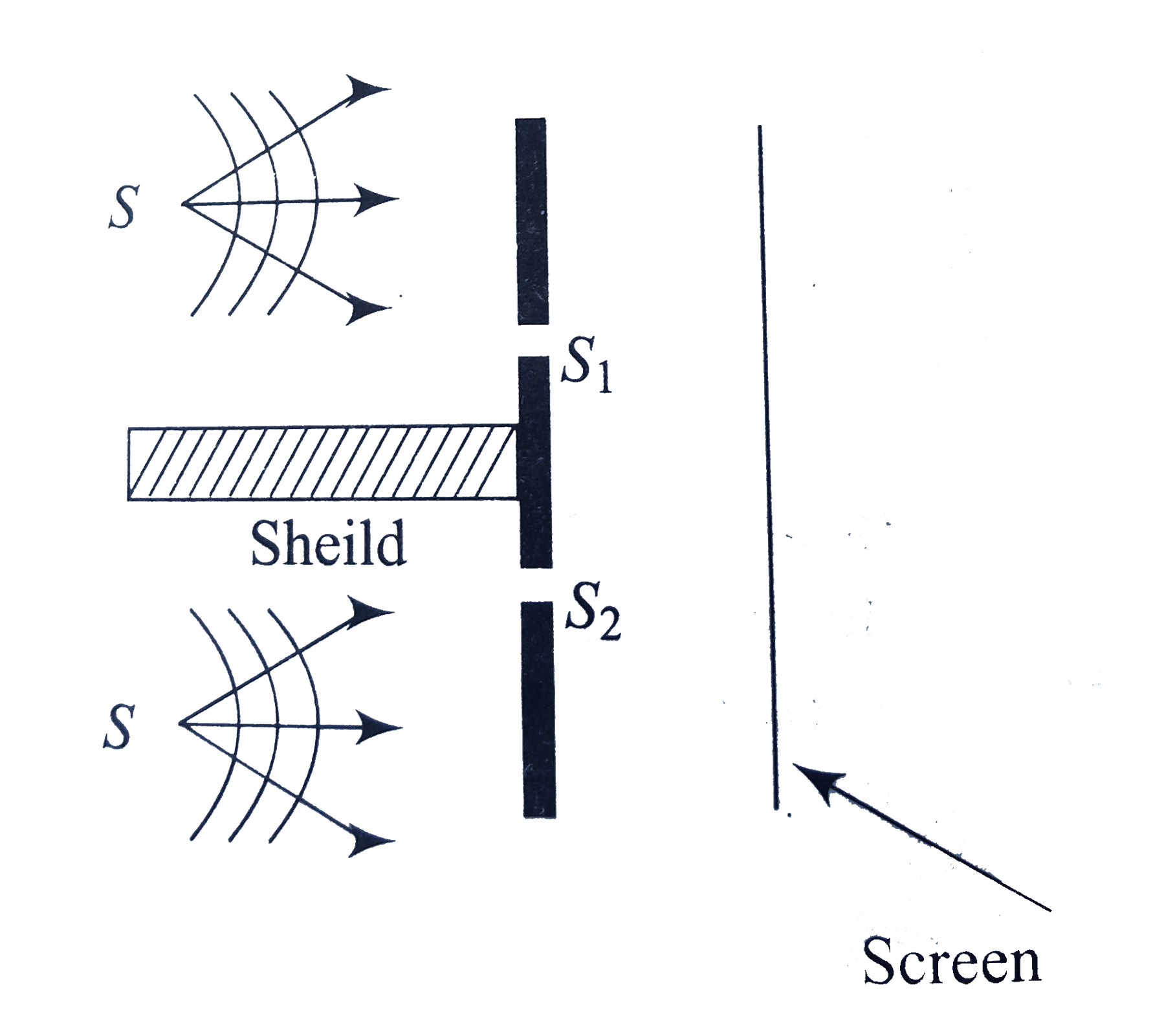
Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
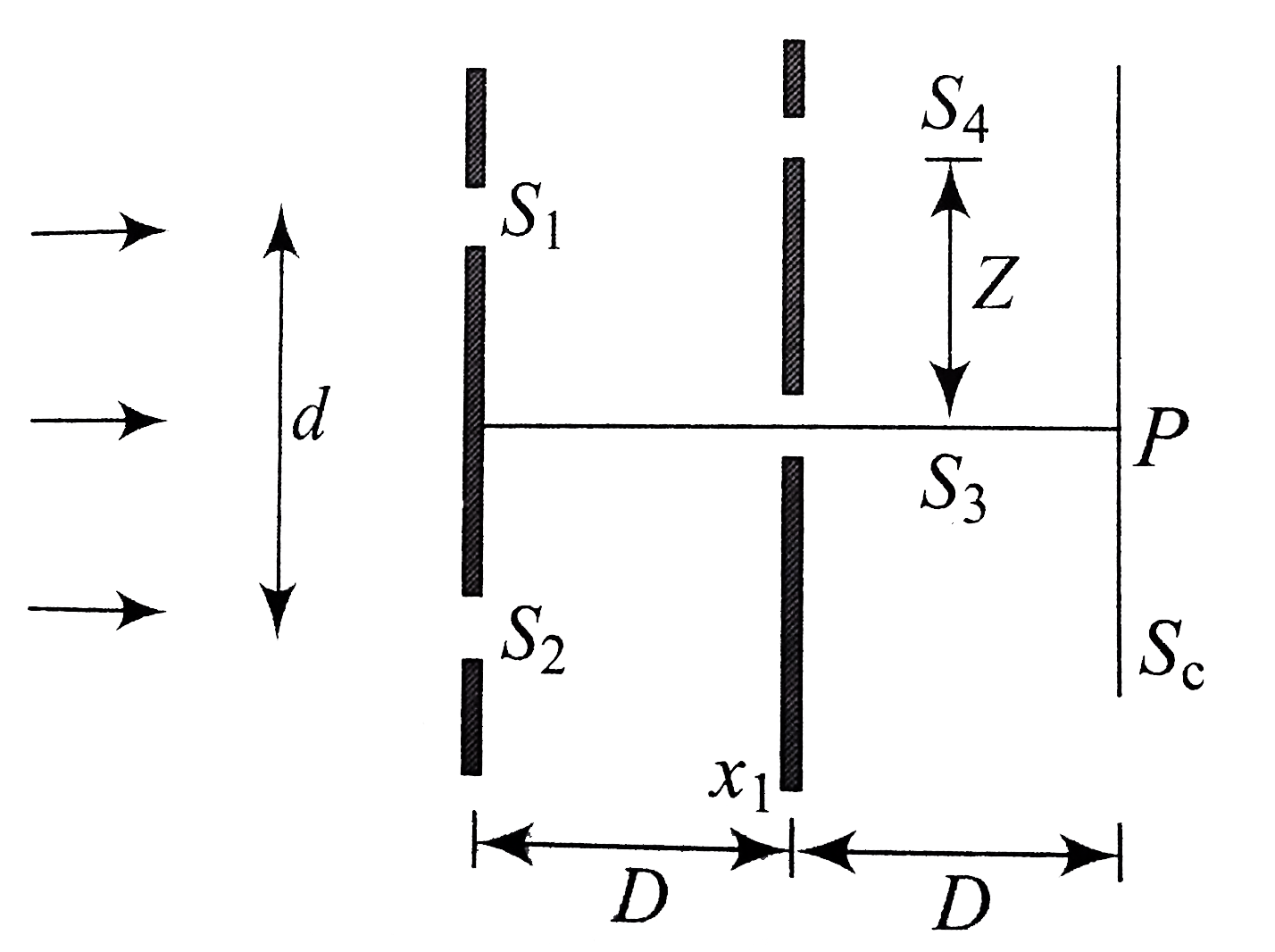
If z=λD2dView SolutionQuestion 105
Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
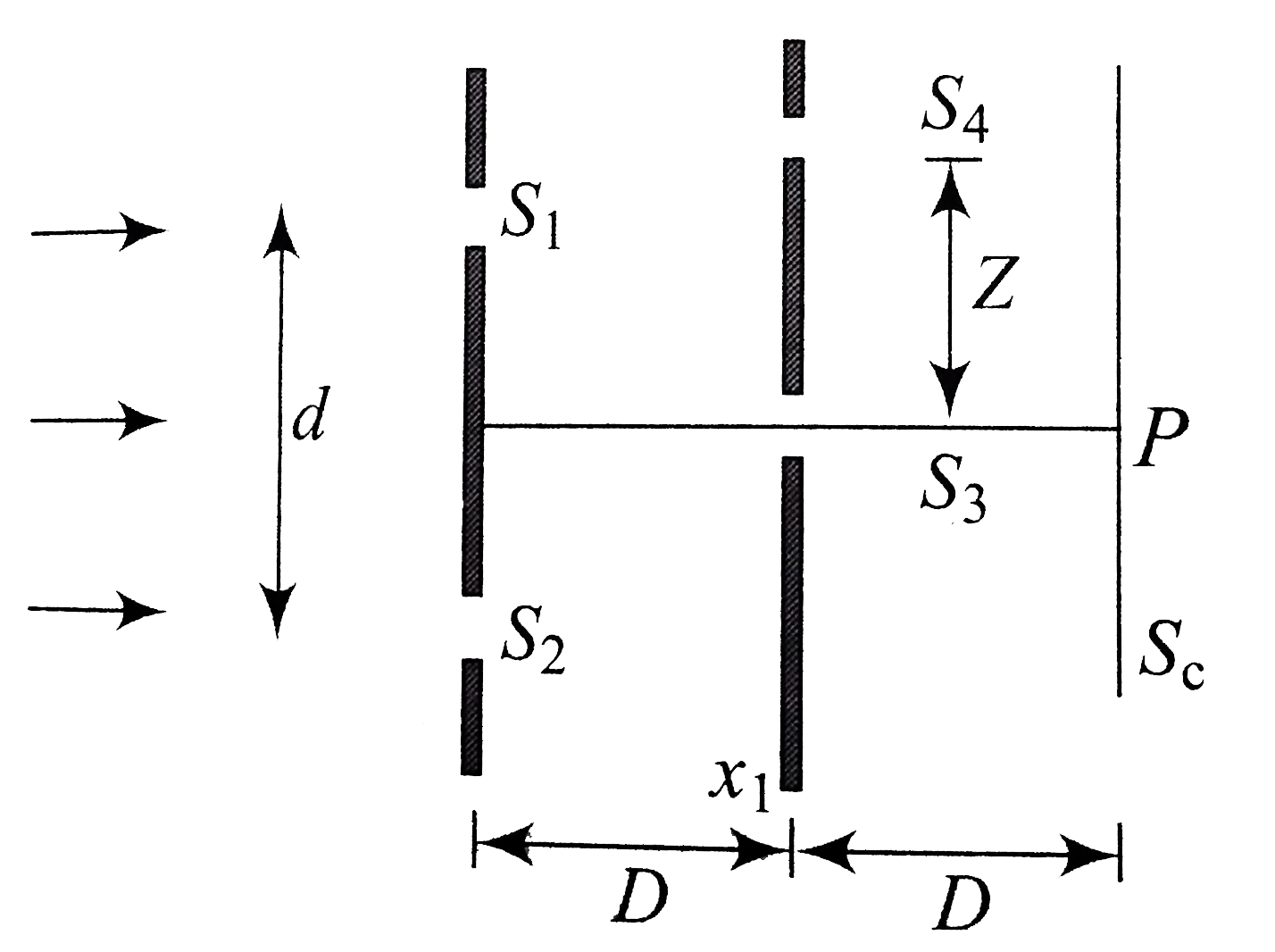
If z=λDdView SolutionQuestion 106
Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
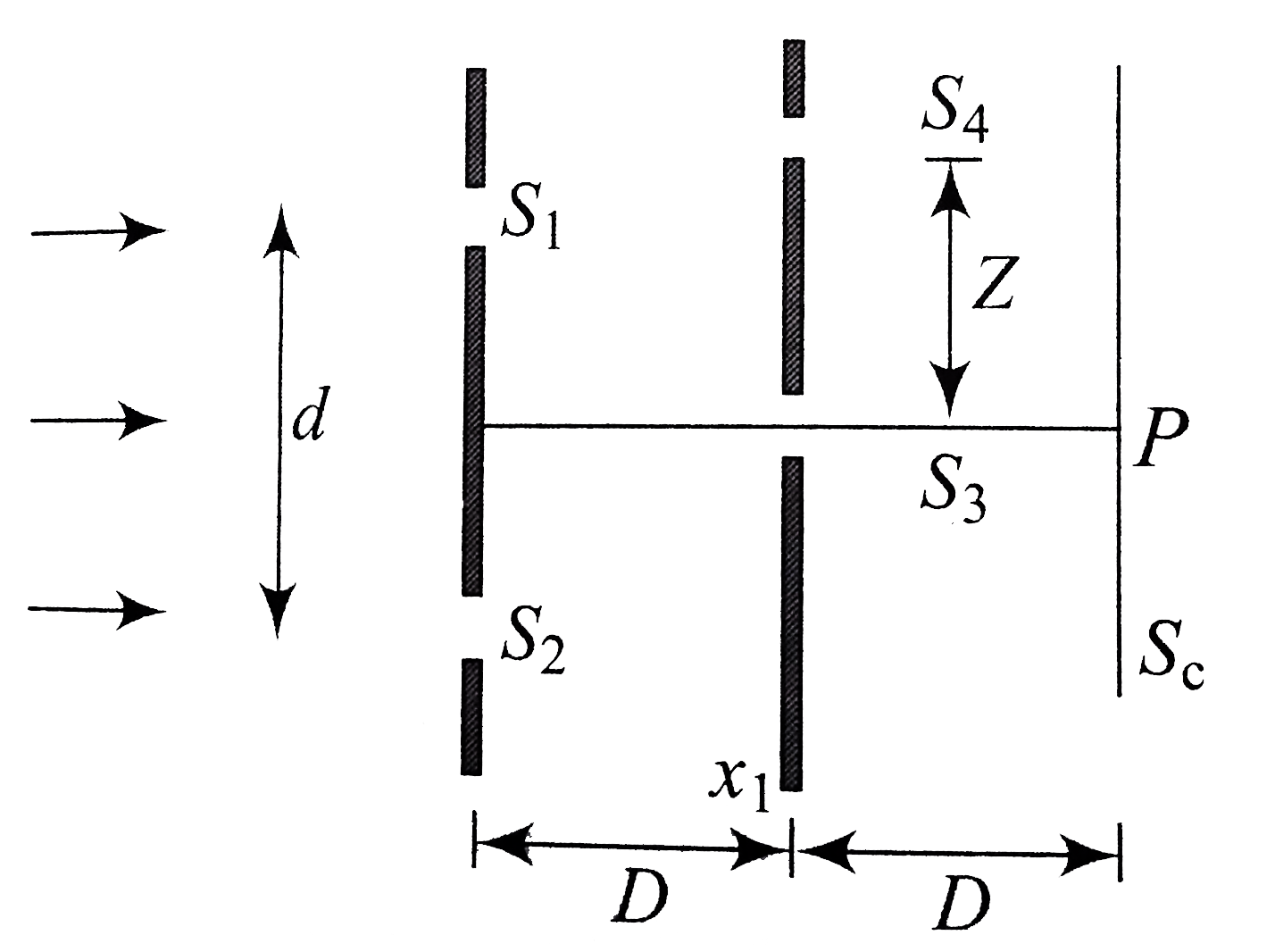
If z=λD4dView SolutionQuestion 107
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic λ. Behind the lens, a screen is located at a distance L front it.
Find the fringe width for the pattern obtained under given arrangement on the screen.View SolutionQuestion 108
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic λ. Behind the lens, a screen is located at a distance L front it.
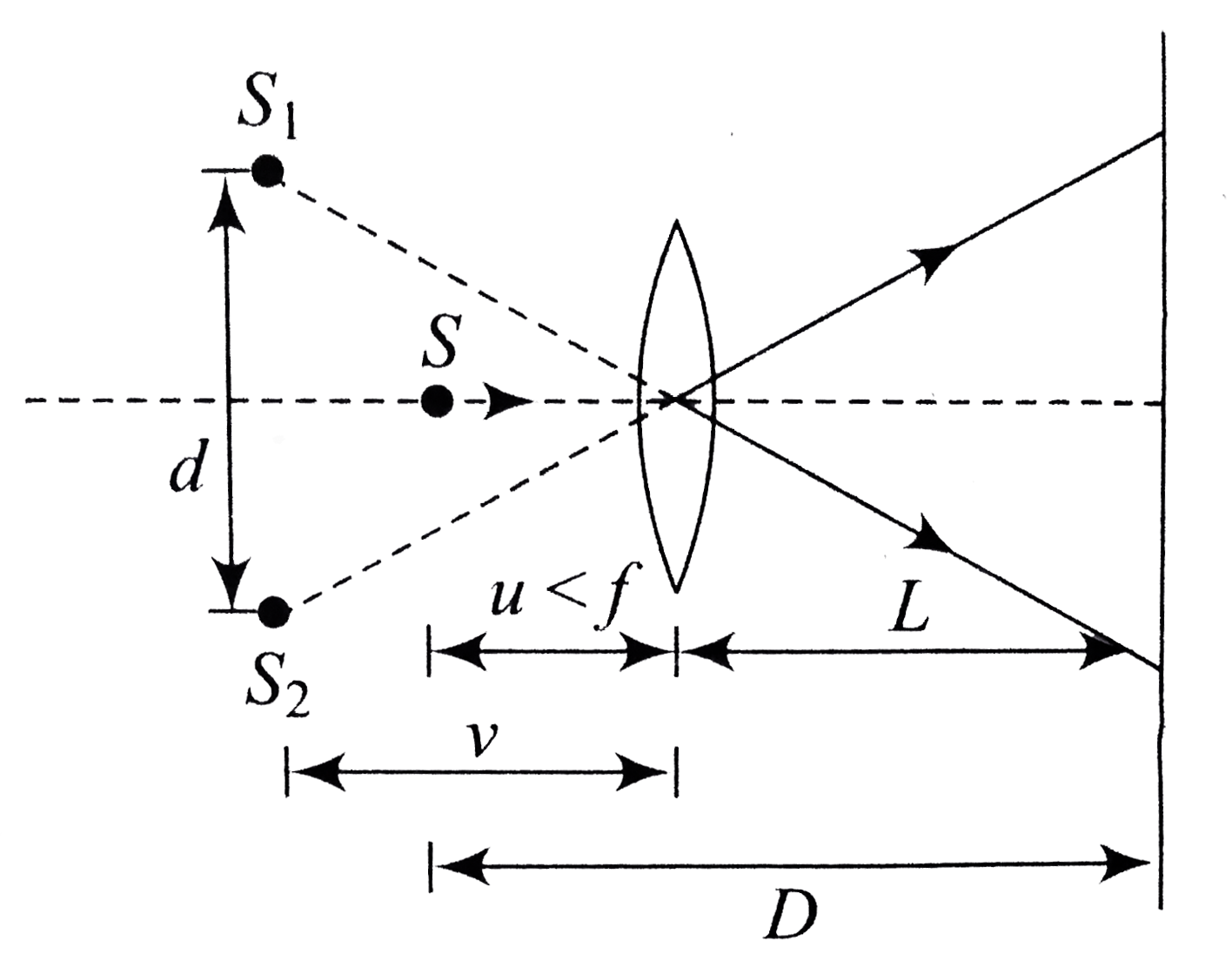
The expression for the number of visible maxima which are obtained through above said arrangement will turn out to beView SolutionQuestion 109
In a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:
If a liquid of refractive index n is filled between the screen and slits, what is the phase difference?View SolutionQuestion 110
In a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:
If a liquid is filled between the slit and the source S, what is the phase difference?View SolutionQuestion 111
Match the statements in Column I labeled as (a), (b), (c), and (d) with those in Column II labeled as (p), (q). (c), and (s). Any given statement in Column I can have correct matching with one or more statements in Column II.
Match the property with the concept it is based on.
View SolutionQuestion 112
Match the statements in Column I labeled as (a), (b), (c), and (d) with those in Column II labeled as (p), (q). (c), and (s). Any given statement in Column I can have correct matching with one or more statements in Column II.
Match the observation given in Column I with the experiments given in Column II.
View SolutionQuestion 113
Interference is an important property of light. In the given table, Column I shows the properties of interfering waves, Column II shows the phase difference, and Column III shows the path difference between two interfering waves
What are the conditions for constructive interference?View SolutionQuestion 114
Interference is an important property of light. In the given table, Column I shows the properties of interfering waves, Column II shows the phase difference, and Column III shows the path difference between two interfering waves
What are the conditions for destructive interference?View SolutionQuestion 115
Interference is an important property of light. In the given table, Column I shows the properties of interfering waves, Column II shows the phase difference, and Column III shows the path difference between two interfering waves
What are the conditions for sustained interference?View SolutionQuestion 116
The amplitudes of two coherent waves are vector quanti- ties. In the given table, Column I shows the phase differ ence between two coherent waves, Column II shows the path difference between them and Column III shows their resultant amplitudes.
When is the phasor diagram at primary maxima?View SolutionQuestion 118
The amplitudes of two coherent waves are vector quanti- ties. In the given table, Column I shows the phase differ ence between two coherent waves, Column II shows the path difference between them and Column III shows their resultant amplitudes.
When is the phasor diagram at secondary maxima?View SolutionQuestion 123
A thin glass plate of thickness t and refractive index μ is between screen &one of the slits in young's experiment.if the intensity at the center of the screen is I ,was the intensity at the same point prior to the introduction of the sheet.
(b) One slit of a young's experiment is covered by a glass plate (μ1=1.4) and the other by another glass plate (μ2=1.7) of the same thickness. The point of central maxima of the screen,before the plates were introduced is now occupied by the third bright fringe.Find the thicknes of the thickness of the plates.the wavelength of light used in 4000Å.View SolutionQuestion 124
In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
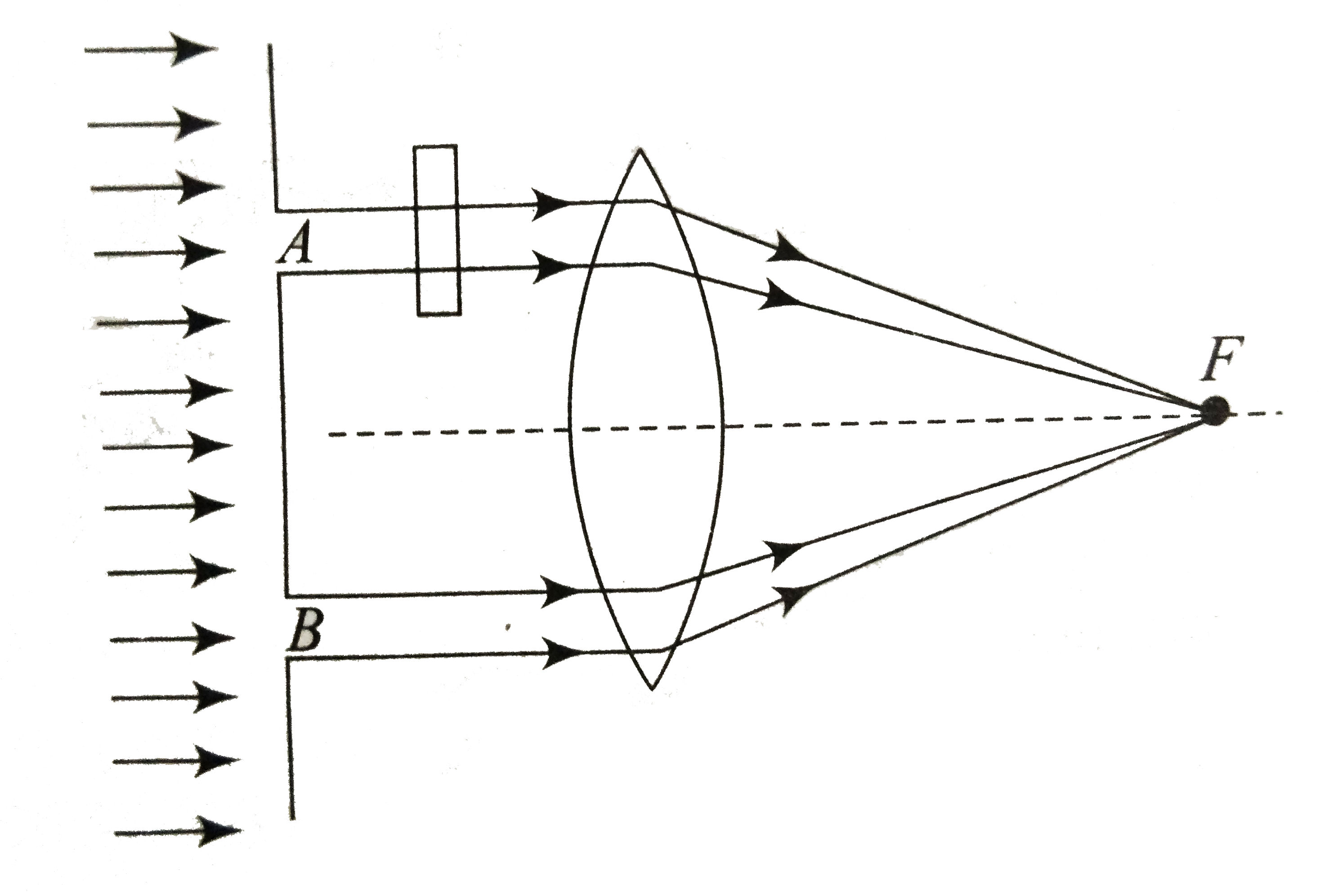View Solution
_E01_080_Q01.png)
