PRACTICE QUESTIONS (Linked Comprehension) from RESNICK AND HALLIDAY PHYSICS Chapter 22 INTERFERENCE AND DIFFRACTION for Class 12

Class 12	PHYSICS
Chapter	INTERFERENCE AND DIFFRACTION
RESNICK AND HALLIDAY PHYSICS	PRACTICE QUESTIONS (Linked Comprehension)
Medium	English
Academic Year	2023-2024

Question 1
The figure shows the interference pattern obtained in a double-slit experiment using light of wavelength 600 nm.

Which fringe is the same distance from both slits?View Solution
Question 2

The figure shows the interfernece pattern obtained in double slit experiment using light of wavelength 600 nm.
Q. The third order bright fringe is View Solution
Question 3
The figure shows the interference pattern obtained in a double-slit experiment using light of wavelength 600 nm.

Which fringe is 300 nm closer to one slit than to the other?View Solution
Question 4
The figure shows the interference pattern obtained in a double-slit experiment using light of wavelength 600 nm.

Which fringe results from a phase difference of $4 π$ ?View Solution
Question 5
Angular width of central maxima in the Fraunhofer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength $6000 Å$ . When the slit is illuminated by light of another wavelength, the angular width decreases by 30%. The wavelength of this light will be View Solution
Question 6
Angular width of central maximum in the Fraunhoffer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength $6000 Å$ . When the slit is illuminated by light of another wavelength, the angular width decreases by $30 %$ . Calculate the wavelength of this light. The same decrease in the angular width of central maximum is obtained when the original apparatus is immersed in a liquid. Find the refractive index of the liquid.View Solution
Question 7
An initially parallel cylindrical beam travels in a medium of refractive index $μ (I) = μ_{0} + μ_{2} I$ , where $μ_{0}$ and $μ_{2}$ are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
31. The initial shape of the wavefront of the beam is View Solution
Question 8
An intially parallel cyclindrical beam travels in a medium of refractive index $μ (I) = μ_{0} + μ_{2} I$ , where $μ_{0}$ and $μ_{2}$ are positive constants and $I$ is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The speed of light in the medium is View Solution
Question 9
An initially parallel cylindrical beam travels in a medium of refractive index $μ (I) = μ_{0} + μ_{2} I$ , where $μ_{0}$ and $μ_{2}$ are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
30 . At the beam enters the medium, it will View Solution
Question 10
When waves from two herent sources, having amplitudes $a$ and $b$ superimpose, the amplitude $R$ of the resultant wave is given by $R = \sqrt{a^{2} + b^{2} + 2 a b cos ϕ}$ where $ϕ$ is the constant phase angle between the two waves. The resultant intensity $I$ is directly proportional to the square of the amplitude of the resultant wave, i.e., $I \propto R^{2}$ ,
i.e., $I \propto (a^{2} + b^{2} + 2 a b cos ϕ)$
For constructive interference, $ϕ = 2 n π$ ,
$I_{max} = {(a + b)}^{2}$
For destructive interference, $ϕ = (2 n - 1) π$
$I_{min} = {(a - b)}^{2}$
If $I_{1}, I_{2}$ are intensities of light from two slits of widths $ω_{1}$ and $ω_{2}$ , then $\frac{I_{1}}{I_{2}} = \frac{ω_{1}}{ω_{2}} = \frac{a^{2}}{b^{2}}$
Light waves from two coherent sources of intensity ratio $81 : 1$ produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of amplitude of two sources is View Solution
Question 11
When waves from two herent sources, having amplitudes $a$ and $b$ superimpose, the amplitude $R$ of the resultant wave is given by $R = \sqrt{a^{2} + b^{2} + 2 a b cos ϕ}$ where $ϕ$ is the constant phase angle between the two waves. The resultant intensity $I$ is directly proportional to the square of the amplitude of the resultant wave, i.e., $I \propto R^{2}$ ,
i.e., $I \propto (a^{2} + b^{2} + 2 a b cos ϕ)$
For constructive interference, $ϕ = 2 n π$ ,
$I_{max} = {(a + b)}^{2}$
For destructive interference, $ϕ = (2 n - 1) π$
$I_{min} = {(a - b)}^{2}$
If $I_{1}, I_{2}$ are intensities of light from two slits of widths $ω_{1}$ and $ω_{2}$ , then $\frac{I_{1}}{I_{2}} = \frac{ω_{1}}{ω_{2}} = \frac{a^{2}}{b^{2}}$
Light waves from two coherent sources of intensity ratio $81 : 1$ produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of slit widths of the two sources is View Solution
Question 12
When waves from two herent sources, having amplitudes $a$ and $b$ superimpose, the amplitude $R$ of the resultant wave is given by $R = \sqrt{a^{2} + b^{2} + 2 a b cos ϕ}$ where $ϕ$ is the constant phase angle between the two waves. The resultant intensity $I$ is directly proportional to the square of the amplitude of the resultant wave, i.e., $I \propto R^{2}$ ,
i.e., $I \propto (a^{2} + b^{2} + 2 a b cos ϕ)$
For constructive interference, $ϕ = 2 n π$ ,
$I_{max} = {(a + b)}^{2}$
For destructive interference, $ϕ = (2 n - 1) π$
$I_{min} = {(a - b)}^{2}$
If $I_{1}, I_{2}$ are intensities of light from two slits of widths $ω_{1}$ and $ω_{2}$ , then $\frac{I_{1}}{I_{2}} = \frac{ω_{1}}{ω_{2}} = \frac{a^{2}}{b^{2}}$
Light waves from two coherent sources of intensity ratio $81 : 1$ produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of amplitude of two sources is View Solution
Question 13
When waves from two coherent source of amplitudes a and b superimpose , the amplitude R of the resultant wave is given by R = $\sqrt{a^{2} + b^{2} + 2 a b cos ϕ} .$
where $ϕ$ is the constant phase angle between the two waves. The resultant intensity I is directly proportional to the square of the amplitude of the resultant wave i.e $I \propto R^{2}$ i.e,
$I \propto (a^{2} + b^{2} + 2 a b cos ϕ)$
For constructive interference ,
$ϕ = 2 n π and I_{max} = {(a + b)}^{2}$
For destructive interference ,
$ϕ = (2 n - 1) π and I_{min} = {(a - b)}^{2}$
If $I_{1} I_{2}$ are intensities from two slits of width $w_{1} and w_{2}$ then
$\frac{I_{1}}{I_{2}} = \frac{w_{1}}{w_{2}} = \frac{a^{2}}{b^{2}}$
Light waves from two coherent sources of intensity ratio 81 : 1 produce interference. With the help of the passage choose the most appropriate alternative for each of the following questions
If two slits in Young's experiment have width ratio 1:4 the ratio of maximum and minimum intensity in the interference pattern would be View Solution
Question 14
When waves from two herent sources, having amplitudes $a$ and $b$ superimpose, the amplitude $R$ of the resultant wave is given by $R = \sqrt{a^{2} + b^{2} + 2 a b cos ϕ}$ where $ϕ$ is the constant phase angle between the two waves. The resultant intensity $I$ is directly proportional to the square of the amplitude of the resultant wave, i.e., $I \propto R^{2}$ ,
i.e., $I \propto (a^{2} + b^{2} + 2 a b cos ϕ)$
For constructive interference, $ϕ = 2 n π$ ,
$I_{max} = {(a + b)}^{2}$
For destructive interference, $ϕ = (2 n - 1) π$
$I_{min} = {(a - b)}^{2}$
If $I_{1}, I_{2}$ are intensities of light from two slits of widths $ω_{1}$ and $ω_{2}$ , then $\frac{I_{1}}{I_{2}} = \frac{ω_{1}}{ω_{2}} = \frac{a^{2}}{b^{2}}$
Light waves from two coherent sources of intensity ratio $81 : 1$ produce interference. With the help of the passsage given above, choose the most appropriate alternative for each of the following questions :
The ratio of amplitude of two sources is View Solution
Question 15
Consider the situation shown in fig. The two slits $S_{1}$ and $S_{2}$ placed symmetrically around the central line are illuminated by monochromatic light of wavelength $λ$ . The separation between the slit is d. The ligth transmitted by the slits falls on a screen $S_{0}$ placed at a distance D form the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance z from $S_{3}$ Another screen $S_{c}$ is placed a further distance D away from $S_{c}$ Find the ratio of the maximum to minimum intensity observed on $S_{c}$

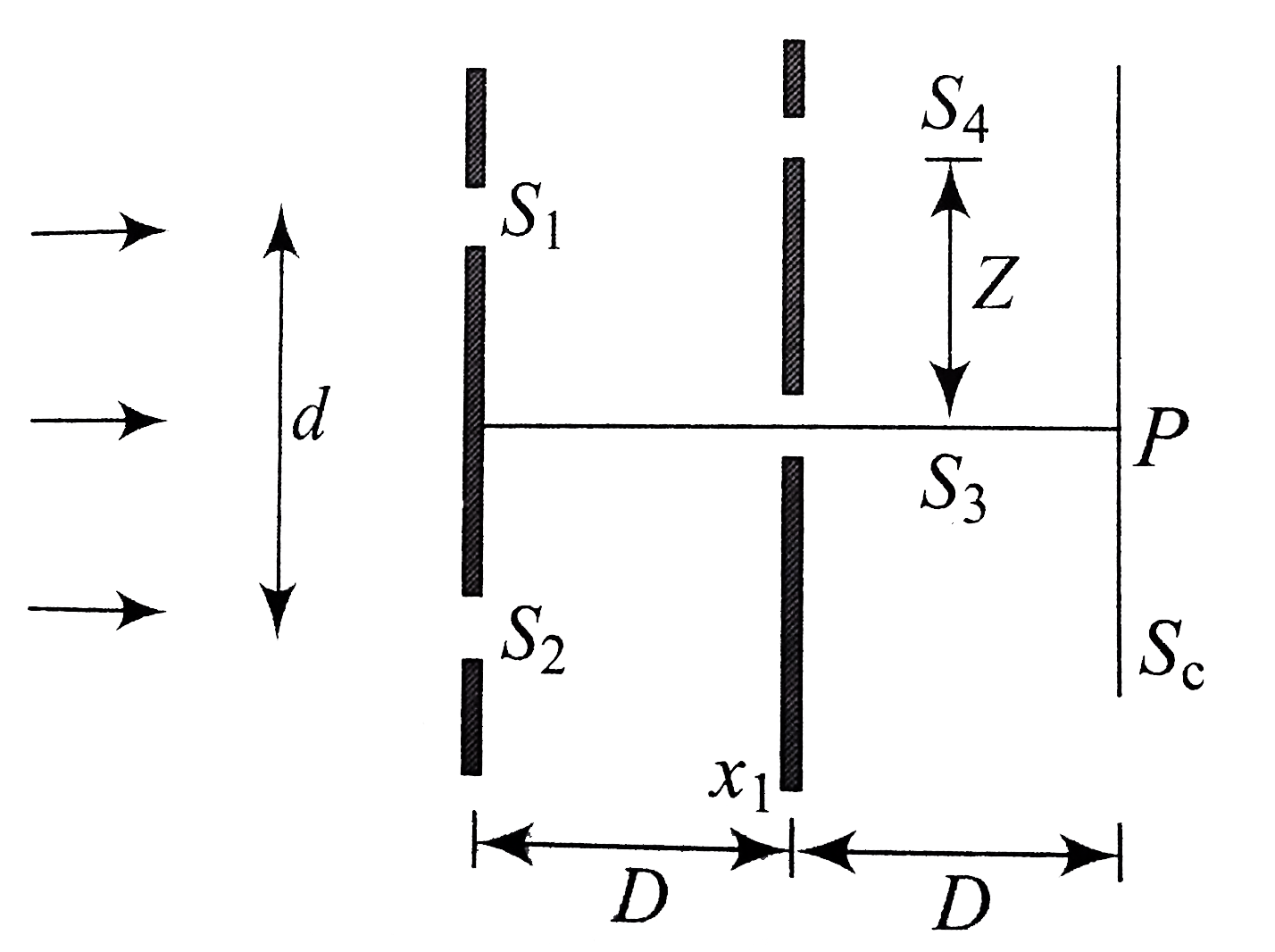
If $z = \frac{λ D}{2 d}$ View Solution
Question 16
Consider the situation shown in fig. The two slits $S_{1}$ and $S_{2}$ placed symmetrically around the central line are illuminated by monochromatic light of wavelength $λ$ . The separation between the slit is d. The ligth transmitted by the slits falls on a screen $S_{0}$ placed at a distance D form the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance z from $S_{3}$ Another screen $S_{c}$ is placed a further distance D away from $S_{c}$ Find the ratio of the maximum to minimum intensity observed on $S_{c}$

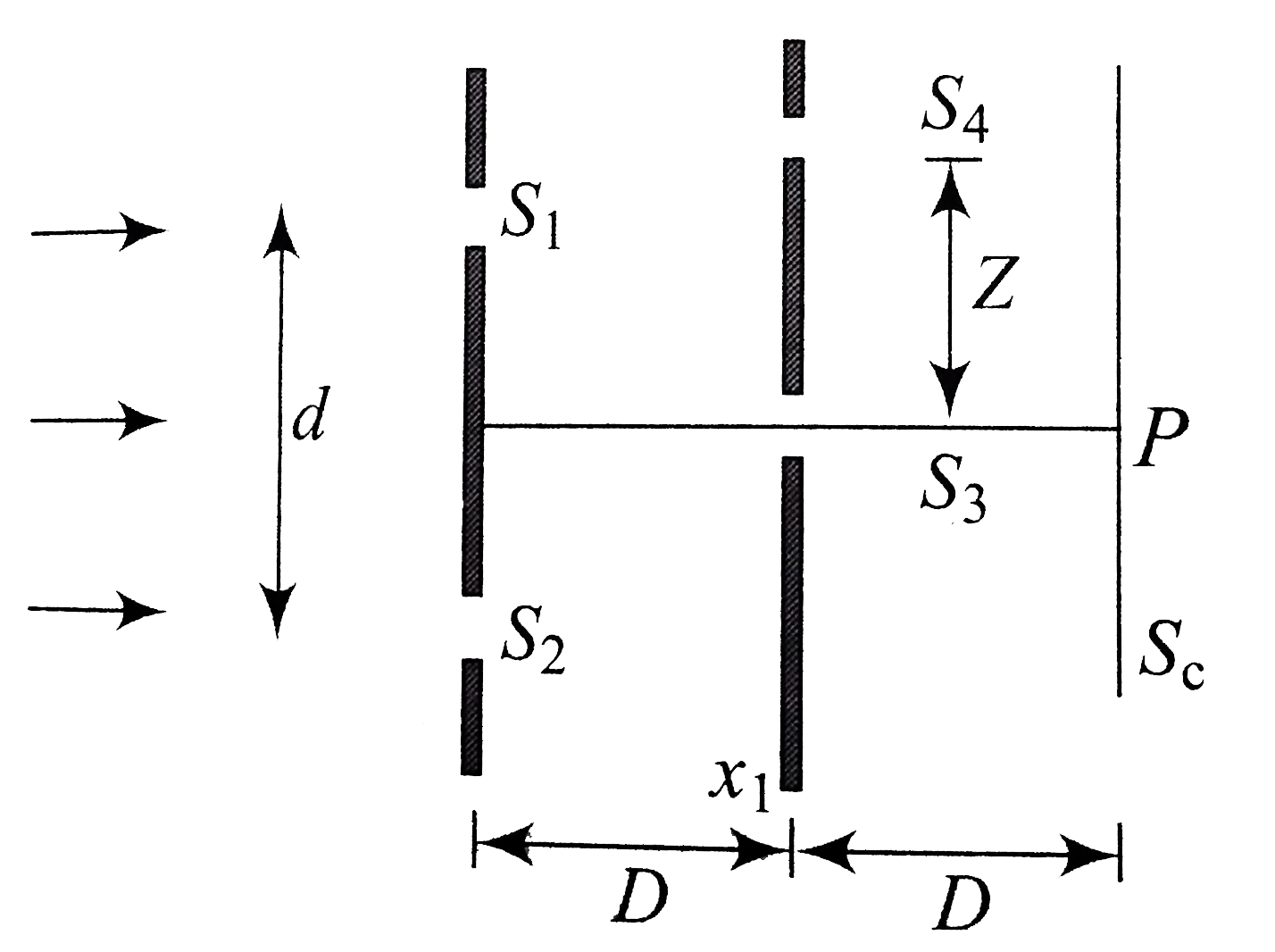
If $z = \frac{λ D}{d}$ View Solution
Question 17
Consider the situation shown in fig. The two slits $S_{1}$ and $S_{2}$ placed symmetrically around the central line are illuminated by monochromatic light of wavelength $λ$ . The separation between the slit is d. The ligth transmitted by the slits falls on a screen $S_{0}$ placed at a distance D form the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance z from $S_{3}$ Another screen $S_{c}$ is placed a further distance D away from $S_{c}$ Find the ratio of the maximum to minimum intensity observed on $S_{c}$

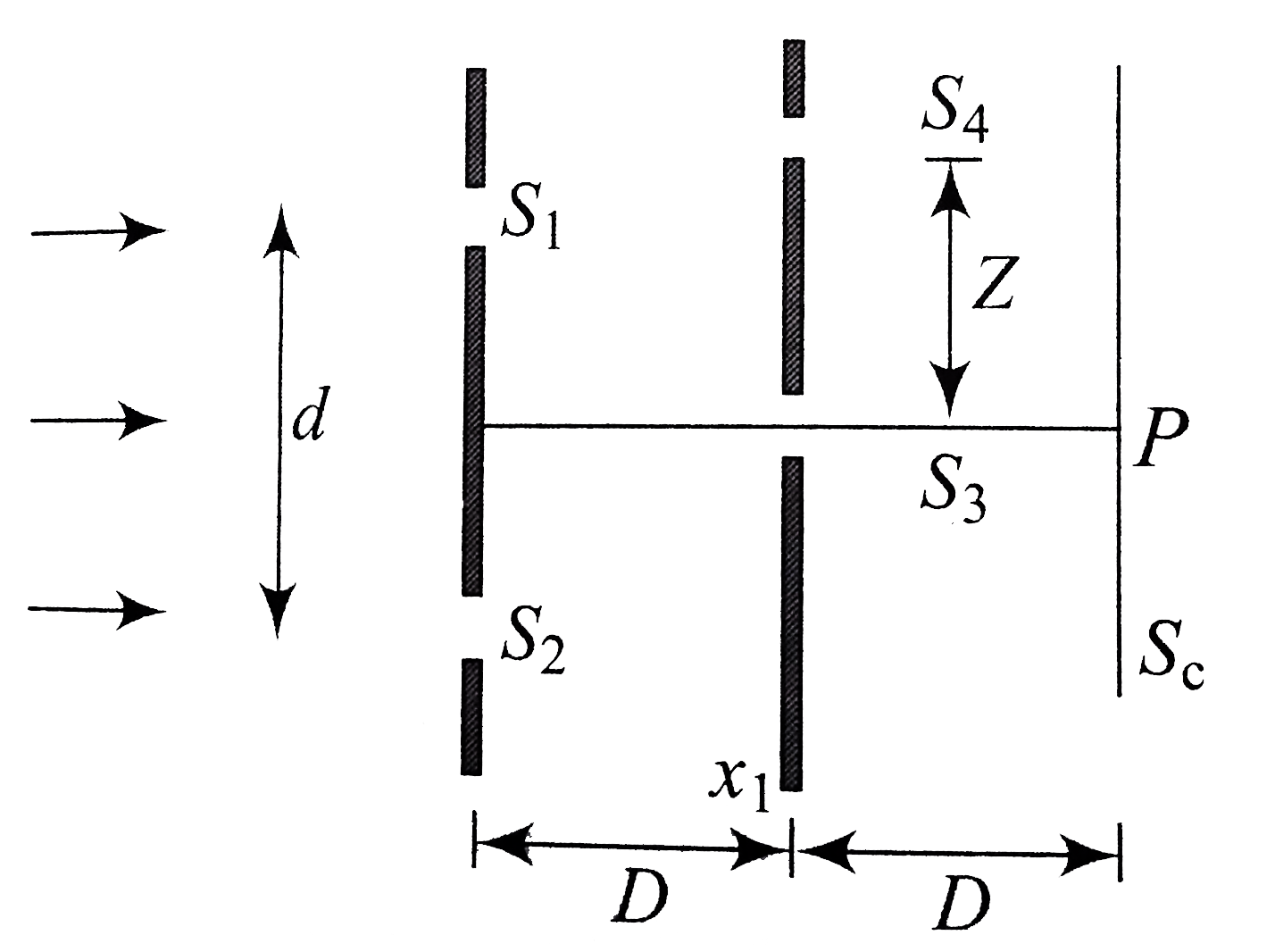
If $z = \frac{λ D}{4 d}$ View Solution
Question 18
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic $λ$ . Behind the lens, a screen is located at a distance L front it.

Find the fringe width for the pattern obtained under given arrangement on the screen.View Solution
Question 19
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic $λ$ . Behind the lens, a screen is located at a distance L front it.

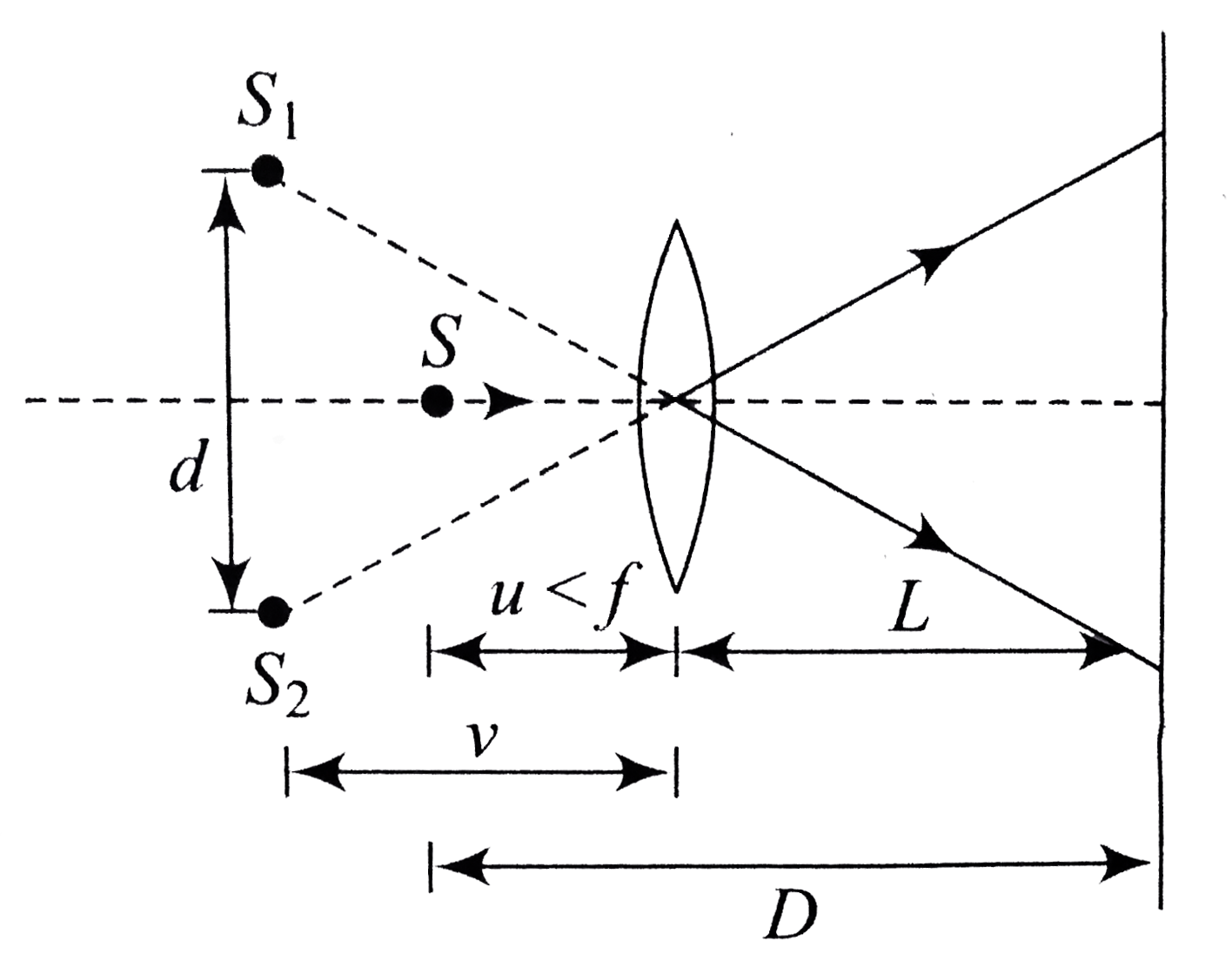
The expression for the number of visible maxima which are obtained through above said arrangement will turn out to be View Solution
Question 20
In a modified Young's double-slit experiment, source S is kept in front of slit $S_{1}$ as shown in the following figure. Find the phase difference at a point that is equidistant from slits $S_{1}$ and $S_{2}$ and point P that is in front of slit $S_{1}$ in the following situations:

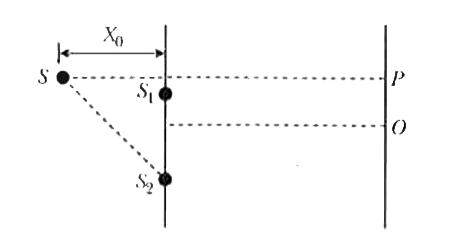
If a liquid of refractive index n is filled between the screen and slits, what is the phase difference?View Solution
Question 21
In a modified Young's double-slit experiment, source S is kept in front of slit $S_{1}$ as shown in the following figure. Find the phase difference at a point that is equidistant from slits $S_{1}$ and $S_{2}$ and point P that is in front of slit $S_{1}$ in the following situations:

If a liquid is filled between the slit and the source S, what is the phase difference?View Solution

All Exercises from RESNICK AND HALLIDAY PHYSICS Class 12 PHYSICS INTERFERENCE AND DIFFRACTION

Home
Ask Doubt
Profile

PRACTICE QUESTIONS (Linked Comprehension﻿) from RESNICK AND HALLIDAY PHYSICS Chapter 22 INTERFERENCE AND DIFFRACTION for Class 12

All Exercises from RESNICK AND HALLIDAY PHYSICS Class 12 PHYSICS INTERFERENCE AND DIFFRACTION

PRACTICE QUESTIONS (Linked Comprehension) from RESNICK AND HALLIDAY PHYSICS Chapter 22 INTERFERENCE AND DIFFRACTION for Class 12