NUCLEI for Class 12 PHYSICS

INTRODUCTION

Jaise ki humne previous chapter me study kiya, atom ke center me nucleus hota hai wo proton aur electrons ko contain karta hai. Rutherford ke experiment se humne atoms ke structure ko find kiya, is experiment me humne ek $α$ beam ko ek thin gold foil me strike kiya, to kuchh alpha rays gold foil se straight pass ho jati hai pr kuchh beams bahut jyada deviate ho jati hai, aisa isliye hota hai kyuki gold foil ke small part me nucleus present hota jo +ve charge carry karta hai aur $α$ beam bhi $+ v e$ hota hai, jaise ki hum jante hai ki same charges ek dusre ko repel karte hai, isliye $α$ beam apne path se deviate hota hai. Is chapter me hum nucleus ke properties ke bare me discuss karenge.

ATOMIC MASS & COMPOSITION OF NUCLEUS

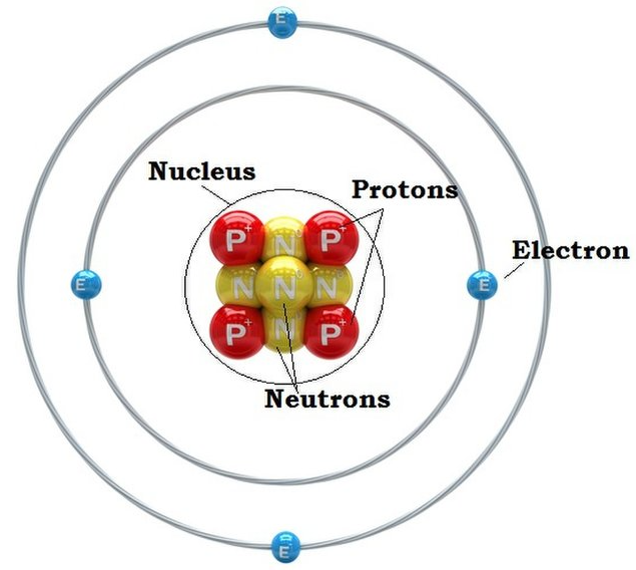
Proton aur neutron ke combination ko nucleus kahte hai. Proton ek $+ v e$ charge particle hai jiska magnitude electron ke barabar hota hai, pr iska mass 1840 times mass of electron hota hai. Neutron ka mass proton se thoda jyada hota hai. Proton aur neutron ke masses :

$m_{p}$ = $1.6726231 \times 10^{- 27}$ kg
$m_{n}$ = $1.6749286 \times 10^{- 27}$ kg

Nuclear physics or higher physics me mass ko energy ke unit me liya jata hai. Conservation of energy

E = m c^{2}

ke anusar mass

m

energy ke equivalent hota hai. For eg. the mass of an electron is

m_{e}

9.1093897 \times 10^{- 31}

kg and the equivalent energy is

m_{e} c^{2}

510.99 k e V

Thus, the mass of an electron is

510.99 k e V c^{2}

. Similarly, the mass of a proton is

938.27231 M e V c^{2}

, and the mass of a neutron is

939.56563 M e V c^{2}

. Particle ke mass ka energy jab rest me hota hai to use rest mass energy kahte hai.

Nuclear physics me mass ko ek aur unit se define karte hai wo unified atomic mass unit hai isi symbol

u

se denote karte hai aur ise

a μ

bhi likha jata hai. Atomic mass unit

{(\frac{1}{12})}^{t h}

part of mass of neutral carbon atom ka hota hai.

1.6605402 \times 10^{- 27}

931.478 M e V c^{2}

Protons and neutrons fermions hai or Pauli exclusion principle ko follow karte hai electrons ki tarah. Koi bhi two protons or two neutrons kabhi bhi same quantum state me nahi ho sakte. Pr one proton and one neutron same quantum state me reh sakte hai. Protons and neutrons ke combination ko nucleons kahte hai.

The number of protons in a nucleus is denoted by Z, the number of neutrons by N and the total number of nucleons by A. Thus, A = Z + N. The total number of nucleons A is also called the mass number of the nucleus. The number of protons Z is called the atomic number. A nucleus is symbolically expressed as

_{Z}^{A} X

in which X is the chemical symbol of the element.
For example $_{2}^{4} H_{e}$ me Z = 2, A = 4, then N = A - Z, i.e., N = 4 - 2 = 2.

Aise nucleus jisme same number of protons Z ho pr different number of neutrons N to use isotopes kahte hai. Nuclei with the same neutron number N but different atomic number Z are called isotones and the nuclei with the same mass number A are called isobars. All nuclei with a given Z and N are collectively called a nuclide. Thus, all the

_{26}^{56} F e

nuclei taken together is one nuclide and all the

_{16}^{32} S

nuclei taken together is another nuclide.

ocr_image

SIZE OF NUCLEUS

Nucleus itna small hota hai ki koi bhi small particle sharp boundary define nahi kr pata. Aisi particles ko sirf wave function me describe karte hai. Wave function ka magnitude itna small ho jata hai ki wo nucleus ke center se distance bana leta hai. Jaha pe wave function ka magnitude appreciable hai waha se roughly nucleus ka size estimate kr sakte hai. Experiments show that the average radius R of a nucleus may be written as R = R_0 A^⅓, where
$R_{0} = 1.1 \times 10^{- 15} m = 1.1$ fm and A is the mass number.

V = \frac{4}{3} π R^{3} = \frac{4}{3} π (R_{0}^{3}) A

As the masses of a proton and a neutron are roughly equal, say m, the mass of a nucleus M is also roughly proportional to the mass number A. We have, M = mA, the density within a nucleus (mass per unit volume)

ρ = \frac{M}{V}

is independent of A.

POINT 1

Nucleus :

The entire positive charge and nearly the entire mass of atom is concentrated in a very small space called the nucleus of an atom.

Atomic Number :

The number of protons in the nucleus of an atom of the element is called atomic number (Z) of the element.

Mass Number :

The total number of protons and neutrons present inside the nucleus of an atom of the element is called mass number (A) of the element.

Nuclear Density :

Nuclear density is independent of mass number and therefore the same for all nuclei.

Atomic Mass Unit :

It is defined as

{(\frac{1}{12})}^{t h}

the mass of the carbon nucleus. It is abbreviated as arnu and often denoted by u.

MASS ENERGY AND NUCLEAR BINDING ENERGY

Einstein ke theory of special relativity se hum mass ko ek energy ke form me treat kr sakte hai. Is theory se pehle mass or energy ko do separate entity me liya jata tha. Lekin Einstein ne show kiya ki mass ek energy ka form hai jo ek energy se dusre energy me change ho sakta hai jaise ki kinetic energy.
Einstein gave the famous mass-energy equivalence relation :

$E = m c^{2}$

Nuclear Binding Energy :

Jaise ki hum jante hai hydrogen atom ke binding concept ke bare me, jisme humne infinity se hydrogen ke constitutes ko la kr hydrogen atom ka formation kiya jisme 13.6 eV energy release hui. Isliye binding energy of hydrogen atom 13.6 eV hai. Aur 13.6 eV energy ki zaroorat hogi hydrogen atom ko separate karne me. Isi tarah nucleons are bound together in a nucleus. Large distance me nucleus me iske constitutes ko separate karne ke liye aur energy supply karna hoga.
Jitna amount lagega energy ka, utne energy ko binding energy kahte hai. Agar nucleus pehle se hi separate ho aur usko pass lana ho to energy release hogi.

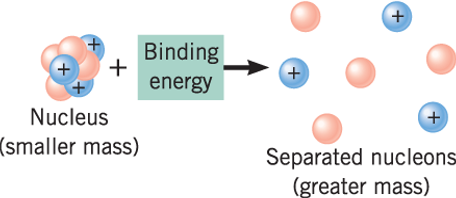
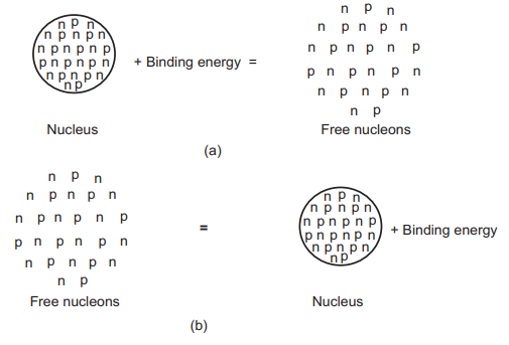
ocr_image

Is se ye pata chalta hai ki rest mass energy of nucleus is smaller than rest mass energy of the constituents on nucleus in free state. Dono energy ke difference ko binding energy kahte hai.

Rest mass energy of free proton is : $m_{p} c^{2}$
Rest mass energy of free neutron is $m_{n} c^{2}$ .
Agar nucleus ka mass $M$ hai, to rest mass energy is $M c^{2}$ .
Agar nucleus Z no. of proton aur N no. of neutron contain karta hai to rest mass energy hoga nucleus ka free state me :
$Z m_{p} c^{2} + N m_{n} c^{2}$ .

Agar binding energy nucleus ka B or

E_{b}

hai to :
$B or E_{b} = [Z m_{P} + N m_{n} - M n] c^{2}$ .
Binding Energy per Nucleon : Is the average energy required to extract one nucleon from the nucleus. Ye nucleus ke stability ko measure karta hai. Jitna energy jayda hota hai utna jayda nucleus stable hota hai.

Binding Energy per Nucleon B.E = $\frac{E_{b}}{A}$ ,

Binding energy curve :

The average of binding energy per nucleon with mass number A is shown below :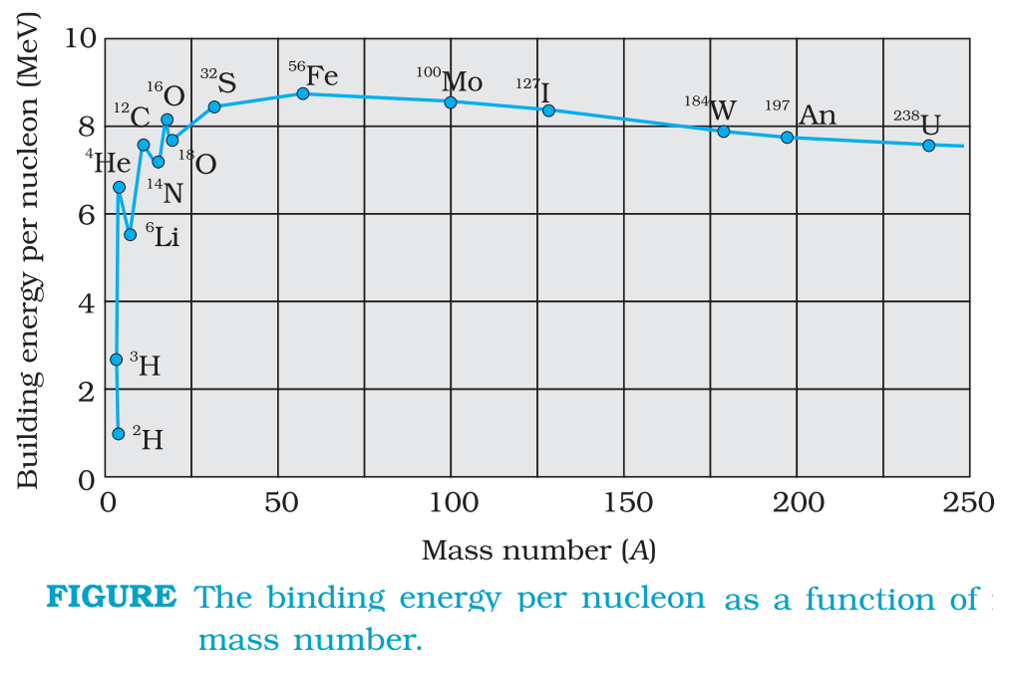

ocr_image

Average binding energy per nucleon for light nuclei like $_{1} H^{4}$ , $_{1} H^{3}$ , $_{1} H^{2}$ , is small.
For mass no. ranging from 2 to 20 there are sharply defined peaks corresponding to $_{1} H e^{4}$ , $_{6} C^{12}$ , $_{8} O^{16}$ . The peak indicates that these nuclei are more stable than their neighbours $_{3} L i^{6}$ , $_{5} B^{10}$ , $_{7} N^{14}$ .
After mass number 20 the binding energy per nucleon increases and for mass no. 40 to 80 the curve becomes more or less flat. For $_{26} F e^{56}$ binding energy/nucleon is maximum and it is equal to 8.75 $m_{e} V$ .
As the mass no. increases the binding energy/nucleon decreases gradually about 7.6 $m_{e} V$ for $_{92} U^{238}$ and it is less stable.
The binding energy/nucleon has low value for both very light and very high for heavy nuclei. In order to maintain higher binding energy/nucleon, the lighter nuclei must be bond together (nuclear fusion) and heavy nucleon must split in to higher nuclei (nuclear fission).

NUCLEAR FORCES

Jab nucleus ko femtometre ( $10^{- 15}$ m) ke order me separate rakha jata hai, to ek new kind ka force act hota hai use nuclear force kahte hai. Jo force nucleus ke inside me ho, or jo force nucleons ke beech me act ho raha ho us force ko Nuclear force kahte hai. Nuclear force sabhi forces jaise gravitational and electromagnetic force se stronger hota hai.
Basically Nuclear force (jo ki attractive force hai) proton or electrons ko hold krke rakhta hai nucleus ke ander.
Important factors of Nuclear Forces are :

Nuclear force ka range short hota hai aur ye attractive force hota hai.
Ye non- central or non-conservative force hai.
Ye force gravitational or electromagnetic force se stronger hota hai.
Nuclear force 100 times hota hai electrostatic force ka aur $10^{38}$ times jayda gravitational force ka.

Various of PE of pair of nucleus with distance :Nuclear binding force dominate karta hai Coulomb repulsive force ko jo present hota hai nucleus me protons ke beech me.

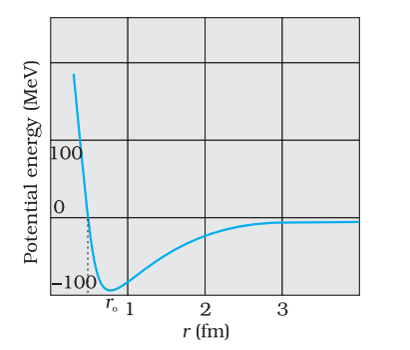
ocr_image

r_{o}

r_{o}

r_{o}

POINT 2

Isotopes :

The atoms of an element having the same atomic number but different mass numbers. are called isotopes.

Isobars :

The atoms of different elements having same mass numbers but different atomic numbers, are called isobars.

Isotones :

The atoms of different elements having different atomic numbers and different mass numbers but having the same number of neutrons, are called isotones.

Isomers :

Atoms having the same mass number and the same atomic number but different radioactive properties are called isomers.

RADIOACTIVITY

Aisa phenomenon jisme radiations ki wajah se heavy elements disintegrate hokar lighter elements me convert hote hai use radioactivity kahte hai. Ye phenomenon A.Henri Becquerel ne discover kiya tha 1896 me. Becquerel ne ek experiment ke dauran note kiya ki Uranium atom kuch invisible rays or radiation produce kar raha hai jo bahut sare thick black papers ko pennetrate krke piche rakhe hue photographic plate ko affect kr raha hai. Us invisible rays or radiation ko alpha $(α)$ , beta $(β)$ or gamma $(γ)$ rays kahte hai.

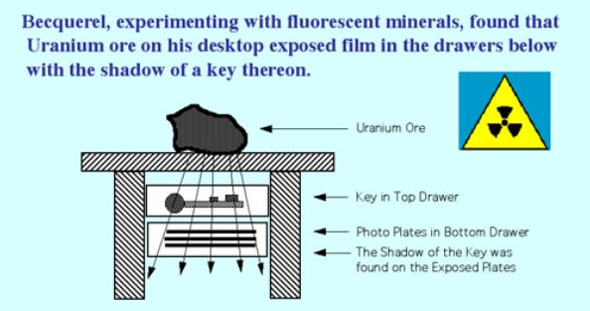
ocr_image

Is experiment me jo unstable nucleus hai wo radiations ke wajah se decay hone lagte hai, aur is decay ko radioactive decay kahte hai. Ye decay 3 types ke hote hai :

α

α

β

γ

Alpha Decay :

Alpha decay me unstable nucleus alpha rays emit karta hai jo number of protons Z or number of neutrons N ko 2 points se reduce karta hai. The alpha decay process may represent as :

$_{Z}^{A} X \to_{Z - 2}^{A - 2} Y +_{2}^{4} H e$

Jaise hi proton Z no. change hota hai to jo original nucleus hota hai wo bhi change ho jata hai. Jo original nucleus ko parent nucleus kahte hai aur second nucleus jo uski jagah le leta hai alpha decay ki wajah se use daughter nucleus kahte hai. For example :

$_{92}^{238} X \to_{90}^{234} Y +_{2}^{4} H e$

The parent nucleus of Uranium contain P = 238, N = 146 and daughter nucleus i.e. Thallium contains P = 234, and N = 144.
Alpha decay sabhi nuclei me hota hai jiska mass no. A > 210. Humne dekha hai ki jyada heavy nucleus unstable hote hai Coulomb repulsive force ke karan. To heavy nucleus stable state me ate hai by releasing alpha particles, us se nucleus ka mass decrease hota hai. Rest mass energy of Uranium jyada hota hai uske product Thallium and Helium ke mass energy se. The difference between the rest mass energy of the initial constituents and that of the final products is called the Q-value of the process. Thus,

U_{i}

initial mass energy hai uranium ka or

U_{f}

final mass energy, to

Q = $U_{i}$ - $U_{f}$

Ye equation sirf alpha decay ke liye hai kisi bhi nuclear process mai. Ye energy hume K.E ke form me available hota hai,

$Q = [m (_{Z}^{A} X)$ - m $(_{Z - 4}^{A - 4} Y) - m (_{2}^{4} H e)] C^{2}$

Beta Decay :

Beta decay me neutron convert hota hai proton me or proton convert hota hai neutron me. Isliye N/Z ke ratio me difference aata hai beta decay me. Jab neutron convert hota hai proton me to ek new particle emit hota hai nucleus se use antineutrino kahte hai.

$n \to p + e + ¯ v$

Beta decay 2 type ke hote hai, jab neutron emit hota hai to use

(β^{-})

se denote karte hai aur jab particle proton emit karta hai to use

(β^{+})

se denote karte hai. For examples :

For $(β^{-})$ : $_{15}^{32} P \to_{16}^{32} S + e^{-} + ¯ v .$
For ( $β^{+})$ : $_{11}^{22} N a \to_{10}^{22} N e + e^{+} + ¯ v .$

Rest mass energy of initial constitutes is :

$U_{i}$ = $[m (C) - Z m_{e}] C^{2}$

Rest mass energy of final constitutes is :

$U_{f}$ = $[m (_{Z + 1}^{A} X) - (Z + 1) m_{e} + m_{e}] C^{2}$

K.E available to the product :

Q = $U_{i} - U_{f}$ = $[m (_{Z}^{A} X) - m (_{Z + 1}^{A} Y)] C^{2}$

K.E ka value 0 se Q ke maximum value ke beech hogi.

Gamma Decay :

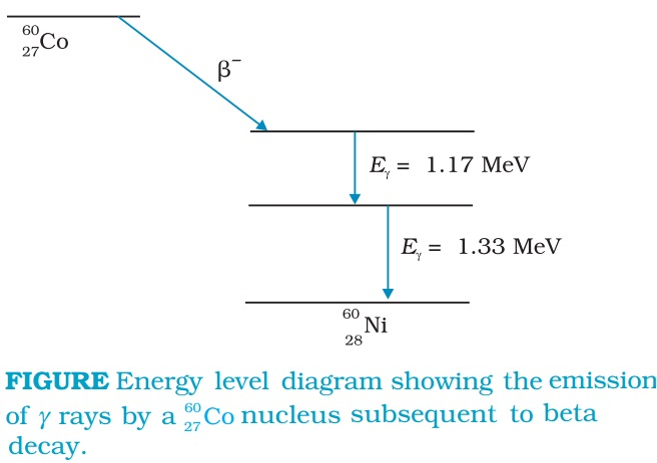
Atoms ki tarah nucleus ke bhi discrete level hote hai - the ground state and excited states. Iska scale energy different hota hai atom se. Atomic energy level gap (spacing) eV ke order me hota hai. Aur nuclear energy level MeV ke order me.
Jab nucleus excited state me hoga to decay ground level me hoga, tabhi ek photon emit hoga jiski energy equal hogi nucleus ke difference energy level se (excited state - ground state) isi ko gamma decay kahte hai. Ye energy (MeV) corresponds to radiation of extremely short wavelength. Gamma decay tabhi hota hai jab alpha or beta decay excited state me ho. A familiar example is the successive emission of gamma rays of energies 1.17 MeV and 1.33 MeV from the deexcitation of

_{60}^{28} N i

nuclei formed from

β^{-}

decay of

_{60}^{27} C o

Law of radioactive decay :

Koi bhi radioactive nucleus tabhi decay hota jab wo nuclear radiation

(α, β, γ)

emit karta hai. Suppose kare ek

α

active nucleus ko time t=0 me liye jaye, hum classical physics me ye determine nahi kr sakte ki nucleus kab decay hoga. Agar bahut sare nucleus liya jaye at t = 0 me waha ke nucleus bahut jaldi decay honge aur bahut lambe samay ke baad, decay ka time pata karna mushkil hai. Per quantum physics me hum particle ke behaviour ke bare me pata kr sakte hai. Kisi bhi radioactive sample me agar N no. of nucleus hai to

Δ N

no. electrons jo decay hui hai in

Δ t

time me.

$N \propto \frac{Δ N}{Δ t}$

or $\frac{Δ N}{Δ t} = λ N$

where

λ

is called the radioactive decay constant or disintegration constant.
The change in the number of nuclei in the sample is dN = -

Δ N

in time

Δ t

. Thus the rate of change of N is (in the limit

Δ t

to 0).

\frac{d N}{d t}

= -

λ N

Δ

N is the number of nuclei that decay, and hence is always positive. dN is the change in N, which may have either sign. Here it is negative, because out of the original N nuclei,

Δ N

have decayed, leaving (N–

Δ N

) nuclei.

$\frac{d N}{N} = - λ d t$ ..........(1)
Integrating both side ............(2)
$\int_{N_{0}}^{N} \frac{d N}{N}$ = $- λ \int_{t_{0}}^{t} d T$ ..............(3)
$ln N - {ln N}_{0}$ = $- λ (t - t_{0})$ .................(4)
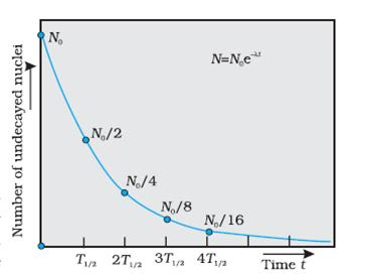
$N = N_{0} e^{- λ t}$ ........................(5)

where

N_{0}

is the number of active nuclei at t = 0. The rate of decay is

$- \frac{d N}{d t} = λ N$ ....................(6)

The quantity(-

\frac{d N}{d t}

) gives the number of decays per unit time and is called the activity of the sample. Thus, the activity of a radioactive sample is A =

λ

N.
From equation (5), we have :

$A = A_{0} e^{- λ t}$ .................(7)

Unit of Activity :

Radioactivity material ke activity ko measure karte hai, in terms of the disintegrations per unit time. Its SI unit is becquerel which is the same as 1 disintegration per second. It is denoted by the symbol Bq. However, the popular unit of activity is curie defined as :

$1 c u r i e = 3.7 \times 10^{10}$ disintegrations $s^{- 1}$ .

The unit ‘curie’ is represented by the symbol Ci. The activity per unit mass is called specific activity.

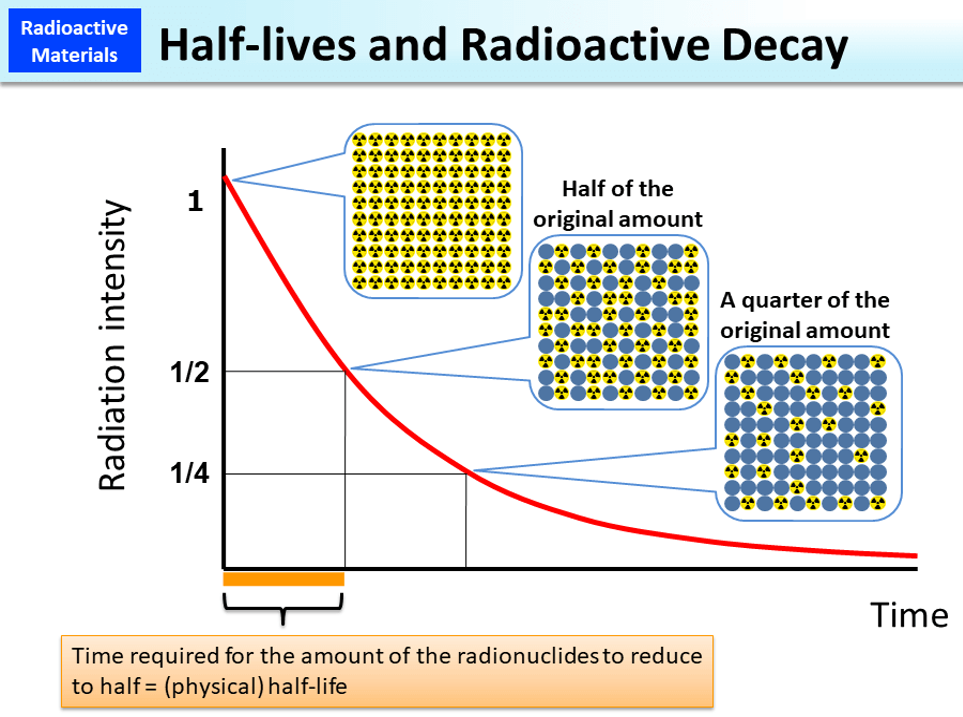
Half Life :

Kitna time laga half the active nuclei hone me use half life kahte hai.
The time elapsed before half the active nuclei decay is called half-life and is denoted by t_(½).Suppose there are

N_{0}

active nuclei at t = 0. The half-life

t_{½}

is the time elapsed before

\frac{N_{0}}{2}

nuclei have decayed and

\frac{N_{0}}{2}

remain active. From equation (5)

$\frac{N_{0}}{2}$ = $N_{0} e_{½}^{- λ t_{½}}$ or,
$e_{½}^{- λ t_{½}}$ = 2,
$t_{½}$ = $\frac{ln 2}{λ}$ = (0.693)/lambda …………..(8)

Using equation 5 and 7 we get,

N = $\frac{N_{0}}{2^{\frac{t}{t_{½}}}}$

Similarly, the activity at time t is :

A = $\frac{A_{0}}{2^{\frac{t}{t_{½}}}}$

Average life :

Sabhi nucleus jo decay ho rahe hai time ke sath un sab ka mean value average life hoga nucleus ka. Consider a sample containing

N_{0}

radioactive nuclei at time t = 0. The number of nuclei which decay between the time t and (t + dt) is

λ

N dt. The life of these nuclei is approximately t each. The sum of the lives of these dN nuclei is t

λ

N dt. The sum of all the lives of all the N nuclei that were active at t = 0 will be

$S = \int_{0}^{\infty} t λ N d t$
= $λ N_{0} \int_{0}^{\infty} t e^{- λ t} d t$
= $λ N_{0} [{(t \frac{e^{- λ t}}{{(- λ)}_{□}})}_{0}^{\infty} - \int_{0}^{\infty} \frac{e^{- λ t}}{- λ} d t]$
= $\frac{N_{0}}{λ}$
Avg life of nuclei is:
$t_{a v} = \frac{S}{N_{0}}$ = $\frac{1}{λ}$ or
$t_{a v} = \frac{t_{½}}{0.693}$

POINT 3

Nuclear Force :

The force acting inside the nucleus or acting between nucleons is called nuclear force.

Mass Defect :

The difference between the sum of masses of all nucleons (M) mass of the nucleus (m) is called mass defect.

Nuclear Binding Energy :

The minimum energy required to separate the nucleons up to an infinite distance from the nucleus, is called nuclear binding energy.

NUCLEAR ENERGY

Jab kisi heavy radioactive nuclei ko break kare two parts me aur use middle weight me laya jaye or do lighter weight nuclei ko bond kar ke middleweight nuclei banaya jaye is process jo energy emit hogi woh nuclear energy hai.

Nuclear Fission :

Jab heavy nuclei ko divide kare do parts me to us process ko nuclear fission kahte hai.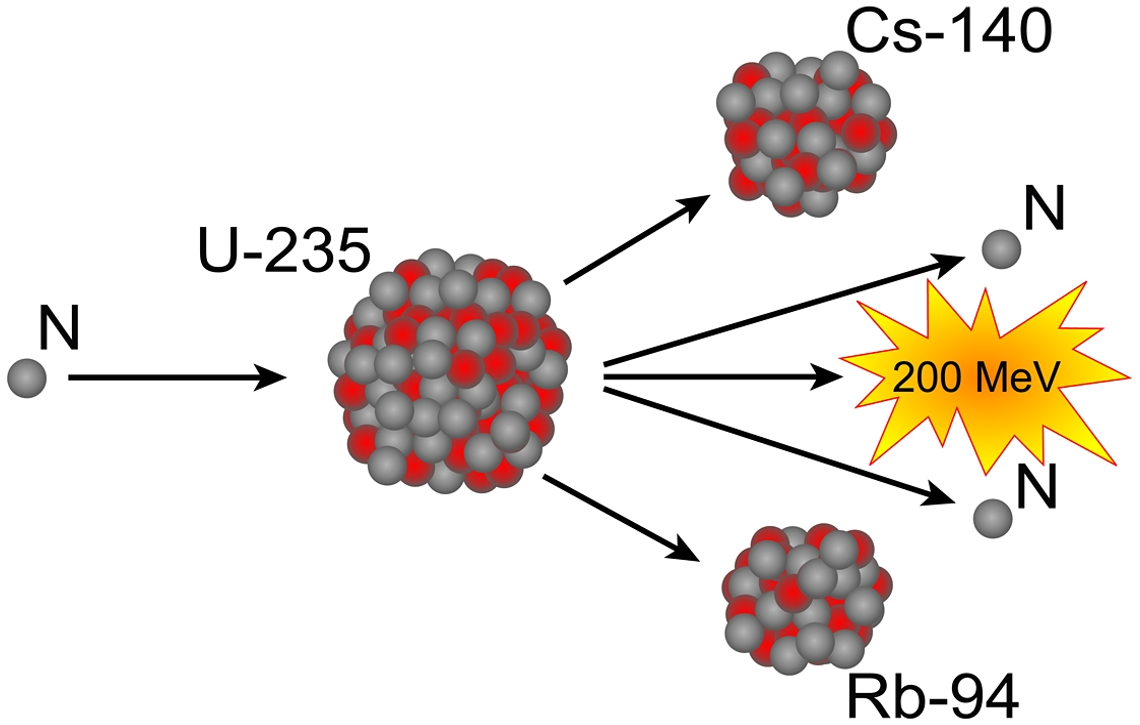

ocr_image

Uper diye gaye figure me aap dekh sate hai ki jab ek neutron ko heavy radioactive element U-235 me bombard kare to U-234 element unstable ho jaega aur break ho kar do middle weight radioactive element Rb-94, Cs-140 me convert hoga. Is conversion ke douron jo radioactive energy emit hoga use nuclear energy kahte hai. For examples :
When a uranium isotope

_{235}^{92} U

bombarded with a neutron breaks into two intermediate mass nuclear fragments

$_{0}^{1} n +_{92}^{235} U$ $\to$ $_{92}^{236} U \to_{36}^{144} B a +_{36}^{89} K r + 3_{0}^{1} n$ .
$_{0}^{1} n +_{92}^{235} U$ $\to$ $_{92}^{236} U \to_{51}^{122} S b +_{41}^{99} N b + 4_{0}^{1} n$ .

The fragment products are radioactive nuclei; they emit

β

particles in succession to achieve stable end products.
The energy released (the Q value ) in the fission reaction of nuclei like uranium is of the order of 200 MeV per fissioning nucleus. This is estimated as follows:
Let us take a nucleus with A = 240 breaking into two fragments each of A = 120.Then

E_{b n}

for A = 240 nucleus is about 7.6 MeV,

E_{b n}

for the two A = 120 fragment nuclei is about 8.5 MeV.

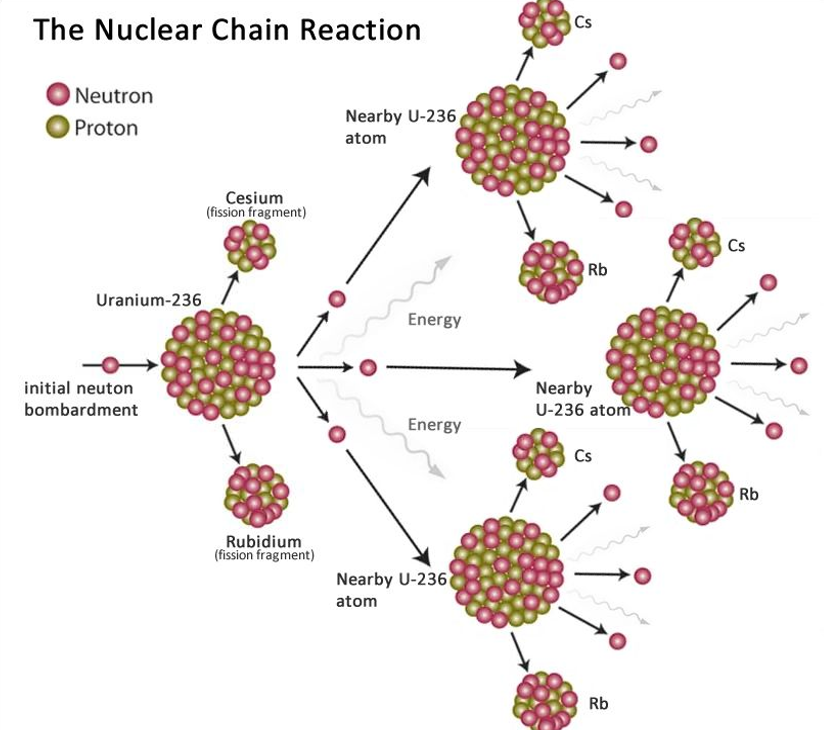
Nuclear Chain Reaction :

Gain in binding energy for nucleon is about 0.9 MeV. Hence the total gain in binding energy is

240 \times 0.9

or 216 MeV.
Jo energy fission process me release hoga wo K.E ke form me hoga aur wo surrounding me heat ki tarah appear hoga.

Jab neutron fission hona shuru hota hai radioactive nucleus U-235 se to neutron kuchh aur neutrons me divide ho jata hai aur wo dusre U-235 jo waha present hote unse fuse hone lagta hai ye rection continue hota is reaction ko chain reaction kahte hai. Number of neutrons increase hota jayega jaise-jaise fission hote jayenge jiski wajah se geometrical progression bhi increase hoga. Ye fission bahut hi kam samay hoga. Jo heat produce hoga wo bahut jayda aur uncontrolled hoga aur ye ek disaster ki aur rukh karega. There are ways to control the chain reaction:
1. Nucleus ke size ko control kare to rate of fission ko bhi control kiya ja sakta hai.
2. The neutrons produced in the fission have kinetic energy ≈ 2 MeV. They are called fast neutrons.
3. The U-235 nucleus has a good probability of absorbing slow neutrons (≈ 0.04eV), but has a poor chance of absorbing fast neutrons. The neutron may not get absorbed in U-235 even if the two meet and collide.
Agar material ka size large ho, to neutron bahut sare nuclei se collide karega. In each collision, ye kinetic energy loss karega aur thodi der baad ye slow hokar thermal energies ≈ 0. 04 eV tak hoga. It may then be absorbed by 235-U. But 238-U nuclei, which are present in large numbers (99. 3%), are extremely good neutron absorbers if they get neutrons of energy 1–100 eV. These neutrons get absorbed in 238U to form 239U which decays generally by means other than fission. A fast neutron has to go through this 1–100 eV range before slowing down to thermal energies ≈ 0. 04 eV and has a fair chance of being absorbed by 238U. This neutron is, therefore, lost as far as fission is concerned.

ocr_image

Nuclear Reactor :

Nuclear reactor works on the principle of controlled chained reaction and provides energy at a constant rate. The main parts of nuclear reactor are as follows :
1. Construction

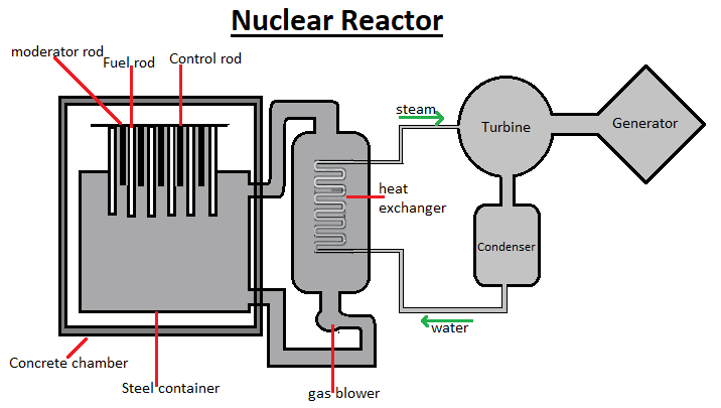
ocr_image

2. Nuclear Fuel : Uranium isotopes (U-235), Thorium (Th-232) are commonly used as nuclear fuel in reactor.
3. Moderator : Fast moving electrons ko slow karne ke liye moderators ka use hota hai. Heavy water, graphite and beryllium oxide are used to slow down fast moving neutrons. Jab heavy water use hota as moderator, to non-enriched U ko fuel ki tarah use kar sakte hai kyuki heavy water me bahut se neutron present hote hai jo fission kar sakte hai.
4. Control Rods : Control rod ka use reaction ko stable rakhne me aur chain reaction ko control karne me use hota hai. Ye neutrons ko control karta hai fission ke liye.
Cadmium or boron rods are good absorbers of neutrons and therefore used to control the fission reaction.
Atom bomb working is based on uncontrolled chain reaction.
5. Coolants : Ye ek cooling material hai jo heat generate hota hai reactor me use cool karta hai. The cold water, liquid oxygen, etc. are used to remove heat generated in the fission process.
6. Protective Shield : Ye protective shield hai jo core ko cover karta, yeh concrete thick wall ke form me rehta hai jo radiation ko bahar ane se rokta hai.

Working : Jab kuch U-235 nuclei ko neutrons se bombard kare jo ki bahut speed se move ho rahe ho. To jo fast moving neutrons jo moderator ke surrounding me hote hai use moderator control karta hai uski speed ko slow karta hai. Jo chain reaction hota hai cadmium rod control karta hai. Fission ki wajah se heat produce hoga nuclear core me. Phir coolant transfer karta hai heat energy ko heat exchanger me jaha steam form hoga. Jo steam produce hoga wo pressure bahut high hoga aur wo turbine ko rotate karega, aur turbine ke rotate hone ke karan generator me electricity generate hoga. Jo steam use ho gaya wo wapas se apne original state me ayega aur wapas heat chamber me jayega. Ye process continue hota hai aur nuclear reactor continuously electricity produce karta hai. Nuclear reactor ka use radioactive isotopes ko produce karne me use hota hai.

Nuclear Fusion :

Jab 2 or more small weight nuclei ko pass laya jaye aur unke bonding ke wajah se wo middle weight nuclei me transfer ho jata hai is process ko nuclear fusion kahte hai. Jab kisi bhi do nuclei ko pass laya jaye (

\approx

1fm) ke range me to fusion hoga. Lekin ye bahut difficult hota hai ki do nucleus ko pass lane ko kyuki dono ke charges same hota hai aur hum jante hai ki same charges repeal each other. Koi bhi bulk material atom se composed hota hai aur uska radius kuchh angstroms me hota hai (

10^{- 10}

m =

10^{5} f m

). Agar hum electrons ko neglect bhi kar de to nuclei khud ek +ve charge hai jo dusre nuclei ko repeal karta hai. Dono nuclei ko fuse karne ke liye use heat kiya jata hai jiske karan electrons bahut speed se move hone lagta hai aur wo fuse hone lagta hai.

Fusion in sun :

Celestial bodies jaha energy produce hota waha sun star se cooler hota hai. Aise stars bhi hai jiska temp sun se jyada hota hai (

\approx 10^{8}

k), aur sun ka temprature (

\approx 10^{7}

k) hai. Yaha pe fusion hota hai proton-proton ke beech me, the chain as follows :

$\frac{\begin{matrix} ^{1} H +^{1} H \to^{2} H + e^{+} + v^{2} H +^{1} H \to^{3} H e + γ^{3} H e +^{3} H e \to^{4} H e + 2^{1} H \end{matrix}}{4^{1} H \to 4 H e + 2 e^{+} + 2 v + 2 γ}$

Note that the first two reactions should occur twice to produce two

^3 H e

nuclei and initiate the third reaction. As a result of this cycle, effectively, four hydrogen nuclei combine to form a helium nucleus. About 26.7 MeV energy is released in the cycle. Thus, hydrogen is the fuel which ‘burns’ into helium to release energy. The sun is estimated to have been radiating energy for the last

4.5 \times 10^{9}

years and will continue to do so till all the hydrogen in it is used up. It is estimated that the present store of hydrogen in the sun is sufficient for the next

5 \times 10^{9}

years.

In hotter stars where the temperature is (

\approx 10^{8}

K), another cycle known as proton–carbon cycle takes place.

$^{1} H +^{12} C \to^{13} N + γ$
$^{13} N \to^{13} C + e^{+} + v$
$^{1} H +^{13} C \to^{14} N + γ$
$^{1} H +^{14} N \to^{15} O + γ$
$^{15} O \to^{15} N + e^{+} + v$
$^{1} H +^{15} N \to^{12} C +^{4} H e$

The end result of this cycle is again the fusion of four hydrogen nuclei into a helium nucleus. Carbon nucleus acts only as a catalyst. When the temperature inside a star rises, such fusions do take place to produce heavier nuclei such as :

$^{4} H e +^{4} H e +^{4} H e \to^{12} C + γ$

The process can continue, finally producing elements in the iron region (A = 56) where the binding energy per nucleon is maximum. Elements heavier than iron can be produced by neutron absorption and subsequent beta decay.

POINT 4

Radioactivity :

The phenomena of disintegration of heavy elements into comparatively lighter elements by the emission of radiations is called radioactivity. This phenomenon was discovered by Henry Becquerel in 1896.

Nuclear Fission :

The process of the splitting of a heavy nucleus into two or more lighter nuclei is called nuclear fission.

Nuclear Chain Reaction :

If the particle starting the nuclear fission reaction is produced as a product and further takes part in the nuclear fission reaction, then a chain of fission reaction starts, which is called nuclear chain reaction.

Thermonuclear Energy :

The energy released during nuclear fusion is known as thermonuclear energy. Protons are needed for fusion while neutrons are needed for the fission process.

EXAMPLE 1

The nuclear mass of $._{26} F^{56}$ is 55.85u. Calculate its nuclear density.

$M_{F e} = 55.85, u = 9.27 \times 10^{- 26} k g$
Nuclear density $= \frac{mass}{volume} = \frac{9.27 \times 10^{- 26}}{(4 π / 3) {(1.2 \times 10^{- 15})}^{3}} \times \frac{1}{56}$
$= 2.29 \times 10^{17} k g m^{- 3}$
The density of matter in neutron stars (an astrophysical object) is comparable to this density. This shows that matter in these objects has been compressed to such an extent that they resemble a big nucleus

Learn more

EXAMPLE 2

Find the energy equivalent of one atomic mass unit, first in joule and then in MeV. Using this, express the mass defect of $._{8} O^{16}$ in Me $V / c^{2}$ . Given $M_{p} = 1.007825 u$ and $M_{n} = 1.008665 u, m_{oxy} = 15.99053$ a.m.u. and Take $1 a . m . u = 933.75 M e V / c^{2}$ .

$l u = 1.6605 \times 10^{- 27} k g$
To convert it into energy units, we multiply it by c2 and find that energy equivalent $= 1.6605 \times 10^{- 27} \times {(2.9979 \times 10^{8})}^{2} k g m^{2} / s 2$
$= 1.4924 \times 10^{- 10} J$
$= \frac{1.4924 \times 10^{- 10}}{1.602 \times 10^{- 19}} e V$
$= 0.9315 \times 10^{9} e V$
$= 931.5 M e V$
or, $l u = 931.5 M e V / c^{2}$
For $._{8}^{16} O, Δ M = 0.13691 u = 0.13691 \times 931.5 M e V / c^{2}$
$= 127.5 M e V / c^{2}$
The energy needed to separate $._{8}^{16} O$ into its constituents is thus $127.5 M e V / c^{2}$ .

Learn more

EXAMPLE 3

The half life of $._{92} U^{238}$ against $α$ -decay is $4.5 \times 10^{9}$ years. What is the activity of 1g sample of $._{92} U^{238}$ ?

$T_{1 / 2} = 4.5 \times 10^{9} y$
$= 4.5 \times 10^{9} y \times 3.16 \times 10^{7} s / y$
$= 1.42 \times 10^{17} s$ One k mol of any isotope contains Avogadro’s number of atoms, and so 1g of $._{92} 238) U$ contains
$\frac{1}{238 \times 10^{- 3} k m o l \times 6.025 \times 10^{26}}$ atoms /Kmol
$= 25.3 \times 10^{20}$ atoms.
The decay rate R is
R = λN
$= \frac{0.693}{T_{1 / 2} N = \frac{0.693 \times 25.3 \times 10^{20}}{1.42 \times 10^{17}} s^{- 1}}$
$= 1.23 \times 10^{4} s^{- 1}$
$= 1.23 \times 10^{4} B q$

Learn more

EXAMPLE 4

(a) Two stable isotope of $._{3} L i^{6}$ and $._{3} L i^{7}$ have respective abundances of $7.5 %$ and $92.5 %$ . These isotopes have masses 6.01512 and 7.01600 u respectively. Find the atomic weight of lithium.
(b) Boron has two stable isotopes $._{5} B^{10}$ and $._{5} B^{11}$ . Their respective masses are 10.01294 u and 11.00931 u, and the atomic weight of boron is 10.81 u. Find the abundances of $._{5} B^{10}$ and $._{5} B^{11}$ .

(a) Mass of lithium isotope $_{(3)}^{6} L i, m_{1} = 6.01512 u$
Mass of lithium isotope $_{3}^{7} L i, m_{2} = 7.01600 u$
Abundance of $_{(3)}^{6} L i, η_{1} = 7.5 %$
$_{(3)}^{7} L i, η_{2} = 92.5 %$
The atomic mass of lithium atom is given as:
$m = \frac{m_{1} η_{1} + m_{2} η_{2}}{η_{1} + η_{2}}$
$= \frac{6.01512 \times 7.5 + 7.01600 \times 92.5}{92.5 + 7.5}$
$= 6.940934 u$
(b) Mass of boron isotope $_{(5)}^{10} B, m_{1} = 10.01294 u$
Mass of boron isotope $_{(5)}^{11} B, m_{2} = 11.00931 u$
Abundance of $_{(5)}^{10} B, μ_{1} = x %$
Abundance of $_{(5)}^{11} B, μ_{2} = (100 - x) %$
Atomic mass of boron, $m = 10.811 u$
The atomic mass of boron atom is given as:
$m = \frac{m_{1} η_{1} + m_{2} η_{2}}{η_{1} + η_{2}}$
$10.811 = \frac{10.01294 \times x + 11.00931 \times (100 - x)}{x + 100 - x}$
$∴ x = \frac{19.821}{0.99637} = 19.89 %$
And $100 - x = 80.11$
Hence, the abundance of $_{(5)}^{10} B is 19.89 %$ and that of $_{(5)}^{11} B is 80.11 %$

Learn more

SUMMARY

An atom has a nucleus. The nucleus is positively charged. The radius of the nucleus is smaller than the radius of an atom by a factor of 104 . More than 99.9% mass of the atom is concentrated in the nucleus.

On the atomic scale, mass is measured in atomic mass units (u). By definition, 1 atomic mass unit (1u) is

\frac{1}{12^{t h}}

mass of one atom of 12C;1u=

1.660563 \times 10^{- 27}

kg.

A nucleus contains a neutral particle called neutron. Its mass is almost the same as that of proton

The atomic number Z is the number of protons in the atomic nucleus of an element. The mass number A is the total number of protons and neutrons in the atomic nucleus; A = Z+N; Here N denotes the number of neutrons in the nucleus.

A nuclear species or a nuclide is represented as

_{Z}^{A} X

, where X is the chemical symbol of the species.

Nuclides with the same atomic number Z, but different neutron number N are called isotopes. Nuclides with the same A are isobars and those with the same N are isotones.
Most elements are mixtures of two or more isotopes. The atomic mass of an element is a weighted average of the masses of its isotopes and calculated in accordance to the relative abundances of the isotopes.

A nucleus can be considered to be spherical in shape and assigned a radius. Electron scattering experiments allow determination of the nuclear radius; it is found that radii of nuclei fit the formula :

R = $R_{0} A^{⅓}$

where

R_{0}

= a constant = 1.2 fm. This implies that the nuclear density is independent of A. It is of the order of

10^{17}

(kg)/

(m^{3})

Neutrons and protons are bound in a nucleus by the short-range strong nuclear force. The nuclear force does not distinguish between neutrons and protons.

The nuclear mass M is always less than the total mass,

Σ

m, of its constituents. The difference in mass of a nucleus and its constituents is called the mass defect

Δ M = (Z m_{p} + (A - Z) m_{n}) - M

Using Einstein’s mass energy relation, we express this mass difference in terms of energy as :

Δ E_{b} = Δ M c^{2}

Energies associated with nuclear processes are about a million times larger than chemical process.

The Q-value of a nuclear process is :
Q = final kinetic energy – initial kinetic energy.
Due to conservation of mass-energy, this is also,
Q = (sum of initial masses – sum of final masses)

c^{2}

Radioactivity is the phenomenon in which nuclei of a given species transform by giving out α or β or γ rays; α-rays are helium nuclei;β-rays are electrons. γ-rays are electromagnetic radiation of wavelengths shorter than X-rays;

Law of radioactive decay : N (t) = N(0)

e^{- λ t}

where λ is the decay constant or disintegration constant. The half-life

T (½)

of a radionuclide is the time in which N has been reduced to one-half of its initial value. The mean life τ is the time at which N has been reduced to

e^{- 1}

of its initial value

$T_{\frac{1}{2}} = \frac{ln 2}{λ} = τ ln 2$

The fact that more neutrons are produced in fission than are consumed gives the possibility of a chain reaction with each neutron that is produced triggering another fission. The chain reaction is uncontrolled and rapid in a nuclear bomb explosion. It is controlled and steady in a nuclear reactor. In a reactor, the value of the neutron multiplication factor k is maintained at 1.

In fusion, lighter nuclei combine to form a larger nucleus. Fusion of hydrogen nuclei into helium nuclei is the source of energy of all stars including our sun.

Home
Ask Doubt
Profile