बीजगणित कक्षा 6 गणित
भूमिका
बच्चों! पिछले अध्यायों मे हमने संख्याओं और आकारों का अध्ययन किया है। गणित की वह शाखा जिसमे संख्याओं पर अध्ययन किया जाता है, अंकगणित कहलाती है। इसी प्रकार आकारों अथवा आकृतियों पर अध्ययन किया जाता है, ज्यामिति कहलाती है।
इस अध्याय मे हम गणित की उस शाखा पर अध्ययन करेंगे जिसमे अक्षरों और प्रतीकों का प्रयोग किया जाता है। इस शाखा को ही बीजगणित कहा जाता है। अक्षरों अथवा प्रतीकों की सहायता से हम नियमों और सूत्रों को आसानी से व्यापक रूप मे लिख सकते है। अक्षर अज्ञात राशियों के स्थान पर भी प्रयोग किए जा सकते है।
आइये जानते है, बीजगणित को और करीब से...
बच्चों, हमने ऊपर पढ़ा कि बीजगणित में अक्षरों और प्रतीकों का प्रयोग किया जाता है। अक्षरों अथवा प्रतीकों की सहायता से हम नियमों और सूत्रों को आसानी से व्यापक रूप मे लिख सकते है।
आइए इसे एक उदाहरण से समझने का प्रयास करते हैं-
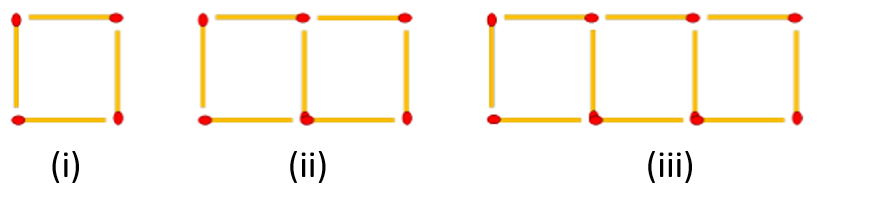
उपर्युक्त आकृतियों मे प्रयुक्त तीलियों की संख्या अलग - अलग है।
(i) एक वर्ग बनाने मे प्रयुक्त तीलियों की संख्या =4
(ii) दो वर्ग बनाने मे प्रयुक्त तीलियों की संख्या =7
(iii) तीन वर्ग बनाने मे प्रयुक्त तीलियों की संख्या =10
उपर्युक्त क्रम को यदि हम इसी प्रकार आगे बढ़ाते रहे तो हमे क्रमबद्ध वर्गों को बनाने मे प्रयुक्त तीलियों की संख्या प्राप्त होती रहेगी।
इस प्रकार यदि यहाँ तीलियों द्वारा बने वर्गों के प्रतिरूप को देखे तो क्रमशः 4,7,10 तीलियों का प्रयोग हुआ हैं।
व्यापक रूप में लिखने पर-
यहां 3n+1 सूत्र का प्रयोग हुआ है। जहाँ n= वर्गों की संख्या है।
अतः अक्षरों एवं संख्याओं के मिश्रित रूप का अध्ययन ही बीजगणित कहलाता है।
उदाहरण :-
50 वर्गों की आकृति बनाने मे कितनी तीलियों का उपयोग किया जाएगा ?
हल : चूंकि यहाँ n=50 वर्ग
अतः सूत्र से :-
=3n+1
=3×50+1
=151 तिलियाँ
अतः 50 वर्गों की आकृति बनाने मे 151 तीलियों की आवश्यकता होगी।
एक चर की अवधारणा
चर की परिभाषा : चर शब्द का अर्थ होता है वह वस्तु जो सदैव विचरण अर्थात बदलती रहती है।
चर का मान स्थिर नहीं रहता है यह कोई भी मान ग्रहण कर सकता है।
उपर्युक्त अध्ययन मे हमने वर्ग का प्रतिरूप बनाने मे आवश्यक तीलियों की संख्या ज्ञात करने के लिए निम्न सूत्र का प्रयोग किया था :-
=3n+1
⇒ यहाँ n वर्ग के प्रतिरूपों की संख्या है। अतः n के मान बदलते रहते है। n के मान मे वृद्धि करने पर परिणाम मे भी वृद्धि होती है।
यहाँ n भी एक चर का उदाहरण है तथा यह कोई भी मान ग्रहण कर सकता है।
चरों के अन्य उदाहरण
आइए चरों को एक और उदाहरण की सहायता से समझते है :-सरिता का कहना कि उसके कंचों के संग्रह में अमीना के कंचों के संग्रह से 10 अधिक कंचे हैं। यदि अमीना के पास 20 कंचे हैं, तो सरिता के पास 30 कंचे होंगे। यदि अमीना के पास 30 कंचे हैं, तो सरिता के पास 40 कंचे होंगे।
हमें यह ज्ञात नहीं है कि अमीना के पास कितने कंचे हैं। उसके पास कंचों की संख्या कुछ भी हो सकती है। परंतु हम जानते हैं कि सरिता के कंचों की संख्या =अमीना के कंचों की संख्या + 10 है।
यदि हम अमीना के कंचों की संख्या को x से दर्शाए। जहाँ x एक चर है, जिसका मान 1,2,3,4,....,10,......,20,....... हो सकता है।
अतः x का प्रयोग करते हुए, हम लिख सकते हैं कि
सरिता के कंचे =x+10 हैं। व्यंजक (x+10) को x धन (+)10 पढ़ा जाता है।
इसका अर्थ है कि x का मान 20 है, तो (x+10) का मान 30 होगा और यदि x का मान 30 है, तो (x+10) का मान 40 होगा इत्यादि।
अतः चर (x) के प्रयोग से हम आसानी से सरिता के कंचों के संग्रह का मान ज्ञात कर सकते है।
सामान्य नियमों मे चरों के प्रयोग
सामान्यतः हम दैनिक जीवन मे चरों का कई प्रकार से अध्ययन करते है। पिछले अध्याय मे हमे आयत, वर्ग आदि के परिमापों की गणना का अध्ययन किया था। वहाँ हमने इनके लिए सूत्रों का उपयोग किया था तथा सूत्रों मे अंग्रेजी वर्णमाला के छोटे अक्षरों का प्रयोग किया था। ये अक्षर ही चर कहलाते है। इसी प्रकार सभी क्षेत्रों मे चरों का प्रयोग किया जाता है।
आइए इनका अलग - अलग अध्ययन करते है :-
ज्यामिति के क्षेत्र मे :
(i) वर्ग का परिमाप :-
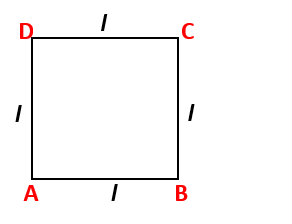
हम जानते हैं कि एक बहुभुज (3 या अधिक रेखाखंडों से बनी बंद आकृति) का परिमाप (perimeter) उसकी सभी भुजाओं की लंबाइयों का योग होता है। वर्ग में चार भुजाएँ होती हैं और प्रत्येक भुजा की लंबाई बराबर होती है ।
अतः वर्ग का परिमाप = वर्ग की भुजाओं की लंबाइयों का योग
=l+l+l+l
=4l यहाँ l= वर्ग की एक भुजा की माप
अतः चर l का प्रयोग करके हम एक सूत्र का निर्माण कर सकते है जिसे वर्ग का परिमाप ज्ञात करने के लिए आसानी से याद रखा जा सकता है।
(ii) आयत का परिमाप :-
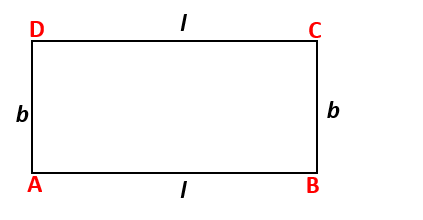
हम जानते हैं कि उपर्युक्त आकृति एक आयत की है। इसकी चार भुजाएँ AB,BC,CD और DA हैं।
एक आयत की सम्मुख भुजाएँ सदैव बराबर होती हैं। इसलिए, आयत ABCD की भुजाएँ AB और CD की लंबाई को l से तथा भुजाएँ AD और BC की लंबाई को b से व्यक्त करते है।
अतः, आयत का परिमाप = AB की लंबाई + BC की लंबाई + CD की लंबाई + AD की लंबाई
=l+b+l+b
=2l+2b
=2(l+b) यहाँ l और b क्रमश: आयत की लंबाई और चौड़ाई हैं।
अतः चर l और b का प्रयोग करके हम एक सूत्र का निर्माण कर सकते है जिसे आयत का परिमाप ज्ञात करने के लिए आसानी से याद रखा जा सकता है।
इस प्रकार ज्यामिति मे हम इन चरों के प्रयोग से आसानी से आकृतियों के क्षेत्रफलों, परिमापों, आयतनों, आदि की गणना के लिए सूत्रों का निर्माण कर सकते है।
अंकगणित के क्षेत्र मे :
(i) दो संख्याओं के योग की क्रमविनिमेयता :- हम जानते हैं कि
4+3=7 और 3+4=7 है अर्थात 4+3=3+4 है।
हम पूर्ण संख्याओं के अध्याय में इस गुण का अध्ययन कर चुके है। संख्याओं का यह गुण संख्याओं के योग की क्रमविनिमेयता (commutativity) कहलाता है।
' क्रमविनिमेय ' का अर्थ है - क्रम बदलना। योग में संख्याओं के क्रम को बदलने से उनके योग में कोई परिवर्तन नहीं होता है।
चरों के प्रयोग से हम इस गुण को संक्षिप्त रूप में व्यक्त करने में समर्थ होते है।
उदाहरण : मान लीजिए a और b दो चर हैं जो कोई भी संख्या का मान ले सकते हैं।
तब a+b=b+a होता है।
(ii) दो संख्याओं के गुणन की क्रमविनिमेयता :- हम पूर्ण संख्याओं के अध्याय में पढ़ चुके हैं कि दो संख्याओं के गुणन के लिए जिन दो संख्याओं का गुणा किया जाता है, उनके क्रम में गुणनफल पर कोई प्रभाव नहीं पड़ता है।
उदाहणार्थ :
4×3=12 है और 3×4=12 अत: 4×3=3×4 है।
संख्याओं का यह गुण संख्याओं के गुणन की क्रमविनिमेयता कहलाता है।
गुणन में संख्याओं के क्रम को बदलने पर गुणनफल में कोई परिवर्तन नहीं आता है। योग की तरह ही चर a और b का प्रयोग करके हम दो संख्याओं के गुणन की क्रमविनिमेयता को a×b=b×a के रूप मे लिख सकते है।
(iii) संख्याओं के योग पर गुणन की वितरणता :- माना कि हमें 7×38 की गणना करनी हो तो हम निम्न प्रकार लिख सकते है :-
7×38=7×(30+8)
=7×30+7×8
=210+56
=266
अतः 7,30 और 8 जैसी सभी तीन संख्याओं के लिए यह गुण सत्य है। यह गुण संख्याओं के योग पर गुणन की वितरणता (distributivity of multiplication over addition of numbers) कहलाती है।
चरों का प्रयोग करके, हम संख्याओं के इस गुण को भी एक व्यापक और संक्षिप्त रूप में लिख सकते हैं।
उदाहरण : मान लीजिए कि a,b और c कोई तीन चर हैं और इनमें से प्रत्येक कोई भी संख्या का मान ग्रहण कर सकता है। तब,
a×(b+c)=a×b+a×c होता है।
OMR (One Minute Revision)
चर का मान स्थिर नहीं रहता है यह कोई मान ग्रहण कर सकता है।
(i) ज्यामिति के क्षेत्र मे :
(ii) अंकगणित के क्षेत्र मे :
उदाहरण 1
एक बस v किमी प्रति घंटा की चाल से चल रही है। यह दासपुर से बीसपुर जा रही है। बस के 5 घंटे चलने के बाद भी बीसपुर 20 किमी दूर रह जाता है। दासपुर से बीसपुर की दूरी क्या है ? इसे v का प्रयोग करते हुए व्यक्त कीजिए।
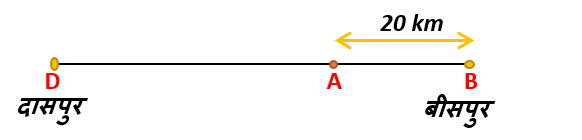
चूंकि दिया है :-
समय = 5 घंटे
चाल =v किमी./ घंटा
सूत्र ⇒ दूरी = चाल × समय
दासपुर से बिन्दु A तक दूरी =v किमी./ घंटा ×5 घंटे =5v किमी.
बिन्दु A से बीसपुर की दूरी =20 किमी.
अतः दासपुर से बीसपुर की कुल दूरी =
= दासपुर से बिन्दु A तक दूरी + बिन्दु A से बीसपुर की दूरी
=(5v+20) किमी.
उदाहरण 2
एक वर्ग की भुजा a है । वर्ग का परिमाप a का प्रयोग करके ज्ञात कीजिए।
चूंकि हम जानते है कि वर्ग की सभी भुजाएँ समान लंबाई की होती है। अतः
दिया है :-
वर्ग की एक भुजा की लंबाई =a
वर्ग का परिमाप = चारों भुजाओं का योग
=a+a+a+a
=4a जहाँ a= वर्ग की एक भुजा की लंबाई
अतः वर्ग का परिमाप 4a होगा।
उदाहरण 3
एक पेंसिल की कीमत 2 रु० और एक कलम की कीमत 15 रु० है। x पेंसिल और y कलमों की कीमत कितनी है ?
चूंकि दिया गया है :-
एक पेंसिल का मूल्य = 2 रुपए
एक कलम का मूल्य = 15 रुपए
माना x पेंसिलों का मूल्य = एक पेंसिल का मूल्य ×x रुपए
=2×x =2x रुपए
माना y कलमों का मूल्य = एक कलम का मूल्य ×y रुपए
=15×y =15y रुपए
अतः x पेंसिलों और y कलमों का मूल्य =(2x+15y) रुपए
चरों वाले व्यंजक
हम जानते हैं कि चर विभिन्न मान ले सकते हैं, इनका कोई निश्चित मान नहीं होता है। परंतु ये संख्याएँ हैं। इसी कारण, संख्याओं की ही तरह इन पर योग, व्यवकलन, गुणन और विभाजन की संक्रियाएँ भी की जा सकती हैं।
चरों वाले व्यंजकों के संबंध में एक महत्त्वपूर्ण बात ध्यान देने योग्य है। एक संख्यात्मक व्यंजक जैसे 4×3+5 का सरलता से मान निकाला जा सकता है।
उदाहरणार्थ:- 4×3+5=12+5=17
परंतु (4x+5) जैसे व्यंजक, जिसमें एक चर x आ रहा है, का मान निकालना संभव नहीं है। यदि चर x का मान दिया हो, केवल तभी व्यंजक का मान निकाला जा सकता है।
उदाहरणार्थ:- जब x=3 है, तो
=4x+5
=4×3+5
=17
यह मान हमे ऊपर पहले भी प्राप्त हुआ था।
इस प्रकार हम चरों का उपयोग करके व्यंजक बना सकते हैं। जैसे:-
2x+2, 4m, 5+t, 2z+1, 6x+4×2x आदि।
व्यंजकों का निर्माण:-
| y में 5 जोड़ने पर | y+5 |
| t में से 7 घटाने पर<td><td>t-7<td><tr><td>bको10सेभागदेनेपर<td><td>b /10<td><tr><td>पहलेy को2 से गुणा करके प्राप्त गुणनफल में से 5घटानेपर<td><td>2 y-5<td><tr><td>पहलेxको3सेगुणाकरकेप्राप्तगुणनफलमें2 जोड़ने पर | 3 x +2<td><tr><td>zको- 5सेगुणाकरनेपर<td><td>-5 z<td><tr><td>nमें2सेगुणाऔरफिरगुणनफलमेंसेlघटानेपर<td><td>2 n-l |
उदाहरण 4
निम्नलिखित में से कौन-से व्यंजक केवल संख्याओं वाले व्यंजक ही हैं ?
(a) y+3
(b) 7×20−8z
(c) 5(21−7)+7×2
(d) 5
(e) 3x
(f) 5−5n
(g) 7×20−5×10−45+p
ऐसा व्यंजक जिसमे केवल अचर राशि शामिल हो, केवल संख्याओं वाले व्यंजक कहलाते है।
(a) y+3
पुष्टि : चूंकि यहाँ y चर राशि है अतः यह केवल संख्याओं वाला व्यंजक नहीं है।
(b) 7×20−8z
=140−8z
पुष्टि : चूंकि यहाँ z चर राशि है अतः यह केवल संख्याओं वाला व्यंजक नहीं है।
(c) 5(21−7)+7×2
=5×14+14
=84
पुष्टि : चूंकि यहाँ कोई चर राशि नहीं है अतः यह केवल संख्याओं वाला व्यंजक है।
(d) 5
पुष्टि : चूंकि यहाँ कोई चर राशि नहीं है अतः यह केवल संख्याओं वाला व्यंजक है।
(e) 3x
पुष्टि : चूंकि यहाँ 3 के साथ गुणा मे x चर राशि है अतः यह केवल संख्याओं वाला व्यंजक नहीं है।
(f) 5−5n
=5(1−n)
पुष्टि : चूंकि यहाँ n चर राशि है अतः यह केवल संख्याओं वाला व्यंजक नहीं है।
(g) 7×20−5×10−45+p
=140−50−45+p
=45+p
पुष्टि : चूंकि यहाँ p चर राशि है अतः यह केवल संख्याओं वाला व्यंजक नहीं है।
उदाहरण 5
निम्नलिखित के लिए बीजीय व्यजंक लिखिए :-
(a) p को 4 से विभाजित करना।
(b) संख्या y को उसके पूर्ववर्ती से गुणा करना।
(c) किसी संख्या K को इसके परवर्ती से विभाजित करना।
(d) x और y के गुणनफल से 5 बड़ी संख्या
(e) y के तीन गुने में x के दो गुने का योग।
चर और अचर का सम्मिलित रूप बीजीय व्यंजक कहलाता है।
(a) p को 4 से विभाजित करना।
=p4
(b) संख्या y को उसके पूर्ववर्ती से गुणा करना।
y का पूर्ववर्ती =y−1
=y×(y−1)
(c) किसी संख्या k को इसके परवर्ती से विभाजित करना।
k का परवर्ती =k+1
=kk+1
(d) x और y के गुणनफल से 5 बड़ी संख्या
=x×y+5
(e) y के तीन गुने में x के दो गुने का योग।
=y×3+x×2
=3y+2x
व्यवहारिक रूप मे व्यंजकों का प्रयोग
| क्रम संo | साधारण भाषा मे वर्णित | चर | व्यंजकों का प्रयोग करते हुए कथन |
|---|---|---|---|
| (i) | सरिता के पास अमीना से 10 कंचे अधिक है। | माना अमीना के पास x कंचे है। | सरिता के पास (x+10) कंचे है। |
| (ii) | बालू राजू से 3 वर्ष छोटा है। | माना राजू की आयु x वर्ष है। | बालू की आयु (x−3) वर्ष है। |
| (iii) | विकास की आयु राजू की आयु की दोगुनी है। | माना राजू की आयु x वर्ष है। | विकास की आयु 2x वर्ष है। |
| (iv) | राजू के पिता की आयु राजू की आयु के तिगुने से 2 वर्ष अधिक है। | माना राजू की आयु x वर्ष है। | राजू के पिता की आयु (3x+2) वर्ष है। |
| (v) | आज से 5 वर्ष बाद वंश की आयु क्या होगी ? | माना वंश की वर्तमान आयु y वर्ष है। | आज से 5 वर्ष बाद वंश की आयु (y+5) वर्ष होगी। |
उदाहरण 6
लीला राधा की छोटी बहन है। लीला राधा से 4 वर्ष छोटी है। क्या आप लीला की आयु राधा की आयु के पदों में लिख सकते हैं ?
राधा की आयु x वर्ष है।
चूंकि दिया गया है :-
राधा की आयु =x वर्ष
लीला राधा से 4 वर्ष छोटी है अतः
लीला की आयु =x−4 वर्ष
उदाहरण 7
संतरों को बड़ी पेटियों में से छोटी पेटियों में रखा जाना है। जब एक बड़ी पेटी को खाली किया जाता है, तो उसके संतरों से दो छोटी पेटियाँ भर जाती हैं और फिर भी 10 संतरे शेष रह जाते हैं। यदि एक छोटी पेटी में संतरों की संख्या को x लिया जाए, तो बड़ी पेटी में संतरों की संख्या क्या है ?
माना बड़ी पेटी मे संतरों की संख्या =y
बड़ी पेटी से छोटी पेटीयो की संख्या =2
दोनों छोटी पेटियों मे संतरों की संख्या =x+x
शेष बचे संतरे =10
अतः बड़ी पेटी मे संतरों की संख्या y=x+x+10
y=2x+10
एक समीकरण
एक समीकरण बनाना
उदाहरण से समझते हैं -
किसी संख्या में 6 का गुणा एवं उसमे 10 जोड़ने पर परिणाम 52 आता हैं।
हल:
चूँकि हम इस संख्या के बारे में कुछ नहीं जानते, अतः यह कोई भी संख्या हो सकता है।
अज्ञात संख्या को एक अक्षर x से व्यक्त करते हैं। (x के स्थान पर कोई अन्य अक्षर जैसे y, t, z भी ले सकते हैं)
प्रश्न के अनुसार,
अज्ञात संख्या (x)×6+10=52
⇒6x+10=52 ................(i)
अतः इस समीकरण का हल अज्ञात संख्या x का मान बताएगा।
इसी प्रकार, किसी अज्ञात संख्या में 10 का गुणा करने पर और गुणनफल में 20 घटाने पर परिणाम 50 आता हैं।
चूँकि हम इस संख्या के बारे में कुछ नहीं जानते, अतः यह कोई भी संख्या हो सकता है।
अज्ञात संख्या को एक अक्षर y से व्यक्त करते हैं।
प्रश्न के अनुसार,
y×10−20=50
⇒10y−20=50 ................(ii)
अतः इस समीकरण का हल अज्ञात संख्या y का मान बताएगा।
समीकरण चर पर एक प्रतिबंध होता है। प्रतिबंध यह है कि दोनों व्यंजकों के मान बराबर होने चाहिए तथा दोनों व्यंजकों में से कम से कम एक में चर अवश्य होना चाहिए या ऐसा बीजीय व्यंजक जिसमे चर के विशिष्ट मान के लिए दोनों पक्ष समान होते हैं। समीकरण कहलाता है।
समीकरण के गुण
4x+5=6x−25 को 6x−25=4x+5 भी लिख सकते हैं।
समीकरण का हल
समीकरण मे चर का वह मान जो समीकरण को संतुष्ट करता है, उस समीकरण का एक हल कहलाता है।
आइए एक उदाहरण से समझते है:-
उदाहरण : 3x+4=7
LHS =3x+4
RHS =7
यहाँ, हम x=1 रखते हैं
LHS=RHS
3×1+4=7
7=7
अतः x=1 के लिए, LHS =RHS अर्थात x=1 समीकरण को संतुष्ट करता हैं।
अर्थात चर के जिस मान से समीकरण के दोनों पक्ष बराबर होते है वही उस समीकरण का हल कहलाता है।
OMR (One Minute Revision)
उदाहरण 8
समीकरण के सम्मुख कोष्ठक में दिए मानों में से समीकरण का हल चुनिए।
दर्शाइए कि अन्य मान समीकरण को संतुष्ट नहीं करते हैं।
q2=7 (7,2,10,14)
चर का वह मान जो समीकरण को संतुष्ट करता है अर्थात दाएँ और बाएँ पक्ष को बराबर करता है, समीकरण का हल कहलाता है।
चूंकि दिया है :- समी. q2=7
(i) q=7 लेने पर
⇒ 72≠7
⇒ यहाँ बायाँ पक्ष ≠ दायाँ पक्ष
अतः q=7 समी. का हल नहीं है।
(ii) q=2 लेने पर
⇒ 22=7
⇒ 1≠7
⇒ यहाँ बायाँ पक्ष ≠ दायाँ पक्ष
अतः q=2 समी. का हल नहीं है।
(iii) q=10 लेने पर
⇒ 102=7
⇒ 5≠7
⇒ यहाँ बायाँ पक्ष ≠ दायाँ पक्ष
अतः q=10 भी समी. का हल नहीं है।
(iv) q=14 लेने पर
⇒ 142=7
⇒ 7=7
⇒ यहाँ बायाँ पक्ष = दायाँ पक्ष
अतः q=14 समी. का हल है।
उदाहरण 9
यदि a=2 और b=3 हो तो निम्नांकित बीजीय व्यंजको के मान ज्ञात करे।
(i) 2x+3b
(ii) 3a−2b+1
चूंकि हमे दिया गया है :-
a=2
b=3
(i) 2a+3b
समी. मे मान रखने पर
=2×2+3×3
=4+9
=13
(ii) 3a−2b+1
समी. मे मान रखने पर
=3×2−2×3+1
=6−6+1
=1
उदाहरण 10
कौन - सा मान समीकरण : n+12=20 को संतुष्ट करता है।
दिया गया है :-
समीकरण : n+12=20
चूंकि हम जानते है कि समीकरण के दोनों पक्षों मे से समान संख्या घटाने से समीकरण के मान पर कोई प्रभाव नहीं पड़ता है। अतः
समीकरण के दोनों पक्षों मे से 12 घटाने पर
n+cancel(12)-cancel(12)=20-12
n=8
अतः n=8, समीकरण n+12=20 को संतुष्ट करता है।
