आधारभूत ज्यामितीय अवधारणाएँ कक्षा 6 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम आधारभूत ज्यामितीय अवधारणाओ का अध्ययन करेंगे। आपने पिछली कक्षाओं मे विभिन्न अवधारणाओ के बारे में पढ़ा है। ज्यामिति, गणित की तीन शाखाओ मे से एक है जिसमे बिन्दुओ, रेखाओ, त्रिभुजों आदि के गुणों, मापन, जैसी स्थितिओ का अध्ययन किया जाता है। इस अध्याय मे हम बिन्दु, रेखाखण्ड, प्रतिच्छेदी रेखाएँ, समांतर रेखाएँ, किरण, वक्र, बहुभुज, कोण, त्रिभुज, चतुर्भुज, वृत्त तथा इनसे संबंधित बिन्दुओ का अध्ययन करेगे।
आइये जानते है, ज्यामितीय अवधारणाओ को और करीब से...
ज्यामिति में सबसे बुनियादी आकार बिंदु है। ज्यामिति में, किसी विशिष्ट स्थान या स्थिति का प्रतिनिधित्व करने के लिए एक बिंदु का उपयोग किया जाता है। एक बिंदु को अंग्रेजी वर्णमाला के बड़े अक्षर से दर्शाया जा सकता है। एक बिंदु की लंबाई, चौड़ाई या मोटाई जैसे कोई आयाम नहीं होते हैं। इस अध्याय मे हम बिन्दु, रेखाखण्ड, प्रतिच्छेदी रेखाएँ, समांतर रेखाएँ, किरण, वक्र, बहुभुज, कोण, त्रिभुज, चतुर्भुज, वृत्त तथा इनसे संबंधित बिन्दुओ का अध्ययन करेंगे।
बिन्दु (Point)
बिना आकृति तथा आकार वाले गणितीय सांकेतिक चिन्ह को बिन्दु कहते है अर्थात इसमे ना तो लंबाई होती है और ना ही चौड़ाई।
इसका प्रयोग केवल समतल मे एक स्थिति को दर्शाने के लिए किया जाता है।

रेखाखण्ड (Line Segment)
दो निश्चित बिन्दुओ के मध्य खिची गई सीधी रेखा, रेखाखण्ड कहलाती है।
यह अनंत तक नहीं बढ़ती है अर्थात इसकी लंबाई निश्चित होती है।
यहाँ चित्र मे A और B निश्चित बिन्दु है तथा AB रेखाखण्ड है।

विभिन्न प्रकार की रेखाएँ
रेखा
ऐसा रेखाखण्ड जिसको दोनों तरफ अनंत लंबाई तक बढ़ाया जा सके, रेखा कहलाती है अर्थात इसकी लंबाई निश्चित नहीं होती है क्योंकि इसका प्रारम्भिक व अंतिम बिन्दु नहीं होता है। रेखाखण्ड, रेखा का ही एक भाग होता है।
रेखाओ के प्रकार
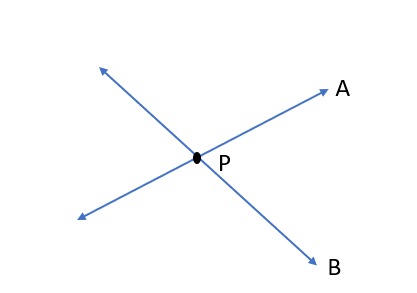
1. प्रतिच्छेदी रेखाएँँ : यदि दो रेखाओ मे एक उभयनिष्ठ बिन्दु हो तो वे रेखाएँ परस्पर प्रतिच्छेदी रेखाएँ कहलाती है।अर्थात जब दो रेखाएँ परस्पर एक दूसरे को काटती है, तो वे रेखाएँ प्रतिच्छेदी रेखाएँ होती है तथा जहाँ ये रेखाएँ काटती है, वह बिन्दु प्रतिच्छेद बिन्दु कहलाता है।
चित्र मे रेखा A और B एक दूसरे को बिन्दु P पर काटती है। अतः बिन्दु P प्रतिच्छेद बिन्दु होगा।

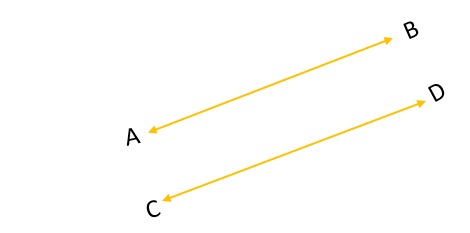
2. समांतर रेखाएँँ : ऐसी दो रेखाएँ जिनकी बीच की दूरी हमेशा समान रहे और वे एक दूसरे को कभी ना काटे अर्थात प्रतिच्छेद नहीं करे, समांतर रेखाएँँ कहलाती है।
इनके बीच का अंतर शून्य से अनंत तक समान रहता है।
चित्र मे रेखा AB व CD की बीच की दूरी समान है इसलिए ये आपस मे कभी नहीं मिलेगी।
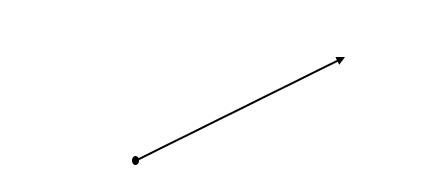
3. किरण : किरण रेखा का ही एक भाग होता है, यह एक निश्चित बिन्दु से प्रारंभ होती है तथा अनंत की ओर बढ़ती है।
4. वक्र : टेढ़ी-मेढ़ी रेखाएँ वक्र कहलाती है। यदि आप कागज मे कोई भी आकृति बनाते है तो वह वक्र का ही उदाहरण है। यदि बिन्दुओ का समूह समतल मे हों तो वह समतल वक्र कहलाता है।
वक्र भिन्न-भिन्न प्रकार के हो सकते है आइए इन्हे देखते है -
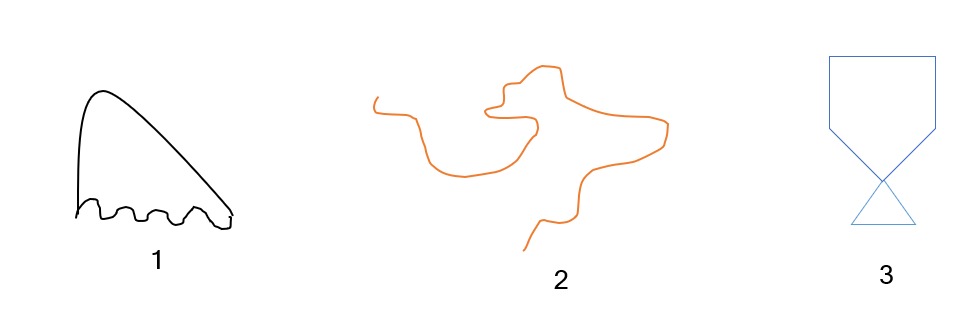
4.1 सरल वक्र : वह वक्र जो कभी स्वयं को ना काटे, अर्थात वक्र की रेखा स्वयं से होकर ना गुजरे सरल वक्र कहलाता है।

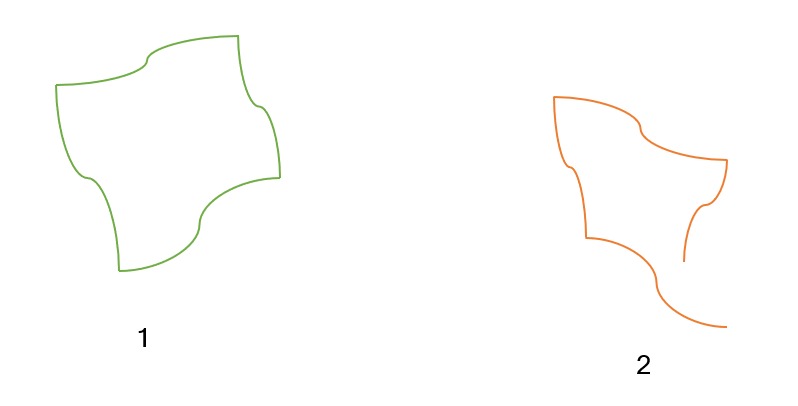
4.2 बंद वक्र : वह वक्र जिसकी रेखा के दोनों सिरों को एक बिन्दु पर मिला दिया जाता है, बंद वक्र कहलाता है। चित्र [1]
4.3 खुला वक्र : वह वक्र जिसकी रेखा के दोनों सिरों को कभी भी ना मिलाया जाए, खुला वक्र कहलाता है। चित्र [2]
OMR (One Minute Revision)
उदाहरण 1
दी गई आकृति मे कितने रेखाखण्ड है? नाम लिखिए।
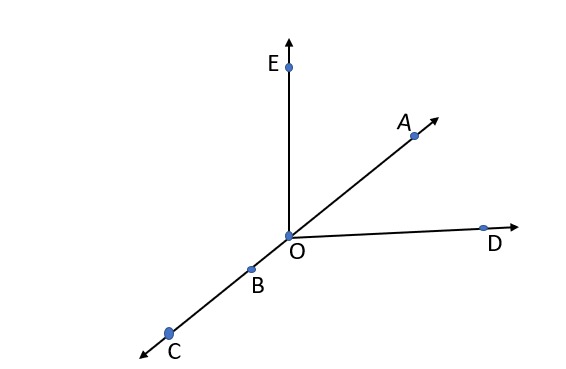
रेखाखण्ड 2 निश्चित बिन्दुओ के मध्य स्थित होता है, दी गई आकृति मे कुल 8 रेखाखण्ड है।
¯¯¯¯¯¯OE
¯¯¯¯¯¯OA
¯¯¯¯¯¯OD
¯¯¯¯¯¯OB
¯¯¯¯¯¯OC
¯¯¯¯¯¯BC
¯¯¯¯¯¯AC
¯¯¯¯¯¯AB
उदाहरण 2
रेखा ¯¯¯¯¯¯AB है तथा इस पर कुछ बिन्दु अंकित है। चित्र की सहायता से निम्न प्रश्नों का सत्य एवं असत्य के अनुसार उत्तर दीजिए ।
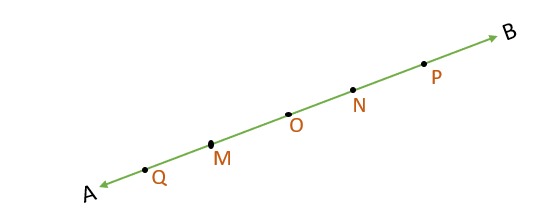
(a) Q,M,O,N और P रेखा ¯¯¯¯¯¯¯¯MN पर स्थित बिंदु है।
(b) M, O और N रेखाखण्ड ¯¯¯¯¯¯¯¯MN के अंतः बिंदु या अंतर्गत स्थित है।
(c) M और N रेखाखण्ड ¯¯¯¯¯¯¯¯MN के अंत बिंदु है।
(d) O और N रेखाखण्ड ¯¯¯¯¯¯OP के अंत बिंदु है।
(e) M, रेखाखण्ड ¯¯¯¯¯¯QO का अंत बिदु में से एक बिंदु है।
(f) M, किरण ¯¯¯¯¯¯OP पर एक बिंदु है।
(g) किरण ¯¯¯¯¯¯OP, किरण ¯¯¯¯¯¯QP से भिन्न है।
(h) किरण ¯¯¯¯¯¯OP वही है जो किरण ¯¯¯¯¯¯¯OM है ।
(i) किरण ¯¯¯¯¯¯¯OM, किरण ¯¯¯¯¯¯OP के विपरीत (Opposite) नहीं है।
(j) O किरण ¯¯¯¯¯¯OP का प्रारभिक बिंदु नहीं है।
(k) N किरण ¯¯¯¯¯¯NP और ¯¯¯¯¯¯¯¯NM का प्रारंभिक बिंदु है।
(a) सत्य (दिए गए सभी बिन्दु रेखा ¯¯¯¯¯¯¯¯MN पर स्थित है, चूंकि रेखा ¯¯¯¯¯¯¯¯MN व ¯¯¯¯¯¯AB एक ही रेखा है चूंकि रेखा ¯¯¯¯¯¯¯¯MN, दोनों सिरों से A व B की ओर बढ़ते हुए अनंत की ओर जा रही है।)
(b) सत्य (M व N रेखाखण्ड ¯¯¯¯¯¯¯¯MN के अंत बिन्दु व O मध्य मे स्थित है अतः अंतर्गत विद्यमान है।)
(c) सत्य (M व N रेखाखण्ड ¯¯¯¯¯¯¯¯MN के अंत अर्थात सिरों मे स्थित है।)
(d) असत्य (O रेखाखण्ड ¯¯¯¯¯¯OP का अंत बिन्दु है परन्तु N मध्य मे स्थित है।)
(e) असत्य (M रेखाखण्ड ¯¯¯¯¯¯QO के मध्य मे स्थित है।)
(f) असत्य (M किरण ¯¯¯¯¯¯OP पर स्थित नहीं है।)
(g) सत्य (किरण ¯¯¯¯¯¯OP व किरण ¯¯¯¯¯¯QP का प्रारम्भिक बिन्दु क्रमशः O व Q है, अतः भिन्न है।)
(h) असत्य (किरण ¯¯¯¯¯¯OP व किरण ¯¯¯¯¯¯¯OM एक दूसरे से विपरीत है, अतः भिन्न है।)
(i) असत्य (रेखा ¯¯¯¯¯¯AB मे बिन्दु M व P, O के क्रमशः बायें व दायें ओर स्थित है अतः किरण ¯¯¯¯¯¯OP व किरण ¯¯¯¯¯¯¯OM एक दूसरे से विपरीत है।)
(j) असत्य (किरण ¯¯¯¯¯¯OP, O से प्रारंभ होकर P की ओर जाती है, अतः O किरण ¯¯¯¯¯¯OP का प्रारम्भिक बिन्दु है।)
(k) सत्य (किरण ¯¯¯¯¯¯NP व किरण ¯¯¯¯¯¯¯¯NM दोनों की शुरुआत N से प्रारंभ होकर क्रमशः P व M की ओर जाती है, अतः N किरण ¯¯¯¯¯¯NP व ¯¯¯¯¯¯¯¯NM का प्रारम्भिक बिन्दु है।)
बहुभुज (Polygons)
एक सरल बंद आकृति, जो केवल रेखाखण्डों से मिलकर बनी होती है बहुभुज कहलाती है।
इसके निम्न भाग होते है -
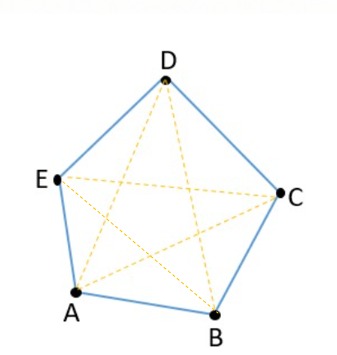
चित्र में ¯¯¯¯¯¯AB, ¯¯¯¯¯¯BC, ¯¯¯¯¯¯CD, ¯¯¯¯¯¯DE और ¯¯¯¯¯¯EA बहुभुज की भुजाएँ है।
चित्र में A, B, C, D और E बहुभुज के शीर्ष हैं।
चित्र मे - ¯¯¯¯¯¯AB और ¯¯¯¯¯¯BC, ¯¯¯¯¯¯BC और ¯¯¯¯¯¯CD, ¯¯¯¯¯¯CD और ¯¯¯¯¯¯DE, ¯¯¯¯¯¯DE और ¯¯¯¯¯¯EA, तथा ¯¯¯¯¯¯EA और ¯¯¯¯¯¯AB बहुभुज की आसन्न भुजाएँ हैं।
चित्र मे A और B, B और C, C और D, D और E तथा E और A बहुभुज के आसन्न शीर्ष हैं।
सूत्र :
बहुभुज के विकर्णों की संख्या =n×(n−3)2
[ जहाँ n= बहुभुज के भुजाओं की संख्या]
चित्र मे रेखाखण्ड - ¯¯¯¯¯¯AC, ¯¯¯¯¯¯AD, ¯¯¯¯¯¯BD, ¯¯¯¯¯¯BE तथा ¯¯¯¯¯¯CE बहुभुज के विकर्ण हैं।
उदाहरण 3
एक बहुभुज की भुजाओंं की संख्या एक अभाज्य संख्या है। यह संख्या दो सबसे छोटी अभाज्य संख्याओं के योग के बराबर है। इस बहुभुज के विकर्णों की संख्या ज्ञात कीजिए।
दो सबसे छोटी अभाज्य संख्याएँ = 2 व 3
अतः बहुभुज की भुजाओं की संख्या =2+3=5
सूत्र =
बहुभुज के विकर्णों की संख्या =n×(n−3)2
[ जहाँ n=भुजाओं की संख्या ]
=5×(5−3)2
=5×22
=102
=5
अतः बहुभुज के विकर्णों की संख्या 5 होगी।
कोण (Angle)
यदि कोई रेखा अपने एक सिरे को स्थिर रखकर, घूमती हुई अपनी स्थिति मे परिवर्तन करती है, तो रेखा के परिक्रमण की माप को कोण कहते है।
अर्थात कोण वह आकृति है जो एक बिन्दु से दो सरल रेखाओ के निकलने पर बनती है।
इसके निम्न भाग होते है। -
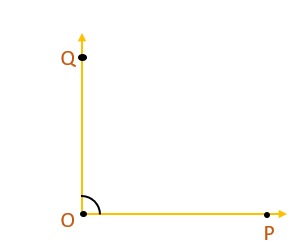
चित्र मे −−→OP व −−→OQ कोण की भुजाएँ है।
चित्र मे O कोण का शीर्ष है।
NOTE− कोण का नामकरण करते समय कोण का शीर्ष बीच मे होना चाहिए।
यहाँ कोण ∠POQ या ∠QOP है।
उदाहरण 4
आकृति में, वे बिंदु लिखिए, जो
(a) ∠DOF के अभ्यंतर में स्थित है।
(b) ∠EOF के बहिर्भाग में स्थित है।
(c) ∠EOF पर स्थित है।
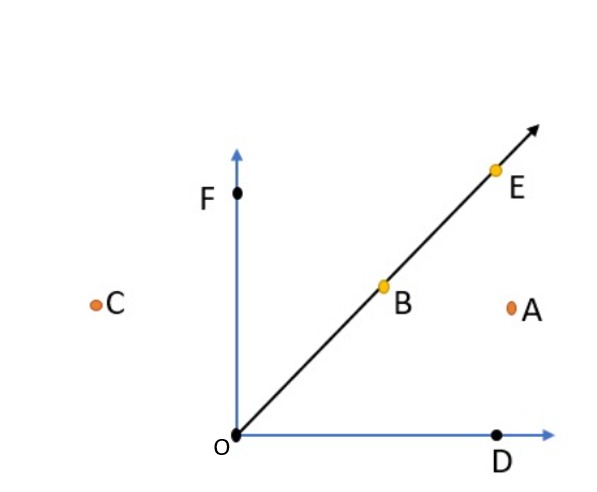
(a) ∠DOF मे अभ्यंतर बिन्दु = B, E,और A
(b) ∠EOF के बहिर्भाग के बिन्दु = A, D और C
(c) ∠EOF पर स्थित बिन्दु = O, B, E और F
उदाहरण 5
आकृति में दिये गए कोणों के नाम तीन अक्षरों में लिखिए :
(a) ∠1 (b) ∠2 (c) ∠3 (d) ∠4 (e) ∠5 (f) ∠6
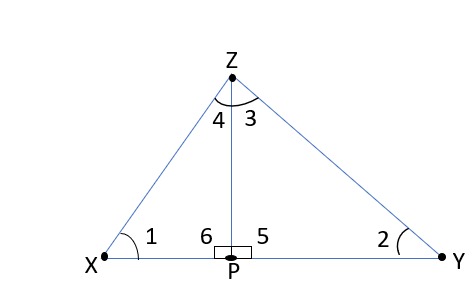
(a) ∠1=∠ZXY
(b)∠2=∠XYZ
(c)∠3=∠YZP
(d)∠4=∠XZP
(e) ∠5=∠YPZ
(f) ∠6=∠XPZ
त्रिभुज (Triangle)
तीन रेखाखण्डों से घिरी बंद आकृति, त्रिभुज कहलाती है।
इसकी निम्न विशेषताएँ होती है -
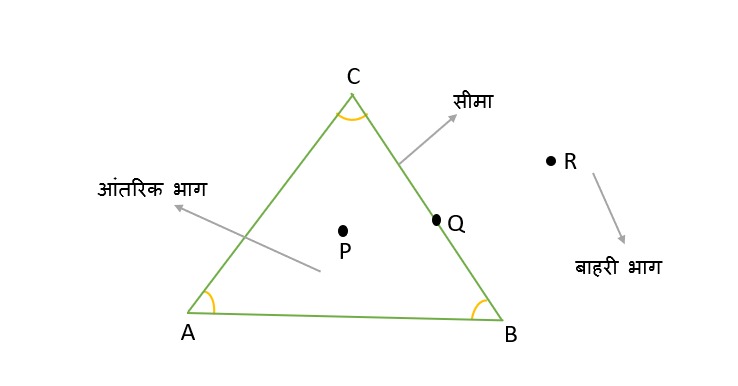
चित्र मे,
⇒¯¯¯¯¯¯AB, ¯¯¯¯¯¯BCऔर ¯¯¯¯¯¯AC इसकी तीन भुजाएँ है।
⇒∠BAC, ∠ABCऔर ∠BCA इसके तीन कोण है।
⇒A,B और C तीन शीर्ष है।
⇒बिन्दु P इसके आंतरिक भाग मे स्थित है तथा बिन्दु R इसके बाहरी भाग मे स्थित है।
संबंधित सूत्र -
त्रिभुज का क्षेत्रफल = 12× ( आधार ) × (ऊंचाई)
त्रिभुज का परिमाप = सभी भुजाओं का योगफल
उदाहरण 6
दी गई आकृति में बने कुल त्रिभुजों के नाम लिखिए।
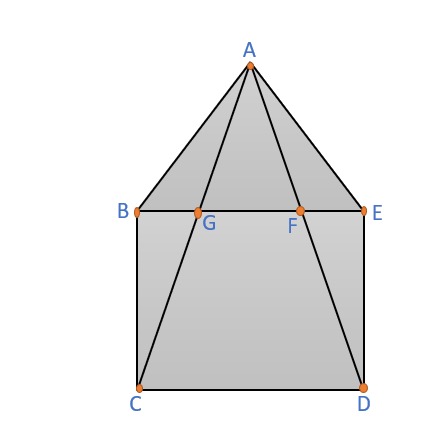
इस चित्र मे कुल 11 त्रिभुज है। -
(1) ΔABC
(2) ΔAED
(3) ΔACD
(4) ΔABE
(5) ΔABG
(6) ΔAGF
(7) ΔAFE
(8) ΔBGC
(9) ΔEFD
(10) ΔAFB
(11) ΔAGE
चतुर्भुज (Quadrilateral)
चार भुजाओंं से घिरी बंद आकृति चतुर्भुज कहलाती है।
इसकी निम्न विशेषताएं होती है -
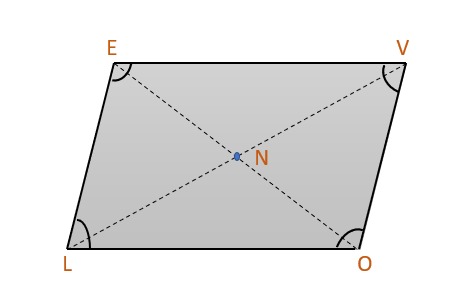
चित्र मे,
⇒¯¯¯¯¯¯LO, ¯¯¯¯¯¯OV, ¯¯¯¯¯¯VE और ¯¯¯¯¯¯EL इसकी चार भुजाएँ है।
⇒∠L, ∠O, ∠V और ∠E चार कोण है।
⇒ ¯¯¯¯¯¯LV और ¯¯¯¯¯¯OE इसके दो विकर्ण है।
⇒ बिन्दु N विकर्णों का कटान बिन्दु है, जो इसके आंतरिक भाग मे स्थित है।
⇒¯¯¯¯¯¯LO व ¯¯¯¯¯¯OV, ¯¯¯¯¯¯OV व ¯¯¯¯¯¯VE, ¯¯¯¯¯¯VE व ¯¯¯¯¯¯EL तथा ¯¯¯¯¯¯EL व ¯¯¯¯¯¯LO आसन्न भुजाओंं के युग्म है।
⇒ ¯¯¯¯¯¯LO व ¯¯¯¯¯¯EV तथा ¯¯¯¯¯¯LE व ¯¯¯¯¯¯OV सम्मुख भुजाओंं के युग्म है।
⇒∠L व ∠V तथा ∠O व ∠E सम्मुख कोणों के युग्म है।
⇒ ∠O व ∠V, ∠V व ∠E, ∠E व ∠L तथा ∠L व ∠O आसन्न कोणों के युग्म है।
संबंधित सूत्र -
चतुर्भुज का क्षेत्रफल = 12×( विकर्णों का गुणनफल )
उदाहरण 7
चित्र में A, B, C, D, P, Q, R, S, T, L और V बिन्दु है। निम्न में से कौन से बिन्दु चतुर्भुज के
(a) अभ्यंतर में है।
(b) बहिर्भाग में है।
(c) चतुर्भुज पर है।
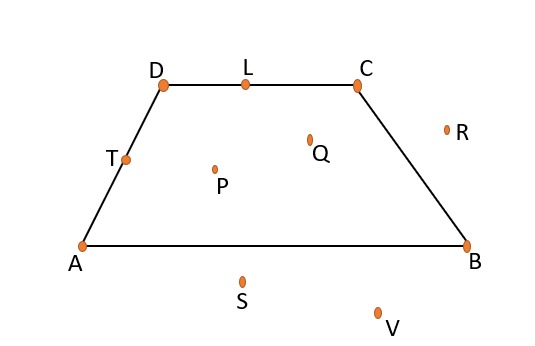
(a) बिन्दु P और Q चतुर्भुज के अभ्यंतर मे है।
(b) बिन्दु R, V और S चतुर्भुज के बहिर्भाग मे है।
(c) बिन्दु A, B, C, D, T और L चतुर्भुज पर स्थित है।
OMR (One Minute Revision)
(a) त्रिभुज के तीनों आंतरिक कोणों का योग 180∘ होता है।
(b) त्रिभुज का परिमाप उसकी तीनों भुजाओं का योग होता है।
(a) चतुर्भुज सरल या जटिल होते है।
(b) चतुर्भुज के चारों अंतः कोणों का योग 360∘ होता है।
(c) प्रत्येक चतुर्भुज मे दो विकर्ण होते है, वह चतुर्भुज सरल या जटिल हो सकता है।
वृत्त (Circle)
वृत्त एक बंद समतलीय आकृति होती है, जिसके मध्य मे एक बिन्दु होता है जो उस वृत्त का केंद्र होता है। वृत्त इसी केंद्र बिन्दु के चारों ओर वक्र रेखा से घिरा होता है ।
केंद्र बिन्दु के चारों ओर समान दूरी पर बिन्दुओ का समूह होता है जिससे वृत्त की सीमा वक्र बनती है। इस निकाय को ही वृत्त कहते है।
वृत्त एक साधारण बंद वक्र होता है जो समतल को दो भागों मे विभाजित करता है -
(i) आंतरिक भाग (अभ्यंतर)
(ii) बाहरी भाग (बहिर्भाग)
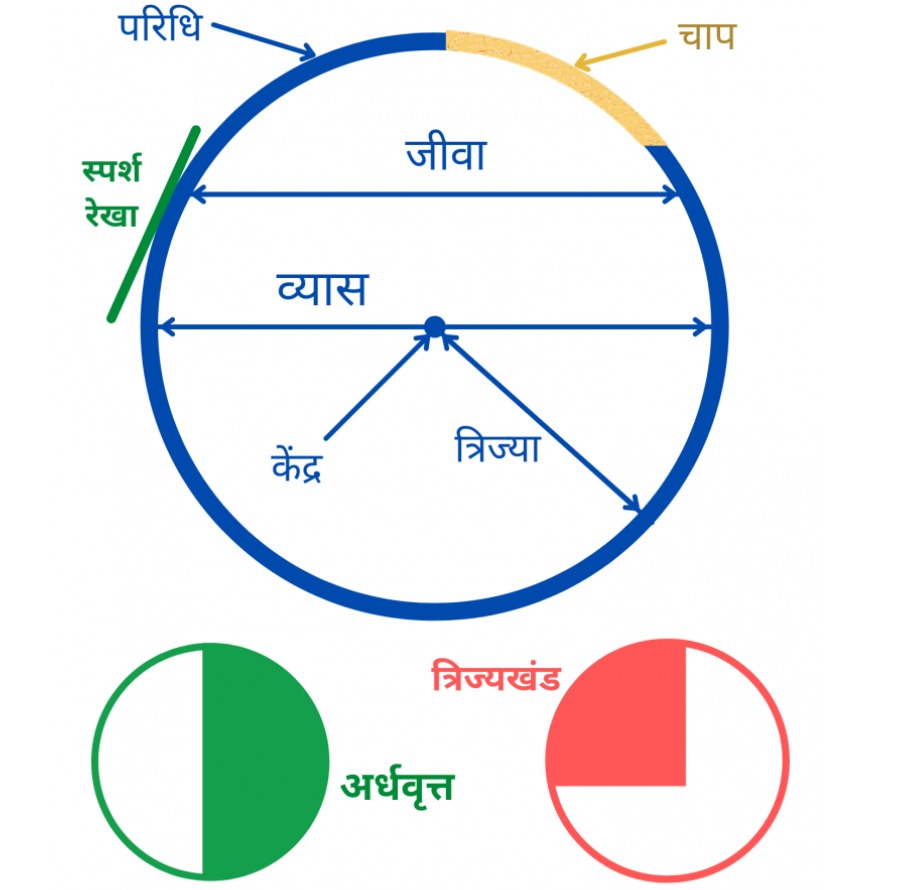
वृत्त के निम्न भाग होते है -
वृत्त का केंद्र: वृत्त के मध्य भाग मे स्थित वह बिन्दु जिसके चारों ओर वक्र रेखा से वृत्त घिरा होता है। वृत्त का केंद्र कहलाता है।
वृत्त की परिधि: वक्र रेखा की लंबाई को वृत्त की परिधि कहते है।
वृत्त की त्रिज्या : वृत्त के केंद्र से लेकर परिधि तक की दूरी को, वृत्त की त्रिज्या कहते है।
वृत्त का व्यास: परिधि पर किन्ही दो बिन्दुओ को मिलाने वाला रेखाखंड, जो वृत्त के केंद्र से होकर जाता है, वृत्त का व्यास कहलाता है।
वृत्त की जीवा: वृत्त पर किन्ही दो बिन्दुओ को मिलाने वाली रेखा वृत्त की जीवा कहलाती है। वृत्त का व्यास वृत्त की सबसे बड़ी जीवा होती है।
वृत्त का चाप: वृत्त की परिधि के किसी भी भाग को वृत्त का चाप कहते है।
वृत्त का त्रिज्यखंड: दो त्रिज्या तथा उनसे कटे चाप के द्वारा जो समतल घिरता है, उसे वृत्त का त्रिज्यखंड कहते है।
वृत्त का वृत्तखंड: वृत्त की एक जीवा और सगंत चाप से घिरा वृत्तीय क्षेत्र का भाग एक वृत्तखंड कहलाता है।
वृत्त के गुण:
वृत्त से संबंधित कुछ सूत्र:
वृत्त का क्षेत्रफल: πr2 वर्ग इकाई
वृत्त की परिधि: 2πr इकाई
अर्द्धवृत्त की परिधि: (πr+2r) इकाई
जहाँ π का मान लगभग 227 या 3.14 होता है तथा r वृत्त की त्रिज्या है।
उदाहरण 8
आकृति में निम्न के नाम बताइए
(a) तीन त्रिज्याएँ
(b) तीन जीवाएँ
(c) एक व्यास
(d) एक त्रिभुज जिसका शीर्ष वृत्त का केन्द्र O हो।
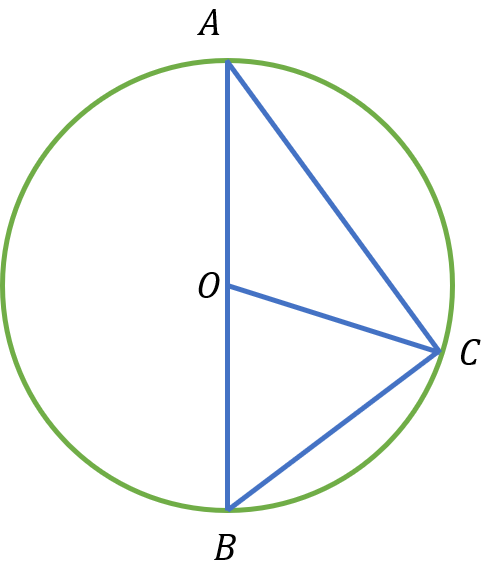
वृत्त का केंद्र O है तथा परिधि पर स्थित बिन्दु A,B और C है। अतः
(a) त्रिज्याएँ =OA,OB,OC
(b) जीवाएँ =AC,BC,AB
(c) व्यास =AB
(d) एक त्रिभुज जिसका शीर्ष वृत्त का केन्द्र O हो -
1.△OCA या
2.△OBC
सारांश
(a) बिन्दु A और B को मिलाने वाले रेखाखण्ड को ¯¯¯¯¯¯AB से दर्शाते है।
(a) यदि कोई वक्र स्वयं को न काटे तो वह एक सरल वक्र (Simple Curve) कहलाता है।
(b) एक वक्र जिसके सिरे मिले हुए हो, बंद वक्र (Closed Curves) कहलाता है।
(c) एक वक्र जिसके सिरे मिले हुए ना हो, खुला वक्र (Open Curves) कहलाता है।
(a) बहुभुज को बनाने वाले रेखाखंड, उसकी भुजाएँ (Arms) कहलाती है।
(b) कोई भी दो भुजाएँ, जिनमें एक उभयनिष्ठ अंत बिंदु हो, बहुभुज की आसन्न भुजाएँ (Adjacent Arms)कहलाती है।
(c) वह बिन्दु जहाँ दो भुजाएँ मिलती है, बहुभुज का शीर्ष (Vertex) कहलाता हैं।
(d) बहुभुज की एक ही भुजा के अंतः बिन्दु, आसन्न शीर्ष (Adjacent Vertex) कहलाते है।
(e) बहुभुज के वे शीर्ष, जो एक दूसरे से सटे नहीं होते है उनको मिलाने से बना रेखाखंड, बहुभुज का विकर्ण (Diagonal) कहलाता है।
(a) दो किरणें −−→OA और −−→OB कोण ∠AOB बनाती हैं।
(b) कोण से संबंधित तीन क्षेत्र हैं - कोण पर, कोण के अभ्यंतर और कोण के बहिर्भाग
(a) वृत्त के मध्य निश्चित बिंदु वृत्त का केंद्र (Centre) कहलाता है।
(b) निश्चित बिन्दु से परिधि तक की दूरी त्रिज्या (Radius) कहलाती है।
(c) वृत्त के चारों ओर निश्चित दूरी पर चली गयी दूरी, उसकी परिधि (circumference) कहलाती है।
(d) वृत्त पर किन्हीं दो बिंदुओं को मिलाने वाला रेखाखंड वृत्त की एक जीवा (chord) कहलाती है।
(e) केंद्र से होकर जाने वाली जीवा वृत्त का व्यास (Dimameter) कहलाती है।
(f) वृत्त की दो त्रिज्याओ और संगत चाप से घिरा वृत्तीय क्षेत्र का भाग त्रिज्यखंड (Sector) कहलाता है।
(g) वृत्त की एक जीवा और संगत चाप से घिरा वृत्तीय क्षेत्र का भाग एक वृत्तखंड (Segment of A Circle) कहलाता है।
(h) वृत्त के एक व्यास के दोनों अंत बिंदु उसे दो बराबर भागों में विभाजित करते हैं प्रत्येक भाग एक अर्धवृत्त (Semicircle) कहलाता है।