भिन्न कक्षा 6 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम भिन्नों का अध्ययन करेंगे। भिन्न (Fraction) एक संख्या होती है, जो पूर्ण के किसी भाग को दर्शाती है। जब हम किसी संख्या या वस्तु को एक से अधिक भागों मे बांटते है तो उस स्थिति मे भिन्न का निर्माण होता है। भिन्न अनेक प्रकार की होती है जैसे उचित भिन्न, अनुचित भिन्न, मिश्रित भिन्न आदि।
इस अध्याय मे हम भिन्नों के सभी प्रकारों, इनके सरलतम रूप, संख्या रेखा पर इनका निरूपण तथा इनके जोड़ एवं व्यवकलन का अध्ययन करेंगे।
आइये जानते है, भिन्नों को और करीब से...
बच्चों! हम जानते है की जब किसी संख्या या वस्तु को एक से अधिक भागों मे बांटते है, तो उस स्थिति मे भिन्न का निर्माण होता है।
जैसे : एक सेब के चार भाग किये जाते है जिनमें से उनके एक हिस्से को निकाल दिया गया है तो उसे 14 के रूप में लिखा जाता हैं और शेष बचे हुए भाग को 34 (1−14=34) के रूप में लिखा जाएगा।
इस अध्याय मे हम भिन्नों का विस्तार से अध्ययन करेंगे।
भिन्नों का परिचय
भिन्न (Fraction) गणित की एक महत्वपूर्ण अवधारणा हैं, जिसमे दो संख्याओंं को (उनके भाग अर्थात हिस्से को) भिन्न के द्वारा प्रदर्शित किया जाता हैं।
अर्थात भिन्न एक ऐसी संख्या होती है जो किसी सम्पूर्ण चीज़ के किसी भाग को निरूपित करती है।
एक भिन्न के दो भाग होते हैं :-
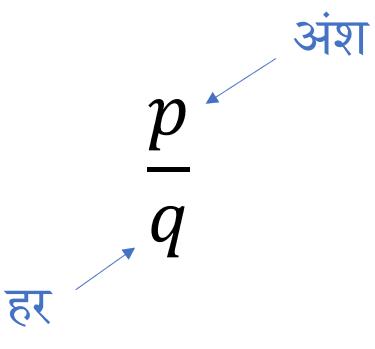
1. अंश : अंश भिन्न का वह भाग होता है जो ऊपर लिखा जाता है।
जैसे : 27 में 2 अंश है क्योंकि यह ऊपर लिखा गया है।
2. हर : हर भिन्न का वह भाग होता है जो अंश के नीचे लिखा जाता है।
जैसे : 27 में 7 हर है क्योंकि यह अंश के नीचे लिखा गया है।
उदाहरण : 12, 53, 634
ये सभी भिन्नों के उदाहरण है परंतु ये भिन्नों का कौनसा प्रकार है और कौनसी भिन्न बड़ी है एवं कौनसी छोटी, इसका अध्ययन आगे इस अध्याय मे करेंगे।
उदाहरण 1
निम्नलिखित भिन्न में अंश और हर को पहचानिए :
1817
चूंकि हम जानते है की
एक भिन्न के दो भाग होते हैं :-
1. अंश : अंश भिन्न का वह भाग होता है जो ऊपर लिखा जाता है।
अतः इस भिन्न (1817) में 18 अंश है क्योंकि यह ऊपर लिखा गया है।
2. हर : हर भिन्न का वह भाग होता है जो अंश के नीचे लिखा जाता है।
अतः इस भिन्न (1817) में 17 हर है क्योंकि यह नीचे लिखा गया है।
उदाहरण 2
6 घंटे एक दिन का कौन-सा भाग अथवा भिन्न है ?
चूंकि हम जानते है की -
एक दिन मे कुल 24 घंटे होते है। अतः
भिन्न =
=624
=14
अतः 6 घंटे एक दिन का 14 भाग होता है।
भिन्नों के प्रकार
बच्चों! मुख्यतः भिन्न 3 प्रकार की होती है :-
(1) साधारण भिन्न
(2) दशमलव भिन्न
(3) सतत या वितत भिन्न
इस अध्याय मे हम केवल साधारण भिन्नों का अध्ययन करेंगे।
साधारण भिन्न निम्न प्रकार की होती है :-
(i) उचित भिन्न (Proper fractions) : जब किसी भिन्न का अंश उसके हर से कम होता है, तो वह भिन्न उचित भिन्न कहलाती हैं।
उचित भिन्नों के अंश का परम मान उनके हर के परम मान से कम होता है। उचित भिन्न मे किसी वस्तु या संख्या के टुकड़े उसके हर के मान से ज्यादा नहीं किए जाते है।
अर्थात उचित भिन्न वह संख्या होती है जो एक पूर्ण (Whole) से छोटे किसी भाग को निरूपित करती है। इसमें हर यह दर्शाता है कि पूर्ण को कितने बराबर भागों में विभाजित किया गया है तथा अंश यह दर्शाता है कि इसमें से कितने भाग चुने गए हैं। अतः एक उचित भिन्न में अंश सदैव हर से छोटा होता है।
उदाहरण : 34
इसमे हर (4) यह दर्शा रहा है की इसे 4 बराबर भागों मे विभाजित किया गया है तथा अंश (3) यह दर्शा रहा है की 4 मे से 3 भाग चुने गए है।
अन्य उदाहरण : 23 , 57 , 12
(ii) अनुचित भिन्न (Improper fractions) : जब किसी भिन्न का अंश उसके हर से ज्यादा होता है, तो वह भिन्न अनुचित भिन्न कहलाती हैं।
अनुचित भिन्नों के अंश का परम मान उनके हर के परम मान से ज्यादा होता है।
अनुचित भिन्न को विषम भिन्न भी कहा जाता है।
अनुचित भिन्न मे किसी वस्तु या संख्या के टुकड़े उसके हर के मान से ज्यादा कर दिए जाते है।
उदाहरण : 54
इसमे हर का मान 4 है जबकि विभाजन 5 भागों मे किया गया है अतः यह अनुचित भिन्न है।
अन्य उदाहरण : 83 , 52 , 97
(iii) मिश्रित भिन्न (Mixed fractions) : वह भिन्न जो एक पूर्णाक एवं एक भिन्न से मिलकर बनी होती है, मिश्र भिन्न कहलाती है।
मिश्रित भिन्नों के दो भाग होते है जिनमे एक भाग पूर्ण संख्या होती है और दूसरा भाग उचित भिन्न होती है।
अनुचित भिन्नों को हल करने पर मिश्रित भिन्ने प्राप्त होती है।
उदाहरण : 634 , 234
अनुचित भिन्न को मिश्रित भिन्न मे बदलना :
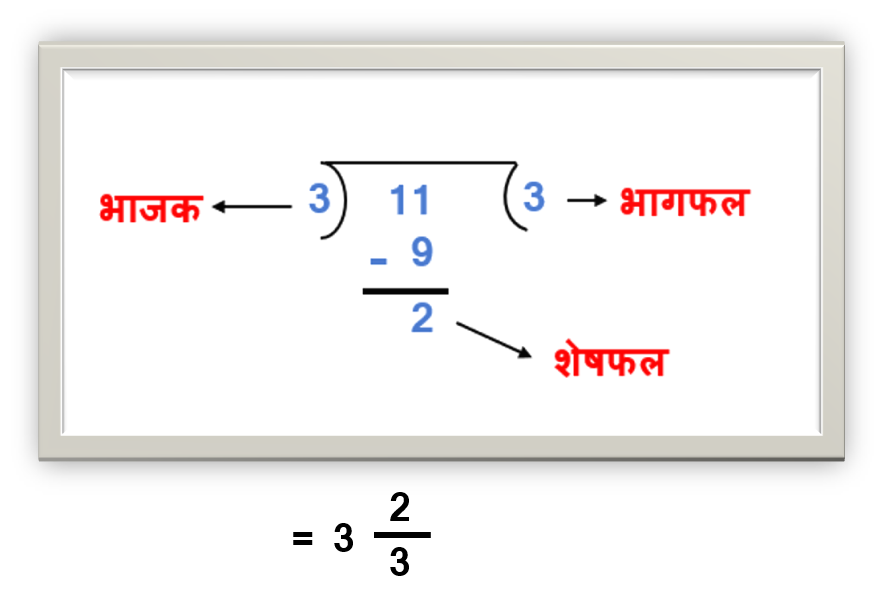
हम एक विषम भिन्न को एक मिश्रित भिन्न के रूप में व्यक्त कर सकते हैं। इसके लिए हम अंश को हर से भाग देकर भागफल और शेषफल प्राप्त करते हैं। फिर इनको निम्न प्रकार लिखते है :-

उदाहरण : 113 को मिश्रित भिन्न मे बदलिए ।
हल :
मिश्रित भिन्न को अनुचित भिन्न मे बदलना :
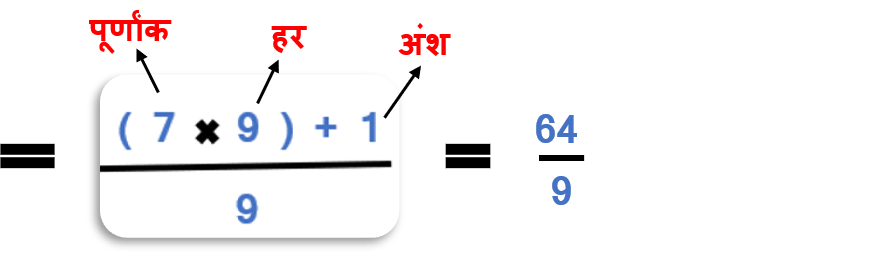
हम एक मिश्रित भिन्न को पुनः एक विषम भिन्न के रूप में व्यक्त कर सकते हैं। इसके लिए हम पूर्णांक को हर से गुणा करके गुणनफल मे अंश को जोड़ते है तथा नीचे हर को पुनः निम्न प्रकार लिख देते है।

उदाहरण : 719 को अनुचित (विषम) भिन्न मे बदलिए ।
हल :
(iv) तुल्य भिन्न (Equivalent fractions) : जब किसी भिन्न के अंश और हर को एक ही संख्या से गुणा करते है तो तुल्य भिन्न प्राप्त होती है।
अर्थात तुल्य भिन्नों की राशियाँ समान होती है। एक भिन्न की एक से अधिक तुल्य भिन्न हो सकती है।
उदाहरण : 12 की 2 तुल्य भिन्न लिखिए।
हल : तुल्य भिन्न प्राप्त करने के लिए हम इसके अंश और हर को 2 से गुणा करते है।
⇒1×22×2=24
एक और तुल्य भिन्न प्राप्त करने के लिए फिर से अंश और हर को 3 से गुणा करते है।
⇒1×32×3=36
इस प्रकार जितनी तुल्य भिन्न प्राप्त करनी है उतनी बार ही उस भिन्न के अंश और हर को समान संख्याओंं से गुणा करते है।
Note : एक दी गई भिन्न की तुल्य भिन्न ज्ञात करने के लिए हम उस भिन्न के अंश और हर को समान संख्या से भाग भी दे सकते है।
जैसे :- 1215 की तुल्य भिन्न लिखिए।
हल : तुल्य भिन्न प्राप्त करने के लिए हम इसके अंश और हर को 3 से भाग देते है।
⇒123153=45
(v) समान भिन्न (Like fractions) : समान हर वाली भिन्न समान भिन्न कहलाती है।
उदाहरण : 115 , 215 , 315 , 815 आदि।
(vi) असमान भिन्न (Unlike fractions) : असमान हर वाली भिन्न असमान भिन्न कहलाती है।
उदाहरण : 215 , 217 , 319 , 322 आदि।
OMR (One Minute Revision)
उदाहरण 3
कंचन ड्रेसों (Dress) को रंगने का कार्य करती है। उसे कुल 30 ड्रेस रंगनी थीं। अब तक वह केवल 20 ड्रेस ही रंग पाई है।
कंचन द्वारा रंगी गई ड्रेसों का भिन्न ज्ञात कीजिए ।
कंचन द्वारा रंगी जाने वाली कुल ड्रेसों की संख्या =30
उसके द्वारा रंगी जा चुकी ड्रेसों की संख्या =20
चूंकि हम जानते है की भिन्नों को pq के रूप लिखते है।
जहाँ p अंश को निरूपित करता है और q हर को निरूपित करता है। अतः
भिन्न =
=2030
=23
अतः कंचन कुल ड्रेसों का 23 भाग रंग चुकी है।
उदाहरण 4
निम्नलिखित मिश्रित भिन्न को विषम भिन्न में व्यक्त कीजिए :
719
मिश्रित भिन्न दो भागों मे विभाजित होती है जिसमे से एक पूर्णांक होता है तथा दूसरा भाग एक उचित भिन्न होती है।
आइये अब मिश्रित भिन्न को अंग्रेजी वर्णमाला से निरूपित करते है।
जैसे :- पूर्णांक को a से तथा उचित भिन्न को bc से निरूपित किया है अतः मिश्रित भिन्न =719=abc
विषम भिन्न मे बदलने के लिए हम a की c से गुणा करके उसमे b को जोड़ते है तथा c को पुनः नीचे निम्न प्रकार लिख देते है -
=a×c+bc
=7×9+19
=63+19
=649
उदाहरण 5
छायांकित भाग को निरूपित करने वाली भिन्न लिखिए ।

उपर्युक्त आकृति मे समान लंबाई - चोड़ाई के 8 भाग है। अतः
कुल भाग (हिस्से) =8
कुल छायांकित भाग =3
कुल छायांकित भाग का भिन्न =
=38
अतः छायांकित भाग का भिन्न 38 है।
उदाहरण 6
निम्नलिखित भिन्न की पाँच तुल्य भिन्न लिखिए ।
29
29 के पाँच तुल्य भिन्न निम्न प्रकार है :-
चूंकि हम जानते है की तुल्य भिन्नों की राशियाँ समान होती है।अतः इस भिन्न के अंश और हर को क्रमश: 2,3,4,5,6 से गुणा करते है।
(i)⇒ 2×29×2=418
(ii)⇒ 2×39×3=627
(iii)⇒ 2×49×4=836
(iv)⇒ 2×59×5=1045
(v)⇒ 2×69×6=1254
अतः 29 के पाँच तुल्य भिन्न =418,627,836,1045 और 1254 है।
संख्या रेखा पर भिन्नों का निरूपण
बच्चों! पिछले अध्यायों मे हम पूर्ण संख्याओंं (0,1,2,3,....) को संख्या रेखा पर दर्शा चुके है। अब हम भिन्नों को संख्या रेखा पर दर्शाना सीखेंगे।
आइये इसे चरणबद्ध तरीके से समझते है :-
चरण 1 : सर्वप्रथम एक संख्या रेखा खींचते है।
चरण 2 : फिर संख्या रेखा को उतने भागों मे बांटते है जितना की भिन्न मे हर का मान होता है। जैसे :
⇒ 12 के लिए संख्या रेखा को 2 बराबर भागों मे बांटते है।
⇒ 14 के लिए संख्या रेखा को 4 बराबर भागों मे बांटते है।
चरण 3 : फिर हम उन विभाजित भागों को देखकर सरलता से दी गई भिन्न को संख्या रेखा पर दर्शा सकते है।
आइये एक उदाहरण से समझते है :-
उदाहरण : संख्या रेखा पर 35 को दर्शाइए।
हल :
चरण 1 : सर्वप्रथम एक संख्या रेखा खींचते है।
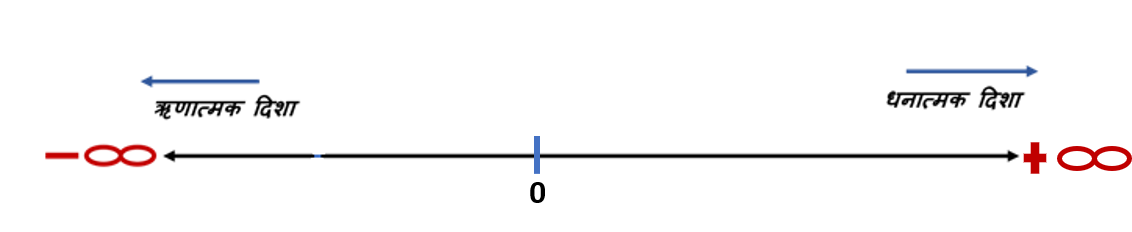
चरण 2 : चूंकि यह एक धनात्मक भिन्न है अतः शून्य के दाईं ओर धनात्मक दिशा मे इस संख्या रेखा पर 1 खाने को 5 बराबर भागों मे बांटते है क्योंकि यहाँ हर का मान 5 है।
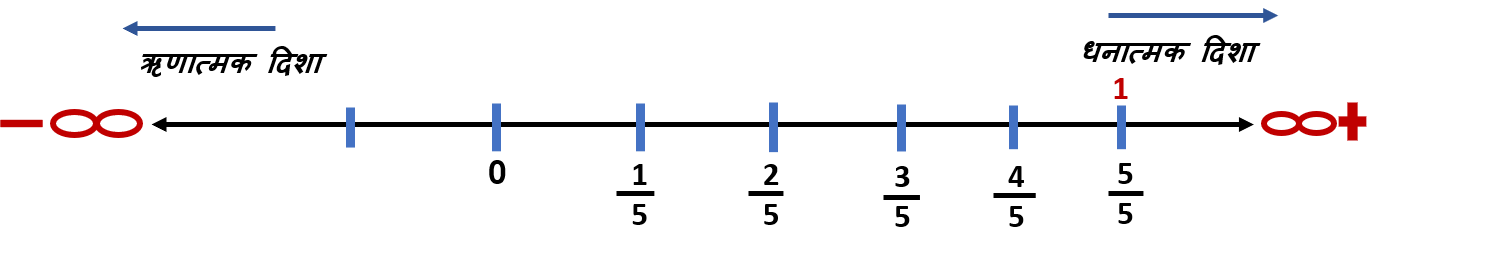
चरण 3 : अतः अब हम सरलता से 35 को निरूपित कर सकते है।
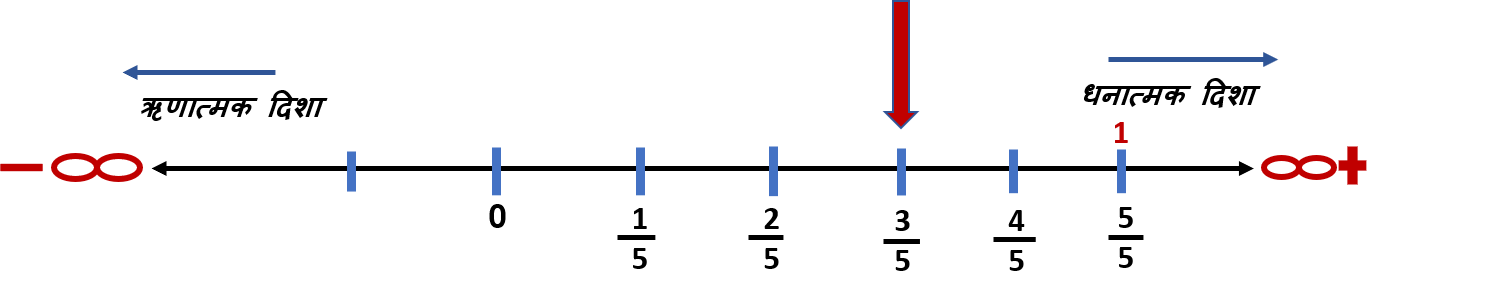
उदाहरण 7
संख्या-रेखा पर निम्नलिखित भिन्न को दर्शाइए:
−67
चरण 1 : सर्वप्रथम एक संख्या रेखा खींचते है।
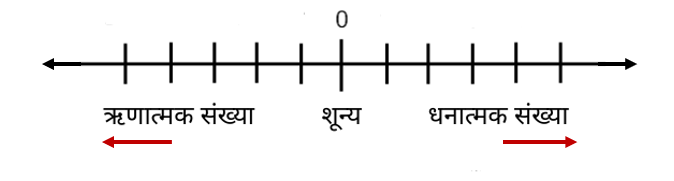
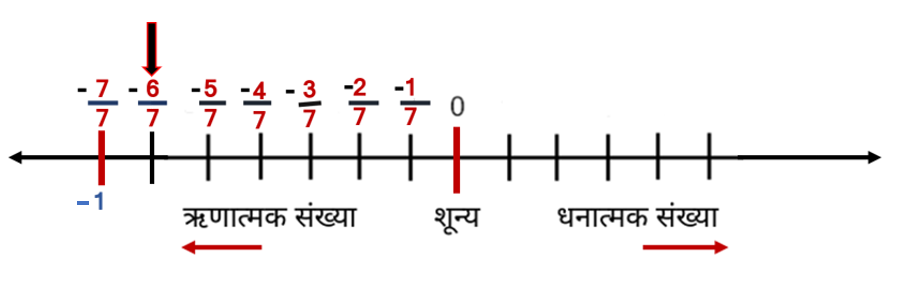
चरण 2 : चूंकि यह एक ऋणात्मक भिन्न है अतः शून्य के बाईं ओर ऋणात्मक दिशा मे इस संख्या रेखा पर 1 खाने को 7 बराबर भागों मे बांटते है क्योंकि यहाँ हर का मान 7 है।
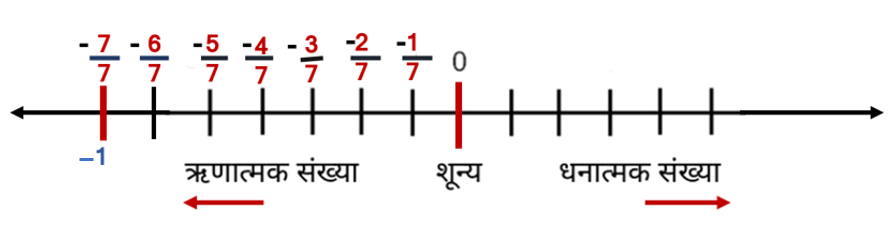
चरण 3 : अतः अब हम सरलता से −67 को निरूपित कर सकते है।
भिन्नों का सरलतम रूप
एक भिन्न सरलतम रूप (Simplest form) या न्यूनतम रूप (Lowest form) में तब कही जाती है, जब उसके अंश और हर में 1 के अतिरिक्त कोई अन्य उभयनिष्ठ गुणनखंड न हो।
अर्थात अंश और हर मे 1 के अलावा कोई अन्य सामान्य गुणनखंड नहीं होने की स्थिति मे वह उस भिन्न का सबसे सरलतम रूप कहलाता है।
आइये एक उदाहरण से समझते है :-
उदाहरण : 3654 का सरलतम रूप ज्ञात कीजिए।
हल : चूंकि हम जानते है की 36 और 54 दोनों 2 से विभाजित है अतः
चरण 1 : 362542=1827
इस स्थिति मे 18 और 27 मे 1 के अलावा अन्य उभयनिष्ठ गुणनखंड भी है जैसे 1,3,9
अतः हमे इसको और सरल करना पड़ेगा।
चरण 2 : 189279=23
इस स्थिति मे 2 और 3 मे 1 के अलावा अन्य कोई उभयनिष्ठ गुणनखंड नहीं है।
अतः यह 3654 का सबसे सरलतम या न्यूनतम रूप है।
सरलतम रूप ज्ञात करने की यह विधि बहुत कठिन होती है क्योंकि इस विधि मे भाग देने के लिए हम कई बार उचित संख्या का चयन नहीं कर पाते है।
अन्य विधि :
सरलतम या न्यूनतम रूप में तुल्य भिन्न ज्ञात करने की सबसे आसान विधि यह है कि दी हुई भिन्न के अंश और हर का म.स. (HCF) निकालकर अंश और हर दोनों को इस म.स. से भाग दिया जाता है।
इस प्रकार, हल करने पर हमे जो तुल्य भिन्न प्राप्त होती है वह उस भिन्न का सबसे सरलतम (न्यूनतम) रूप होता है।
उदाहरण : 3654 का सरलतम रूप ज्ञात कीजिए।
हल : चूंकि ल. स. और म. स. का अध्ययन हम पिछले अध्यायों मे कर चुके है।
अतः हम जानते है की 36 और 54 का म. स. 18 होता है। अब 18 का अंश और हर मे भाग देते है -
⇒36185418=23
अतः हम देख सकते है की इस विधि से हमने बहुत कम समय मे सरलता से भिन्न का सरलतम रूप ज्ञात किया है।
उदाहरण 8
7296 को सरलतम रूप में बदलिए।
चूंकि हम जानते है की एक भिन्न सरलतम रूप (Simplest form) या न्यूनतम रूप (Lowest form) में तब कही जाती है, जब उसके अंश और हर में 1 के अतिरिक्त कोई अन्य उभयनिष्ठ गुणनखंड न हो।
अतः इसके लिए हमे पहले इस भिन्न के अंश और हर का म. स. (HCF) निकालेंगे तथा फिर इस म. स. का अंश और हर मे भाग देंगे।
72 के गुणनखंड =2×2×2×3×3
96 के गुणनखंड =2×2×2×2×2×3
दोनों मे उभयनिष्ठ गुणनखंड =2×2×2×3
दोनों मे उभयनिष्ठ गुणनखंडों का गुणनफल ही इनका म. स. होगा अतः
72 और 96 का म. स. =24
अब इस म. स. का दी गई भिन्न के अंश और हर मे भाग देते है।
=72249624
=34
अतः इस प्राप्त भिन्न के अंश और हर मे 1 के अतिरिक्त अन्य कोई गुणनखंड नहीं है।
इसलिए 34 दी गई भिन्न (7296) का सबसे सरलतम रूप है।
भिन्नों की तुलना
216 और 338
बच्चों! उपर्युक्त भिन्नों को देखकर हम सरलता से बता सकते है की 338 बड़ी भिन्न है क्योंकि इसका पूर्णांक बड़ा है, परंतु हम 1517 और 2530 को केवल देखकर यह नहीं बता सकते है की इन दोनों मे से कोनसी भिन्न बड़ी है और कौनसी छोटी ।
अतः हम भिन्नों की तुलना करने के लिए एक क्रमबद्ध विधि का अध्ययन करेंगे।
(i) समान भिन्नों की तुलना : समान हर वाली भिन्ने समान भिन्ने कहलाती है।
चूंकि इनके हर समान होते है इसलिए इनकी तुलना अंशों के आधार पर की जाती है।
समान हर वाली भिन्न की स्थिति मे हमेशा वह भिन्न बड़ी होती है जिसका अंश बड़ा होता है।
उदाहरण : 35 और 45 मे से कोनसी भिन्न बड़ी है ?
हल : 45 बड़ी भिन्न है क्योंकि इसका अंश बड़ा है।
हम इसको निम्न प्रकार भी दर्शा सकते है - 45>35
(ii) असमान भिन्नों की तुलना :
(a) समान अंश वाली विषम (असमान) भिन्नों की तुलना : यदि दो भिन्नों के अंश समान हो तो इस स्थिति मे छोटे हर वाली भिन्न बड़ी होती है।
उदाहरण : 23 और 25 मे से कोनसी भिन्न बड़ी है ?
हल : 23 बड़ी भिन्न है क्योंकि इसका हर छोटा है।
अर्थात 23 मे इसका केवल एक भाग शेष बचा है जबकि 25 मे इसके 3 भाग शेष बचे है। इसलिए
⇒23>25
(b) भिन्न - भिन्न अंश और हर वाली विषम (असमान) भिन्नों की तुलना : यदि दी गई भिन्नों के अंश और हर दोनों अलग - अलग होते है तो इस स्थिति मे हम पहले दोनों भिन्नों की समतुल्य भिन्न ज्ञात करके हरो को समान करते है फिर उनकी समान भिन्नों की तरह तुलना करते है।
उदाहरण : 67 और 35 की तुलना कीजिए।
हल : चूंकि दी गई दोनों भिन्नों के अंश एवं हर असमान है अतः इस स्थिति मे इनकी तुलना करना असंभव है।
इसलिए हमे पहले इनके हरो को समान करना होगा। इसके लिए प्रत्येक भिन्न के अंश और हर को दूसरी भिन्न के हर से गुणा करते है।
⇒6×57×5
⇒3×75×7
अब इनको हल करके इनकी तुलना समान भिन्नों की तरह करते है।
⇒3035 और 2135
अब हम सरलता से बता सकते है 3035 बड़ी भिन्न है क्योंकि इसका अंश बड़ा है अतः
⇒67>35
जब हम भिन्नों को घटते हुए क्रम मे व्यवस्थित करते है, तो उसे अवरोही क्रम कहते है।
जब हम भिन्नों को बढ़ते हुए क्रम मे व्यवस्थित करते है, तो उसे आरोही क्रम कहते है।
OMR (One Minute Revision)
उदाहरण 9
□ स्थान मे <,=,> में से सही चिह्न भरिए:
413□316
चूंकि हमे पता है की दी गई भिन्ने असमान भिन्ने है, क्योंकि इनमे अंश ओर हर दोनों असमान है।
चरण 1 : अतः पहले हम दोनों भिन्नों के हरो को समान करते है। इसके लिए हम प्रत्येक भिन्न के अंश और हर को दूसरी भिन्न के हर से गुणा करते है।
⇒4×1613×16 और ⇒3×1316×13
चरण 2 : अब इनको हल करके समान भिन्नों की तरह तुलना करते है।
⇒64208 और ⇒39208
चरण 3 : अतः अब हम सरलता से बता सकते है की 64208 बड़ी भिन्न है, क्योंकि इसका अंश बड़ा है।
चूंकि 64208 दी गई भिन्न 413 की तुल्य भिन्न है अतः
⇒413>316
पिछले अध्यायों मे हम प्राकृत संख्याओंं, पूर्ण संख्याओंं तथा पूर्णांकों पर आधारित जोड़ एवं व्यवकलन कर चुके है। अब हम भिन्नों पर आधारित जोड़ एवं व्यवकलन करना सीखेंगे।
आइये इन्हे विस्तार से समझते है :-
समान भिन्नों का योग एवं व्यवकलन
समान भिन्नों का योग : समान भिन्नों का योग करना आसान होता है क्योंकि इसमे हर समान रहते है।
आइये एक उदाहरण से समझते है :-
उदाहरण : 35 और 15 को जोड़िए।
हल : आइये चरणबद्ध तरीके से समझते है -
चरण 1: सर्वप्रथम दोनों अंशों को जोड़ते है।
=3+1
चरण 2: फिर इसके नीचे उभयनिष्ठ हर को लिखते है।
=3+15
चरण 3: अब चरण 2 को हल करते है।
=45
समान भिन्नों का व्यवकलन : समान भिन्नों का व्यवकलन करना भी आसान होता है क्योंकि इसमे भी हर समान रहते है।
उदाहरण : 78 मे से 38 को घटाइए।
हल : आइये चरणबद्ध तरीके से समझते है -
चरण 1: सर्वप्रथम बड़े अंश मे से छोटे अंश को घटाते है।
=7−3
चरण 2: इसके नीचे उभयनिष्ठ हर को लिखते है।
=7−38
चरण 3: अब चरण 2 को आगे हल करते है।
=48
=12
अतः समान भिन्नों ( जिनका हर समान हो ) का योग एवं व्यवकलन करना बहुत ही आसान होता है।
उदाहरण 10
सुजाता ने 345 मी० कपड़ा खरीदा और उसकी बहन ने 415 मी० कपड़ा खरीदा।
उन दोनों ने मिलकर कुल कितना कपड़ा खरीदा ?
सुजाता द्वारा खरीदे गए कपड़े की माप =345 मी० ⇒ A
उसकी बहन द्वारा खरीदे गए कपड़े की माप =415 मी० ⇒ B
अतः उन दोनों द्वारा खरीदे गए कुल कपड़े की माप =A+B
=345+415
पहले इन मिश्र भिन्नों को हल करते है।
=(3×5)+45+(4×5)+15
=195+215
चूंकि इन दोनों भिन्नों के हर समान है अतः हर को नीचे कॉमन लेते है और फिर जोड़ते है।
=19+215
=405
=8 मीटर
अतः दोनों ने मिलकर कुल 8 मीटर कपड़ा खरीदा।
असमान भिन्नों का योग एवं व्यवकलन
असमान भिन्नों मे इनके हर अलग - अलग होते है ऐसी स्थिति मे इनका योग या व्यवकलन करना बहुत कठिन होता है। इसलिए असमान भिन्नों के योग एवं व्यवकलन करने के लिए पहले इनके हरो को समान करना होता है फिर इनको आगे हल किया जाता है।
असमान भिन्नों का योग : आइये चरणबद्ध तरीके से समझते है :-
उदाहरण : 45 और 38 को जोड़िए।
हल : चूंकि हम जानते है की दी गई भिन्ने असमान भिन्ने है अतः पहले इनके हरो को समान करते है।
चरण 1: सर्वप्रथम दी गई भिन्नों के हरो का ल. स. (LCM) लेते है।
चूंकि हम जानते है की 5 और 8 का ल. स. 40 होता है।
चरण 2: फिर प्रत्येक भिन्न के अंश और हर को दूसरी भिन्न के हर से गुणा करते है जिससे उनके हर समान अर्थात 40 हो जाए।
⇒ 4×85×8=3240
⇒ 3×58×5=1540
चरण 3: अब इन्हे समान भिन्नों की तरह जोड़ते है।
⇒ 3240+1540
⇒ 32+1540=4740
Note : दोनों भिन्नों का ल. स. लेने से हमे यह ज्ञात होता है की दोनों भिन्नों का उभयनिष्ठ हर कितना होगा।
असमान भिन्नों का व्यवकलन : आइये इसे भी चरणबद्ध तरीके से समझते है :-
उदाहरण : 45 मे से 38 को घटाइए।
चरण 1: सर्वप्रथम दी गई भिन्नों के हरो का ल. स. (LCM) लेते है।
चूंकि हम जानते है की 5 और 8 का ल. स. 40 होता है।
चरण 2: फिर प्रत्येक भिन्न के अंश और हर को दूसरी भिन्न के हर से गुणा करते है जिससे उनके हर समान हो जाए।
⇒ 4×85×8=3240
⇒ 3×58×5=1540
चरण 3: अब इन्हे समान भिन्नों की तरह घटाते है।
⇒ 3240−1540
⇒ 32−1540=1740
उदाहरण 11
रवि ने 534 किग्रा. चावल, 215 किग्रा. चीनी और 1025 किग्रा. आटा खरीदा।
ज्ञात कीजिए कि उसने कुल कितना वजन का सामान खरीदा ?
चावल का वजन =534 किग्रा. ⇒ A
चीनी का वजन =215 किग्रा. ⇒ B
आटा का वजन =1025 किग्रा. ⇒ C
अतः रवि द्वारा खरीदे गए कुल सामान का वजन =A+B+C
=534+215+1025
=5×4+34+2×5+15+10×5+25
=234+115+525
चूंकि ये असमान भिन्ने है अतः पहले इनका ल. स. (LCM) लेकर इनके हरो को समान करते है।
4,5 और 5 का ल. स. 20 होता है।
=(23×5)+(11×4)+(52×4)20
अब हम इन्हे समान भिन्नों की तरह हल कर सकते है क्योंकि तीनों भिन्नों का हर समान है।
=115+44+20820
=36720
=18720 किग्रा.
अतः रवि ने कुल 18720 किलोग्राम वजन का सामान खरीदा।
उदाहरण 12
56 मीटर कपड़ा में से 14 मीटर काट लिया गया। कितना कपड़ा शेष बचा ?
कुल कपड़े की माप =56 मी. ⇒ A
काटे गए कपड़े की माप =14 मी. ⇒ B
अतः बचे हुए कपड़े की माप =A−B
=56−14
चूंकि हम जानते है की ये असमान भिन्ने है अतः इनको हल करने के लिए पहले इनका ल. स. (LCM) लेते है।
6 और 4 का ल. स. 12 होता है।
अतः हर समान करने पर
=1012−312
अब हम इन्हे समान भिन्नों की तरह हल कर सकते है क्योंकि दोनों भिन्नों का हर समान है।
=10−312
=712
अतः कुल 712 मीटर कपड़ा बचा।