पूर्णांक कक्षा 6 गणित
भूमिका
बच्चों! इस अध्याय के शीर्षक के अनुसार इस अध्याय मे हम पूर्णांकों का अध्ययन करेंगे। इससे पहले के अध्याय मे हमने प्राकृत एवं पूर्ण संख्याओं का परिचय देखा है जिसमे हमने इन संख्याओं पर विभिन्न संक्रियाएँ ( जैसे - जोड़ना, घटाना आदि ) देखी थी। इस अध्याय मे हम पूर्णांकों के विभिन्न अंकगणितीय संक्रियाओं तथा उनके गुणों का अध्ययन करेंगे।
आइये जानते है, पूर्णांकों को और करीब से...
इससे पूर्व के अध्याय में हमने निम्न संख्याओं का अध्ययन किया हैं आइये उन्हे पुनः दोहराते हैं :-
प्राकृत संख्या (Natural Numbers)
जिन अंको का प्रयोग किसी भी चीज की गणना के लिए किया जाता है उन्हें प्राकृत संख्या कहते है।उदाहरण के लिए ;
1,2,3,......,∞
पूर्ण संख्या (Whole Numbers)
शून्य सहित सभी प्राकृत संख्याएँ पूर्ण संख्याएँ कहलाती हैं।उदाहरण के लिए ;
0,1,2,3,......,∞
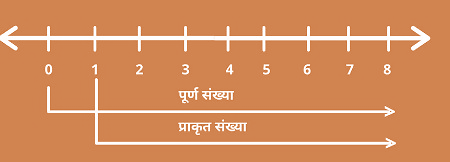
पूर्णांक
पूर्णांक (Integer) वे संख्याएँ होती हैं जो धनात्मक, ऋणात्मक या शून्य हो सकती हैं, लेकिन भिन्न नहीं हो सकती। इन संख्याओं का उपयोग विभिन्न अंकगणितीय संक्रियाओं जैसे जोड़, घटाव, गुणा और भाग को करने के लिए किया जाता है।
संख्याएँ निम्न प्रकार की होती है :-
धनात्मक संख्या :
1,2,3,4,...∞ तक कोई भी संख्या हो सकती है।
ऋणात्मक संख्या :
−1,−2,−3,...−∞ तक कोई भी संख्या हो सकती है।
शून्य संख्या : =0
अतः हम कह सकते है, की
−∞....−4,−3,−2,−1,0,1,2,3,4,5......+∞
तक सभी संख्याएँ पूर्णांक संख्याएँ होंगी।
जैसे की 10,15,0,50,−89,−28 ये सभी पूर्णांक संख्याएँ है।
उदाहरण 1
−4 और 4 के बीच सभी पूर्णाकों को आरोही क्रम मे लिखिए।
संख्या रेखा की सहायता से हम इसे आसानी से हल कर सकते है।
अतः एक संख्या रेखा पर कुछ संख्याएँ दर्शाते है -
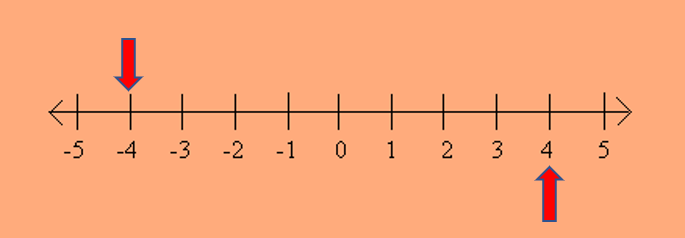
चित्र से हम देख सकते है की तीर का चिन्ह 4 और −4 पर है।
अतः इन दोनों अंकों को छोड़कर बाकी सभी अंकों की गणना करनी है।
4 और −4 के बीच 3,2,1,0,−1,−2,−3 ये सभी पूर्णांक है।
आरोही क्रम मे लिखने पर - −3,−2,−1,0,1,2,3
संख्या रेखा पर पूर्णांकों का निरूपण
संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
मध्य मे शून्य को रखते हैं ।
अब संख्या रेखा में ऋणात्मक पूर्णांक संख्या को शून्य के बायीं ओर एवं धनात्मक पूर्णांक संख्या को दायीं ओर अंकित कर लेते हैं।
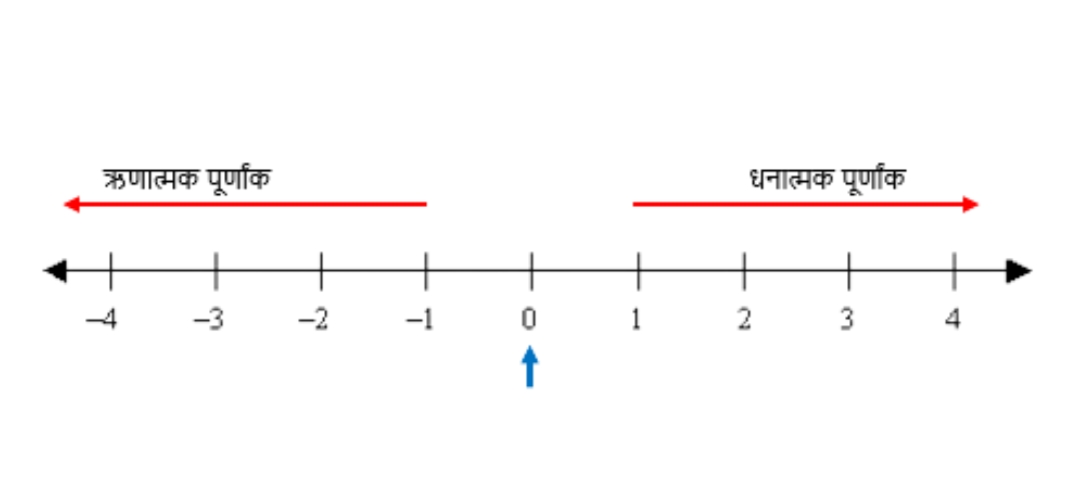
संख्या रेखा में बाएं से दायें → जाने पर संख्या बढ़ती है, दायें से बाएं ←जाने पर संख्या का मान घटता है। इसमें हम किसी पूर्णांक संख्या को आसानी से दर्शा सकते हैं।
संख्या रेखा की सहायता से हम दो पूर्णांको को आसानी से जोड़ या घटा सकते हैं।
उदाहरण 2
संख्या रेखा पर −5 अंकित कीजिये ।
संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
मध्य मे शून्य को रखते हैं ।
अब संख्या रेखा में ऋणात्मक पूर्णांक संख्या को शून्य के बायीं ओर एवं धनात्मक पूर्णांक संख्या को दायीं ओर अंकित कर लेते हैं।
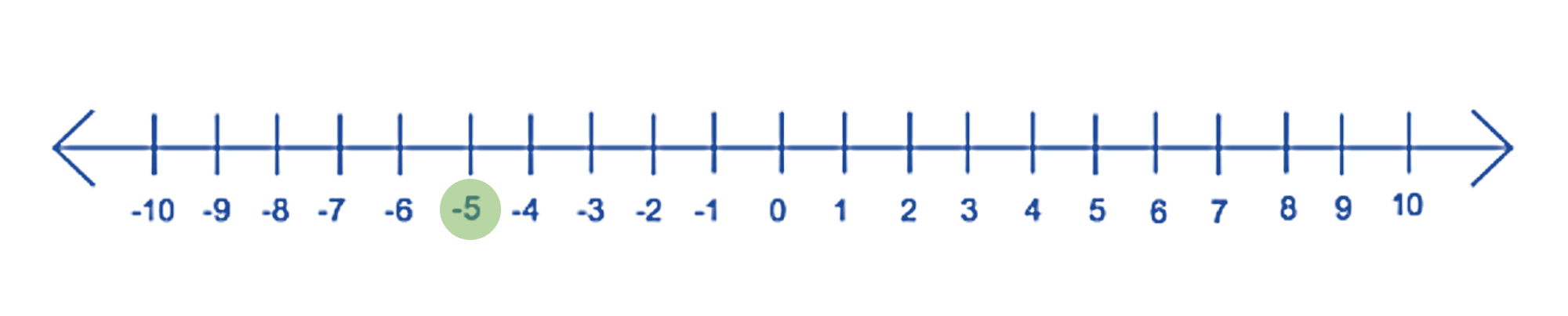
चित्र मे शून्य के बायीं ओर 5 इकाई जाने पर पूर्णांक −5 को संख्या रेखा में निरूपित किया गया है।
उदाहरण 3
निम्नलिखित संख्याओं को संख्या रेखा पर व्यवस्थित कीजिये और उनको आरोही और अवरोही क्रम में लिखिए :-
7,−5,4,0 और −4
संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
मध्य मे शून्य को रखते हैं ।
अब संख्या रेखा में ऋणात्मक पूर्णांक संख्या को शून्य के बायीं ओर एवं धनात्मक पूर्णांक संख्या को दायीं ओर अंकित कर लेते हैं।
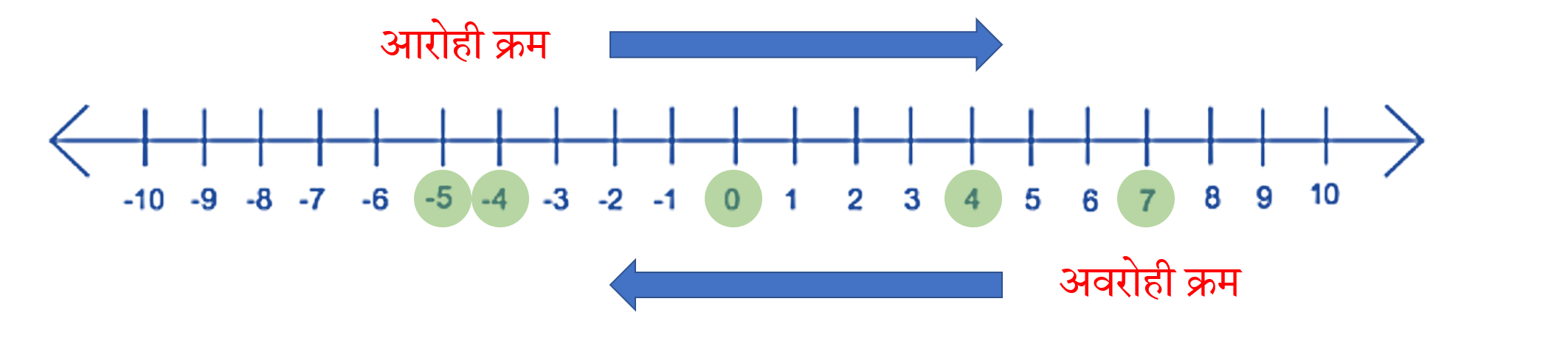
संख्या रेखा में बाएं से दायें →जाने पर संख्या बढ़ती है, दायें से बाएं ←जाने पर संख्या का मान घटता है अतः
आरोही क्रम :−5,−4,0,4,7
अवरोही क्रम : 7,4,0,−4,−5
पूर्णांकों मे क्रमबद्धता
संख्या रेखा पर जब हम दाईं ओर चलते हैं, तो संख्या का मान बढ़ता है और जब हम बाईं ओर चलते है , तो संख्या का मान घटता है।
अतः, −3<−2,−2<−1,−1<0,0<1,1<2,2<3 इत्यादि।
अतः, पूर्णाकों के संग्रह को −5,−4,−3,−2,−1,0,1,2,3,4,5 लिखा जा सकता है।

उदाहरण 4
हल कीजिए :-
(a) −3 पर एक बटन रखा गया है।
−9 पर पहुँचने के लिए , हम किस दिशा में और कितने कदम चलें ?
(b) यदि हम संख्या −6 के दाई ओर 4 कदम चलें , तो किस संख्या पर पहुँच जाएँगे ?
(a) संख्या रेखा की सहायता से समझते है :-
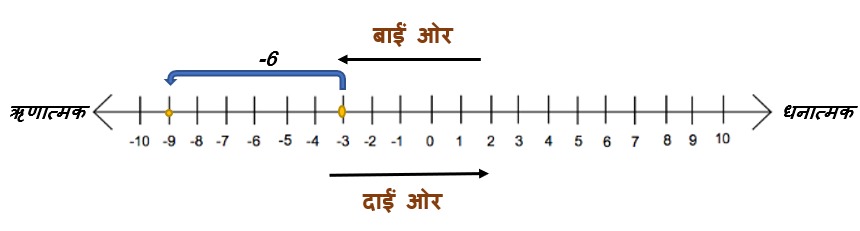
दिया है :-
−3 पर बटन रखा है।
−9 तक पहुचने के लिए हम −3 से प्रारंभ करके −3 की बाईं दिशा मे 6 कदम चलते है तथा −9 पर पहुचते है।
अतः −9 पर पहुचने के लिए हमे 6 कदम −3 की बाईं दिशा मे चलना पड़ेगा।
(b)
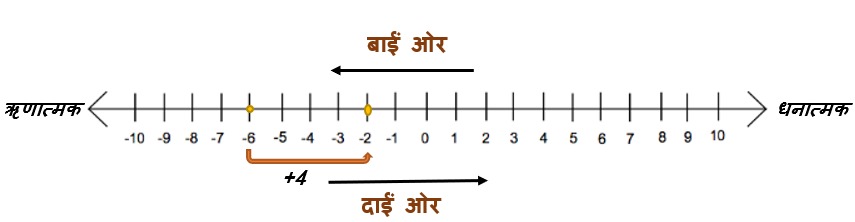
यदि हम संख्या −6 के दाईं ओर 4 कदम चलेंगे, तो हम −2 पर पहुँच जाएँगे।
पूर्णांकों का योग
बच्चों! हम पूर्णांकों का योग तीन प्रकार से कर सकते है-
1. दो धनात्मक पूर्णांकों का योग :-
2. दो ऋणात्मक पूर्णांकों का योग :-
3. एक ऋणात्मक और एक धनात्मक पूर्णांक का योग :-
1. दो धनात्मक पूर्णांकों का योग : दो धनात्मक पूर्णांकों को जोड़ने के लिए हम उन्हें केवल प्राकृत संख्याओं के रूप में जोड़ते है और फिर उत्तर पर धनात्मक चिह्न लगाते है।
इसका मान सदैव धनात्मक होता है।
उदाहरण :
(i) (+6)+(+7)=(6+7)=+13
(ii) (+12)+(+15)=(15+12)=+27
2. दो ऋणात्मक पूर्णांकों का योग : दो ऋणात्मक पूर्णांकों को जोड़ने के लिए हम उन्हें भी केवल प्राकृत संख्याओं के रूप में जोड़ते है और फिर उत्तर पर ऋणात्मक चिह्न लगाते है।
इसका मान सदैव ऋणात्मक होता है।
उदाहरण :
(i) (−5)+(−9)=−(5+9)=−14
(ii) (−13)+(−20)=−(13+20)=−33
3. एक ऋणात्मक और एक धनात्मक पूर्णांक का योग : एक ऋणात्मक और एक धनात्मक पूर्णांक को जोड़ने के लिए हमेशा बड़ी संख्या ( पूर्णांक ) मे से छोटी संख्या ( पूर्णांक ) को घटाते है और उत्तर मे बड़ी संख्या वाला चिह्न ही लगाते है।
क्योंकि परिणामी संख्या का चिन्ह सदैव बड़ी संख्या ( पूर्णांक ) के चिह्न पर निर्भर करता है।
उदाहरण :
(i) (−6)+(7)=+1 ( यहाँ बड़ा पूर्णांक 7 धनात्मक पूर्णांक है अतः उत्तर भी धनात्मक ही होगा )
(ii) (+9)+(−18)=−9 ( यहाँ बड़ा पूर्णांक 18 ऋणात्मक पूर्णांक है अतः उत्तर भी ऋणात्मक ही होगा )
गुणन के नियम :-
(i)'+'×'+'='+'
अर्थात धन की गुणा धन से करने पर परिणाम धन ही आता है।
(ii)'+'×'−'='−'
अर्थात धन की गुणा ऋण से करने पर परिणाम ऋण आता है।
(iii)'−'×'+'='−'
अर्थात ऋण की गुणा धन से करने पर भी परिणाम ऋण ही आता है।
(iv)'−'×'−'='+'
अर्थात ऋण की गुणा ऋण से करने पर परिणाम धन आता है।
OMR (One Minute Revision)
जैसे 5 , 6 , 25 ( ये सभी धनात्मक संख्या हैं। )
- दो धनात्मक पूर्णांको का गुणन धनात्मक होता है।
उदाहरण:⇒(+)×(+)=(+) - दो ऋणात्मक पूर्णांको का गुणन धनात्मक होता है।
उदाहरण:⇒ (−)×(−)=(+) - एक धनात्मक और एक ऋणात्मक का गुणन ऋणात्मक होता हैं।
उदाहरण:
⇒(+)×(−)=(−)
या (−)×(+)=(−)
उदाहरण 5
निम्नलिखित का योग ज्ञात कीजिए :
137 और −354
चूंकि हमे यहाँ दो संख्याएँ दी गई है -
137 और −354
चरण 1 : इनको जोड़ने लिए 'और' को हटाकर धन का चिन्ह लगाते है तथा −354 को कोष्ठक मे लिखते है -
=137+(−354)
चरण 2 : हम जानते है की धन की गुणा ऋण से करने पर परिणाम ऋण ही आता है अतः
=137−354
चरण 3 : चूंकि हम जानते है की एक ऋणात्मक और एक धनात्मक पूर्णांक को जोड़ने के लिए हमेशा बड़ी संख्या ( पूर्णांक ) मे से छोटी संख्या ( पूर्णांक ) को घटाते है और परिणाम (उत्तर) मे बड़ी संख्या वाला चिह्न ही लगाते है अतः
=−217
उदाहरण 6
निम्नलिखित का योग ज्ञात कीजिए :
−389 और −1032
चूंकि हमे यहाँ दो संख्याएँ दी गई है -
−389 और −1032
चरण 1 : इनको जोड़ने लिए 'और' को हटाकर धन का चिन्ह लगाते है तथा −1032 को कोष्ठक मे लिखते है -
=−389+(−1032)
चरण 2 : हम जानते है की धन की गुणा ऋण से करने पर परिणाम ऋण ही आता है अतः
=−389−1032
चरण 3 : चूंकि हम जानते है की दो ऋणात्मक पूर्णांकों को जोड़ने के लिए हम उन्हें केवल प्राकृत संख्याओं के रूप में जोड़ते है अतः
=1421
चरण 4 : फिर उत्तर पर ऋणात्मक चिह्न लगाते है क्योंकि इसका मान सदैव ऋणात्मक होता है अतः
=−1421
संख्या रेखा पर पूर्णांकों का योग
संख्या रेखा पर हम पूर्णांकों का योग निम्न प्रकार से कर सकते है-
1. दो धनात्मक पूर्णांकों का योग : आइये एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर 3 और 5 को जोड़िए।
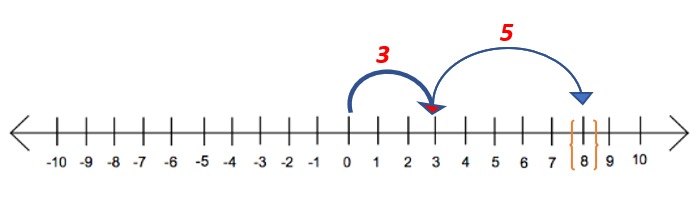
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के दाईं ओर 3 कदम चलते हैं और 3 पर पहुँचते हैं।
फिर हम 3 के दाईं ओर 5 कदम पुनः चलते हैं और 8 पर पहुँचते हैं।
इस प्रकार, हमें 3+5=8 प्राप्त होता है।
2. दो ऋणात्मक पूर्णांकों का योग : आइये इसे भी एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर -3 और -5 को जोड़िए।
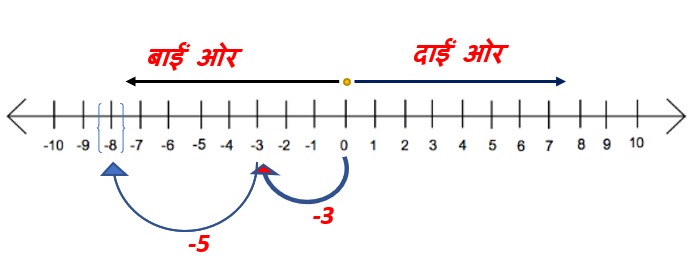
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के बाईं ओर 3 कदम चलते हैं और -3 पर पहुँचते हैं।
अब हम -3 के बाईं ओर 5 कदम फिर से चलते हैं और -8 पर पहुँचते हैं।
इस प्रकार, हमें (−3)+(−5)=(−3−5)=(−8) प्राप्त होता है।
3. एक धनात्मक और एक ऋणात्मक पूर्णांक का योग : आइये एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर (+5) और (-3) को जोड़िए।
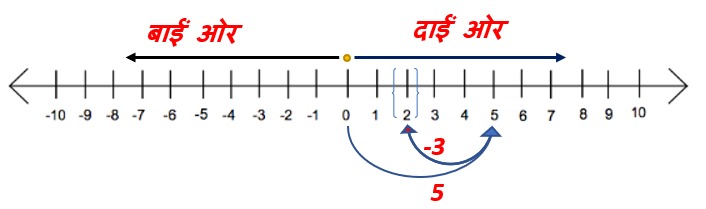
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के दाईं ओर 5 कदम चलते हैं और 5 पर पहुँचते हैं।
फिर हम 5 के बाईं ओर 3 कदम चलते हैं और 2 पर पहुँचते हैं।
इस प्रकार, हमें (+5)+(−3)=(+5−3)=(+2) प्राप्त होता है।
4. एक ऋणात्मक और एक धनात्मक पूर्णांक का योग : आइये एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर (-5) और (+3) को जोड़िए।
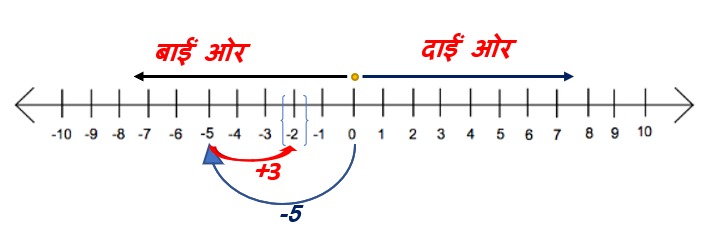
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के बाईं ओर 5 कदम चलते हैं और -5 पर पहुँचते हैं।
फिर हम -5 के दाईं ओर 3 कदम चलते हैं और -2 पर पहुँचते हैं।
इस प्रकार, हमें (−5)+(+3)=(−5+3)=(−2) प्राप्त होता है।
NOTE :
उदाहरण 7
संख्या रेखा का प्रयोग करते हुए निम्नलिखित योग ज्ञात कीजिए :-
9+(−6)
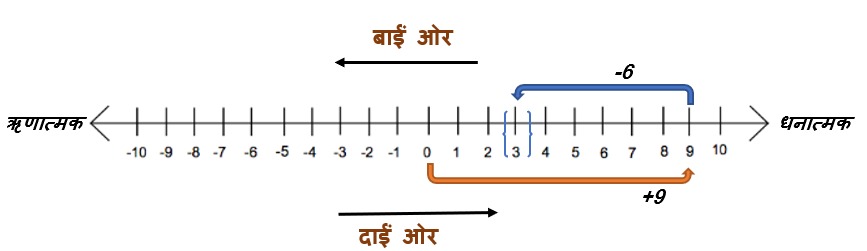
चरण 1 : सर्वप्रथम हम एक संख्या रेखा खींचते है तथा उसके मध्य मे शून्य (0) अंकित करते है। फिर शून्य के दाईं तरफ धनात्मक पूर्णांक और बाईं तरफ ऋणात्मक पूर्णांक अंकित करते है।
चूंकि हम जानते है की दाईं तरफ जाने पर मान बढ़ता है अर्थात '+' होता है तथा बाईं तरफ जाने पर मान घटता है अर्थात '−' होता है।
चरण 2 : हम सबसे पहले संख्या रेखा पर, 0 (शून्य) से प्रारंभ करके 0 के दाईं ओर 9 कदम चलते हैं और +9 पर पहुँचते हैं।
चरण 3 : फिर हम +9 के बाईं ओर 6 कदम वापिस चलते हैं अर्थात ऋणात्मक दिशा की तरफ वापिस आते है और +3 पर पहुँचते हैं।
चरण 4 : इस प्रकार, हमें 9+(−6)=+3 प्राप्त होता है।
संख्या रेखा पर पूर्णांकों का व्यवकलन
अब तक हमने संख्या रेखा पर पूर्णांकों का योग करना सीखा है। अब हम संख्या रेखा पर पूर्णांकों का व्यवकलन करना सीखेंगे।
हम संख्या रेखा पर पूर्णांकों का व्यवकलन निम्न प्रकार से कर सकते है-
1. दो धनात्मक पूर्णांकों का व्यवकलन : आइये एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर +5 मे से +2 को घटाइए।
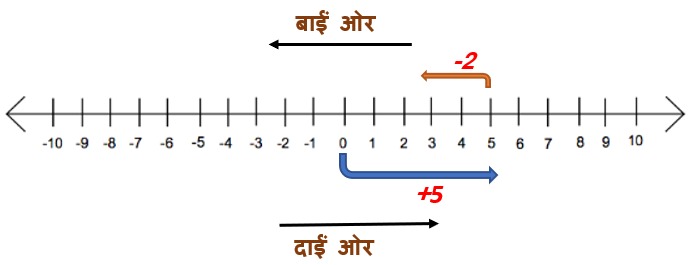
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के दाईं ओर 5 कदम चलते हैं और 5 पर पहुँचते हैं।
फिर हम 5 के बाईं ओर 2 कदम वापिस आते हैं और 3 पर पहुँचते हैं।
इस प्रकार, हमें (+5)−(+2)=(+5−2)=+3 प्राप्त होता है।
2. दो ऋणात्मक पूर्णांकों का व्यवकलन : आइये इसे भी एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर −4 मे से −8 को घटाइए।
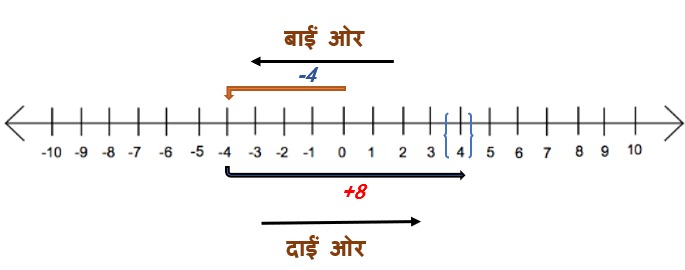
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के बाईं ओर 4 कदम चलते हैं और -4 पर पहुँचते हैं।
फिर हम -4 के दाईं ओर 8 कदम चलते हैं और 4 पर पहुँचते हैं।
इस प्रकार, हमें (−4)−(−8)=(−4+8)=+4 प्राप्त होता है। चूंकि यहाँ दो ऋणात्मक चिन्ह गुणा होकर धनात्मक हो जाते है।
3. एक धनात्मक पूर्णांक मे से एक ऋणात्मक पूर्णांक का व्यवकलन : आइये एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर (+4) मे से (-3) को घटाइए।
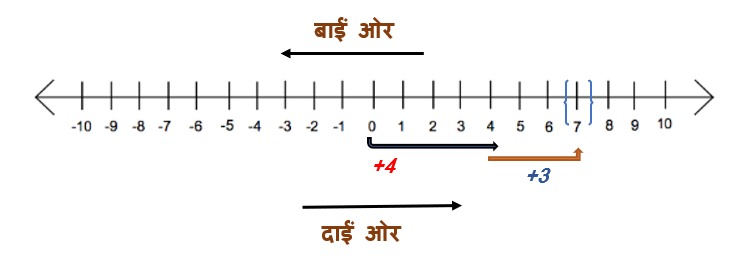
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के दाईं ओर 4 कदम चलते हैं और 4 पर पहुँचते हैं।
फिर हम 4 के दाईं ओर पुनः 3 कदम चलते हैं और 7 पर पहुँचते हैं।
इस प्रकार, हमें (+4)−(−3)=(+4+3)=(+7) प्राप्त होता है। चूंकि यहाँ भी दो ऋणात्मक चिन्ह गुणा होकर धनात्मक हो जाते है।
4. एक ऋणात्मक पूर्णांक मे से एक धनात्मक पूर्णांक का व्यवकलन : आइये एक उदाहरण की सहायता से समझते है-
उदा. संख्या रेखा पर (−4) मे से (+3) को घटाइए।
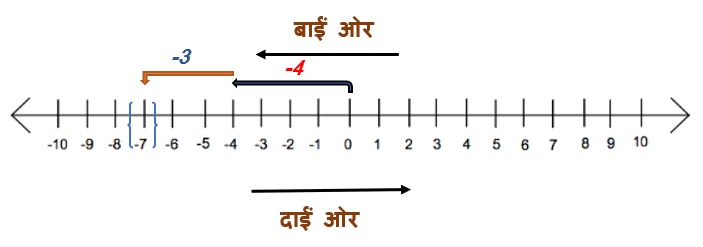
संख्या रेखा पर, पहले हम 0 (शून्य) से प्रारंभ करके 0 के बाईं ओर 4 कदम चलते हैं और -4 पर पहुँचते हैं।
फिर हम -4 के बाईं ओर पुनः 3 कदम चलते हैं और -7 पर पहुँचते हैं।
इस प्रकार, हमें (−4)−(+3)=(−4−3)=(−7) प्राप्त होता है।
OMR (One Minute Revision)
उदाहरण 8
संख्या रेखा की सहायता से (−8)−(−10) का मान ज्ञात कीजिए ।
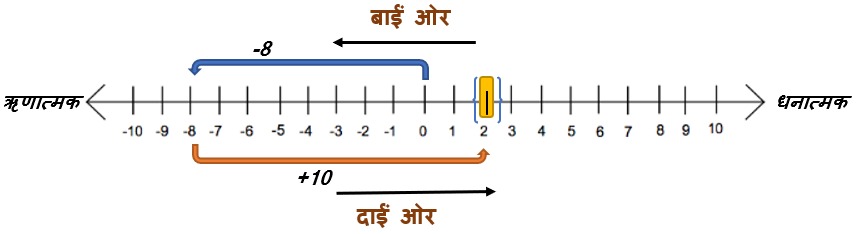
चरण 1 : सर्वप्रथम हम एक संख्या रेखा खींचते है तथा उसके मध्य मे शून्य (0) अंकित करते है। फिर शून्य के दाईं तरफ धनात्मक पूर्णांक और बाईं तरफ ऋणात्मक पूर्णांक अंकित करते है।
चूंकि हम जानते है की दाईं तरफ जाने पर मान बढ़ता है अर्थात '+' होता है तथा बाईं तरफ जाने पर मान घटता है अर्थात '−' होता है।
चरण 2 : हम सबसे पहले संख्या रेखा पर, 0 (शून्य) से प्रारंभ करके 0 के बाईं ओर 8 कदम चलते हैं और −8 पर पहुँचते हैं।
चरण 3 : चूंकि हम जानते है की दो ऋणात्मक चिन्ह आपस मे गुणा होकर धनात्मक हो जाते है ।
अतः फिर हम −8 के दाईं ओर 10 कदम चलते हैं अर्थात धनात्मक दिशा मे वापिस आते है और 2 पर पहुँचते हैं।
चरण 4 : इस प्रकार, हमें (−8)−(−10)=(−8+10)=+2 प्राप्त होता है।
उदाहरण 9
(−10) में से (−4) को घटाइए ।
चूंकि हमे यहाँ (−10)में से (−4)को घटाना है अतः
चरण 1 : इनको घटाने लिए 'मे से ' को हटाकर ऋण (−) का चिन्ह लगाते है -
=−10−(−4)
चरण 2 : हम जानते है की ऋण की गुणा ऋण से करने पर परिणाम धन आता है अतः
=−10+4
चरण 3 : चूंकि अब इसका मान ज्ञात करने के लिए हम इनको जोड़ते है।
एक ऋण और एक धन पूर्णांक को जोड़ने के लिए हमेशा बड़े पूर्णांक मे से छोटे पूर्णांक को घटा देते है अतः
=6
चरण 4 : फिर उत्तर पर ऋणात्मक चिह्न लगाते है क्योंकि यहाँ बड़ी संख्या ऋणात्मक है अतः
=−6
सारांश
[ जैसे, (+3)+(+2)=+(3+2)=+5]
[ जैसे, (−2)+(−1)=−(2+1)=−3]
जैसे, (+4)+(−3)=(4−3)=(+1)
(−4)+(+3)=(−4+3)=(−1)