क्षेत्रमिति कक्षा 6 गणित
भूमिका
इस अध्याय मे हम क्षेत्रमिति के अंतर्गत आने वाले द्विविमीय (समतल) आकृतियों के क्षेत्रफल तथा परिमाप का अध्ययन करेंगे। समतल आकृतियों का परिमाप इसकी सीमा से संबंधित माप और समतल आकृतियों का क्षेत्रफल इसके द्वारा घेरे गए क्षेत्र या सतह से संबंधित माप होती है।
आइये जानते है, क्षेत्रमिति को और करीब से...
क्षेत्रमिति के अंतर्गत हम द्विविमीय और त्रिविमीय आकृति के बारे में पड़ते है। जहाँ हम आयतन, क्षेत्रफल, परिमाप या परिमिति आदि को निकालना सीखते है लेकिन इस अध्याय में हम केवल द्विविमीय आकृतियों का अध्ययन करेंगे तथा क्षेत्रफल और परिमाप की गणना करना सीखेंगे।
द्विविमीय आकृतियां : आयत, वर्ग, समकोण त्रिभुज, समद्विबाहु त्रिभुज, समबाहु त्रिभुज, विषमबाहु त्रिभुज आदि।
क्षेत्रफल (AREA) : किसी आकृति के उसके सभी भुजाओं से घिरे हुए तल को उस आकृति का क्षेत्रफल कहते हैं।
क्षेत्रफल की इकाई (Unit) वर्गमीटर, वर्ग सेंटीमीटर, वर्ग किलोमीटर आदि होती हैं।
परिमाप (PERIMETER) : किसी आकृति की सभी भुजाओं की लंबाइयों का योग उस आकृति का परिमाप या परिमिति कहलाता हैं।
परिमाप की इकाई (unit) मीटर, सेंटीमीटर, किलोमीटर आदि होती हैं।
परिमाप
यदि एक बंद आकृति बनाने के लिए उसकी सीमा के साथ आकृति के चारों ओर घूमते हैं तो तय की गई दूरी उस आकृति की परिधि कहलाती है। यह परिधि ही उस आकृति का परिमाप कहलाती है।
अतः परिमाप एक बंद आकृति की सीमा की लंबाई को दर्शाता है।
यदि कोई आकृति केवल रेखाखंडों से बनी है तो हम दी गई आकृति की सभी भुजाओं की लंबाइयों को जोड़कर उसका परिमाप ज्ञात कर सकते हैं।
आइए एक उदाहरण से समझते है :-
उदाहरण : दी गई आकृति का परिमाप ज्ञात कीजिए।

हल : चूंकि दी गई आकृति का परिमाप ज्ञात करने के लिए हमे इसकी सभी भुजाओं का योग करना होगा। अतः ⇒
परिमाप = सभी भुजाओं का योग
= AB+BC+CD+DE+EF+FA
=100+120+90+45+60+80
=495 मीटर
इस प्रकार हम आकृति की सभी भुजाओं का योग करके उसके परिमाप की गणना कर सकते है।
आयत का परिमाप
आयत एक बंद आकृति होती है जिसमे समान विपरित भुजाओं के दो जोड़े होते है अर्थात इसमे आमने - सामने की भुजाएँ समान होती है।
उपर्युक्त आकृति मे :-
AB=CD
AD=BC
अतः इसका परिमाप = चारों भुजाओं का योग
=AB+BC+CD+DA
=AB+BC+AB+BC
=2AB+2BC
=2(AB+BC)
=2(15+9)
=2(24)
=48 सेमी.
उपर्युक्त प्रश्न मे हमने देखा कि
आयत का परिमाप = लंबाई + चौड़ाई + लंबाई + चौड़ाई
अर्थात 2 लंबाई + 2 चौड़ाई
आयत का परिमाप =2 (लंबाई + चौड़ाई )
आइए एक उदाहरण की सहायता से समझते है :-
उदाहरण : सारिका 5 मीटर लंबाई और 7 मीटर चौड़ाई के एक आयताकार टेबल कवर के चारों ओर एक किनारी लगाना चाहती है। बताइए कि सारिका को कितनी लंबी किनारी की आवश्यकता है।
हल :
आयताकार टेबल कवर की लंबाई = 5 मीटर
आयताकार टेबल कवर की चौड़ाई =7 मीटर
चूंकि सारिका टेबल के चारों ओर किनारी लगाना चाहती है अतः उसे टेबल का परिमाप ज्ञात करना होगा।
आयताकार टेबल कवर का परिमाप = 2× ( लंबाई + चौड़ाई )
=2×( 5 मी. + 7 मी.)
=2× ( 12 मी.)
=24 मीटर
अतः सारिका को कुल 24 मीटर किनारी की आवश्यकता है।
सम आकृतियों का परिमाप
ऐसी आकृतियाँ जिनकी सभी भुजाओं और कोणों की माप समान हो, सम आकृतियाँ कहलाती है।जैसे :- वर्ग, समबाहु त्रिभुज आदि।
वर्ग का परिमाप
चूंकि हम जानते है कि वर्ग एक सम आकृति है क्योंकि इसकी सभी भुजाएँ तथा कोण समान होते है। इसके परिमाप की गणना के लिए इसकी चारों भुजाओं का योग करते है।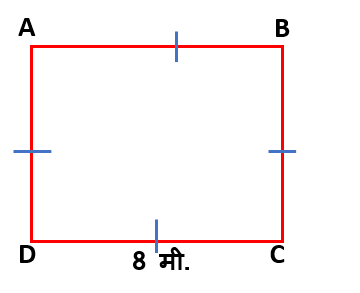
उपर्युक्त आकृति मे :-
AB=BC=CD=DA=8 मीटर
अतः वर्ग ABCD का परिमाप = चारों भुजाओं का योग
अर्थात =AB+BC+CD+DA
=8+8+8+8 मीटर
=32 मीटर
चूंकि यहाँ सभी भुजाएँ समान है अतः अलग - अलग योग के स्थान पर भुजाओं की संख्या को एक ही भुजा की माप से गुणा कर सकते है।
अर्थात वर्ग का परिमाप =4× एक भुजा की माप
=4×8 मीटर
=32 मीटर
आइए एक अन्य उदाहरण से समझते है :-
उदाहरण : महिमा 45 मीटर भुजा वाले वर्गाकार पार्क के चारों ओर 3 चक्कर लगाती है। उसके द्वारा तय की गई दूरी की गणना कीजिए।
हल : वर्गाकार पार्क का परिमाप =4× एक भुजा की माप
=4×45 मीटर
=180 मीटर
अतः महिमा एक चक्कर लगाने के लिए 180 मीटर की दूरी तय करती है।
3 चक्कर मे महिमा द्वारा तय की गई दूरी =3×180 =540 मीटर
अतः 3 चक्कर मे वह कुल 540 मीटर की दूरी तय करेंगी।
समबाहु त्रिभुज का परिमाप
जिस प्रकार वर्ग की सभी भुजाएँ तथा कोण समान होते है उसी प्रकार समबाहु त्रिभुज के भी सभी कोण एवं भुजाएँ समान होती है।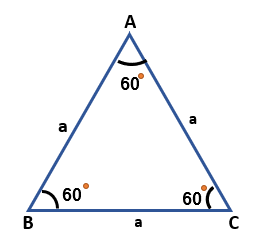
चूंकि इसमे तीन भुजाएँ होती है तो :−
समबाहु त्रिभुज का परिमाप =3× एक भुजा की माप
अतः उपर्युक्त आकृतियों के परिमापों की गणना से हम समझ सकते है कि जिन आकृतियों की सभी भुजाओं की लंबाई एवं कोणों की माप समान होती है, बंद सम आकृतियाँ कहलाती है।
ऐसी सभी सम आकृतियों का परिमाप निम्न सूत्र की सहायता से ज्ञात कर सकते है :-
सम आकृति का परिमाप = भुजाओं की संख्या × एक भुजा की माप
आइए इस सूत्र का प्रयोग करते है :-
उदाहरण : एक सम षट्भुज का परिमाप 18 सेमी. है। इसकी भुजा की लंबाई ज्ञात कीजिए।
हल : चूंकि हम जानते है कि समषट्भुज मे 6 समान लंबाई की भुजाएँ होती है।
समषट्भुज का परिमाप = भुजाओं की संख्या × एक भुजा की माप
18=6× भुजा की माप
186= भुजा की माप
3= भुजा की माप
अतः इस समषट्भुज की प्रत्येक भुजा 3 सेमी. की होगी।
OMR (One Minute Revision)
जैसे :- वर्ग, समबाहु त्रिभुज आदि।
सम आकृति का परिमाप = भुजाओं की संख्या × एक भुजा की माप
उदाहरण 1
40 सेमी. लम्बाई और 10 सेमी. चौड़ाई वाले एक आयताकार ढक्कन को चारो ओर से पूरी तरह एक टेप द्वारा बंद कर दिया जाता है। आवश्यक टेप की लम्बाई ज्ञात कीजिए।
चूंकि आयताकार ढक्कन को चारों तरफ से टेप से बंद करना है अतः आयताकार ढक्कन के परिमाप की गणना करनी होगी।
आयताकार ढक्कन की लंबाई (l) =40 सेमी.
आयताकार ढक्कन की चौड़ाई (b) =10 सेमी.

चूंकि यह एक आयताकार ढक्कन है अतः आमने - सामने की भुजाएँ समान होगी।
AB=CD
BC=AD
अतः टेप की कुल लंबाई =AB+BC+CD+AD
=AB+BC+AB+BC
=2AB+2BC
=2(AB+BC)
=2(l+b) = आयत का परिमाप
=2(40+10) सेमी.
=100 सेमी.
अतः इस आयताकार ढक्कन को चारों तरफ से बंद करने लिए 100 सेमी. टेप की आवश्यकता होगी।
उदाहरण 2
एक सम पंचभुज का परिमाप 120 सेमी हैं। प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
चूंकि हम जानते है कि यह एक सम आकृति है।
अतः सम आकृति परिमाप सूत्र से :-
समपंचभुज का परिमाप = भुजाओं की संख्या × एक भुजा की माप
120 सेमी. =5× भुजा की माप
1205 सेमी. = भुजा की माप
24 सेमी. = भुजा की माप
अतः इस पंचभुज की प्रत्येक भुजा की लंबाई 24 सेमी. होगी।
उदाहरण 3
एक मेज की ऊपरी सतह की विमाएँ 2 मी 50 सेमी और 1 मी 50 सेमी है। मेज की ऊपरी सतह का परिमाप ज्ञात कीजिए।
चूंकि
100 सेमी. =1 मी.
1 सेमी. =1100 मी.
50 सेमी. =50100=510 मी. =0.5 मी.
मेज की लंबाई (l) = 2 मी. 50 सेमी. = 2.5 मी.
मेज की चोड़ाई (b) = 1 मी. 50 सेमी. = 1.5 मी.
मेज की सतह का परिमाप = 2× ( लंबाई + चौड़ाई )
=2×(2.5+1.5)
=2×4
=8 मीटर
अतः मेज की ऊपरी सतह का परिमाप 8 मीटर होगा।
उदाहरण 4
स्वीटी 75 मी भुजा वाले वर्ग के चारो ओर दौड़ती है और बुलबुल 60 मी लम्बाई और 45 मी चौड़ाई वाले आयत के चारों ओर दौड़ती है। ज्ञात कीजिए कि कौन कम दुरी तय करती है ?
चूंकि यह दूरी ज्ञात करने के लिए इनके परिमापों की गणना करनी होगी।
वर्ग का परिमाप =4× भुजा
आयत का परिमाप =2×( लंबाई + चौड़ाई )
(i) स्वीटी द्वारा तय की गई दूरी = वर्ग का परिमाप
=4× भुजा
=4×75
=300 मीटर
(ii) बुलबुल द्वारा तय की गई दूरी = आयत का परिमाप
=2× ( लंबाई + चौड़ाई )
=2× ( 60 + 45 )
=2× 105
=210 मीटर
अतः बुलबुल द्वारा कम दूरी तय की गई।
उदाहरण 5
एक धागे का टुकड़ा 30 सेमी लंबाई का हैं। प्रत्येक भुजा की लंबाई क्या होगी, यदि धागे से बनाया जाता हैं : -
(a) एक वर्ग ?
(b) एक समबाहु त्रिभुज ?
(c) एक सम षट्भुज ?
चूंकि हमे यहाँ निम्न आकृतियों की सभी भुजाओं की लंबाइयों का योग अर्थात परिमाप दिया गया है।
(i) जब इस धागे से एक वर्ग बनाया जाए :-
वर्ग का परिमाप =4× भुजा
30 सेमी. =4× भुजा की लंबाई
304 सेमी. = भुजा की लंबाई
7.5 सेमी. = भुजा की लंबाई
अतः जब इस धागे से एक वर्ग बनाया जाए तो उस वर्ग की प्रत्येक भुजा 7.5 सेमी. की होगी।
(ii) जब इस धागे से एक समबाहु त्रिभुज बनाया जाए :-
समबाहु त्रिभुज का परिमाप =3× भुजा की लंबाई
30 सेमी. =3× भुजा की लंबाई
303 सेमी. = भुजा की लंबाई
10 सेमी. = भुजा की लंबाई
अतः जब इस धागे से एक समबाहु त्रिभुज बनाया जाए तो उस समबाहु त्रिभुज की प्रत्येक भुजा 10 सेमी. की होगी।
(iii) जब इस धागे से एक समषट्भुज बनाया जाए :-
समषट्भुज का परिमाप =6× भुजा
30 सेमी. =6× भुजा की लंबाई
306 सेमी. = भुजा की लंबाई
5 सेमी. = भुजा की लंबाई
अतः जब इस धागे से एक समषट्भुज बनाया जाए तो उस समषट्भुज की प्रत्येक भुजा 5 सेमी. की होगी।
क्षेत्रफल
जब हम एक बंद आकृति बनाते हैं, तो आकृति उस क्षेत्र को ढकती है जो उससे घिरा होता है। उस क्षेत्र को आकृति के क्षेत्रफल के रूप में जाना जाता है। यहाँ कुछ बंद आकृतियाँ दी गई हैं।
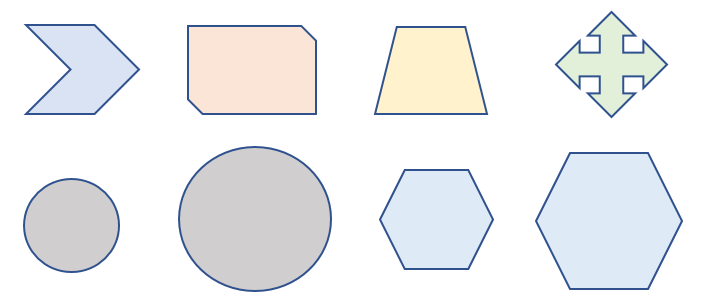
उपरोक्त सभी आकृतियाँ सतह के कुछ भाग को ढकती हैं। हम देख सकते हैं कि जो आकृति बड़ी है, वह सतह के अधिक भाग को ढक रही है। कभी-कभी हम यह नहीं कह सकते कि किस आकृति का क्षेत्रफल अधिक है। इस स्थिति में, हम क्षेत्रफल की गणना के लिए वर्गाकार कागज या ग्राफ पेपर का उपयोग करते हैं।
आइए एक उदाहरण लेते हैं:
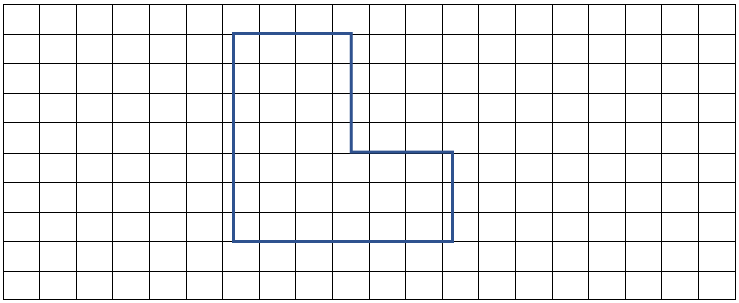
वर्गाकार कागज में, प्रत्येक वर्ग की प्रत्येक भुजा की माप 1 सेमी है। वर्गाकार कागज पर क्षेत्रफल की गणना करने के लिए, हमें कुछ नियमों पर ध्यान देना होगा।
अब, उपरोक्त उदाहरण से,
अत: दी गई आकृति का क्षेत्रफल होगा =23+2+7=32 वर्ग इकाई
Note:- हम किसी भी बंद आकृति का क्षेत्रफल वर्ग इकाई में मापते हैं। यदि किसी आकृति की भुजाएं सेंटीमीटर में हों तो क्षेत्रफल का मात्रक वर्ग सेंटीमीटर (वर्ग सेमी) होगा।
आयत का क्षेत्रफल
यदि हम एक वर्गांकित कागज (जिसकी प्रत्येक वर्ग की प्रत्येक भुजा की माप 1 सेमी है) पर एक आयत बनाते हैं और क्षेत्रफल की गणना करते हैं, तो हम पाएंगे कि आयत द्वारा ढके हुए वर्ग उसकी लंबाई और चौड़ाई के गुणन के बराबर हैं।उदाहरण से समझते हैं:
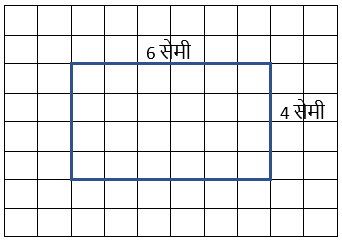
आयत द्वारा ढके हुए वर्ग =24 वर्ग
लंबाई और चौड़ाई का गुणन =6×4=24
चूँकि आयत द्वारा ढके हुए वर्ग और लंबाई व चौड़ाई का गुणन बराबर है।
इसलिए, हम आयत की लंबाई और चौड़ाई को गुणा करके आयत के क्षेत्रफल की गणना कर सकते हैं।
अत: आयत का क्षेत्रफल = लंबाई × चौड़ाई
उदाहरण: यदि एक आयताकार मेज की लंबाई और चौड़ाई क्रमशः 10 सेमी और 7 सेमी है, तो मेज का क्षेत्रफल ज्ञात कीजिए।
हल: यहाँ, मेज की लंबाई =10 सेमी
मेज की चौड़ाई =7 सेमी
अत: आयताकार मेज का क्षेत्रफल = लंबाई × चौड़ाई
=10 सेमी ×7 सेमी
=70 वर्ग सेमी
वर्ग का क्षेत्रफल
वर्ग का क्षेत्रफल आयत के क्षेत्रफल के समान ही ज्ञात किया जा सकता है। हम जानते हैं कि यदि किसी आयत की लंबाई और चौड़ाई समान हो तो वह वर्ग होता हैं।आइए समझते हैं
यहाँ हम एक वर्गांकित कागज (जिसकी प्रत्येक वर्ग की प्रत्येक भुजा की माप 1 सेमी है) पर एक वर्ग बनाते हैं और क्षेत्रफल की गणना करते हैं।
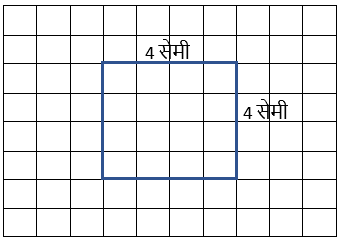
वर्ग द्वारा ढके हुए वर्ग =16 वर्ग
इसकी दोनों भुजाओं का गुणन =4×4=16
चूँकि दोनों का मान समान है, इसलिए हम वर्ग की दो भुजाओं को गुणा करके उसके क्षेत्रफल की गणना कर सकते हैं।
अत: वर्ग का क्षेत्रफल = भुजा × भुजा
उदाहरण:एक वर्गाकार टाइल का क्षेत्रफल ज्ञात कीजिए, यदि इसकी प्रत्येक भुजा 5 सेमी है।
हल: एक वर्गाकार टाइल की प्रत्येक भुजा =5 सेमी
अतः वर्गाकार टाइल का क्षेत्रफल = भुजा × भुजा
=5 सेमी ×5 सेमी
=25 वर्ग सेमी
OMR (One Minute Revision)
उदाहरण 6
60 मीटर लंबाई वाले एक आयताकार बग़ीचे का क्षेत्रफल 480 वर्ग मीटर हैं। बग़ीचे की चौड़ाई ज्ञात कीजिए।
दिया है;
बगीचे की लंबाई =60 मीटर
बगीचे का क्षेत्रफल =480 वर्ग मीटर
बगीचे की चौड़ाई =?
हम जानते हैं कि
बगीचे का क्षेत्रफल = लम्बाई × चौड़ाई
⇒480=60× चौड़ाई
⇒ चौड़ाई =48060= (48cancel(0)) /(6cancel(0)) = 48/6
⇒ चौड़ाई =8 मीटर
अतः बगीचे की चौड़ाई =8 मीटर
उदाहरण 7
एक आयताकार गत्ते का क्षेत्रफल 54 वर्ग सेमी तथा इसकी लंबाई 9 सेमी हैं। गत्ते की चौड़ाई ज्ञात कीजिए।
दिया है;
आयताकार गत्ते की लंबाई =9 सेमी
आयताकार गत्ते का क्षेत्रफल =54 वर्ग सेमी
आयताकार गत्ते की चौड़ाई =?
हम जानते हैं कि
आयताकार गत्ते का क्षेत्रफल = लम्बाई × चौड़ाई
⇒54=9× चौड़ाई
⇒ चौड़ाई =549
⇒ चौड़ाई =6 सेमी
अतः आयताकार गत्ते की चौड़ाई =6 सेमी
उदाहरण 8
तीन आयतों की विमाएँ निम्नलिखित है :
(a) 9 मी और 6 मी
(b) 3 मी और 17 मी
(c) 4 मी और 14 मी
इनमे से किसका क्षेत्रफल सबसे अधिक है और किसका सबसे कम हैं ?
(a) लंबाई =9m
चौड़ाई =6m
आयत का क्षेत्रफल = लंबाई × चौड़ाई =9m×6m=54m2
(b) लंबाई =3m
चौड़ाई =17m
आयत का क्षेत्रफल = लंबाई × चौड़ाई =3m×17m=51m2
(c) लंबाई =4m
चौड़ाई =14m
आयत का क्षेत्रफल = लंबाई × चौड़ाई =4m×14m=56m2
अतः, आयत (c) का क्षेत्रफल सबसे अधिक और आयत (b) का क्षेत्रफल सबसे कम है।
उदाहरण 9
400 मी लंबाई तथा 150 मी चौड़ाई वाले एक आयताकार भूखंड पर Rs10 प्रति 100 वर्ग मीटर की दर से टाइल लगाने का व्यय ज्ञात कीजिए।
भूखंड की लंबाई =400 m तथा चौड़ाई =150 m
आयताकर भूखंड का क्षेत्रफल = लंबाई × चौड़ाई
⇒आयताकर भूखंड का क्षेत्रफल =400m×150m
⇒आयताकर भूखंड का क्षेत्रफल =60,000 m2
चूंकि 100 वर्ग मीटर भूखंड पर टाइल लगवाने का व्यय = ₹10
∴1 वर्ग मीटर भूखंड पर टाइल लगवाने का व्यय = ₹10100
अतः 60,000 वर्ग मीटर भूखंड पर टाइल लगवाने का व्यय
=10100×60000
= 10/(1cancel(00))xx600cancel(00)
=10×600
=₹6,000
उदाहरण 10
एक फर्श की लंबाई 5 मी तथा चौड़ाई 4 मी हैं। 3 मी भुजा वाले एक वर्गाकार गलीचे को फर्श पर बिछाया गया है। फर्श के उस भाग जिस पर गलीचा नहीं बिछाया गया है का क्षेत्रफल ज्ञात कीजिए।
यहाँ,
फर्श की लंबाई =5m तथा चौड़ाई =4m
फर्श का क्षेत्रफल = लंबाई × चौड़ाई =5m×4m=20m2
अब, वर्गाकार गलीचे की भुजा =3m
गलीचे का क्षेत्रफल = भुजा × भुजा =3×3=9m2
प्रश्न के अनुसार,
एक वर्गाकार गलीचे को फर्श पर बिछाया गया है।
अतः फर्श के उस भाग का क्षेत्रफल, जिस पर गलीचा नहीं बिछा है
= फर्श का क्षेत्रफल−गलीचे का क्षेत्रफल
=20m2−9m2
=11m2
सारांश
(b) वर्ग का परिमाप =4× भुजा की लंबाई
(c) समबाहु त्रिभुज का परिमाप =3× भुजा की लंबाई
(a) जिन वर्गों का आधे से कम भाग आकृति से घिरा है, उन्हें छोड़ दीजिए।
(b) यदि किसी वर्ग का आधे से अधिक भाग आकृति से घिरा है, तो ऐसे वर्गों को हम एक पूरा वर्ग ही गिनते हैं।
(c) यदि किसी वर्ग का आधा भाग आकृति से घिरा हो तो उसके क्षेत्रफल का 12 वर्ग इकाई लेते हैं।
(b) वर्ग का क्षेत्रफल = भुजा× भुजा
