संख्याओं के साथ खेलना कक्षा 6 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम संख्याओं का अध्ययन करेंगे। आपने पिछली कक्षाओं मे विभिन्न संख्याओ के बारे में पढ़ा है तथा इससे पहले अध्याय में पूर्ण संख्या का अध्ययन किया हैं। इस अध्याय में आप गुणनखंड (Factors), गुणज (Multiples), सार्व गुणनखंड एवं सार्व गुणज (Common Factors and Common Multiples), विभिन्न प्रकार की संख्याएँ, भाजकता के नियम (Divisibility Law), अभाज्य गुणनखंडन (Prime Factorisation), महत्तम समापवर्तक (HCF), लघुत्तम समापवर्तक (LCM) आदि के बारे पढ़ेंगे।
आइये जानते है, संख्या को और करीब से ...
संख्या एक गणितीय वस्तु है जिसका उपयोग गिनने, मापने और तुलना करने के लिए किया जाता है। संख्याओं को प्रतीकों द्वारा दर्शाया जा सकता है, जिन्हें अंक कहा जाता है। इन संख्याओं को सामान्य रूप में एक अंक, दोहरे अंक, तीन अंकों में लिखा जा सकता है। उदाहरण के लिए, "5" एक अंक है जो संख्या पांच का प्रतिनिधित्व करता है। इस अध्याय में हम संख्याओं को अन्य संख्याओं के गुणनफल में व्यक्त करना सीखेंगे इसके अतिरिक्त इस अध्याय में हम गुणनखंड और गुणज, सार्व गुणनखंड एवं सार्व गुणज, विभिन्न प्रकार की संख्याएँ, भाजकता के नियम, अभाज्य गुणनखंडन, महत्तम समापवर्तक (HCF), लघुत्तम समापवर्तक (LCM) आदि के बारे पढ़ेंगे।
गुणनखंड और गुणज
गुणनखंड
वे संख्याएँ जो दी गई संख्या को पूर्णतः विभाजित करती हैं, उस संख्या के गुणनखंड कहलाती हैं। अर्थात किसी संख्या का गुणनखंड उस संख्या का पूर्ण भाजक होता है।उदाहरण
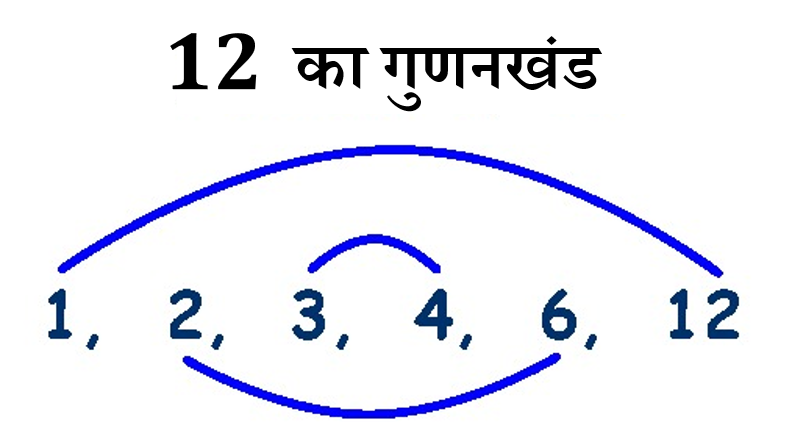
हम देख सकते हैं कि हमें संख्या 12 के निम्न गुणनखंड प्राप्त होते है
1×12,2×6,3×4,4×3,6×2 और 12×1
इसलिये,
1, 2, 3, 4, 6 और 12, 12 के गुणनखंड हैं।
गुणज
गुणज , हमेशा दी गई संख्या से अधिक या उसके बराबर होते हैं। इसे हम निम्न उदाहरण से समझ सकते हैं -
20,4 और 5 दोनों का गुणज है।
OMR (One Minute Revision)
गुणनखंडों और गुणकों के बारे में कुछ तथ्य
गुणनखंड
गुणज
उदाहरण 1
निम्नलिखित संख्याओं के सभी गुणनखंड लिखिए:
(a)24
(b)15
(c)21
(d)27
(e)12
(f)20
(g)18
(h)23
(i)36
(a)24=
1,2,3,4,6,8,12,24
(b)15=
1,3,5,15
(c)21=
1,3,7,21
(d)27=
1,3,9,27
(e)12=
1,2,3,4,6,12
(f)20=
1,2,4,5,10,20
(g)18=
1,2,3,6,9,18
(h)23=
1,23
(i)36=
1,2,3,4,6,9,12,18,36
उदाहरण 2
निम्न संख्याओं के प्रथम पांच गुणज लिखिए: (a)5
(b)8
(c)9
(a)5=
5,10,15,20,25
(b)8=
8,16,24,32,40
(c)9=
9,18,27,36,45
सार्व गुणनखंड एवं सार्व गुणज
सार्व गुणनखंड
एक से अधिक संख्याओं के गुणनखंडो में उभयनिष्ठ गुणनखंडो को उन संख्याओं का सार्व गुणनखंड कहते हैं। अर्थात किन्ही संख्याओं का सार्व गुणनखंड, उन संख्याओं का उभयनिष्ठ गुणनखंड होता है।उदाहरण
25 और 55 के सार्व गुणनखंड =
25 के गुणनखंड 1, 5 , 25 हैं
55 के गुणनखंड 1, 5, 11, 55 हैं
25 और 55 के सार्व गुणनखंड 1 और 5 होंगे
सार्व गुणज
एक से अधिक संख्याओं के गुणजो में उभयनिष्ठ गुणजो को उन संख्याओं का सार्व गुणज कहते हैं।
उदाहरण
3 और 4 के सार्व गुणज=
3 के गुणज:
=3,6,9,12,15,18,21,24...
4 के गुणज
=4,8,12,16,20,24,28...
3 और 4 के सार्व गुणज =12,24 इत्यादि हैं।
उदाहरण 3
निम्न के सार्व गुणनखंड ज्ञात कीजिए:
(a) 4,8 और 12
(b) 5,15 और 25
(a) 4,8 और 12
4 के गुणनखंड =1,2,4
8 के गुणनखंड =1,2,4,8
12 के गुणनखंड =1,2,3,4,6,12
4, 8 और 12 का उभयनिष्ठ/सार्व गुणनखंड =
1,2,4
(b) 5,15 और 25
5 के गुणनखंड =1,5
15 के गुणनखंड =1,3,5,15
25 के गुणनखंड =1,5,25
5,15 और 25 का उभयनिष्ठ/सार्व गुणनखंड =
1,5
उदाहरण 4
निम्न के प्रथम तीन सार्व गुणज ज्ञात कीजिए:
(a) 6 और 8
(b) 12 और 18
(a) 6 और 8
6 के गुणज =6,12,18,24,30,36,42,48,54,60,66,72
8 के गुणज =8,16,24,32,40,48,56,64,72
6, 8 के उभयनिष्ठ गुणज या सार्व गुणज=
24,48,72
(b) 12 और 18
12 के गुणज =12,24,36,48,60,72,84,96,108
18 के गुणज =18,36,54,72,90,108
12, 18 के उभयनिष्ठ गुणज या सार्व गुणज=
36,72,108
विभिन्न प्रकार की संख्याएँ
संपूर्ण संख्या (perfect number)
वह संख्या जिसके सभी गुणनखंडों का योग उस संख्या का दोगुना हो, एक संपूर्ण संख्या (perfect number) कहलाती है। 6 और 28 संपूर्ण संख्याएँ हैं।उदाहरण के लिए:
| सम्पूर्ण संख्या (perfect number) | गुणनखंड (Factors) | सभी गुणनखंडो का योग (Sum of all Factors) |
|---|---|---|
| 6 | 1,2,3,6 | 12 |
| 28 | 1,2,4,7,14,28 | 56 |
| 496 | 1,2,4,8,16,31,62,124,248,496 | 992 |
अभाज्य संख्याए [Prime Numbers ]
वे संख्या जिनके गुणनखंड 1 या वह संख्या स्वयं होती है अभाज्य संख्या कहलाती है।उदाहरण के लिए =2 ,3 ,5 ,7
भाज्य संख्याए [Composite Numbers ]
वे संख्याए जिनके 2 से अधिक गुणनखंड होते है भाज्य संख्याए कहलाती है।उदहारण के लिए =4 ,6 ,8 ,9
NOTE =1 ना तो भाज्य संख्या है ना ही अभाज्य।
सह-अभाज्य संख्याएँ (Co-prime Numbers)
यदि दो संख्याओं के बीच केवल 1 ही उभयनिष्ठ गुणनखंड है तो वे सह-अभाज्य संख्याएँ कहलाती हैं।
उदाहरण
7 और 15 सह-अभाज्य संख्याएँ हैं
चुकि
7 और 15 का उभयनिष्ठ/सार्व गुणनखंड केवल 1 है। इसलिए ये सह-अभाज्य संख्याएँ हैं।
सम संख्याएँ (Even Numbers )
वे संख्याएँ जिनका इकाई का अंक 0,2,4,6,8 होता हैं उन्हें सम संख्याएँ कहते हैंउदहारण के लिए =10 ,32 ,68
विषम संख्याएँ ( Odd Numbers)
वे संख्याएँ जिनका इकाई का अंक 1,3,5,7,9 होता हैं उन्हें विषम संख्याएँ कहते हैंउदहारण के लिए =13 ,15 ,27
OMR (One Minute Revision)
- NOTE:
- वे संख्या जिनके गुणनखंड 1 या वह संख्या स्वयं होती है अभाज्य संख्या कहलाती है।
तथा वे संख्याए जिनके 2 से अधिक गुणनखंड होते है भाज्य संख्याए कहलाती है। - यदि इकाई के स्थान पर संख्या 0,2,4,6 और 8 हो तो वह संख्या सम संख्या होती है।
वे संख्याएँ जो सम नहीं होती हैं, विषम संख्याएँ कहलाती हैं। - 2 सबसे छोटी सम अभाज्य संख्या है, 2 को छोड़कर सभी अभाज्य संख्याएँ विषम संख्याएँ हैं।
- 1 न तो अभाज्य संख्या है और न ही भाज्य संख्या।
उदाहरण 5
निम्नलिखित में से कौन-से युग्म सह-अभाज्य है?
(a) 18 और 35
(b) 15 और 37
(c) 30 और 415
(d) 17 और 68
(a) 18 और 35
18 के गुणनखंड
=1,2,3,6,9,18
35 के गुणनखंड
=1,5,7,35
18 और 35 का उभयनिष्ठ/सार्व गुणनखंड केवल 1 है। इसलिए ये सह-अभाज्य संख्याएँ हैं।
(b) 15 और 37
15 के गुणनखंड
=1,3,5,15
37 के गुणनखंड
=1,37
15 और 37 का उभयनिष्ठ/सार्व गुणनखंड केवल 1 है। इसलिए ये सह-अभाज्य संख्याएँ हैं।
(c) 30 और 415
30 के गुणनखंड
=1,2,3,5,6,10,15,30
415 के गुणनखंड
=1,5,83
30 और 415 का उभयनिष्ठ/सार्व गुणनखंड 1, 5 है। इसलिए ये सह-अभाज्य संख्याएँ नहीं हैं।
(a) 17 और 68
17 के गुणनखंड
=1,17
68 के गुणनखंड
=1,2,4,17,34
17 और 68 का उभयनिष्ठ/सार्व गुणनखंड 1, 17 है। इसलिए ये सह-अभाज्य संख्याएँ नहीं हैं।
भाजकता के नियम (Divisibility Law)
भाजकता का नियम यह निर्धारित करने की एक विधि है कि क्या दी गयी संख्या एक निश्चित भाजक (divisor) द्वारा विभाज्य (divisible) है या नहीं
हमारे पास 2, 3, 4, 5, 6, 7, 8, 9, 10 और 11 के लिए विभाज्यता नियम हैं।
यदि किसी संख्या के इकाई का अंक 0, 2, 4, 6 या 8 है, तो वह संख्या 2 से विभाज्य होती है।
उदाहरण:
12, 34, 56 और 78
एक संख्या 3 से विभाज्य है, यदि उसके अंकों का योग 3 से विभाज्य है
उदाहरण:
27
क्योकि
2+7=9
जो की 3 से विभाज्य हैं
अत: 27, 3 से विभाज्य है
कोई संख्या 4 से विभाज्य होती है यदि उसके अंतिम दो अंकों (अर्थात इकाई और दहाई) से बनी संख्या 4 से विभाज्य हो
उदाहरण:
1396, 4 से विभाज्य है क्योंकि इसके अंतिम दो अंक यानी 96, 4 से विभाज्य है।
यदि किसी संख्या का इकाई का अंक 5 या 0 है, तो वह 5 से विभाज्य है।
उदाहरण:
75, 90, 100 और 125
यदि कोई संख्या 2 और 3 दोनों से विभाज्य है, तो वह 6 से भी विभाज्य है।
उदाहरण:
120,
चुकि 120, 2 और 3 से विभाज्य है। इसलिए, यह 6 से भी विभाज्य है
कोई संख्या 7 से विभाजित होगी यदि जब संख्या के इकाई के अंक को दुगुना करे तथा इसे शेष अंकों से बनी संख्या से घटाया जाए यदि प्राप्त संख्या 7 से विभाजित है तो वह पूरी संख्या भी 7 से विभाजित होगी
NOTE= यह नियम 1 से अधिक बार भी प्रयोग किया जा सकता है ।
उदाहरण :1 = 3541
step1 इकाई का अंक =1
step2 दुगुना = 1×2=2
step3 शेष संख्या = 354−2
=352
step4 प्राप्त संख्या 352 , 7 से विभाजित नहीं है अतः यह पूरी संख्या भी 7 से विभाजित नहीं होगी।
इसी प्रकार इस नियम को फिर से प्रयोग करने पर भी यह संख्या 7 से विभाजित नहीं होगी ।
उदाहरण :2
826
क्योंकि
82−(6×2)
=82−12
=70,
यहा प्राप्त संख्या 70, 7 से विभाजित है अतः यह पूरी संख्या भी 7 से विभाजित होगी ।
कोई संख्या 8 से विभाज्य होती है, यदि उसके अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य हो।
उदाहरण:
73512, 8 से विभाज्य है क्योंकि इसके अंतिम तीन अंक यानी 512, 8 से विभाज्य हैं।
एक संख्या 9 से विभाज्य होती है यदि उसके अंकों का योग 9 के द्वारा विभाज्य है
उदाहरण:
126
इसके अंकों का योग = 1+2+6=9,
जो 9 से विभाज्य है।
अत: 126, 9 से विभाज्य है।
यदि किसी संख्या का इकाई का अंक 0 है, तो वह 10 से विभाज्य है।
उदाहरण:
90, 100
किसी संख्या के विषम स्थानों (दाईं ओर से) के अंकों के योग और सम स्थानों (दाईं ओर से) के अंकों के योग के बीच अंतर ज्ञात कीजिए यदि अंतर या तो 0 है या 11 से विभाज्य है, तो संख्या 11 से विभाज्य है।
उदाहरण =
1234321, 11 से विभाज्य है,
क्योंकि
(1+3+3+1)−(2+4+2)
=8−8
=0
जो 11 से विभाज्य है।
कुछ और विभाज्यता नियम
(1) मान लीजिए a और b दो दी गई संख्याएं हैं। यदि a, b से विभाज्य है तो यह b के सभी गुणनखंडों से भी विभाज्य होगा।
उदाहरण
यदि 24, 12 से विभाज्य है, तो 24, 12 के सभी गुणनखंडों (अर्थात 2, 3, 4, 6) से भी विभाज्य होगा।
(2) मान लीजिए a और b दो सह-अभाज्य संख्याएँ हैं। यदि c, a और b से विभाज्य है तो c, a और b के गुणनफल से विभाज्य होगा
उदाहरण
यदि 24, 2 और 3 से विभाज्य है जो सह-अभाज्य संख्याएँ हैं तो 24 भी 2 और 3 (2×3=6) के गुणनफल से विभाज्य होगा।
(3) यदि a और b, c से विभाज्य हैं तो (a+b) भी c से विभाज्य होगा।
उदाहरण
यदि 24 और 12, 4 से विभाज्य हैं तो (24+12)=36 भी 4 से विभाज्य होंगे।
(4) यदि a और b, c से विभाज्य हैं तो a−b भी c से विभाज्य होंगे।
उदाहरण
यदि 24 और 12, 4 से विभाज्य हैं तो 24−12=12 भी 4 से विभाज्य होगा।
OMR (One Minute Revision)
(Divisibility Test)
उदाहरणतः =1298,1221,123321,12344321,1234554321,123456654321
उदाहरण 6
विभाज्यता की जांच के नियमो का प्रयोग करते हुए, पता कीजिए की निम्नलिखित संख्याओं में से कौन से संख्या 2 से विभाज्य है, 3 से विभाज्य है, 4 से विभाज्य है, 5 से विभाज्य है, 6 से विभाज्य है, 8 से विभाज्य है, 9 से विभाज्य है, 10 से विभाज्य है या 11 से विभाज्य है (हाँ या नहीं कहिये):

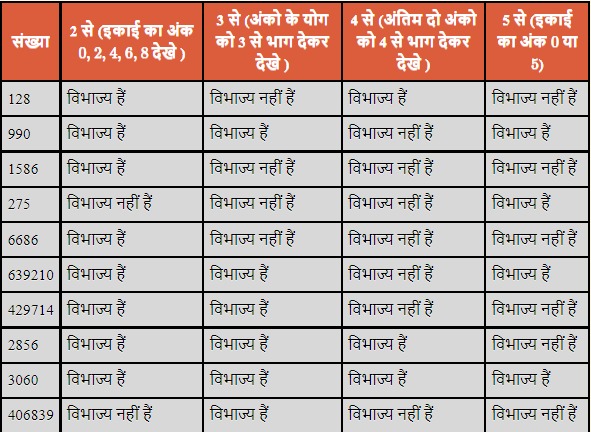
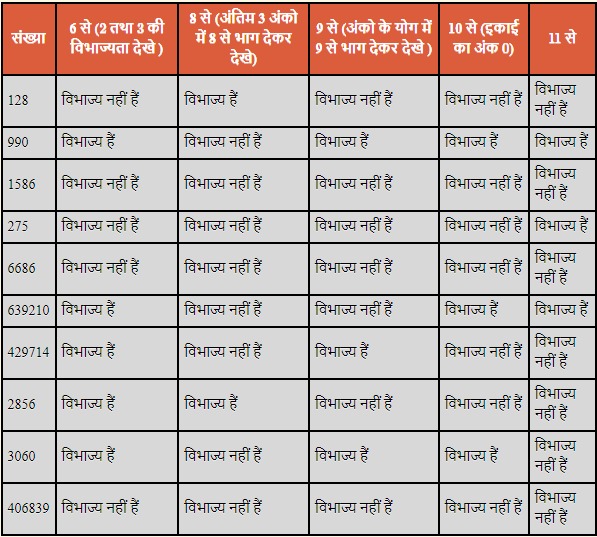
अभाज्य गुणनखंडन
अभाज्य गुणनखंडन, एक संख्या के सभी अभाज्य गुणनखंडों को खोजने की प्रक्रिया है।
यदि किसी संख्या को उसके गुणनखंडों के गुणनफल के रूप में व्यक्त किया जाए, तो हम उस संख्या को गुणनखंडित (factorised) करते है
उदाहरण
24=8×3 लिखते हैं, तो हम कहते हैं कि हमने 24 के गुणनखंड कर लिए हैं। यह 24 के गुणनखंडो में से एक गुणनखंड है, इसके अन्य गुणनखंडन निम्न हैं :
24=2×2×2×3
किसी संख्या के अभाज्य गुणनखंड ज्ञात करने की दो विधियाँ हैं
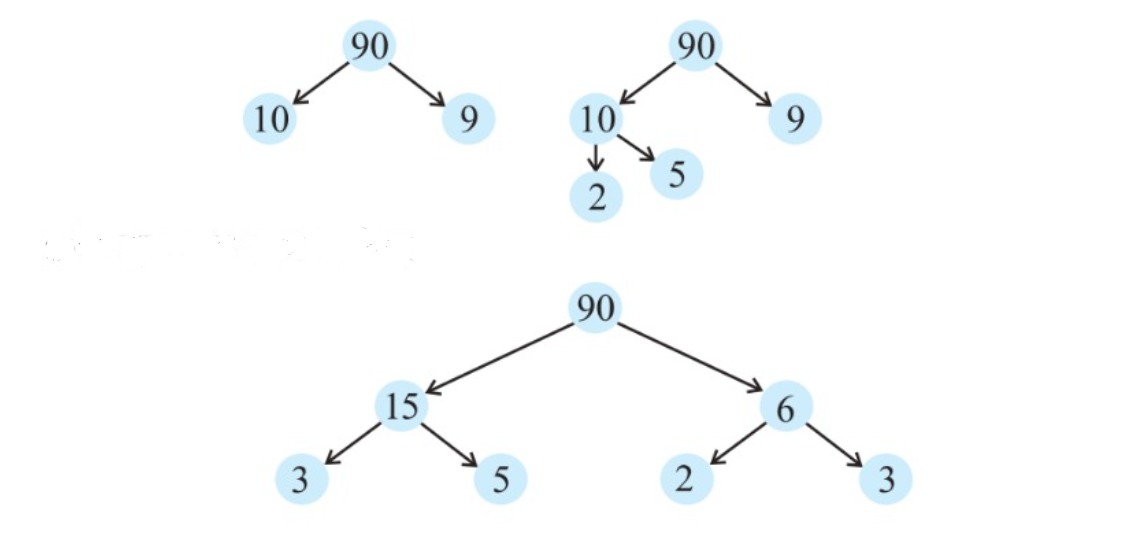
गुणनखंड वृक्ष
हम 90 के अभाज्य गुणनखंड निम्न प्रकार से ज्ञात कर सकते हैं।
बार-बार विभाजन विधि
हम 680 के अभाज्य गुणनखंड निम्न प्रकार से ज्ञात कर सकते हैं।
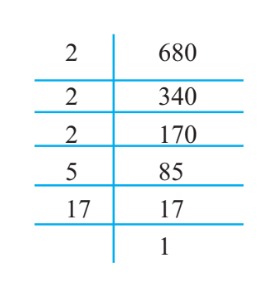
उदाहरण 7
980 का अभाज्य गुणनखंड ज्ञात कीजिए
संख्या 980 को 2, 3, 5, 7 इत्यादि से इसी क्रम में बार-बार भाग देते हैं। यह प्रक्रिया हम तब तक जारी रखते हैं, जब तक कि भागफल इनसे विभाजित होता रहे।

इस प्रकार 980 का अभाज्य गुणनखंडन है :
980=2×2×5×7×7
उदाहरण 8
पांच अंको की सबसे छोटी संख्या लिखिए और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए!
चूंकि पांच अंको की सबसे छोटी संख्या =
10000
संख्या 10000 को 2,3,5,7 इत्यादि से इसी क्रम में बार-बार भाग देते हैं। यह प्रक्रिया हम तब तक जारी रखते हैं, जब तक कि भागफल इनसे विभाजित होता रहे।
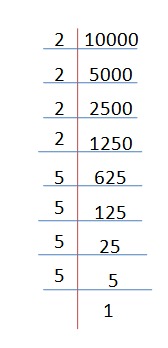
इस प्रकार 10000 का अभाज्य गुणनखंडन है :
10000=2×2×2×2×5×5×5×5
महत्तम समापवर्तक (HCF)
दो या दो से अधिक दी गई संख्याओं का महत्तम समापवर्तक (HCF), उनके सामान्य गुणनखंडों में सबसे बड़ा होता है।
इसका दूसरा नाम (GCD) (Greatest Common Divisior) है।
HCF ज्ञात करने की विधि
दी गई संख्याओं का HCF ज्ञात करने के लिए, हमें प्रत्येक संख्या का अभाज्य गुणनखंड ज्ञात करना होगा और फिर HCF ज्ञात करना होगा।
उदाहरण 9
निम्न का म.स. ज्ञात कीजिए:
(i)24और 36
(ii)15,25 और 30
(iii)8 और 12
(iv)12,16 और 28
(i) 24, 36
सर्वप्रथम हमे दी गई संख्याओं का अभाज्य गुणनखंड ज्ञात करना हैं
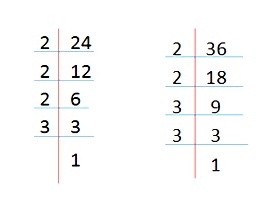
24=2×2×2×3
36=2×2×3×3
यहाँ 24 और 36 में सार्व गुणनखंड 2 ,(दो बार) और 3 एक बार है इसलिए 24 ,36 का म.स.=
2×2×3=12
(ii) 15 ,25 ,और 30
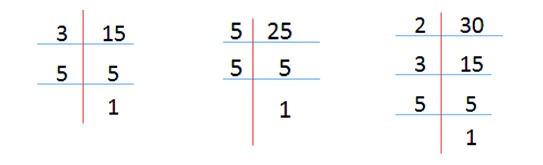
15=3×5
25=5×5
30=2×3×5
यहाँ 15 , 25 और 30 में सार्वगुणनखंड 5, है इसलिए 15 ,25 और 30 का म.स.5 होगा।
(iii) 8 और 12

8=2×2×2
12=2×2×3
यहाँ 8और 12 में सार्वगुणनखंड 2 , दो बार आया है। इसलिए 8 और12 का म.स.=4 होगा
(iv) 12, 16 और 28
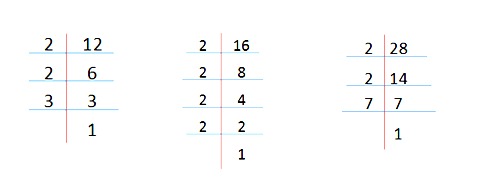
12=2×2×3
16=2×2×2×2
28=2×2×7
यहाँ 12,16और 28 में सार्वगुणनखंड 2 , दो बार आया है। इसलिए 12,16 और28 का म.स.=4 होगा
उदाहरण 10
किसी कमरे की लम्बाई ,चौड़ाई तथा ऊंचाई क्रमश: 825 सेमी. ,675 सेमी. और 450 सेमी. है, ऐसा सबसे लम्बा फीता ज्ञात कीजिए जो कमरे की तीनो विमाओ को पूरा-पूरा माप ले
825, 675, 450
सर्वप्रथम हमे दी गई संख्याओं का अभाज्य गुणनखंड ज्ञात करना हैं

825=3×5×5×11
675=3×3×3×5×5
450=2×3×3×5×5
यहाँ 825, 675 और 450 में सार्व गुणनखंड 5 ,(दो बार) और 3 एक बार है इसलिए 825,625,450 का म.स.=
3×5×5=75
लघुत्तम समापवर्तक (LCM)
(Lowest common multiple)(LCM)
दो या दो से अधिक दी गई संख्याओं का सबसे छोटा सामान्य गुणज (लघुत्तम समापवर्तक), उनके सामान्य गुणकों में सबसे छोटा होता है।
LCM ज्ञात करने का तरीका
LCM ज्ञात करने के लिए हमें दी गई सभी संख्याओं का अभाज्य गुणनखंड ज्ञात करना होगा और फिर उन सभी अभाज्य गुणनखंडों को गुणा करना होगा जो अधिकतम बार आए हैं।
उदाहरण 11
20,25 और 30 का ल.स. ज्ञात कीजिए!
METHOD-1

step (a) सबसे छोटी अभाज्य संख्या 2 से भाग देने पर, चुकि 25 जैसी संख्या 2 से विभाज्य नहीं है इसलिए इन्हें अगली पंक्ति में वैसा का वैसा ही रख दिया जाता है
step (b) पुन: 2 से भाग देने पर, इसे तब तक जारी रखेंगे जब तक 2 के गुणज मिलते रहें
step (c) अगली अभाज्य संख्या 3 से भाग दीजिए।
step (d) अगली अभाज्य संख्या 5 से भाग दीजिए
step (e) पुन: 5 से भाग दीजिए
अतः ल.स. =
2×2×3×5×5=300
METHOD-2
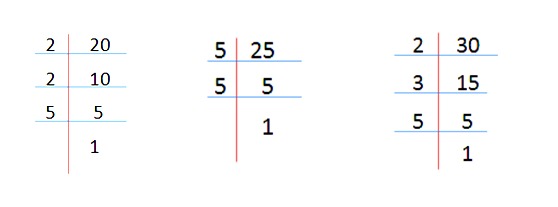
20=2×2×5
25=5×5
30=2×3×5
अतः ल.स. =
2×2×3×5×5=300
उदाहरण 12
तीन लड़के एक ही स्थान से एक साथ कदम उठाकर चलना प्रारंभ करते है! उनके कदमो की माप क्रमश: 63 सेमी., 70 सेमी. और 77 सेमी. है! इनमे से प्रत्येक कितनी न्यूनतम दूरी तय करे की वह दूरी पुरे-पुरे कदमो में तय हो जाये?
63, 70, 77
सर्वप्रथम हमे दी गई संख्याओं का अभाज्य गुणनखंड ज्ञात करना हैं

यहाँ 63, 70, 77 के गुणनखंड में 2×3×3×7×11 , आया है इसलिए 63, 70, 77 का ल.स.1386 होगा।
उदाहरण 13
वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 6,15 और 18 से भाग देने पर प्रत्येक दशा में 5 शेष रहे!
6, 15, 18
सर्वप्रथम हमे दी गई संख्याओं का अभाज्य गुणनखंड ज्ञात करना हैं
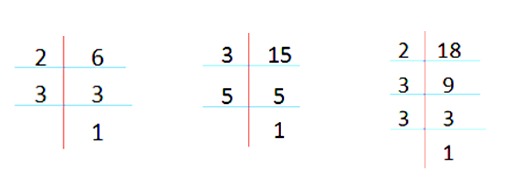
15=3×5
6=2×3
18=2×3×3
यहाँ 6 ,15 और 18 के गुणनखंड में 2×3×3×5 , आया है इसलिए 6 ,15 और 18 का ल.स.90 होगा।
चुकी हमे प्रत्येक दशा मे 5 शेष चाहिए इसलिए
90+5=95
अतः वह संख्या 95 होगी ।
सारांश
गुणनखंडों और गुणकों के बारे में कुछ तथ्य
गुणनखंड
गुणज
तथा वे संख्याए जिनके 2 से अधिक गुणनखंड होते है भाज्य संख्याए कहलाती है।
वे संख्याएँ जो सम नहीं होती हैं, विषम संख्याएँ कहलाती हैं।
उदाहरणतः =1298,1221,123321,12344321,1234554321,123456654321
