अनुपात और समानुपात कक्षा 6 गणित
भूमिका
बच्चों! अध्याय के शीर्षक के अनुसार इस अध्याय में हम अनुपात और समानुपात का अध्ययन करेंगे। दो समान राशियों के तुलनात्मक अध्ययन को अनुपात कहते है। अन्य शब्दों में वह संबंध जो एक ही प्रकार की दो राशियों में यह बताता है कि एक राशि, दूसरी राशि से कितना गुना है, अनुपात कहलाता है तथा समानुपात दो भिन्नों या अनुपातों की समानता बताता है। इस अध्याय मे हम अनुपात, समानुपात तथा एकिक विधि का अध्ययन करेंगे।
आइये जानते है, अनुपात और समानुपात को और करीब से...
हमारे दैनिक जीवन में अनेक बार हमें दो एक जैसी राशियों की तुलना करनी पड़ती है।
उदाहरण:- राम और श्याम ने दुकानदार से चित्र बनाने के लिए कुछ पेंसिल खरीदते हैं।
राम ने 10 पेंसिल और श्याम ने 20 पेंसिल खरीदा।
इन दोनों की पेंसिलों की संख्या में अंतर द्वारा तुलना करने पर हम जान सकते हैं कि श्याम ने राम से (20−10=10) 10 पेंसिल अधिक खरीदा।
यदि हम तुलना भाग द्वारा करें तो वह इस प्रकार होगी:
अतः, श्याम के द्वारा खरीदें गये पेंसिलों की संख्या =2× राम के द्वारा खरीदें गये पेंसिलों की संख्या
अतः हम कह सकते हैं कि श्याम के द्वारा खरीदें गये पेंसिलों की संख्या, राम के द्वारा खरीदें गये पेंसिलों की संख्या से दोगुनी हैं।
एक और उदाहरण से समझते हैं:-
एक कार का मूल्य ₹2,50,000 है और एक मोटर साइकिल का मूल्य ₹50,000 है यदि हम उनके मूल्यों का अंतर लें तो यह ₹2,50,000− ₹50,000= ₹2,00,000 होगा।

यदि हम तुलना भाग द्वारा करें तो वह इस प्रकार होगी:
(250000)/(50000)= (25cancel0000)/(5cancel0000) =25/5= 5/1
अतः हम कह सकते हैं कि कार का मूल्य मोटरसाइकिल के मूल्य का पाँच गुना है।
इस प्रकार कुछ परिस्थितियों में भाग द्वारा तुलना अंतर द्वारा तुलना से ज्यादा सार्थक है। भाग द्वारा तुलना को ही अनुपात कहा जाता है तथा जब दो अनुपात आपस मे बराबर होते हैं तो वे समानुपात कहलाते हैं।
अनुपात में किन्हीं दो राशियों की तुलना करनी होती है, जबकि समानुपात में दो अनुपातों के बीच तुलना की जाती है।
अनुपात
दो समान राशियों के तुलनात्मक अध्ययन को अनुपात कहते है। अन्य शब्दों में वह संबंध जो एक ही प्रकार की दो राशियों में यह बताता है कि एक राशि दूसरी राशि से कितना गुना है, अनुपात कहलाता है।
अनुपात को प्रदर्शित करने के लिए संकेत : का प्रयोग किया जाता हैं।
जैसे:- यदि, a तथा b दोनों एक ही प्रकार की दो राशियाँ हो, तो a तथा b के अनुपात को a:b के रूप में लिखा जाता हैं और a अनुपात b पढा जाता हैं।
a:b को ab के रूप में भी लिखा जा सकता है, जहाँ, b≠0 होता हैं।
उदाहरण से समझते हैं:
एक कक्षा में 20 लड़के तथा 40 लड़कियाँ हैं। अनुपात ज्ञात कीजिए :
(a) लड़कियों की संख्या का कुल विद्यार्थियों से
(b) लड़कों की संख्या का कुल विद्यार्थियों से
हल:- सर्वप्रथम हमें कुल विद्यार्थियों की संख्या की आवश्यकता है जो कि इस प्रकार है:
कुल विद्यार्थियों की संख्या = लड़कियों की संख्या + लड़कों की संख्या
=20+40=60
अतः, लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से अनुपात
=4060=46=23=2:3
लड़कों की संख्या का कुल विद्यार्थियों की संख्या से अनुपात
=2060=26=13=1:3
अतः, लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से अनुपात 2:3 तथा लड़कों की संख्या का कुल विद्यार्थियों की संख्या से अनुपात 1:3 हैं।
दो राशियों की तुलना तभी की जा सकती है जब वे एक ही इकाई में हों।
यदि दो राशि दिया गया हो, जिनकी इकाई अलग - अलग हो, तो सबसे पहले उन्हे एक ही इकाई मे बदलना होता हैं।
उदाहरण से समझते हैं:
रमन की ऊंचाई का राधा की ऊंचाई से अनुपात क्या है यदि रमन की ऊंचाई 175 सेमी और राधा की ऊंचाई 1.35 मीटर है?
हल:-
रमन की ऊंचाई =175 सेमी
राधा की ऊंचाई =1.35 मीटर
रमन और राधा की ऊंचाई की इकाई समान नहीं है (रमन की ऊंचाई सेमी मे दिया हैं और राधा की ऊंचाई मीटर में) इसलिए उन्हें एक ही इकाई में परिवर्तित करना होगा।
∵1 मीटर =100 सेमी
∴1.35 मीटर =1.35×100 सेमी =135 सेमी
अतः, राधा की ऊंचाई =135 सेमी
∴ रमन की ऊंचाई का राधा की ऊंचाई से अनुपात
=175135=3527=35:27
अतः, रमन की ऊंचाई का राधा की ऊंचाई से अनुपात =35:27 हैं।
Note:- यहाँ रमन की ऊंचाई का राधा की ऊंचाई से अनुपात 35:27 हैं, अतः राधा की ऊंचाई का रमन की ऊंचाई से अनुपात 27:35 होगा।
तुल्य अनुपात: किसी भी अनुपात का तुल्य अनुपात अंश और हर में एक समान संख्या (अशून्य संख्या) से गुणा या भाग द्वारा प्राप्त कर सकते हैं।
उदाहरण: 2:4 के दो तुल्य अनुपात ज्ञात कीजिए।
हल:- ∵ तुल्य अनुपात प्राप्त करने के लिए अंश और हर दोनों को एक ही संख्या से गुणा या भाग करते हैं।
2:4=24=2×24×2=48=4:8
इसी प्रकार,
2:4=24=2÷24÷2=12=1:2
अतः 2:4 के दो तुल्य अनुपात 4:8 और 1:2 हैं।
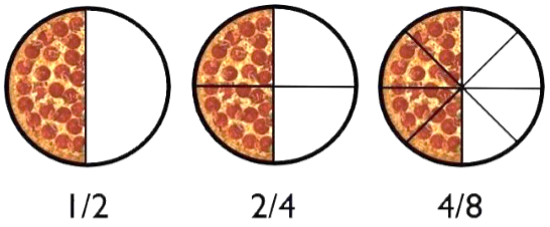
उपरोक्त आकृति से, हम देख सकते हैं कि सभी समान अनुपातों में केवल समान भागों की संख्या बदल रही है लेकिन सभी अनुपात केवल वृत्त के आधे भाग का प्रतिनिधित्व कर रहे हैं। अतः तुल्य अनुपात के मामले में केवल उनके मूल्य में परिवर्तन होता है लेकिन वे मात्रा के समान हिस्से का प्रतिनिधित्व करते हैं।
अनुपात का निम्नतम रूप: यदि 1 को छोड़कर अंश और हर का कोई उभयनिष्ठ गुणनखंड नहीं है, तो यह अनुपात का निम्नतम रूप होता हैं।
Note:- अनुपात का निम्नतम रूप ज्ञात करने के लिए उसके अंश व हर का महत्तम समापवर्तक ज्ञात कर, उसे अंश व हर दोनों मे विभाजित करके भी प्राप्त किया जा सकता हैं।
जैसे:- 40:60 का निम्नतम रूप ज्ञात करते हैं।
40 व 60 का महत्तम समापवर्तक =20
अतः, 4060 के अंश एवं हर मे 20 को भाग देने पर, निम्नतम रूप प्राप्त हो जाएगा।
40:60=4060=40÷2060÷20=23=2:3
उदाहरण: 10:40 का निम्नतम रूप ज्ञात कीजिए।
हल:- 10 व 40 का म.स. =10, इसलिए अंश और हर दोनों को 10 से विभाजित करते हैं।
∴10:40=1040=10÷1040÷10=14=1:4
अतः 10:40 का निम्नतम रूप 1:4 हैं।
OMR (One Minute Revision)
उदाहरण 1
सौरभ घर से स्कूल पहुँचने में 15 मिनट लेता है और सचिन 1 घंटा लेता है। सौरभ द्वारा लिए गए समय और सचिन द्वारा लिए गए समय का अनुपात ज्ञात करों।
दिया हैं;
सौरभ द्वारा घर से स्कूल पहुँचने में लिया गया समय =15 मिनट
सचिन द्वारा घर से स्कूल पहुँचने में लिया गया समय =1 घंटा
स्पष्ट हैं कि दोनों की इकाई समान नहीं हैं, अतः समान इकाई मे बदलते हैं।
हम जानते हैं कि, 1 घंटा =60 मिनट
∴ सचिन द्वारा घर से स्कूल पहुँचने में लिया गया समय =60 मिनट
अतः, सौरभ द्वारा लिए गए समय और सचिन द्वारा लिए गए समय का अनुपात
15:60=1560=14=1:4
अतः, सौरभ द्वारा लिए गए समय और सचिन द्वारा लिए गए समय का अनुपात 1:4 हैं।
उदाहरण 2
30 मिनट का 1.5 घंटे से अनुपात ज्ञात कीजिये।
स्पष्ट हैं कि, दोनों की इकाई समान नहीं हैं, अतः समान इकाई मे बदलते हैं।
∵1 घंटा =60 मिनट
∴ 1.5 घंटा =60×1.5=90 मिनट
अतः, 30 मिनट का 90 मिनट से अनुपात
30:90 = (3cancel(0))/(9cancel(0)) = 3/9 =1/3=1:3
उदाहरण 3
3:2 के दो तुल्य अनुपात लिखिए।
हम जानते हैं कि, जब हर और अंश में एक समान संख्या से गुणा या भाग करने पर जो अनुपात मिलता है तुल्य अनुपात कहलाता है।
3:2=32=3×22×2=64=6:4
इसी प्रकार,
3:2=32=3×32×3=96=9:6
अतः 3:2 के दो तुल्य अनुपात 6:4 और 9:6 हैं।
उदाहरण 4
आकृति को देखकर आयत के अंदर के सभी त्रिभुजों की संख्या का वृत्तों की संख्या से अनुपात निकालिये।
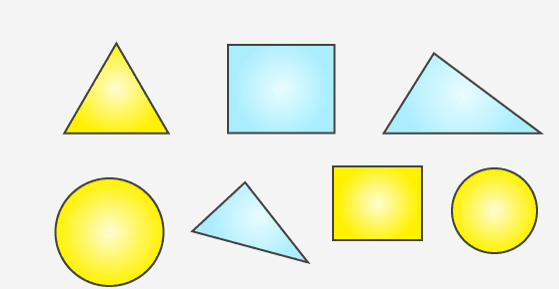
दिया हैं;
आयत में त्रिभुजों की संख्या =3
आयत में वृत्तों की संख्या =2
अतः, त्रिभुजों की संख्या का वृत्तों की संख्या से अनुपात =3:2
उदाहरण 5
एक स्कूल में एक वर्ष में 73 छुट्टियाँ बनती हैं। छुट्टियों का वर्ष के कुल दिनों के साथ अनुपात ज्ञात कीजिए।
दिया हैं;
छुट्टियों की संख्या =73 दिन
हम जानते हैं, कि एक साल में दिनों की संख्या =365 दिन
अतः, छुट्टियों का वर्ष के कुल दिनों के साथ अनुपात
73:165=73165=15=1:5
अतः छुट्टियों का वर्ष के कुल दिनों के साथ अनुपात 1:5 हैं।
उदाहरण 6
शीला और संगीता के बीच 20 पेनों को 3:2 में बाँटिए।
शीला और संगीता के बीच पेनों का अनुपात =3:2
अनुपात के अंकों का कुल योग =3+2=5
इसलिए, शीला का हिस्सा = कुल पेनों का 35 भाग
=35×20=3×4=12 पेन
संगीता का हिस्सा = कुल पेनों का 25 भाग
=25×20=2×4=8 पेन
अतः 20 पेनों को 3:2 मे बांटने पर, 12 पेन शीला के और 8 पेन संगीता के होंगे।
समानुपात
समानुपात दो शब्दों सम + अनुपात से बना है जिसका अर्थ है समान अनुपात, अतः जब दो अनुपात बराबर होते हैं तो वे समानुपात कहलाते हैं।
समानुपात को प्रदर्शित करने के लिए संकेत :: का प्रयोग किया जाता हैं।
यदि ab=cd है, तो इसे हम a:b::c:d या a:b=c:d लिखते हैं और a अनुपात b बराबर c अनुपात d पढ़ते हैं।
उदाहरण: एक व्यक्ति 2 घंटे में 35 किमी चलता है। एक अन्य व्यक्ति 4 घंटे में 70 किमी चलता है तब क्या उनकी चाल समानुपातिक है?
हल:- दोनों व्यक्ति द्वारा चली गई दूरियों का अनुपात =35:70
35:70=3570=12=1:2
दोनों व्यक्ति द्वारा लिए गए समय का अनुपात =2:4
2:4=24=12=1:2
अतः दोनों अनुपात समान है।
अर्थात् 35:70::2:4 या 35:70=2:4
इसे 35 अनुपात 70 बराबर 2 अनुपात 4 पढ़ते हैं।
यदि दो अनुपात समान नहीं होते हैं, तो वे राशियाँ समानुपाती नहीं होती हैं।
उदाहरण: 3 किग्रा सेब का मूल्य ₹360 है और 15 किग्रा तरबूज का मूल्य ₹90 है।
दोनों के वजनों का अनुपात =3:15
3:15=315=15=1:5
दोनों के मूल्यों का अनुपात =360:90
360:90=(36cancel(0))/(9cancel(0))=36/9= 4/1= 4:1
अतः 3:15 और 360:90 समान नहीं है।
अर्थात् 3:15≠360:90
∴ चारों राशियाँ 3, 15, 360 और 90 समानुपात में नहीं है।
समानुपात के कथन में, क्रम में ली गई चारों राशियाँ पद कहलाती हैं। पहले और चौथे पद को चरम पद (या सिरों के पद) कहते हैं तथा दूसरे और तीसरे पद को मध्य पद कहते हैं।
जैसे: 35:70::2:4 में 35, 70, 2 और 4 चार पद हैं।
जिसमें से 35 तथा 4 चरम पद हैं और 70 तथा 2 मध्य पद हैं।
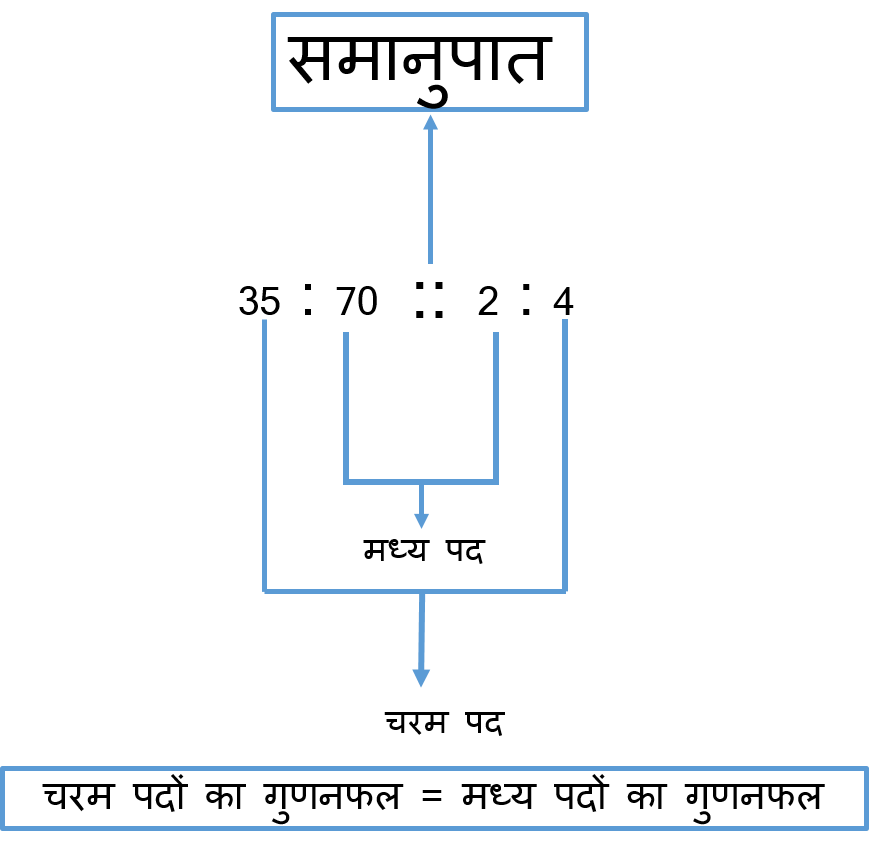
दोनों चरम पदों के गुणनफल तथा दोनों मध्य पदों के गुणनफल आपस में बराबर होते हैं।
अतः, चरम पदों का गुणनफल = मध्य पदों का गुणनफल
⇒35×4=70×2
⇒140=140
उदाहरण: जाँच कीजिए कि 4:12 और 9:27 समानुपाती हैं अथवा नहीं ?
हल:- यहाँ,
4:12=412=13=1:3
9:27=927=13=1:3
अतः दोनों अनुपात समान हैं। इसलिए 4:12 और 9:27 समानुपाती हैं।
Note:- उपरोक्त उदाहरण में चरम पदों का गुणनफल और मध्य पदों का गुणनफल आपस मे बराबर होंगे क्योंकि दिया गया अनुपात समानुपाती हैं।
∴ चरम पदों का गुणनफल = मध्य पदों का गुणनफल
⇒4×27=12×9
⇒108=108
OMR (One Minute Revision)
चरम पदों का गुणनफल = मध्य पदों का गुणनफल
⇒ad=bc
उदाहरण 7
क्या राशियाँ 30,25,42,35 समानुपात में है ?
यहाँ,
30:25=3025=65=6:5
42:35=4235=65=6:5
अतः दोनों अनुपात 30:25 और 42:35 समान हैं।
3025=4235 या 30:25=42:35
इसलिए राशियाँ 30,25,42,35 समानुपात में है।
उदाहरण 8
16:24::20:30 सत्य हैं या असत्य लिखिए।
यहाँ,
16:24=1624=46=23=2:3
20:30=2030=23=2:3
अतः दोनों अनुपात 16:24 और 20:30 समान हैं।
अतः, दिया गया कथन सत्य हैं।
उदाहरण 9
जाँचिए की क्या निम्न अनुपात, समानुपात बनाते है? यदि समानुपात बनता हो, तो मध्य पद और चरम पद भी लिखिए:
25 सेमी :1 मीटर और ₹40 : ₹160
25 सेमी का 1 मीटर से अनुपात
=25 सेमी : 1×100 सेमी (1 मीटर =100सेमी)
=25:100=25100=14=1:4
₹40 का ₹160 से अनुपात
40:160=40160=416=14=1:4
चूंकि दोनों अनुपात समान हैं। अतः दिये हुए अनुपात, समानुपात बनाते हैं।
यहाँ, मध्य पद =1 मीटर, ₹40 और चरम पद =25 सेमी, ₹160
एकिक विधि
वह विधि जिसमें हम पहले एक इकाई का मान निकालते हैं और फिर वांछित इकाइयों का मान निकालते हैं, एकिक विधि कहलाती है।
उदाहरण से समझते हैं
उदाहरण:-यदि 3 पुस्तकों का मूल्य ₹320 है, तो 6 पुस्तकों का मूल्य क्या होगा?

हल:- यहाँ, 6 पुस्तकों का मूल्य इकाई विधि से ज्ञात करने के लिए, हम पहले 1 पुस्तक का मूल्य ज्ञात करेंगे।
∵3 पुस्तकों का मूल्य =₹320
∴1 पुस्तक का मूल्य =₹3203
अतः, 6 पुस्तकों का मूल्य
=3203×6
=320×2
=₹640
अत: 6 पुस्तकों का मूल्य ₹640 होगा।
उदाहरण:-एक मोटर साइकिल 2 लीटर पेट्रोल में 120 किमी दूरी तय करती है। बताइए 300 किमी दूरी तय करने में कितने लीटर पेट्रोल की आवश्यकता होगी?

हल:- 120 किमी दूरी तय करने में मोटर साइकिल में पेट्रोल की खपत =2 लीटर
∴1 किमी दूरी तय करने में पेट्रोल की खपत =2120 लीटर
अतः, 300 किमी दूरी तय करने में पेट्रोल की खपत
=2120×300 लीटर
=600120 लीटर
=5 लीटर
अतः, एक मोटर साइकिल को 300 किमी दूरी तय करने में 5 लीटर पेट्रोल की आवश्यकता होगी।
उदाहरण 10
यदि 22 मीटर कपड़े का मूल्य ₹704 है, तो 20 मीटर कपड़े का मूल्य क्या होगा?
∵22 मीटर कपड़े का मूल्य = ₹704
∴1 मीटर कपड़े का मूल्य =₹70422
अतः, 20 मीटर कपड़े का मूल्य
=70422×20
=70411×10
=64×10
=₹640
अतः, 20 मीटर कपड़े का मूल्य ₹640 है।
उदाहरण 11
63 पुस्तकों का भार 9 किग्रा है। ऐसी 49 पुस्तकों का भार कितना होगा ?
∵63 पुस्तकों का भार =9 किग्रा
∴1 पुस्तक का भार =963 किग्रा
अतः, 49 पुस्तकों का भार
=963×49 किग्रा
=17×49 किग्रा
=1×7 किग्रा
=7 किग्रा
अतः, 49 पुस्तकों का भार 7 किग्रा होगा।
उदाहरण 12
2 दर्जन केले का मूल्य ₹60 है ₹12.50 में कितने केले खरीदें जा सकते है।
2 दर्जन केले का मूल्य = ₹60
∵1 दर्जन =12
∴2 दर्जन =12×2=24
इसलिए, 24 केले का मूल्य = ₹60
∵ ₹60 में खरीदें गए केले =24
∴ ₹1 में खरीदें गए केले =2460=25
अतः, ₹12.50 में खरीदें गए केले
=25×12.50 (∵12.50⇒1250100)
= 2/5 xx(125cancel(0))/(10cancel(0))
= cancel(2)/5 xx25/cancel(2)
=5 केले
अतः, ₹12.50 में 5 केले खरीदें जा सकते है।
उदाहरण 13
मोहन ने 7 ओवर में 63 रन बनाए और सोहन ने 6 ओवर में 42 रन बनाए। 1 ओवर में किसने अधिक रन बनाए ?
मोहन द्वारा 7 ओवर में बनाए गए रन =63
∴ मोहन द्वारा 1 ओवर में बनाए गए रन =637=9 रन
सोहन द्वारा 6 ओवर में बनाए गए रन =42
∴ सोहन द्वारा 1 ओवर में बनाए गए रन =426=7 रन
अतः, 1 ओवर में मोहन ने अधिक रन बनाए।
उदाहरण 14
एक महिला की 15 महीने की बचत ₹18,000 है ?
(a) उसकी 7 महीने की बचत क्या होगी ?
(b) कितने महीने में उसकी बचत ₹30,000 हो जाएगी ?
(a) एक महिला की 15 महीने की बचत = ₹18,000
∴ 1 महीने की बचत =₹1800015
∴ 7 महीने की बचत =1800015×7
=1200×7
= ₹8400
अतः 7 महीने की बचत ₹8400 होगी।
(b) ∵एक महिला की 15 महीने की बचत = ₹18,000
अतः, महिला ₹18,000 बचत करती हैं =15 महीने
₹1 बचत करती हैं =1518000 महीने
∴₹30,000 बचत करती हैं
=1518000×30,000
= 15/(18cancel(000)) xx30cancel(000)
=5×5=25 महीने
अतः, 25 महीने में महिला की बचत ₹30,000 हो जाएगी।
सारांश
- एक जैसी राशियों की तुलना करने के लिए हम साधारणत: राशियों के अंतर द्वारा तुलना विधि प्रयोग करते हैं।
- अधिकतर परिस्थितियों में भाग द्वारा तुलना अधिक अच्छी होती है। अर्थात् एक राशि दूसरी राशि का कितना गुना है। इस विधि को भाग द्वारा तुलना कहते हैं।
उदाहरण के लिए ईशा का भार 25 किग्रा है और उसके पिता का भार 75 किग्रा है। हम कहेंगे कि ईशा के पिता के भार का ईशा के भार के साथ अनुपात 3:1 है।
- अनुपात द्वारा तुलना में, दोनों राशियों की इकाइयाँ समान होनी चाहिए। यदि वे समान नहीं हैं, तो अनुपात लेने से पहले उन्हें समान बना लेना चाहिए।
- अलग-अलग परिस्थितियों में अनुपात समान हो सकता है।
- अनुपात 3:2 और 2:3 एक दूसरे से भिन्न हैं। इस प्रकार जिस क्रम में राशियाँ ली गई हैं वह महत्वपूर्ण है।
- अनुपात को भिन्न के रूप में भी लिखा जा सकता है, जैसे 10:3=103 हैं।
- दो अनुपात तुल्य होंगे, यदि उनकी संगत भिन्न भी तुल्य हों। अत: 3:2 तुल्य है 6:4 या 12:8 के।
- एक अनुपात को न्यूनतम रूप में बदला जा सकता है। उदाहरण के लिए अनुपात 50:15 को 5015 भी लिख सकते हैं और न्यूनतम रूप में 5015=103 है। इस प्रकार न्यूनतम रूप में 50:15=10:3 हैं।
- चार राशियाँ समानुपात में कहलाएँगी, यदि पहली और दूसरी राशि का अनुपात, तीसरी और चौथी राशि के अनुपात के बराबर हो। इस प्रकार 3,10,15,50 समानुपात में है क्योंकि 310=1550 है।
हम समानुपात को 3:10::15:50 के रूप में दर्शाते हैं और 3 अनुपात 10 बराबर 15 अनुपात 50 के रूप में पढ़ते हैं। ऊपर लिखे समानुपात में 3 और 50 चरम पद हैं तथा 10 और 15 मध्य पद हैं।
- समानुपात में क्रम महत्वपूर्ण है। 3,10,15 और 50 समानुपात में हैं लेकिन 3,10,50 और 15 नहीं हैं क्योंकि 310≠5015 है।
- वह विधि जिसमें हम पहले एक इकाई का मान निकालते है और फिर एक से अधिक इकाइयों का मान निकालते हैं, एकिक विधि कहलाती है।
