सममिति कक्षा 6 गणित
भूमिका
बच्चों! अध्याय के शीर्षक के अनुसार इस अध्याय में सममिति का अध्ययन करेंगे। ऐसी आकृति जो बराबर संतुलित अनुपात में हो अर्थात एक आकृति के दो भाग एक - दूसरे के पूर्णतः बराबर हो, सममित आकृति (Symmetric Figure) कहलाती है। एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बांटती हो, तो यह रेखा सममित रेखा (Symmetric Line) कहलाती है। इस अध्याय मे हम सममित आकृतियाँ बनाना, दो सममित रेखाओं वाली एवं अनेक सममित रेखाओं वाली आकृतियाँ तथा प्रतिबिंब और सममिति का अध्ययन करेंगे।
आइये जानते है, सममिति को और करीब से...
हमारे दैनिक जीवन मे हमे बहुत से सममित आकृतियाँ देखने को मिलती रहती हैं।

ऊपर आकृति मे हम देख सकते हैं, कि तितली और पुष्प के दोनों भाग पूर्णतः एक - दूसरे के बराबर हैं। अतः ये सममित आकृति हैं।
इसी प्रकार,
प्रकृति मे पुष्प, मछली, गाय, कछुआ और बहुत से प्राणियों की आकृतियाँ सममित होती हैं।

बहुत से वस्तुओं, इमारतों को बनाने में भी सममिति का ध्यान रखा जाता हैं।
जैसे: नीचे आकृति में देख सकते हैं:


यदि, एक खींची गई रेखा आकृति को दो बराबर या समान भागों में विभाजित करती हैं, तो रेखा सममित रेखा कहलाती है।
आइए समझते हैं:-
जब किसी कागज को इस प्रकार मोड़ते हैं कि चित्र दो बराबर भागों में विभाजित हो जाता है, तो विभाजित करने वाली रेखा ही सममित रेखा है।

यहाँ, रेखा तारा को दो पूर्णतः बराबर भागों में विभाजित करती है इसलिए यह सममिति की रेखा है। इसे दर्पण रेखा भी कहा जाता है क्योंकि अगर हम उस रेखा पर दर्पण रखेंगे तो आकृति का एक भाग बिल्कुल दूसरी भाग के जैसा दिखेगा।
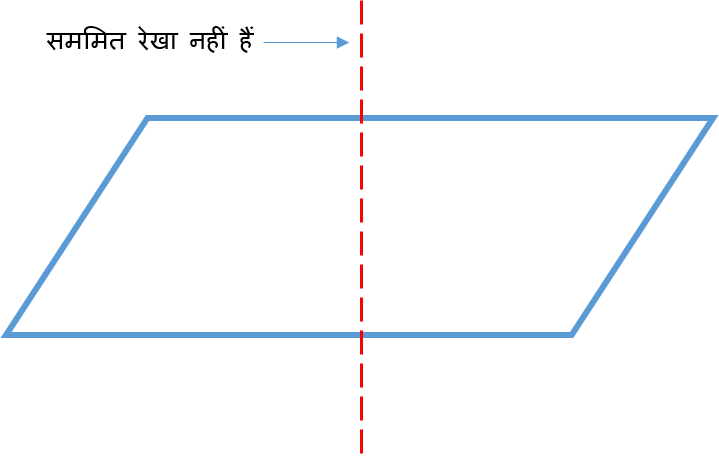
यह, आकृति सममित नहीं है क्योंकि यदि हम इस आकृति को दो भागों मे विभाजित करते हैं, तो इसके दोनों भाग एक - दूसरे के बराबर नहीं है।
सममित आकृतियाँ बनाना: इंक - ब्लाट डेविल्स
आइए सममित आकृति बनाने के लिए कुछ क्रियाकलाप करते हैं:

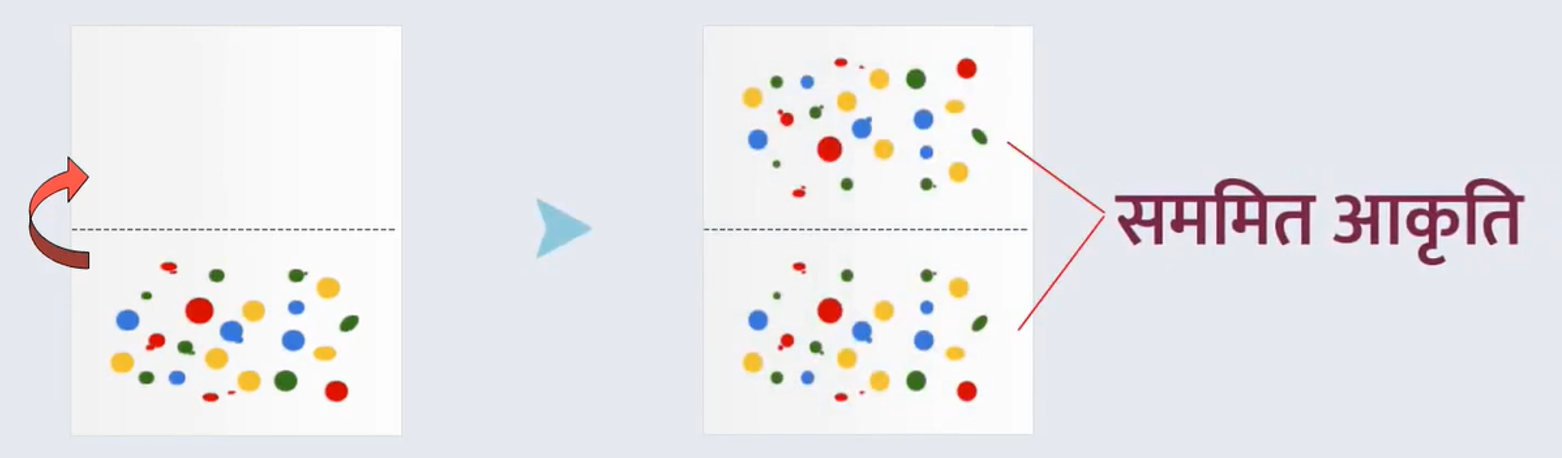
इस क्रियाकलाप में हमने देखा की कागज में स्याही (इंक) की मदद से सममित आकृति कैसे प्राप्त कर सकते हैं।
आइए एक और क्रियाकलाप करते हैं:
यह, क्रियाकलाप भी ऊपर हमने जो क्रियाकलाप किया हैं उसी के जैसा ही हैं, यहाँ हम कागज मे स्याही से भीगी हुई धागे को रखेंगे।


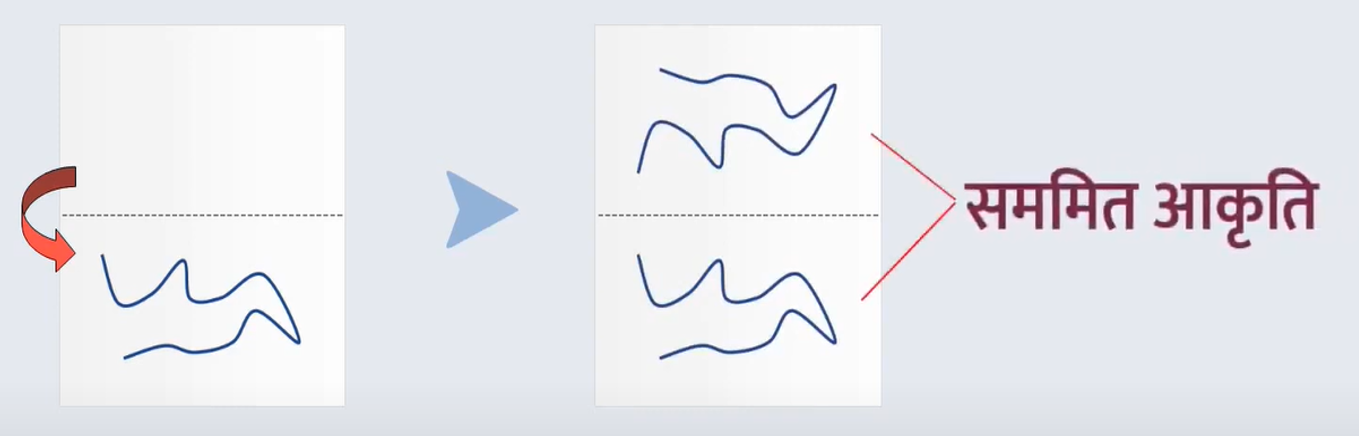
अतः, दोनों भागों मे बनी स्याही का निशान से स्पष्ट हैं कि पहले भाग में बनी आकृति दूसरे भाग में बनी आकृति से सममित हैं।
उदाहरण 1
दी गई आकृति में जाँच कीजिए कि क्या ये आकृतियाँ सममित हैं या नहीं तथा उनकी सममित रेखा खींचिये।
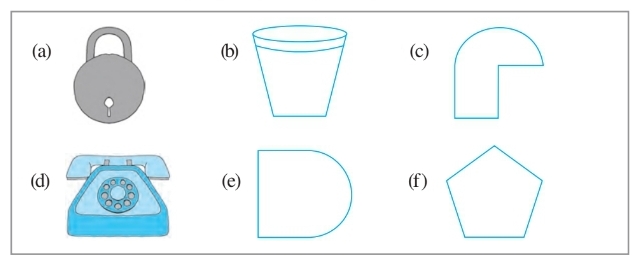
हम जानते है कि, किसी आकृति को दो भागों मे बांटने से, आकृति के दोनों भाग एक - दूसरे के पूर्णतः बराबर हो, तो आकृति सममित आकृति कहलाती है तथा आकृति को दो बराबर भागों में बांटने वाली रेखा, सममित रेखा होती है।
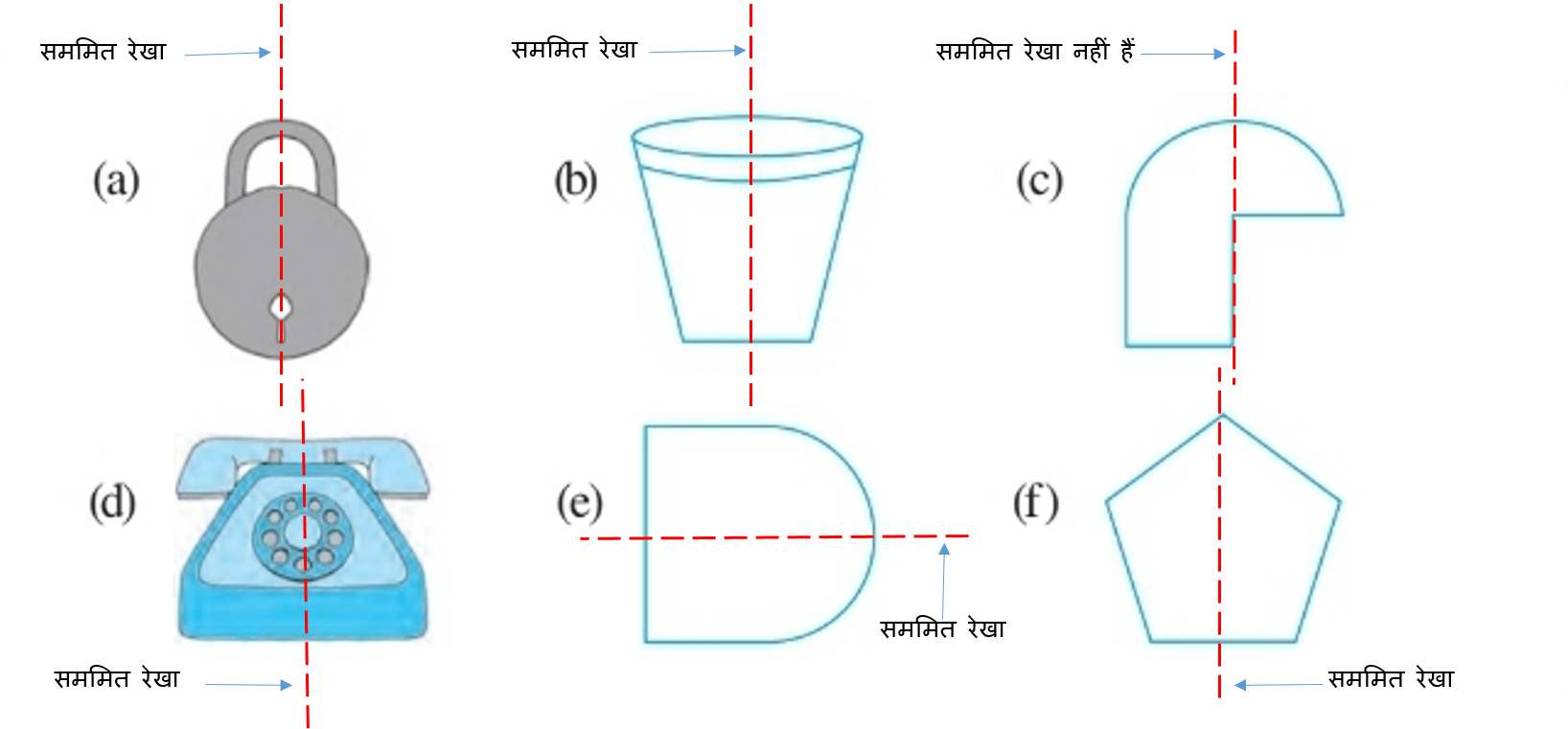
अतः दिए गये आकृति मे आकृति (a), आकृति (b), आकृति (d), आकृति (e) और आकृति (f) सममित आकृति हैं क्योंकि आकृति को दो भागों में बांटने पर इनके दोनों भाग एक - दूसरे के पूर्णतः बराबर हैं।
आकृति (c) सममित आकृति नहीं हैं क्योंकि आकृति को दो भागों में बांटने पर इनके दोनों भाग एक - दूसरे के बराबर नहीं हैं।
उदाहरण 2
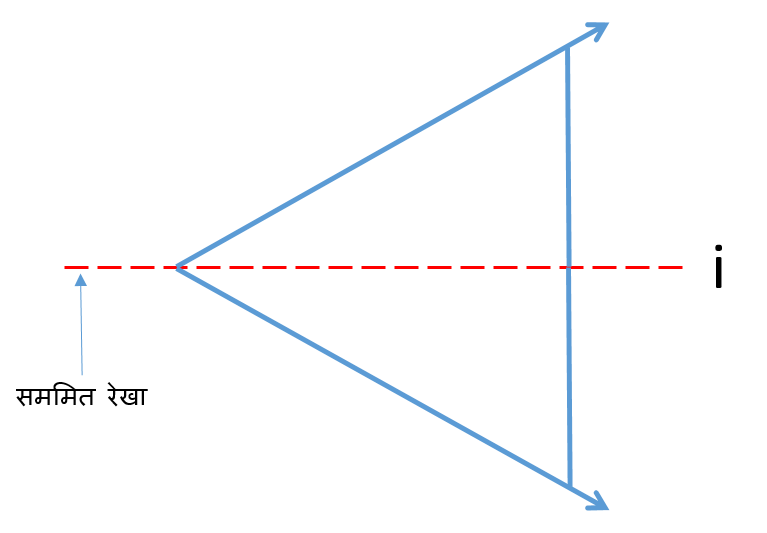
नीचे दी गई आकृति में, i सममित रेखा है। इस आकृति को पूरा कीजिए, जिससे यह सममित हो जाए।
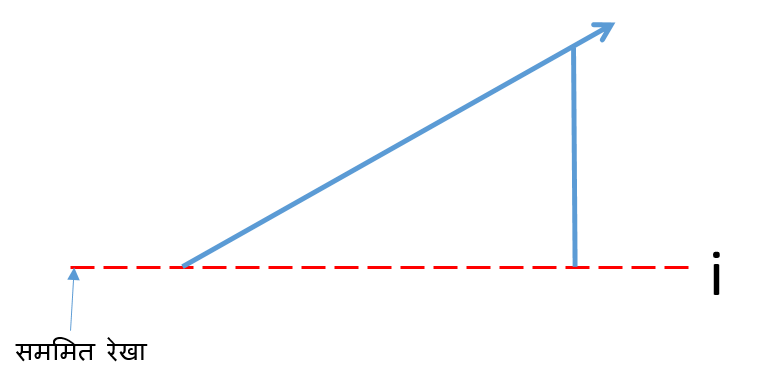
हम जानते हैं, कि सममित रेखा किसी भी आकृति को दो भागों मे विभाजित करती है, जो एक - दूसरे के पूर्णतः बराबर होते हैं। आकृति में सममित रेखा के ऊपर का भाग दिया है, अतः हमे सममित रेखा के नीचे भी ऊपर के जैसा ही बनाना होगा।
∴
उदाहरण 3
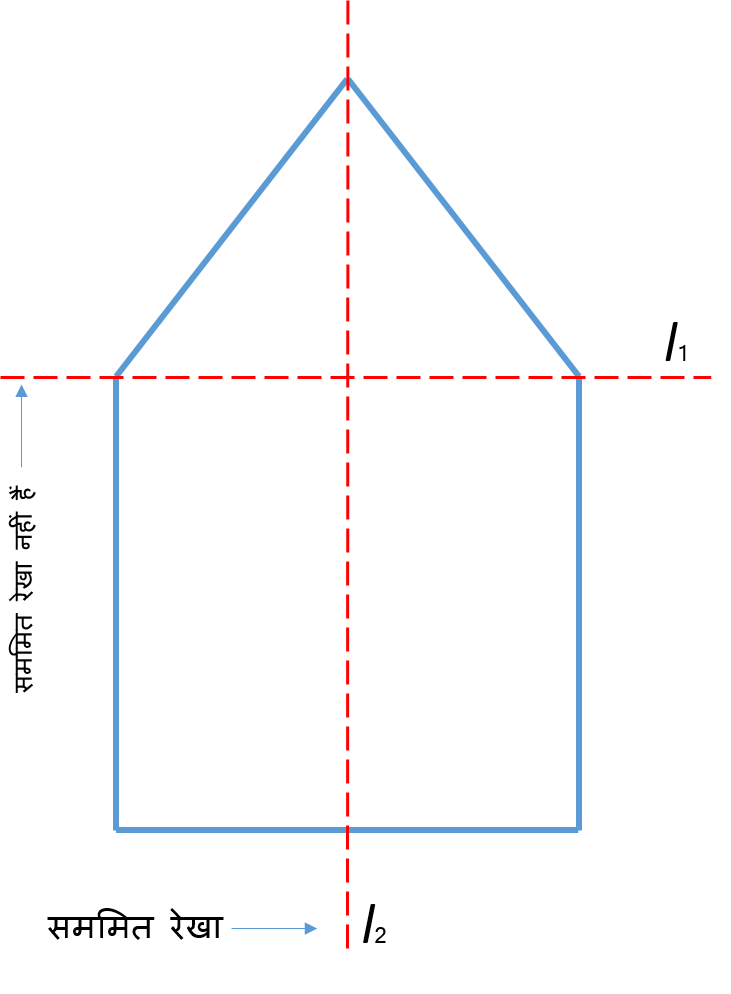
जाँच कीजिए कि दी गई आकृति सममित हैं या नहीं तथा सममित रेखा भी खींचिए।
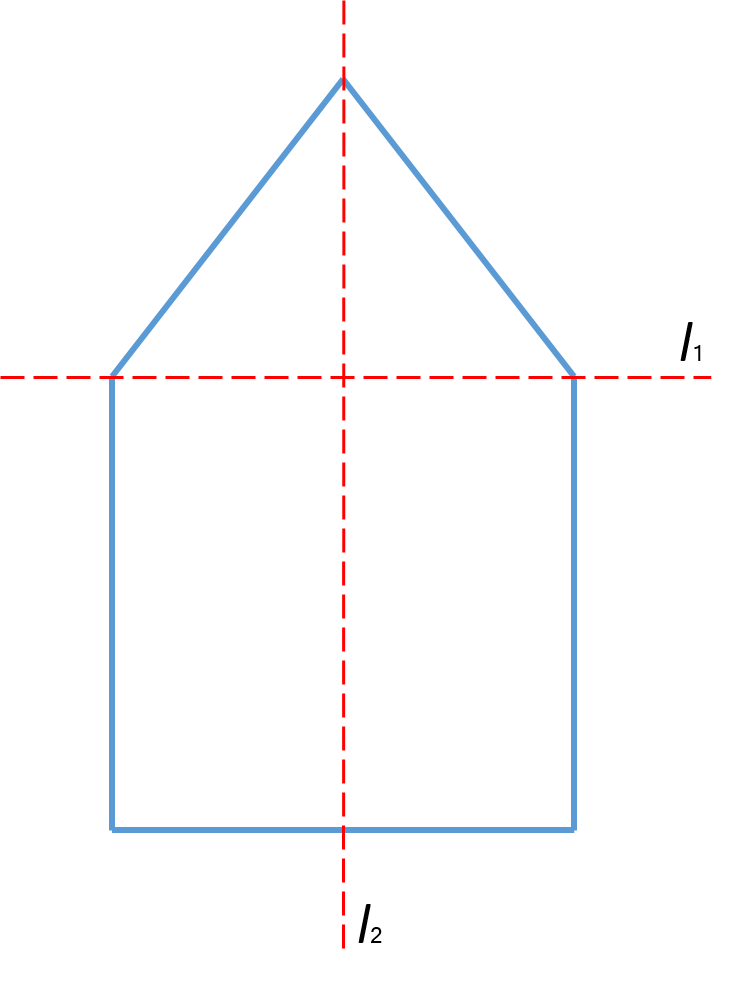
चूंकि आकृति में दो रेखाएँ दी गई हैं, l1 और l2
यहाँ, रेखा l2 के द्वारा विभाजित दोनों भाग एक - दूसरे के पूर्णतः बराबर हैं, अतः आकृति सममित है, तथा l1 के द्वारा विभाजित दोनों भाग एक-दूसरे के बराबर नहीं हैं।
अतः स्पष्ट हैं कि, l2 सममित रेखा हैं तथा l1 सममित रेखा नहीं हैं।
उदाहरण 4
संलग्न चित्र में दी गई आकृति एक सममित आकृति नहीं है। क्या आप बता सकते हैं क्यों नहीं?

∵ दी गई आकृति मे कोई भी सममित रेखा नहीं खींचा जा सकता हैं।
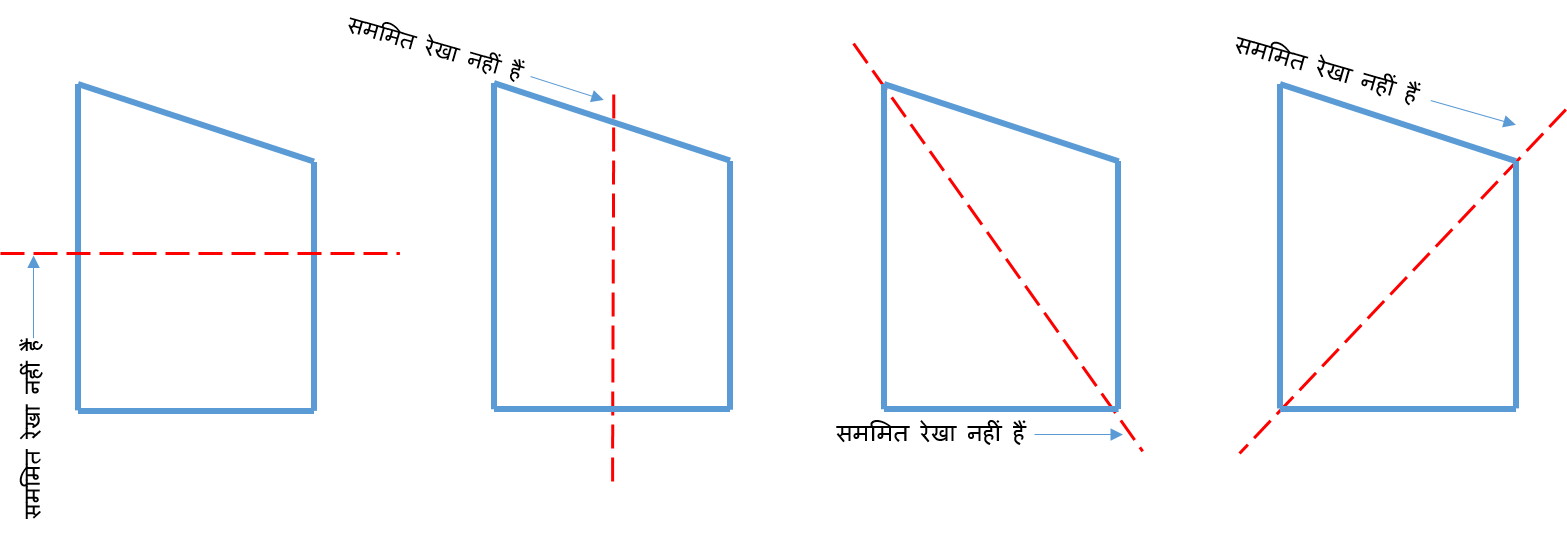
∴ आकृति सममित आकृति नहीं है।
आकृतियाँ जिनमें दो सममित रेखाएँ हों
हम जानते हैं कि, एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बांटती हो, यह रेखा सममित रेखा या दर्पण रेखा कहलाती है।
जैसे:-

कुछ आकृतियों में दो सममित रेखाएँ होती हैं।
एक आयताकार कागज लेते हैं इसे एक बार लंबाई की ओर मोड़ते हैं जिससे कि एक आधा भाग, दूसरे आधे भाग को पूर्णतया ढ़क लेंता हैं। अब एक बार चौड़ाई की ओर से समान तरीके से मोड़ते हैं।
अतः, इसे खोलने पर हमें दो सममित रेखाएँ प्राप्त होती हैं।
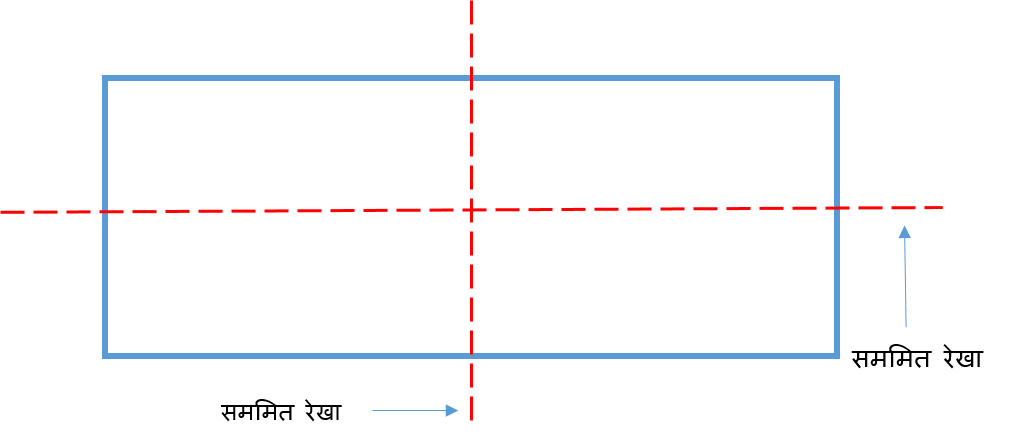
दो सममित रेखाओं वाली आकृति का निर्माण:- यदि हम कागज का एक आयताकार टुकड़ा लें और उसे दो बार मोड़कर दो सममित रेखाएँ बना लें और उसे किसी नए आकार में काट लें, तो उसे खोलने के बाद हमें दो सममित रेखाएँ के साथ आकृति प्राप्त होता हैं।
OMR (One Minute Revision)
यदि आकृति को दो भागों मे बांटने से, आकृति के दोनों भाग एक - दूसरे के पूर्णतः बराबर हो, तो आकृति सममित आकृति कहलाती है।
साधारणतः यदि हम किसी आकृति को मोड़कर इसके दो भाग बना सकते हैं जो एक - दूसरे को पूर्णतः ढ़क ले अर्थात एक-दूसरे के प्रतिबिंब हो, तो हम कहते हैं कि वह आकृति सममित हैं।
एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बांटती हो। यह रेखा सममित रेखा कहलाती है।
उदाहरण 5
निम्नलिखित कथन सत्य है या असत्य:-
एक समकोण त्रिभुज में अधिकतम एक सममिति रेखा हो सकती है?
माना ΔABC समकोण त्रिभुज है तथा ∠B=90∘, AB=BC
जैसा की आकृति मे देख सकते हैं, यदि AB=BC हैं, तो समकोण त्रिभुज में एक सममिति रेखा हो सकती है।
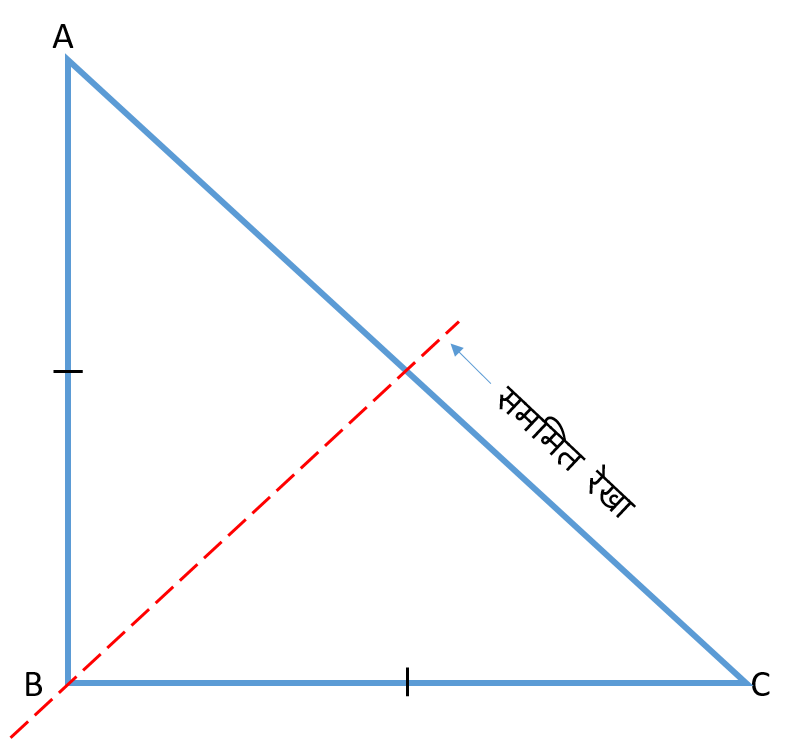
अतः दिया गया कथन सत्य हैं क्योंकि दोनों भाग एक - दूसरे पूर्णतः बराबर हैं।
उदाहरण 6
नीचे दी गई अंग्रेजी वर्णमाला के अक्षरों में सममित अक्षरों को चुनिए।
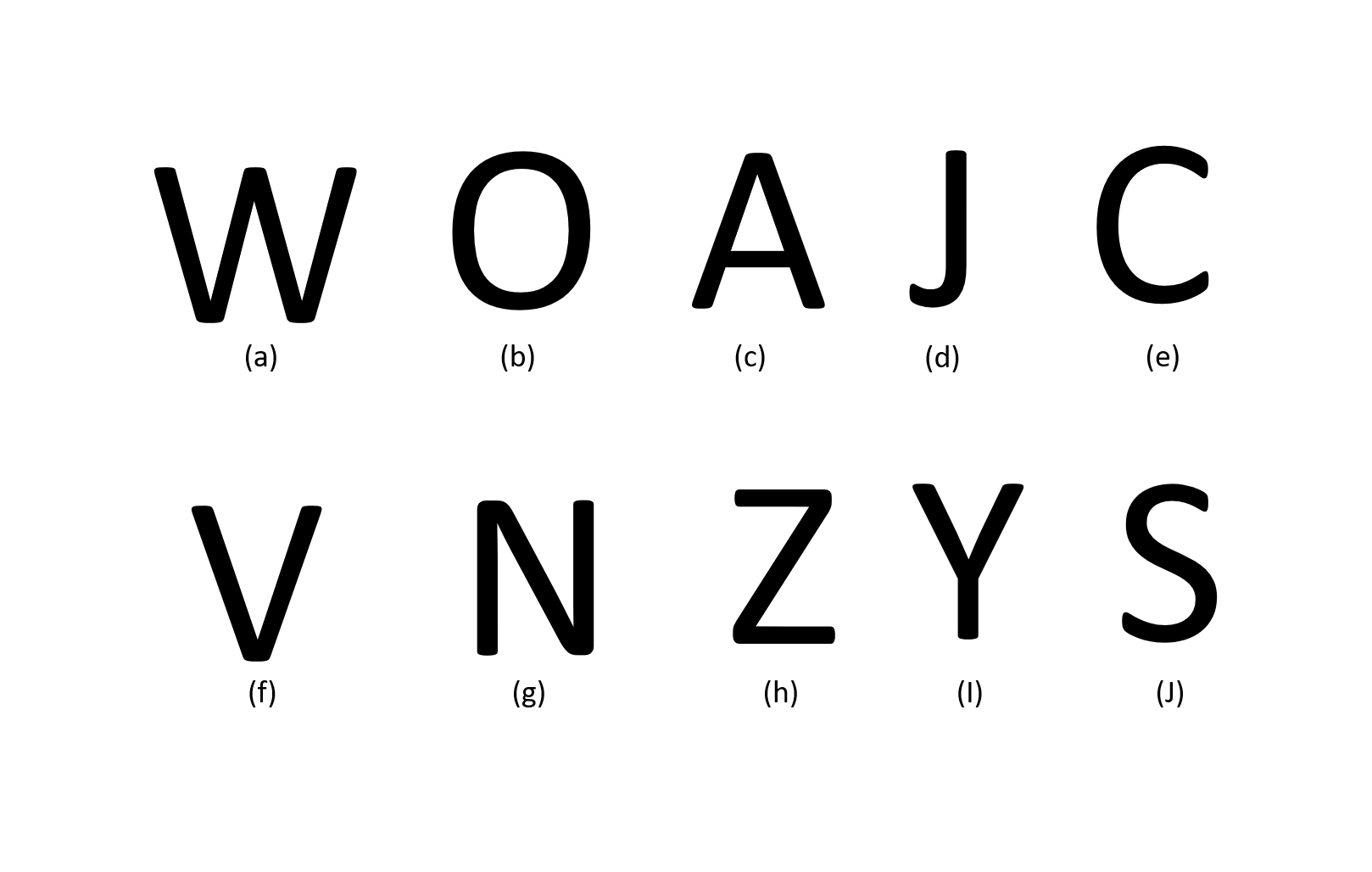
(a) यदि हम W को ऊर्ध्वाधर दो भागों में विभाजित करे तो, इसके दोनों भाग (दायाँ एवं बायाँ) एक - दूसरे के पूर्णतः बराबर होंगे।
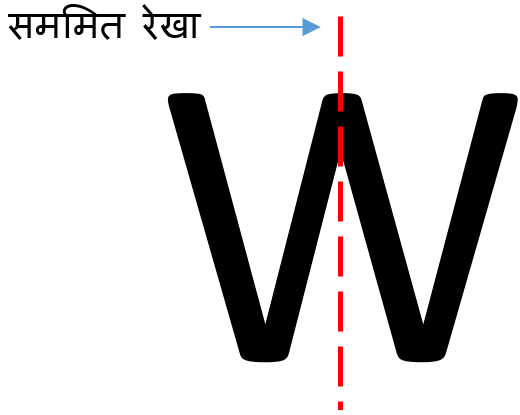
∴ W एक सममित अक्षर हैं।
(b) यदि हम O को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
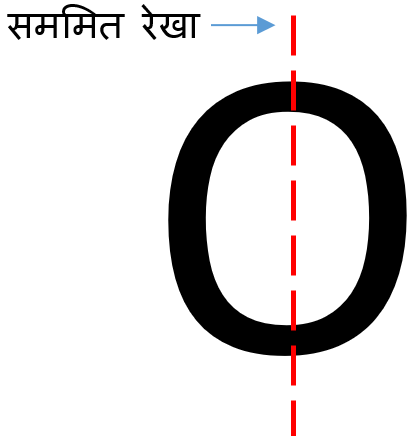
∴ O एक सममित अक्षर हैं।
(C) यदि A को ऊर्ध्वाधर दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
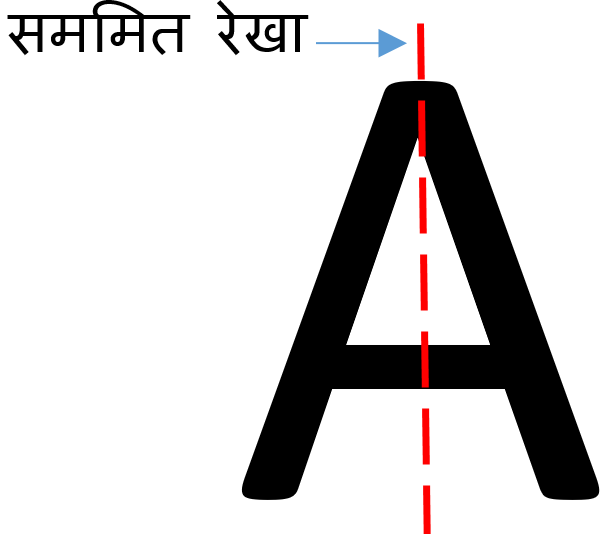
∴ A एक सममित अक्षर हैं।
(d) यदि j को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
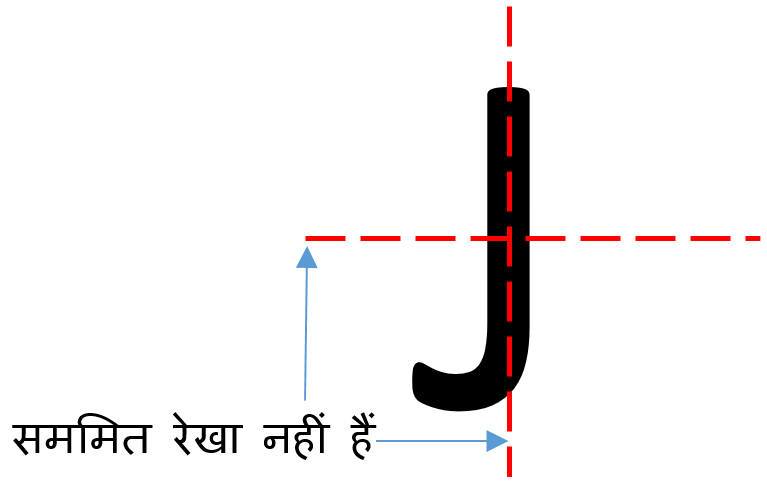
∴J एक सममित अक्षर नहीं हैं।
(e) यदि C को क्षैतिज दो भागों में विभाजित करे, इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
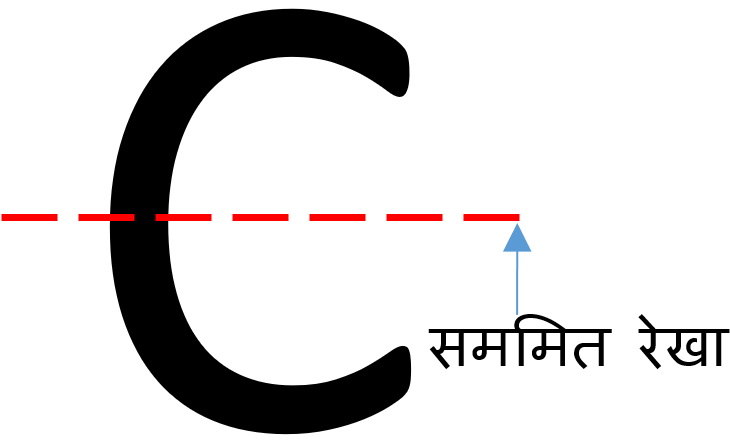
∴ C एक सममित अक्षर हैं।
(f) यदि V को ऊर्ध्वाधर दो भागों में ऊर्ध्वाधर विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
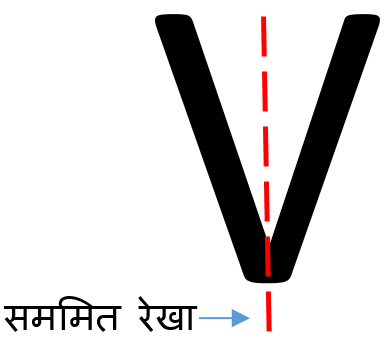
∴ V एक सममित अक्षर हैं।
(g) यदि N को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
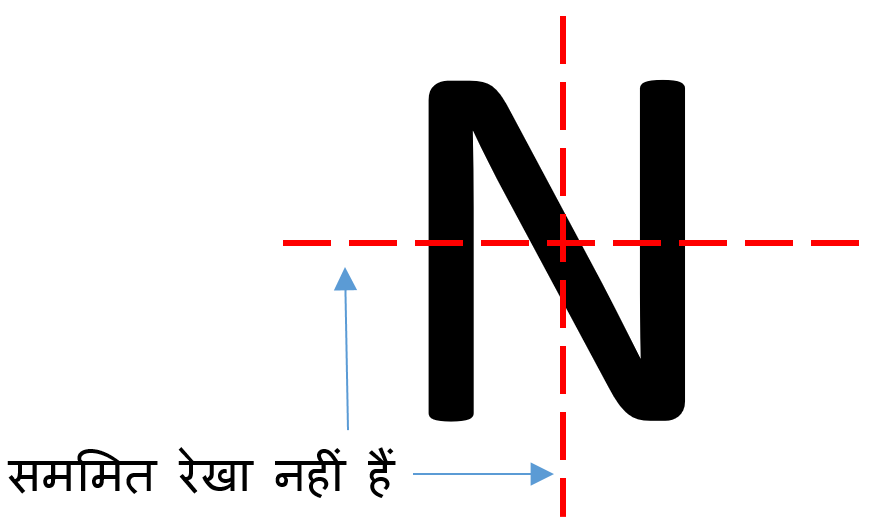
∴ N एक सममित अक्षर नहीं हैं।
(h) यदि Z को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
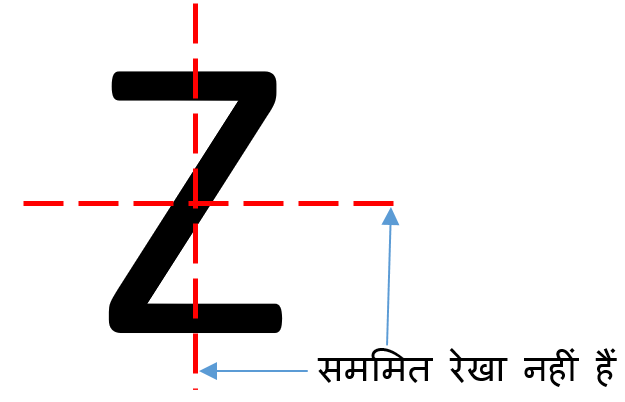
(i) यदि Y को ऊर्ध्वाधर दो भागों में ऊर्ध्वाधर विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
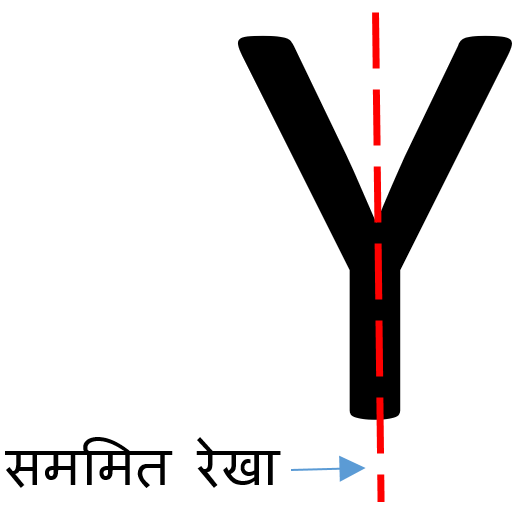
∴ Y एक सममित अक्षर हैं।
(J) यदि S को दो भागों में विभाजित करे, इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
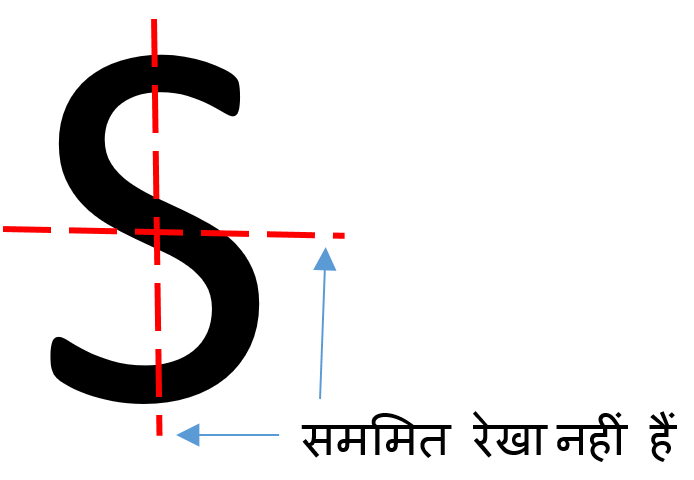
∴ S एक सममित अक्षर नहीं हैं।
अतः स्पष्ट है कि, W, O, A, C, V, और Y सममित अक्षर हैं।
उदाहरण 7
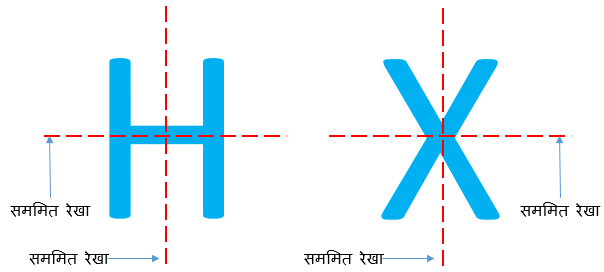
M, H, E, V में से किस अक्षर में ऊर्ध्वाधर सममित रेखा नहीं है ?
यदि M, H तथा V को एक ऊर्ध्वाधर सममित रेखा खींचकर दो भागों में विभाजित करे, तो इनके दोनों भाग एक - दूसरे के पूर्णतः बराबर होते हैं, तथा एक भाग को दूसरे के ऊपर रखेंगे तो उसे पूरी तरह से ढ़क लेगा।
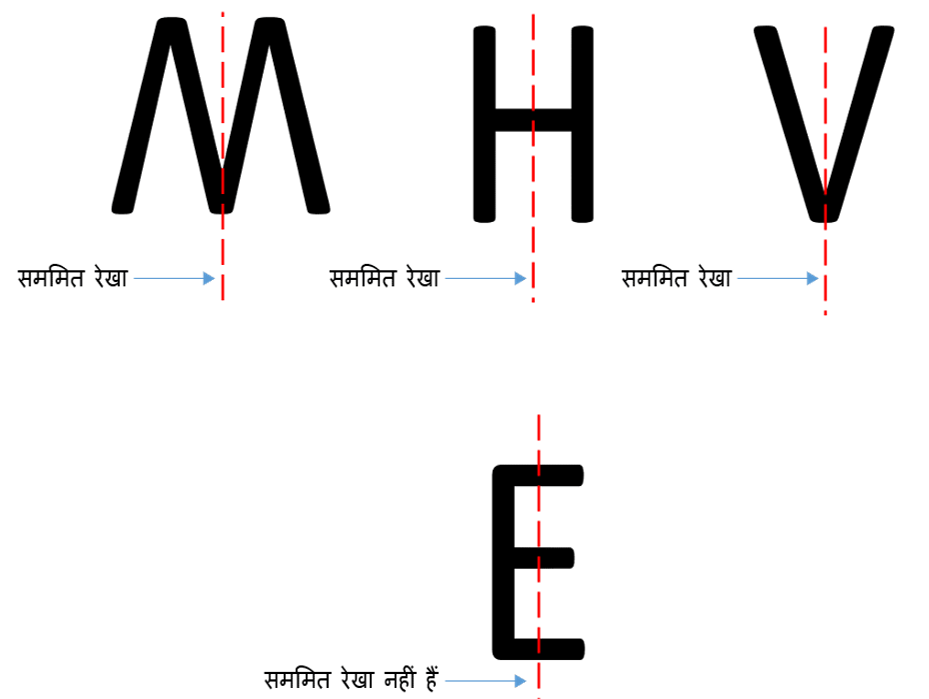
लेकिन E को एक ऊर्ध्वाधर सममित रेखा खींचकर दो भागों में विभाजित करे तो इसके दोनों भाग बराबर नहीं होंगे। अतः E में, ऊर्ध्वाधर सममित रेखा नहीं खींचा जा सकता हैं।
अनेक सममित रेखाओं (दो से अधिक) वाली आकृतियाँ
बच्चों! अब तक हमने आकृतियों में एक और दो सममित रेखाओं वाले आकृति का अध्ययन किया है।
आइए अब हम दो से अधिक सममित रेखाओं वाली आकृति देखते हैं।
एक वर्गाकार कागज़ का टुकड़ा लेते हैं।
इसे ऊर्ध्वाधर (vertically) में आधे से मोड़ते हैं और पुन: क्षैतिज (horizontally) से आधे भाग से मोड़ते हैं (अर्थात् इसे दो बार मोड़ते हैं)।
इसे खोलकर पुनः वर्ग को आधे भाग से मोड़ते हैं (अर्थात् तीसरी बार), लेकिन इस बार विकर्ण के साथ-साथ जैसा कि आकृति में दिखाया गया है।
इसे पुनः खोलिए और आधे भाग से मोड़िए (चौथी बार) दूसरे विकर्ण के साथ।
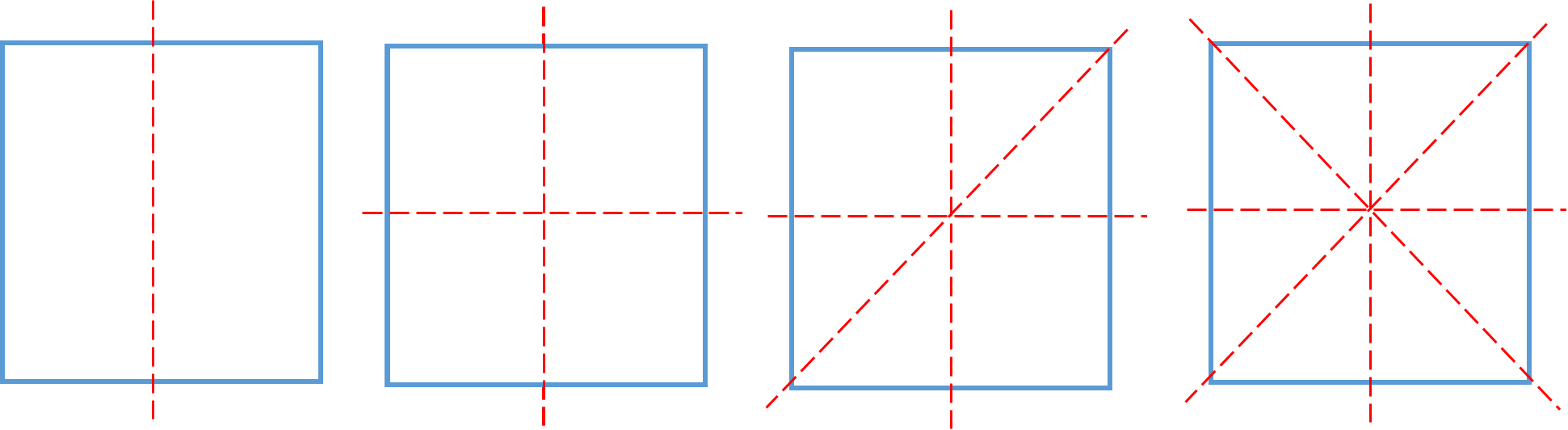
अब जैसे की हम देख सकते हैं कि वर्ग में हमे 4 सममित रेखाएँ प्राप्त होती हैं।
दो से अधिक सममित रेखाओं वाली कुछ और आकृति:
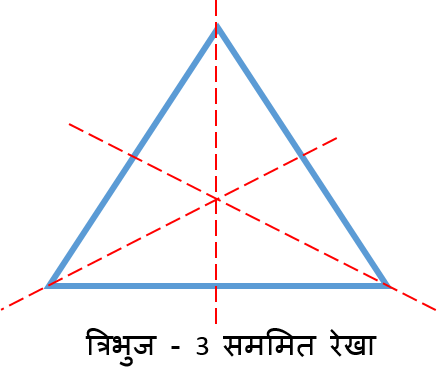
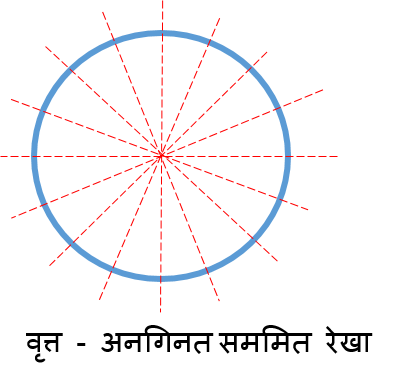
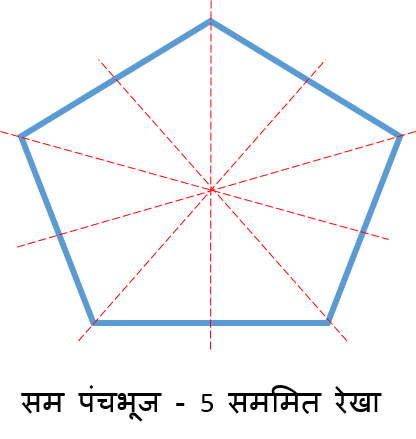
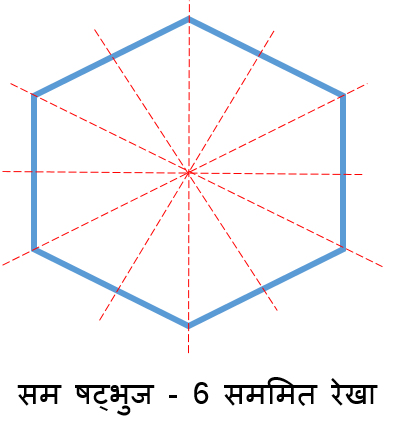
उदाहरण 8
किस प्रकार के त्रिभुज में
(a) कोई सममिति रेखा नहीं होती है।
(b) एक सममिति रेखा होती है।
(c) तीन सममिति रेखाएँ होती हैं। उनके चित्र भी खींचें।
(a) माना कि ΔABC एक विषमबाहु त्रिभुज हैं।
∵ विषमबाहु त्रिभुज की तीनों भुजाओं की माप अलग-अलग होती हैं, इसलिए इन्हे बराबर भागों मे विभाजित करने पर, दोनों भाग बराबर नहीं होते हैं।
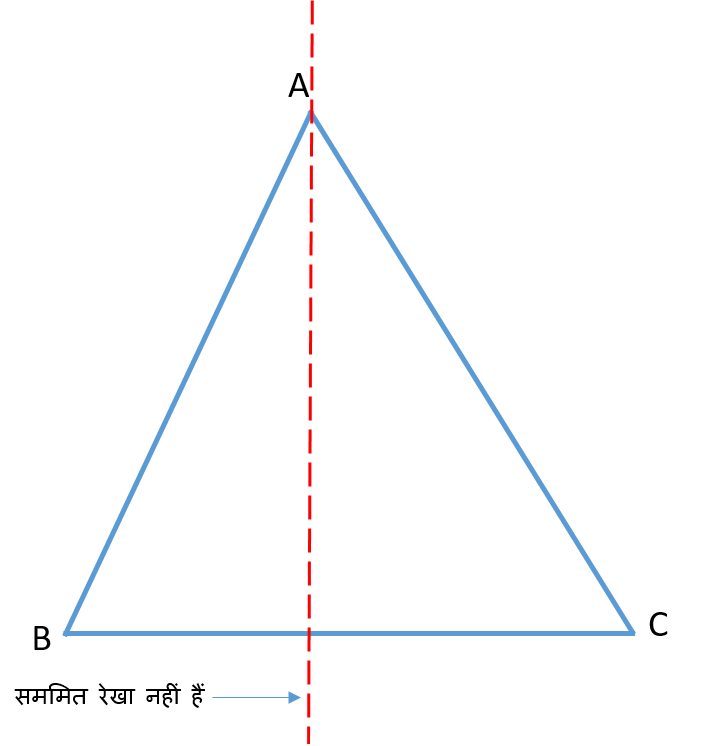
अतः, विषमबाहु त्रिभुज में कोई सममिति रेखा नहीं होती है।
(b) माना कि ΔDEF एक समद्विबाहु त्रिभुज हैं।
∵ समद्विबाहु त्रिभुज की दो भुजाओं की माप बराबर होती हैं, यहाँ भुजा DE=DF हैं।
∴ यदि समद्विबाहु त्रिभुज को दो बराबर भागों मे विभाजित करे तो, दोनों भाग एक - दूसरे के पूर्णतः बराबर होते हैं।
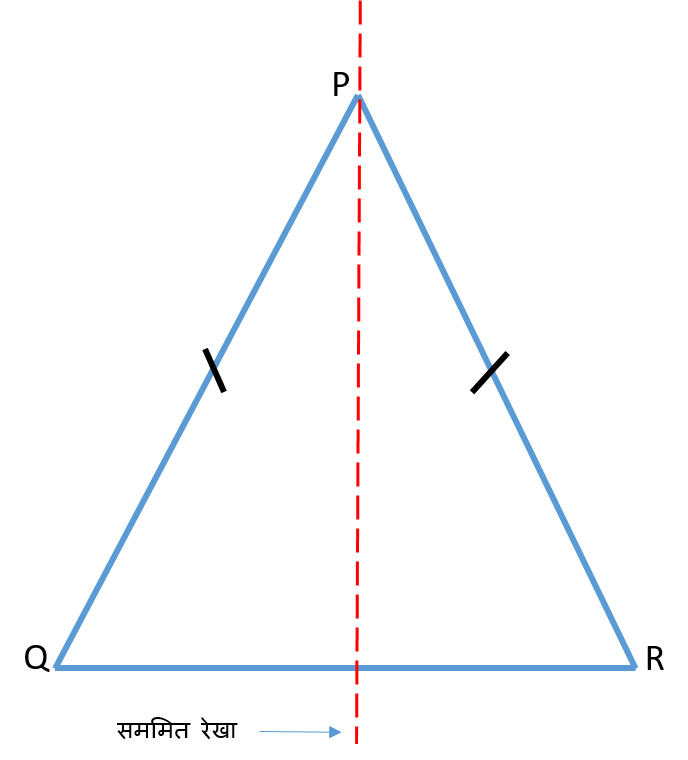
अतः, समद्विबाहु त्रिभुज में 1 सममिति रेखा होती है।
(c) माना कि ΔPQR एक समबाहु त्रिभुज हैं।
∵ समबाहु त्रिभुज की तीनों भुजाओं की माप बराबर होती हैं, यहाँ PQ=QR=RP
∴ समबाहु त्रिभुज में तीन सममिति रेखाएँ खींची जा सकती हैं, जैसा कि आकृति में दिखाया गया हैं।
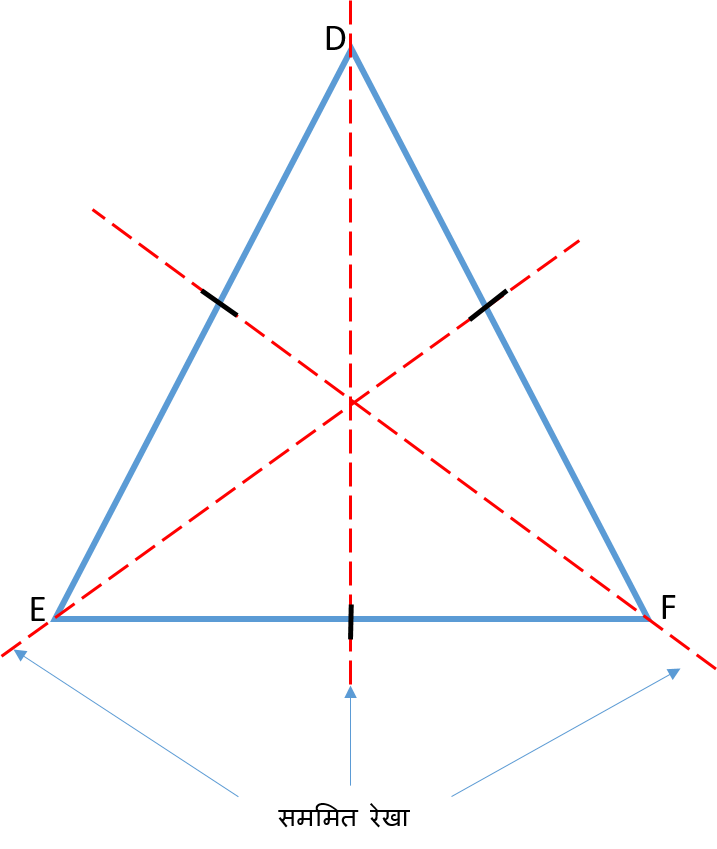
अतः समद्विबाहु त्रिभुज में 3 सममिति रेखा होती है।
प्रतिबिंब और सममिति
सममित रेखा को दर्पण रेखा भी कहते हैं क्योंकि यदि सममित रेखा के स्थान पर एक दर्पण को रख देते है, तो आकृति का एक भाग बिल्कुल दूसरी भाग के जैसा दिखेगा। जब हम किसी वस्तु को दर्पण में देखते हैं तो वस्तु की लंबाई और कोण में कोई परिवर्तन नहीं होता है केवल प्रतिबिंब, मूल प्रतिबिंब के विपरीत होता है अर्थात वस्तु का दायाँ भाग प्रतिबिंब मे बायाँ और वस्तु का बायाँ भाग प्रतिबिंब में दायाँ भाग होता हैं।
जैसे:-
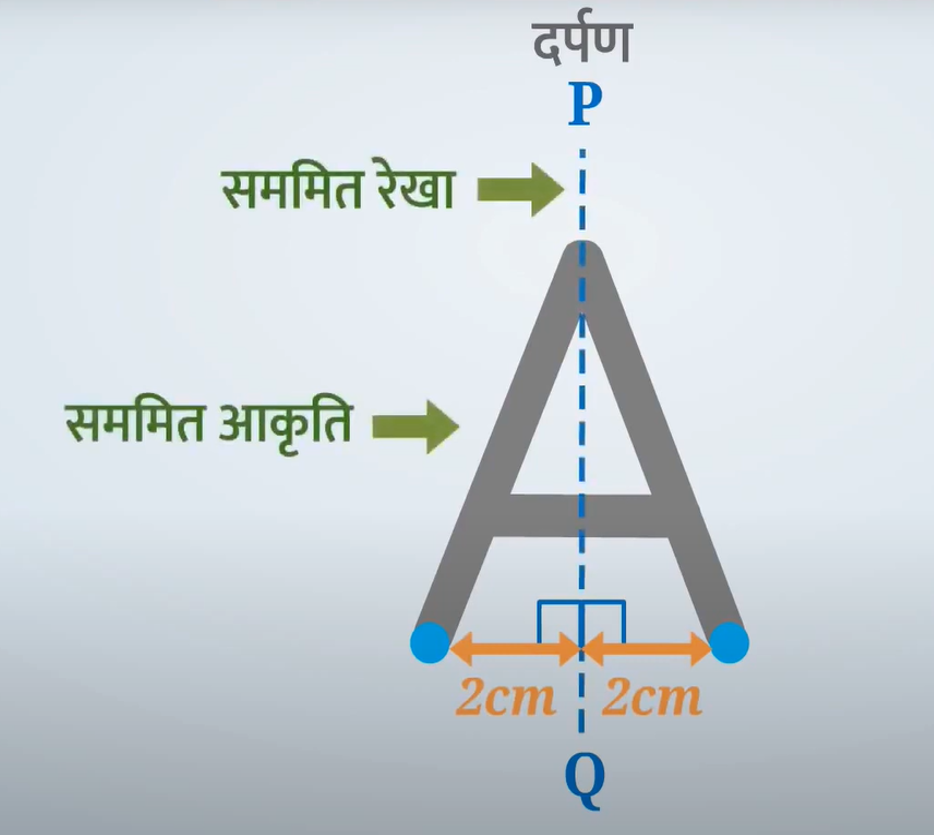
आइए कुछ उदाहरण देखते हैं:
नीचे आकृति मे देख सकते हैं शतरंज बोर्ड के मध्य मे दर्पण रेखा हैं।

यदि हम इस पर कोई वस्तु रखते हैं, चूंकि हमने वस्तु को दर्पण रेखा के तीसरे डिब्बे मे रखा हैं, अतः इसका प्रतिबिंब में वस्तु, दर्पण रेखा से तीसरे डिब्बे मे होगा। प्रतिबिंब मे वस्तु उतनी ही दूरी पर दिखाई देती हैं, जितनी दूरी पर वह दर्पण के सामने होती हैं तथा लंबाई की तरह कोण भी आपस में बराबर होते हैं।
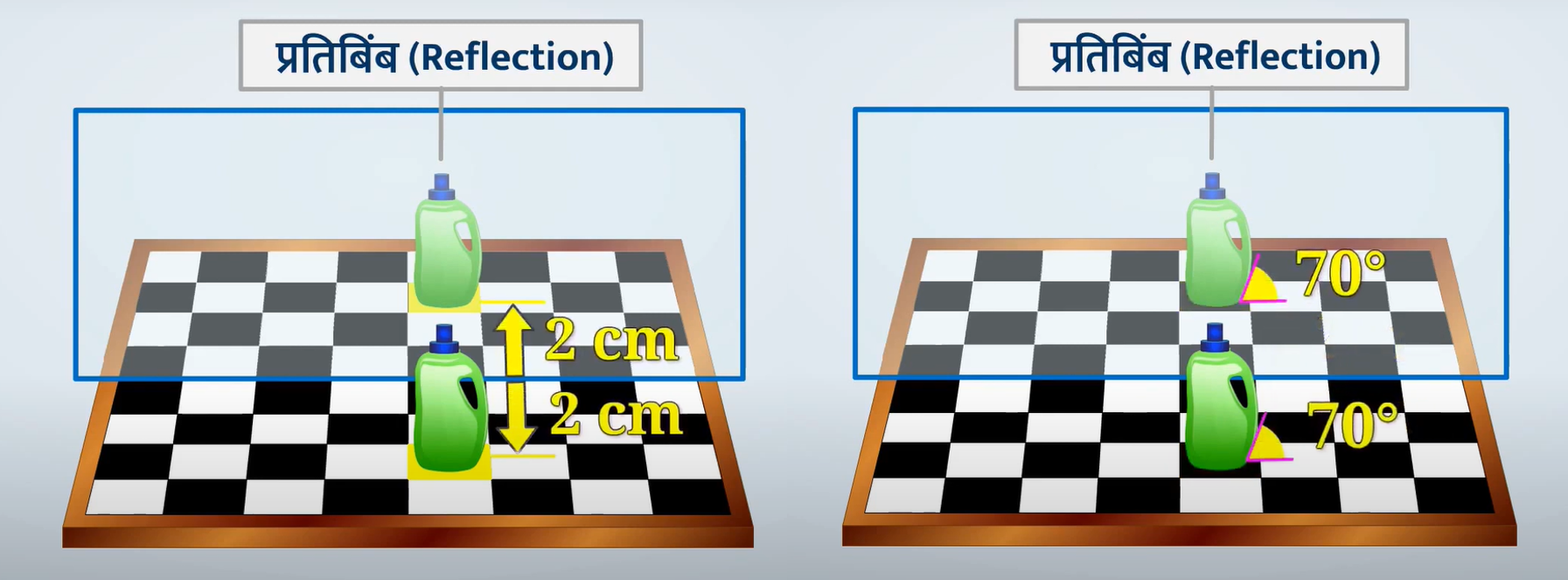
लेकिन वस्तु का दायाँ भाग प्रतिबिंब में बायाँ और वस्तु का बायाँ भाग प्रतिबिंब में दायाँ भाग होता हैं।
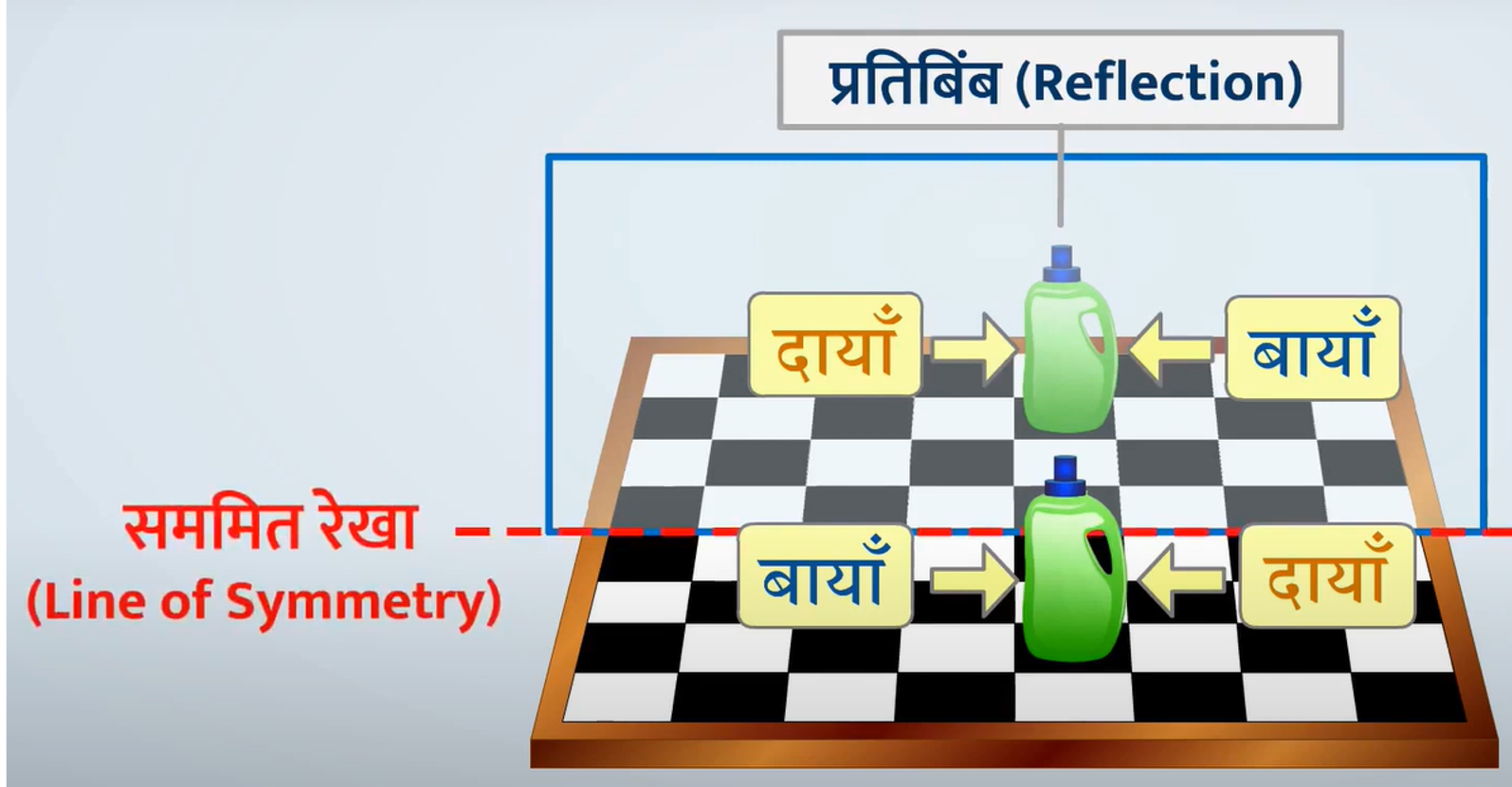
अतः स्पष्ट हैं कि वस्तु और उसका प्रतिबिंब दर्पण रेखा के संदर्भ में सममित होते हैं।
Note:- सममिति जिसमें किसी आकार का आधा भाग उसके दूसरे आधे भाग का दर्पण प्रतिबिंब हो परावर्तीय सममिति कहलाता हैं।
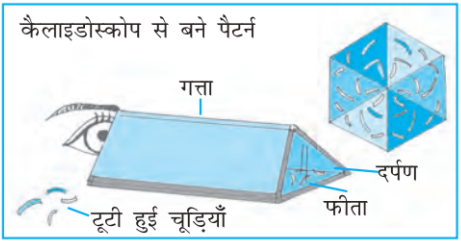
कैलाइडोस्कोप:- अनेक दर्पणों वाले एक केलाइडोस्कोप में कई प्रतिबिंब बनते हैं जिनमें अनेक सममिति की रेखाएँ होती हैं (जैसा यहाँ उदाहरण में दिखाया गया है)। प्रायः दो दर्पण पट्टियों को V आकार में रखकर प्रयोग किया जाता है। दर्पणों के बीच बने कोण सममित रेखाओं या सममित रेखाओं की संख्या को बताते हैं।
प्रश्न:- परावर्तन सममिति के बाद कौन-सा अक्षर समान रहेगा? R, C, N, A और T के लिए जाँच करें।
वर्णमाला परावर्तन सममिति में अक्षर दर्पण में विपरीत दिखते हैं अर्थात दाएँ से बाएँ लिखा हुआ अक्षर बाएँ से दाएँ लिखा हुआ दिखाई देगा।
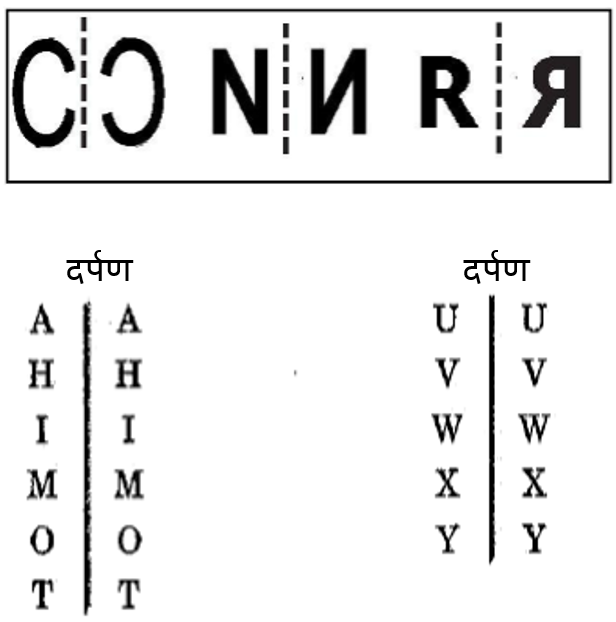
इसलिए C, N और R परावर्तन के बाद समान नहीं दिख रहे है, लेकिन A और T समान दिखाई दे रहे हैं।
OMR (One Minute Revision)
सममित रेखा को दर्पण रेखा भी कहते हैं क्योंकि यदि सममित रेखा के स्थान पर एक दर्पण को रख देते है, तो आकृति का एक भाग बिल्कुल दूसरी भाग के जैसा दिखेगा।
जब हम किसी वस्तु को दर्पण में देखते हैं, तो वस्तु का दायाँ भाग प्रतिबिंब मे बायाँ भाग और वस्तु का बायाँ भाग प्रतिबिंब में दायाँ भाग होता हैं। जितनी दूरी किसी वस्तु की दर्पण से होंगी, उतनी ही दूरी पर वस्तु का प्रतिबिंब दिखेगा।
उदाहरण 9
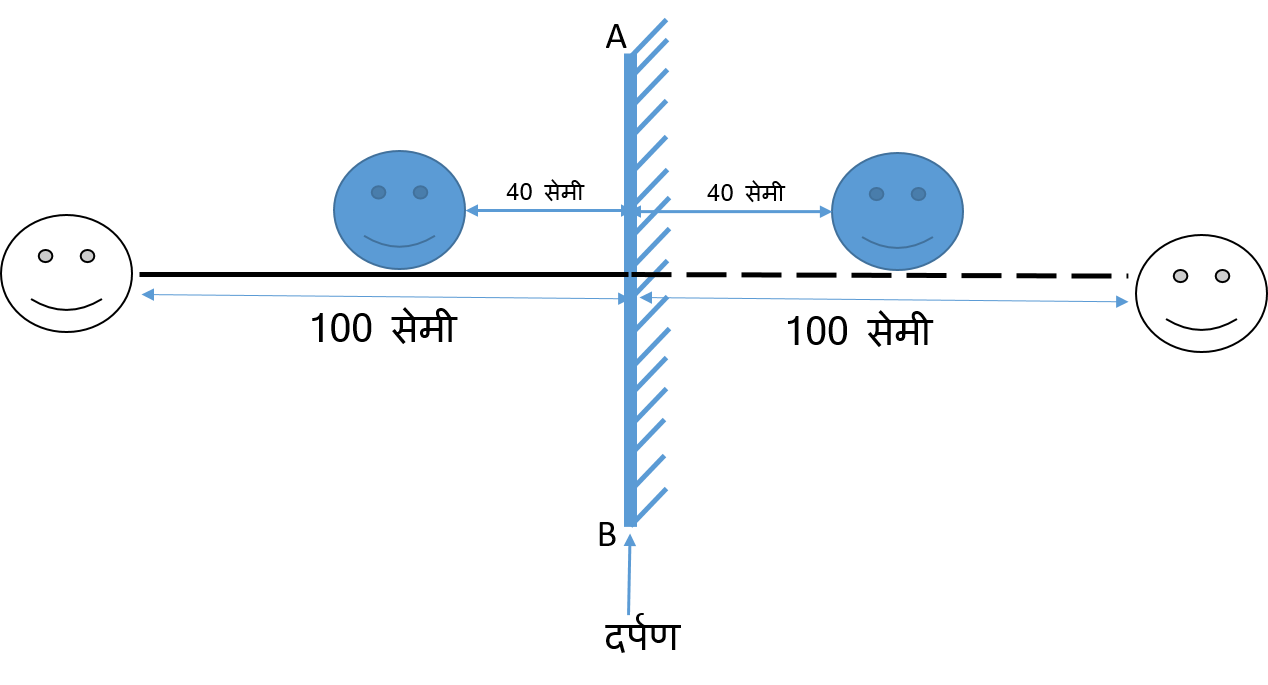
यदि आप दर्पण के सामने 100 सेमी की दूरी पर हैं। आपका प्रतिबिंब कहाँ होगा? यदि आप दर्पण की ओर चलते हैं, तो आपका प्रतिबिंब किस प्रकार चलता है?
नीचे आकृति में देख सकते हैं कि AB दर्पण हैं।
यदि आप दर्पण के सामने 100 सेमी की दूरी पर हैं, तो आपका प्रतिबिंब भी दर्पण मे 100 सेमी की दूरी पर बनेगा।
यदि आप दर्पण की ओर आते हैं, तो आपका प्रतिबिंब भी दर्पण की ओर आएगा।
सारांश
- एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बांटती हो, यह रेखा सममित रेखा कहलाती है।
- एक आकृति में कोई भी सममित रेखा नहीं हो सकती, केवल एक सममित रेखा, दो सममित की रेखाएँ या अनेक सममित की रेखाएँ हो सकती हैं। यहाँ पर कुछ उदाहरण दिए गए हैं।
आकार सममित रेखाओं की संख्या समबाहु त्रिभुज 3 वर्ग 4 आयत 2 समद्विबाहु त्रिभुज 1 समचतुर्भुज 2 वृत्त अनंत
- रैखिक सममिति परावर्तन से संबंधित होती है। जब हम परावर्तन के बारे में बात करते हैं, तो हमें बायें ↔ दायें अभिमुख होने का ध्यान रखना चाहिए। सममिति का हमारे दैनिक जीवन में बहुत उपयोग होता है, जैसे कला में, वस्त्र प्रौद्योगिकी, डिजाइन बनाना, ज्यामितीय तर्क, रंगोली इत्यादि।