प्रारंभिक आकारों को समझना कक्षा 6 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम प्रारम्भिक आकारों का अध्ययन करेंगे। हमने पिछली कक्षाओं मे विभिन्न आधारभूत ज्यामितीय अवधारणाओं के बारे में पढ़ा है। हमारे चारों ओर बहुत - सी ऐसी आकृतियाँ होती है जो रेखाओं और वक्रों से मिलकर बनी होती है। जैसे - रेखाखंड, कोण, त्रिभुज, बहुभुज और त्रिविमीय आकृतियाँ आदि। ये सभी आकृतियाँ विभिन्न आकारों और मापों की होती हैं। इस अध्याय मे हम इनसे संबंधित बिन्दुओं पर अध्ययन करेंगे।
आइये जानते है, प्रारंभिक आकारों को और करीब से...
पिछले अध्यायों मे हमने रेखाखण्डों का अध्ययन किया है तथा इनके प्रयोगों से अनेक आकृतियों जैसे- रेखाखंड, कोण का निर्माण भी कर चुके है।
इस अध्याय में हम आगे रेखाखंडो से बनने वाली विभिन्न आकृतियों जैसे- त्रिभुज, चतुर्भुज आदि के बारे में पढ़ेंगे।
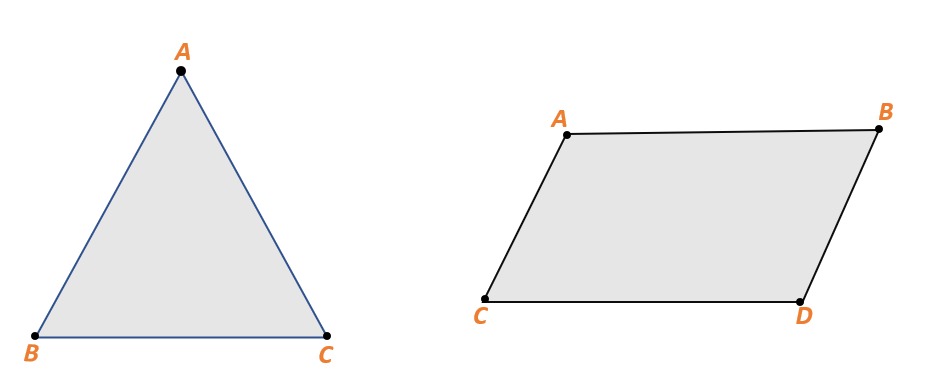
एक त्रिभुज तीन रेखाखंडों से बनता है और एक चतुर्भुज चार रेखाखंडों से बनता है। ये सभी आकृतियाँ विभिन्न आकारों और मापो की होती हैं।
इसके अतिरिक्त इस अध्याय मे हम आगे रेखाखंडों का मापन, कोण एवं इसके प्रकार, त्रिभुजों और उनके प्रकारों का वर्गीकरण, बहुभुज, चतुर्भुज और अन्य त्रिविमीय आकृतियों के संबंध में अध्ययन करेंगे।
रेखाखण्डों का मापन
रेखाखण्ड :
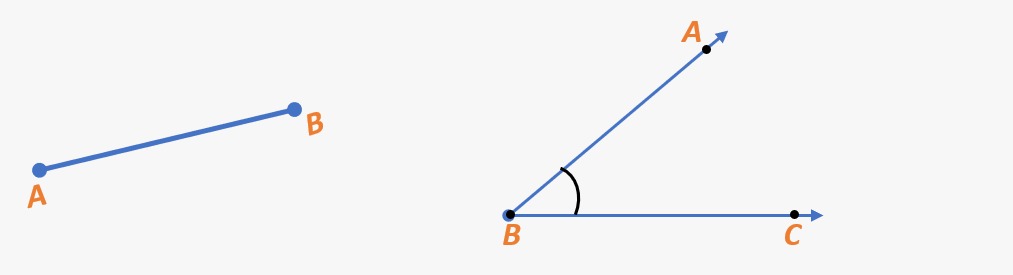
दो निश्चित बिन्दुओं के मध्य खींची गई सीधी रेखा, रेखाखण्ड ( Line Segment ) कहलाती है। यह अनंत तक नहीं बढ़ती है अर्थात इसकी लंबाई निश्चित होती है।यहाँ चित्र मे A और B निश्चित बिन्दु है तथा AB रेखाखण्ड है।

रेखाखंड ( Line Segment ) एक रेखा ( Line ) का वह निश्चित भाग होता है जिससे रेखाखंड के मापन मे सहायता मिलती है। प्रत्येक रेखाखंड की यह माप ( Measure ) एक अद्वितीय संख्या होती है, जो उसकी लंबाई ( Lenght ) कहलाती है।
एक रेखाखंड की लंबाई को उसके अंतिम बिंदुओं के बीच की दूरी के रूप में भी परिभाषित किया जा सकता है।
दो रेखाखण्डों की तुलना करने के लिए हम उनकी लंबाइयों के मध्य एक संबंध स्थापित करते है। इसकी तीन विधियाँ है -
(i) अवलोकन ( देखकर ) तुलना
(ii) अक्स द्वारा तुलना
(iii) रूलर और डिवाइडर द्वारा तुलना
(i) अवलोकन ( देखकर ) तुलना : इसमे हम केवल दो रेखाखंडों को देखकर ही बता सकते हैं कि दोनों मे से कौनसा रेखाखंड दूसरे से बड़ा है। जैसे -
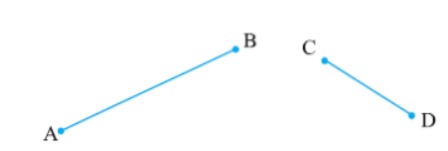
यहाँ हम स्पष्ट रूप से कह सकते हैं कि AB>CD
परंतु कभी-कभी यह बताना आसान नहीं होता की दोनों मे से कौनसा रेखाखण्ड बड़ा है। जैसे -
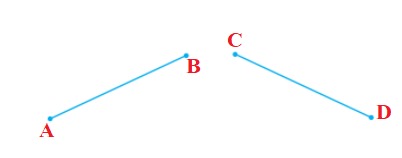
इन दोनों रेखाखण्डों की लंबाइयों का अंतर इतना स्पष्ट नहीं है की हम इनकी लंबाइयों के बारे मे बता सके। अतः हमे मापन के लिए अन्य विधियों की आवश्यकता है।
(ii) अक्स द्वारा तुलना : इस विधि में हम दो अक्स कागजों ( Tracing Paper ) पर अलग - अलग रेखाखण्ड खींचते है फिर दोनों अक्स कागजों पर बने रेखाखण्डों को एक - दूसरे के ऊपर रखकर यह जांच करते है कि कोनसा रेखाखण्ड बड़ा है।
परंतु यह विधि बहुत कठिन है क्योंकि हर बार रेखाखण्ड के अलग - अलग आकार को मापने के लिए हमें एक अलग रेखाखण्ड बनाना पड़ता है।
(iii) रूलर और डिवाइडर द्वारा तुलना : इस विधि को पढ़ने से पहले हम रूलर और डिवाइडर के बारे मे जानेंगे । रूलर और डिवाइडर को नीचे चित्र में दर्शाया गया हैं
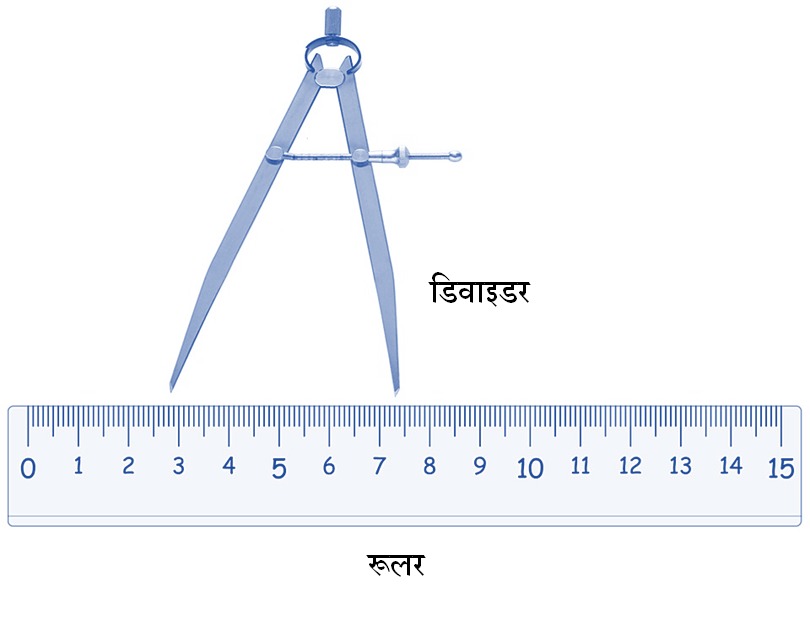
रूलर 15 बराबर भागों में विभाजित होता है, तथा प्रत्येक भाग की लंबाई 1 cm होती है। एवं इसमें प्रत्येक भाग को आगे और उपविभाजित (Sub Divide) किया गया है अर्थात 1 cm को 10 बराबर भागों में उपविभाजित किया गया है, जिसमे प्रत्येक भाग की लंबाई 1 mm है।
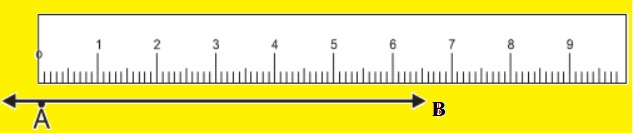
रूलर से गणना के लिए बिंदु A पर शून्य अंकित करते है और फिर रेखाखंड की लंबाई मापने के लिए B की ओर बढ़ते है। परंतु कभी - कभी रूलर की मोटाई के कारण इस गणना मे कुछ त्रुटियाँ रह जाती है। ( उपर्युक्त आकृति )
परंतु डिवाइडर के प्रयोग से इन त्रुटियों की संभावना नहीं रहती है।

हमारे पास AB रेखाखण्ड है इसकी माप ज्ञात करने के लिए हम एक सिरे को बिंदु A पर रखते है तथा दूसरे सिरे को बिंदु B तक खोलते है। अब डिवाइडर को बिना अव्यवस्थित किये उठाकर रूलर पर इस तरह रखते है कि एक सिरा 0 ( शून्य ) पर हो तथा दूसरे सिरे पर माप को पढ़ते है। इस तरह हम दो रेखाखण्डों की तुलना कर सकते हैं।
NOTE:
रेखाखंडों की लंबाई ज्ञात करने के लिए सामान्यतः रूलर या डिवाइडर का उपयोग किया जाता है।
उदाहरण 1
एक रेखाखण्ड की लम्बाई मापने के लिए रूलर की अपेक्षा डिवाइडर का प्रयोग करना क्यों अधिक अच्छा है ?
एक रेखाखण्ड की लम्बाई मापने के लिए रूलर की अपेक्षा डिवाइडर का प्रयोग करना अधिक अच्छा होता है क्योंकि रूलर ( पैमाना ) पर बहुत छोटी mm की लाइने होती है। कई बार हमारी रूल / पेंसिल की नोंक मोटी होती है तो हम उस mm की रेखा पर इसे सही से रख नहीं पाते है जिससे माप मे त्रुटि (गलती) होने की संभावना रहती है।
परंतु डिवाइडर के दोनों सिरे नुकीले होते है जिससे वे छोटी से छोटी mm की लाइन को भी पूरी शुद्धता से मापता है।
अतः एक शुद्ध माप प्राप्त करने के लिए डिवाइडर का प्रयोग करना चाहिए।
कोणों का वर्गीकरण
बच्चों ! अगर हम दिशाओं की बात करे तो आप सभी जानते है की कुल चार दिशाएँ होती है -
(i) उत्तर [ North ]
(ii) दक्षिण [ South ]
(iii) पूर्व [ East ]
(iv) पश्चिम [ West ]
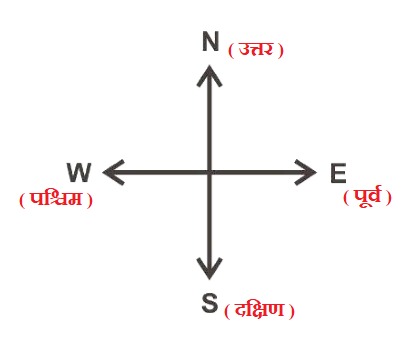
चित्र से समझ सकते है की उत्तर (N) के विपरीत दक्षिण (S) दिशा होती है तथा पूर्व (E) के विपरीत पश्चिम (W) दिशा होती है।
अब हम इन दिशाओं की सहायता से कोणों का अध्ययन करेंगे।
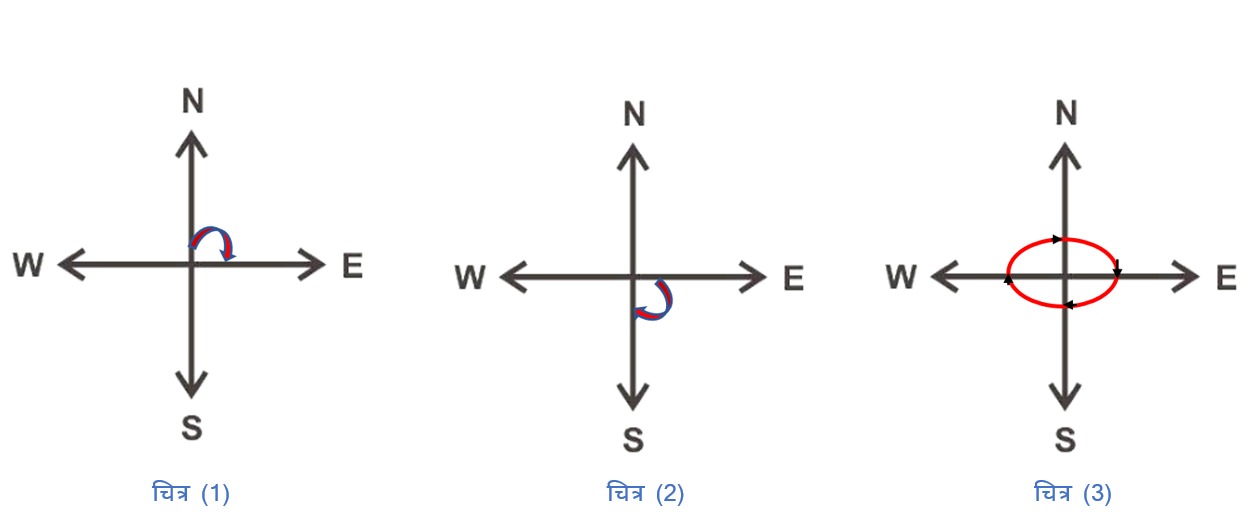
(i) यदि हम घड़ी की दिशा ( दक्षिणावर्त दिशा ) (clock-wise) में उत्तर से पूर्व की ओर घूमते है तो हम एक समकोण अर्थात 90∘ घूम जाते है। इस कोण को समकोण ( Right Angle ) कहते है। [ चित्र 1 ]
(ii) अब हम पूर्व से दक्षिण की तरफ घड़ी की सुई की दिशा ( दक्षिणावर्त दिशा ) मे घूमते है तो हम एक समकोण और घूम जाते है अर्थात उत्तर से दक्षिण तक आने मे हम दो समकोण ( 180∘ ) घूमते है तो इस कोण को ऋजुकोण ( Straight angle) कहते हैं। [ चित्र 2 ]
(iii) अब हम दक्षिण दिशा पर खड़े है। अब तक हमने देखा की उत्तर से दक्षिण तक आने के लिए हम एक ऋजुकोण अर्थात दो समकोण घूमते है। अतः अब हमे दक्षिण से पुनः उत्तर तक जाने के लिए एक और ऋजुकोण अर्थात दो समकोण और घूमना पड़ता है।
इस प्रकार हमे उत्तर से पुनः उत्तर पर आने के लिए दो ऋजुकोण अर्थात चार समकोण [ 360∘ ] का चक्कर पूरा करना पड़ेगा।
यह पूरा चक्कर एक घूर्णन कहलाता है। और इस एक घूर्णन से बना कोण संपूर्ण कोण ( Complete Angle ) कहलाता है। [ चित्र 3 ]
आइये इन घूर्णनों को घड़ी की सहायता से और समझते है -
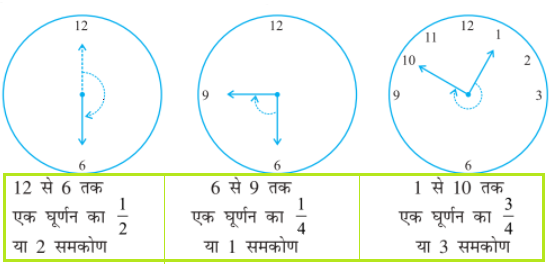
इन घड़ियों से हम एक घूर्णन के चारों भागों को अच्छे से समझ सकते हैं।
(iv) न्यून कोण ( Acute Angle ) : वह कोण जो एक समकोण से भी छोटा हो, न्यून कोण कहलाता है।
इस कोण का मान 0∘ से 90∘ के बीच मे होता है।
उदाहरण -
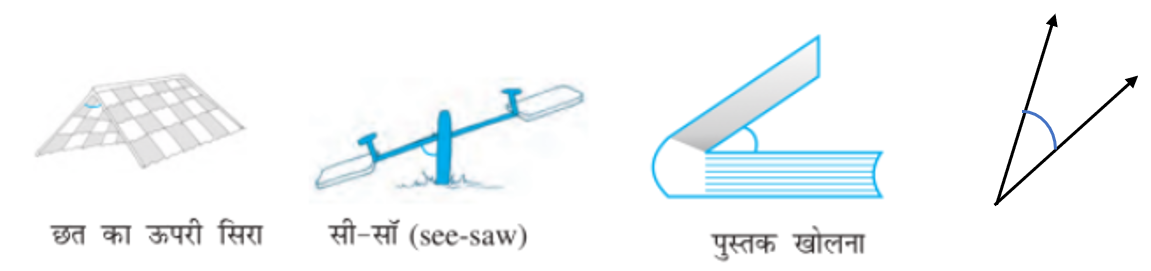
(v) अधिक कोण ( Obtuse angle ) : वह कोण जो एक समकोण से बड़ा और एक ऋजुकोण से छोटा होता है, अधिक कोण कहलाता है।
इस कोण का मान 90∘ से 180∘ के बीच मे होता है।
उदाहरण -

(vi) प्रतिवर्ती कोण ( Reflex Angle ) : यह कोण एक ऋजुकोण से बड़ा और एक संपूर्ण कोण से छोटा होता है।
इस कोण का मान 180∘ से 360∘ के बीच मे होता है।
उदाहरण -
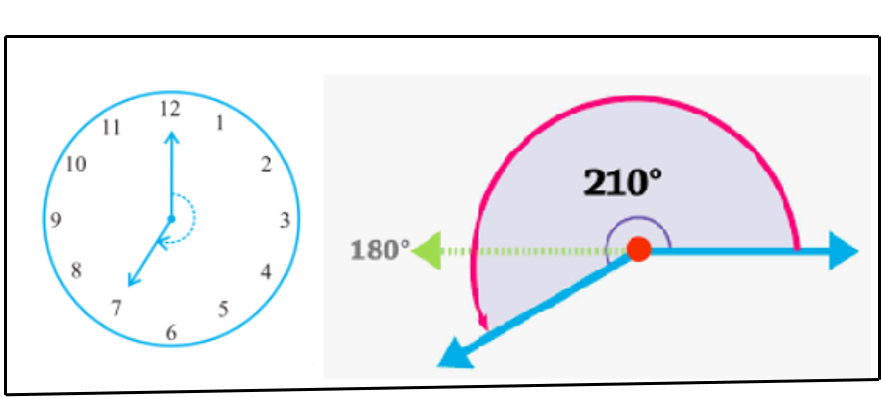
कोणों का मापन
अब तक हमने कोणों के विभिन्न प्रकारों के बारे मे पढ़ा है हम न्यूनकोण एवं अधिककोण में देखकर बता सकते हैं कि यह कौन-सा कोण हैं परंतु यदि हमे दो अधिक कोण या दो न्यून कोण दिए जाए तो हम केवल देखकर उनकी तुलना नहीं कर सकते, अतः कोणों की ठीक से तुलना करने के लिए हमें इनके मापन की आवश्यकता होती है।
चांदा ( Protractor ) : कोणों के मापन के लिए सबसे आवश्यक उपकरण चांदा होता है। इसके वक्रीय किनारे ( Edge ) 180 भागों में विभाजित होते है। प्रत्येक भाग का एक अंश 1 डिग्री ( Degree ) कहलाता है।
चांदे पर चिह्न, दायी से बायीं ओर तथा बायीं से दायी ओर, 0° से 180° तक लिखे होते हैं।
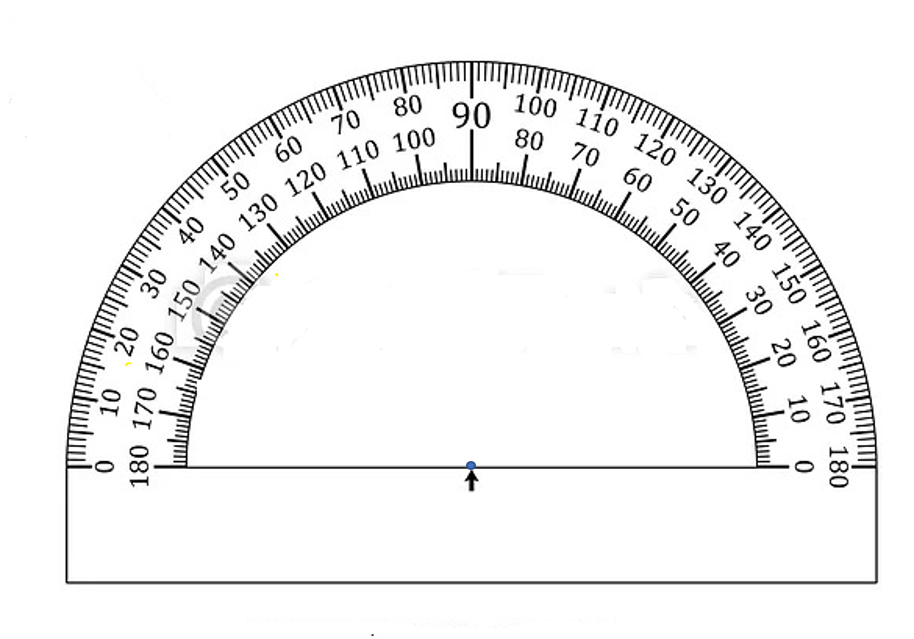
उसी प्रकार एक पूर्ण घूर्णन 360 बराबर भागों में विभाजित होता है। हम इसे 360° लिखते हैं और तीन सौ साठ डिग्री पढ़ते हैं।
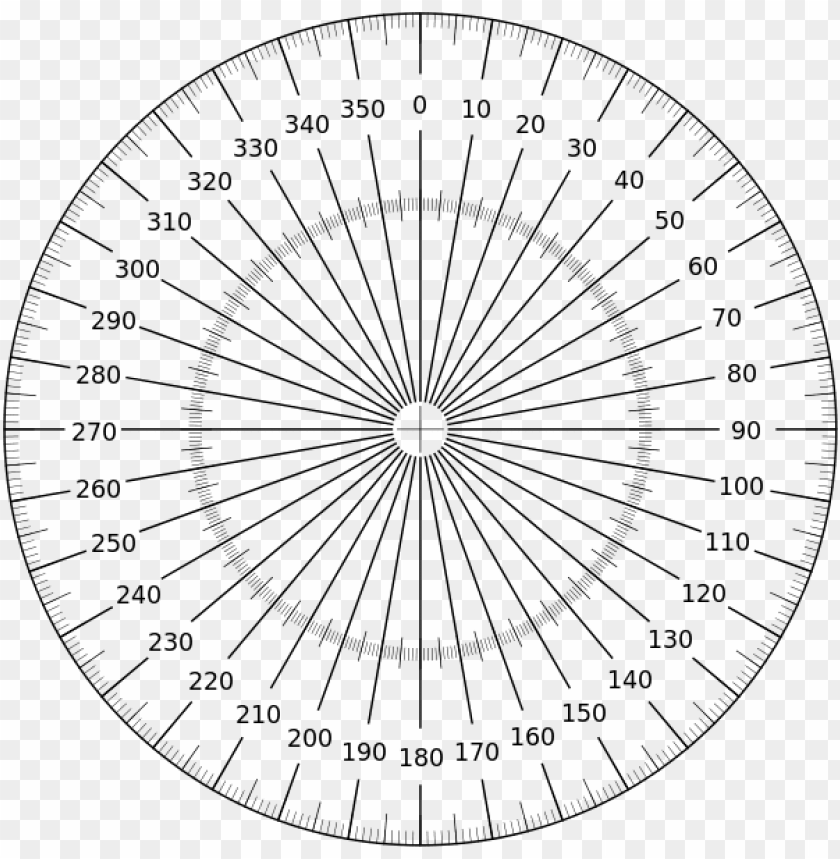
परंतु मापन के लिए अर्धचाँदा ही सरल होता है। आइये इसकी सहायता से एक कोण का मापन करते है।
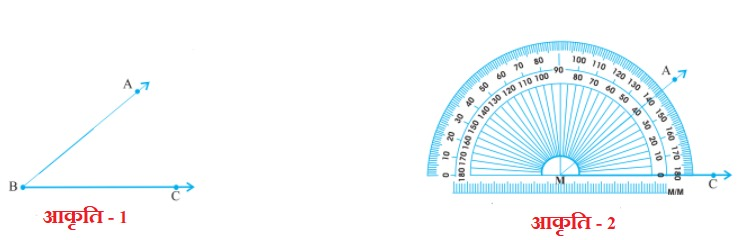
आकृति (1) मे हमे ∠ ABC का मान ज्ञात करना है -
उदाहरण 2
घड़ी की घण्टे वाली सुई एक घूर्णन में कितना घूम सकती है, जब वह: 6 से 3 पर पहुँचती है?
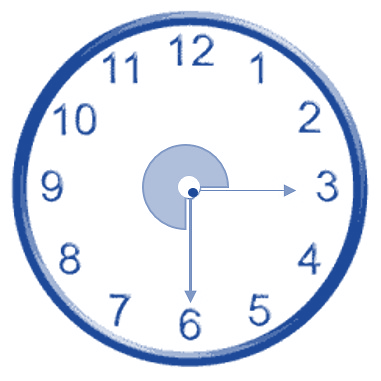
चूंकि घड़ी की सुई चलना प्रारंभ करती है : 6 बजे से
घड़ी की सुई रुकती है : 3 बजे
अतः 6 बजे से 3 बजे तक कुल घंटे = 9
चुकि घड़ी मे कुल घंटों की संख्या : 12
12 घंटों मे कुल डिग्री कोण : 360∘
अतः 1 घंटे मे घड़ी की सुई कोण बनाएगी : 360∘12=30∘
∴ 9 घंटे मे घड़ी की सुई कोण बनाएगी : 30∘×9=270∘
अतः घड़ी की घंटे की सुई 6 बजे से 3 बजे तक कुल 270∘ का कोण बनाएगी।
भिन्न मे बदलने पर : 270∘360∘ = (34)∘
उदाहरण 3
घड़ी की घंटे वाली सुई कहाँ रुकेगी, यदि वह 7 से प्रारम्भ करें और 2 ऋजुकोण घूम जाए ?

चूंकि हम जानते है :
एक ऋजुकोण = 180∘
अतः दो ऋजुकोण = 180∘×2=360∘
घड़ी की सुई दो ऋजुकोण (360∘) 12 घंटे मे घूमेगी तथा एक घूर्णन पूरा करेगी।
अर्थात घड़ी की सुई एक ऋजुकोण मे 1 पर पहुचेगी तथा दूसरे ऋजुकोण मे पुनः 7 पर पहुच जाएगी। जैसा चित्र मे दर्शाया गया है।
अतः घड़ी की घंटे वाली सुई 7 बजे से प्रारंभ होकर पुनः 12 घंटे बाद 7 पर ही आकर रुकेगी।
लंब रेखाएँ
यदि दो रेखाएँ परस्पर एक - दूसरे को प्रतिच्छेद करें और उनके बीच का कोण समकोण हो, तो वे रेखाएँ एक - दूसरे पर लंब ( Perpendicular ) रेखाएँ कहलाती हैं।
यदि एक रेखा MN, रेखा AB पर लंब है, तो इसे MN⊥AB लिखते हैं। आइये चित्र से समझते है -
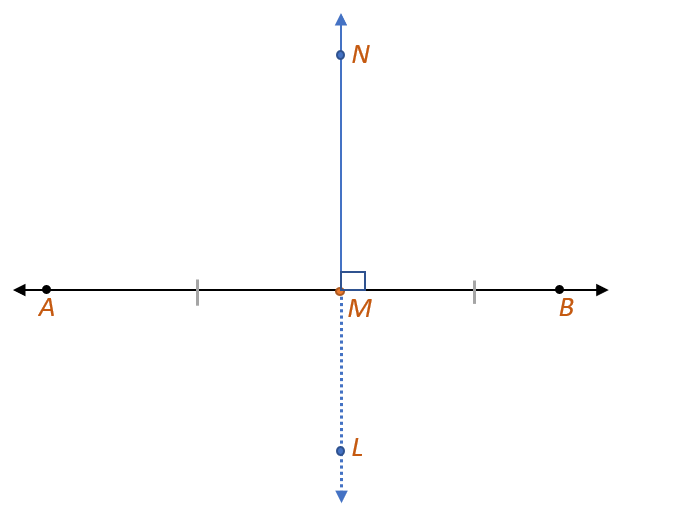
चित्र मे रेखा AB और रेखा NL एक - दूसरे को बिन्दु M पर प्रतिच्छेद करती है। MN, रेखाखण्ड AB को समद्विभाजित करती है (अर्थात् दो बराबर भागों में विभाजित करती है) और उस पर लंब भी है।
अतः रेखा MN रेखाखंड AB का लंब समद्विभाजक ( Perpendicular Bisector ) है।
उदाहरण 4
रेखाखण्ड PQ तथा XY परस्पर लम्ब है तथा ये परस्पर बिंदु A पर प्रतिच्छेद करते हैं।
∠PAY की माप ज्ञात कीजिए

चूंकि हमे दिया गया है -
रेखाखण्ड PQ और XY परस्पर लंब है अर्थात ये रेखाएँ एक दूसरे को 90∘ पर काटती है।
अतः ∠PAY=90∘ होगा क्योंकि रेखा PQ और रेखा XY परस्पर लंब पर प्रतिच्छेद करती है।
त्रिभुजों का वर्गीकरण
तीन रेखाखण्डों से घिरी बंद आकृति, त्रिभुज कहलाती है। त्रिभुज सबसे कम भुजाओं वाला बहुभुज होता है। जिसमे तीन भुजाएँ, तीन कोण और तीन शीर्ष होते है।
त्रिभुज से संबंधित कुछ महत्वपूर्ण तथ्य -
• यदि किसी त्रिभुज के सभी कोण बराबर होते है तो उसकी सभी भुजाएँ भी बराबर होती है।
• यदि किसी त्रिभुज की सभी भुजाएँ बराबर होती है तो उसके सभी कोण भी बराबर होते है।
• यदि किसी त्रिभुज की दो भुजाएँ बराबर हैं तो उस त्रिभुज के दो कोण भी बराबर होंगे।
• यदि किसी त्रिभुज की तीनों भुजाएँ आपस मे बराबर नहीं है तो उस त्रिभुज के तीनों कोण भी आपस मे बराबर नहीं होंगे।
अर्थात त्रिभुज की भुजाओं ओर कोणों मे एक विशेष संबंध होता है।
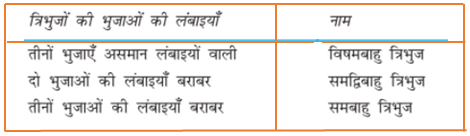
भुजाओं के आधार पर त्रिभुजों का नामकरण -
( i ) समबाहु त्रिभुज ( Equilateral triangle ) : ऐसा त्रिभुज जिसकी तीनों भुजाएँ बराबर हों, समबाहु त्रिभुज कहलाता है।
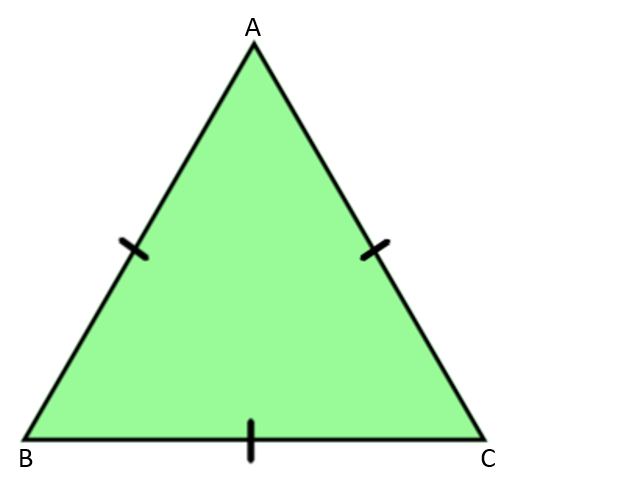
( ii ) समद्विबाहु त्रिभुज ( Lsosceles triangle ) : ऐसा त्रिभुज जिसकी दो भुजाएँ बराबर हों, समद्विबाहु त्रिभुज कहलाता है।
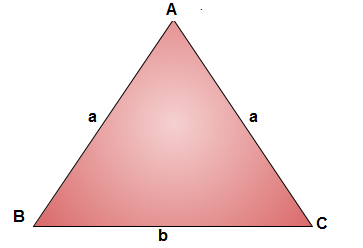
( iii ) विषमबाहु त्रिभुज ( Scalene triangle ) : ऐसा त्रिभुज जिसकी तीनों भुजाएँ बराबर नहीं हों, विषमबाहु त्रिभुज कहलाता है।
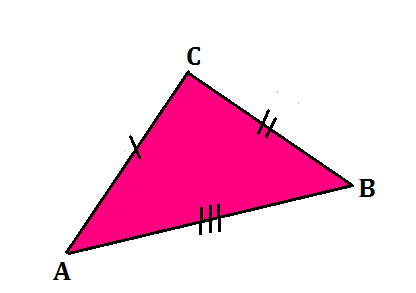
कोणों के आधार पर त्रिभुजों का नामकरण -
( i ) न्यून कोण त्रिभुज ( Acute angled triangle ) : ऐसा त्रिभुज जिसका प्रत्येक कोण 90° से कम हो, न्यून कोण त्रिभुज कहलाता है।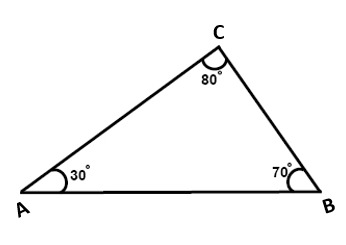
( ii ) समकोण त्रिभुज ( Right angled triangle ) : ऐसा त्रिभुज जिसका कोई एक कोण समकोण हो, समकोण त्रिभुज कहलाता है।
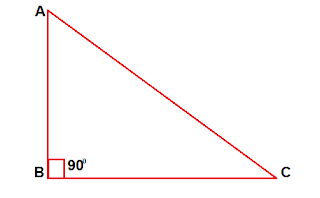
( iii ) अधिक कोण त्रिभुज ( Obtuse angled triangle ) : ऐसा त्रिभुज जिसका कोई एक कोण 90° से अधिक हो, अधिक कोण त्रिभुज कहलाता है।
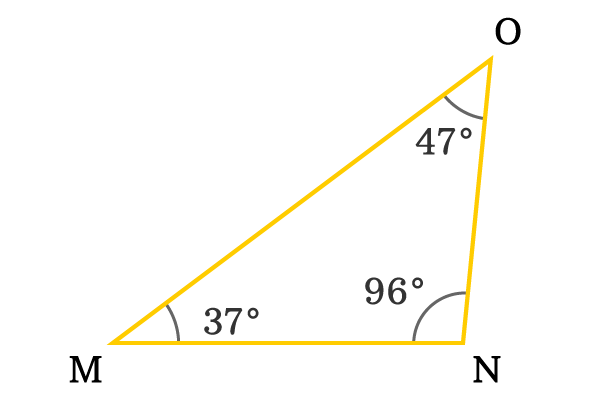
उदाहरण 5
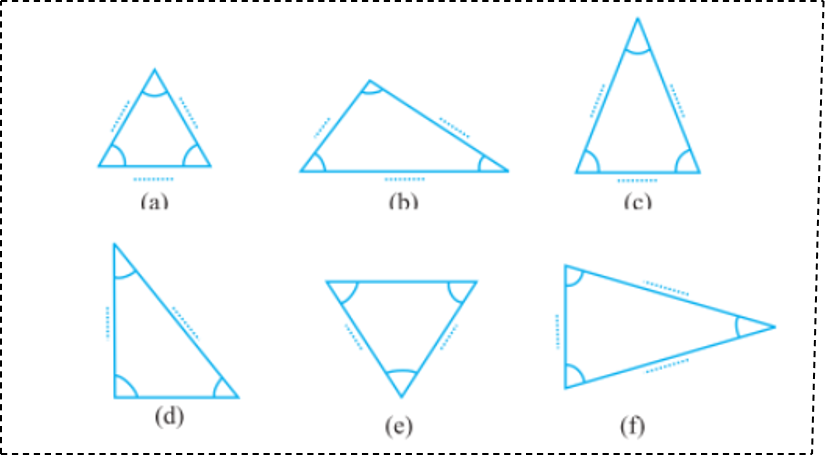
निम्न को उनके गुणों के आधार पर सुमेलित कीजिएः
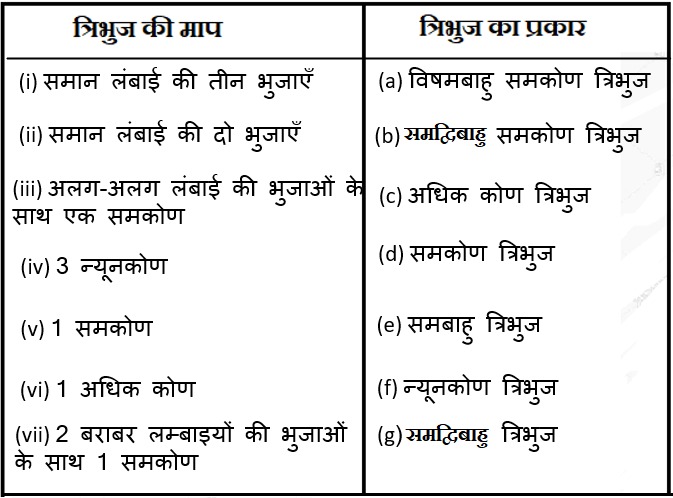
(i) समान लंबाई की तीन भुजाएँ : चूंकि यह गुण एक समबाहु त्रिभुज का होता है।
अतः (e) समबाहु त्रिभुज
(ii) समान लंबाई की दो भुजाएँ : चूंकि यह एक समद्विबाहु त्रिभुज का गुण होता है।
अतः (g) समद्विबाहु त्रिभुज
(iii) अलग - अलग लम्बाइयों के साथ एक समकोण : चूंकि यह गुण एक विषमबाहु समकोण त्रिभुज का होता है।
अतः (a) विषमबाहु समकोण त्रिभुज
(iv) 3 न्यून कोण : चूंकि यह गुण न्यूनकोण त्रिभुज का होता है।
अतः (f) न्यून कोण त्रिभुज
(v) 1 समकोण : यह गुण एक समकोण कोण त्रिभुज का होता है।
अतः (d) समकोण त्रिभुज
(vi) 1 अधिक कोण : यह गुण अधिक कोण त्रिभुज का होता है।
अतः (c) अधिक कोण त्रिभुज
(vii) 2 बराबर लंबाइयों की भुजाओं के साथ एक समकोण : चूंकि यह गुण एक समद्विबाहु समकोण त्रिभुज का होता है।
अतः (b) समद्विबाहु समकोण त्रिभुज
चतुर्भुज
चार भुजाओंं से घिरी बंद आकृति चतुर्भुज कहलाती है।
इसकी निम्न विशेषताएँ होती है -
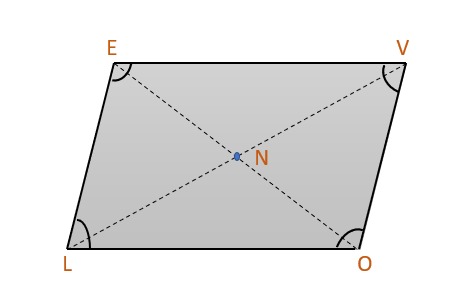
चित्र मे,
⇒¯¯¯¯¯¯LO, ¯¯¯¯¯¯OV, ¯¯¯¯¯¯VE और ¯¯¯¯¯¯EL इसकी चार भुजाएँ है।
⇒∠L, ∠O, ∠V और ∠E चार कोण है।
⇒ ¯¯¯¯¯¯LV और ¯¯¯¯¯¯OE इसके दो विकर्ण है।
इस अध्याय मे हम पाँच प्रकार के चतुर्भुजों का अध्ययन करेंगे -
( i ) आयत
( ii ) वर्ग
( iii ) समांतर चतुर्भुज
( iv ) समचतुर्भुज
( v ) समलंब चतुर्भुज
इनकी पहचान हम सेट स्कवेयर की सहायता से भी कर सकते है। हमारे पास दो प्रकार के सेट स्कवेयर होते है -
( i ) 45° - 45° - 90° सेट स्कवेयर
( ii ) 30° - 60° - 90° सेट स्कवेयर
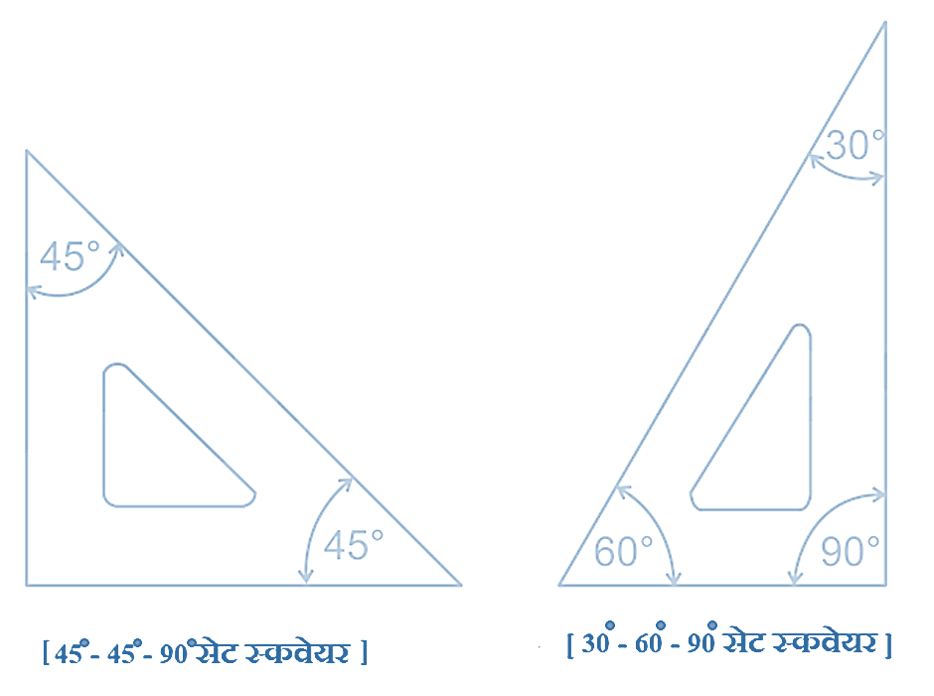
आइये इनकी सहायता से चतुर्भुजों की पहचान करते है।
( i ) आयत :
यदि हम 30° - 60° - 90° के सेट स्कवेयर के एक युग्म को चित्रानुसार रखते है तो हमे आयत की आकृति प्राप्त होती है।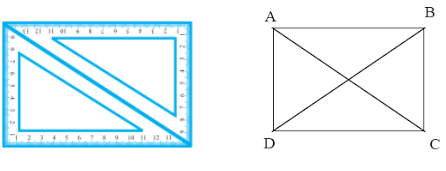
आयत के गुण -
(i) आयत की सम्मुख भुजाएँ बराबर होती हैं।
(ii) आयत की सम्मुख भुजाएँ समांतर होती हैं।
(iii) आयत की आसन्न भुजाओं से बने कोण 90∘ के होते हैं अर्थात प्रत्येक कोण 90∘ का होता है।
(iv) आयत के विकर्ण बराबर होते हैं।
(v) आयत के विकर्ण एक दूसरे को समद्विभाजित करते है।
( ii ) वर्ग :
यदि हम 45° - 45° - 90° के सेट स्कवेयर के एक युग्म का प्रयोग चित्रानुसार करते है तो हमे वर्ग की आकृति प्राप्त होती है।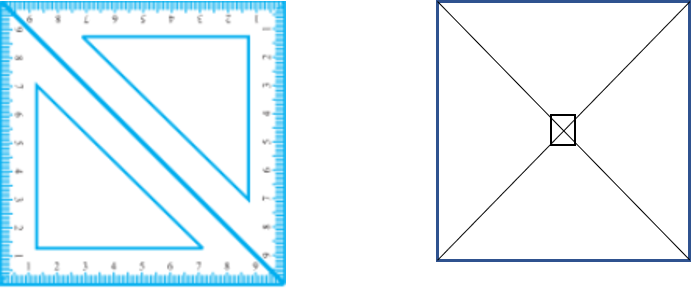
वर्ग के गुण -
(i) वर्ग की सभी भुजाएँ बराबर होती हैं।
(ii) वर्ग की सम्मुख भुजाएँ समांतर होती हैं।
(iii) वर्ग के चारों कोण 90∘ के होते हैं अर्थात समकोण होते है।
(iv) वर्ग के विकर्ण बराबर होते हैं।
(v) वर्ग के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते है।
( iii ) समांतर चतुर्भुज :
यदि हम 30° - 60° - 90° के सेट स्कवेयर के एक युग्म को चित्रानुसार रखते है तो हमे समांतर चतुर्भुज की आकृति प्राप्त होती है।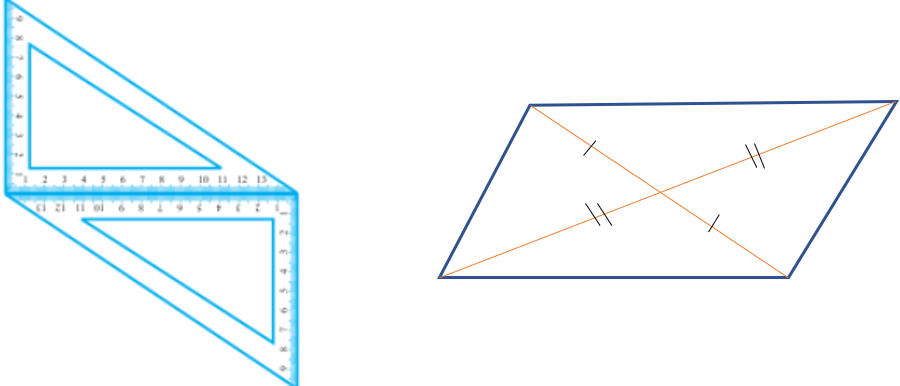
समांतर चतुर्भुज के गुण -
(i) समांतर चतुर्भुज की आमने - सामने की भुजाएँ (सम्मुख भुजाएँ) समांतर होती हैं।
(ii) समांतर चतुर्भुज के आमने - सामने के कोण (सम्मुख कोण) आपस में बराबर होते हैं।
(iii) समांतर चतुर्भुज की आमने - सामने की भुजाएँ (सम्मुख भुजाएँ) आपस में बराबर होती हैं।
(iv) समांतर चतुर्भुज के विकर्ण एक दूसरे को दो बराबर भागों में बाँटते हैं।
( iv ) समचतुर्भुज :
यदि हम 30° - 60° - 90° के सेट स्कवेयर के एक युग्म को चित्रानुसार रखते है तो हमे समचतुर्भुज की आकृति प्राप्त होती है।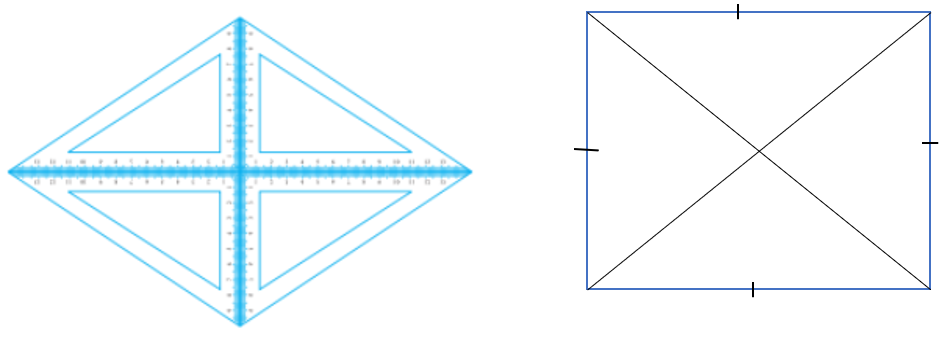
समचतुर्भुज के गुण -
(i) समचतुर्भुज की सम्मुख भुजाएँ समांतर होती हैं।
(ii) समचतुर्भुज की सभी भुजाएँ आपस में बराबर होती हैं।
(iii) समचतुर्भुज के सम्मुख कोण बराबर होते है।
(iv) समचतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं तथा एक दूसरे पर लम्ब होते हैं।
( v ) समलंब चतुर्भुज :
यदि हम कई सेट स्कवेयरो को चित्रानुसार रखते है तो हमे एक ऐसा चतुर्भुज प्राप्त होता है जिसकी दो सम्मुख भुजाओं का एक युग्म समांतर है अर्थात वह चतुर्भुज एक समलंब चतुर्भुज होता है।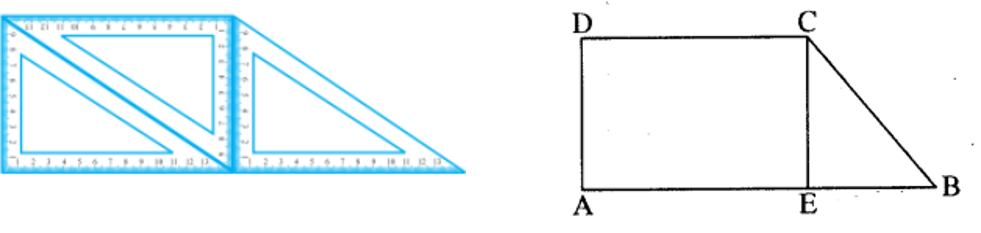
समलंब चतुर्भुज के गुण -
(i) समलंब चतुर्भुज की कोई भी दो भुजाएँ समांतर और आपस मे असमान होती है।
(ii) इसके चारों आंतरिक कोणों का योग 360∘ होता है।
उदाहरण 6
सत्य एवं असत्य के आधार पर उत्तर दीजिए :
(a) आयत का प्रत्येक कोण समकोण होता है ।
(b) आयत की सम्मुख भुजाओं की लंबाई बराबर होती है।
(c) वर्ग के विकर्ण एक दूसरे पर लंब होते हैं।
(d) समचतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(e) समांतर चतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती है।
(f) समलंब की सम्मुख भुजाएँ समांतर होती है।
(a) सत्य
आयत का प्रत्येक कोण समकोण होता हैं।
(b) सत्य
आयत की सम्मुख भुजाओं की लंबाई बराबर होती है।
(c) सत्य
वर्ग के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते है।
(d) सत्य
समचतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(e) असत्य
क्योंकि समांतर चतुर्भुज की केवल आमने - सामने की भुजाएँ (सम्मुख भुजाएँ) आपस में बराबर होती हैं।
(f) असत्य
क्योंकि समलंब चतुर्भुज की सम्मुख भुजाओं का एक युग्म समांतर होता हैं जबकि दूसरा असमान्तर होता हैं।
बहुभुज
बहुभुज के प्रकार
बहुभुज को उनकी भुजाओं की संख्या के आधार पर वर्गीकृत किया जा सकता है -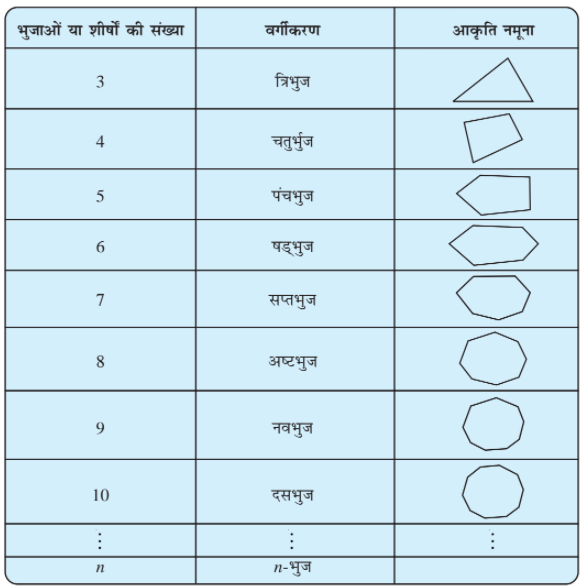
(i) त्रिभुज : ऐसा बहुभुज, जिसमें तीन भुजाएँ होती हैं।
दूसरे शब्दों में तीन भुजाओं वाले बहुभुज को त्रिभुज कहा जाता है।
(ii) चतुर्भुज : ऐसा बहुभुज, जिसकी चार भुजाएँ होती हैं।
दूसरे शब्दों में चार भुजाओं वाले बहुभुज को चतुर्भुज कहा जाता है।
(iii) पंचभुज : पाँच भुजाओं वाले बहुभुज को पंचभुज कहा जाता है।
(iv) षष्टभुज : छ: भुजाओं वाले बहुभुज को षष्टभुज कहा जाता है।
(v) सप्तभुज : सात भुजाओं वाले बहुभुज को सप्तभुज कहा जाता है।
(vi) अष्टभुज : आठ भुजाओं वाले बहुभुज को अष्टभुज कहा जाता है।
(vii) नवभुज : नौ भुजाओं वाले बहुभुज को नवभुज कहा जाता है।
(viii) दशभुज : दस भुजाओं वाले बहुभुज को दशभुज कहा जाता है।
उदाहरण 7
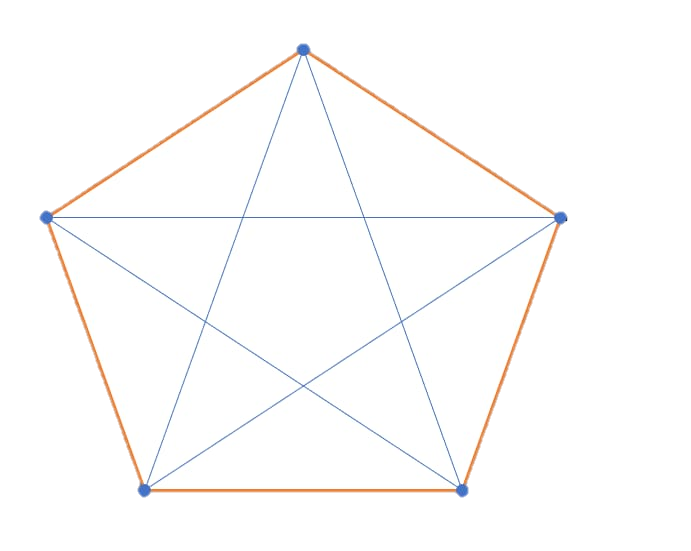
पंचभुज की आकृति बनाइये और उसके विकर्ण खींचिए।
पंचभुज : पाँच भुजाओं वाले बहुभुज को पंचभुज कहा जाता है।
त्रिविमीय आकृतियाँ
समतल आकारों में, दो मापन ( लंबाई और चौड़ाई ) होते हैं, इसलिए इन्हें द्विविमीय आकार कहते हैं, जबकि ठोस आकारों में, तीन मापन ( लंबाई, चौड़ाई और ऊँचाई या गहराई ) होते हैं, इसलिए इन आकारों को त्रिविमीय आकार कहते हैं।
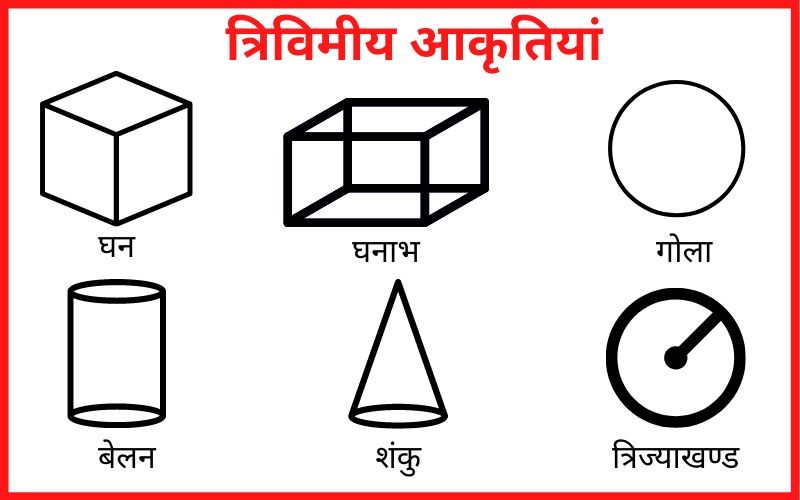
त्रिविमीय आकारों के उदाहरण : घन, घनाभ, गोला, बेलन, शंकु, त्रिज्याखण्ड, पिरामिड आदि
त्रिविमीय आकृतिया निम्न प्रकार की होती है -
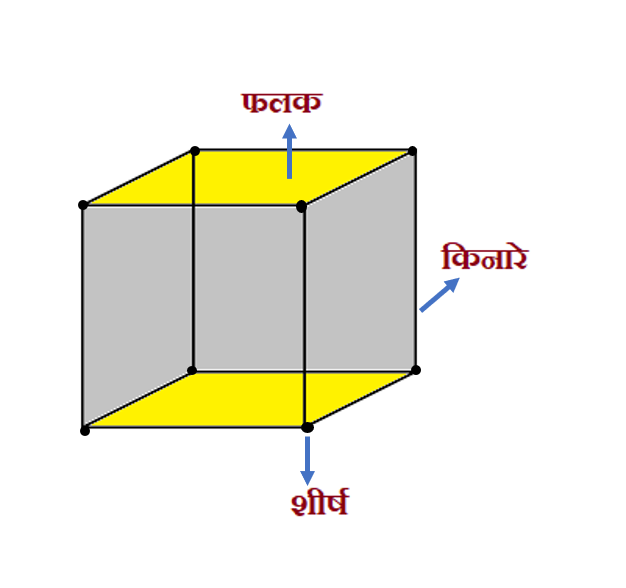
(1) घन :
(i) इसकी लम्बाई, चौड़ाई एवं ऊँचाई समान होती हैं।
(ii) एक घन में 6 फलक, 12 किनारे एवं 8 शीर्ष ( कोने ) होते हैं।
(iii) इसके 6 बराबर-बराबर आकार के फलक होते हैं हर फलक एक वर्ग होता हैं।
(iv) 6 फलक होने के कारण यह एक प्रकार का षट्फलकी भी कहलाता हैं।
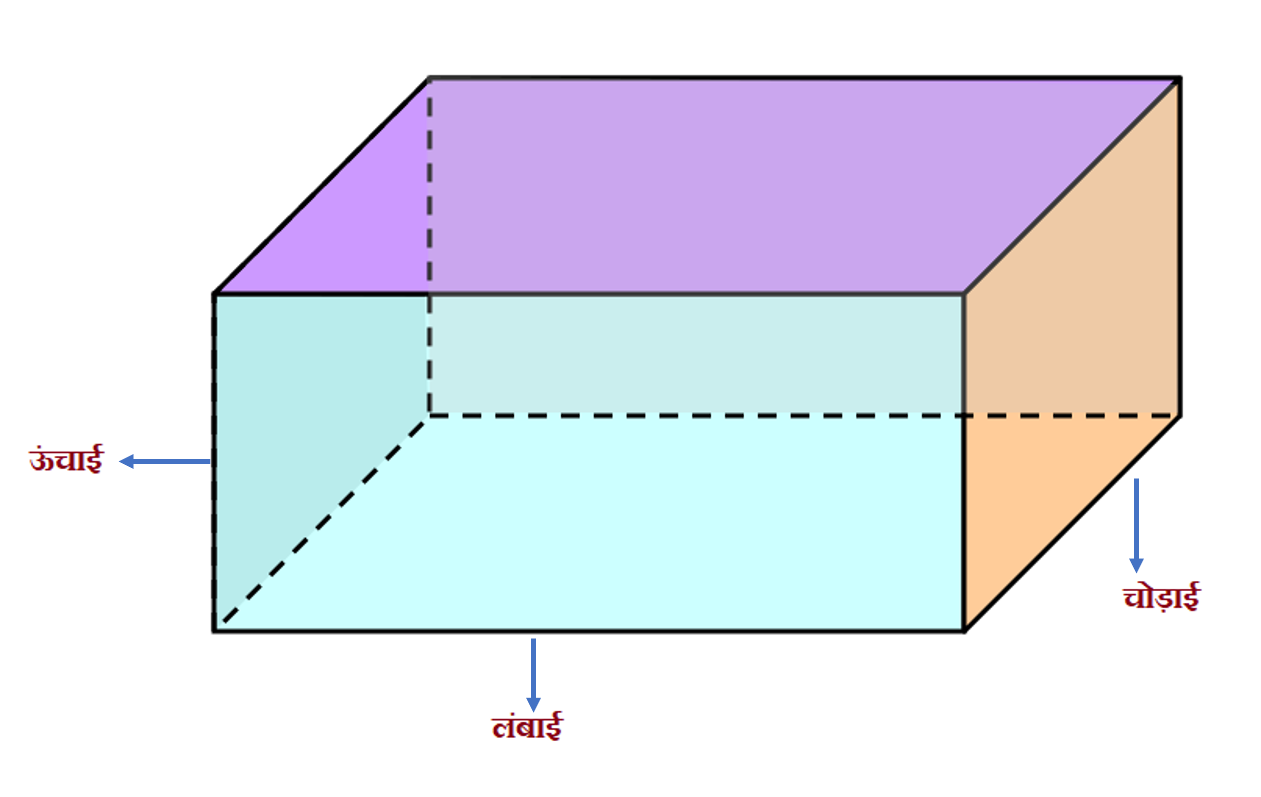
(2) घनाभ :
(i) घनाभ 6 आयताकार आकृतियों से मिलकर बना होता है।
(ii) घनाभ मे 6 फलक, 12 किनारे एवं 8 शीर्ष ( कोने ) होते है।
(iii) इसका प्रत्येक पृष्ठ एक आयत होता हैं।
(iv) घनाभ 6 आयताकार फलको से मिलकर बना होता है इसलिए इसे बहुफलक भी कहा जाता है।
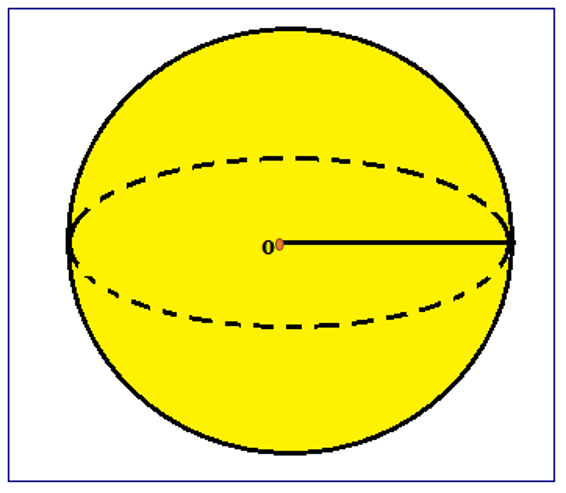
(3) गोला :
(i) गोला एक ऐसी त्रिविमीय आकृति है, जिसमें केवल एक तल होता है और इसके तल का प्रत्येक बिन्दु एक निश्चित बिन्दु से समान दूरी पर होता है।
(ii) इस बिन्दु को गोले का केन्द्र कहते हैं।
(iii) केन्द्र से गोले के किसी बिन्दु की दूरी को गोले की त्रिज्या कहते हैं।
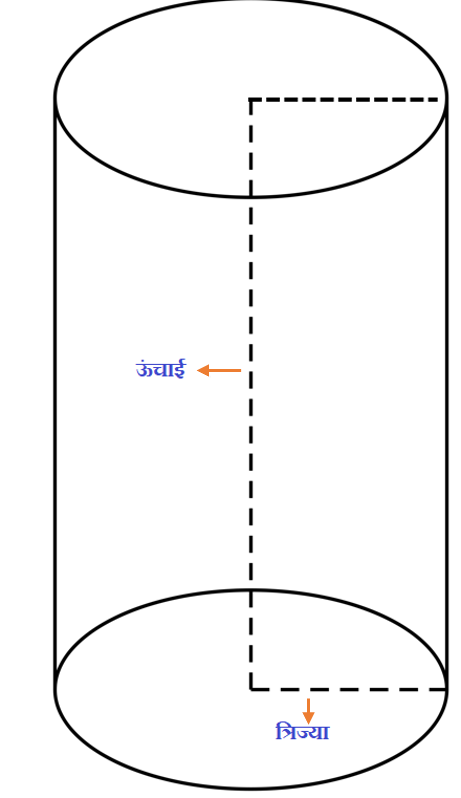
(4) बेलन :
(i) बेलन एक ऐसी त्रिविमीय आकृति होती है जिसमे दो समान त्रिज्या वाले वृत्ताकार भाग होते है।
(ii) बेलन सरल रूप में एक रोलर या समान व्यास वाला गिलास होता है।
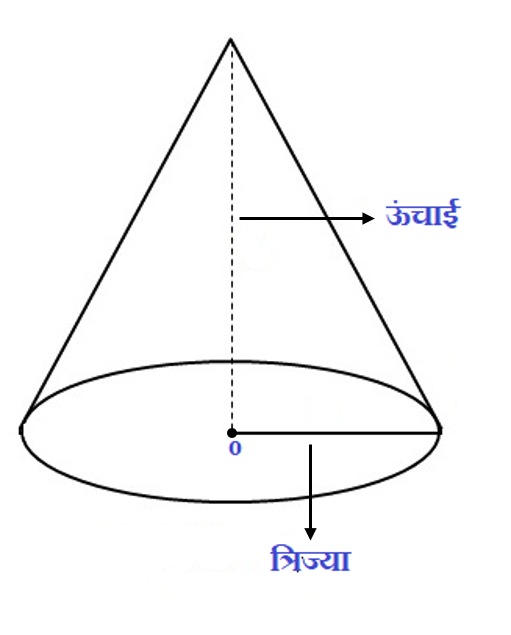
(5) शंकु :
(i) शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं।
(ii) किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।
(iii) यह समान आधार और ऊंचाई वाले बेलन के 13 भाग के बराबर होता है।
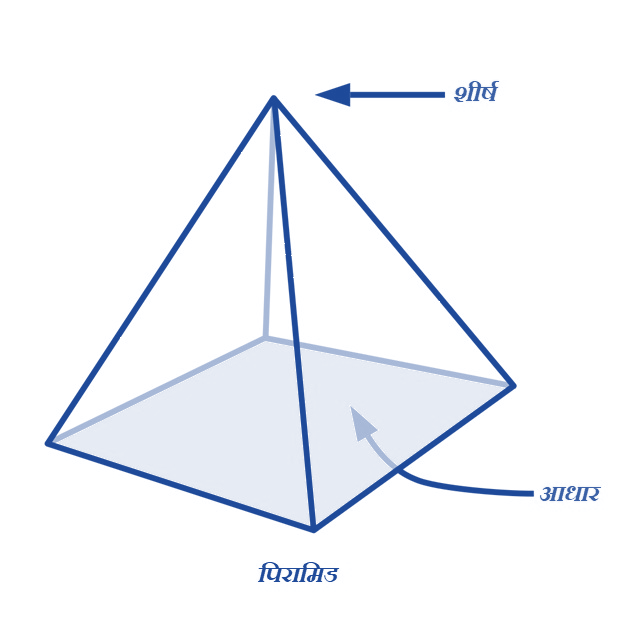
(6) पिरामिड : ठोस ज्यामिति में पिरामिड उस बहुफलकीय ठोस को कहते हैं जिसका आधार कोई बहुभुज हो तथा शेष सभी त्रिभुजाकार फलक एक बिन्दु (शीर्ष) पर मिलते हों।
अर्थात आधार के प्रत्येक कोर और शीर्ष मिलकर एक त्रिभुजाकार फलक बनाते हैं।
उदाहरण 8
निम्न का सुमेलन कीजिए :


शंकु :
(i) शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं।
(ii) किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।
(iii) यह समान आधार और ऊंचाई वाले बेलन के 13 भाग के बराबर होता है।
a→(ii)
गोला :
(i) गोला एक ऐसी त्रिविमीय आकृति है, जिसमें केवल एक तल होता है और इसके तल का प्रत्येक बिन्दु एक निश्चित बिन्दु से समान दूरी पर होता है।
(ii) इस बिन्दु को गोले का केन्द्र कहते हैं।
(iii) केन्द्र से गोले के किसी बिन्दु की दूरी को गोले की त्रिज्या कहते हैं।
b→(iv)
बेलन :
(i) बेलन एक ऐसी त्रिविमीय आकृति होती है जिसमे दो समान त्रिज्या वाले वृत्ताकार भाग होते है।
(ii) बेलन सरल रूप में एक रोलर या समान व्यास वाला गिलास होता है।
c→(v)
घनाभ :
(i) घनाभ 6 आयताकार आकृतियों से मिलकर बना होता है।
(ii) घनाभ मे 6 फलक, 12 किनारे एवं 8 शीर्ष ( कोने ) होते है।
(iii) इसका प्रत्येक पृष्ठ एक आयत होता हैं।
d→(iii)
पिरामिड :
(i) पिरामिड उस बहुफलकीय ठोस को कहते हैं जिसका आधार कोई बहुभुज हो तथा शेष सभी त्रिभुजाकार फलक एक बिन्दु (शीर्ष) पर मिलते हों।
(ii) आधार के प्रत्येक कोर और शीर्ष मिलकर एक त्रिभुजाकार फलक बनाते हैं।
e→(i)
सारांश