पूर्ण संख्याएँ कक्षा 6 गणित

भूमिका

बच्चों इस अध्याय के शीर्षक के अनुसार इस अध्याय मे हम पूर्ण संख्याओं का अध्ययन करेंगे। आपने पिछली कक्षाओं मे विभिन्न संख्या के बारे में पढ़ा है तथा इससे पहले के अध्याय में हमने संख्याओं को जोड़ना, घटाना गुणा करना देखा था। इस अध्याय मे हम पूर्ण संख्या को संख्या रेखा पर जोड़ना, घटाना, तथा गुणा करना सीखेंगे इसके अतिरिक्त इस अध्याय में हम पूर्ण संख्याओं के गुणधर्म, पूर्ण संख्याओं के तत्समक अवयव, पूर्ण संख्याओं में प्रतिरूप आदि के बारे में अध्ययन करेंगे।

आइये जानते है, संख्या को और करीब से ...

अध्याय के शीर्षक के अनुसार इस अध्याय मे हम पूर्ण संख्याओं (Whole Numbers) का अध्ययन करेंगे, हम पिछली कक्षाओं में प्राकृत संख्याओं (Natural Numbers) का अध्ययन कर चुके हैं, आइए उसे पुनः दोहराते है $-$

प्राकृत संख्या (Natural Numbers)

जिन अंको का प्रयोग किसी भी चीज की गणना के लिए किया जाता है उन्हें प्राकृत संख्या कहते है।
उदाहरण के लिए ;

1, 2, 3, ... ..., \infty

परवर्ती (successor)

किसी भी प्राकृत संख्या में 1 जोड़ने पर हमे उस संख्या का परवर्ती प्राप्त होता है।
उदाहरण के लिए ;
16+1 =17
13+1 =14

पूर्ववर्ती (predecessor)

किसी भी प्राकृत संख्या मे से 1 घटाने पर हमे उस संख्या का पूर्ववर्ती प्राप्त होता है।
उदाहरण के लिए ;

23 - 1 = 22

8 - 1 = 7

Note :

1 को छोड़कर प्रत्येक प्राकृत संख्या का पूर्ववर्ती (predecessor) होता है।

पूर्ण संख्या (Whole Numbers)

शून्य सहित सभी प्राकृत संख्याएँ पूर्ण संख्याएँ कहलाती हैं।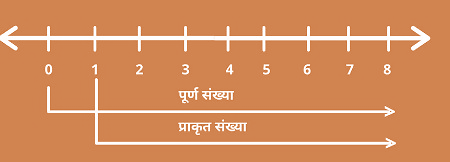

ocr_image

उदाहरण 1

$19, 1997, 12000,$ $49, 100000,$ $2440701, 100199$ और $208090$ के पूर्ववर्ती और परवर्ती लिखिए।

(1) 19
पूर्ववर्ती $=$ 18
परवर्ती $=$ 20

(2) 1997
पूर्ववर्ती $=$ 1996
परवर्ती $=$ 1998

(3) 12000
पूर्ववर्ती $=$ 11999
परवर्ती $=$ 12001

(4) 49
पूर्ववर्ती $=$ 48
परवर्ती $=$ 50

(5) 100000
पूर्ववर्ती $=$ 99999
परवर्ती $=$ 100001

(6) 2440701
पूर्ववर्ती $=$ 2440700
परवर्ती $=$ 2440702

(7) 100199
पूर्ववर्ती= $100198$
परवर्ती = $100200$

(8) 208090
पूर्ववर्ती= $208089$
परवर्ती = $208091$

Learn more

उदाहरण 2

10001 से ठीक पहले आने वाली तीन पूर्ण संख्याएं लिखिए।

10001 से ठीक पहले आने वाली तीन पूर्ण संख्याएं $= 9998, 9999, 10000$

Learn more

OMR (One Minute Revision)

संख्याएँ 1, 2, 3,... जिनका प्रयोग हम गिनने के लिए करते हैं, प्राकृत संख्याएँ कहलाती हैं।

यदि किसी प्राकृत संख्या में 1 जोड़ते हैं तो हमे इसका परवर्ती (successor) मिलता है। यदि किसी प्राकृत संख्या में से 1 घटाते हैं, तो इसका पूर्ववर्ती (predecessor) प्राप्त होता है।

1 को छोड़कर प्रत्येक प्राकृत संख्या का एक पूर्ववर्ती होता है।

यदि प्राकृत संख्याओं के संग्रह में हम संख्या 0 जोड़ते हैं, तो हमें पूर्ण संख्याओं का संग्रह प्राप्त होता है।
इस प्रकार संख्याएँ 0, 1, 2, 3, पूर्ण संख्याओं का संग्रह बनाती हैं।

0 को छोड़कर प्रत्येक पूर्ण संख्या का एक पूर्ववर्ती होता है।

सभी प्राकृत संख्याएँ, पूर्ण संख्याएँ भी हैं। लेकिन सभी पूर्ण संख्याएँ प्राकृत संख्याएँ नहीं हैं।

पूर्ण संख्याओं का निरूपण

पूर्ण संख्याएँ (whole number) वे संख्याएँ होती हैं जो धनात्मक (Positive), या शून्य हो सकती हैं, लेकिन भिन्न (Fraction), ऋणात्मक (Negative) नहीं हो सकती हैं। इन संख्याओं का उपयोग विभिन्न अंकगणितीय संक्रियाओं जैसे जोड़, घटाव, गुणा और भाग को करने के लिए किया जाता है।

धनात्मक संख्या (Positive Numbers)
$1, 2, 3, 4, ... \infty$ तक कोई भी संख्या हो सकती है|

शून्य संख्या $= 0$

अतः हम कह सकते है,की
$0, 1, 2, 3, 4, 5 ... + \infty$

तक सभी संख्या पूर्ण संख्या होंगे|
जैसे की $10, 15, 0,$ $50$ ये सभी पूर्ण संख्या है|

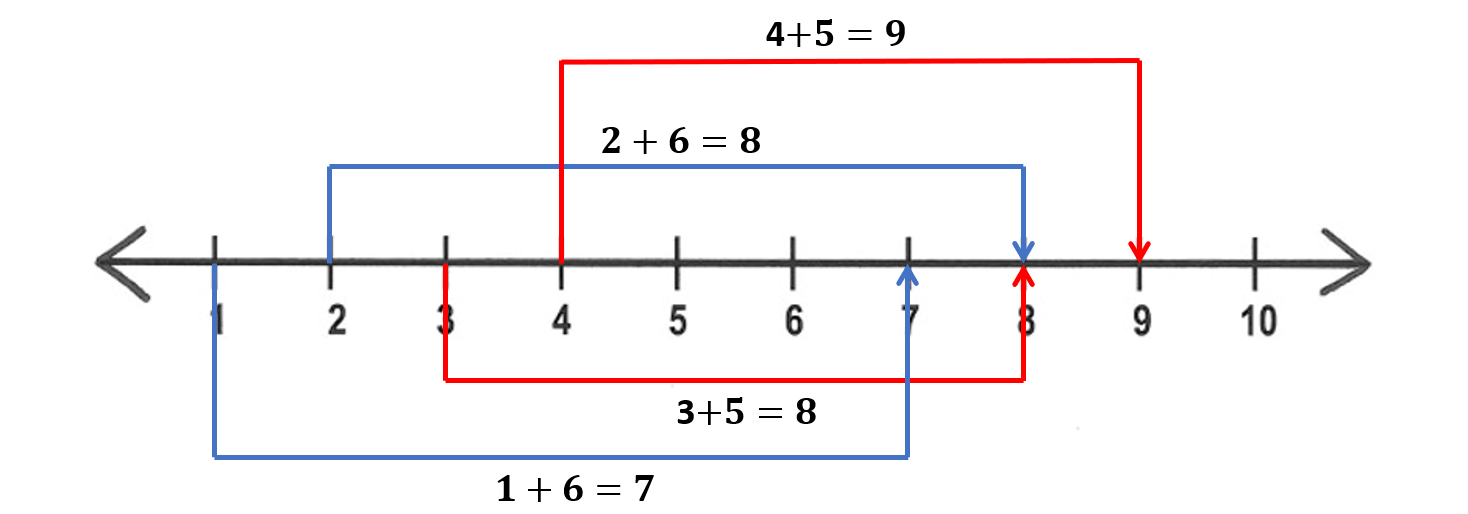
संख्या रेखा (Number Line)

संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
सबसे बायीं ओर (Left Side) शून्य को रखते हैं ।
अब संख्या रेखा में धनात्मक दिशा मे शून्य के दायीं ओर (Right Side) 1, 2, 3..... अंकित कर लेते हैं।

ocr_image

संख्या रेखा में बाएं से दायें

\to

(Left to Right) जाने पर संख्या बढ़ती है, दायें से बाएं

\leftarrow

(Right to Left) जाने पर संख्या का मान घटता है। इसमें हम किसी पूर्ण संख्या को आसानी से दर्शा सकते हैं। संख्या रेखा की सहायता से हम दो पूर्ण संख्याओं को आसानी से जोड़ या घटा सकते हैं।

OMR (One Minute Revision)

हम एक रेखा लेते हैं। इस पर एक बिंदु अंकित करते हैं जिसे 0 से नामांकित करते हैं। फिर हम 0 के दाईं ओर समान अंतराल (दूरी) पर बिंदु अंकित करते जाते हैं। इन्हें क्रमशः 1, 2, 3,... से नामांकित करते हैं। इस प्रकार हमें एक संख्या रेखा प्राप्त होती है जिस पर पूर्ण संख्याओं को दर्शाया जाता है।
हम इस संख्या रेखा पर आसानी से संख्याओं का जोड़, व्यवकलन, गुणा और भाग जैसी सक्रियाएँ कर सकते हैं।

संख्या रेखा पर दाई ओर चलने पर संगत योग प्राप्त होता है जबकि बाई ओर चलने पर संगत व्यवकलन प्राप्त होता है।
शून्य (0) से प्रारंभ करके समान दूरी के कदम से गुणा प्राप्त होता है।

उदाहरण 3

संख्या रेखा का प्रयोग करके, $4 + 5, 2 + 6, 3 + 5$ और $1 + 6$ को ज्ञात कीजिये।

Learn more

पूर्ण संख्याओं के गुणधर्म

1. संवृत (Closed)

यदि दो पूर्ण संख्याओं की संक्रिया [ योग, व्यवकलन , गुणा या भाग ] से हमें पूर्ण संख्या ही प्राप्त हो तो पूर्ण संख्या उस संक्रिया के अंतर्गत संवृत होगा।

संक्रिया	संवृत गुण की जांच	टिप्पणी
योग $(+)$ (addition)	दो पूर्ण संख्या $1$ एवं $5$ को जोड़ते हैं - $1 + 5$ $= 6$ एक पूर्ण संख्या है	संवृत है
व्यवकलन $(-)$ (subtraction)	दो पूर्ण संख्या $1$ एवं $3$ को घटाते हैं - $1 - 3$ $= - 2$ यह एक पूर्ण संख्या नहीं है	संवृत नहीं है
गुणा $(\times)$ (multiplication)	दो पूर्ण संख्या $6$ एवं $4$ का गुणा करते हैं - $6 \times 4 = 24$ $24$ एक पूर्ण संख्या है	संवृत है
भाग $(\div)$ (division)	पूर्ण संख्या $5$ को पूर्ण संख्या $3$ से भाग देते हैं - $(5) \div (3)$ $\frac{5}{3}$ एक पूर्ण संख्या नहीं है Ex.=b यदि यहाँ भाजक $3$ की जगह अन्य पूर्ण संख्या $0$ लेते हैं तो यह भाग अपरिभाषित होगा क्यूंकि हर में शून्य होने पर संख्या अपरिभाषित होती है अथवा हमें पूर्ण संख्या प्राप्त नहीं होगी। अतः सभी पूर्ण संख्याओं के लिए भाग करने पर पूर्ण संख्या प्राप्त नहीं होगी।	संवृत नहीं है

2. क्रम विनिमेयता (commutative)

यदि दो पूर्ण संख्याओं के मध्य संक्रिया करने पर प्राप्त परिणाम संख्याओं के क्रम पर निर्भर नहीं करता है (क्रम बदलने पर भी परिणाम नहीं बदलता) तब वह संक्रिया पूर्ण संख्या पर क्रम विनिमेय होगी।

संक्रिया	क्रम विनिमेयता की जांच	टिप्पणी
योग $(+)$ (addition)	दो पूर्ण संख्या $1$ एवं $5$ के लिए $1 + 5 = 6$ क्रम बदलने पर - $5 + 1 = 6$ दोनों स्थितियों में परिणाम समान है	क्रम विनिमेय है
व्यवकलन $(-)$ (subtraction)	दो पूर्ण संख्या $1$ एवं $4$ को घटाते हैं - $1 - 4 = - 3$ क्रम बदलने पर - $4 - 1 = + 3$ दोनों स्थितियों में परिणाम समान नहीं है	क्रम विनिमेय नहीं है
गुणा $(\times)$ (multiplication)	दो पूर्ण संख्या $4$ एवं $8$ का गुणा करते हैं - $4 \times 8 = 32$ क्रम बदलने पर - $8 \times 4 = 32$ दोनों स्थितियों में परिणाम समान है	क्रम विनिमेय है
भाग $(\div)$ (division)	पूर्ण संख्या $5$ को पूर्ण संख्या $3$ से भाग देते हैं - $(5) \div (3)$ = $\frac{5}{3}$ क्रम बदलने पर - $(3) \div (5)$ = $\frac{3}{5}$ दोनों स्थितियों में परिणाम समान नहीं है	क्रम विनिमेय नहीं है

3. साहचर्यता (Associative)

यदि

⋆

एक संक्रिया (योग, व्यवकलन, गुणा अथवा भाग ) हो तब साहचर्यता से -

a ⋆ (b ⋆ c) = (a ⋆ b) ⋆ c

संक्रिया	साहचर्यता की जांच	टिप्पणी
योग $(+)$ (addition)	तीन पूर्ण संख्या $1$ , $3$ एवं $5$ के लिए $1 + (3 + 5)$ $= 1 + 8$ $= 9$ अब - $(1 + 3) + 5$ $= 4 + 5$ $= 9$ दोनों स्थितियों में परिणाम समान है	साहचर्य है
व्यवकलन $(-)$ (subtraction)	तीन पूर्ण संख्या $4$ , $2$ एवं $3$ के लिए - $4 - (2 - 3)$ $= 4 - (- 1)$ $= 4 + 1$ $= 5$ अब - $(4 - 2) - 3$ $= 2 - 3 = - 1$ दोनों स्थितियों में परिणाम समान नहीं है	साहचर्य नहीं है
गुणा $(\times)$ (multiplication)	तीन पूर्ण संख्या $6,$ $2$ एवं $3$ का गुणा करते हैं - $6 \times (2 \times 3)$ $= 6 \times 6 = 36$ अब - $(6 \times 2) \times 3$ $= 12 \times 3 = 36$ दोनों स्थितियों में परिणाम समान है	साहचर्य है
भाग $(\div)$ (division)	तीन पूर्ण संख्या $6,$ $2$ एवं $3$ का भाग देते हैं - $6 \div (\frac{2}{3})$ $6 \times \frac{3}{2} = 9$ अब - $(\frac{6}{2}) \div 3$ $3 \div 3 = 1$ दोनों स्थितियों में परिणाम समान नहीं है	साहचर्य नहीं है

OMR (One Minute Revision)

दो पूर्ण संख्याओं का योग हमेशा एक पूर्ण संख्या ही होता है।

दो पूर्ण संख्याओं का गुणनफल हमेशा एक पूर्ण संख्या होता है।

इस प्रकार पूर्ण संख्याएँ योग, गुणनफल के अंतर्गत संवृत (Closed) हैं।
जबकि, पूर्ण संख्याएँ व्यवकलन (घटाना) और भाग (विभाजन) के अंतर्गत संवृत नहीं हैं।

दो पूर्ण संख्याओं को किसी भी क्रम में जोड़ सकते हैं। तथा दो पूर्ण संख्याओं को किसी भी क्रम में गुणा (गुणन) कर सकते हैं।अर्थात पूर्ण संख्याओं के लिए योग और गुणन क्रमविनिमेय (commutative) हैं।

पूर्ण संख्याओं के लिए योग और गुणन साहचर्य (Associative) हैं।

पूर्ण संख्याओं के क्रमविनिमेय और साहचर्य गुण, परिकलन को आसान बनाने में उपयोगी हैं

उदाहरण 4

उपयुक्त क्रम में लगाकर योग ज्ञात कीजिये:
(a) $837 + 208 + 363$
(b) $1962 + 453 + 1538 + 647$

(a) $837 + 208 + 363$
$= (837 + 208) + 363$
[साहचर्यता के प्रयोग से]

$= 1045 + 363$
$= 1408$

(b) $1962 + 453 + 1538 + 647$
$= (1962 + 453)$ $+ (1538 + 647)$
[साहचर्यता के प्रयोग से]

$= 2415 + 2185$
$= 4600$

Learn more

उदाहरण 5

उपयुक्त क्रम में लगाकर गुणनफल ज्ञात कीजिये:
(a) $2 \times 1768 \times 50$
(b) $4 \times 166 \times 25$
(c ) $8 \times 291 \times 125$

(a) $2 \times 1768 \times 50$
$= (2 \times 50) \times 1768$
[साहचर्यता के प्रयोग से]

$= 100 \times 1768$
$= 176800$

(b) $4 \times 166 \times 25$
$= (4 \times 25)$ $\times 166$
[साहचर्यता के प्रयोग से]

$= 100 \times 166$
$= 16600$

(c ) $8 \times 291 \times 125$
$= (8 \times 125)$ $\times 291$
[साहचर्यता के प्रयोग से ]

$= 1000 \times 291$
$= 291000$

Learn more

पूर्ण संख्याओं के तत्समक अवयव

1.योज्य तत्समक (additive identity)

पूर्ण संख्याओं के योग के लिए शून्य योज्य तत्समक हैं अतः जब पूर्ण संख्याओं मे शून्य जोड़ा जाता हैं, तो योग फिर से वही पूर्ण संख्या देता हैं |

जैसे

2 + 0 = 2

माना कि a पूर्ण संख्या हैं -

अतः a + 0 = a

2. गुणात्मक तत्समक (multiplicative identity)

पूर्ण संख्याओं के गुणन के लिए 1 गुणात्मक तत्समक हैं अतः जब पूर्ण संख्याओं मे 1 का गुणा किया जाता हैं | तो गुणन फिर से वही पूर्ण संख्या देता हैं |

जैसे

2 \times 1 = 2

माना कि a पूर्ण संख्या हैं -

अतः $a \times 1 = a$

वितरण (distributive)

वितरण गुण (distributive property) एक ब्रैकेट के भीतर किसी अन्य गणितीय ऑपरेशन पर संचालन की वितरण क्षमता की व्याख्या करता है। यह या तो जोड़ पर गुणन का वितरण गुण हो सकता है या घटाव पर गुणन का वितरण गुण हो सकता है। यहां, पूर्ण संख्या को पहले जोड़ा या घटाया जाता है और फिर कोष्ठक के भीतर प्रत्येक संख्या के साथ गुणा किया जाता है और फिर जोड़ा या घटाया जाता है। इसे किसी भी पूर्ण संख्या a , b और c के लिए इस प्रकार दर्शाया जा सकता है,

अतः
$a \times (b + c) = a \times b + a \times c$
एवं
$a \times (b - c) = a \times b - a \times c$

उदाहरण

504 \times 25

= (500 + 4) \times 25

= 500 \times 25

+ 4 \times 25

= 12500 + 100

= 12600

OMR (One Minute Revision)

शून्य को पूर्ण संख्याओं के योग के लिए तत्समक अवयव (identity element) या (तत्समक) कहते हैं।

पूर्ण संख्या 1 को पूर्ण संख्याओं के गुणन के लिए तत्समक कहते हैं।

पूर्ण संख्याओं के लिए योग पर गुणन का वितरण (या बंटन) होता है।

उदाहरण 6

सरल कीजिये:
$126 \times 55 + 126 \times 45$

$126 \times 55$ $+ 126 \times 45$
$= 126 \times (55 + 45)$
[वितरण गुणधर्म से]

$= 126 \times 100$
$= 12600$

Learn more

उदाहरण 7

वितरण गुण का प्रयोग करते हुए, $15 \times 68, 17 \times 23$ और $69 \times 78 + 22 \times 69$ के मान ज्ञात कीजिये।

(i) $15 \times 68$
$= 15 \times (70 - 2)$
$= 15 \times 70$ $- 15 \times 2$
$= 1050 - 30$
$= 1020$

(ii) $17 \times 23$
$= 17 \times (20 + 3)$
$= 17 \times 20$ $+ 17 \times 3$
$= 340 + 51$
$= 391$

(iii) $69 \times 78 + 22 \times 69$
$= 69 \times (78 + 22)$
$= 69 \times 100$
$= 6900$

Learn more

उदाहरण 8

मिलान करें|

(i) $2 + 8 = 8 + 2$
दो पूर्ण संख्याओं को किसी भी क्रम में जोड़ सकते हैं अर्थात जोड़ की क्रमविनिमयता (commutative of addition)

(ii) $8 \times 90 = 90 \times 8$
दो पूर्ण संख्याओं को किसी भी क्रम में गुणा (गुणन) कर सकते हैं, अर्थात गुणन की क्रमविनिमयता (commutative of multiplication)

(iii) $885 \times 145$ $= 885 \times (100 + 40 + 5)$
पूर्ण संख्याओं के लिए योग पर गुणन का वितरण (या बंटन)

(iv) $5 \times (4 \times 28)$ $= (5 \times 4) \times 28$
पूर्ण संख्याओं के लिए गुणन साहचर्य (Associative) हैं। अर्थात गुणन का साहचर्य नियम

Learn more

उदाहरण 9

किसी टैक्सी-ड्राइवर ने अपने गाड़ी की पेट्रोल टंकी में सोमवार को 40 लीटर पेट्रोल भरवाया। अगले दिन, उसने टंकी में 50 लीटर पेट्रोल भरवाया। यदि पेट्रोल का मूल्य रु 44 प्रति लीटर था, तो उसने पेट्रोल पर कुल कितना व्यय किया?

कुल भरवाया गया पेट्रोल (petrol)
$= 40 + 50 = 90$ लीटर
1 लीटर पेट्रोल की कीमत $= 44$ रुपये

पेट्रोल पर कुल व्यय $= 90 \times 44$ $= 3960$ रुपये

Learn more

पूर्ण संख्याओं में प्रतिरूप

चुकि हम संख्याओं को बिंदुओं द्वारा दर्शा सकते हैं तथा उन बिंदुओं के द्वारा हम संख्याओं को एक रेखा, एक आयत, एक वर्ग, एक त्रिभुज के रूप में व्यवस्थित करेंगे।

प्रत्येक संख्या को एक रेखा के रूप में व्यवस्थित किया जा सकता है;
संख्या 2 को इस प्रकार दिखाया जा सकता है

संख्या 3 को इस प्रकार दिखाया जा सकता है

...

कुछ संख्याओं को आयतों के रूप में दर्शाया जा सकता है।
उदाहरणार्थ, संख्या 6 को आयत के रूप में दर्शाया जा सकता है। ध्यान दीजिए कि यहाँ 2 पंक्तियाँ और 3 स्तंभ हैं।

...
...

कुछ संख्याओं जैसे 4 और 9 को वर्गों के रूप में भी दर्शाया जा सकता है उदाहरणार्थ,

..
..

...
...
...

कुछ संख्याओं जैसे

3, 6 ...

को त्रिभुजों के रूप में भी दर्शाया जा सकता है। उदाहरणार्थ,

ocr_image

प्रतिरूपो के गुण

ये प्रतिरूप हमे संख्याओं को जोड़ने, घटाने , गुणा करने तथा भाग करने के लिए आसान और मौखिक विधियाँ प्रदान करते हैं
जैसे-(a)

117 + 9

= 117 + 10 - 1

= 127 - 1

= 126

(b)

117 - 9

= 117 - 10 + 1

= 107 + 1

= 108

(c)

117 + 99

= 117 + 100 - 1

= 217 - 1

= 216

(d)

117 - 99

= 117 - 100 + 1

= 17 + 1

= 18

Ex (2)
(a)

96 \times 5 = 96 \times \frac{10}{2}

= \frac{960}{2} = 480

(b)

96 \times 25 = 96 \times \frac{100}{4}

= \frac{9600}{4} = 2400

(c)

96 \times 125 = 96 \times \frac{1000}{8}

= \frac{96000}{8} = 12000

Ex (3)
(a)

64 \times 5 = 64 \times \frac{10}{2}

= 32 \times 10 = 320 \times 1

(b)

64 \times 15 = 64 \times \frac{30}{2}

= 32 \times 30 = 320 \times 3

(c) 64 \times 25 = 64 \times \frac{50}{2}

= 32 \times 50 = 320 \times 5

(d)

64 \times 35 = 64 \times \frac{70}{2}

= 32 \times 70 = 320 \times 7

उदाहरण 10

कौन-सी संख्याएं आयतों के रूप में दर्शाइए जा सकती हैं?

अभाज्य संख्याओं को छोड़कर सभी संख्याएँ आयत के रूप में दर्शायी जा सकती हैं
अभाज्य संख्याएँ $= 2, 3, 5, 7, 11, 13, 17, 19, 21, 23, 29 ... ... . .$
उपर्युक्त संख्याओं के अलावा सभी संख्याओं को आयत के रूप में दर्शाया जा सकता हैं
अर्थात आयत के रूप में दर्शायी जा सकने वाली संख्याएं $= 4, 6, 8, 10, 12, 14, 15 ... . .$

Learn more

सारांश

संख्याएँ 1, 2, 3,... जिनका प्रयोग हम गिनने के लिए करते हैं, प्राकृत संख्याएँ कहलाती हैं।

यदि किसी प्राकृत संख्या में 1 जोड़ते हैं तो हमे इसका परवर्ती मिलता है। यदि किसी प्राकृत संख्या में से 1 घटाते हैं, तो इसका पूर्ववर्ती प्राप्त होता है।

1 को छोड़कर प्रत्येक प्राकृत संख्या का एक पूर्ववर्ती होता है।

यदि प्राकृत संख्याओं के संग्रह में हम संख्या 0 जोड़ते हैं, तो हमें पूर्ण संख्याओं का संग्रह प्राप्त होता है।
इस प्रकार संख्याएँ 0, 1, 2, 3, पूर्ण संख्याओं का संग्रह बनाती हैं।

0 को छोड़कर प्रत्येक पूर्ण संख्या का एक पूर्ववर्ती होता है।

सभी प्राकृत संख्याएँ, पूर्ण संख्याएँ भी हैं। लेकिन सभी पूर्ण संख्याएँ प्राकृत संख्याएँ नहीं हैं।

हम एक रेखा लेते हैं। इस पर एक बिंदु अंकित करते हैं जिसे 0 से नामांकित करते हैं। फिर हम 0 के दाईं ओर समान अंतराल (दूरी) पर बिंदु अंकित करते जाते हैं। इन्हें क्रमशः 1, 2, 3,... से नामांकित करते हैं। इस प्रकार हमें एक संख्या रेखा प्राप्त होती है जिस पर पूर्ण संख्याओं को दर्शाया जाता है।
हम इस संख्या रेखा पर आसानी से संख्याओं का जोड़, व्यवकलन, गुणा और भाग जैसी सक्रियाएँ कर सकते हैं।

संख्या रेखा पर दाई ओर चलने पर संगत योग प्राप्त होता है जबकि बाई ओर चलने पर संगत व्यवकलन प्राप्त होता है।
शून्य (0) से प्रारंभ करके समान दूरी के कदम से गुणा प्राप्त होता है।

दो पूर्ण संख्याओं का योग हमेशा एक पूर्ण संख्या ही होता है।

दो पूर्ण संख्याओं का गुणनफल हमेशा एक पूर्ण संख्या होता है।

इस प्रकार पूर्ण संख्याएँ योग, गुणनफल के अंतर्गत संवृत (Closed) हैं।
जबकि, पूर्ण संख्याएँ व्यवकलन (घटाना) और भाग (विभाजन) के अंतर्गत संवृत नहीं हैं।

दो पूर्ण संख्याओं को किसी भी क्रम में जोड़ सकते हैं। तथा दो पूर्ण संख्याओं को किसी भी क्रम में गुणा (गुणन) कर सकते हैं।अर्थात पूर्ण संख्याओं के लिए योग और गुणन क्रमविनिमेय (commutative) हैं।

पूर्ण संख्याओं के लिए योग और गुणन साहचर्य (Associative) हैं।

पूर्ण संख्याओं के क्रमविनिमेय और साहचर्य गुण, परिकलन को आसान बनाने में उपयोगी हैं

शून्य को पूर्ण संख्याओं के योग के लिए तत्समक अवयव (identity element) या (तत्समक) कहते हैं।

पूर्ण संख्या 1 को पूर्ण संख्याओं के गुणन के लिए तत्समक कहते हैं।

पूर्ण संख्याओं के लिए योग पर गुणन का वितरण (या बंटन) होता है।

Home
Ask Doubt
Profile