KNOWING OUR NUMBERS for Class 6 MATHS

Hello baccho, hum sab jaante hai ki numbers, mathematics ka ek bohot badha aur bohot important part hai. Chaahe simple addition ho, ya fir kisi shape ki measurement, we all use numbers to express them. Ab hum numbers k baare m thora aur detail m pdhenge ki hum numbers ko kaise compare krte hai, place value kya hota hai, ascending-descending, importance of commas while writing numbers, etc. ye saare topics hum iss chapter m cover krenge. So let’s start!

Toh bacho sabse pehle hum suruaat karnge numbers ke comparision se , comparision of numbers se matlab hai ye pehchanna ke konsa number bada hai konsa equal hai ya chota hai , iss type ke sabhi problems ko hum yaha deal karne wale hai. In math, to compare means to examine the differences between numbers, quantities or values to decide if it is greater than, smaller than or equal to another quantity. Here, for instance, we are comparing numbers.

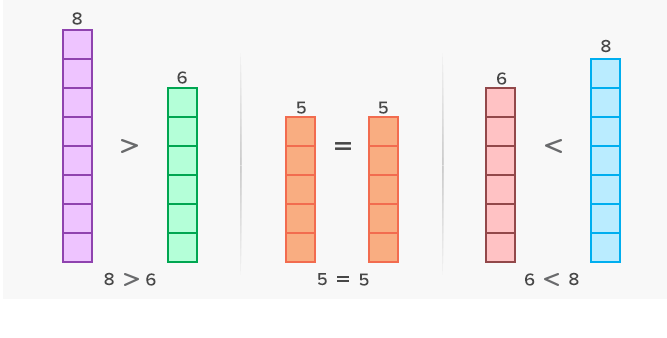
To baccho, numbers ko compare krne k lie basically do tareeke hote hai. Pehla hota h ki hum number of digits se compare kre , yaani ki agar ek number m 3 digits hai aur dusre number m 2 digits hai , to we can directly conclude ki 3 digits vala number 2 digits wale number se badha hai. For example , agar mai aapse puchu ki 2000 aur 30 m se konsa number badha hai to aap within seconds , sirf digits dekh k mujhe ye bta skte hai ki 2000 badha hai.
Second method hota hai jisme place value involved hoti hai. Agar dono numbers equal digits k hai to hum leftmost digit ko dekh kr identify kr skte hai ki bdha number konsa hai. For example, If i give you these two numbers : 3269 and 7392 , what you think which is the greater number?
It’s very easy, aap simply leftmost numbers ko compare krke answer kr skte hai. Since, 7 is greater than 3, therefore 7392 is greater than 3269.
Note: When the two numbers have the same number of digits, we start comparing the digits from the left most place until we come across unequal digits.
For example: Compare 29,384 and 20,364
Both numbers are 5-digit number. Let us compare the digits in left most place, we find that both numbers have same digit. Next, we compare the digits in the second most left place, we find that $9>0$.
So, $29,384>20,364$

To baccho ab hum seekhenge ki if we are given a bunch of numbers, to hum unse alag alag numbers kaise bna skte hai.
For example, aap sabko 1,3,5,7 ko use krke ek aisa four digit ka number bnana h jisme no number repeats itself. So, you can make numbers like 7531, 5731, 1375, etc. But you cannot make numbers like 5513 or 3375, because inme 5 aur 7 repeat horha hai.
Now, If I ask you to make the largest possible four digit number using those same numbers ( 1,3,5,7 ) to ye kaise krenge? It’s very simple!
largest number bnane k lie aapko simply highest to lowest numbers arrange krne hai, like : 7531, and that would be our answer!
Similarly, agar hume smallest number banana ho, to hum lowest to highest numbers arrange krenge, like : 1357
Aise questions mai baccho aapko arrangement of numbers par specially focus krna hai and you can make any type of number using existing numbers.

Find the difference between the greatest and the least number that can be written using the digits 6, 2, 7, 4, 3 each only once.

So baccho humare pas kuch numbers given hain i.e. $6,2,7,4\text{and}3$.
And hume ye pta hai ki agar hume greatest number chaiye to numbers ko descending order me likha hota hai.
So, Greatest Number $=76432$
Similarly students hum ye bhi jante hai ki agar hume smallest number chaiye to numbers ko ascending order me likhna hoga i.e.
Smallest Number $=23467$
So, the difference is $76432-23467=52965$

Ascending order means arranging numbers (or other items) smallest to highest.

Yaani sabse chote number se start krke sabe bdhe number tk arrange krna.
For example, Arrange the following numbers in ascending order 2, 9, 7 , 3 ,6 , 4
so, it will be arranged like this : 2, 3, 4, 6, 7, 9
Note: Aise questions m baccho, there is a possibility ki aap galti se kisi number ko miss kr jaaye. So, in order to avoid that, always count the number of digits in the question and in your answer. Jaise ki, question mai 6 numbers h total and humare answer m bhi 6 numbers hai, so we can be sure ki we did not miss any number.

Descending order means arranging numbers (or other items) highest to smallest .

For example, Arrange the following numbers in descending order 2, 9, 7 , 3 ,6 , 4
so, it will be arranged like this : 9, 7, 6, 4, 3, 2

To baccho, shifting digits bhi re-arranging numbers se related hi hai. It’s a very interesting concept. Sirf kuch numbers ko shift krne se uss number ki puri value badal jaati hai. Imagine ki aapko lucky draw m ek coupon mila jispe value likhi hai Rs. 1000 . Aap bohot khush honge, but now imagine ki agar usme first digit aur last digit exchange hojaye to!
The resultant number would be Rs. 0001 :( which is way less than the initial amount.
A small number like 358 can become as large as 853 by simply shifting the first and last numbers.

Toh bacho humne dekha digits ki place value change karne se numbers me ek huge difference aa jaata hai. So let's move to some larger numbers now .

We have learnt in our previous classes, that the largest two digit number is 99, the largest 3 digit number is 999 and similarly the largest 4 digit number is 9999 .
Ab hum ek bohot hi interesting cheez notice krenge. We will add “1” to all these three numbers and will observe the resultant figure.

We also know that, 100 is the smallest 3 digit number, 1000 is the smallest 4 digit number and 10000 is the smallest 5 digit number. Iss pattern ko observe krke hum ye conclude kr skte hai ki when we add 1 to the largest 2 digit number, it becomes the smallest 3 digit number. Similarly, when we add 1 to the largest 3 digit number, it becomes the smallest 4 digit number and when we add 1 to the largest 4 digit number, it becomes the smallest 5 digit number.
We can convert every large numbers in terms of smaller numbers: Remember, 1 hundred = 10 tens
1 thousand = 10 hundreds = 100 tens
1 lakh = 100 thousands = 10000 tens
1 crore = 100 lakhs = 1000000 tens

To baccho, abhi tk jo humne pdha usse humne ye seekh lia hai ki har digit ki ek value hoti h jiske shift hone se pure number ki value badal jaati hai. Each digit of a number has a certain value which is known as its place value. Har digit ki value uske next number k 10 times jitni hoti hai.
For example, consider the number 435.
In this number, the rightmost digit has the place value of ones. Which means, 5 is at the ones place.
3 ki place value will be 10 times the value of 5 ( 10 X (place value of 5) )
Since place value of 5 is ones, therefore, place value of 3 will be 10 X 1 = 10 Which implies, 3 is at the tens place.Using the same concept, we get to know that 4 is at the hundreds place.

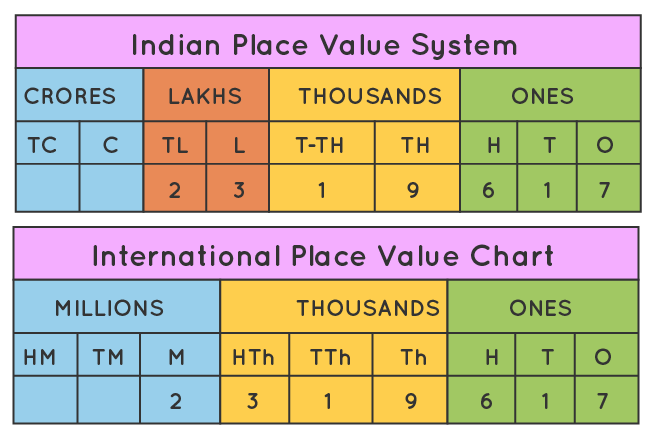
Toh bacho upar di hui images me 2 alag alg type ki place value system ka use hua hai , one is Indian Place value system and other one is International place value system.Let's discuss them in detail
Indian Place value system: The Indian place value chart is a table that is used to find the value of each digit in a number based on its position, as per the Indian numeral system. Every digit in a number has its own value depending on its position in the place value chart. The place value of a number shows how much a digit is worth based on its position. In order to avoid confusion while reading very large numbers, we arrange the numbers into periods with the help of a comma as the separator.
Observe the following Indian place value chart. We use this to read and write numbers accurately according to their place values.

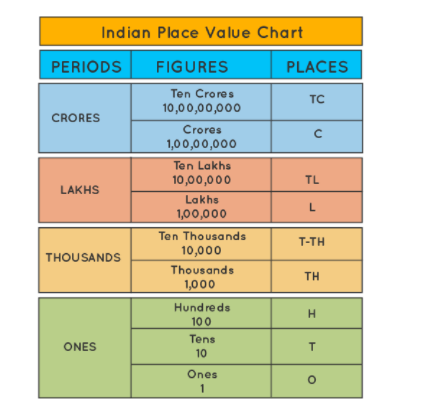
Steps to read or write numbers in Indian place value system:

Insert commas suitably and write the names according to International System of Numeration :
(a) 78921092 (b) 7452283 (c) 99985102 (d) 48049831

To bacchon jaisa ki aapne upar dekha ki in international system hum 3 numbers ki grouping karte hai and ye hum right to left karte hai. After grouping hume kya karna hai ye hum upar likhe steps ko follow krte huye dekh sakte hai.
(a) 78,921,092
Seventy eight million nine hundred twenty one thousand ninety two.
(b) 7,452,283
Seven million four hundred fifty two thousand two hundred eighty three.
(c) 99,985,102
Ninety nine million nine hundred eighty five one hundred two.
(d) 48,049,831
Forty eight million forty nine thousand eight hundred thirty one

Insert commas suitably and write the names according to Indian System of Numeration :
(a) 87595762 (b) 8546283 (c) 99900046 (d) 98432701

To bacchon yha jab baat Indian system ki aati hai to hum international number system ke jaise hi numbers ki grouping karte hai lakin right to left jate huye sabse pehle grouping hum 3 numbers ki karte hai then 2 numbers ki grouping hoti hai
(a) $8,75,95,762$
Eight crore seventy five lakh ninety five thousand seven hundred sixty two
(b) $85,46,283$
Eighty five lakh forty six thousand two hundred eighty three
(c) $9,99,00,046$
Nine crore ninety nine lakh forty six
(d) $9,84,32,701$
Nine crore eighty four lakh thirty two thousand seven hundred one

Bacho ab hum large numbers ko kuch real life problems ke through discuss karnge , but for that we need to understand about measurement . Aapne apni daily life m kahi na kahi units of measurements ko use hote hue suna hoga. Jaise aapki mummy aapse bolti hongi ki dukaan se 100 gram(g) paneer le aao. Ya aapne apne papa se suna hoga ki unka office ghr se 10 kilometer (km) door hai. Ya aapne kabhi bahar se 1 litre(l) wali pepsi ki bottle khareedi hogi. To baccho, ye units of measurement hume day to day life m bohot help krte hai alag alag cheezo ko measure krne k lie.
Dhyaan de ki in sabhi measurements m hum milli, centi aur kilo ka use krte hai , jaise ki 10 millimeter, 10 centimeter, 10 kilometer.
kilo shows 1000 times greater, milli shows 1000 times smaller.
1 kilogram = 1000 grams, 1 gram = 1000 milligrams.
Similarly, centi shows 100 times smaller, 1 metre = 100 centimetres.

A vessel has 4 litres and 500 ml of curd. In how many glasses, each of 25 ml capacity, can it be filled?

So bacchon hum ye jante hai ki there are $1000ml$ in one liter.
$\therefore 4$liter $=4\times 1000ml$
$\therefore$ Total curd in vessel $=4liter\text{and}500ml=4000+500ml=4500ml$
Capacity of a glass $=25ml$
$\therefore$ Number of glasses that can be filled with curd = Total curd in vessel/ Capacity of a glass= $\frac{4500}{25}=180$ glasses

Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10,000 runs. How many more runs does he need?

Runs scored by Shekhar so far = 6980
Total runs need to be completed = 10000
So more runs required = Total runs need to be completed - Runs scored by Shekhar so far = 10000- 6980 = 3020

Toh bacho we do estimation to find a value that is close enough to the right answer, usually with some thought or calculation involved. Example: One student Alex estimated there were 10,000 sunflowers in the field , now you might be wondering how he did that ?

So basically he did by counting one row then multiplying by the number of rows. Now we will understand the process of estimation with more examples.

In order to estimate to nearest tens, we follow the following procedure:
Step 1:Obtain the number.
Step 2: Examine the digit at ones place.
Step 3: If the digit at ones place is less than 5, then replace the ones digit by 0 and keep the other digits as they are. If the digit at ones place is 5 or greater than 5, then increase tens digit by 1 and replace the ones digit by 0. The number so obtained is the number obtained by rounding off the given number to the nearest tens.

Round off the following to nearest tens:
(a) 75 (b) 1574

(i) Toh bacho here ones digit is 5 so we will add 1 to tens place digit (7) and replace ones digit by 0
So, 75 will be rounded as 80 agar hum tens ko roundoff karne ki baat karte hai.
(ii) Similarly 1547 ko tens ke respect me roundoff karna ho to our answer will be 1550.

In order to estimate to nearest thousands we follow the following procedure:
Step 1:Obtain the number.
Step 2:Examine the digit at hundreds place.
Step 3:If the digit at hundreds place is less than 5, replace each one of the digits at hundreds, tens and ones or units place by 0 and keep all other digits as they are. If the digit at hundreds place is 5 or greater than 5, increase the digit at thousands place by 1 and replace each one of the digits at hundreds, tens and ones place by 0.The number so obtained is the number rounded off to the nearest thousands.

Round off 85642 to nearest thousands?

So bacchon yaha hundred place digit 6 hai jo ki 5 se jayda hai so we will replace hundreds , tens and ones place digit by 0 and and add 1 to thousands place ( 5 + 1 = 6) .
So if we roundoff to nearest thousand, the number $85642$ is $86000$.

Toh bacho for estimating a sum or a difference first we need to round the numbers, by changing them to the nearest power of ten, hundred, thousand etc. and then we add or subtract them according to given problem. Let's understand it better by an example : Suppose you have to estimate the sum 58 + 22
To estimate this answer, first round both numbers to the nearest ten.
58 rounds up to 60. 22 rounds down to 20.
Then sum the rounded values: 60 + 20 = 80.
The estimated answer is 80.

Estimate: 5290+17986.

$5290$ rounded off to nearest $1000$ is $5000$
$17986$ rounded off to nearest $1000$ is $18000$
$\therefore$estimated sum = $18000+5000$
= $23000$ answer

Toh bacho just as we estimate the sum and difference of numbers , we can also estimate the products of numbers.The general rule that we can make is round off each factor to its greatest place, then multiply the rounded off factors.

Estimate the following products using general rule:
(a) 578 × 161 (b) 5281 × 3491 (c) 1291 × 592 (d) 9250 × 29

(a) We have to estimate $578\times 161$
Here we can roundoff $578\text{to}600\text{and}161\text{to}200$
$\therefore \text{estimated product}600\times 200=120000$
(b) We have to estimate $5281\times 3491$
Here we can roundoff $5281\text{to}5000\text{and}3491\text{to}3000$
So the estimated product $=5000\times 3000=15000000$
(c) We have to estimated $1291\times 592$
Here we can roundoff $1291\text{to}1000\text{and}592\text{to}600$
$\therefore \text{estimated product}1000\times 600=600000$
(d) We have to estimate $9250\times 29$
Here we can roundoff $9250\text{to}9000\text{and}29\text{to}30$
$\therefore \text{estimated product}=9000\times 30=270000$

Toh bacho , I will tell you a story of three students , Salman , Amir and John .

One day they decide to have a party , so Salman and Amir went to market to purchase some eatables . Salman purchased 6 Fruit pastries each of 10 Rs. and Amir purchased 7 truffle pastries again 10 for each. When they came back they showed their expenditure in the following manner.

You can see that Salman’s and Amir’s ways to get the answer are a bit different. But both give the correct result. How?
Salman says, what Amir has done is 7 + 6 × 10.
John points out that 7 + 6 × 10 = 7 + 60 = 67. Thus, this is not what Amir had done. All the three friends get confused now. But then Katrina came there and explain all this confusion arises because of not using brackets , and she explained brackets are very helpful in doing any operations like addition , multiplication , division etc. Use of brackets keeps us away from confusion and calculation error , now you must be curious about how exactly brackets work , so let's learn it together.
Note :First, turn everything inside the brackets ( ) into a single number and then do the operation outside

Solve the following using brackets :
(i) 7 × 109
(ii)102 × 103

To bacchon aise sawal bahut hi aasan trike se hum kar sakte hai jise sikhna bahut hi aasan hai aao dekhe or samjhe. Is type ke questions me hume koshis ye karni hai ki humara calculation aasan ho jaye.
(i) $7\times 109=7\times (100+9)$
$=7\times 100+7\times 9$
$=700+63$
$=763$
(ii) $102\times 103=102\times (100+3)$
$102\times 100+102\times 3$
$=10200+306$
$=10506$

Bacho ap sabhi ne watch dekhi hai .

Toh bacho isme likhe time ke symbols hamare hindu arabic numbers se kuch alag dikhte hai right , but kya unka meaning humare hindu arabic system se alag hai?
Toh answer hai nahi. Countings ko represent karne ke liye bahut saare alag alag symbols ka use kiya jata hai jinme se ek hai Roman Numeral System .Chaliye dekhte hai Roman numbers ko likhne ke kya rules hote hai. Toh bacho the symbols are I, V, X, L, C, D, and M, standing respectively for 1, 5, 10, 50, 100, 500, and 1,000 in the Hindu-Arabic numeral system.

Write in Roman Numerals:
(a) 69 (b) 98.

To bacchon humne numbers ko Roman Numerals me likhna sikh liya hai.
(a) $69=50+10+9=$ LXIX [L= fifty, X= ten, IX= nine]
(b) $98=90+8=$ XCVIII [XC = 90 and VIII = 8]

1.Given two numbers, one with more digits is the greater number. If the number of digits in two given numbers is the same, that number is larger, which has a greater leftmost digit. If this digit also happens to be the same, we look at the next digit and so on.
2. In forming numbers from given digits, we should be careful to see if the conditions under which the numbers are to be formed are satisfied. Thus, to form the greatest four digit number from 7, 8, 3, 5 without repeating a single digit, we need to use all four digits, the greatest number can have only 8 as the leftmost digit.
3. If we arrange the numbers from the smallest to the greatest then it is said to be an Ascending order.
4. If we arrange the numbers from the greatest to the smallest then it is said to be Descending order.
4. Use of commas helps in reading and writing large numbers. In the Indian system of numeration we have commas after 3 digits starting from the right and thereafter every 2 digits. The commas after 3, 5 and 7 digits separate thousand, lakh and crore respectively. In the International system of numeration commas are placed after every 3 digits starting from the right. The commas after 3 and 6 digits separate thousand and million respectively.
5.Remember kilo shows 1000 times larger, Centi shows 100 times smaller and milli shows 1000 times smaller, thus, 1 kilometre = 1000 metres, 1 metre = 100 centimetres or 1000 millimetres etc.
6.Estimation involves approximating a quantity to an accuracy required. Thus, 4117 may be approximated to 4100 or to 4000, i.e. to the nearest hundred or to the nearest thousand depending on our need.
7.Use of brackets allows us to avoid confusion in the problems where we need to carry out more than one number operation.
8. We use the Hindu-Arabic system of numerals. Another system of writing numerals is the Roman system.

Rules for comparing numbers:
Rule I: We know that a number with more digits is always greater than the number with less number of digits.
Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits.