MENSURATION for Class 6 MATHS
Explanation
Bachcho ab hum mensuration kai bare mai padhege jisme humare pass 2D or 3D figures hote hai 1st 2D hote h jisme square or rectangle or circle jaise figure aate hai jin figures ko hum plane surface par draw kar sakte hai unn ko hum 2Dfigure kehte hai or 2D figures mai hum area or perimeter calculate kar sakte hai.
Ab hum mensuration kai 2nd type figure kai bare mai padhege jis ko hum 3D figures bolte hai in figure mai cube, cuboid, cylinder etc. aate hai in figures mai 3 dimension hote hai length, breadth and height/depth in figures ko hum physically touch kr kte hai jaise book, cane, box etc. basically hum in figures mai area or perimeter calculate nahi krte 3D figures mai hum volume (V), total surface area(TSA), curve surface area(CSA) calculate krte hai
MENSURATION
Mensuration (mathematics), a branch of mathematics that deals with measurement of various parameters of geometric figures and many more.
Perimeter
Bachcho ab hum padhege perimeter kai bare mai jo ki basically 2D figures mai hota hai. Perimeter ka matlab hota hai ki sum of all side of figure. For example square, rectangle, circle, etc. Hum rectangle ka perimeter calculate karte hai rectangle mai 4 sides hote hai iss figure mai parallel/opposite side hote rectangle main parallel side equal hote hai or rectangle perimeter ka formula 2×(length + breadth) hota h jaise ki hum figure mai dekh sakte hai length 12cm or breadth 7cm show ho rhe hai ab hum in ko formula mai put krte hai 2×(12+7)=2×19<br≥38cm hoga.
Ab hum padhenge square kai bare mai square mai 4 side hote hai or sare side equal hote hai . Square kai perimeter ka formula (4×s) hota hai jaise ki hum figure mai dekh sakte hai ki square ki sare side 2cm ki hai. Ab hum square ka perimeter calculate krne kai liye formula apply karte hai (4×s=4×2cm<br≥8cm) iss tarah hum perimeter of square calculate karte hai
EXAMPLE 1
The lengths of two sides of an isosceles triangle are 2016 cm and 2017 cm, then the maximum possible perimeter of a triangle is
The two sides of an isosceles triangle are 2016 cm and 2017 cm
Since the given triangle is an isosceles triangle. So, that third side is either 2016 cm or 2017 cm.
The maximum possible perimeter of the triangle =2016+2017+2017=6050cm
EXAMPLE 2
The side of an equilateral triangle is 672 cm long, then the perimeter of the triangle is
The side of an equilateral triangle (a)=672cm
∴ Perimeter of the equilateral triangle =3a=3(672)=2016cm
Area
The amount of surface enclosed by a closed figure is called its area.
Area
" Area of a rectangle
Rectangle ki dono side ki length and breadth equal hoti hain aur agar hum rectangle ki ek length and ek breadth ko multiply karte hai to hume rectangle ka area pta chal jayega. Ab hum rectangle ka area calculate karenge jaise ki figure mai show ho rha hai.
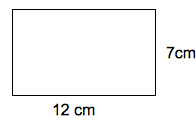
Rectangle ki length 12cm or breadth 7cm hai or area of rectangle ka formula (length × breath). Ab hum rectangle ka area calculate karenge (12cm×7cm=84cm2)
Area of a square
Square ke sari sides equal hote hain agar hum square ki ek side ko dusri side se multiply karte hai to hume square ka area mil jata hai. Ab hum area kai bare mai padhenge jaise humare pass 2 figure hote hai 1st square and 2nd rectangle jab hum in figures ko flat surface par draw karte hai jo area yai figure occupied/cover karte hai unn area ko calculate karne ko hum calculation of area kehte hain.
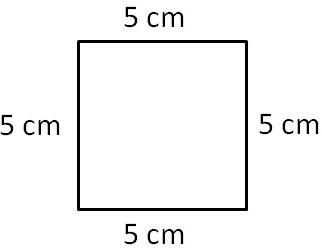
For example jaise ki hum figure mai dekh sakte hai ki humare pass ek square hai jis ki 4 side 5cm hai or square ka area nikalne ka formula (side × side). Ab hum area of square nikalege (5cm×5cm=25cm2) "
EXAMPLE 3
Four identical cubes of edge 5cm are placed side by side to form a cuboid of length 20cm. Find the total surface area and volume of the cuboid.
Edge of each cube 5cm
Since four identical cubes are placed side by side to form a cuboid.
Length of the cuboid =20cm
Breadth of the cuboid =5cm
Height of the cuboid = 5cm
Total surface area of the cuboid
2(20×5+5×5+5×20)
2(100+25+100)=2(225)=450sq.cm
Volume of the cuboid =20×5×5=500cm.
EXAMPLE 4
From a square sheet of side 8 cm , a piece of a paper width 2 cm is removed along the border. Then find the area of the removed piece of paper.
Side of an outer square sheet =8cm
Area of an outer square =82=64sq.cm
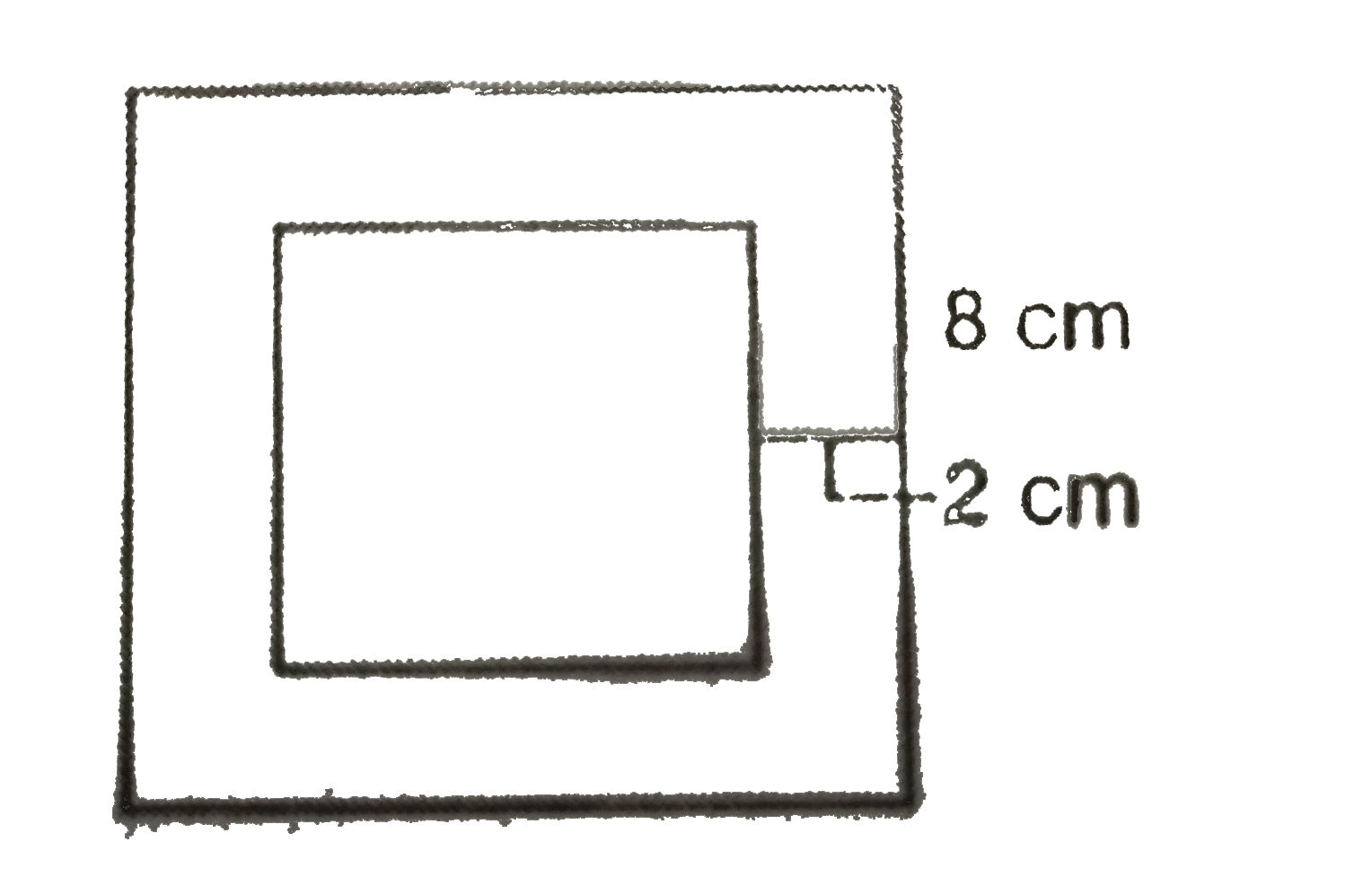
Width of a removed piece of paper =2cm
Side of the inner square =8−2(2)=8−4=4cm
Area of the inner square =42=16sq.cm
Area of the removed paper =Area of the outer square -Area of the inner square
64−16=48sq.cm
Summary
We have discussed so many things in this chapter:-
- Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.
- (a) Perimeter of a rectangle = 2 × (length + breadth)
(b) Perimeter of a square = 4× length of its side
(c) Perimeter of an equilateral triangle = 3 × length of a side - Figures in which all sides and angles are equal are called regular closed figures.
- The amount of surface enclosed by a closed figure is called its area.
- To calculate the area of a figure using a squared paper, the following conventions
are adopted :
(a) Ignore portions of the area that are less than half a square.
(b) If more than half a square is in a region. Count it as one square.
(c) If exactly half the square is counted, take its area as 12 sq units. - (a) Area of a rectangle = length × breadth
(b) Area of a square = side × side