UNDERSTANDING ELEMENTARY SHAPES for Class 6 MATHS
Introduction
Baccho jab hum apne surroundings ko notice krte hai to hum ye dekhte hai ki humare aas paas bohot saari alag alag shapes hoti hai. Sirf shapes hi nahi balki humare aas paas aur bhi bohot saare alag alag elements hote hai jaise ki lines, curves, edges, planes and corners. Hum ye bhi dekhte hai ki ye saare elements alag alag size aur measures k hote hai. Baccho iss chapter m hum inn sab elements k baare m detail m pdhenge. Saath hi saath hum ye bhi seekhenge ki inn sabhi elements ko measure aur compare krne k lie hum kon konse mathematical tools use kr skte hai. Chapter start krne se phle chlo baccho, I have a fun exercise for you all.
Look at the following composition and locate

Measuring Line Segments
Baccho jaisa ki humne apni previous classes m pdha hai, line segment basically ek line ka fixed part hota hai jisko hum definite values m measure kr skte hai. Hum do line segments ko unki length k basis p compare kr skte hai. We will learn three different ways jisse ki hum line segments ko compare kr skte hai
NULL
1. Comparison by Observation
We can tell which line segment is greater than other just by observing the two line segments. For example, we can clearly see that ¯¯¯¯¯¯AB is longer than ¯¯¯¯¯¯CD
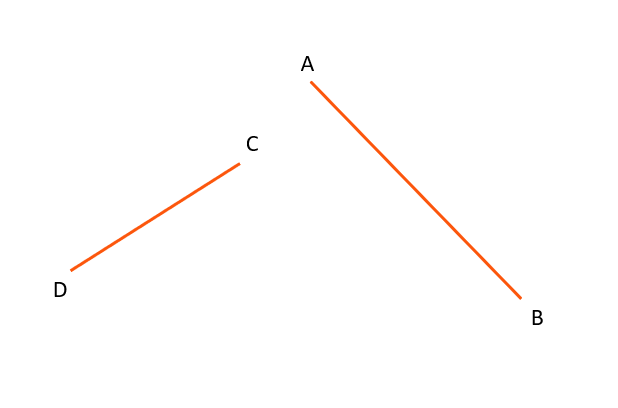
But we can not be sure. If there is only a small difference between the lengths of the two line segments it becomes difficult to observe. For example, look at the following lines segments ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD.
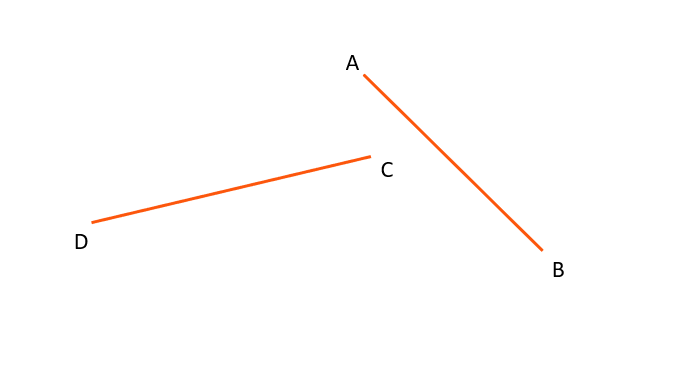
2.Comparison by Tracing
In this method we have to trace one line on a tracing paper then put the traced line segment on the other line to check which one is greater.
But this is a difficult method because every time to measure the different size of line segments we have to make a separate line segment.
3. Comparison using Ruler and a Divider
We can use a ruler to measure the length of a line segment. A regular ruler is divided into 15 parts. Each of these 15 parts is of
length 1 cm. Each centimeter is divided into 10 subparts.
Each subpart of the division of a cm is 1mm.
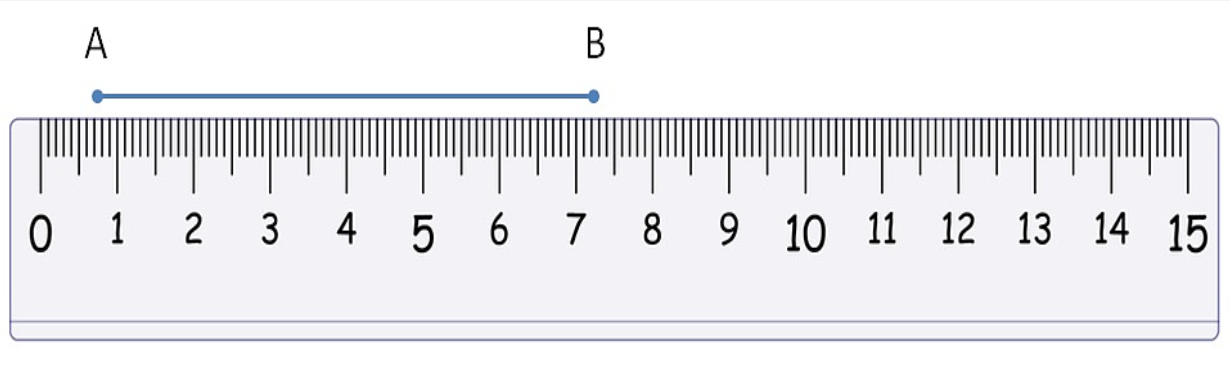
Put the zero mark at point A and then read the mark at point B to measure the length of the line segment, but it may have some errors on the basis of the thickness of the ruler.
This could be made accurate by using a Divider.
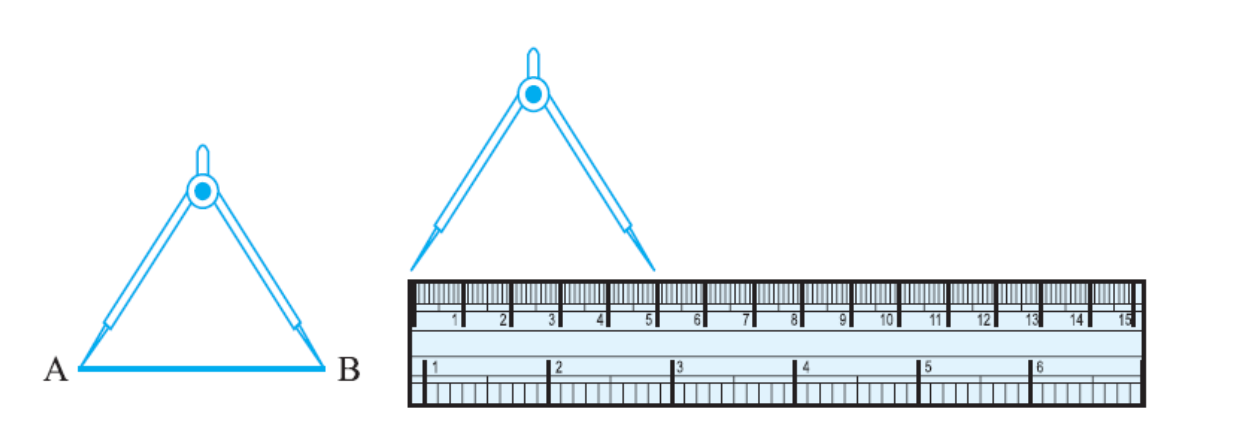
a. Put the one end of the divider on point A and open it to put another end on point B.
b. Now pick up the divider without disturbing the opening and place it on the ruler so that one end lies on 0.
c. Read the marking on the other end and we can compare the two line.
ANGLES
Baccho humne previous chapter m angles k baare m kuch basic cheezein pdhi thei. Hume ye pta hai ki jab corners form hote hai tab hume angles milte hai. Hum apni daily lives m bhi alag alag jagah angles form hote hue dekh skte hai
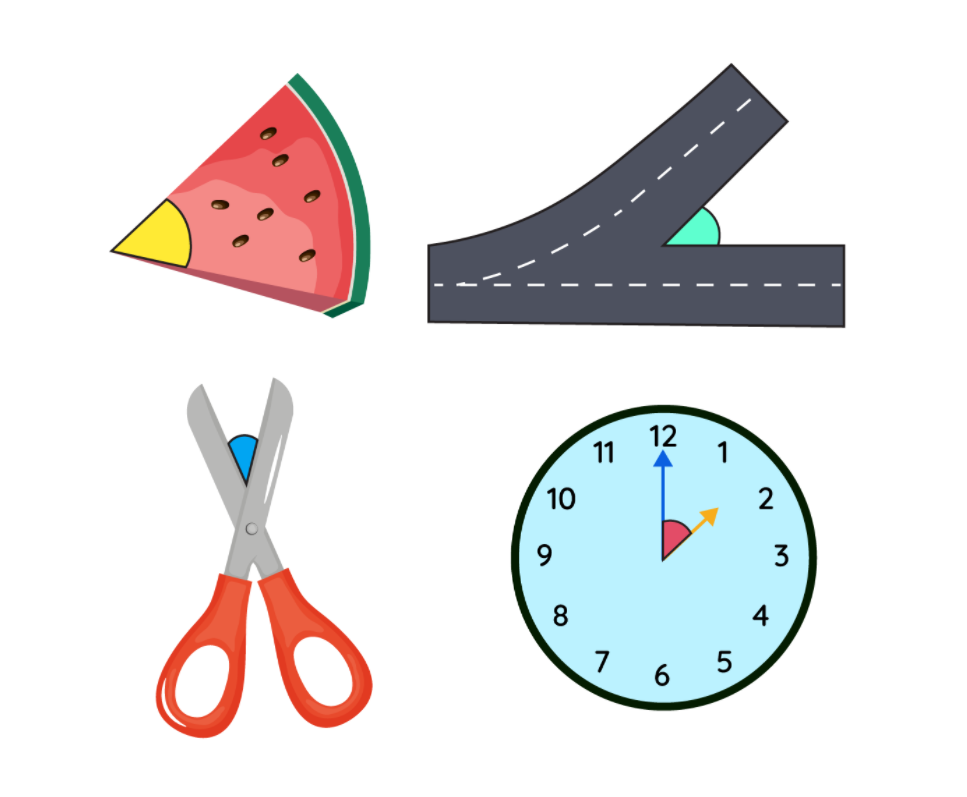
Let's revise some previous concepts first:
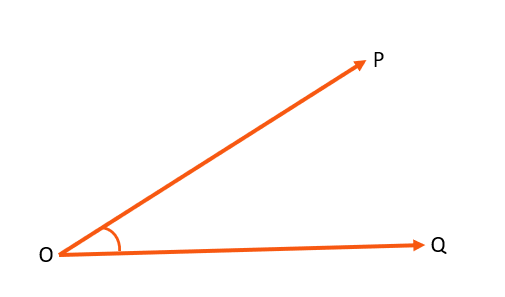
MEASURING ANGLES
Baccho jaise ki hume line segments ko measure aur compare krna seekha ab hum dekhenge ki angles ko hum kaise measure krte hai. Angles are used in daily life. Engineers and architects use angles for designs, roads, buildings and sporting facilities. Carpenters use angles to make chairs, tables and sofas.
To compare two angles exactly, we need the measures of the angles. This is done with the help of a protractor. The curved
edge is divided into 180 equal parts. One complete revolution is divided into 360 parts. Each part is called a degree. The measure of the angle is called ‘degree measure’. We write 360 degrees as 360∘.
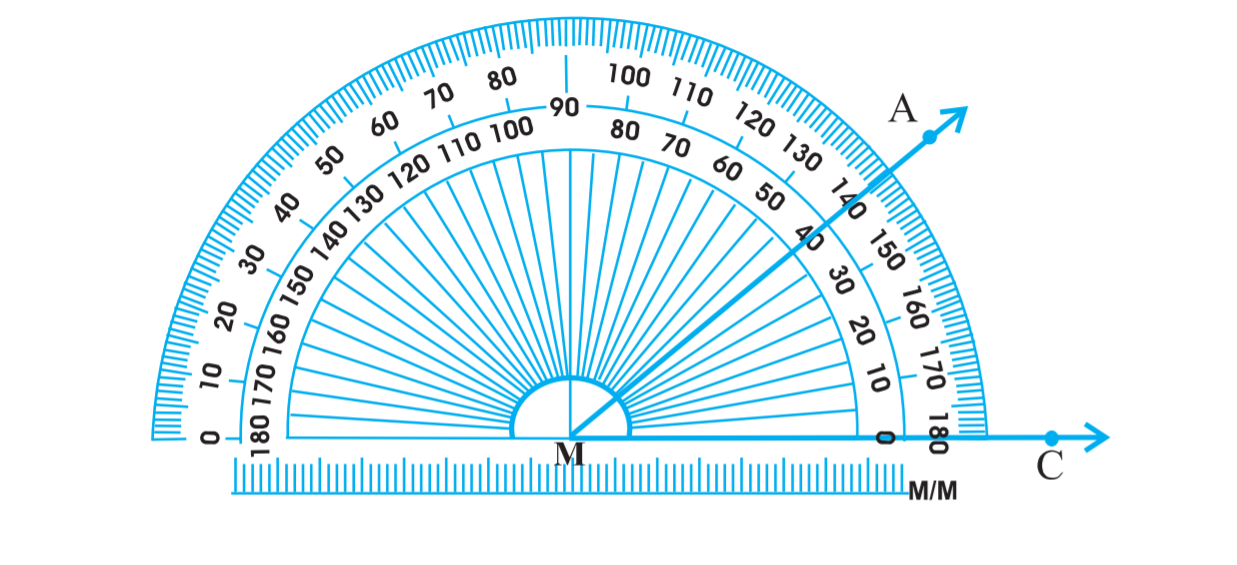
To measure an angle using protractor-
NULL
Example 1
Shikha is rowing a boat due north-east. In which direction will she be rowing if she turns it through:
(i) a straight angle
(ii) a complete angle
(i) South-West
(ii) North-East
Example 2
A ship sailing in river Jhelam moves towards east. If it changes to north, through what angle does it turn?
The ship turns at an angle of 90∘
PERPENDICULAR LINES
Baccho, perpendicular lines vo lines hoti h jo ki intersection p 90∘ ka angle form krti hai. Hum apni daily life m bohot jagah p perpendicualr lines dekh skte hai. For example:

NULL
If two lines intersect with each other and form an angle of 90∘ then they must be perpendicular to each other.
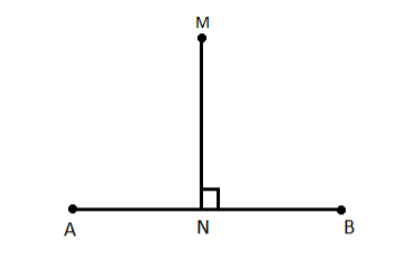
Here AB and MN are intersecting at point N and form a right angle. We will write it as:
AB⊥MN or MN⊥AB
Reads as AB is perpendicular to MN or MN is perpendicular to AB.
PERPENDICULAR BISECTOR
If a perpendicular divides another line into two equal parts then it is said to be a perpendicular bisector of that line.
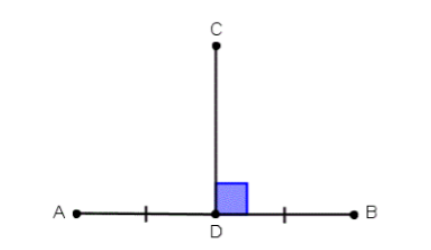
Here, CD is the perpendicular bisector of AB as it divides AB into two equal parts i.e. AD=DB.
Example 3
Let PQ be the perpendicular to the line segment XY. Let PQ and XY intersect in the point A. What is the measure of ∠PAY.
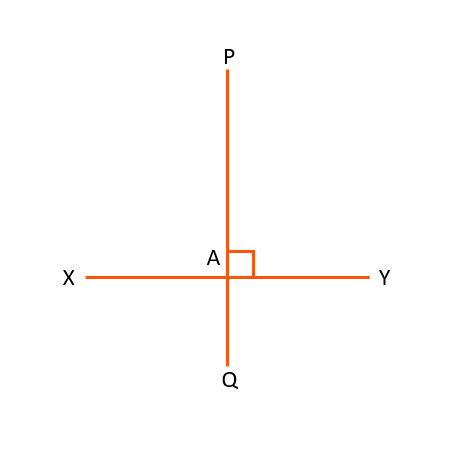
After making diagrams from given information.
∠PAY=900.
Example 4
Which of the following are models for perpendicular lines :
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter ‘L’.
(d) The letter V.
(a)Yes
(b)No
(c)Yes
(d)No
CLASSIFICATION OF TRIANGLES
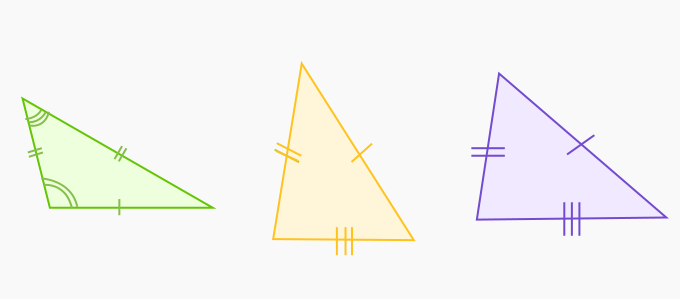
Baccho aapne ye observe kia hoga ki saare triangles same nhi dikhte. This is because of the difference in the lengths of their side and angle measurements. Look at the following triangles and notice the difference in their sides and angles.

After making diagrams from given information.
Let us learn about the different classifications of triangles:
Classifying triangles based on sides.
(i) Scalene Triangle: A triangle having all three unequal sides is called a Scalene Triangle
After making diagrams from given information.
(ii) Isosceles Triangle: A triangle having two equal sides is called an Isosceles Triangle
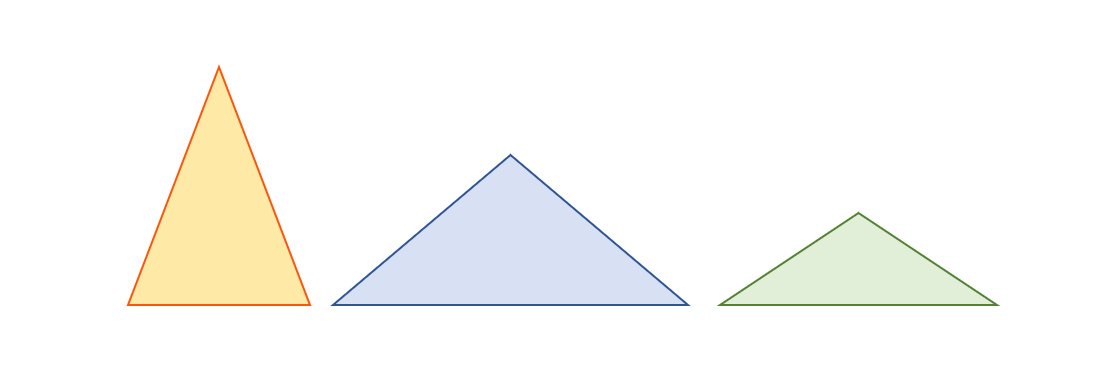
After making diagrams from given information.
(iii) Equilateral Triangle: A triangle having three equal sides is called an Equilateral Triangle

After making diagrams from given information.
Classifying triangles based on angles.
(i) Acute angled triangle: If each angle is less than 90∘, then the triangle is called an acute angled triangle

After making diagrams from given information.
(ii) Right angled triangle: If any one angle is a right angle(90∘) then the triangle is called a right angled triangle.

(iii) Obtuse angled triangle: If any one angle is greater than 90∘, then the triangle is called an obtuse angled triangle.

Example 5
Name the types of following triangles :
(a) Triangle with lengths of sides 7cm,8cmand9cm.
(b) △ABC with AB=8.7cm, AC=7cm and BC=6cm.
(c) △PQR such that PQ=QR=PR=5cm.
(d) △DEF with ∠D=90∘
(e) △XYZ with ∠Y=90∘ and ∠XY=∠YZ
(f) △LMN with ∠L=30∘, ∠M=70∘ and ∠N=80∘.
a) Scalene triangle
b) Scalene triangle
c) Equilateral triangle
d) Right angled triangle
e) Isosceles right angled triangle
f) Acute angle triangle.
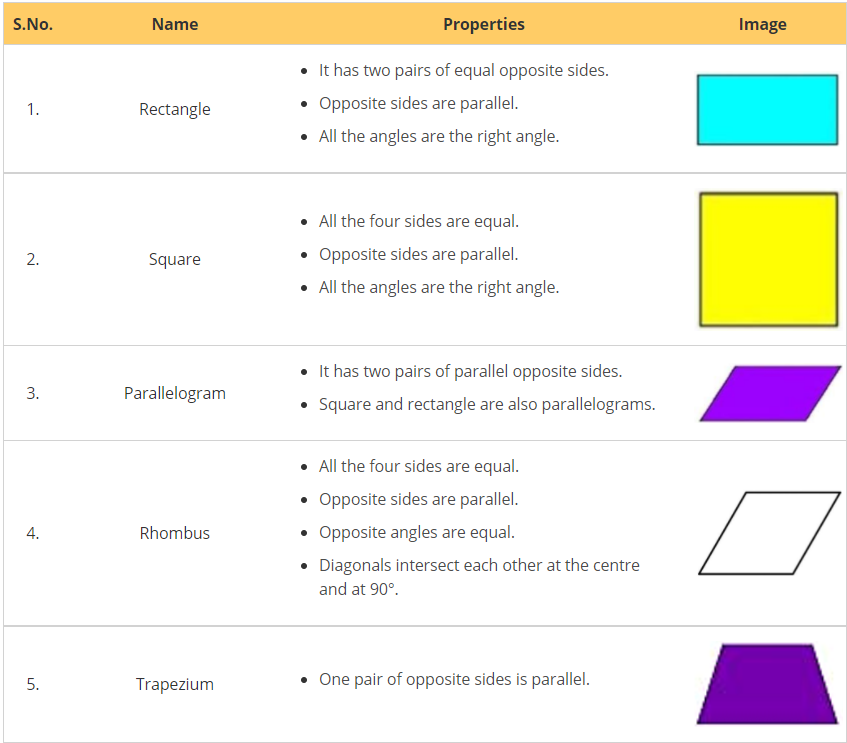
QUADRILATERALS
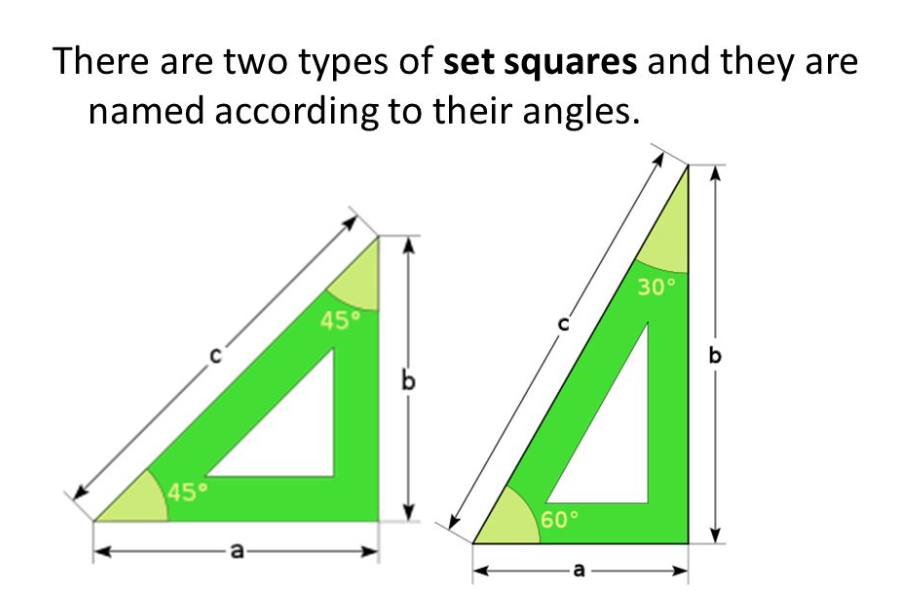
Bacch hume ye pta hai ki ek four sided closed figure ko quadrilateral kaha jaata hai. Because it has four sides, it means it has four corners and four internal angles too. Jaise ki humne abhi angles measure krne k lie protractor use kia tha, now we'll see how we can use another tool called Set Square to understand the different types of quadrilaterals.
A set square is in the shape of a right angled triangle. There are two set-squares in your instrument box. One is 30∘–60∘–90∘
set-square, the other is 45∘–45∘–90∘ set square.
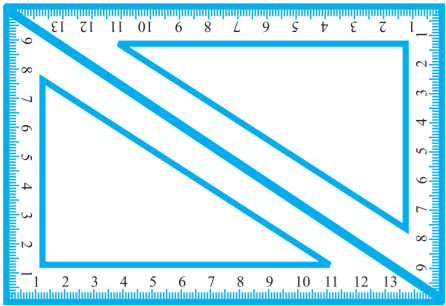
Let's form the different types of quadrilaterals using these set squares.
(i) Rectangle: When we place two 30∘−60∘−90∘ set squares like the figure below, we'll get a rectangle.
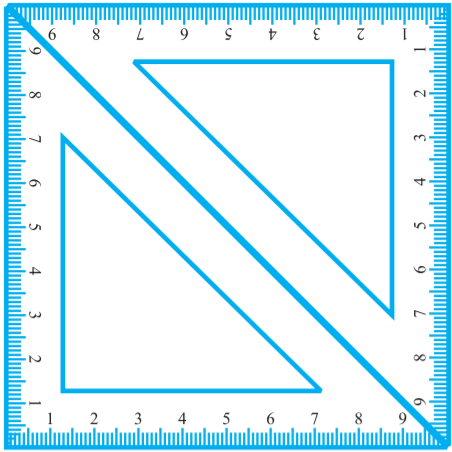
(ii) Square: If you use a pair of 45∘–45∘–90∘ set-squares, you get another quadrilateral this time.
It is a square.
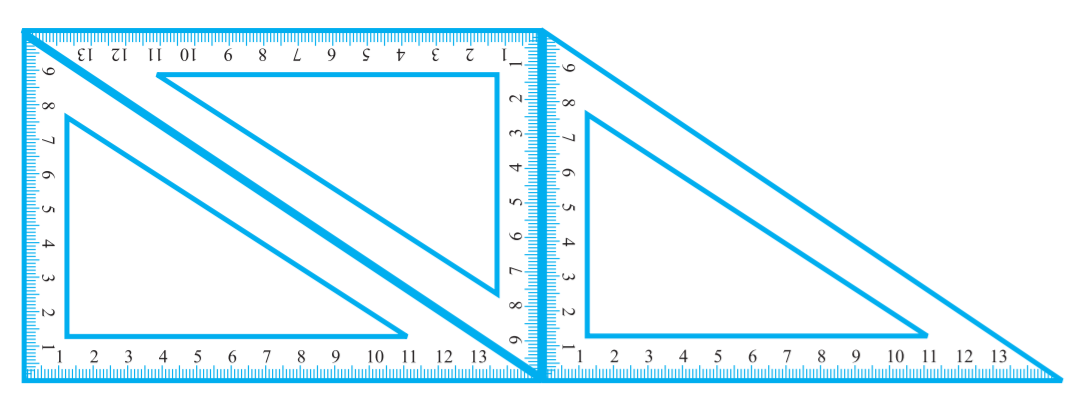
(iii) Parallelogram: If you place the pair of 30∘–60∘–90∘ set-squares like the figure given below, you'll get a parallelogram.
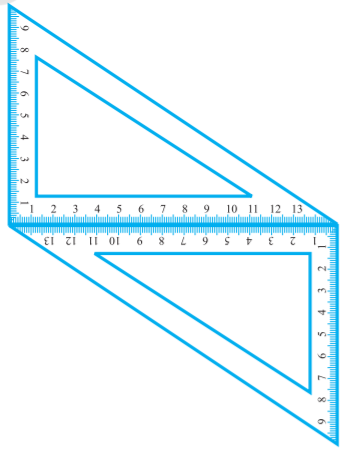
(iv) Rhombus: If you use four 30∘–60∘–90∘ set-squares you'll get a rhombus.
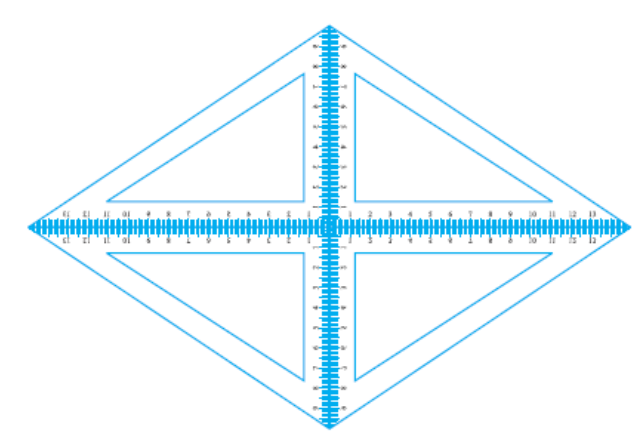
(v) Trapezium:If you use several set-squares you can build a shape like the one given below.
POLYGONS
Polygons are closed geometric shapes having at least 3 sides and 3 angles. Based on the number of sides, a polygon can be categorised into multiple types. Some of the most common polygons are-
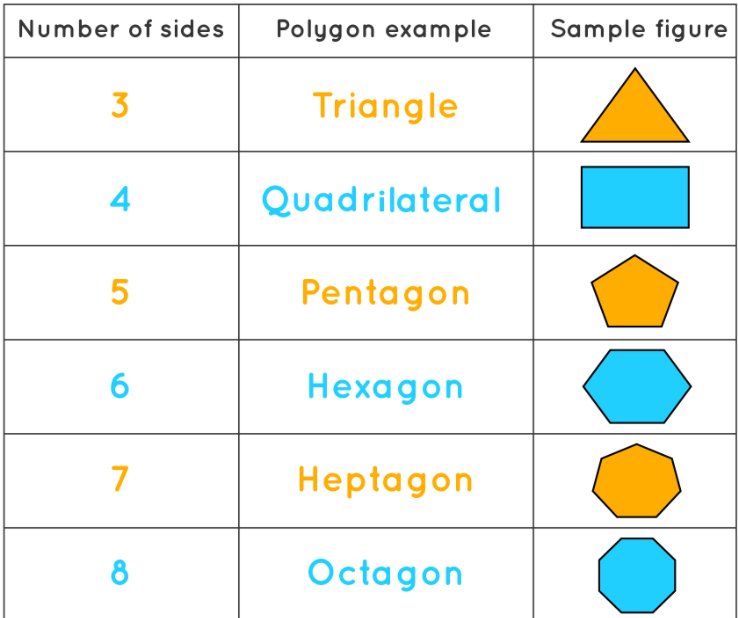
POLYGONS AROUND US
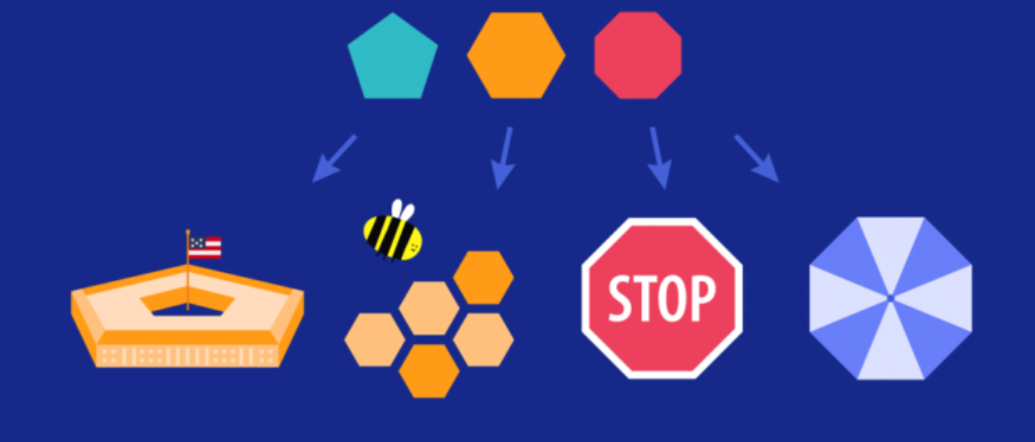
We often come across various polygons in our day to day life. Let's see some of those:
Example 6
Give reasons for the following :
(a) A square can be thought of as a special rectangle.
(b) A rectangle can be thought of as a special parallelogram.
(c) A square can be thought of as a special rhombus.
(d) Squares, rectangles, parallelograms are all quadrilaterals.
(e) Square is also a parallelogram.
a) Because square have all properties of rectangle but rectangle does not have all properties of square.
b) Because parallelogram have all properties of rectangle but rectangle does not have all properties of parallelogram.
c) Because square have all properties of rhombus but rhombus does not have all properties of square.
d) Properties of quadrilateral are that they have 4 sides and sum of 4 angles is 3600 which are same as square, rectangle, parallelogram.
e) Because square have parallel sides and sum of all 4 angles is 3600
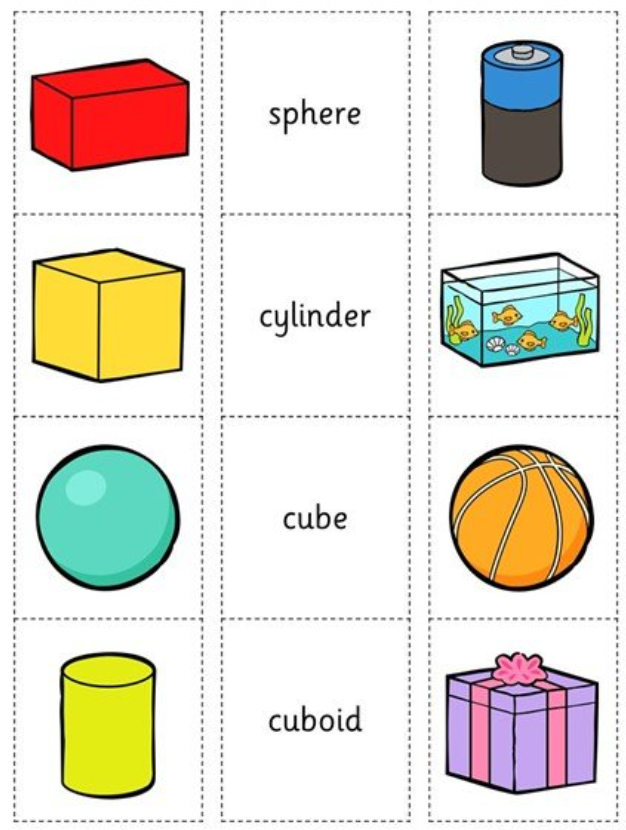
THREE DIMENSIONAL SHAPES
Baccho hum sab ek 3D yaani Three Dimensional world m rehte hai jiska mtlb hai ki humare around aisi cheezein hai jo ki flat nahi hoti, instead they have a proper length, breadth and height jisse hume unka volume pta chlta hai. We have a lot of such things around us like a football is a sphere and a book is a cuboid. Let's do a quick exercise and match the following things with their shapes:
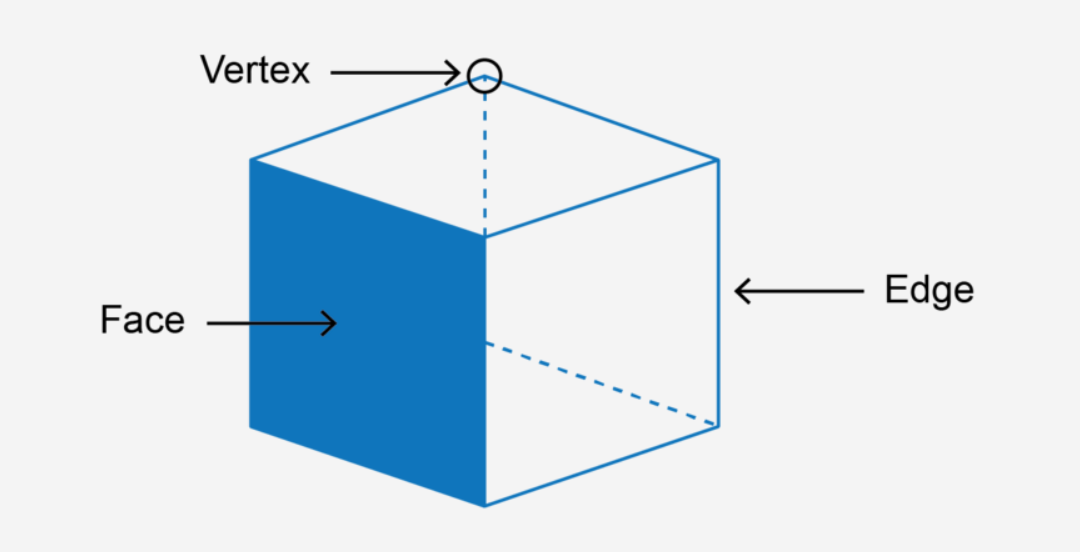
Faces, Edges and Vertices
LET'S SUMMARIZE
1. The distance between the end points of a line segment is its length.
2. A graduated ruler and the divider are useful to compare lengths of line
segments.
3. When a hand of a clock moves from one position to another position we have
an example for an angle.
A right angle is 14 revolution and a straight angle is 12 a revolution.
4. Two intersecting lines are perpendicular if the angle between them is 90∘.
5. The perpendicular bisector of a line segment is a perpendicular to the line segment that divides it into two equal parts.
6. Triangles can be classified as follows based on their angles:
| Nature of angles in the triangle | Name |
|---|---|
| Each angle is acute | Acute angled triangle |
| One angle is a right angle | Right angled triangle |
| One angle is obtuse | Obtuse angled triangle |
7. Triangles can be classified as follows based on the lengths of their sides:
| Nature of sides in the triangle | Name |
|---|---|
| All the three sides are of unequal length | Scalene triangle |
| Any two of the sides are of equal length | Isosceles triangle |
| All the three sides are of equal length | Equilateral triangle |
8. Polygons are named based on their sides:
| Number of sides | Name of the Polygon |
|---|---|
| 3 | Triangle |
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 8 | Octagon |
9. Quadrilaterals are further classified with reference to their properties:
| Properties | Name of the Quadrilateral |
|---|---|
| One pair of parallel sides | Trapezium |
| Two pairs of parallel sides | Parallelogram |
| Parallelogram with 4 right angles | Rectangle |
| Parallelogram with 4 sides of equal length | Rhombus |
| A rhombus with 4 right angles | Square |
10. We see around us many three dimensional shapes. Cubes, cuboids, spheres, cylinders, cones, prisms and pyramids are some of them.
LET'S REVISE
1. Baccho humne iss chapter m basic shapes k baare m pdha aur humne ye bhi seekha ki inn sabhi shapes ko measure aur compare krne k lie kon konse tools and techniques available hoti hai.
2. Ek line segment basically ek line ka part hota hai jiski ek fixed measurement hoti hai. Do line segments ko compare krne k lie hum 3 methods use krte hai:
(a) Comparison by Observation: Baccho iss method m hum directly apni observation se line segments ko compare krte hai. Lekin ye method humesha accurate nahi hota kyunki hum isme minimal differences nahi observe kr paate.
(b) Comparison by tracing: Iss method m hum ek tracing paper ko use krke first line segment ko trace krlete hai aur use dusri line segment k uppr rakh k compare krte hai.
(c) Comparison using Ruler and a Divider: Iss method m hum ek ruler aur ek divider ko use krke line segments ki lengths ko compare krte hai. Divider use krne se hume accurate measurements mil skti hai jo ki ruler se nahi mil paati kyunki ruler m thickness ki vjh se errors k chances hote hai.
3.Jab bhi ek corner ya intersection form hota hai, we get an angle. Angles ko measure krne k lie hum degrees ko use krte hai as a unit of measurement. We use the geometric tool "protractor" to measure angles.
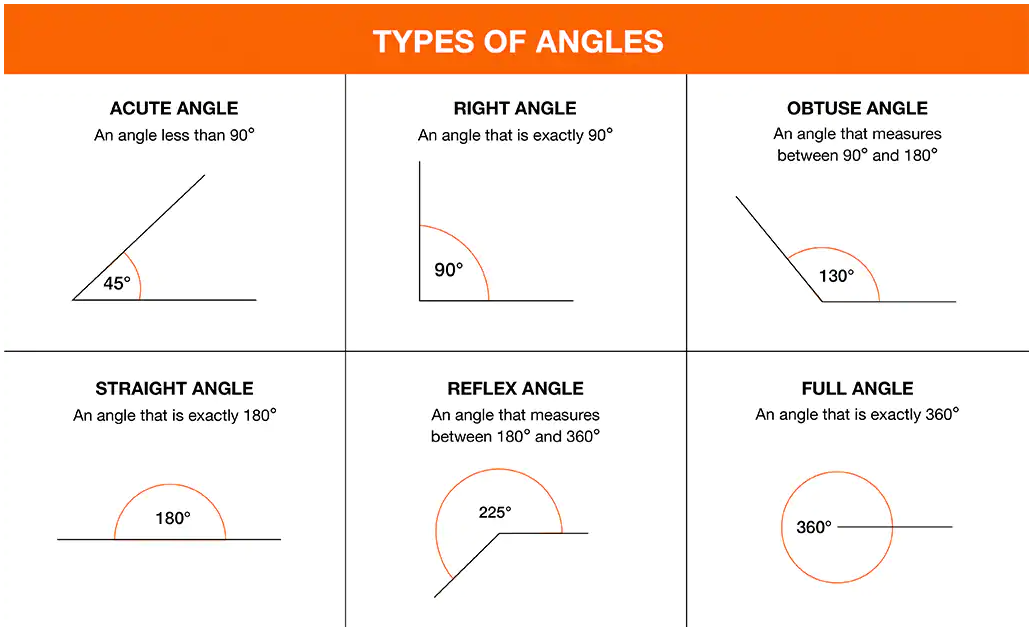
4. There are five different classifications of an angle:
5. Perpendicular lines vo lines hoti hai jo ki intersection p 90∘ ka angle form krti hai. Jab ek line segment dusri line segment ko 90 degrees k angle p do equal parts m divide krti hai, then it's called a perpendicular bisector of that line.
6. Triangle is a three sided polygon. It has three corners and three internal angles. They are classified based on sides as: Scalene, Isosceles and Equilateral triangle.
On the basis of angles, they're classified as : Acute angled triangle, Obtuse angled triangle and Right angled triangle.
7. Quadrilateral ek four sided polygon hota hai with four internal angles. There are different types of quadrilaterals based on the length of their sides and angle measurements. In this chapter we learnt about:
Rectangle
Square
Parallelogram
Rhombus
Trapezium
8. Polygons are geometric shapes formed by joining atleast 3 line segments.
9. Hum apni daily life m bohot saari 3D shapes dekhte hai. Jaise ki ek football is in the form of a sphere, a pencil is in the form of a cylinder and so on. 3d shapes have vertices, faces and edges. In this chapter we got to know about cube, cuboid, sphere, cylinder, cone and a prism.