त्रिभुजों की सर्वांगसमता कक्षा 7 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम त्रिभुजों की सर्वांगसमता का अध्ययन करेंगे। दो त्रिभुज सर्वांगसम कहलाते हैं यदि वे एक-दूसरे की प्रतियाँ हों और वे एक-दूसरे को पूर्णतया ढके हों। इस अध्याय में हम तल-आकृतियों की सर्वांगसमता, कोणों की सर्वांगसमता, त्रिभुजों की सर्वांगसमता तथा त्रिभुजों की सर्वांगसमता के लिए प्रतिबंधों का अध्ययन करेंगे।
आइये जानते है, त्रिभुजों की सर्वांगसमता को और करीब से ...
गणित में सर्वांगसम शब्द से आशय दो आकृतियों में सभी संगत भाग का बराबर होना है।
दैनिक जीवन में एक ही ताले की दो चाबियाँ, एक ही माप की दो चूड़ियाँ और एक ही बैंक द्वारा जारी किए गए दो एटीएम (ATM) कार्ड आदि के आकार व उनके संगत भागों की माप बराबर होती हैं। ये आकृतियों परस्पर सर्वांगसम होती हैं। आकृतियों के बीच का यह संबंध उनकी सर्वांगसमता कहलाता है।

कोई भी दो आकृतियाँ परस्पर सर्वांगसम होंगी, यदि उनमें बिना आकार या माप बदले प्रत्येक को उठाकर दूसरी पर इस प्रकार रखा जा सके कि नीचे रखी आकृति को ठीक-ठीक पूरा ढक ले। आकृतियों में सर्वांगसमता की जाँच के लिए एक को उठाकर दूसरी पर रखने की इस विधि को अध्यारोपण विधि कहते हैं।
सर्वांगसमता को ≅ संकेत से दर्शाया जाता है।
यदि एक आकृति A1, एक दूसरी आकृति A2 के सर्वांगसम है, तो हम इसे:
लिखते हैं आकृति A1≅ आकृति A2
पढ़ते हैं आकृति A1 सर्वांगसम है आकृति A2 के
इसी प्रकार, एक त्रिभुज को दूसरे त्रिभुज पर अध्यारोपित करने पर पहला त्रिभुज दूसरे त्रिभुज को पूर्णतया ढक लेता है तो, वे त्रिभुज सर्वांगसम होते हैं।
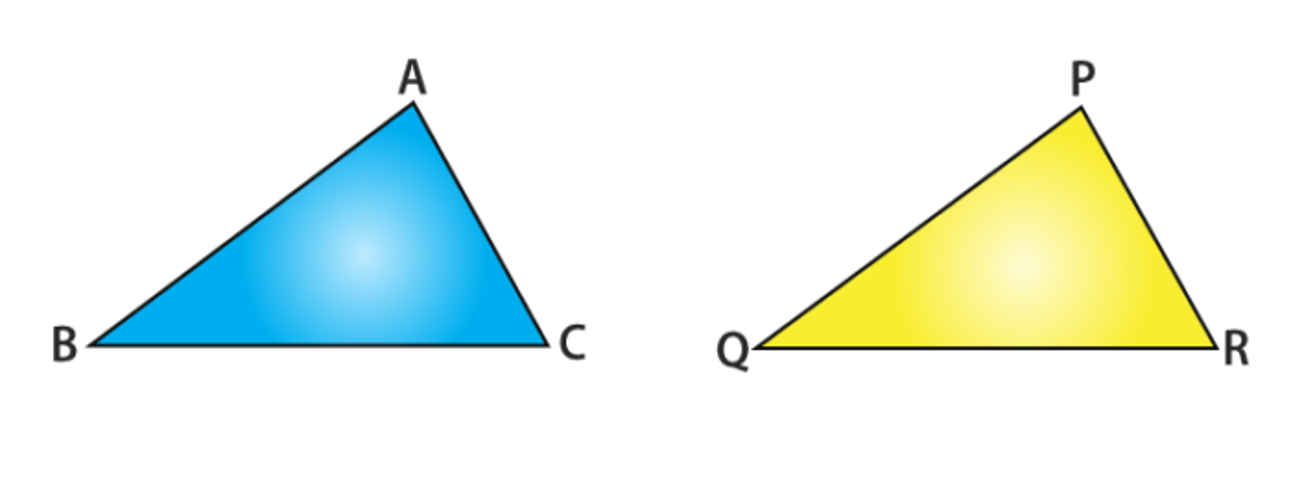
ऊपर दी गयी आकृति में जैसा कि हम देख सकते हैं यहाँ हमें दो त्रिभुज दे रखे हैं। ये दो त्रिभुज बिल्कुल समान हैं। अगर हम इन्हें एक के ऊपर एक रखेंगे तो फिर एक त्रिभुज दुसरे त्रिभुज को पूरी तरह ढक लेगा।
तल-आकृतियों की सर्वांगसमता
दो सर्वांगसम आकृतियों में जब एक आकृति दूसरे के ऊपर रखी जाती है तब वे एक दूसरे को पूरा पूरा ढक लेती हैं और एक रूप हो जाती है। दूसरे शब्दों में एक सर्वांगसम आकृति के सभी भाग दूसरी आकृति के संगत भागों के बराबर होते हैं।
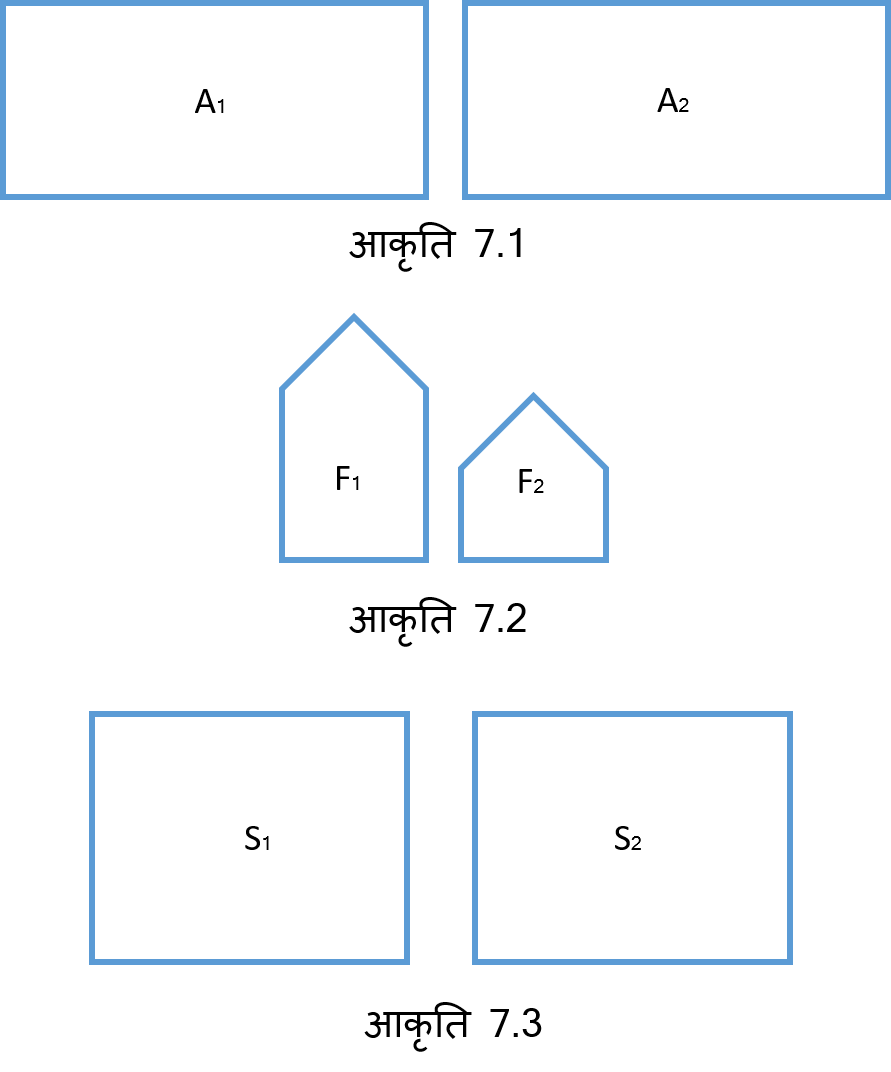
चित्र के युग्मों की आकृतियाँ सामान्य दृष्टि में ही सर्वांगसम दिख रही हैं।
आकृति 7.1 में आयत A1≅ आयत A2 तथा आकृति 7.3 में वर्ग S1≅ वर्ग S2
आकृति 7.2 के युग्मों की आकृतियाँ यद्यपि परस्पर आकार (Shape) में समान हैं। किन्तु मापों में भिन्न-भिन्न होने से सर्वांगसम नहीं है।
Note: प्रत्येक युग्म की एक आकृति का अक्स (ट्रेसिंग) कागज पर ट्रेस करके उसे उसी युग्म की दूसरी आकृति पर अध्यारोपित करने से पता चलता है कि आकृतियाँ सर्वांगसम हैं या नहीं।
रेखाखंडों में सर्वांगसमता
यदि दो रेखाखंडों की लंबाई समान (यानी बराबर) है तो वे सर्वांगसम होते हैं। यदि दो रेखाखंड सर्वांगसम हैं तो उनकी लंबाइयाँ समान होती हैं।
जब दो रेखाखंड सर्वांगसम होते हैं तो हम कहते हैं कि रेखाखंड बराबर हैं और हम लिखते हैं AB=CD (हमारा वास्तव में अर्थ है कि ¯¯¯¯¯¯AB≅¯¯¯¯¯¯CD)
जैसे:-

यहाँ चित्र में दोनों ही रेखाखंडों की लंबाई समान हैं।
अतः, ¯¯¯¯¯¯AB≅¯¯¯¯¯¯CD
उदाहरण 1
नीचे दो रेखाखंड दिए गए हैं, दोनो रेखाखंड सर्वांगसम हैं। यदि AB=4 सेमी, तो CD की लंबाई कितनी होंगी ?

यहाँ हमे रेखाखंड AB=4 सेमी दिया गया हैं।
हम जानते हैं यदि कोई आकृति सर्वांगसम है तो उनके संगत भाग बराबर होते है।
चूंकि AB=4 सेमी
अतः AB≅CD होगा, यदि CD=4 सेमी होगा।
∴CD=4 सेमी
उदाहरण 2
निम्नांकित आयत-युग्मो में कौन-सा आयत-युग्म सर्वांगसम है ?
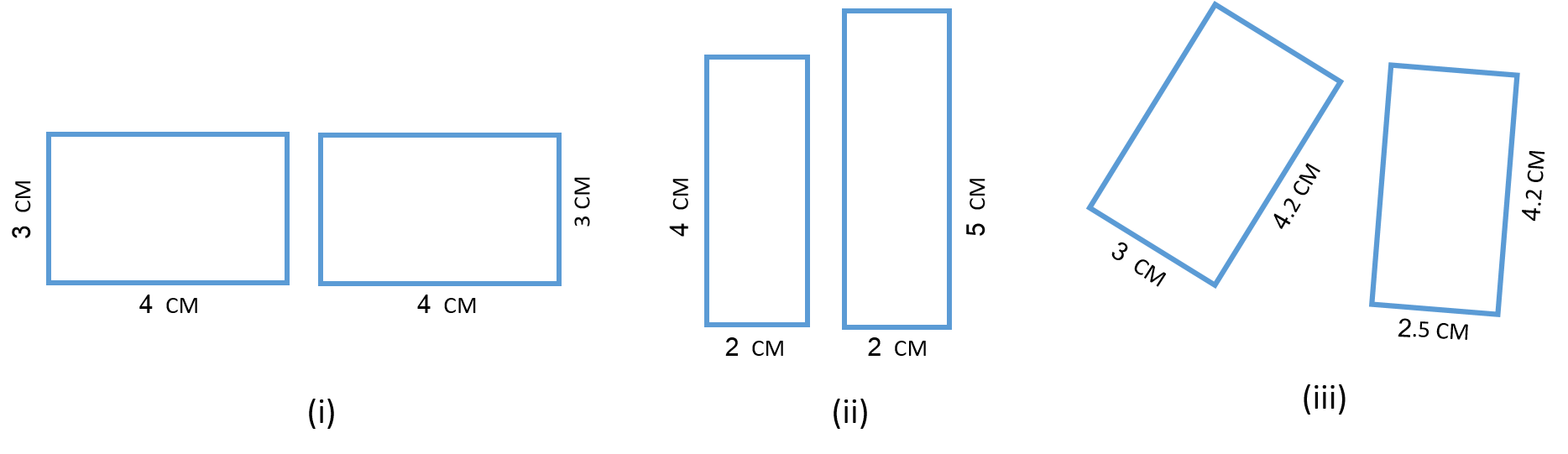
हम जानते हैं कि कोई भी दो आकृतियाँ परस्पर सर्वांगसम होंगी, यदि उनमें बिना आकार या माप बदले प्रत्येक को उठाकर दूसरी पर इस प्रकार रखा जा सके कि नीचे रखी आकृति को ठीक-ठीक पूरा ढक ले।
अतः, यहाँ आयत युग्म की लंबाई, लंबाई के बराबर और चौड़ाई, चौड़ाई के बराबर हो, तो वह आयत युग्म सर्वागसम होंगे।
(i) यहाँ दोनों आयतों की लंबाई और चौड़ाई बराबर हैं।
अतः आयत युग्म सर्वांगसम होंगे।
(ii) यहाँ दोनों आयतों की लंबाई बराबर नहीं हैं।
अतः आयत युग्म सर्वांगसम नहीं होंगे।
(iii) यहाँ दोनों आयतों की चौड़ाई बराबर नहीं हैं।
अतः आयत युग्म सर्वांगसम नहीं होंगे।
कोणों की सर्वांगसमता
यदि दो कोणों की माप समान हो तो वे सर्वांगसम होते हैं। कोणों की सर्वांगसमता पूर्णतया उनके मापों की समानता के ऊपर निर्भर करती है जैसा कि रेखाखंडों की स्थिति में बताया गया है। हम कई बार केवल यही कहते हैं कि कोण बराबर हैं और हम लिखते हैं:
∠ABC=∠PQR (अर्थात ∠ABC≅∠PQR या m∠ABC=m∠PQR)
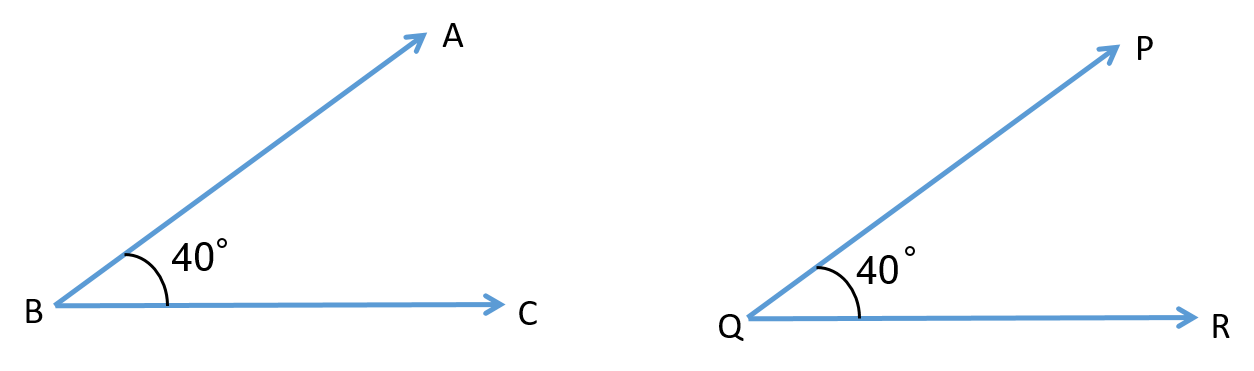
इसी प्रकार, नीचे चित्र मे देख सकते हैं
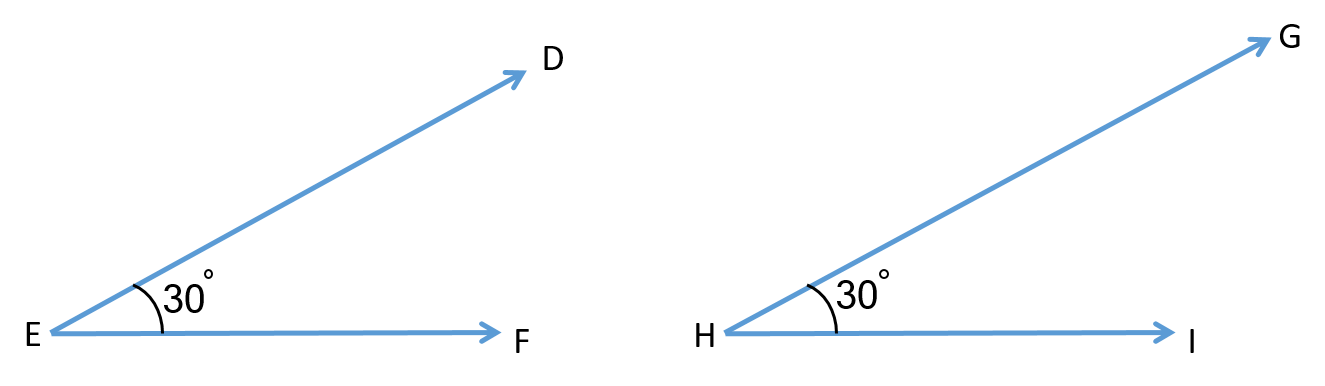
यहाँ ∠DEF तथा ∠GHI के कोण बराबर हैं
अतः, ∠DEF≅∠GHI
Note:- यहाँ किरण केवल दिशा को ही प्रदर्शित करती है अतः किरण के आधार पर सर्वांगसमता को नहीं बताया जा सकता हैं।
त्रिभुजों की सर्वांगसमता
दो त्रिभुजों में यदि एक त्रिभुज की सभी भुजाएँ तथा सभी कोण, दूसरे त्रिभुज की सभी संगत भुजाओं तथा संगत कोणों के बराबर हों, तो वे सर्वांगसम होते हैं। जब ऐसा होता हैं, तो एक त्रिभुज को दूसरे त्रिभुज पर अध्यारोपित करने पर पहला त्रिभुज, दूसरे त्रिभुज को पूर्णतया ढक लेता है।
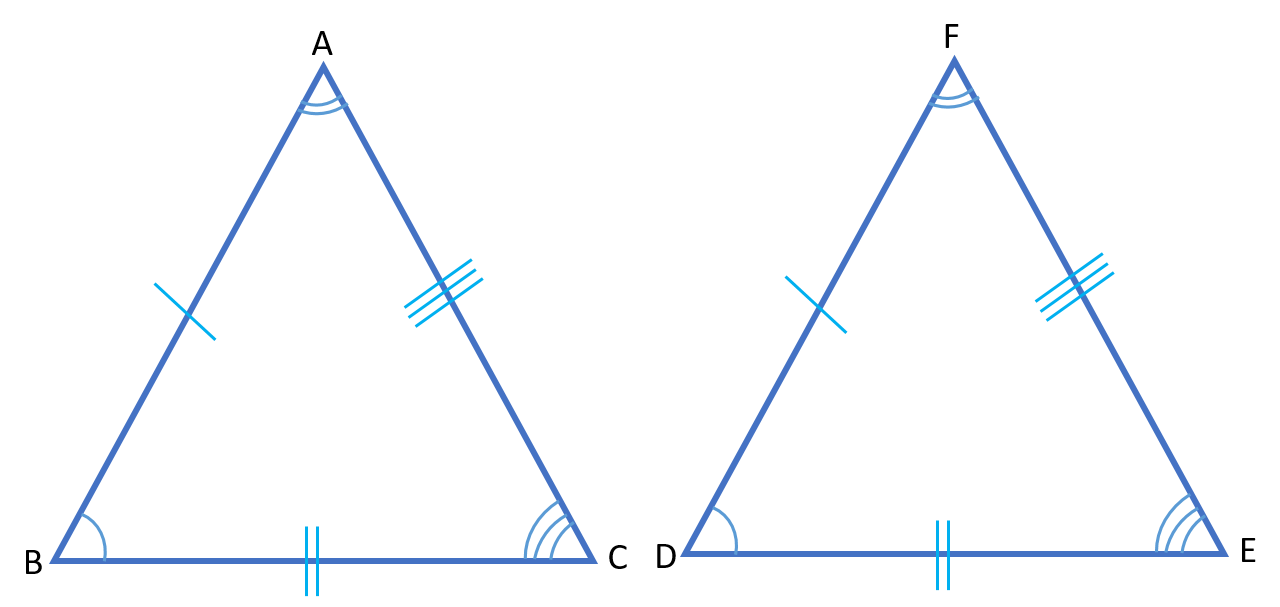
ऊपर दी गयी आकृतियों में जैसा कि हम देख सकते हैं यहाँ हमें दो त्रिभुज दे रखे हैं। ये दो त्रिभुज बिल्कुल समान हैं। अगर हम इन्हें एक के ऊपर एक रखेंगे तो फिर एक त्रिभुज, दुसरे त्रिभुज को पूरी तरह ढक लेगा।
∴ यहाँ, ΔABC≅ΔFDE
सर्वांगसम त्रिभुजों की दशा में:
एक त्रिभुज की सभी भुजाएँ दूसरे त्रिभुज की संगत भुजाओं के बराबर होनी चाहिए।
यहाँ, AB↔FD, BC↔DE, AC↔FE
एक त्रिभुज के सभी कोण दूसरे त्रिभुज के संगत कोणों के बराबर होने चाहिए।
यहाँ, ∠A↔∠F, ∠B↔∠D, ∠C↔∠E
एक त्रिभुज के सभी शीर्ष दूसरे त्रिभुज के शीर्षों के संगत होने चाहिए।
यहाँ, A↔F, B↔D, C↔E
Note:- यहाँ त्रिभुजों के नामों के अक्षरों का क्रम है जो दो त्रिभुजों के बीच संबंधित संबंधों को बताता है। यदि हम इसे ΔABC≅ΔFDE से ΔBCA≅ΔFDE में बदलते हैं, तो यह आवश्यक नहीं है कि दोनों त्रिभुज सर्वांगसम हों क्योंकि यह महत्वपूर्ण है कि सभी संगत भुजाएँ, कोण और शीर्ष समान हों।
OMR (One Minute Revision)
उदाहरण 3
यदि ΔDEF≅ΔBCA हो, तो ΔBCA के उन भाग को लिखिए जो ∠F के संगत हो।
दिया हैं;
ΔDEF≅ΔBCA
∠F का संगत भाग ज्ञात करना हैं।
दो त्रिभुजों में यदि एक त्रिभुज की सभी भुजाएँ तथा सभी कोण, दूसरे त्रिभुज की सभी संगत भुजाओं तथा संगत कोणों के बराबर हों, तो वे सर्वांगसम होते हैं।
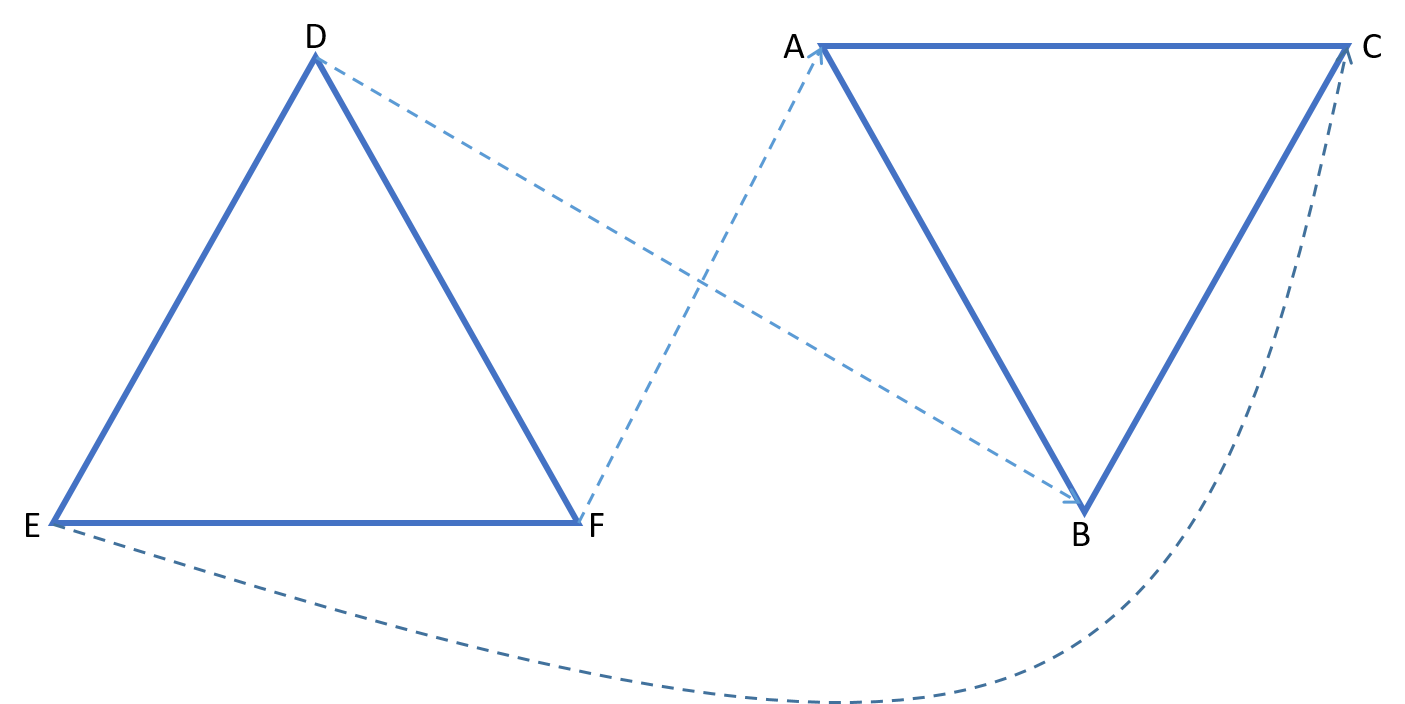
अतः स्पष्ट हैं कि, ∠F=∠A
∴∠F का संगत भाग ∠A होगा।
उदाहरण 4
यदि सुमेलन ABC↔FED के अंतर्गत ΔABC≅ΔFED तो त्रिभुजों के सभी संगत सर्वांगसम भागों को लिखिए।
दिया हैं;
ΔABC≅ΔFED
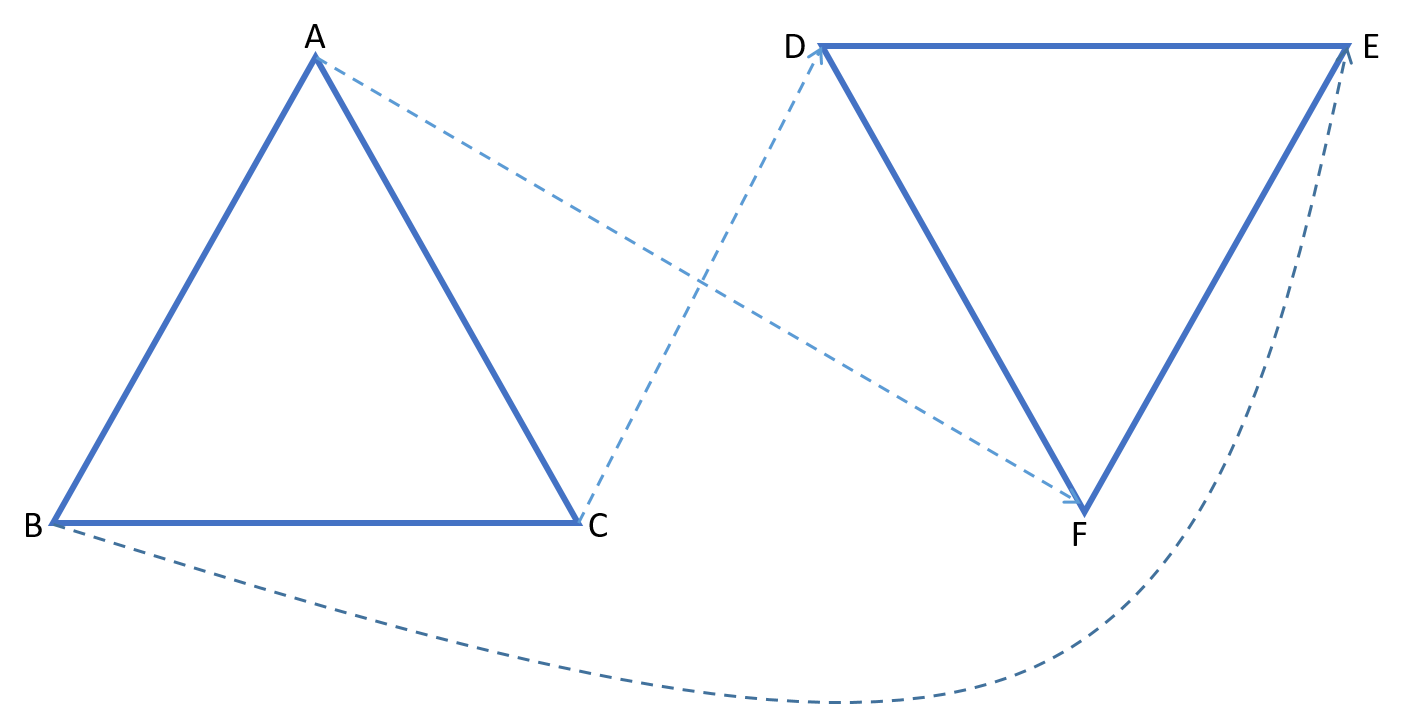
त्रिभुजों के सभी संगत सर्वांगसम भाग निम्नलिखित हैं:
(i) ∠A↔∠F
(ii) ∠B↔∠E
(iii) ∠C↔∠D
(iv) ¯¯¯¯¯¯AB↔¯¯¯¯¯¯FE
(v) ¯¯¯¯¯¯BC↔¯¯¯¯¯¯ED
(vi) ¯¯¯¯¯¯AC↔¯¯¯¯¯¯FD
उदाहरण 5
दी गई आकृति में AB=AC और D, BC का मध्य बिंदु हैं। ΔADB और ΔADC में बराबर भागों के तीन युग्म बताइए।

दिया हैं;
AB=AC
अतः, ΔABD और ΔACD में,
चूंकि D, BC का मध्य बिंदु हैं
∴BD=DC
भुजा AD उभयनिष्ठ हैं
∴AD=AD
ΔABD और ΔACD में बराबर भागों के तीन युग्म
(AB,AC), (AD,AD), (BD,DC) हैं।
त्रिभुजों की सर्वांगसमता के लिए प्रतिबंध
हम जानते हैं कि किसी त्रिभुज की रचना उसके निम्नलिखित भागों के दिए जाने पर ही की जा सकती है।
(i) दो भुजाएँ और अन्तर्गत कोण
(ii) दो कोण और अन्तर्गत भुजा
(iii) तीनों भुजाएँ
(iv) समकोण त्रिभुज में उसकी एक भुजा और कर्ण
आइए देखें कि किन्हीं दो त्रिभुजों के अलग-अलग छः अवयवों (तीनों कोण व तीनों भुजाओं) में से कम से कम कितने और कौन-कौन से सर्वांगसम होने पर वे त्रिभुज भी सर्वांगसम होंगे।
अतः हम एक सी माप वाले दो त्रिभुज खींचेंगे और उनकी सर्वांगसमता पर विचार करेंगे।
SSS (भुजा-भुजा-भुजा) सर्वांगसमता नियम: यदि किसी त्रिभुज की तीनों भुजाओं की माप दूसरे त्रिभुज की तीनों संगत भुजाओं की माप के बराबर हो तो दोनों त्रिभुज SSS सर्वांगसमता नियम से सर्वागसम होंगे।
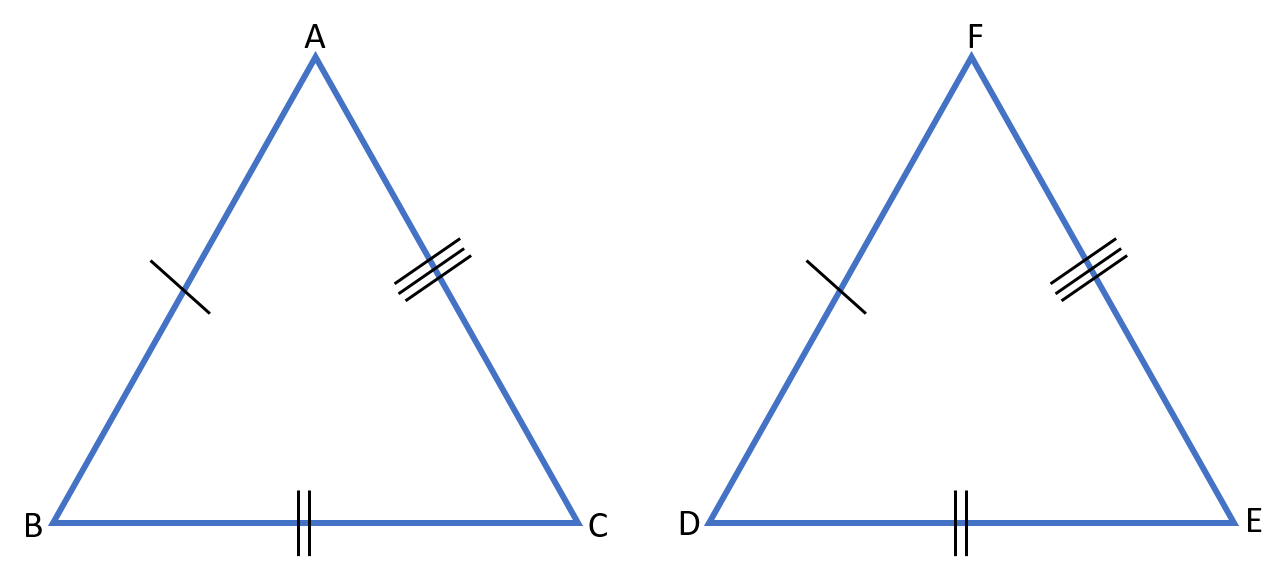
दिये गए त्रिभुजों में,
भुजा AB=FD
भुजा BC=DE
भुजा CA=EF
अतः ΔABC≅ΔFDE
उदाहरण: दिए गए दो त्रिभुजों में, ΔABC और ΔDEF में AB=7 सेमी, BC=5 सेमी, AC=9 सेमी, DE=7 सेमी, DF=9 सेमी और EF=5 सेमी। जाँच कीजिए कि दोनों त्रिभुज सर्वांगसम हैं या नहीं।
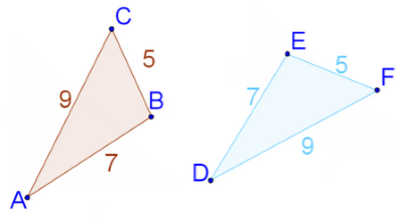
हल: ΔABC और ΔDEF में,
AB=DE=7 सेमी
BC=EF=5 सेमी
AC=DF=9 सेमी
यह दर्शाता है कि ΔABC की तीनों भुजाएँ ΔDEF की तीनों संगत भुजाओं के बराबर हैं।
∴ΔABC≅ΔDEF
अत: SSS (भुजा-भुजा-भुजा) सर्वांगसमता नियम से दोनों त्रिभुज सर्वांगसम हैं।
SAS (भुजा-कोण-भुजा) सर्वांगसमता नियम: यदि एक त्रिभुज की कोई दो भुजाएँ और उनके बीच का कोण दूसरे त्रिभुज की दो संगत भुजाओं व उनके बीच के कोण के बराबर हों, तो वे दोनों त्रिभुज SAS सर्वांगसमता नियम से सर्वांगसम होंगे।
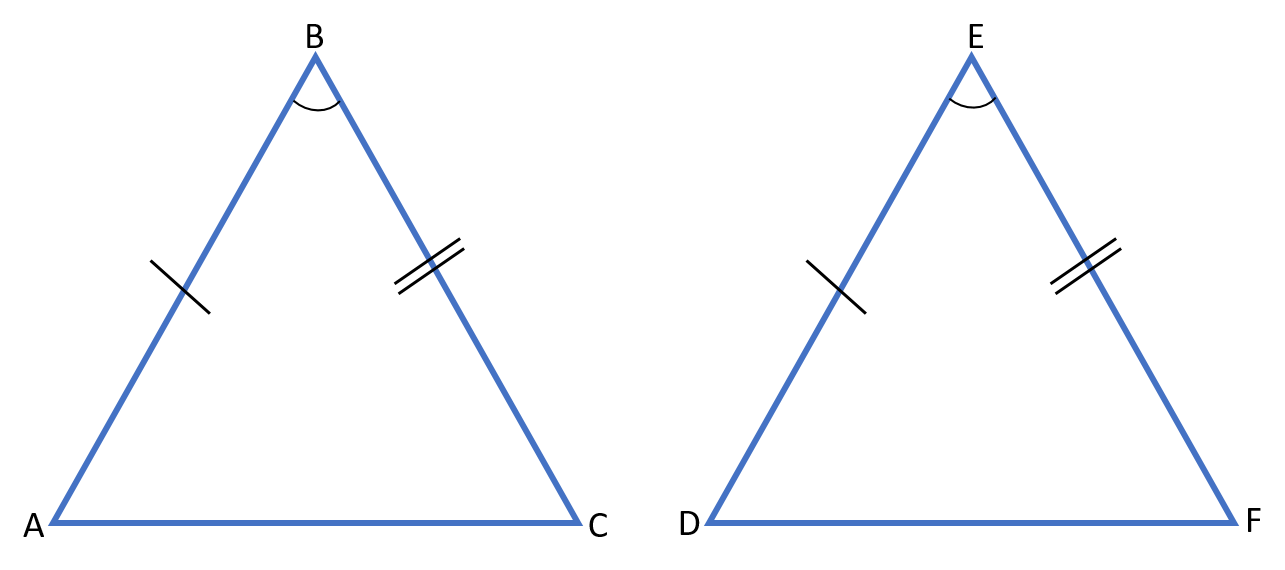
दिये गए त्रिभुजों में,
भुजा AB=DE
कोण ∠B=∠E
भुजा BC=EF
अतः ΔABC≅ΔDEF
उदाहरण: दो त्रिभुजों के कुछ भागों की माप नीचे दी गई है। SAS सर्वांगसमता नियम का प्रयोग करके जाँच कीजिए कि दोनों त्रिभुज सर्वांगसम हैं या नहीं। यदि त्रिभुज सर्वांगसम हों तो इसे प्रतीकात्मक रूप में लिखिए। ΔABC के लिए, AB=7 सेमी, BC=5 सेमी, ∠B=50∘ और ΔDEF के लिए, DE=5 सेमी, EF=7 सेमी, ∠E=50∘
हल:
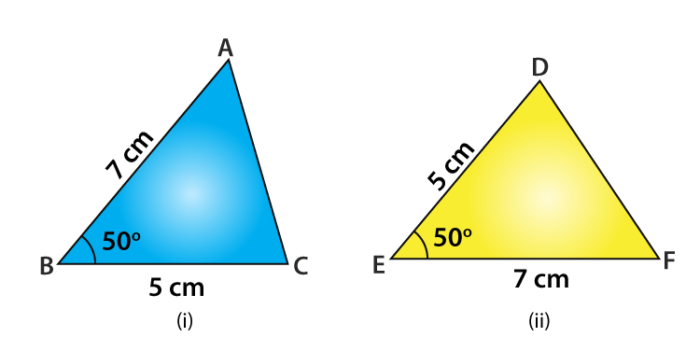
दिये गए त्रिभुजों में,
AB=EF=7 सेमी
∠B=∠E=50∘
BC=DE=5 सेमी
अतः SAS सर्वांगसमता नियम से,
ΔABC≅ΔFED
ASA (कोण-भुजा-कोण) सर्वांगसमता नियम: यदि किसी त्रिभुज के कोई दो कोण और एक भुजा, दूसरे त्रिभुज के दो संगत कोण और एक संगत भुजा के बराबर हों, तो वे त्रिभुज सर्वांगसम होते हैं।
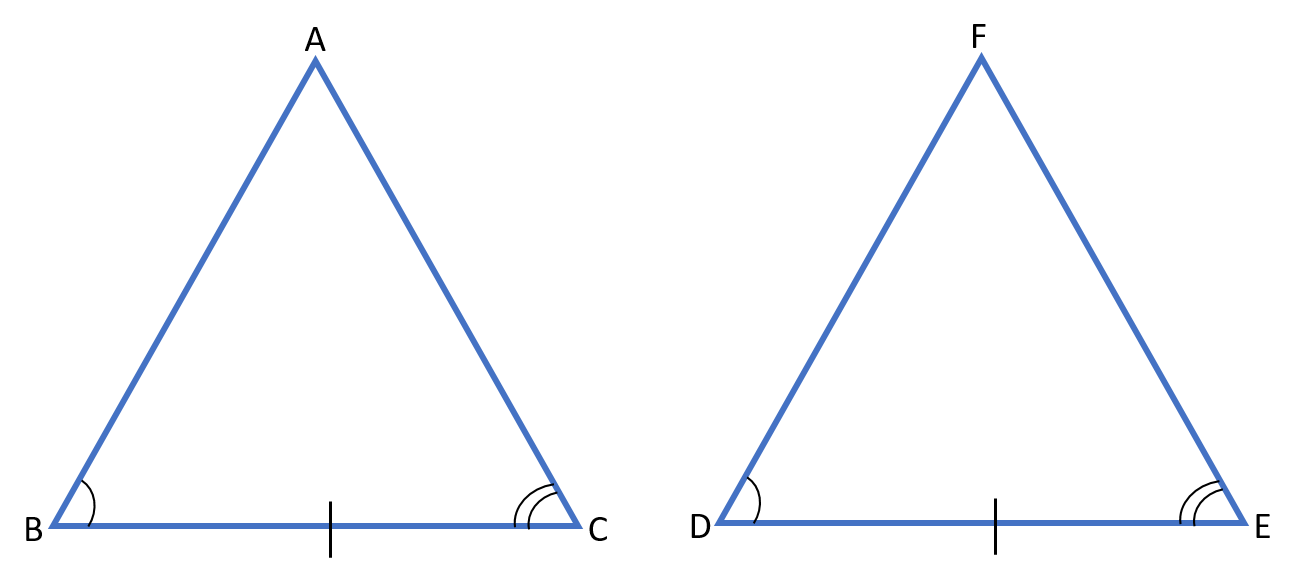
दिये गए त्रिभुजों में,
कोण ∠B=∠D
भुजा BC=DE
कोण ∠C=∠E
अतः ΔABC≅ΔFDE
उदाहरण: दिए गए चित्र से ASA सर्वांगसमता नियम का प्रयोग करते हुए निष्कर्ष निकालें कि ΔAOC≅ΔBOD हैं।
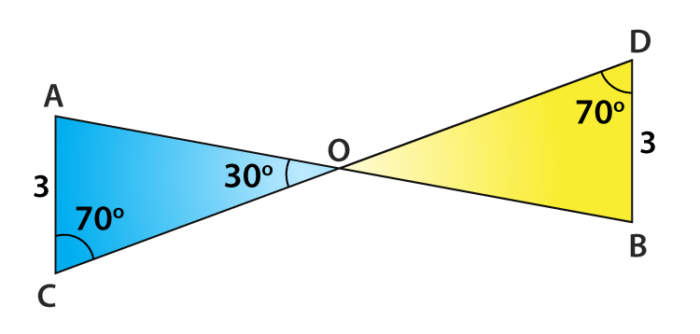
हल:
दिया गया है कि ∠C=∠D=70∘
साथ ही, ध्यान दें कि ∠AOC=∠BOD=30∘ जो शीर्षाभिमुख कोण हैं।
अतः, ∠A=180∘−(70∘+30∘)=80∘ (त्रिभुज के कोणों के योग के गुण से)
इसी प्रकार, ∠B=180∘−(70∘+30∘)=80∘
तो, हमारे पास ∠A=∠B, AC=BD और ∠C=∠D है।
अब, ∠A और ∠C के अंतर्गत भुजा AC तथा ∠B और ∠D के अंतर्गत भुजा BD है।
अतः ASA सर्वांगसमता प्रतिबंध से, ΔAOC≅ΔBOD
Note:-यदि एक त्रिभुज के दो कोण दिए हुए हों तो हम त्रिभुज के तीसरे कोण को हमेशा ज्ञात कर सकते हैं। अतः जब एक त्रिभुज के दो कोण और एक भुजा किसी दूसरे त्रिभुज के दो संगत कोणों और एक भुजा के बराबर हो, तब हम इसे दो कोणों और अंतर्गत भुजा वाली सर्वांगसमता में रूपांतरित कर सकते हैं और तब सर्वांगसमता नियम का उपयोग कर सकते हैं।
Note:- यदि दो त्रिभुजों के सभी कोण समान हैं तो यह अनिवार्य नहीं है कि उनकी भुजाएँ भी समान हों। त्रिभुजों में से एक का आकार दूसरे त्रिभुज से बड़ा हो सकता है।
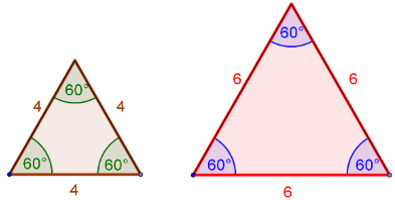
उपरोक्त आकृति में, दो त्रिभुजों के कोण समान हैं लेकिन उनकी भुजाओं की लंबाई समान नहीं है, इसलिए वे सर्वांगसम त्रिभुज नहीं हैं।
उदाहरण 6
दिए गए आकृति में PQ=7 सेमी, PR=7 सेमी, ∠QPM=30∘,∠QPR=60∘ है, तो क्या ΔPMQ≅ΔPMR होगा? सर्वांगसमता के किस प्रतिबंध पर आधारित है, उसे लिखिए।
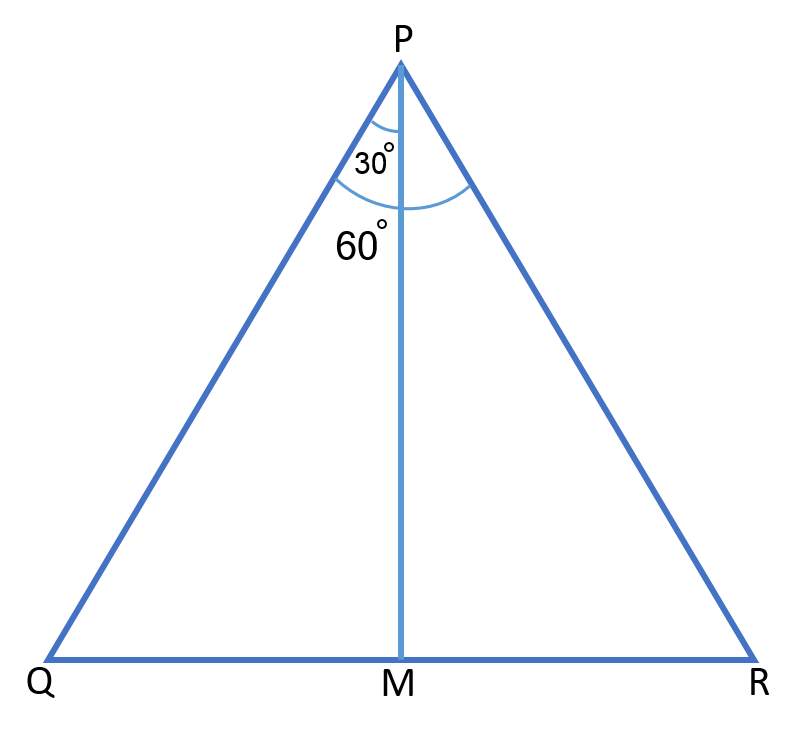
दिया हैं;
PQ=PR=7 सेमी
∠QPM=30∘
∠QPR=60∘
यहाँ, ∠QPR=∠QPM+∠RPM
⇒60∘=30∘+∠RPM
⇒∠RPM=60∘−30∘
⇒∠RPM=30∘
अतः, ∠QPM=∠RPM=30∘
यहाँ,
भुजा PQ=PR
कोण ∠QPM=∠RPM
भुजा PM=PM (उभयनिष्ठ)
हम जानते हैं, कि यदि एक त्रिभुज की कोई दो भुजाएँ और उनके बीच का कोण दूसरे त्रिभुज की दो संगत भुजाओं व उनके बीच के कोण के बराबर हों, तो वे दोनों त्रिभुज SAS सर्वांगसमता नियम से सर्वांगसम होंगे।
अतः ΔQPM≅ΔRPM
उदाहरण 7
आकृति में AC=BD और AD=BC है। निम्नलिखित कथन सत्य है: ΔABC≅ΔBAD

ΔABC और ΔABD में,
भुजा AC=BD
भुजा BC=AD
भुजा AB=AB (उभयनिष्ठ)
हम जानते हैं कि यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की संगत भुजाओं के बराबर हो, तो दोनो त्रिभुज SSS सर्वांगसमता नियम से सर्वांगसम होते हैं।
अतः ΔACB≅ΔBDA
चूंकि A↔B, C↔D, B↔A
∴ΔABC≅ΔBAD
अतः दिया गया कथन सत्य हैं।
उदाहरण 8
ΔABC में, ∠A=30∘, ∠B=40∘ और ∠C=110∘, ΔPQR में, ∠P=30∘,∠Q=40∘ और ∠R=110∘ एक विधार्थी कहता है कि, AAA सर्वांगसमता प्रतिबंध से ΔABC≅ΔPQR है। क्या यह कथन सत्य है? क्यों या क्यों नहीं?
कथन सत्य नहीं है, क्योंकि एक त्रिभुज सभी कोण यदि दूसरे त्रिभुज के सभी संगत कोणों के बराबर हो, तो भी वह एक दूसरे आकर में छोटे या बड़े हो सकते हैं।
समकोण त्रिभुजों में सर्वांगसमता
यदि किसी समकोण त्रिभुज की एक भुजा और कर्ण दूसरे समकोण त्रिभुज की संगत भुजा तथा कर्ण के बराबर हों, तो वे त्रिभुज सर्वांगसम होते हैं। इस नियम को RHS सर्वांगसमता नियम भी कहते हैं।
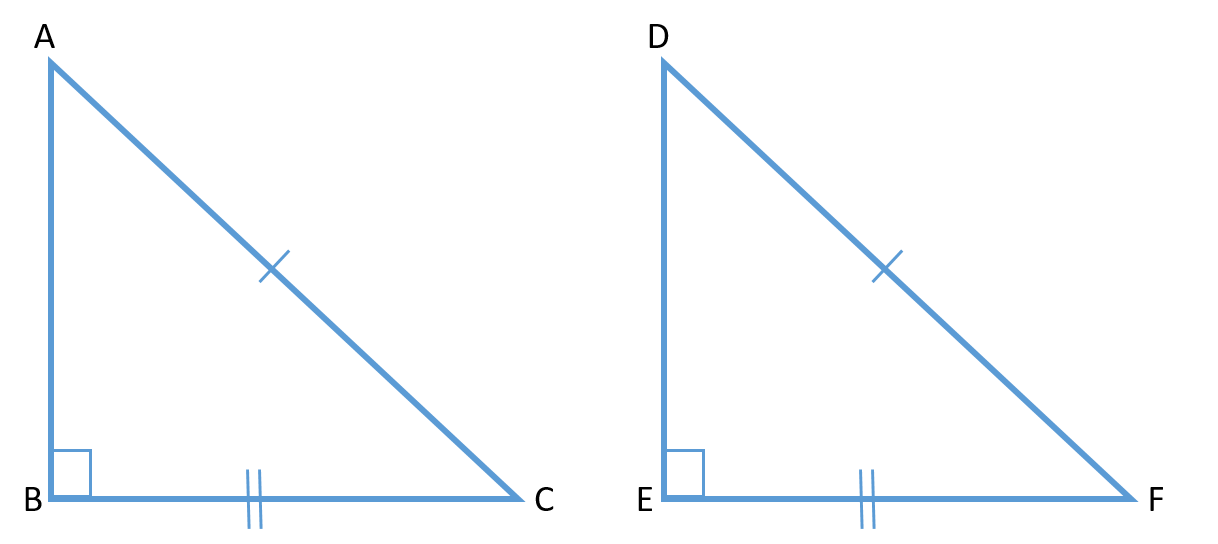
दिये गए त्रिभुजों में,
यहाँ, ∠B=∠E
कर्ण AC=DF
भुजा BC=EF
चूंकि यहाँ किसी त्रिभुज की एक भुजा और कर्ण दूसरे समकोण त्रिभुज की संगत भुजा तथा कर्ण के बराबर हैं अतः दोनों त्रिभुज RHS सर्वांगसमता नियम से सर्वागसम होंगे।
ΔABC≅ΔDEF
उदाहरण: दो त्रिभुजों के मापन के कुछ भाग नीचे दिए गए हैं। RHS सर्वांगसमता नियम का प्रयोग करते हुए, जाँच कीजिए कि दिए गए दो त्रिभुज सर्वांगसम हैं या नहीं। यदि त्रिभुज सर्वांगसम हैं तो परिणाम को प्रतीकात्मक रूप में लिखें। ΔABC और ΔPQR के लिए, माप नीचे दिए गए हैं। त्रिभुज ABC के लिए ∠B=90∘, AC=8 सेमी, AB=3 सेमी और त्रिभुज PQR के लिए ∠P=90∘, PR=3 सेमी, QR=8 सेमी।
हल:
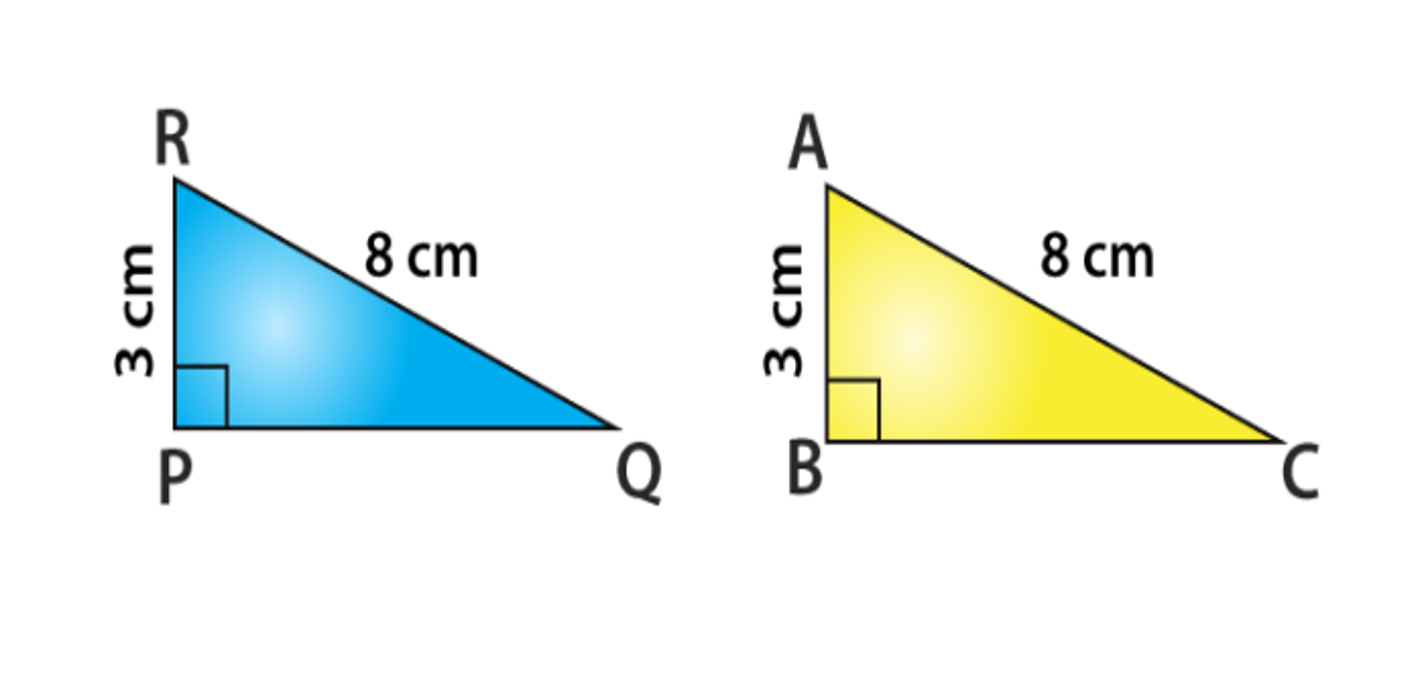
कर्ण AC=RQ=8 सेमी
भुजा AB=RP=3 सेमी
अत: RHS सर्वांगसमता नियम से,
ΔABC≅ΔRPQ
OMR (One Minute Revision)
उदाहरण 9
दी गई आकृति में त्रिभुजों के भागों की माप दी गई है। RHS सर्वांगसमता प्रतिबंध का उपयोग करके बताइए कि कौन-कौन से त्रिभुज युग्म सर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में, उन्हें सांकेतिक रूप में लिखिए।
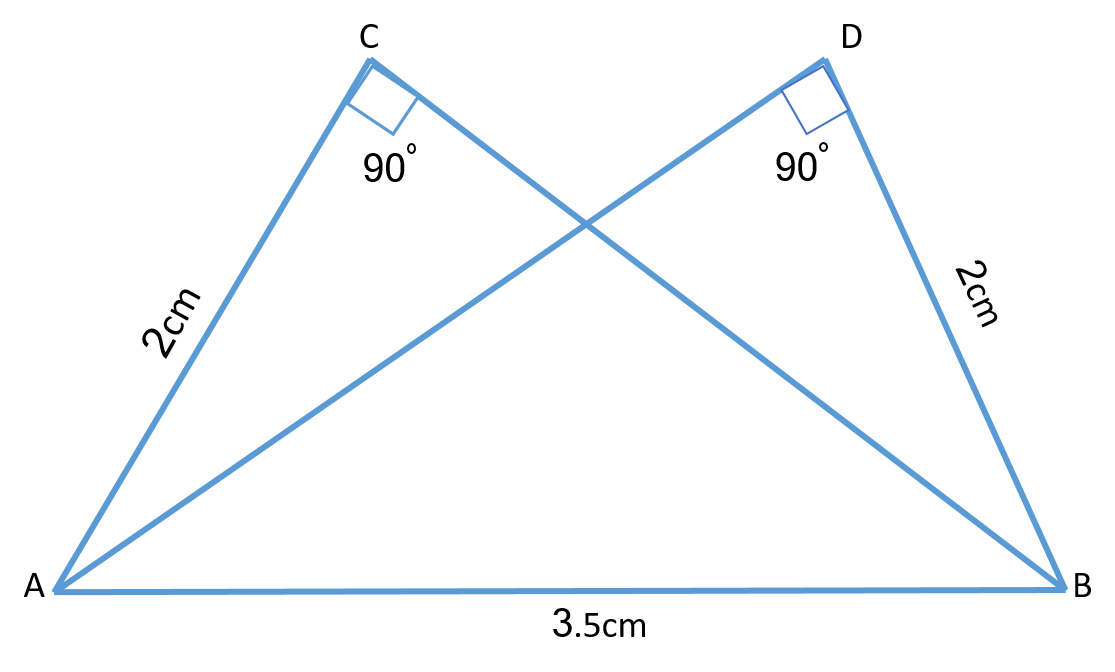
यहाँ, ΔACB और ΔADB में
∠C=∠D=90∘
AC=BD=8 सेमी
AB=AB=3 सेमी (उभयनिष्ठ भुजा)
अत: हम जानते हैं कि, यदि किसी समकोण त्रिभुज की एक भुजा और कर्ण दूसरे समकोण त्रिभुज की संगत भुजा तथा कर्ण के बराबर हों, तो वे त्रिभुज RHS सर्वांगसमता नियम से सर्वांगसम होते हैं।
अतः, ΔACB≅ΔBDA
उदाहरण 10
यदि आप ΔABC≅ΔDEF दर्शाना चाहते हैं।

RHS प्रतिबंध का उपयोग कीजिए। दिया है ∠BAC=∠DEF=90∘ और AB=DE है। अभीष्ट तीसरी शर्त बताइए।
हम जानते हैं कि, यदि किसी समकोण त्रिभुज की एक भुजा और कर्ण दूसरे समकोण त्रिभुज की संगत भुजा तथा कर्ण के बराबर हों, तो वे त्रिभुज RHS सर्वांगसमता नियम से सर्वांगसम होते हैं।
यहाँ ∠BAC=∠DEF=90∘ (समकोण)
BC=DF (कर्ण)
AB=DE (भुजा)
अतः ΔABC≅ΔDEF मे अभीष्ट तीसरी शर्त BC=DF हैं।