भिन्न एवं दशमलव कक्षा 7 गणित

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय मे हम भिन्न एवं दशमलव का अध्ययन करेंगे । जैसा कि हमने पिछली कक्षाओं में उचित भिन्न, विषम भिन्न, मिश्रित भिन्न एवं भिन्नों के योग एवं व्यवकलन के बारे मे अध्ययन किया हैं | इसके अतिरिक्त हमने, भिन्नों की तुलना, तुल्य भिन्न, भिन्नों को संख्या रेखा पर निरूपित करना, भिन्नों को क्रमबद्ध करना, के बारे में भी अध्ययन किया है। दशमलवों के अध्ययन में हम, उनकी तुलना, संख्या रेखा पर उनका निरूपण और उनका योग एवं व्यवकलन के बारे में चर्चा कर चुके हैं। अब हम भिन्नों एवं दशमलवों के गुणन एवं भाग के बारे में अध्ययन करेंगे।

आइये जानते है, भिन्नों को और करीब से ...

भिन्न (Fraction) एक संख्या है जो पूर्ण के किसी भाग को दर्शाती है।

जैसे : एक सेब के चार भाग किये जाते है जिनमें से उनके एक हिस्से को निकाल दिया गया है तो उसे $\frac{1}{4}$ के रूप में लिखा जाता हैं और शेष बचे हुए भाग को $\frac{3}{4}$ $(1 - \frac{1}{4} = \frac{3}{4})$ के रूप में लिखा जाएगा।

$\frac{2}{4}, \frac{5}{2}, \frac{6}{4}$ आदि भिन्न के उदाहरण हैं।

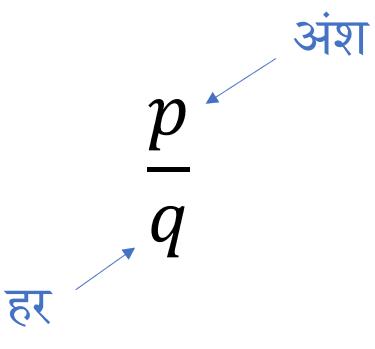
एक भिन्न के दो भाग होते हैं

1. अंश

अंश भिन्न का वह भाग होता है जो ऊपर लिखा जाता है। जैसे : $\frac{2}{7}$ में $2$ अंश है क्योंकि यह ऊपर लिखा जा रहा है।

2. हर

हर भिन्न का वह भाग होता है जो अंश के निचे लिखा जाता है। जैसे : $\frac{2}{7}$ में $7$ हर है क्योंकि यह अंश के नीचे लिखा जा रहा है।

भिन्न के प्रकार

भिन्न के मुख्यतः तीन प्रकार होते हैं:

1. उचित भिन्न

2. विषम भिन्न या अनुचित भिन्न

3. मिश्रित भिन्न

1. उचित भिन्न

जब किसी भिन्न का अंश उसके हर से कम होता है तो वह उचित भिन्न कहलाती हैं।

जैसे:

\frac{1}{4}, \frac{4}{9}, \frac{3}{5}, \frac{12}{17}

आदि।

2. विषम भिन्न

जब किसी भिन्न का अंश उसके हर से बड़ा होता है तो वह भिन्न विषम भिन्न कहलाती है।

जैसे:

\frac{4}{3}, \frac{9}{7}, \frac{5}{2}

आदि।

3. मिश्रित भिन्न

ऐसी भिन्न जिसके दो भाग होते हैं। उन भागों में से एक भाग तो पूर्ण संख्या होता है एवं दूसरा भाग उचित भिन्न होता है। या वह भिन्न जो एक पूर्णांक एवं भिन्न से मिलकर बनी होती है, मिश्रित भिन्न कहलाती है।

जैसे:

6 \frac{3}{4}, 2 \frac{3}{4}

आदि।

उदाहरण 1

निम्नलिखित में प्रत्येक का मान निकालिए :
$\frac{3}{10} + \frac{5}{15} - \frac{1}{30}$

दिया है,

$\frac{3}{10} + \frac{5}{15} - \frac{1}{30}$

अतः 10 ,15 ,30 का लघुत्तम समापवर्त्य $= 60$

$\frac{18 + 20 - 2}{60}$

$\Rightarrow \frac{38 - 2}{60}$

$\Rightarrow \frac{36}{60}$

चूंकि
$36 = 2 \times 2 \times 3 \times 3$ , $60 = 2 \times 2 \times 3 \times 5$

इसलिए ,

$\Rightarrow \frac{2 \times 2 \times 3 \times 3}{2 \times 2 \times 3 \times 5}$

implies( cancel(2)xxcancel(2)xxcancel(3)xx3)/(cancel(2)xxcancel(2)xxcancel(3)xx5)

$\Rightarrow \frac{3}{5}$ उत्तर

Learn more

उदाहरण 2

निम्नलिखित विषम भिन्न को मिश्रित भिन्न में परिवर्तित कीजिए -
$\frac{287}{21}$

दिया हैं,

$\frac{287}{21}$ को सरलतम रूप मे लिखने पर

$\Rightarrow \frac{7 \times 41}{7 \times 3}$

$\Rightarrow \frac{41}{3}$

41 को 3 से भाग देने पर , भाजक $= 3$ , भागफल $= 13$ , शेषफल $= 2$

अतः मिश्रित भिन्न $= 13 \frac{2}{3}$ उत्तर

Learn more

भिन्नों का गुणा

हम जानते हैं कि एक आयत का क्षेत्रफल कैसे ज्ञात किया जाता है। चूँकि आयत का क्षेत्रफल लंबाई $\times$ चौड़ाई के बराबर होता है। यदि किसी आयत की लंबाई एवं चौड़ाई क्रमश: 7 cm और 4 cm है तो इसका क्षेत्रफल क्या होगा?
इसका क्षेत्रफल $7 \times 4 = 28 c m^{2}$ होगा।

यदि आयत की लंबाई एवं चौड़ाई क्रमश: $7 \frac{1}{2}$ cm एवं $3 \frac{1}{2}$ cm है तो इसका क्षेत्रफल क्या होगा?

आप कहेंगे कि यह $7 \frac{1}{2} \times 3 \frac{1}{2} = \frac{15}{2} \times \frac{7}{2} c m^{2}$ है।

संख्याएँ $\frac{15}{2}$ और $\frac{7}{2}$ भिन्न हैं।

दिए हुए आयत का क्षेत्रफल ज्ञात करने के लिए यह ज्ञात करना आवश्यक है कि भिन्नों को गुणा कैसे किया जाए।

अतः हम अब सीखेंगे भिन्नो का गुणन ।

एक भिन्न का पूर्ण संख्या से गुणा

नीचे दिए गए आकृति को देखे जिसमे वृत को 4 बराबर भागों मे बांटा गया हैं जिसका प्रत्येक छायांकित भाग वृत का

\frac{1}{4}

भाग होगा |

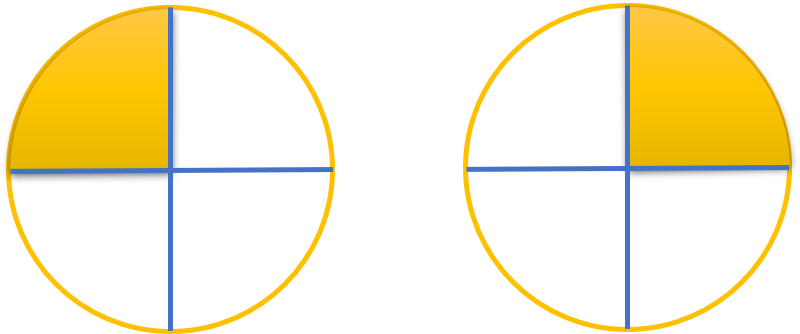
ocr_image

यदि ऊपर के दोनों वृतो को मिला दिया जाए तो

\frac{1}{4} + \frac{1}{4} = 2 \times \frac{1}{4}

भाग को निरूपित करेंगे, जिसे नीचे दिए गए आकृति मे दर्शाया गया हैं अतः यह वृत के

\frac{2}{4}

भाग को निरूपित करेगा |

ocr_image

या इसे गुणन से भी हल किया जा सकता हैं:

2 \times \frac{1}{4} = \frac{2}{4}

होगा | ( अंश का गुणा अंश के साथ

2 \times 1 = 2

एवं हर का गुणा हर के साथ

1 \times 4 = 4

, अतः

\frac{2}{4}

होगा )

एक और उदाहरण से समझते है नीचे दिए गए चित्र को देखे

ocr_image

दिए गये चित्र में बायीं ओर तीन बॉक्स तथा दायीं ओर एक बॉक्स है, जो पाँच बराबर भागों में बँटे हुए हैं। बायीं ओर के प्रत्येक बॉक्स में एक भाग में रंग भरा हुआ है,

अर्थात बायीं ओर के प्रत्येक बॉक्स में रंग भरा हुआ भाग

\frac{1}{5}

भाग को दर्शाता है।

तथा दायीं ओर के बॉक्स के तीन भाग में रंग भरा हुआ है अर्थात दायीं ओर के रंग भरे हुए भाग

\frac{3}{5}

भाग को दर्शाता है।

बायीं ओर के एक बॉक्स का रंग भरा हुआ भाग

\frac{1}{5}

भाग को दर्शाता है, अत: तीनों बॉक्स मिलकर

3 \times \frac{1}{5}

को दर्शाता है।

अतः

3 \times \frac{1}{5} = \frac{3 \times 1}{5} = \frac{3}{5}

होगा |

निम्न भिन्नों का गुणनफल ज्ञात कीजिए,
और यदि गुणनफल एक विषम भिन्न हैं तो इसे मिश्रित भिन्न मे व्यक्त कीजिए |

(1) $4 \times \frac{1}{3}$

हल:-

दिया है,

4 \times \frac{1}{3}

हम जानते हैं कि यदि किसी संख्या में हर नहीं हो, तो उसका हर 1 माना जाता है।

\Rightarrow

\frac{4}{1} \times \frac{1}{3}

हम जानते हैं कि दो या दो से अधिक भिन्न को गुणा करने के लिए एक के अंश को दूसरे के अंश से तथा एक के हर को दूसरे के हर से गुणा किया जाता है।

\Rightarrow

\frac{4 \times 1}{1 \times 3}

\Rightarrow \frac{4}{3}

अंश, हर से बड़ा है अतः एक विषम भिन्न हैं तो इसे मिश्रित भिन्न मे बदलने पर

\Rightarrow 1 \frac{1}{3}

उत्तर

(2) $\frac{2}{7} \times 3$

हल:-

दिया है,

\frac{2}{7} \times 3

हम जानते हैं कि यदि किसी संख्या में हर नहीं हो, तो उसका हर 1 माना जाता है।

\Rightarrow

\frac{2}{7} \times \frac{3}{1}

हम जानते हैं कि दो या दो से अधिक भिन्न को गुणा करने के लिए एक के अंश को दूसरे के अंश से तथा हर को दूसरे के हर से गुणा किया जाता है।

\Rightarrow

\frac{2 \times 3}{7 \times 1}

\Rightarrow \frac{6}{7}

उत्तर ( हर, अंश से बड़ा है , उचित भिन्न होगा )

(3) $\frac{9}{7} \times 6$

हल:-

दिया है,

\frac{9}{7} \times 6

हम जानते हैं कि यदि किसी संख्या में हर नहीं हो, तो उसका हर 1 माना जाता है।

\Rightarrow

\frac{9}{7} \times \frac{6}{1}

\Rightarrow \frac{9 \times 6}{7 \times 1}

\Rightarrow \frac{54}{7}

अंश , हर से बड़ा है अतः एक विषम भिन्न हैं तो इसे मिश्रित भिन्न मे बदलने पर

\Rightarrow 7 \frac{5}{7}

उत्तर

(4) $5 \times 2 \frac{3}{7}$

हल:-

दिया है,

5 \times 2 \frac{3}{7}

हम जानते हैं , कि किसी मिश्रित भिन्न को एक पूर्ण संख्या से गुणा करने से पहले मिश्रित भिन्न को विषम भिन्न मे बदलते हैं उसके बाद गुणा करते हैं

\Rightarrow 5 \times \frac{17}{7}

हम जानते हैं कि यदि किसी संख्या में हर नहीं हो, तो उसका हर 1 माना जाता है।

\Rightarrow

\frac{5}{1} \times \frac{17}{7}

\Rightarrow \frac{5 \times 17}{1 \times 7}

\Rightarrow \frac{85}{7}

अंश, हर से बड़ा है अतः एक विषम भिन्न हैं तो मिश्रित भिन्न मे बदलने पर

\Rightarrow 12 \frac{1}{7}

उत्तर

भिन्न का भिन्न से गुणन

\frac{2}{5} \times \frac{3}{7}

जैसा की आप देख सकते है कि ऊपर दो भिन्न दी गई है

हम जानते हैं की भिन्नों के गुणा मे, अंश का गुणा अंश के साथ

= (2 \times 3)

तथा हर का गुणा हर के साथ

= (5 \times 7)

अतः

= \frac{2 \times 3}{5 \times 7}

\Rightarrow \frac{6}{35}

ज्ञात कीजिए

(1) $\frac{2}{3} \times \frac{1}{5}$

हल:

दिया हैं,

\frac{2}{3} \times \frac{1}{5}

अतः अब हम जानते हैं कि भिन्नों के गुणा मे, अंश का गुणा अंश के साथ एवं हर का गुणा हर के साथ होता है

\Rightarrow \frac{2 \times 1}{3 \times 5}

\Rightarrow \frac{2}{15}

उत्तर

(2) $\frac{3}{5}$ का $\frac{1}{4}$

हल:

दिया हैं,

\frac{3}{5}

का

\frac{1}{4}

हम जानते हैं कि गणित में "का" का अर्थ "गुणा" होता है, अत: "का" को "(×)" से बदलने पर

\Rightarrow \frac{3}{5} \times \frac{1}{4}

अतः अब हम जानते हैं कि भिन्नो के गुणा मे, अंश का गुणा अंश के साथ एवं हर का गुणा हर के साथ होता है

\Rightarrow \frac{3 \times 1}{5 \times 4}

\Rightarrow \frac{3}{20}

उत्तर

3. $\frac{1}{7}$ का $\frac{2}{3}$

हल:

दिया हैं,

\frac{1}{7}

का

\frac{2}{3}

हम जानते हैं कि गणित में "का" का अर्थ "गुणा" होता है, अत: "का" को "(×)" से बदलने पर

\Rightarrow \frac{1}{7} \times \frac{2}{3}

\Rightarrow \frac{1 \times 2}{7 \times 3}

\Rightarrow \frac{2}{21}

उत्तर

गुणा कीजिए और न्यूनतम रूप मे बदलिए यदि संभव है तो

1. $\frac{2}{3} \times 2 \frac{2}{3}$

हल:

दिया हैं,

\frac{2}{3} \times 2 \frac{2}{3}

हम जानते हैं, कि किसी मिश्रित भिन्न को गुणा करने से पहले मिश्रित भिन्न को विषम भिन्न मे बदलते हैं उसके बाद गुणा करते हैं

\Rightarrow \frac{2}{3} \times \frac{8}{3}

(2 \frac{2}{3} = 2 + \frac{2}{3} = \frac{3 \times 2 + 2}{3} = \frac{8}{3})

अतः अब हम जानते हैं कि भिन्नो का गुणा मे, अंश का गुणा अंश के साथ एवं हर का गुणा हर के साथ होता है

\Rightarrow \frac{2 \times 8}{3 \times 3}

\Rightarrow \frac{16}{9}

अंश , हर से बड़ा है अतः एक विषम भिन्न हैं तो इसे मिश्रित भिन्न मे बदलने पर

\Rightarrow 1 \frac{7}{9}

उत्तर

2. $\frac{3}{8} \times \frac{6}{4}$

हल:

दिया हैं,

\frac{3}{8} \times \frac{6}{4}

\Rightarrow \frac{3 \times 6}{8 \times 4}

संख्या

4 (2 \times 2), 6 (2 \times 3), 8 (2 \times 2 \times 2)

को अभाज्य गुणनखंड रूप मे बदला जा सकता हैं

\Rightarrow \frac{3 \times 3 \times 2}{2 \times 2 \times 2 \times 2 \times 2}

\Rightarrow \frac{3 \times 3 \times 2}{2 \times 2 \times 2 \times 2 \times 2}

\Rightarrow \frac{3 \times 3}{2 \times 2 \times 2 \times 2}

\Rightarrow \frac{9}{16}

उत्तर

दिया हैं,

$\frac{3}{2} \times 5 \frac{1}{3}$

हम जानते हैं , कि किसी मिश्रित भिन्न को गुणा करने से पहले मिश्रित भिन्न को विषम भिन्न मे बदलते हैं उसके बाद गुणा करते हैं

$\Rightarrow \frac{3}{2} \times \frac{16}{3}$

$(5 \frac{1}{3} = 5 + \frac{1}{3} = \frac{5 \times 3 + 1}{3} = \frac{16}{3})$

अतः अब हम जानते हैं कि भिन्नो के गुणा मे, अंश का गुणा अंश के साथ एवं हर का गुणा हर के साथ होता है

$\Rightarrow \frac{3 \times 16}{2 \times 3}$

संख्या $16 (2 \times 2 \times 2 \times 2)$ को अभाज्य गुणनखंड मे बदला जा सकता हैं

$\Rightarrow \frac{3 \times 2 \times 2 \times 2 \times 2}{2 \times 3}$

implies (cancel(3)xxcancel(2 )xx2xx2xx2)/(cancel(2)xxcancel(3))

$\Rightarrow 2 \times 2 \times 2$

$\Rightarrow 8$

हम जानते है कि किसी भी संख्या के हर मे कुछ नहीं हो तो वहाँ 1 होगा

$\Rightarrow \frac{8}{1}$

उदाहरण 3

गुणा कीजिए और गुणनफल को न्यूनतम रूप में व्यक्त कीजिए -
$\frac{3}{2} \times 5 \frac{1}{3}$

Learn more

गुणनफल का मान

हमने देखा है कि दो पूर्ण संख्याओं का गुणनफल उन दोनों संख्याओं में से प्रत्येक से बड़ा होता है।

उदाहरण:
$3 \times 4 = 12$ और $12 > 4, 12 > 3$ . अतः अब हम भिन्नो के गुणनफल के मान की तुलना करेंगे -

दो या दो से अधिक भिन्नों की तुलना करने के लिए सबसे पहले हमे उनके हर को समान करना पड़ता हैं |

हर को समान करने के लिए आप LCM ले सकते हैं |

अब आगे जिसका अंश बड़ा होगा वह बड़ा भिन्न होगा |

उदाहरण:
$\frac{2}{3}$ और $\frac{8}{15}$ कि तुलना करते हैं

अतः तुलना करने के लिए पहले हर को समान करना होगा

अतः

\frac{2}{3}

के अंश और हर मे 5 से गुणा करने पर

\frac{2 \times 5}{3 \times 5}

\frac{8}{15}

\frac{10}{15}, \frac{8}{15}

अब दोनों का हर समान हैं अतः जिसका अंश बड़ा होगा वही बड़ा भिन्न होगा

स्पष्ट हैं की,

\frac{10}{15} > \frac{8}{15}

अतः

\frac{2}{3} > \frac{8}{15}

उचित भिन्नो के गुणनफल की तुलना

\frac{2}{3} \times \frac{4}{5} = \frac{8}{15}

ऊपर दो उचित भिन्न दी गयी हैं जिनका गुणनफल का मान

\frac{8}{15}

हैं

अतः

\frac{2}{3}

एवं

\frac{4}{5}

की तुलना

\frac{8}{15}

से करने पर

हर को समान करने के लिए

\frac{2}{3}

के अंश और हर मे 5 का तथा

\frac{4}{5}

के अंश और हर मे 3 का गुणा करने पर, हर समान हो जाएगा

\frac{2 \times 5}{3 \times 5}

\frac{8}{15}

और

\frac{4 \times 3}{5 \times 3}, \frac{8}{15}

\Rightarrow \frac{10}{15}, \frac{8}{15}

और

\frac{12}{15}, \frac{8}{15}

अतः

\frac{10}{15} > \frac{8}{15}

और

\frac{12}{15} > \frac{8}{15}

\Rightarrow \frac{2}{3} > \frac{8}{15}

और

\frac{4}{5} > \frac{8}{15}

हम पाते हैं कि जब दो उचित भिन्नों को गुणा किया जाता हैं तो गुणनफल दोनों भिन्नों से कम होता है।

विषम भिन्नों के गुणनफल की तुलना

\frac{7}{3} \times \frac{5}{2} = \frac{35}{6}

ऊपर दो विषम भिन्न दी गयी हैं जिनका गुणनफल का मान

\frac{35}{6}

हैं |

अतः

\frac{7}{3}

एवं

\frac{5}{2}

की तुलना

\frac{35}{6}

से करने पर

\frac{7}{3}

\frac{35}{6}

और

\frac{5}{2}

\frac{35}{6}

हर को समान करने के लिए

\frac{7}{3}

के अंश और हर मे 2 का तथा

\frac{5}{2}

मे 3 का गुणा करने पर,हर समान हो जाएगा

\frac{7 \times 2}{3 \times 2}

\frac{35}{6}

और

\frac{5 \times 3}{2 \times 3}, \frac{35}{6}

\Rightarrow \frac{14}{6}, \frac{35}{6}

और

\frac{15}{6}, \frac{35}{36}

अतः

\frac{14}{6} < \frac{35}{6}

और

\frac{15}{6} < \frac{35}{36}

\Rightarrow \frac{7}{3} < \frac{35}{6}

और

\frac{5}{2} < \frac{35}{36}

हम पाते हैं कि जब दो विषम भिन्नों को गुणा किया जाता हैं तो गुणनफल का मान प्रत्येक भिन्न से अधिक होता है।

उदाहरण 4

$\frac{3}{4}$ का $\frac{2}{7}$ अथवा $\frac{5}{8}$ का $\frac{3}{5}$ कौन बड़ा है ?

दिया हैं,

$\frac{3}{4}$ का $\frac{2}{7}$ अथवा $\frac{5}{8}$ का $\frac{3}{5}$

हम जानते हैं कि गणित में "का" का अर्थ "गुणा" होता है, अत: "का" को "(×)" से बदलने पर

अतः $\frac{3}{4} \times \frac{2}{7}$ अथवा $\frac{5}{8} \times \frac{3}{5}$

अब हम जानते हैं कि भिन्नों का गुणा मे, अंश का गुणा अंश के साथ एवं हर का गुणा हर के साथ होता है

$\Rightarrow \frac{3 \times 2}{4 \times 7}$ अथवा $\frac{5 \times 3}{8 \times 5}$

$\Rightarrow \frac{3 \times 2}{2 \times 2 \times 7}$ अथवा $\frac{5 \times 3}{8 \times 5}$

implies (3 xx cancel(2))/( cancel(2)xx2 xx 7)अथवा ( cancel(5)xx3)/(8xx cancel(5))

$\Rightarrow \frac{3}{14}$ अथवा $\frac{3}{8}$

प्राप्त भिन्न के हर का लघुत्तम समापवर्तक (एलसीएम) = 56

अब दिये गये भिन्न की तुलना करने के लिए और उनके हर को बराबर करने के लिए उनके अंश तथा हर को आवश्यक संख्या से गुणा करते हैं,

$\Rightarrow \frac{3 \times 4}{14 \times 4}$ अथवा $\frac{3 \times 7}{8 \times 7}$

$\Rightarrow \frac{12}{56}$ अथवा $\frac{21}{56}$

स्पष्ट हैं, $\frac{12}{56} < \frac{21}{56}$

अतः $\frac{5}{8}$ का $\frac{3}{5}$ बड़ा हैं |

Learn more

उदाहरण 5

निम्नलिखित को अवरोही क्रम मे लिखिए ?

$\frac{1}{5}, \frac{3}{7}, \frac{7}{10}$

दिया है,

$\frac{1}{5}, \frac{3}{7}, \frac{7}{10}$

हम जानते हैं की , अवरोही क्रम अर्थात घटते क्रम ,

अतः 5,7,10 का LCM (ल.स.) = 70

अब दिए गए भिन्न के हर को 70 के बराबर करना हैं

$\Rightarrow \frac{1}{5} = \frac{1 \times 14}{5 \times 14} = \frac{14}{70}$

$\Rightarrow \frac{3}{7} = \frac{3 \times 10}{7 \times 10} = \frac{30}{70}$

$\Rightarrow \frac{7}{10} = \frac{7 \times 7}{10 \times 7} = \frac{49}{70}$

स्पष्ट हैं, $\frac{49}{70} > \frac{30}{70} > \frac{14}{70}$

इसलिए, $\frac{7}{10} > \frac{3}{7} > \frac{1}{5}$

अतः दिए गए भिन्न का अवरोही क्रम $\frac{7}{10} > \frac{3}{7} > \frac{1}{5}$ हैं |

Learn more

भिन्न का व्युत्क्रम

ऐसी शून्येतर संख्याएँ जिनका परस्पर गुणनफल 1 है, एक दूसरे के व्युत्क्रम कहलाती हैं।

इस प्रकार $\frac{5}{9}$ का व्युत्क्रम $\frac{9}{5}$ और $\frac{9}{5}$ का $\frac{5}{9}$ हैं

अतः $\frac{5}{9} \times \frac{9}{5} = 1$

उदाहरण :

2 का व्युत्क्रम $\frac{1}{2}$ है ।

जब 2 को $\frac{1}{2}$ से गुणा किया जाता है, तो गुणनफल 1 होता है।

अर्थात $2 \times \frac{1}{2} = 1$

इसी प्रकार , $\frac{1}{4}$ का व्युत्क्रम 4 है।

अर्थात, $\frac{1}{4} \times 4 = 1$

उसी प्रकार, $\frac{3}{4}$ का व्युत्क्रम $\frac{4}{3}$ है

क्योंकि $\frac{3}{4} \times \frac{4}{3} = 1$

उदाहरण 6

निम्नलिखित भिन्नो का व्युत्क्रम लिखिए :
$13 \frac{2}{9}$

दिया हैं,

$13 \frac{2}{9}$

अतः मिश्रित भिन्न को विषम भिन्न मे बदलने पर ,

$13 \frac{2}{9} = \frac{119}{9}$

हम जानते हैं की किसी भी संख्या का उसके व्युत्क्रम के साथ गुणनफल हमेशा 1 होता हैं

अतः $\frac{119}{9}$ का व्युत्क्रम $\frac{9}{119}$ होगा

क्योंकि $\frac{119}{9} \times \frac{9}{119} = 1$

Learn more

भिन्नों का भाग

किसी पूर्ण संख्या का भिन्न से भाग

किसी पूर्ण संख्या को एक भिन्न से भाग करने के लिए उस पूर्ण संख्या को उस भिन्न के व्युत्क्रम से गुणा करना होता है।

उदाहरण 1

3 को

\frac{5}{4}

से भाग दीजिए ?

हल:

3 \div \frac{5}{4}

यहाँ

\frac{5}{4}

का व्युत्क्रम

= \frac{4}{5}

होगा |

अतः ,

3 \div \frac{5}{4} = 3 \times \frac{4}{5}

\Rightarrow 3 \times \frac{4}{5}

\Rightarrow \frac{12}{5}

उदाहरण 2

5 को

\frac{7}{2}

से भाग दीजिए ?

हल:

5 \div \frac{7}{2}

यहाँ

\frac{7}{2}

का व्युत्क्रम

= \frac{2}{7}

होगा |

अतः ,

5 \div \frac{7}{2} = 5 \times \frac{2}{7}

\Rightarrow 5 \times \frac{2}{7}

\Rightarrow \frac{10}{7}

किसी भिन्न का पूर्ण संख्या से भाग

किसी भिन्न को एक पूर्ण संख्या से भाग देने के लिए, उस भिन्न को दिए गये पूर्ण संख्या के व्युत्क्रम से भी गुणा करना होता हैं।

उदाहरण 1

\frac{5}{4}

को 3 से भाग दीजिए ?

हल:

\frac{5}{4} \div 3

हम जानते हैं कि किसी भी संख्या के हर मे कुछ नहीं दिया गया हैं इसका मतलब संख्या के हर मे 1 होता है |

\frac{5}{4} \div \frac{3}{1}

यहाँ

\frac{3}{1}

का व्युत्क्रम

= \frac{1}{3}

होगा |

अतः ,

\frac{5}{4} \div \frac{3}{1} = \frac{5}{4} \times \frac{1}{3}

\Rightarrow \frac{5 \times 1}{4 \times 3}

\Rightarrow \frac{5}{12}

उदाहरण 2

\frac{7}{2}

को 5 से भाग दीजिए ?

हल:

\frac{7}{2} \div 5

\frac{7}{2} \div \frac{5}{1}

यहाँ

\frac{5}{1}

का व्युत्क्रम

= \frac{1}{5}

होगा |

अतः ,

\frac{7}{2} \div \frac{5}{1} = \frac{7}{2} \times \frac{1}{5}

\Rightarrow \frac{7 \times 1}{5 \times 2}

\Rightarrow \frac{7}{10}

एक भिन्न की दूसरे भिन्न से भाग

किसी भिन्न को दूसरे भिन्न से भाग देने के लिए पहले भिन्न को दूसरे भिन्न के व्युत्क्रम से गुणा करना होता है।

उदाहरण 1

\frac{5}{4}

को

\frac{3}{7}

से भाग दीजिए ?

हल:

\frac{5}{4} \div \frac{3}{7}

यहाँ

\frac{3}{7}

का व्युत्क्रम

= \frac{7}{3}

होगा |

अतः ,

\frac{5}{4} \div \frac{3}{7} = \frac{5}{4} \times \frac{7}{3}

\Rightarrow \frac{5 \times 7}{4 \times 3}

\Rightarrow \frac{35}{12}

उदाहरण 2

\frac{7}{2}

को

\frac{5}{3}

से भाग दीजिए ?

हल:

\frac{7}{2} \div \frac{5}{3}

यहाँ

\frac{5}{3}

का व्युत्क्रम

= \frac{3}{5}

होगा |

अतः ,

\frac{7}{2} \div \frac{5}{3} = \frac{7}{2} \times \frac{3}{5}

\Rightarrow \frac{7 \times 3}{2 \times 5}

\Rightarrow \frac{21}{10}

दशमलव संख्या

आपने पिछली कक्षाओं में दशमलव संख्याओं के बारे में अध्ययन किया है। आइए यहाँ हम संक्षिप्त में इनका स्मरण करते हैं। निम्नलिखित सारणी को देखिए


सैकड़ा	दहाई	इकाई	दशांक	शतांश	सहसत्रांश	संख्या
2	5	3	1	4	7	253.147
6	2	9	3	2	1	629.321
0	4	3	1	9	2	43.192

उपर्युक्त सारणी में आपने ऐसी दशमलव संख्याएँ लिखी हैं जिनका प्रसारित स्थानीय मान दिया हुआ था। आप विलोम भी कर सकते हैं। अर्थात् यदि आपको संख्या दी हुई है तो आप इसका प्रसारित रूप लिख सकते हैं।

उदाहरण:

253.417 = 2 \times 100 + 5 \times 10 + 3 \times 1 + 4 \times \frac{1}{10} + 1 \times \frac{1}{100} + 7 \times \frac{1}{1000}

हम यह भी जानते हैं की दशमलव संख्या को कैसे जोड़ा और घटाया जाता हैं |

इस प्रकार

21.36 + 37.35 = 58.71

39.87 + 21.98 = 61.85

उदाहरण 7

कौन सी संख्या बड़ी है?
0.77 या 7

दिया हैं,

7 अथवा 0.77

यहाँ, 7 = 7.00

दिए गये दशमलव वाली संख्याओं की तुलना करने के लिए यदि दिए गये दशमलव वाली संख्याओं में दशमलव के पूर्व कोई अंक है, तो दशमलव के पहले वाली संख्याओं की तुलना की जाती है।

अत: यहँ स्पष्ट रूप से, 7 > 1

अर्थात 7 बड़ा है।

अत:, 7 > 0.77

अत:, 7 बड़ा है।

Learn more

उदाहरण 8

कौन सी संख्या बड़ी है?
1.37 या 1.39

दिया हैं,

1.37 अथवा 1.39

दिए गये दशमलव वाली संख्याओं की तुलना करने के लिए यदि दिए गये दशमलव वाली संख्याओं में दशमलव के पूर्व की संख्या बराबर है, तो दशमलव के बाद वाली संख्याओं की तुलना की जाती है।

यहाँ दी गयी संख्याओं में दशमलव के पहले वाली संख्याएँ बराबर है।

तथा दशमलव के बाद की संख्याएँ 37 तथा 39 है।

अत:, स्पष्ट रूप से, 39 बड़ी है 37 से। अत:, 1.37 < 1.39

अत:, 1.39 बड़ी है।

Learn more

दशमलव संख्याओं का गुणा

रेशमा ने ₹ 8.50 प्रति kg की दर से 1.5kg सब्जी खरीदी। उसे कितने धन का भुगतान करना चाहिए ?

निश्चित रूप से यह ₹ $8.50 \times 1.50$ होगा।

8.5 और 1.5 दोनों ही दशमलव संख्याएँ हैं।

इस प्रकार हमें एक ऐसी परिस्थिति मिलती है जहाँ हमें यह ज्ञात करने की आवश्यकता होती है ।

आइए अब दो दशमलव संख्याओं का गुणा सीखते हैं।

दशमलव संख्या का गुणा करने से पहले हमे उन्ही सख्याओं का बिना दशमलव का गुणा करना होता हैं अर्थात साधारण संख्याओं की तरह गुणा करना ।

इन संख्याओं को गुणा करने पर जो उत्तर आएगा हम उसमे दशमलव बिंदु लगायेंगे। बिंदु किस जगह लगाना है हम यह इस प्रकार ज्ञात कर सकते हैं। जिन दो संख्याओं को हमने गुणा किया है हम उन संख्याओं के दशमलव स्थानों का योग करेंगे एवं जो योग आएगा वही उन दो संख्याओं के गुणनफल का दशमलव स्थान होगा।

उदाहरण से समझते हैं -

0.08 \times 3.2

ऊपर जैसा कि आप देख सकते हैं हमारे पास दो दशमलव संख्याएं हैं जिनका हमें गुणा करना है। तो सबसे पहले हम उनमे से दशमलव बिंदु को हटाकर साधारण संख्याओं की तरह गुणा करना है |

अर्थात,

008 \times 32

\Rightarrow 8 \times 32

\Rightarrow 256

जिन दो संख्याओं को हमने गुणा किया है हम उन संख्याओं के दशमलव स्थानों का योग करेंगे एवं जो योग आएगा वही उन दो संख्याओं के गुणनफल का दशमलव स्थान होगा |

0.08 = 2 (दशमलव स्थान)
3.2 = 1 (दशमलव स्थान)
गुणनफल का दशमलव स्थान = 2+1 = 3

अतः इसका हल होगा : 0.256 उत्तर

एक और उदाहरण से समझते हैं -

1.22 \times 2.9

ऊपर जैसा कि आप देख सकते हैं हमारे पास दो दशमलव संख्या हैं जिनका हमें गुणा करना है तो सबसे पहले हम उनमे से दशमलव बिंदु को हटाकर साधारण संख्याओं की तरह गुणा करते है |

अर्थात,

122 \times 29 = 3538

जिन दो संख्याओं को हमने गुणा किया है हम उन संख्याओं के दशमलव स्थानों का योग करेंगे एवं जो योग आएगा वही उन दो संख्याओं के गुणनफल का दशमलव स्थान होगा |

1.22 = 2 (दशमलव स्थान)
2.9 = 1 (दशमलव स्थान)
गुणनफल का दशमलव स्थान = 2+1 = 3
अतः इसका हल होगा : 3.538 उत्तर

दशमलव संख्याओं का 10, 100, 1000 से गुणा

जब किसी दशमलव संख्या को 10,100 अथवा 1000 से गुणा किया जाता है तो गुणनफल के अंक वही होते हैं जो अंक दशमलव संख्या में होते हैं परंतु गुणनफल में दशमलव बिंदु दाईं तरफ उतने ही स्थानों से विस्थापित होता है। जितने 1 के अतिरिक्त शून्य होते हैं।

उदाहरण :

2.345 \times 10 = 23.45, 2.345 \times 100 = 234.5, 2.345 \times 1000 = 2345

अतः स्पष्ट हैं कि किसी दशमलव संख्या को यदि 10 से गुणा करते है तो उसका गुणनफल मे दशमलव दाई तरफ 1 स्थान आगे बड़ जाएगा |

जैसे,

2.156 \times 10 = 21.56

इसी प्रकार यदि किसी दशमलव संख्या को यदि 100 से गुणा करते है तो उसका गुणनफल मे दशमलव दाई तरफ 2 स्थान आगे बड़ जाएगा |

जैसे,

2.156 \times 100 = 215.6

इसी प्रकार यदि किसी दशमलव संख्या को यदि 1000 गुणा करते है तो उसका गुणनफल मे दशमलव दाई तरफ 3 स्थान आगे बड़ जाएगा |

2.156 \times 1000 = 2156

किसी भी दशमलव संख्या मे दशमलव को हटाने के लिए उसे भिन्न मे परिवर्तित किया जा सकता हैं | इसमे सबसे पहले दी गई संख्या मे दशमलव के बाद कितनी संख्या है उसे गिन लीजिए उसके बाद दशमलव के बाद जितनी संख्या होगी उतनी ही 0 उसके भिन्न मे 1 के बाद होगा |

इसी प्रकार ,

1.25 = \frac{125}{100}

आइए देखते हैं क्या हम दशमलव संख्याओं को 10 अथवा 100 अथवा 1000 से गुणा करने का कोई प्रतिरूप (पैटर्न) प्राप्त कर सकते हैं।

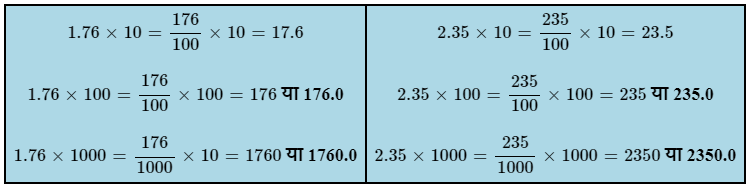
ocr_image

सारणी में गुणनफल के दशमलव बिंदु के विस्थापन को देखिए। यहाँ संख्याओं को 10,100 एवं 1000 से गुणा किया गया है।

1.76 \times 10 = 17.6

में अंक वही हैं अर्थात् दोनों तरफ 1, 7 और 6 है। क्या आपने इसे दूसरे गुणनफलों में भी देखा है? 1.76 और 17.6 को भी देखिए। दशमलव बिंदु दाईं अथवा बाईं, किस तरफ़ विस्थापित हुआ है ध्यान दीजिए 10 में 1 के अतिरिक्त एक शून्य है।

1.76 \times 100 = 176.0

में 1.76 एवं 176.0 को देखिये कि किस तरफ और कितने स्थानों से दशमलव बिंदु का विस्थापन हुआ है। दशमलव बिंदु दाईं तरफ़ दो स्थानों से विस्थापित हुआ है।

उदाहरण 9

शुभम 15 किग्रा सब्जी खरीदता है, जिसमें 3 किग्रा 250 ग्रा. प्याज, 4 किग्रा टमाटर और शेष आलू है। यदि प्रति किग्रा आलू का मूल्य 8 रु० है, तो शुभम द्वारा खरीदी गई आलू का मूल्य ज्ञात कीजिए।

दिया है,

कुल खरीदी गई सब्जी = 15 किग्रा

प्याज = 3.250 किग्रा

टमाटर = 4 किग्रा

शेष = आलू

1 किग्रा आलू का मूल्य = 8 रु०

आलू का कुल मूल्य = ?

अतः प्याज + टमाटर $= 3.250 + 4 = 7.250$ किग्रा

शेष आलू $= 15 - 7.250 = 7.750$ किग्रा

आलू का कुल मूल्य
$= 7.750 \times 8$
$= 62$ रु० उत्तर

Learn more

दशमलव संख्याओं का भाग

सविता अपनी कक्षा की सजावट के लिए एक डिजाईन तैयार कर रही थी। उसे $1.9 c m$ लंबाई वाली कुछ रंगीन कागज़ की पट्टियों की आवश्यकता थी। उसके पास $9.5 c m$ लंबाई वाली एक रंगीन कागज़ की पट्टी थी। इस पट्टी में से वह अभीष्ट लंबाई के कितने टुकड़े प्राप्त कर सकेगी। उसने सोचा शायद यह $\frac{9.5}{1.9}$ होगा।

$9.5$ और $1.9$ दोनों ही दशमलव संख्याएँ हैं। इसलिए हमें दशमलव संख्याओं की भाग भी जानने की आवश्यकता है।

दशमलव संख्याओं का 10, 100, 1000 से भाग

एक दशमलव संख्या को 10, 100 अथवा 1000 से भाग करने के लिए दशमलव संख्या में दशमलव बिंदु को बाईं तरफ उतने ही स्थान से विस्थापित करते हैं जितने 1 के अतिरिक्त शून्य होते हैं। इस प्रकार भागफल की प्राप्ति होती है। आइए अब हम एक दशमलव संख्या की 10, 100 और 1000 से भाग ज्ञात करते हैं। हम

31.5 \div 10

ज्ञात करते हैं।

31.5 \div 10

\Rightarrow \frac{315}{10} \times \frac{1}{10}

\Rightarrow \frac{315 \times 1}{10 \times 10}

\Rightarrow \frac{315}{100}

\Rightarrow 3.15

इसी प्रकार ,

31.5 \div 100

\Rightarrow \frac{315}{10} \times \frac{1}{100}

\Rightarrow \frac{315 \times 1}{10 \times 100}

\Rightarrow \frac{315}{1000}

\Rightarrow 0.315

इसी प्रकार ,

31.5 \div 1000

\Rightarrow \frac{315}{10} \times \frac{1}{1000}

\Rightarrow \frac{315 \times 1}{10 \times 1000}

\Rightarrow \frac{315}{10000}

\Rightarrow 0.0315

आइए हम यह देखते हैं कि क्या हम संख्याओं को 10, 100 अथवा 1000 से भाग करने का कोई प्रतिरूप ज्ञात कर सकते हैं। यह संख्याओं को 10, 100 अथवा 1000 से, संक्षिप्त विधि से भाग करने में हमारी सहायता कर सकता है।

$31.5 \div 10 = 3.15$ $31.5 \div 100 = 0.315$ $31.5 \div 1000 = 0.0315$	$231.5 \div 10 = 23.15$ $231.5 \div 100 = 2.315$ $231.5 \div 1000 = 0.2315$	$1.5 \div 10 = 0.15$ $1.5 \div 100 = 0.015$ $1.5 \div 1000 = 0.0015$

दशमलव संख्या का पूर्ण संख्या से भाग

एक दशमलव संख्या को पूर्ण संख्या से भाग करने के लिए सर्वप्रथम हम उन्हें पूर्ण संख्याओं के रूप में भाग देते हैं। तब भागफल में दशमलव बिंदु को वैसे ही रखा जाता है जैसे दशमलव संख्या में।

आइए, हम

6.4 \div 2

ज्ञात करते हैं। याद कीजिए हम इसे

\frac{6.4}{2}

के रूप में भी लिखते हैं।

इसलिए, जैसा कि हमने भिन्नों से सीखा है

\Rightarrow 6.4 \div 2 = (\frac{64}{10}) \div 2

\Rightarrow (\frac{64}{10}) \times (\frac{1}{2})

\Rightarrow \frac{64 \times 1}{10 \times 2}

\Rightarrow \frac{2 \times 32 \times 1}{10 \times 2}

implies(cancel(2 )xx32 xx 1)/(10xxcancel(2 ))

\Rightarrow \frac{32}{10}

\Rightarrow 3.2

अथवा, आइए सर्वप्रथम हम 64 को 2 से भाग करते है। हम 32 प्राप्त करते हैं। 6.4 में दशमलव बिंदु के दाईं तरफ एक अंक है। 32 में दशमलव इस प्रकार रखिए ताकि दशमलव के दाईं तरफ़ केवल एक ही अंक रह पाए। हम फिर से 3.2 प्राप्त करते हैं।

अतः ,

\frac{64}{2} = 32

\Rightarrow 3.2

चूंकि 6.4 में दशमलव बिंदु के दाईं तरफ एक अंक है। अतः संख्या 32 मे दशमलव के दाईं तरफ़ केवल एक ही अंक रह पाए

\Rightarrow 3.2

इसी तरह

19.5 ÷ 5 ज्ञात करने के लिए पहले 195÷ 5 ज्ञात करते हैं तो 39 प्राप्त करते हैं। 19.5 में दशमलव बिंदु के दाईं तरफ एक अंक है। 39 में दशमलव बिंदु को इस प्रकार रखते हैं की दाईं तरफ केवल एक अंक रह पाए। अतः 3.9 प्राप्त होगा ।

एक दशमलव संख्या का दूसरे दशमलव संख्या से भाग

आइए हम

\frac{25.5}{0.5}

को अर्थात

25.5 \div 0.5

ज्ञात करते हैं

हल: दिया हैं ,

25.5 \div 0.5

अतः अब हम जानते हैं की किसी दशमलव संख्या मे दशमलव को हटाने के लिए उसे भिन्न मे बदल जाता हैं दशमलव संख्या मे दशमलव के बाद जितनी संख्या होती है, उसके हर मे 1 के बाद उतनी ही शून्य लगानी पड़ती हैं

इसलिए ,

25.5 \div 0.5 = \frac{255}{10} \div \frac{5}{10}

\Rightarrow \frac{255 \times 10}{10 \times 5}

\Rightarrow \frac{255 \times 10}{10 \times 5}

implies(255xxcancel(10 ))/(cancel(10 )xx5)

\Rightarrow \frac{255}{5}

\Rightarrow 51

हम पाते हैं कि 0.5 में दशमलव के दाई तरफ़ एक अंक है। अतः 0.5 को भिन्न रूप में लिखने के लिए 5 को 10 से भाग दिया गया हैं | इसी तरह से 25.5 को भिन्न रूप में लिखने के लिए 255 को 10 से भाग दिया गया हैं |

उदाहरण 10

सीमेंट की कुछ बोरियों का मूल्य 3150.40 रु० है। यदि एक बोरी सीमेंट का मूल्य 196.90 रु० है, तो सीमेंट की बोरियों की संख्या ज्ञात कीजिए।

दिया हैं,

सीमेंट की कुछ बोरियों का मूल्य 3150.40 रु०

एक बोरी सीमेंट का मूल्य 196.90 रु०

ज्ञात करना हैं सीमेंट की बोरियों की संख्या ?

अतः सीमेंट की बोरियों की संख्या = $\frac{3150.40}{196.90}$

$\Rightarrow \frac{\frac{315040}{100}}{\frac{19690}{100}}$

$\Rightarrow \frac{315040}{100} \times \frac{100}{19690}$

implies(315040xxcancel(100))/(cancel(100)xx19690)

$\Rightarrow \frac{315040}{19690}$ = 16 उत्तर

Learn more

सारांश

हमने पिछली कक्षा में भिन्न एवं दशमलव के बारे में, तथा उन पर योग एवं व्यवकलन की संक्रियाओं सहित अध्ययन किया हुआ है।

अब हमने भिन्नों एवं दशमलवों पर गुणन एवं भाग की संक्रियाओं का अध्ययन किया है।

हमने अध्ययन किया है कि भिन्नों को कैसे गुणा किया जाए। दो भिन्नों को गुणा करने के लिए उनके अंशों एवं हरों को पृथक्-पृथक् गुणा किया जाता है और फिर गुणनफल को अंशों का गुणनफल

/

हरों का गुणनफल के रूप में लिखा जाता है।

उदाहरण:

\frac{2}{3} \times \frac{5}{7} = \frac{2 \times 5}{3 \times 7} = \frac{10}{21}

भिन्नों का गुणा प्रचालक 'का' के रूप में काम करती है।

उदाहरण: 2 का

\frac{1}{2}

होता है

\frac{1}{2} \times 2 = 1

(a) दो उचित भिन्नों का गुणनफल, गुणा किए गए प्रत्येक भिन्न से कम होता है।

(b) एक उचित और एक विषम भिन्न का गुणनफल विषम भिन्न से कम होता है और उचित भिन्न से अधिक होता है।

(c) दो विषम भिन्नों का गुणनफल, गुणा किए गए दोनों भिन्नों में से प्रत्येक से बड़ा होता है।

एक भिन्न का व्युत्क्रम इसके अंश और हर को परस्पर बदलने से प्राप्त होता है।

हमने देखा है कि दो भिन्नों को कैसे भाग दिया जाता है :

(a) एक पूर्ण संख्या को किसी भिन्न से भाग करते समय हम पूर्ण संख्या को भिन्न के व्युत्क्रम से गुणा करते हैं।

उदाहरण:

2 \div \frac{3}{5} = 2 \times \frac{5}{3} = \frac{2 \times 5}{3 \times 1} = \frac{10}{3}

(b) एक भिन्न को पूर्ण संख्या से भाग करने के लिए हम भिन्न को पूर्ण संख्या के व्युत्क्रम से गुणा करते हैं।

उदाहरण:

\frac{3}{5} \div 2 = \frac{3}{5} \times \frac{1}{2} = \frac{3 \times 1}{5 \times 2} = \frac{3}{10}

\frac{3}{5} \div \frac{2}{7}

= \frac{3}{5} \times \frac{7}{2} = \frac{3 \times 7}{5 \times 2} = \frac{21}{10}

हमने यह भी सीखा है कि दो दशमलव संख्याएँ कैसे गुणा की जाती हैं। दो दशमलव संख्याओं को गुणा करने के लिए सर्वप्रथम हम उन्हें पूर्ण संख्याओं के रूप में गुणा करते हैं। दोनों दशमलव संख्याओं में दशमलव बिंदु के दाईं तरफ अंकों की संख्या को गिनते हैं। गिनी हुई अंकों की संख्या का योग ज्ञात करते हैं। सबसे दाएँ स्थान से अंकों को गिनते हुए गुणनफल में दशमलव बिंदु रखा जाता है। यह गिनती पूर्व में प्राप्त योग के समान होनी चाहिए।

उदाहरण:

0.5 \times 0.7 = 0.35

एक दशमलव संख्या को 10, 100 अथवा 1000 से गुणा करने के लिए हम उस संख्या में दशमलव बिंदु को दाईं तरफ उतने ही स्थान से विस्थापित करते हैं जितने 1 के अतिरिक्त शून्य होते हैं।

अतः

0.53 \times 10 = 5.3, 0.53 \times 100 = 53, 0.53 \times 1000 = 530

हमने देखा है कि दशमलव संख्याएँ कैसे विभाजित की जाती है।

(a) एक दशमलव संख्या को पूर्ण संख्या से भाग करने के लिए सर्वप्रथम हम उन्हें पूर्ण संख्याओं के रूप में भाग देते हैं। तब भागफल में दशमलव बिंदु को वैसे ही रखा जाता है जैसे दशमलव संख्या में।

उदाहरण:

8.4 \div 4 = 2.1

ध्यान दीजिए हम यहाँ पर केवल ऐसे विभाजनों की बात कर रहे हैं जिनमें शेषफल शून्य है।

(b) एक दशमलव संख्या को 10, 100 अथवा 1000 से भाग करने के लिए दशमलव संख्या में दशमलव बिंदु को बाईं तरफ उतने ही स्थान से विस्थापित करते हैं जितने 1 के अतिरिक्त शून्य होते हैं। इस प्रकार भागफल की प्राप्ति होती है।

इसलिए,

23.9 \div 10 = 2.39, 23.9 \div 100 = 0.239, 23.9 \div 1000 = 0.02390

(c) दो दशमलव संख्याओं को भाग करते समय सर्वप्रथम हम दोनों संख्याओं में दशमलव बिंदु को दाईं तरफ़ समान स्थानों से विस्थापित करते हैं और तब भाग देते हैं। अतः

12.4 \div 0.2 = 124 \div 2 = 62

Home
Ask Doubt
Profile