पूर्णांक कक्षा 7 गणित
भूमिका
बच्चों इस अध्याय के शीर्षक के अनुसार इस अध्याय मे हम पूर्णांको का अध्ययन करेंगे| आपने कक्षा 6 मे पूर्णांक संख्या का परिचय देखा है जिसमे हमने संख्या रेखा पर पूर्णांकों को प्रदर्शित करने के साथ संख्या रेखा पर पूर्णांकों की संक्रिया (जोड़ना, घटाना) देखा था| इस अध्याय मे हम पूर्णांकों के विभिन्न अंकगणितीय संक्रियाओ तथा उनके गुणों का अध्ययन करेंगे|
आइये जानते है, पूर्णांकों को और करीब से ...
पूर्णांक (Integer) वे संख्याएँ होती हैं जो धनात्मक, ऋणात्मक या शून्य हो सकती हैं, लेकिन भिन्न नहीं हो सकती हैं। इन संख्याओं का उपयोग विभिन्न अंकगणितीय संक्रियाओं जैसे जोड़, घटाव, गुणा और भाग को करने के लिए किया जाता है।
धनात्मक संख्या
1,2,3,4,...∞ तक कोई भी संख्या हो सकती है|
ऋणात्मक संख्या
−1,−2,−3,...−∞ तक तक कोई भी संख्या हो सकती है|
शून्य संख्या =0
अतः हम कह सकते है,की
−∞....−4,−3,−2,−1,0,1,2,3,4,5−...+∞
तक सभी संख्या पूर्णांक संख्या होंगे|
जैसे की 10,15,0,50−89,−28 ये सभी पूर्णांक संख्या है|
संख्या रेखा
संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
मध्य मे शून्य को रखते हैं।
अब संख्या रेखा में ऋणात्मक पूर्णांक संख्या को शून्य के बायीं ओर एवं धनात्मक पूर्णांक संख्या को दायीं ओर अंकित कर लेते हैं।
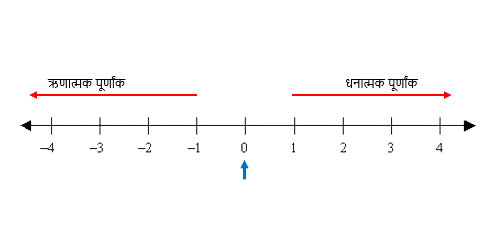
संख्या रेखा में बाएं से दायें → जाने पर संख्या बढ़ती है, दायें से बाएं ←जाने पर संख्या का मान घटता है। इसमें हम किसी पूर्णांक संख्या को आसानी से दर्शा सकते हैं। संख्या रेखा की सहायता से हम दो पूर्णांको को आसानी से जोड़ या घटा सकते हैं।
उदाहरण 1
संख्या रेखा मे −5 अंकित कीजिये
संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
मध्य मे शून्य को रखते हैं ।
अब संख्या रेखा में ऋणात्मक पूर्णांक संख्या को शून्य के बायीं ओर एवं धनात्मक पूर्णांक संख्या को दायीं ओर अंकित कर लेते हैं।
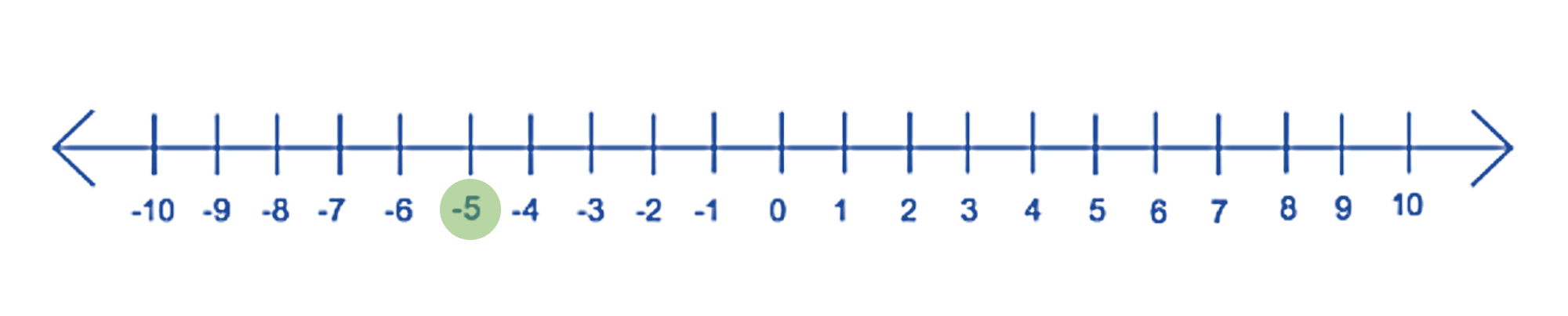
चित्र मे शून्य के बायीं ओर 5 इकाई जाने पर पूर्णांक −5 को संख्या रेखा में निरूपित किया गया है।
उदाहरण 2
निम्नलिखित संख्याओं को संख्या रेखा पर व्यवस्थित कीजिये और उनको आरोही और अवरोही कम में लिखिए 7,−5,4,0 और −4
संख्या रेखा बनाने के लिए सबसे पहले एक सीधी रेखा खींचते हैं।
मध्य मे शून्य को रखते हैं ।
अब संख्या रेखा में ऋणात्मक पूर्णांक संख्या को शून्य के बायीं ओर एवं धनात्मक पूर्णांक संख्या को दायीं ओर अंकित कर लेते हैं।
−7 एक ऋणात्मक पूर्णांक है अतः इसे हम शून्य से बायीं ओर 7 इकाई दूरी पर अंकित करेंगे।
−5 एक ऋणात्मक पूर्णांक है अतः इसे हम शून्य से बायीं ओर 5 इकाई दूरी पर अंकित करेंगे।
4 एक धनात्मक पूर्णांक है अतः इसे हम शून्य से दायीं ओर 4 इकाई दूरी पर अंकित करेंगे।
शून्य 0 संख्या रेखा के मध्य में स्थित है।
−4 एक ऋणात्मक पूर्णांक है अतः इसे हम शून्य से बायीं ओर 4 इकाई दूरी पर अंकित करेंगे।
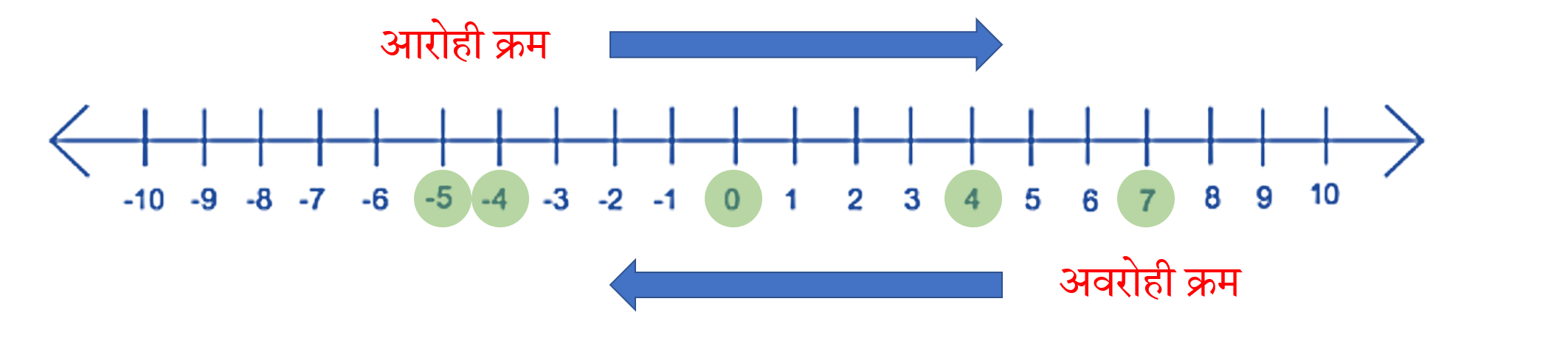
संख्या रेखा में बाएं से दायें →जाने पर संख्या बढ़ती है, दायें से बाएं ←जाने पर संख्या का मान घटता है।
अतः आरोही क्रम : −5,−4,0,4,7
एवं अवरोही क्रम : 7,4,0,−4,−5
पूर्णांकों के विभिन्न अंकगणितीय संक्रिया
पूर्णांकों का गुणन
जब हम पूर्णांकों का जोड़, घटाव करेंगे तो उसमे दो धनात्मक पूर्णांक या ऋणात्मक पूर्णांक का जोड़, घटाव करना होता हैं तो हम पूर्णांकों के गुणन मे सीखेंगे दो पूर्णांकों का चिन्ह अलग-अलग हो या एक जैसा हो तो कौन सी संक्रिया प्रयुक्त होगी।जैसे 7–(−3)
⇒7+3
⇒10
आइए समझते है –
| पूर्णांकों का गुणन | परिणाम | |
| धनात्मक × धनात्मक {(+) × (+)} | धनात्मक (+) | |
| ऋणात्मक × ऋणात्मक {(-) × (-)} | धनात्मक (+) | |
| धनात्मक × ऋणात्मक {(+) × (-)} | ऋणात्मक (-) | |
| ऋणात्मक × धनात्मक {(-) × (+)} | ऋणात्मक (-) |
| पूर्णांक | परिणाम | उदाहरण |
|---|---|---|
| धनात्मक + धनात्मक | धनात्मक | 2 + 2 = 4 |
| ऋणात्मक + ऋणात्मक | ऋणात्मक | (-2) + (-2) =-4 |
| धनात्मक + ऋणात्मक | धनात्मक ऋणात्मक शून्य | 10+(−5)=5 10+(−20)=−10 10+(−10)=0 |
| ऋणात्मक + धनात्मक | धनात्मक ऋणात्मक शून्य | (−5)+10=5 (−10)+5=−5 10+(−10)=0 |
घटाने के नियम
• दो धनात्मक पूर्णांकों को घटाने पर पूर्णांक धनात्मक, ऋणात्मक या शून्य हो सकता है |जैसे: 10 - 5 = 5 (यहाँ पर बड़ी संख्या धनात्मक है इसलिए घटाने पर धनात्मक पूर्णांक आएगा )
5 – 10 = -5 (यहाँ पर बड़ी संख्या ऋणात्मक है इसलिए घटाने पर ऋणात्मक पूर्णांक आएगा )
5 - 5 = 0 (यहाँ पर दोनों ही संख्या समान इसलिए घटाने पर शून्य आएगा )
• दो ऋणात्मक पूर्णांकों को घटाने पर पूर्णांक धनात्मक, ऋणात्मक या शून्य हो सकता है |
जैसे (-10) - (-5) = -10 + 5 = -5 ( पूर्णांकों के गुणन मे हमने सीखा है कि {(-) × (-)} = (+) इसलिए –(-5) धनात्मक 5 आया है उसके बाद बड़ी संख्या ऋणात्मक ही इसलिए जोड़ने पर ऋणात्मक पूर्णांक आएगा )
-5 – (-10) = -5 + 10 = 5 (यहाँ पर बड़ी संख्या धनात्मक है इसलिए घटाने पर धनात्मक पूर्णांक आएगा)
-5 – (-5) = -5 + 5 = 0 (यहाँ पर दोनों ही संख्या समान तथा उनके चिन्हों को हाल करने से एक ऋणात्मक और एक धनात्मक हो जा रहा हैं इसलिए घटाने पर शून्य आएगा )
• एक धनात्मक और एक ऋणात्मक पूर्णांक को घटाने पर पूर्णांक धनात्मक होगा और एक ऋणात्मक और एक धनात्मक पूर्णांक को घटाने पर पूर्णांक ऋणात्मक होगा |
जैसे (-10) - (-5) = -5 एवं (-5) - 10 = -15
| पूर्णांक | परिणाम | उदाहरण |
|---|---|---|
| धनात्मक - धनात्मक | धनात्मक ऋणात्मक शून्य | 10−5=5 5–10=−5 5−5=0 |
| ऋणात्मक - ऋणात्मक | धनात्मक ऋणात्मक शून्य | (−5)–(−10)=5 (−10)−(−5)=−5 −5–(−5)=0 |
| धनात्मक - ऋणात्मक | धनात्मक | 10−(−5)=20 |
| ऋणात्मक - धनात्मक | ऋणात्मक | (−5)−10=−15 |
उदाहरण 5
एक ऐसा पूर्णाक युग्म लिखिए जिसके योग से हमे निम्नलिखित प्राप्त होता है:
शून्य
योग शून्य प्राप्त करने के लिए किसी भी पूर्णांक में उसका योज्य प्रतिलोम जोड़ते हैं ।
यदि पूर्णांक a है तो योज्य प्रतिलोम −a होगा।
a+(−a)=0
अतः पूर्णांक युग्म जिसके योग से हमे शून्य प्राप्त होगा -
(i) 4 तथा −4
(ii)7 तथा −7
उदाहरण 6
प्रश्न को हल करके पूर्णांकों की पहचान कीजिए
(1.) (−5)−(−10)
(2.) 10+(−5)
(3.) (−5)+(−10)+(−7)
(4.) 6+(−2)−4
(5.) −25+5
( 6.) धनात्मक 4 और ऋणात्मक 25 का जोड़ क्या होगा ?
(7.) ऋणात्मक 9 और धनात्मक 9 का घटाव क्या होगा ?
(8.) (−2)+2+(−4) कौन सा पूर्णांक होगा ?
(9.) यदि 10 मे – ऋणात्मक 5 को घटाया जाता हैं तो कौन सा पूर्णांक होगा ?
(10.) −5×(−3)
(11.) −10×2×(−3)
1.)(−5)−(−10)
⇒−5+10 ( गुणन के नियमानुसार )
⇒5
⇒धनात्मक पूर्णांक
2.)10+(−5)
⇒10−5
⇒5
⇒धनात्मक पूर्णांक
3.)(−5)+(−10)+(−7)
⇒−5−7−10)
⇒−22
⇒ऋणात्मक पूर्णांक
4.)6+(−2)−4
⇒6−2−4
⇒−12
⇒ऋणात्मक पूर्णांक
5.)−25+5
⇒20
⇒धनात्मक पूर्णांक
6.)4+(−25)
⇒−21
⇒ऋणात्मक पूर्णांक
7.)−9+9
⇒0
⇒शून्य पूर्णांक
8.)−2+2+(−4)
⇒0+(−4)
⇒0−4
⇒0
⇒शून्य पूर्णांक
9.)10−(−5)
⇒10+5
⇒15
⇒धनात्मक पूर्णांक
10.)−5×(−3)
⇒−(−15)
⇒15
⇒धनात्मक पूर्णांक
11.)−10×2×(−3)
⇒−20×(−3)
⇒60
⇒ धनात्मक पूर्णांक
पूर्णांकों का विभाजन
पूर्णांकों के विभाजन को निम्न सारणी से समझते है –
| पूर्णांकों का विभाजन | परिणाम |
| धनात्मक / धनात्मक {(+) / (+)} | धनात्मक (+) |
| ऋणात्मक / ऋणात्मक {(-) / (-)} | धनात्मक (+) |
| धनात्मक / ऋणात्मक {(+) / (-)} | ऋणात्मक (-) |
| ऋणात्मक / धनात्मक {(-) / (+)} | ऋणात्मक (-) |
उदाहरण:
5−5=−1
−55=−1
105=2
उदाहरण 7
निम्नलिखित में कौन -सा कथन सत्य और कौन -सा कथन असत्य है ?
(−15)÷(−1)=15
चूंकि हम जानते हैं समान चिह्नों का भाग करने पर धनात्मक चिह्न प्राप्त होता है।
यहाँ −15 और −1 दोनों ही ऋणात्मक पूर्णांक हैं इसलिए
(−15)÷(−1)=+15=15
अतः भागफल/विभाजन का चिह्न धनात्मक है एवं दिया गया कथन सत्य है
उदाहरण 8
निम्नलिखित में कौन -सा कथन सत्य और कौन -सा कथन असत्य है ?
(−125)÷(+5)=25
चूंकि हम जानते हैं असमान चिह्नों का भाग करने पर ऋणात्मक चिह्न प्राप्त होता है।
यहाँ −125 और +5 दोनों ही अलग - अलग चिह्न वाले पूर्णांक हैं इसलिए
(−125)÷(+5)=−25
अतः भागफल/विभाजन का चिह्न ऋणात्मक है एवं दिया गया कथन असत्य है
पूर्णांकों के गुण
संवृत गुण
(1) योग के लिए - पूर्णांक संख्याएँ योग के लिए संवृत गुण का पालन करती हैं अर्थात इस नियम के अनुसार दो पूर्णांक को जोड़ने पर पूर्णांक ही प्राप्त होता हैं।
माना कि a और b पूर्णांक हैं
अतः a+b= पूर्णांक
उदाहरण:
5+5=10,2+4=6
(2) व्यवकलन के लिए- पूर्णांक संख्याएँ व्यवकलन के लिए भी संवृत गुण का पालन करती हैं अर्थात दो पूर्णांक को घटाने पर पूर्णांक ही प्राप्त होता हैं।
अतः a−b= पूर्णांक
उदाहरण:
5−5=0,2−4=−2
(3) गुणन के लिए – गुणन के लिए भी पूर्णांक संख्या संवृत गुण का पालन करती हैं।
अतः a×b= पूर्णांक
उदाहरण:
5×6=30,10×0=0
(4) विभाजन के लिए – पूर्णांक संख्या विभाजन के लिए संवृत गुण का पालन नहीं करती हैं।
अतः ab≠ पूर्णांक
उदाहरण:
12=0.5
(हम जानते हैं की भिन्न कभी भी पूर्णांक नहीं होता हैं)
क्रम विनिमय गुण
इसके अनुसार दो पूर्णांकों के क्रम मे बदलाव करके जोड़, घटाव, गुणा और भाग करते हैं।
माना कि a और b पूर्णांक हैं,
(1) योग के लिए - पूर्णांक संखयाएं योग के लिए क्रम विनिमय गुण का पालन करती हैं। इसके अनुसार दो पूर्णांकों का योग तथा उनके क्रम को बदलकर योग करने पर उत्तर समान आता है।
अतः a+b=b+a
उदाहरण
5+6=6+5=11,
2+3=3+2=5
(2) गुणन के लिए पूर्णांक संख्याएँ गुणन के लिए क्रम विनिमय गुण का पालन करती हैं।
अतः a×b=b×a
उदाहरण:
5×2=10=2×5
अतः a−b≠b−a
उदाहरण:
4−(−6)=10
(−6)–4=−10
⇒4 - (-6) ≠(−6) – 4
उदाहरण:
102=5
210=15
⇒102≠210
अतः ab≠ba
साहचर्य गुण
इस गुण के अनुसार संख्याओं का समूहन कैसा भी हो परंतु परिणाम एक जैसा आना चाहिए। योग और गुणन के लियें पूर्णांक साहचर्य गुण का पालन करती है।
माना कि a,b और c पूर्णांक हैं
a+(b+c)=(a+b)+c
इसी प्रकार गुणा के लिए;
a×(b×c)=(a×b)×c
उदाहरण:
1+[2+(−3)]=0
=(1+2)+(−3)=0
1×[2×(−3)]=−6
=(1×2)×(−3)=−6
वितरण गुण
वितरण गुण एक ब्रैकेट (कोष्ठक) के भीतर किसी अन्य गणितीय संक्रिया पर संचालन की वितरण क्षमता की व्याख्या करता है। यह या तो जोड़ पर गुणन का वितरण गुण हो सकता है या घटाव पर गुणन का वितरण गुण हो सकता है। यहां, पूर्णांकों को पहले जोड़ा या घटाया जाता है और फिर कोष्ठक के भीतर प्रत्येक संख्या के साथ गुणा किया जाता है और फिर जोड़ा या घटाया जाता है। इसे किसी भी पूर्णांक a,b और c के लिए इस प्रकार दर्शाया जा सकता है,
a×(b+c) =a×b+a×c
एवं
a×(b−c)=a×b−a×c
उदाहरण:
5(2+1)=5×2+5×1
⇒15=15
⇒LHS = RHS
योज्य तत्समक
जब किसी पूर्णांक को शून्य से जोड़ा जाता है तो वह वही संख्या देता है।इसलिए शून्य, पूर्णांकों के लिए योज्य तत्समक हैं। पूर्णांक a के लिए
अतः a+0=a=0+a
उदाहरण:
5+0=5,0+5=5
गुणात्मक तत्समक
जब कोई पूर्णांक को 1 से गुणा किया जाता हैं वह वही संख्या देता है।इसलिए 1 पूर्णांकों के लिए गुणात्मक तत्समक हैं। पूर्णांक a के लिए
अतः a⋅1=a
उदाहरण:
5×1=5
6×1=6
उदाहरण 9
सत्यापित कीजिए।
(−30)×[13+(−3)]=[(−30)×13]+[(−30)×(−3)]
दिया है -
(−30)×[13+(−3)]=[(−30)×13]+[(−30)×(−3)]
LHS=−30[13+(−3)]
=−30⋅[13−3]
=−30⋅10
=−300
RHS=[(−30)⋅13]+[(−30)(−3)]
=[−3⋅10⋅13]+[30⋅3]
=[−3⋅13⋅10]+[90]
=(−39⋅10)+90
=−390+90
=−(390−90)
=−300
चूंकि LHS=RHS
दिया गया समीकरण सिद्ध हुआ।
उदाहरण 10
जाँच कीजिये कि क्या
(−23)×20=23×(−20) है।
(−23)×20=23×(−20)
धनात्मक एवं ऋणात्मक पूर्णांक का गुणा करने पर ऋणात्मक चिह्न प्राप्त होता है
⇒−(23×20)=−(23×20)
⇒−460=−460
सारांश
| पूर्णांकों का गुणधर्म | योग | व्यवकलन |
| संवृत गुण | a+b= पूर्णांक | a−b= पूर्णांक |
| क्रम विनिमय गुण | a+b=b+a | a−b≠b−a |
| साहचर्य गुण | a+(b+c) = (a+b)+c | a−(b−c) ≠ (a−b)−c |
| पूर्णांकों का गुणधर्म | गुणा | विभाजन |
| संवृत गुण | a×b= पूर्णांक | ab≠ पूर्णांक |
| क्रम विनिमय गुण | a×b=b×a | (a÷b)≠(b÷a) |
| साहचर्य गुण | a×(b×c) = (a×b)×c | (a÷b)÷c ≠ a÷(b÷c) |
1. पूर्णांक संख्याओं का एक विशाल संग्रह है जिसमें पूर्ण संख्याएँ और उनके ऋणात्मक सम्मिलित हैं। इनका परिचय कक्षा VI मे कराया गया था।
2. आपने पिछली कक्षा में पूर्णांकों को संख्या रेखा पर निरूपित करने के बारे में एवं उनके योग और व्यवकलन के बारे में अध्ययन किया है।
3. अब हमने योग एवं व्यवकलन द्वारा संतुष्ट होने वाले गुणों का अध्ययन किया है।
(a) पूर्णांक योग एवं व्यवकलन दोनों के लिए संवृत्त है। अर्थात्, a + b और a - b दोनों पुनःपूर्णाक होते हैं, जहाँ a और b कोई भी पूर्णांक हैं।
(b) पूर्णांकों के लिए योग क्रमविनिमेय है, अर्थात् सभी पूर्णाकों तथा a , b के लिए,a+b = b+a
(c) पूर्णांकों के लिए योग साहचर्य है, अर्थात् सभी पूर्णाकों a, b तथा c के लिए (a+b)+c=a+(b+c) होता है।
(d) योग के अंतर्गत पूर्णांक शून्य तत्समक है, अर्थात किसी भी पूर्णाक के लिए, a+0=a=0+a होता है।
4. हमने यह भी अध्ययन किया है कि पूर्णांकों को कैसे गुणा किया जा सकता है और हमने पाया कि एक धनात्मक एवं एक ऋणात्मक पूर्णांक का गुणनफल एक ऋणात्मक पूर्णांक है, जबकि दो ऋणात्मक पूर्णाकों का गुणनफल एक धनात्मक पूर्णाक है।
उदाहरण: - 2x7 =14 और 3 x 8 = 24 है।
5. ऋणात्मक पूर्णांकों की संख्या सम होने पर उनका गुणनफल धनात्मक होता है जबकि यह संख्या विषम होने पर उनका गुणनफल ऋणात्मक होता है।
6. पूर्णाक गुणन के अंतर्गत कुछ गुणों को दर्शाते हैं।
(a) गुणन के अंतर्गत पूर्णांक संवृत होते हैं, अर्थात् किन्हीं दो पूर्णाकों a तथा b के लिएaxxb एक पूर्णांक होता है।
(b) पूर्णांकों के लिए गुणन क्रमविनिमेय होता है, अर्थात् किन्हीं दो पूर्णाको तथा b के लिए a×b=b×a होता है।
(c) गुणन के अंतर्गत पूर्णांक 1. तत्समक है, अर्थात् किसी भी पूर्णांक के लिए 1×a=a×l=a होता है।
(d) पूर्णांकों के लिए गुणन साहचर्य होता है, अर्थात् किन्हीं तीन पूर्णांकों a,b व c तथा के लिए, (a×b)×c=a×(b×c) होता है।
7. योग एवं गुणन के अंतर्गत पूर्णांक एक गुण को दर्शाते हैं, जिसे वितरण गुण कहा जाता है, अर्थात् किन्हों तीन पूर्णाको a ,b तथा c के लिए, a×(b+c)
=
a×b+a×c होता है।
8. योग एवं गुणन के अंतर्गत क्रमविनिमेयता सहचारिता और वितरणता के गुण हमारे परिकलन को आसान बनाते हैं।
9. हमने यह भी सीखा है कि पूर्णाकों को कैसे भाग दिया जाता है। हमने पाया कि
(a) जब एक धनात्मक पूर्णांक को एक ऋणात्मक पूर्णाक से भाग दिया जाता है या जब एक ऋणात्मक पूर्णाक को एक धनात्मक पूर्णांक से भाग दिया जाता है तो प्राप्त भागफल एक ऋणात्मक पूर्णांक होता है।
(b) एक ऋणात्मक पुर्णाक को दूसरे ऋणात्मक पूराक से भाग देने पर प्राप्त भागफल एक धनत्मक पूर्ण होता है।
10. किसी भी पूर्ण संख्या के लिए, हम पाते हैं कि
(a) a0 परिभाषित नहीं है।
(b) a1 =a