परिमाप और क्षेत्रफल कक्षा 7 गणित
भूमिका
इस अध्याय मे हम क्षेत्रमिति के अंतर्गत आने वाले द्विविमीय (समतल) आकृतियों के क्षेत्रफल तथा परिमाप का अध्ययन करेंगे। समतल आकृतियों का परिमाप इसकी सीमा से संबंधित माप और समतल आकृतियों का क्षेत्रफल इसके द्वारा घेरे गए क्षेत्र या सतह से संबंधित माप होती है।
आइये जानते है, परिमाप और क्षेत्रफल को और करीब से...
क्षेत्रमिति के अंतर्गत हम द्विविमीय और त्रिविमीय आकृति के बारे में पढ़ते है। जहाँ हम आयतन, क्षेत्रफल, परिमाप या परिमिति आदि को निकालना सीखते है लेकिन इस अध्याय में हम केवल द्विविमीय आकृतियों का अध्ययन करेंगे तथा क्षेत्रफल और परिमाप की गणना करना सीखेंगे।
द्विविमीय आकृतियां : आयत, वर्ग, त्रिभुज, समांतर चतुर्भुज, वृत आदि।
क्षेत्रफल (AREA) : किसी आकृति के उसके सभी भुजाओं से घिरे हुए तल को उस आकृति का क्षेत्रफल कहते हैं।
⇒ क्षेत्रफल की इकाई (Unit) वर्गमीटर, वर्ग सेंटीमीटर, वर्ग किलोमीटर आदि होती हैं।
परिमाप (PERIMETER) : किसी आकृति की सभी भुजाओं की लंबाइयों का योग उस आकृति का परिमाप या परिमिति कहलाता हैं।
⇒ परिमाप की इकाई (unit) मीटर, सेंटीमीटर, किलोमीटर आदि होती हैं।
कुछ द्विविमीय (2D) आकृतियों का क्षेत्रफल और परिमाप
| आलेख | आकार | क्षेत्रफल | परिमाप |
|---|---|---|---|
 | वर्ग | a×a | 4×a |
 | आयत | l×b | 2(l+b) |
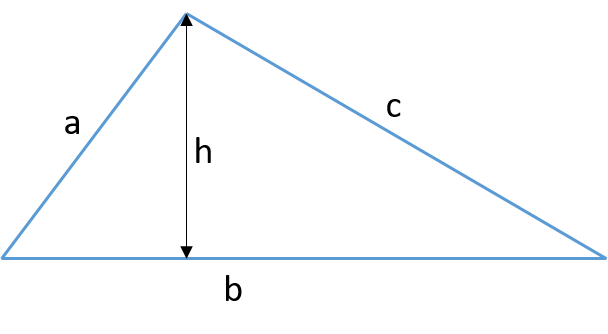 | त्रिभुज | 12×b×h | a+b+c |
 | समांतर चतुर्भुज | b×h | 2(b+h) |
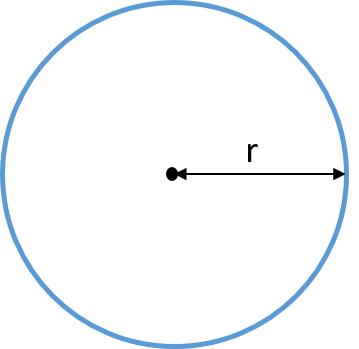 | वृत्त | πr2 | 2πr |
आयत
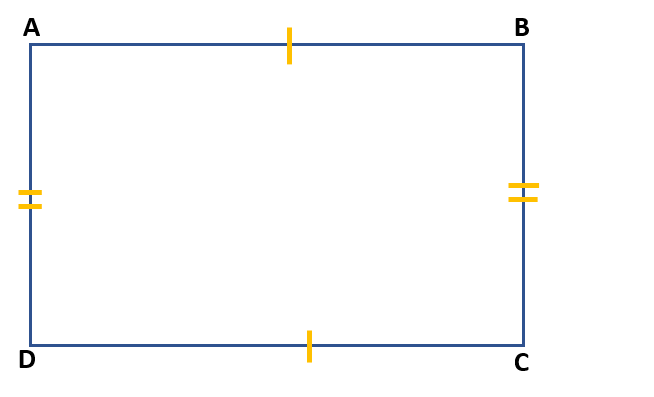
उपर्युक्त आकृति मे हम देख सकते है कि AB=CD तथा AD=BC है।
परिभाषा : चार भुजाओं वाली ऐसी बंद आकृति जिसमे आमने - सामने की भुजाओं के युग्म बराबर लंबाई के हो, आयत कहलाता है।
यदि हम इस आकृति के द्वारा घेरे गए क्षेत्रफल की गणना करे तो हम इसकी लंबाई और चौड़ाई का गुणा करके क्षेत्रफल ज्ञात कर सकते है।
परिमाप की गणना के लिए हमे इसकी चारों भुजाओं की लंबाई का योग करना होता है।
=AB+BC+CD+DA
चूंकि हम जानते है कि आमने - सामने की रेखाओं के युग्म बराबर लंबाई के है अर्थात
⇒AB=CD तथा AD=BC
⇒AB+BC+AB+BC
⇒ 2AB+2BC
⇒ 2(AB+BC)
अर्थात इसके परिमाप की गणना के लिए इसकी लंबाई और चौड़ाई को 2 से गुणा करके योग किया जाता है।
आइए एक उदाहरण की सहायता से समझते है :-
उदाहरण : दी गई आकृति के क्षेत्रफल और परिमाप की गणना कीजिए।
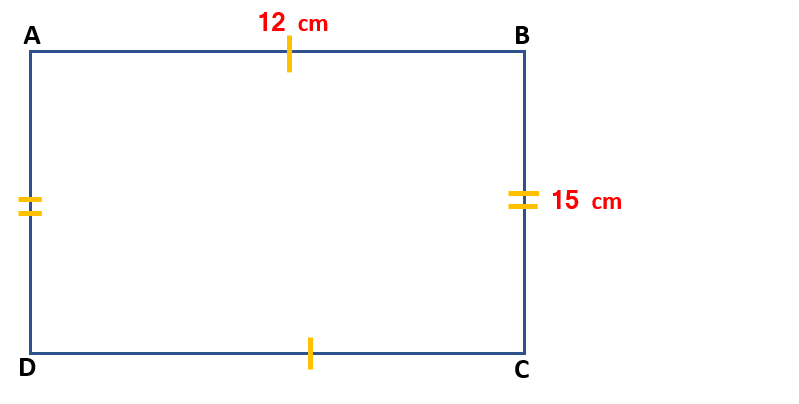
हल : चूंकि हम देख सकते है कि दी गई आकृति आयत है। अतः इसके आमने - सामने की भुजाएँ समान होगी।
लंबाई (AB)=12 cm
चौड़ाई (BC)=15 cm
क्षेत्रफल = लंबाई × चौड़ाई
=(12cm×15cm)
=180 cm2
क्षेत्रफल की गणना हमेशा वर्ग इकाई मे होती है।
परिमाप =2( लंबाई + चौड़ाई )
=2(12+15) cm
=2(27) cm
=54 cm
इस प्रकार यदि हमसे किसी भी आकार की आकृति के चारों तरफ बाढ़ अथवा दीवार पर पेंट करने जैसे किसी कार्य लिए कहा जाए तो हमे उस आकृति के क्षेत्रफल एवं परिमाप की सहायता लेनी चाहिए।
आइए समझते है :-
यदि हमे उपर्युक्त आकृति के चारों तरफ बाढ़ लगानी है तथा बाढ़ लगाने का खर्च 2 रुपए प्रति सेमी हो तो कुल खर्च ज्ञात कीजिए।
हल : चूंकि बाढ़ केवल आकृति के चारों तरफ किनारों पर लगाई जाती है अतः इसके लिए हमे उसके परिमाप की आवश्यकता होती है।
= परिमाप × दर
=54×2
=108 रुपए
अतः आयत के चारों तरफ बाढ़ लगाने का खर्च 2 रुपए प्रति सेमी की दर से 108 रुपए होगा।
परंतु यदि हमे इस आयत को पूरी तरह पेंट करने के लिए कहा जाए तो हमे प्रश्न मे निम्न प्रकार पूछा जाएगा :-
आकृति को पूरी तरह पेंट करने का खर्च 2 रुपए प्रति वर्ग सेमी हो तो कुल खर्च ज्ञात कीजिए।
हल : चूंकि पेंट आकृति के चारों तरफ की सतहों पर भी किया जाएगा अतः इसके लिए हमे उसके क्षेत्रफल की आवश्यकता होती है:-
= क्षेत्रफल × दर
=180×2
=360 रुपए
इस प्रकार हम आसानी से कुल खर्च की गणना कर सकते है।
उदाहरण 1
एक आयताकार भूखंड की चौड़ाई ज्ञात कीजिए। यदि इसका क्षेत्रफल 440m2 और लंबाई 22m हो। इसका परिमाप भी ज्ञात कीजिए।
दिया हैं,
आयताकार भूखंड की लंबाई =22 m
आयताकार भूखंड का क्षेत्रफल =440 m2
∵ आयताकार भूखंड का क्षेत्रफल = लंबाई × चौड़ाई
∴ 440 m2=22 m× चौड़ाई
⇒ चौड़ाई =440m222m=20m
∵ आयताकार भूखंड का परिमाप =2 (लंबाई + चौड़ाई )
=2(22+20) m
=2×42 m
=84m
अतः, आयताकार भूखंड की चौड़ाई 20 m तथा परिमाप 84 m हैं।
उदाहरण 2
2m लंबाई और 1m चौड़ाई वाले दरवाजे को एक दीवार में लगाया जाता है। दीवार की लंबाई 4.5m तथा चौड़ाई 3.6m है। ₹ 20 प्रति m2 की दर से दीवार पर सफेदी कराने का व्यय ज्ञात कीजिए।
आयताकार दरवाजे का क्षेत्रफल = लंबाई × चौड़ाई
=2 m×1 m=2 m2
दरवाजे सहित, दीवार का क्षेत्रफल = लंबाई × चौड़ाई
=4.5 m×3.6 m=16.2 m2
दरवाजे रहित, दीवार का क्षेत्रफल
= दरवाजे सहित, दीवार का क्षेत्रफल − दरवाजे का क्षेत्रफल
=(16.2−2) m2=14.2 m2
∵1 m2 दीवार पर सफेदी कराने का व्यय =₹20
∴14.2 m2 दीवार पर सफेदी कराने का व्यय =20<br><br>×14.2 =₹284
अतः, ₹20 प्रति m2 की दर से दीवार पर सफेदी कराने का व्यय ₹284 है।
वर्ग
परिभाषा : चार भुजाओं से बंद ऐसी आकृति जिसकी चारों भुजाएँ लंबाई मे समान हो, वर्ग कहलाता है।
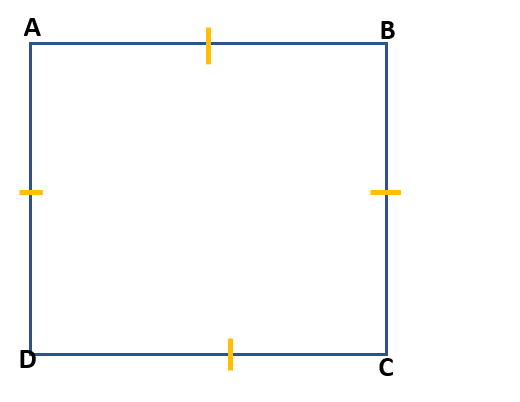
उपर्युक्त आकृति मे देख सकते है :-
⇒AB=BC=CD=DA
क्षेत्रफल : भुजा × भुजा
परिमाप : 4× भुजा
आइए एक उदाहरण से समझते है :-
उदाहरण :
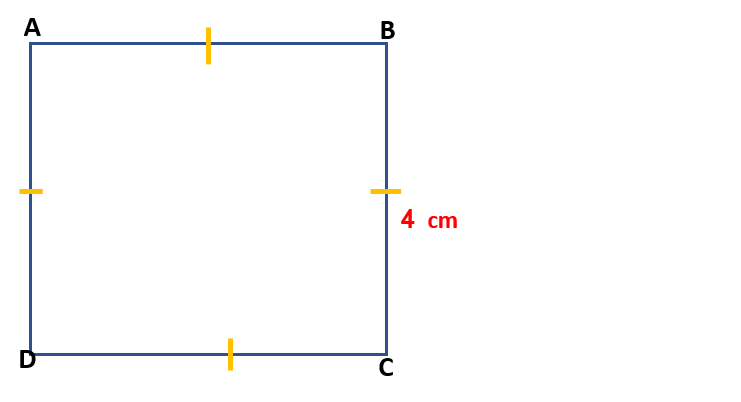
उपर्युक्त आकृति के क्षेत्रफल और परिमाप की गणना कीजिए।
हल :
आकृति से :- भुजा =4 cm
चूंकि वर्ग की प्रत्येक भुजा बराबर होती है अतः
AB=BC=CD=DA=4 cm
क्षेत्रफल = भुजा × भुजा
=4cm ×4 cm
=16 cm2
परिमाप = 4 × भुजा
=4 ×4 cm
=16 cm
उदाहरण 3
एक वर्गाकार पार्क का क्षेत्रफल ज्ञात कीजिए जिसका परिमाप 320m है।
दिया हैं,
वर्गाकार पार्क का परिमाप =320m
4× भुजा =320 (∵ वर्ग का परिमाप =4× भुजा)
⇒ भुजा =3204=80m
वर्गाकार पार्क का क्षेत्रफल = (भुजा) 2
=(80 m)2
=80 m×80 m=6400 m2
अतः, वर्गाकार पार्क का क्षेत्रफल 6400 m2 हैं।
उदाहरण 4
वर्गाकार भूखंड की एक भुजा 300m है। इसका क्षेत्रफल ज्ञात कीजिए। इसको समतल करवाने का व्यय भी ज्ञात कीजिए। यदि समतल करने का व्यय ₹0.50 प्रति m2 है।
वर्गाकार भूखंड की भुजा की लंबाई =300m
वर्गाकार भूखंड का क्षेत्रफल = भुजा × भुजा
=300 m×300 m
=90,000m2
∵ प्रति वर्ग मीटर समतल कराने का व्यय =₹0.50
∴ वर्गाकार भूखंड को समतल कराने का व्यय = क्षेत्रफल × दर
=90,000×0.50
=90,000×50100
=90,000×12
=₹45,000
उदाहरण 5
एक वर्ग और एक आयत का क्षेत्रफल समान है। यदि वर्ग की भुजा 40cm हो और आयत की चौड़ाई 25cm हो, तो आयत की लंबाई ज्ञात कीजिए। आयत का परिमाप भी ज्ञात कीजिए।
दिया है,
वर्ग का क्षेत्रफल = आयत का क्षेत्रफल
⇒(भुजा) 2= लंबाई × चौड़ाई
⇒(40 cm)2= लंबाई ×25 cm
⇒1600 cm2= लंबाई ×25 cm
⇒ लंबाई =1600cm225cm=64 cm
आयत का परिमाप =2× (लंबाई + चौड़ाई)
=2×(64+25) cm
=2×89 cm=178 cm
समांतर चतुर्भुज
परिभाषा : चार भुजाओं से बंद ऐसी आकृति जिसमे आमने - सामने की भुजाओं के युग्म समांतर एवं समान लंबाई के हो, समांतर चतुर्भुज कहलाता है।

उपर्युक्त आकृति मे :-
PQ ∣∣ SR और PS ∣∣ QR
PQ=SR तथा PS=QR
समांतर चतुर्भुज का क्षेत्रफल : क्षेत्रफल की गणना के लिए हमे इसके आधार और ऊंचाई की आवश्यकता होती है।
ऊंचाई इसके किसी भी शीर्ष से सामने वाली भुजा पर डाले गए लंब को कहा जाता है।
सूत्र : आधार × संगत ऊंचाई
आइए एक उदाहरण से समझते है :-
उदाहरण : दी गई आकृति का क्षेत्रफल ज्ञात कीजिए।

चूंकि हमे दिया है :-
आधार (SR) = 7 cm
ऊंचाई (PN) = 4 cm
क्षेत्रफल = आधार × संगत ऊंचाई
= SR × PN
= 7 cm ×4 cm
= 28 cm2
समांतर चतुर्भुज का परिमाप : परिमाप आकृति के चारों भुजाओं का योग होता है। चूंकि इसकी आमने - सामने की समांतर भुजाओं के युग्म समान होते है, इसलिए इसे निम्न सूत्र की सहायता से हल कर सकते है :-
सूत्र : 2× (a+b) ⇒ जहाँ a और b समांतर चतुर्भुज की असमान भुजाओं की मापे होती है।
उदाहरण : दिए गए समांतर चतुर्भुज के परिमाप की गणना कीजिए।

चूंकि दी गई आकृति समांतर चतुर्भुज की है अतः आमने सामने की भुजाओं के युग्म समान लंबाई के होंगे।
AB=DC=(a)=12 cm
AD=BC=(b)=15 cm
परिमाप : 2×(a+b)
=2×(12+15) cm
=2×(27) cm
=54 cm
उदाहरण 6
समांतर चतुर्भुज का आधार ज्ञात कीजिए जिसका क्षेत्रफल 560m2 और शीर्षलंब 1400cm है।
दिया गया है :-
समांतर चतुर्भुज का क्षेत्रफल = 560 m2
समांतर चतुर्भुज का शीर्षलंब =1400 cm
मीटर मे बदलने पर :-
∵ 1 m = 100 cm
∴ 1400100=14 मीटर
सूत्र :
समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊंचाई
560 m2 = आधार × 14 m
आधार =560m214m
आधार =40 मीटर
उदाहरण 7
DL और BM समांतर चतुर्भुज ABCD की क्रमशः भुजाएँ AB और AD पर लंब है। यदि समांतर चतुर्भुज का क्षेत्रफल 1470cm2 है। AB=35cm और AD=49cm है तो BM तथा DL की लंबाई ज्ञात कीजिए।
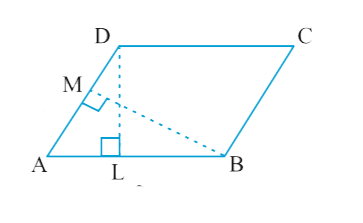
हमे दिया गया है :-
समांतर चतुर्भुज ABCD का क्षेत्रफल =1470 cm2
AB =35 cm
AD =49 cm
ज्ञात करना है :- (i) BM =? (ii) DL =?
(i) समांतर चतुर्भुज का क्षेत्रफल = आधार × संगत ऊंचाई
⇒ 1470 cm2 =AD×BM
⇒ 1470 cm2 =49cm×BM
⇒ 1470cm249cm=BM
⇒ 30 cm =BM
⇒ BM=30 cm
(ii) समांतर चतुर्भुज का क्षेत्रफल = आधार × संगत ऊंचाई
⇒ 1470 cm2 =AB×DL
⇒ 1470 cm2 =35cm×DL
⇒ 1470cm235cm=DL
⇒ 42 cm =DL
⇒ DL=42 cm
त्रिभुज
परिभाषा : तीन रेखाखंडों से घिरी बंद आकृति त्रिभुज कहलाती है।
त्रिभुज का क्षेत्रफल : त्रिभुज की तीनों भुजाओं द्वारा आपस मे मिलकर जितने क्षेत्र को घेरा जाता है, उसे त्रिभुज का क्षेत्रफल कहते है।
त्रिभुज के क्षेत्रफल की गणना के लिए हम निम्न सूत्र का प्रयोग कर सकते है :-
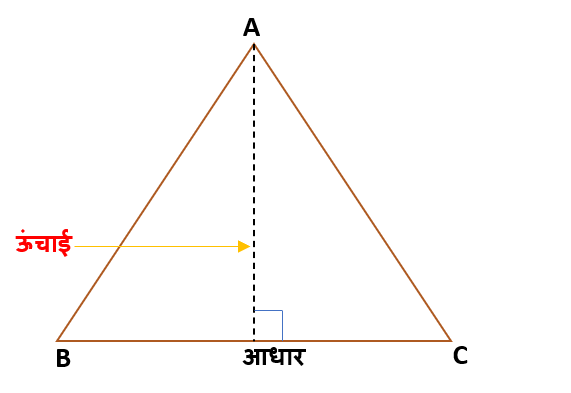
सूत्र :
(i) 12 (आधार × ऊंचाई ) ⇒ जब केवल त्रिभुज दिया गया हो।
(ii) 12 ( समांतर चतुर्भुज का क्षेत्रफल ) ⇒ जब त्रिभुज समांतर चतुर्भुज के रूप मे दिया गया हो।
आइए एक उदाहरण से समझते है :-
उदाहरण : दी गई आकृति के क्षेत्रफल की गणना कीजिए।
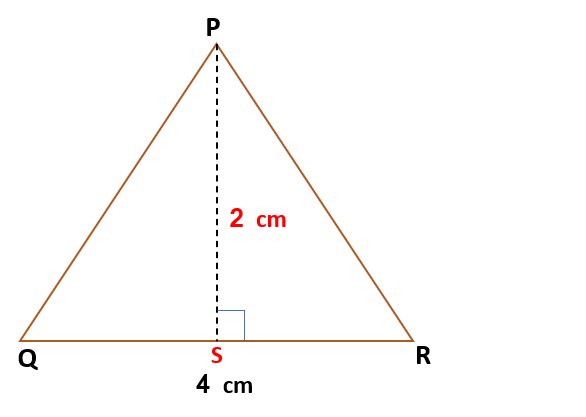
हल :
दी गई आकृति त्रिभुज की है।
आधार (QR) =4 cm
ऊंचाई (PS) =2 cm
क्षेत्रफल : 12 (आधार × ऊंचाई )
=12× (4 cm × 2 cm)
=12× (8 cm2)
=4 cm2
इस प्रकार हम इस सूत्र की सहायता से क्षेत्रफल के साथ - साथ आधार और ऊंचाई की गणना भी कर सकते है।
OMR (One Minute Revision)
क्षेत्रफल की इकाई (Unit) वर्गमीटर, वर्ग सेंटीमीटर, वर्ग किलोमीटर आदि होती हैं।
परिमाप की इकाई (unit) मीटर, सेंटीमीटर, किलोमीटर आदि होती हैं।
उदाहरण 8
त्रिभुज PQR, मे P पर समकोण है। PS,QR पर लंब है। यदि PQ=12cm,QR=20cm और PR=16cm है, तो
(i) ΔPQR का क्षेत्रफल ज्ञात कीजिए।
(ii) PS की लंबाई भी ज्ञात कीजिए।
दी गई माप से त्रिभुज की आकृति बनाते है :-
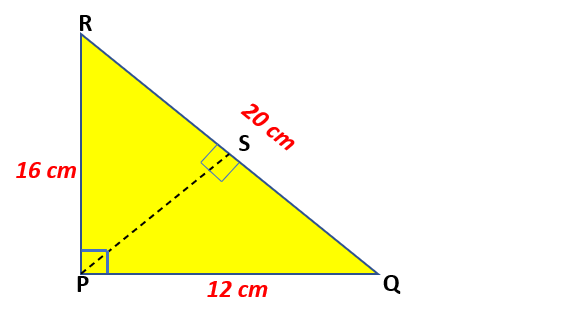
(i) △PQR का क्षेत्रफल = 12 (आधार × ऊंचाई)
=12×PQ×PR
=12×12 cm×16 cm
=96 cm2
(ii) अब हम आकृति को निम्न प्रकार व्यवस्थित करते है :-
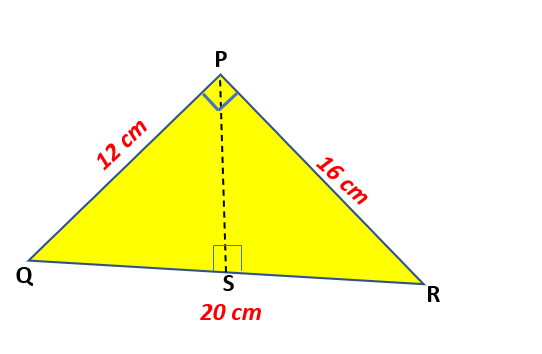
△PQR का क्षेत्रफल = 12 (आधार × ऊंचाई)
96 cm2 =12×QR×PS
96 cm2 =12×20×PS
96 cm2 =10×PS
96cm210cm =PS
9.6 cm =PS
उदाहरण 9
त्रिभुज का आधार ज्ञात कीजिए जिसका शीर्षलंब 12 cm और क्षेत्रफल 96 cm2 है।
दिया गया है :-
त्रिभुज का शीर्षलंब =12 cm
त्रिभुज का क्षेत्रफल =96 cm2
ज्ञात करना है :- त्रिभुज का आधार =?
त्रिभुज का क्षेत्रफल =12 (आधार × ऊंचाई )
96 cm^2=1/(cancel2)xx (आधार × cancel12)cm
96 cm2= (आधार × 6 cm)
आधार =96cm26cm
आधार =16 cm
वृत
वृत्त एक बंद समतलीय आकृति होती है, जिसके मध्य मे एक बिन्दु होता है जो उस वृत्त का केंद्र होता है। वृत्त इसी केंद्र बिन्दु के चारों ओर वक्र रेखा से घिरा होता है ।
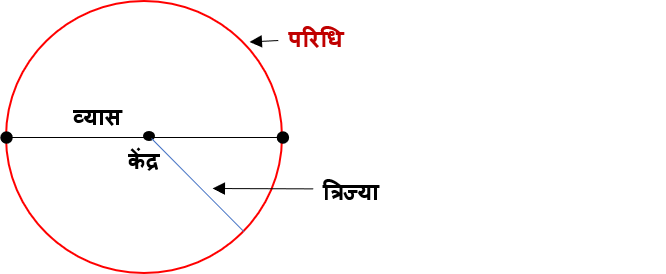
वृत्त के निम्न भाग होते है -
वृत्त का केंद्र : वृत्त के मध्य भाग मे स्थित वह बिन्दु जिसके चारों ओर वक्र रेखा से वृत्त घिरा होता है। वृत्त का केंद्र कहलाता है।
वृत्त की परिधि : वक्र रेखा की लंबाई को वृत्त की परिधि कहते है।
वृत्त की त्रिज्या : वृत्त के केंद्र से लेकर परिधि तक की दूरी को, वृत्त की त्रिज्या कहते है।
वृत्त का व्यास : परिधि पर किन्ही दो बिन्दुओं को मिलाने वाला रेखाखंड, जो वृत्त के केंद्र से होकर जाता है, वृत्त का व्यास कहलाता है।
वृत का व्यास त्रिज्या का दुगुना होता है।
वृत्त से संबंधित कुछ सूत्र :
वृत्त का क्षेत्रफल : πr2 वर्ग इकाई
वृत्त की परिधि : 2πr इकाई
अर्द्धवृत्त की परिधि : (12×2πr)=πr इकाई
अर्द्धवृत्त का परिमाप : अर्द्धवृत्त की परिधि + व्यास = (πr+2r) इकाई
त्रिज्या : व्यास ÷ 2
जहाँ π का मान लगभग 227 या 3.14 होता है, r वृत्त की त्रिज्या तथा d वृत का व्यास होता है।
आइए कुछ उदाहरणों की सहायता से समझते है :-
उदाहरण : 10 सेमी. व्यास वाले वृत की परिधि ज्ञात कीजिए। (π=3.14)
हल : दिया है :-
व्यास (d) = 10 सेमी
त्रिज्या (r) = d2 =102=5 सेमी.
परिधि =2πr
=2×3.14×5
=10×3.14
=31.4 सेमी
उदाहरण : निधि एक 7 सेमी त्रिज्या वाले वृत को दो बराबर भागों मे विभाजित कर देती है। प्रत्येक अर्धवृत का परिमाप ज्ञात कीजिए। (π=227)
हल : दिया है :-
त्रिज्या (r) =7 सेमी
अर्द्धवृत्त का परिमाप : अर्द्धवृत्त की परिधि + व्यास
अर्धवृत के परिमाप की गणना के लिए हमे पहले अर्धवृत की परिधि और व्यास की गणना करनी होगी। अतः
अर्धवृत की परिधि = πr
=227×7
=22 सेमी
व्यास =2r =2×7=14 सेमी
अतः अर्द्धवृत्त का परिमाप : अर्द्धवृत्त की परिधि + व्यास
=(22+14) सेमी
=36 सेमी
उदाहरण : एक वृताकार बगीचे का व्यास 9.8 मीटर है। इसका क्षेत्रफल ज्ञात कीजिए।
हल : दिया है :-
व्यास (d) =9.8 मीटर
त्रिज्या (r) =d2=9.82=4.9 मीटर
क्षेत्रफल =πr2
=227×4.9 m×4.9 m
=227×24.01 m2
=75.46 m2
नोट : जब π का मान नहीं दिया गया हो तो उस स्थिति मे हमेशा π=227 का प्रयोग करते है।
उदाहरण 10
21 cm त्रिज्या वाले वृत्त की परिधि ज्ञात कीजिए : (π=227) लीजिये
दिया गया है :-
त्रिज्या (r)=21 cm
परिधि = 2πr
=2×227×21 cm
=132 cm
उदाहरण 11
यदि एक वृत्ताकार शीट की परिधि 154 m हो, तो इसकी त्रिज्या ज्ञात कीजिए। शीट का क्षेत्रफल भी ज्ञात कीजिए। (π=227 लीजिये )
परिधि =154 m
2πr=154 m
2×227×r=154 m
r=154×744 m
r=492 m
r=24.5 m ( त्रिज्या )
क्षेत्रफल =πr2
=227×492 m×492 m
=37732 m2
=1886.5 m2
उदाहरण 12
21 m व्यास वाले एक वृत्ताकार बगीचे के चारों ओर माली बाड़ लगाना चाहता है। खरीदे जाने वाले आवश्यक रस्से की लंबाई ज्ञात कीजिए। यदि वह 2 पूरे चक्कर की बाड़ बनाना चाहता है तो ₹ 4 प्रति मीटर की दर से रस्से पर व्यय ज्ञात कीजिए। (π=227 लीजिये)
दिया गया है :-
वृत का व्यास (d)=21 m
त्रिज्या (r) =d2=212=10.5 m
वृत की परिधि =2πr
=2×227×212
=66 m
अतः रस्से की कुल लंबाई =66 m
2 चक्कर लगाने पर रस्से की कुल लंबाई =2×66 m=132 m
4 रुपए प्रति मीटर की दर से रस्से पर व्यय =4×132 =528 रुपए
इकाइयों का रूपांतरण
बच्चों! इकाइयों के रूपांतरण से हमे प्रश्नों को हल करने मे काफी सहायता मिलती है। जैसे यदि हमे प्रश्न मे दो अलग - अलग इकाइयाँ दी हुई हो तो हम उस स्थिति मे प्रश्न को आसानी से हल नहीं कर सकते परंतु यदि हम उनमे से किसी एक इकाई का रूपांतरण दूसरी इकाई मे कर दे तो हम सरलता से प्रश्न का हल कर सकते है।
जब हम बड़ी इकाई को छोटी इकाई मे बदलते है तो परिणामस्वरूप इकाइयों की संख्या अधिक प्राप्त होती है।
जब हम छोटी इकाई को बड़ी इकाई मे बदलते है तो इकाइयों की संख्या कम प्राप्त होती है।
उदाहरण के लिए :-
यदि हम 1 cm को mm बदले तो हमे 1 mm को 10 से गुणा करना होगा।
1cm=10mm
| इकाई | परिवर्तन |
|---|---|
| 1 cm | 10 mm |
| 1 m | 100 cm |
| 1 km | 1000 m |
| वर्ग इकाई | अन्य वर्ग इकाई मे परिवर्तन |
| 1 cm2 | 100 mm2 |
| 1 m2 | 10000 cm2 |
| 1 km2 | 1000000 m2 |
| 1 ha (हेक्टेयर ) | 10000 m2 |
उदाहरण : 1000 cm2 को mm2 मे बदलिए।
हल : चूंकि 1 cm =10 mm
दोनों तरफ वर्ग करने पर :-
(1cm)2 =(10mm)2
12 cm2 = 102 mm2
1 cm2 = 100 mm2
अतः 1000 cm2 = 1000×100 mm2 =100000 mm2
इस प्रकार हम अधिकांश इकाइयों को परिवर्तित कर सकते है।
उदाहरण 13
10m2 को cm2 में बदलिए।
चूंकि 1 m = 100 cm
दोनों पक्षों का वर्ग करने पर :-
(1m)2=(100cm)2
12 m2=1002 cm2
1m2=10000 cm2 (∵1002=100×100=10000)
10 m2=10×10000 cm2
10 m2=100000 cm2
अनुप्रयोग
हम अपने दैनिक जीवन में समतल आकृतियों के क्षेत्रफल और परिमाप की इन अवधारणाओं का अधिकतर उपयोग करते है। जैसे :-
⇒ यदि हमारे पास एक आयताकार क्षेत्र है और हम गणना करना चाहते हैं कि उस क्षेत्र को कवर करने के लिए आवश्यक बाड़ की लंबाई कितनी होगी, तो हम परिधि का उपयोग करते है।
⇒ यदि किसी बच्चे को फीते से वृत्ताकार कार्ड सजाना है तो वह कार्ड की परिधि आदि की गणना करके आवश्यक फीते की लंबाई की गणना कर सकता है।
⇒ बगीचों के बीच मे छोड़े गए पथ के क्षेत्रफल की गणना के लिए भी हम इन इकाइयों का प्रयोग करते है।
उदाहरण : एक आयताकार पार्क 45 m लंबा और 30 m चौड़ा है। पार्क के बाहर चारों ओर एक 2.5 m चौड़ा एक पथ बनाया गया है। पथ का क्षेत्रफल ज्ञात कीजिए।
हल :
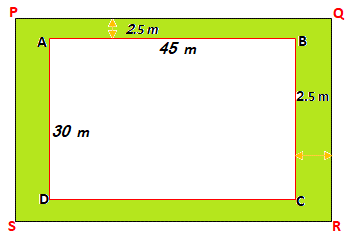
पथ का क्षेत्रफल ज्ञात करने के लिए हमे {आयत PQRS का क्षेत्रफल − आयत ABCD का क्षेत्रफल } ज्ञात करना होगा।
आयत PQRS का क्षेत्रफल :
लंबाई (l) =PQ=[45+2.5+2.5]m=50 m
चौड़ाई (b) =PS=[30+2.5+2.5]m=35 m
क्षेत्रफल =l×b
=50 m×35 m
=1750 m2
आयत ABCD का क्षेत्रफल :
लंबाई (l) =AB=45 m
चौड़ाई (b) =AD=30 m
क्षेत्रफल =l×b
=45 m×30 m
=1350 m2
पथ का क्षेत्रफल = {आयत PQRS का क्षेत्रफल − आयत ABCD का क्षेत्रफल }
={1750−1350} m2
=400 m2
OMR (One Minute Revision)
उदाहरण 14
निम्नलिखित आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
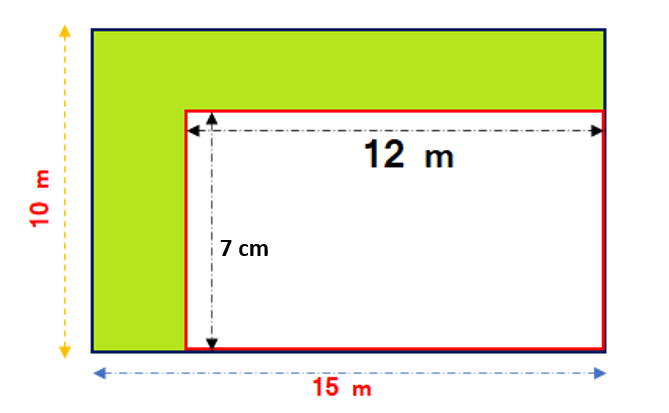
बड़े आयत के लिए :-
लंबाई (l)= 15 m
चौड़ाई (b)= 10 m
क्षेत्रफल =l×b
=15 m×10 m
=150 m2
छोटे आयत के लिए :-
लंबाई (l)= 12 m
चौड़ाई (b)= 7 m
क्षेत्रफल =l×b
=12 m×7 m
=84 m2
अतः छायांकित भाग का क्षेत्रफल = बड़े आयत का क्षेत्रफल − छोटे आयत का क्षेत्रफल
=(150−84) m2
=66 m2
उदाहरण 15
100 m भुजा वाले एक वर्गाकार पार्क के भीतर उसकी परिसीमा से लगा 5 m चौड़ा पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए। ₹ 250 प्रति 10m2 की दर से इसको सीमेंट करवाने का व्यय भी ज्ञात कीजिए।
दी गई माप से एक कच्ची आकृति बनाते है :-
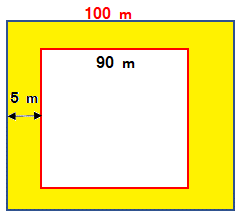
आकृति मे हम देख सकते है कि 5 मीटर चौड़ा पथ बनाने के बाद उसमे अंदर की तरफ एक 90 मीटर वर्गाकार क्षेत्र बचता है।
अतः पथ के क्षेत्रफल के लिए हम 100 मीटर भुजा वाले वर्ग के क्षेत्रफल मे से 90 मीटर भुजा वाले वर्ग के क्षेत्रफल को घटा देते है।
वर्गाकार पार्क का क्षेत्रफल = भुजा × भुजा
=100 m×100 m
=10000 m2
पथ की चौड़ाई को छोड़कर शेष बचे क्षेत्र का क्षेत्रफल = भुजा × भुजा
=90 m×90 m
=8100 m2
अतः पथ का क्षेत्रफल =(10000−8100) m2 =1900 m2
250 रुपए प्रति 10 m2 पर व्यय होता है।
1m2 पर व्यय =25010=25 रुपए
1900 m2 पर व्यय =1900×25 =47500 रुपए