परिमेय संख्याएँ कक्षा 7 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय में हम परिमेय संख्याओं का अध्ययन करेंगे। ऐसी वास्तविक संख्या जिसको दो पूर्ण संख्याओं के बटा अर्थात भाग के रूप में व्यक्त किया जा सकता हो, परिमेय संख्या (Rational Number) कहलाती हैं।
अर्थात कोई संख्या pq; जहाँ p और q दोनों पूर्ण संख्याएँ हो तथा q≠0 हो, परिमेय संख्या कहलाती है।
उदाहरण : 1,2,4,34,0 आदि।
इस अध्याय मे हम परिमेय संख्याओं से संबंधित सभी तथ्यों जैसे :- धनात्मक एवं ऋणात्मक रूप, संख्या रेखा पर इनका निरूपण, मानक रूप, इनकी तुलना और इन पर विभिन्न संक्रियाओं का अध्ययन करेंगे।
आइये जानते है, परिमेय संख्याओं को और करीब से...
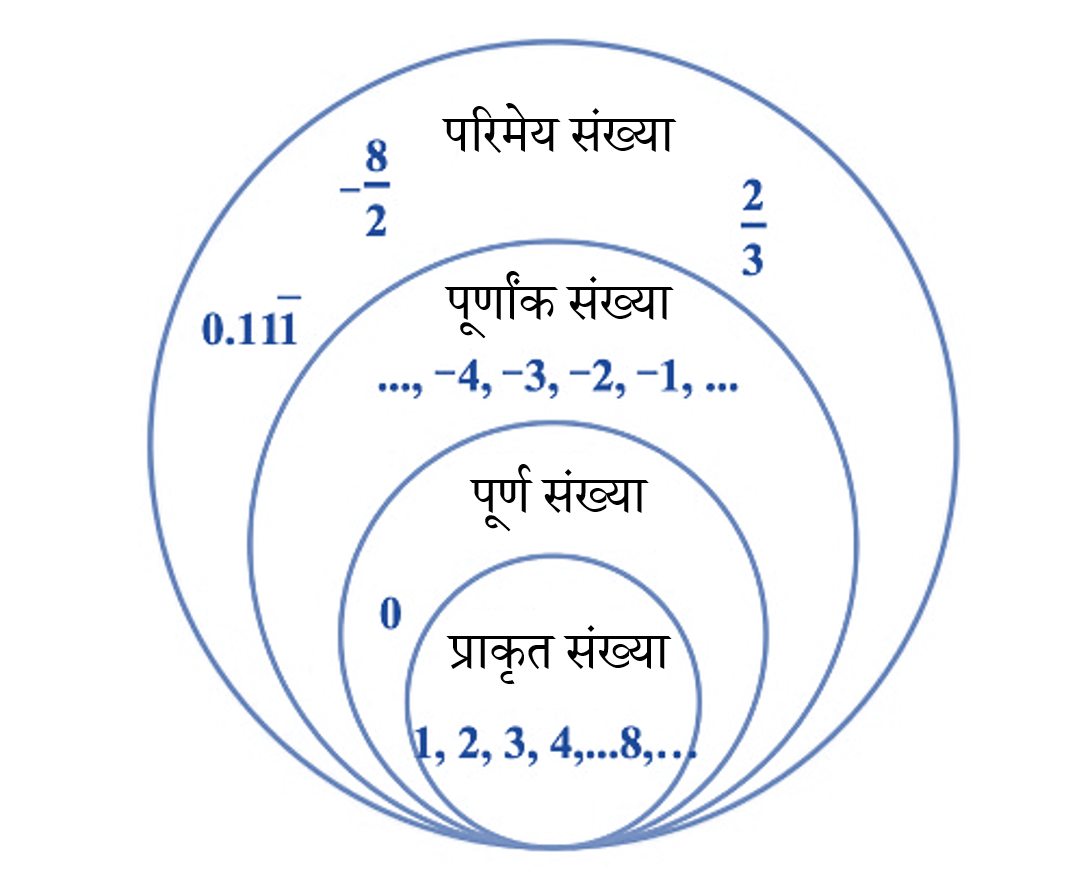
बच्चों! संख्याओं का अध्ययन हमने अपने परिवेश की वस्तुओं के गिनने के कार्य से प्रारंभ किया। इस कार्य में प्रयोग की गई संख्याओं को गणन संख्याएँ (Counting Numbers) या प्राकृत संख्याएँ (Natural Numbers) कहा जाता है अर्थात 1,2,3,4,.....। इन प्राकृत संख्याओं में 0 को सम्मिलित करने पर हमें पूर्ण संख्याएँ (Whole Numbers) अर्थात् 0,1,2,3,...... प्राप्त हुई। इसके बाद पूर्णांक (Integers) प्राप्त करने के लिए पूर्ण संख्याओं में प्राकृत संख्याओं के ऋणात्मको (Negatives) को सम्मिलित किया गया अर्थात .........,−3,−2,−1,0,1,2,3,...... पूर्णांक संख्याएँ हैं। इस प्रकार, हमने संख्या पद्धति (Number System) को प्राकृत संख्याओं से पूर्ण संख्याओं तक और पूर्ण संख्याओं से पूर्णांकों तक विस्तृत किया।
इसके अलावा पिछले अध्यायों मे हमने भिन्नों (Fractions) का अध्ययन किया है जिसमे हम भिन्न संख्या को pq के रूप मे निरूपित करते है जहाँ p अंश तथा q हर को दर्शाता है।
इस प्रकार परिमेय संख्याएँ वे संख्याएँ होती है जिन्हे pq के रूप मे व्यक्त किया जा सकता हो और जहाँ p व q पूर्णांक हो (q≠0)
इस अध्याय में, हम संख्या पद्धति का और आगे विस्तार करेंगे। हम परिमेय संख्याओं की अवधारणा का परिचय देकर उनकी तुलना, संख्या रेखा पर इनका निरूपण, मानक रूप तथा इन पर योग, व्यवकलन, गुणन और विभाजन (भाग) की संक्रियाएँ करना सीखेंगे।
परिमेय संख्याओं का परिचय
परिमेय संख्याओं के अध्ययन से पहले सामान्य संख्याओं का अध्ययन करते है :-
(1) प्राकृत संख्या : 1,2,3,......,∞ तक सभी धनात्मक पूर्णांक प्राकृत संख्याएँ कहलाती है।
(2) पूर्ण संख्या : शून्य सहित सभी प्राकृत संख्याएँ पूर्ण संख्याएँ कहलाती हैं।
(3) पूर्णांक संख्या : शून्य सहित सभी ऋणात्मक और धनात्मक संख्याएँ पूर्णांक कहलाती हैं। (जिसमे भिन्न सम्मिलित नहीं होगा।)
परिमेय संख्या
जहाँ p और q पूर्णांक हैं (q≠0)
समतुल्य परिमेय संख्याएँ
एक परिमेय संख्या के अंश और हर को एक ही पूर्णांक से गुणा या विभाजित करके हम दी गई परिमेय संख्या के बराबर एक और परिमेय संख्या प्राप्त कर सकते है।
उदाहरण :-
12=1×22×2=24
इस प्रकार 24, 12 के समतुल्य है।
उदाहरण 1
निम्नलिखित परिमेय संख्या में अंश तथा हर को पहचानिए।
3−7
चूंकि हम जानते है कि परिमेय संख्या को pq के रूप मे लिखते है जहाँ p अंश को तथा q हर को दर्शाता है अतः
दी गई परिमेय संख्या मे : 3−7=pq
⇒ p = 3 = अंश
⇒ q = -7 = हर
उदाहरण 2
निम्नलिखित के समतुल्य चार परिमेय संख्याएँ लिखिए :
−27
ऐसी संख्याएँ जो एक - दूसरे के बराबर हो अर्थात सरल करने पर समान मान प्राप्त हो, समतुल्य परिमेय संख्याएँ कहलाती है।
हम जानते है कि परिमेय संख्या के अंश और हर को समान पूर्णांक से गुणा करके हम एक और समतुल्य परिमेय संख्या प्राप्त कर सकते है अतः
(i) अंश और हर को 2 से गुणा करने पर :
⇒ −2×27×2=−414
(ii) अंश और हर को 3 से गुणा करने पर :
⇒ −2×37×3=−621
(iii) अंश और हर को 4 से गुणा करने पर :
⇒ −2×47×4=−828
(iv) अंश और हर को 5 से गुणा करने पर :
⇒ −2×57×5=−1035
उदाहरण 3
निम्नलिखित पूर्णांकों को परिमेय संख्या pq के रूप में लिखिए :
−13
चूंकि परिमेय संख्या को pq के रूप मे लिखा जाता है जहाँ q≠0 होना आवश्यक होता है।
हमे ऐसी संख्या दी गई है जिसमे q का मान नहीं दिया गया है अतः इसे pq के रूप मे निरूपित करने के लिए इसके हर मे एक ऐसा पूर्णांक रखना होगा जिससे इसके मान मे भी कोई बदलाव नहीं हो तथा q≠0 भी हो।
⇒ −13 =pq=−131
अतः q=1 रखने पर इसके मान मे कोई बदलाव नहीं हुआ अतः −13 एक परिमेय संख्या है।
धनात्मक एवं ऋणात्मक परिमेय संख्याएँ
धनात्मक परिमेय संख्याएँ : ऐसी परिमेय संख्या जिसके अंश और हर दोनों धनात्मक (+) हो, धनात्मक परिमेय संख्या कहलाती है।
उदाहरण : 34, 1224, 1527 आदि।
ऋणात्मक परिमेय संख्याएँ : ऐसी परिमेय संख्या जिसके अंश और हर दोनों मे से कोई एक ऋणात्मक (-) हो, ऋणात्मक परिमेय संख्या कहलाती है।
उदाहरण : −34, 12−24, −1527 आदि।
OMR (One Minute Revision)
जहाँ p और q पूर्णांक हैं (q≠0)
उदाहरण 4
ऐसी पांच परिमेय संख्या लिखिए जिनमे से प्रत्येक का अंश एक ऋणात्मक पूर्णांक हो और हर एक धनात्मक पूर्णांक हो।
चूंकि हम जानते है कि परिमेय संख्या को pq के रूप मे लिखते है जहाँ p अंश को तथा q हर को दर्शाता है। जहाँ q≠0 होना आवश्यक होता है।
अंश एक ऋणात्मक पूर्णांक हो और हर एक धनात्मक पूर्णांक हो,इसके लिए p का मान ऋणात्मक पूर्णांक रखना होगा तथा q का मान धनात्मक पूर्णांक रखना होगा।
⇒ pq= −12,−23,−34,−45,−56
उदाहरण 5
निम्नलिखित में से कौन-सी संख्याएँ ऋणात्मक परिमेय संख्याएँ है ?
(i) −23
(ii) 57
(iii) 3−5
(iv) 0
(v) 611
(vi) −2−9
चूंकि हम जानते है कि कोई भी परिमेय संख्या निम्न स्थितियों मे धनात्मक या ऋणात्मक होती है।
स्थिति : 1 यदि परिमेय संख्या के अंश अथवा हर मे से कोई एक ऋणात्मक होता है तो वह परिमेय संख्या ऋणात्मक परिमेय संख्या होती है।
स्थिति : 2 यदि परिमेय संख्या के अंश और हर दोनों ही या तो धनात्मक हो या ऋणात्मक उस स्थिति मे वह परिमेय संख्या धनात्मक परिमेय संख्या होती है।
(i) −23 = इस परिमेय संख्या मे अंश ऋणात्मक है अतः यह ऋणात्मक परिमेय संख्या है।
(ii) 57 = इस परिमेय संख्या मे अंश और हर दोनों ही धनात्मक है अतः यह धनात्मक परिमेय संख्या है।
(iii) 3−5 = इस परिमेय संख्या मे हर ऋणात्मक है अतः यह ऋणात्मक परिमेय संख्या है।
(iv) 0= यह ना तो धनात्मक परिमेय संख्या है ना ही ऋणात्मक।
(v) 611 = इस परिमेय संख्या मे अंश और हर दोनों ही धनात्मक है अतः यह धनात्मक परिमेय संख्या है।
(vi) −2−9=(cancel(-)2)/(cancel(-)9)= 2/9= इस परिमेय संख्या मे अंश और हर दोनों ही ऋणात्मक है। चूंकि ऋणात्मक चिह्न भाग प्रक्रिया मे धनात्मक हो जाते है अतः यह धनात्मक परिमेय संख्या है।
संख्या रेखा पर परिमेय संख्या का निरूपण
बच्चों! उपर्युक्त अध्ययन मे हम धनात्मक और ऋणात्मक परिमेय संख्याओं को समझ चुके है। आइए अब इनका संख्या रेखा पर निरूपण समझते है :-
परिमेय संख्याओं का संख्या रेखा पर निरूपण निम्न प्रकार से किया जाता हैं :-
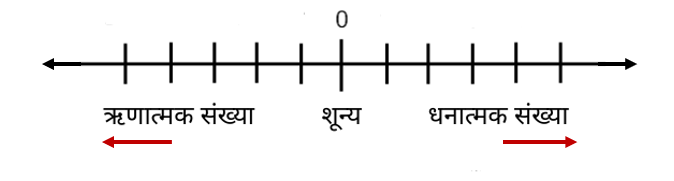
इस आकृति मे हम देख सकते है कि शून्य के दाईं ओर धनात्मक संख्या तथा शून्य के बाईं ओर ऋणात्मक संख्या अंकित है।
आइए अब एक उदाहरण से समझते है :-
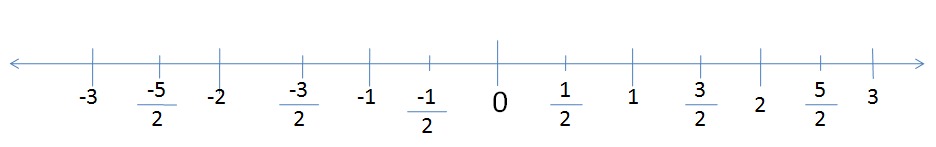
यह रेखा संख्या रेखा कहलाती है।
हम किन्हीं दो परिमेय संख्याओं के बीच अपरिमित रूप से अनेक परिमेय संख्याएँ ज्ञात कर सकते हैं।
उदाहरण 6
निम्नलिखित कथन सत्य है अथवा असत्य जांच कीजिए।
परिमेय संख्या 7−4 रेखा पर शून्य के दाईं ओर होती है।
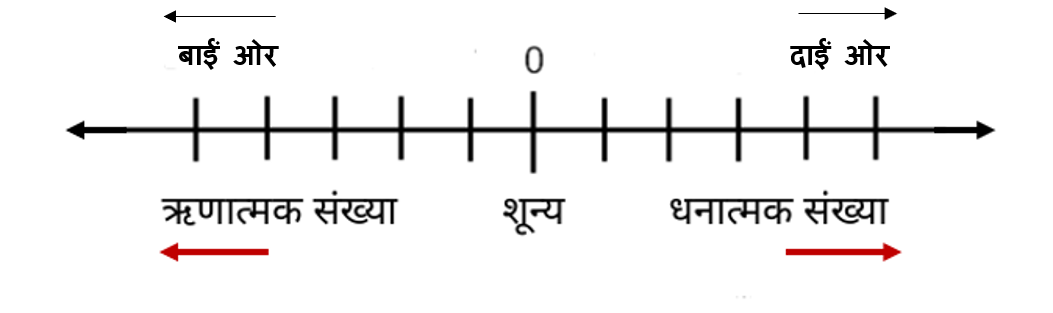
चूंकि हम जानते है कि धनात्मक संख्या शून्य के दाईं ओर तथा ऋणात्मक संख्या शून्य के बाईं ओर होती है।
हमे संख्या दी गई है : 7−4
यह परिमेय संख्या एक ऋणात्मक परिमेय संख्या है अतः यह शून्य के बाईं ओर प्रदर्शित की जाएगी।
अतः दिया गया कथन असत्य है।
उदाहरण 7
संख्या रेखा पर निम्नलिखित परिमेय संख्या को प्रदर्शित कीजिए।
34
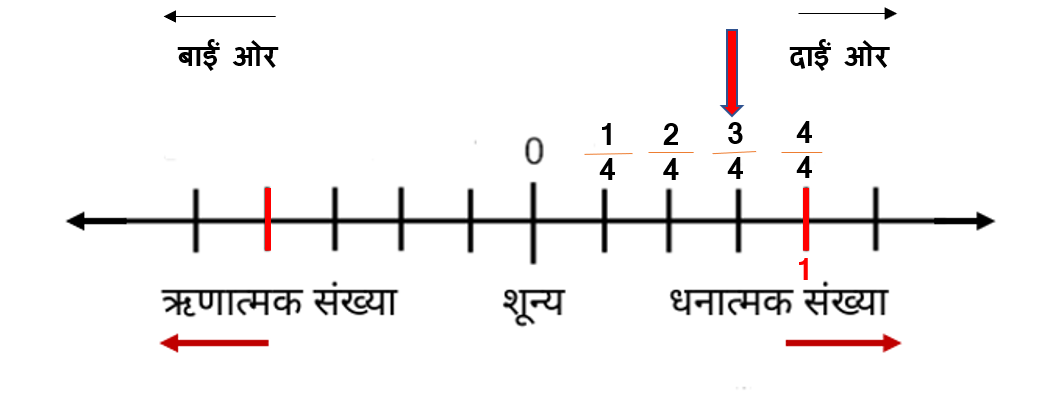
चरण : 1 सर्वप्रथम एक संख्या रेखा खीचते है।
चरण : 2 चूंकि यह एक धनात्मक परिमेय संख्या है अतः शून्य के दाईं ओर धनात्मक दिशा मे इस संख्या रेखा पर एक भाग को 4 बराबर भागों मे बाटते है क्योंकि यहाँ हर का मान 4 है।
चरण : 3 अब सरलता से 34 को दर्शा सकते है।
मानक रूप मे परिमेय संख्या
कोई परिमेय संख्या मानक रूप मे उस स्थिति मे कही जाती है जब उस परिमेय संख्या का हर एक धनात्मक पूर्णांक हो तथा उसके अंश और हर मे 1 के अलावा अन्य कोई उभयनिष्ठ गुणनखंड ना हो।
अर्थात परिमेय संख्या का अंतिम सरलतम रूप ही उस परिमेय संख्या का मानक रूप कहलाता है।
किसी भी परिमेय संख्या का मानक रूप ज्ञात करने के लिए हम परिमेय संख्या के अंश और हर का HCF (म. स.) निकालकर उस म.स. से अंश और हर को विभाजित करते है।
इस प्रकार हम सरलता से उस परिमेय संख्या का मानक रूप या निम्नतम रूप प्राप्त कर सकते है।
आइए उदाहरण की सहायता से समझते है :-
उदाहरण : 1218 का मानक रूप ज्ञात कीजिए।
हल : चूंकि हम जानते है कि 12 और 18 का म. स. 6 होता है।
अतः 6 का अंश और हर मे भाग देने पर :-
⇒ 126186=23
इस प्रकार हम सरलता से किसी भी परिमेय संख्या का मानक रूप ज्ञात कर सकते है।
नोट : यदि परिमेय संख्या के अंश मे ऋणात्मक चिह्न हो तो उस पर बिना ध्यान दिए म.स. से विभाजित करके मानक रूप मे अंश मे ऋणात्मक चिह्न लगा देते है परंतु यदि हर मे ऋणात्मक चिह्न हो तो ऋणात्मक म.स. (- म.स.) से विभाजित करते है क्योंकि मानक रूप का हर धनात्मक पूर्णांक होना आवश्यक है।
उदाहरण 8
मानक रूप ज्ञात कीजिए।
−1845
चूंकि हम जानते है कि किसी भी परिमेय संख्या का मानक रूप ज्ञात करने के लिए हम परिमेय संख्या के अंश और हर का HCF (म. स.) निकालकर उस म.स. से अंश और हर को विभाजित करते है।
−1845
चूंकि हम जानते है कि 18 और 45 का म. स. 9 होता है।
चूंकि यहाँ अंश ऋणात्मक है अतः इस पर बिना ध्यान दिए अंश और हर को म. स. से विभाजित करते है तथा मानक रूप के अंश पर ऋणात्मक चिह्न लगा देते है।
अतः 9 का अंश और हर मे भाग देने पर :-
⇒ 189459=25
अंश मे ऋणात्मक चिह्न लगाने पर : −25
अतः अंतिम सरलतम रूप अथवा मानक रूप : −25
उदाहरण 9
मानक रूप में व्यक्त कीजिए :
240−840
चूंकि हम जानते है कि किसी भी परिमेय संख्या का मानक रूप ज्ञात करने के लिए हम परिमेय संख्या के अंश और हर का HCF (म. स.) निकालकर उस म.स. से अंश और हर को विभाजित करते है।
240−840=24−84
चूंकि हम जानते है कि 24 और 84 का म. स. 12 होता है।
चूंकि हम जानते है कि यदि हर मे ऋणात्मक चिह्न हो तो अंश और हर को ऋणात्मक म.स. (- म.स.) से विभाजित करते है क्योंकि मानक रूप का हर धनात्मक पूर्णांक होना आवश्यक है।
अतः अंश और हर को −12 से विभाजित करने पर :
⇒ 24−12−84−12=−27
अतः परिमेय संख्या 240−840 का मानक रूप −27 होगा।
परिमेय संख्याओं की तुलना
परिमेय संख्याओं की तुलना निम्न प्रकार की जा सकती है :-
(i) दो धनात्मक परिमेय संख्याओं की तुलना : धनात्मक परिमेय संख्याओं की तुलना के लिए पहले उनके हरो को समान करते है फिर उनकी तुलना सामान्य प्रक्रिया द्वारा करते है।
इसमे हमेशा बड़े अंश वाली परिमेय संख्या बड़ी होती है।
उदाहरण : 45 और 38 मे से कोनसी परिमेय संख्या बड़ी है ?
हल : दोनों परिमेय संख्याओं के अंश और हरो को ऐसी संख्या से गुणा करते हैं जिससे कि उनका हर समान हो जाए। अतः
⇒4×85×8=3240
⇒3×58×5=1540
चूंकि अब देख सकते कि 3240 ; 1540 से बड़ी है अतः 45>38
(ii) दो ऋणात्मक परिमेय संख्याओं की तुलना : ऋणात्मक परिमेय संख्याओं की तुलना के लिए भी पहले उनके हरो को समान करते है फिर उनकी भी तुलना सामान्य प्रक्रिया द्वारा करते है।
इसमे हमेशा छोटे ऋणात्मक अंश वाली परिमेय संख्या बड़ी होती है।
उदाहरण : −25 और −37 मे से कोनसी परिमेय संख्या बड़ी है ?
हल : दोनों परिमेय संख्याओं के अंश और हरो को ऐसी संख्या से गुणा करते हैं जिससे कि उनका हर समान हो जाए। अतः
⇒−2×75×7=−1435
⇒−3×57×5=−1535
अतः हम देख सकते है कि दोनों संख्याओं मे से −1435 का अंश छोटा है अर्थात −25 परिमेय संख्या बड़ी है।
−25>−37
(iii) एक धनात्मक और एक ऋणात्मक परिमेय संख्याओं की तुलना : यह तुलना सुस्पष्ट होती है क्योंकि हम जानते है कि धनात्मक संख्या हमेशा ऋणात्मक संख्या से बड़ी होती है। अतः हम केवल देखकर ही इनकी तुलना कर सकते है।
उदाहरण : −25 और 37 मे से कोनसी परिमेय संख्या बड़ी है ?
हल : चूंकि −25 एक ऋणात्मक परिमेय संख्या है जबकि 37 एक धनात्मक संख्या है अतः 37 बड़ी परिमेय संख्या होंगी।
37>−25
दो परिमेय संख्याओं के बीच परिमेय संख्या ज्ञात करना
दो परिमेय संख्याओं के बीच अनंत परिमेय संख्याएँ होती हैं।
आइए समझते हैं -
310 और 710 के बीच मे कितनी परिमेय संख्या हैं ?
शायद आप सोच रहे होंगे कि वे संख्याएँ 410,510,610 होंगी। इन परिमेय संख्याओं की संख्या तीन हैं।
परंतु हम 310 को 30100 और 710 को 70100 के रूप मे भी लिख सकते हैं।
अब संख्याएँ 31100,32100,33100.....68100,69100 सभी 310 और 710 के बीच की परिमेय संख्याएँ हैं। इन परिमेय संख्याओं की संख्या 39 है।
इसके अतिरिक्त 310 को 300010000 और 710 को 700010000 इसके के रूप में लिखा जा सकता है।
अब हम पाते हैं कि परिमेय संख्याएँ 3000110000,3000210000......699810000,699910000 सभी संख्याएँ 310 और710 के बीच की परिमेय संख्याएँ है। ये कुल 3999 संख्याएँ हैं।
इस प्रकार हम 310 और 710 के बीच में अधिक से अधिक संख्याओं का समावेश कर सकते है। यह संख्याएँ 39999,399999999........अनंत तक हो सकती हैं।
उपर्युक्त उदाहरण से हम समझ सकते है कि दो परिमेय संख्याओं के बीच परिमेय संख्या ज्ञात करने के लिए हम उनके हरो को समान करके अर्थात समान अंकों से गुणा या भाग करके हम उनके बीच मे अनंत परिमेय संख्याएँ प्राप्त कर सकते है।
आइए एक उदाहरण से समझते है :-
उदाहरण : 35 और 37 के बीच परिमेय संख्या ज्ञात कीजिए।
हल : यहाँ दोनों परिमेय संख्याओं के हर असमान है अतः सर्वप्रथम इनके हरों को समान करते है।
3×75×7=2135
3×57×5=1535
अतः इनके बीच परिमेय संख्या : 1635,1735,1835,1935,2035
अब यदि हमे 35 और 37 के बीच और अधिक परिमेय संख्या ज्ञात करनी है तो हम इनको समान संख्या से गुणा कर सकते है :-
21×235×2=4270
15×235×2=3070
अतः इनके बीच परिमेय संख्या : 3170,3270,.........4170
इस प्रकार हम दो परिमेय संख्याओं के बीच अनंत परिमेय संख्या ज्ञात कर सकते है।
उदाहरण 10
परिमेय संख्याओं की तुलना कीजिए :
2115 और 1927
दो परिमेय संख्याओ की तुलना करने के लिए हमे सर्वप्रथम उनके हरो को समान करना होता है।
हरो को समान करने के लिए हम एक परिमेय संख्या के हर से दूसरी परिमेय संख्या के अंश और हर को गुणा करते है तथा इसी प्रकार दूसरी परिमेय संख्या के हर से पहली संख्या के अंश और हर को गुणा करते है। अतः
2115=21×2715×27=567405
1927=19×1527×15=285405
अब इनकी तुलना सरलता से कर सकते है।
चूंकि हम जानते है कि बड़े अंश वाली परिमेय संख्या बड़ी होती है अतः
⇒ 567405>285405
⇒ 2115>1927
उदाहरण 11
संकेतों >,< और = में से सही संकेत चुन कर रिक्त स्थानों को भरिए :
−57□23
चूंकि हम जानते है कि ऋणात्मक हमेशा धनात्मक से छोटा होता है अतः ऋणात्मक परिमेय संख्या भी धनात्मक परिमेय संख्या से छोटी होगी।
⇒ −57<23
उदाहरण 12
−57 और −38 के बीच में पाँच परिमेय संख्याएँ ज्ञात कीजिए।
दो परिमेय संख्याओं के बीच परिमेय संख्या ज्ञात करने के लिए उनके हरो को समान करते है।
हरो को समान करने के लिए हम एक परिमेय संख्या के हर से दूसरी परिमेय संख्या के अंश और हर को गुणा करते है तथा इसी प्रकार दूसरी परिमेय संख्या के हर से पहली संख्या के अंश और हर को गुणा करते है।
−57 और −38
⇒ −57=−5×87×8=−4056
⇒ −38=−3×78×7=−2156
अतः अब इनके बीच सरलता से अन्य परिमेय संख्याएँ ज्ञात कर सकते है।
−4056,−3956,−3856,−3756 −3656........,−2156
ये सभी परिमेय संख्याएँ −57 और −38 के बीच की परिमेय संख्याएँ है।
परिमेय संख्याओं पर संक्रियाएँ
परिमेय संख्याओं का योग
दो या दो से अधिक परिमेय संख्याओं के योग के लिए सर्वप्रथम उन्हे योग (+) के चिह्न द्वारा एक साथ लिखते है। फिर उन सभी परिमेय संख्याओं के हरो का LCM (ल.स.) लेकर सामान्य विधि द्वारा हल करते है।
आइए एक उदाहरण से समझते है :-
उदाहरण : 43 और 59 को जोड़िए।
हल :
=43+59
चूंकि यहाँ दोनों परिमेय संख्याओं के हर 3 व 9 है अतः
3 और 9 का ल.स. = 9
=12+59
=179
परिमेय संख्याओं का व्यवकलन
दो परिमेय संख्याओं के व्यवकलन के लिए सर्वप्रथम उन्हे व्यवकलन (−) के चिह्न द्वारा एक साथ लिखते है। फिर उन दोनों परिमेय संख्याओं के हरो का LCM (ल.स.) लेकर सामान्य विधि द्वारा हल करते है।
आइए एक उदाहरण से समझते है :-
उदाहरण : 59 मे से 43 को घटाइए।
हल :
=59−43
चूंकि यहाँ दोनों परिमेय संख्याओं के हर 9 व 3 है अतः
9 और 3 का ल.स. = 9
=5−129
=−79
परिमेय संख्याओं का गुणन
दो या दो से अधिक परिमेय संख्याओं के गुणन के लिए उनके अंशों को गुणा अंशों से तथा हरो का गुणा हरो से करते है फिर गुणनफल को परिमेय संख्या के रूप मे ही लिखते है।
आइए एक उदाहरण से समझते है :-
उदाहरण : 59,43 और 73 का गुणनफल ज्ञात कीजिए।
हल :
=5×4×79×3×3
=14081
नोट :
⇒ दो ऋणात्मक चिह्न गुणन प्रक्रिया मे धनात्मक हो जाते है जबकि तीन ऋणात्मक चिह्न गुणन प्रक्रिया मे पुनः ऋणात्मक हो जाते है।
⇒ यदि गुणनफल मे अंश और हर दोनों मे ऋणात्मक चिह्न हो तो वह मान धनात्मक प्राप्त होता है जबकि यदि दोनों मे से किसी एक मे ऋणात्मक चिह्न हो तो गुणनफल का मान ऋणात्मक ही प्राप्त होता है।
परिमेय संख्याओं का विभाजन
परिमेय संख्या का व्युत्क्रम : दी गई परिमेय संख्या के अंश और हर का मान परस्पर बदलने पर प्राप्त संख्या दी गई परिमेय संख्या का व्युत्क्रम कहलाती है।
उदाहरण : 27 का व्युत्क्रम =72
दो परिमेय संख्याओं का विभाजन निम्न प्रकार समझ सकते है :-
उदाहरण : 37 ÷ 411 का मान ज्ञात कीजिए।
हल :
एक परिमेय संख्या को दूसरी परिमेय संख्या से भाग देने के लिए हम एक परिमेय संख्या के व्युत्क्रम को दूसरी परिमेय संख्या से गुणा करते है। अतः
=37÷411
यहाँ हम 37 को 411 के व्युत्क्रम से गुणा करते है :-
=37×114
=3328
OMR (One Minute Revision)
उदाहरण 13
योग ज्ञात कीजिए :
−910+2215
दो या दो से अधिक परिमेय संख्याओं के योग के लिए सर्वप्रथम उन्हे योग (+) के चिह्न द्वारा एक साथ लिखते है। फिर उन सभी परिमेय संख्याओं के हरो का LCM (ल.स.) लेकर सामान्य विधि द्वारा हल करते है।
=−910+2215
10 और 15 का ल.स. = 30
=−9×3+22×230
=−27+4430
=1730
उदाहरण 14
गुणनफल ज्ञात कीजिए :
92×−74
दो या दो से अधिक परिमेय संख्याओं के गुणन के लिए उनके अंशों को गुणा अंशों से तथा हरो का गुणा हरो से करते है फिर गुणनफल को परिमेय संख्या के रूप मे ही लिखते है।
=92×−74
=9×−72×4
=−638
उदाहरण 15
निम्नलिखित का मान ज्ञात कीजिए :
−213÷17
एक परिमेय संख्या को दूसरी परिमेय संख्या से भाग देने के लिए हम एक परिमेय संख्या के व्युत्क्रम को दूसरी परिमेय संख्या से गुणा करते है।अतः
−213÷17
यहाँ हम −213 को 17 के व्युत्क्रम से गुणा करते है :-
17 का व्युत्क्रम =71
⇒ −213×71
⇒ −1413