सरल समीकरण कक्षा 7 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम सरल समीकरण का अध्ययन करेंगे। आपने पिछली कक्षा 6 में भी समीकरणों के बारे मे पढ़ा हैं, चर राशियों के बारे मे जाना था, साथ ही हमने अनेक बीजीय व्यंजकों और समीकरणों के बारे में अध्ययन किया हैं। इस अध्याय मे सीखेंगे समीकरण बनाना, समीकरण हल करना, हल से समीकरण बनाना और व्यावहारिक स्थितियों में सरल समीकरणों के अनुप्रयोग का अध्ययन करेंगे।
आइये जानते है, सरल समीकरण को और करीब से ...
किसी भी समीकरण के मुख्यत: दो भाग होते हैं। LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) तथा दोनों पक्षों के बीच एक बराबर का चिन्ह होता है जिसे समता कहते हैं। समीकरण में कम से कम एक चर एवं दो बीजीय व्यंजक अवश्य होते है।
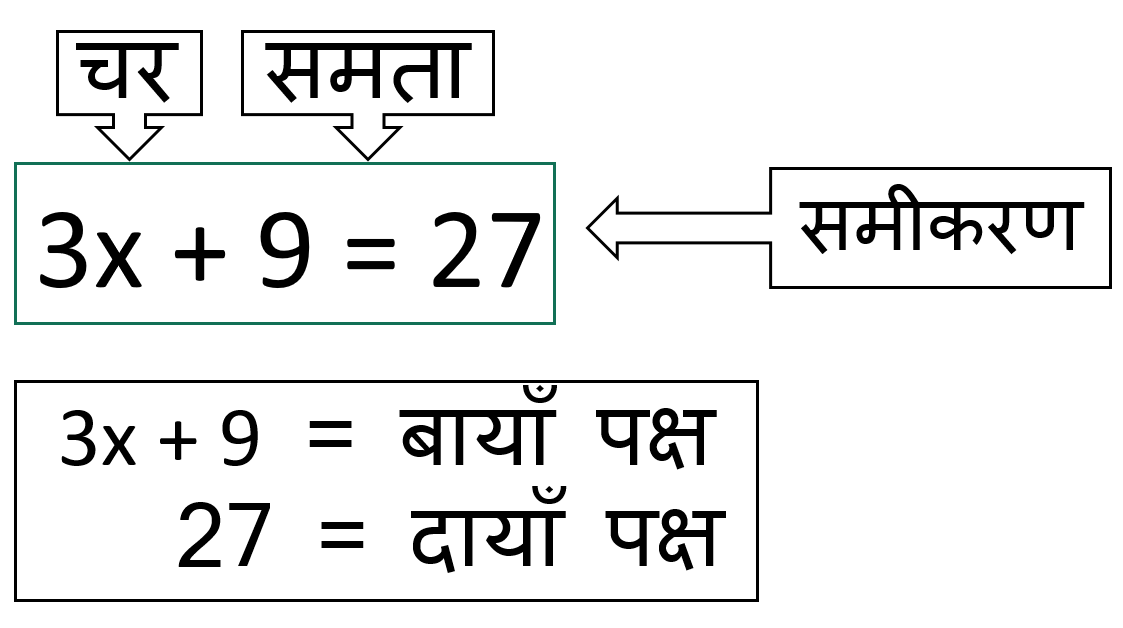
सरल समीकरण के कुछ उदाहरण:
(a) 10x=5
(b) 4m+8=20
(c) m+3=4m+7
समीकरण बनाना
उदाहरण से समझते हैं -
किसी संख्या में 6 का गुणा एवं उसमे 10 जोड़ने पर परिणाम 52 आता हैं।
हल:
चूँकि हम इस संख्या के बारे में कुछ नहीं जानते, अतः यह कोई भी संख्या हो सकता है।
अज्ञात संख्या को एक अक्षर x से व्यक्त करते हैं। (x के स्थान पर कोई अन्य अक्षर जैसे y, t, z भी ले सकते हैं)
प्रश्न के अनुसार,
अज्ञात संख्या (x)×6+10=52
⇒6x+10=52 ................(i)
अतः इस समीकरण का हल अज्ञात संख्या x का मान बताएगा।
इसी प्रकार, किसी अज्ञात संख्या में 10 का गुणा करने पर और गुणनफल में 20 घटाने पर परिणाम 50 आता हैं।
चूँकि हम इस संख्या के बारे में कुछ नहीं जानते, अतः यह कोई भी संख्या हो सकता है।
अज्ञात संख्या को एक अक्षर y से व्यक्त करते हैं।
प्रश्न के अनुसार,
y×10−20=50
⇒10y−20=50 ................(ii)
अतः इस समीकरण का हल अज्ञात संख्या y का मान बताएगा।
जो हमे ज्ञात हैं उसकी समीक्षा
यहाँ, समीकरण (i) में चर x तथा समीकरण (ii) में चर y है।
चर (Variable)
चर का अर्थ है, जिस राशि में परिवर्तन होता रहता है अर्थात् इसका मान निश्चित या स्थिर नहीं होता है। एक चर विभिन्न संख्यात्मक मान ले (ग्रहण कर) सकता है। चरों को प्रायः अंग्रेजी वर्णमाला के अक्षरों x, y, z, l, m, n, p इत्यादि से व्यक्त किया जाता है। चरों पर योग, व्यवकलन, गुणन और विभाजन जैसी संक्रियाएँ करके हम व्यंजकों (expressions) को बनाते हैं।
जैसे - चर से हमने व्यंजक (6x+10) बनाया था। इसके लिए, हमने पहले x को 6 से गुणा किया और फिर गुणनफल में 10 जोड़ा था।
इसी प्रकार, हमने व्यंजक (10y−20) बनाया था। इसके लिए, हमने y को 10 से गुणा किया और फिर गुणनफल में से 20 को घटाया था। ये सभी व्यंजकों के उदाहरण हैं।
इस प्रकार के बनाए व्यंजक का मान, चर के मान पर निर्भर करता हैं।
जैसे की अगर व्यंजक (6x+10) में x=1 हो, तो
6×1+10=6+10=16
अतः 6x+10=16 होगा। (समीकरण संतुष्ट हैं जब x=1 हो )
जब x=5 हैं, तो
6×5+10=30+10=40
अतः 6x+10=40 होगा। (समीकरण संतुष्ट हैं जब x=5 हो)
उदाहरण 1
निम्नलिखित सारणी के अंतिम स्तम्भ को पूरा कीजिए :
| क्रम संo | समीकरण | चर का मान | बताइए कि समीकरण संतुष्ट होती है या नहीं (हाँ/नहीं) |
|---|---|---|---|
| (i) | x+3=0 | x=3 | |
| (ii) | x+3=0 | x=0 | |
| (iii) | x+3=0 | x=−3 | |
| (iv) | x−7=1 | x=7 | |
| (v) | x−7=1 | x=8 | |
| (vi) | 5x=25 | x=0 | |
| (vii) | 5x=25 | x=5 | |
| (viii) | 5x=25 | x=−5 | |
| (ix) | m3=2 | m=−6 | |
| (x) | m3=2 | m=0 | |
| (xi) | m3=2 | m=6 |
| क्रम संo | समीकरण | चर का मान | बताइए कि समीकरण संतुष्ट होती है या नहीं (हाँ/नहीं) |
|---|---|---|---|
| (i) | x+3=0 | x=3 | नहीं |
| (ii) | x+3=0 | x=0 | नहीं |
| (iii) | x+3=0 | x=−3 | हाँ |
| (iv) | x−7=1 | x=7 | नहीं |
| (v) | x−7=1 | x=8 | हाँ |
| (vi) | 5x=25 | x=0 | नहीं |
| (vii) | 5x=25 | x=5 | हाँ |
| (viii) | 5x=25 | x=−5 | नहीं |
| (ix) | m3=2 | m=−6 | नहीं |
| (x) | m3=2 | m=0 | नहीं |
| (xi) | m3=2 | m=6 | हाँ |
(i) x+3=0 जब x=3
अतः समीकरण में x=3 रखने पर,
3+3=0
⇒6=0
अत: मान x=3 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(ii) x+3=0 जब x=0
अतः समीकरण में x=3 रखने पर,
0+3=0
⇒3=0
अत: मान x=0 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(iii) x+3=0 जब x=−3
अतः समीकरण में x=−3 रखने पर,
−3+3=0
⇒0=0
अत: मान x=−3 दिये गये समीकरण को संतुष्ट करता है।
अत: उत्तर हाँ होगा।
(iv) x−7=1 जब x=7
अतः समीकरण में x=7 रखने पर,
7−7=1
⇒0=1
अत: मान x=7 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(v) x−7=1 जब x=8
अतः समीकरण में x=8 रखने पर,
8−7=1
⇒1=1
अत: मान x=8 दिये गये समीकरण को संतुष्ट करता है।
अत: उत्तर हाँ होगा।
(vi) 5x=25 जब x=0
अतः समीकरण में x=0 रखने पर,
5×0=25
⇒0=25
अत: मान x=0 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(vii) 5x=25 जब x=5
अतः समीकरण में x=5 रखने पर,
5×5=25
⇒25=25
अत: मान x=5 दिये गये समीकरण को संतुष्ट करता है।
अत: उत्तर हाँ होगा।
(viii) 5x=25 जब x=−5
अतः समीकरण में x=−5 रखने पर,
5×(−5)=25
⇒−25=25
अत: मान x=−5 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(ix) m3=2 जब m=–6
अतः समीकरण में m=–6 रखने पर,
−63=2
⇒−2=2
अत: मान m=–6 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(x) m3=2 जब m=0
अतः समीकरण में m=0 रखने पर,
03=2
⇒0=2
अत: मान m=0 दिये गये समीकरण को संतुष्ट नहीं करता है।
अत: उत्तर नहीं होगा।
(xi) m3=2 जब m=6
अतः समीकरण में m=6 रखने पर,
63=2
⇒2=2
अत: मान m=6 दिये गये समीकरण को संतुष्ट करता है।
अत: उत्तर हाँ होगा।
समीकरण क्या हैं`?`
समीकरण चर पर एक प्रतिबंध होता है। प्रतिबंध यह है कि दोनों व्यंजकों के मान बराबर होने चाहिए तथा दोनों व्यंजकों में से कम से कम एक में चर अवश्य होना चाहिए या ऐसा बीजीय व्यंजक जिसमे चर के विशिष्ट मान के लिए दोनों पक्ष समान होते हैं। समीकरण कहलाता है।
समीकरण के गुण
जैसे 4x+5=6x−25 को 6x−25=4x+5 भी लिख सकते हैं।
जैसे, 3x+4=7
LHS =3x+4
RHS =7
यहाँ, हम x=1 रखते हैं
LHS = 3×1+4=7
अतः x=1 के लिए, LHS =RHS अर्थात x=1 समीकरण को संतुष्ट करता हैं।
उदाहरण 2
निम्नलिखित कथनों को समीकरण के रूप में लिखिए:
(i) x के तिगुने और 11 का योग 32 है।
(ii) किसी संख्या के 6 गुने में 5 घटाने पर 7 प्राप्त होता है।
(iii) m का एक चौथाई 7 से 3 अधिक है।
(iv) किसी संख्या के एक तिहाई में 5 जोड़ने पर 8 प्राप्त होता है।
दिया हैं,
(i) x के तिगुने और 11 का योग 32 है।
अतः x का तिगुना =3x
प्रश्न के अनुसार,
x का तिगुना +11=32
⇒3x+11=32
अतः समीकरण, 3x+11=32 होगा।
(ii) किसी संख्या के 6 गुने में 5 घटाने पर 7 प्राप्त होता है।
माना की वह संख्या x हैं।
अतः x का 6 गुना =6x
प्रश्न के अनुसार,
संख्या (x) का 6 गुना −5=7
⇒6x−5=7
अतः समीकरण, 6x−5=7 होगा।
(iii) m का एक चौथाई 7 से 3 अधिक है।
m का एक चौथाई =m(14)=m4
यह 7 से 3 अधिक हैं।
अतः m4=7+3
⇒m4=10
अतः समीकरण m4=10 होगा।
(iv) किसी संख्या के एक तिहाई में 5 जोड़ने पर 8 प्राप्त होता है।
माना की वह संख्या z हैं।
संख्या (z) का एक तिहाई =z(13)=z3
प्रश्न के अनुसार,
संख्या (z) का एक तिहाई +5=8
⇒z3+5=8
अतः समीकरण z3+5=8 होगा।
उदाहरण 3
प्रयत्न और भूल विधि से निम्नलिखित समीकरणों को हल कीजिए:
(i) 5p+2=17
(ii) 3m−14=4
दिया है,
(i)5p+2=17
(a) माना कि, p=1
अत:, समीकरण में p=1 रखने पर,
5×1+2=17
⇒5+2=17
⇒7=17
यहाँ LHS≠RHS अर्थात मान p=1 दिये गये समीकरण का हल नहीं है।
(b) माना कि p=2
अत:, समीकरण में p=2 रखने पर,
5×2+2=17
⇒10+2=17
⇒12=17
यहाँ LHS≠RHS अर्थात मान p=2 दिये गये समीकरण का हल नहीं है।
(c) माना कि p=3
अत:, समीकरण में p=3 रखने पर,
5×3+2=17
⇒15+2=17
⇒17=17
यहाँ LHS=RHS अर्थात मान p=3 दिये गये समीकरण का हल है।
अत:, p=3 उत्तर
(ii) 3m−14=4
दिया गया है, 3m−14=4
(a) माना कि m=5
अत:, समीकरण में m=5 रखने पर,
3×5−14=4
⇒15−14=4
⇒1=4
यहाँ LHS≠RHS अर्थात मान m=5 दिये गये समीकरण का हल नहीं है।
(b) माना कि m=6
अत:, समीकरण में m=6 रखने पर हम पाते हैं कि
3×6−14=4
⇒18−14=4
⇒4=4
यहाँ LHS=RHS अर्थात मान m=6 दिये गये समीकरण का हल है।
अत:, m=6 उत्तर
उदाहरण 4
निम्नलिखित समीकरणों को सामान्य कथनों के रूप में लिखिए:
(i) p+4=15
(ii) m−7=3
(iii) 2m=7
(iv) m5=3
दिया हैं,
(i) p+4=15
P और 4 का योग 15 हैं।
(ii) m−7=3
m में से 7 घटाने पर 3 प्राप्त होता है।
(iii) 2m=7
m का दो गुणा 7 है।
(iv) m5=3
m को 5 से भाग देने पर 3 प्राप्त होता हैं।
एक समीकरण को हल करना
आइए इसे समझने के लिए एक समिका लेते है -
8−3=4+1
अतः समिका सत्य है, क्योंकि इसके दोनों पक्ष बराबर हैं।
LHS=8−3=5
RHS=4+1=5
LHS=8−3+2=5+2=7
RHS=4+1+2=5+2=7
पुनः, समिका सत्य है क्योंकि इसके दोनों पक्ष बराबर हैं।
इस प्रकार, यदि हम एक समिका के दोनों पक्षों में एक ही संख्या जोड़ें, तो भी वह समिका सत्य होती है।
LHS=8−3−2=5−2=3
RHS=4+1−2−5−2=3
पुनः, समिका सत्य है क्योंकि इसके दोनों पक्ष बराबर हैं।
इस प्रकार, यदि हम एक समिका के दोनों पक्षों में से एक ही संख्या घटाएँ, तो भी वह समिका सत्य होती है।
LHS=3×(8–3)=3×5=15
RHS=3×(4+1)=3×5=15
अतः समिका सत्य है क्योंकि इसके दोनों पक्ष बराबर हैं।
इसी प्रकार, यदि हम एक समिका के दोनों पक्षों को एक ही शून्येतर (non−zero) संख्या से गुणा करें, तो भी वह समिका सत्य होती है।
LHS=8−32=52=52
RHS=4+12=52=52
अतः समिका सत्य है क्योंकि इसके दोनों पक्ष बराबर हैं।
इसी प्रकार, यदि हम एक समिका के दोनों पक्षों को एक ही शून्येतर (non−zero) संख्या से भाग दें, तो भी वह समिका सत्य होती है।
उदाहरण के लिए,
8−3=4+1
अब, इसके बाएँ पक्ष में 2 जोड़े और दाएँ पक्ष में 3 जोड़े।
अतः
LHS=8−3+2=5+2=7 है।
RHS=4+1+3=5+3=8 है।
अब, समिका सत्य नहीं है, क्योंकि LHS और RHS बराबर नहीं हैं।
इस प्रकार, यदि हम एक समिका के दोनों पक्षों में कोई गणितीय संक्रिया एक ही संख्या के साथ न करें, तो समिका सत्य नहीं होती है।
उपरोक्त निष्कर्ष समीकरणों के लिए भी मान्य होते हैं, क्योंकि प्रत्येक समीकरण में चर केवल संख्या ही निरूपित करता है।
उदाहरण 5
चर को पृथक करने वाला चरण बताइये और फिर समीकरण को हल कीजिए :
(a)x−1=0
(b) x+1=0
(c) x−1=5
(d) x+6=2
दिया है,
(a) x−1=0
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 1 जोड़ने पर,
x−1+1=0+1
⇒x=1
अत: दोनों तरफ 1 जोड़ना है, x=1 उत्तर
(b) x+1=0
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 1 घटाने पर,
x+1−1=0−1
⇒x=−1
अत: दोनों तरफ 1 घटाना है, x=−1 उत्तर
(c) x−1=5
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 1 जोड़ने पर,
x−1+1=5+1
⇒x=6
अत: दोनों पक्षों में 1 जोड़ना है, x=6 उत्तर
(d) x+6=2
समीकरण के दोनों तरफ अर्थात LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 6 घटाने पर,
x+6−6=2−6
⇒x=−4
अत:, दोनों पक्षों में 6 घटाना है, x=−4 उत्तर
उदाहरण 6
निम्नलिखित समीकरणों को हल कीजिए :
(a) 10p=100
(b) 10p+10=100
(c) 20p3=40
(d) 3p10=6
(a) 10p=100
दिया हैं,
10p=100
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 10 से भाग देने पर,
⇒10p10=10010
चूँकि 100=10×10
implies(cancel (10) p)/cancel (10) = [cancel (10) xx 10]/cancel (10)
⇒p=10
अत: p=10 उत्तर
(b) 10p+10=100
दिया है,
10p+10=100
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 10 घटाने पर,
⇒10p+10−10=100−10
⇒10p=90
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) में 10 से भाग देने पर,
⇒10p10=9010
( चूँकि 90=10×9)
implies(cancel (10)p)/ cancel (10) = (cancel (10) xx 9)/ cancel (10)
⇒p=9
अत: p=9 उत्तर
(c) 20p3=40
दिया है,
20p3=40
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) को 3 से गुणा करने पर,
⇒20p3×3=40×3
implies(20p) / cancel (3) xxcancel (3)= 40xx3
⇒20p=40×3
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) को 20 से भाग करने पर,
⇒20p20=40×320
चूँकि 40=20×2
implies(cancel(20)p)/cancel(20) = (cancel(20)xx 2 xx 3)/cancel(20)
⇒p=2×3
⇒p=6
अत: p=6 उत्तर
(d) 3p10=6
दिया है,
3p10=6
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) को 10 से गुणा करने पर,
⇒3p10×10=6×10
implies(3p) / cancel (10) xxcancel (10)= 6xx10
⇒3p=6×10
समीकरण के दोनों तरफ LHS (बायाँ पक्ष) और RHS (दायाँ पक्ष) को 3 से भाग करने पर,
⇒3p3=6×103
चूँकि 6=3×2
implies( cancel(3)p)/cancel(3) = (cancel(3) xx 2xx10)/cancel(3)
⇒p=2×10
⇒p=20
अत: p=20 उत्तर
स्थानापन्न
अब, समीकरणों को हल करते समय, हम एक संख्या को स्थानापन्न (transpose) करने अर्थात् एक पक्ष से दूसरे पक्ष में ले जाने के बारे में सीखेंगे।
किसी संख्या को, समीकरण के दोनों पक्षों में जोड़ने या घटाने के स्थान पर, स्थानापन्न (जिसे पक्षांतर भी कह सकते हैं) कर सकते हैं।
जैसे - समीकरण x+3=8 में +3 का स्थानापन्न LHS से RHS करने पर −3 हो जायेगा।
अतः x=8−3
जैसे - समीकरण 8x=56 में 8, LHS में गुणात्मक रूप में हैं जिसे RHS में ले जाने पर हर में चला जायेगा।
अतः x=56×18
जैसे - समीकरण 18x=7 में 8, LHS के हर में गुणात्मक रूप में हैं जिसे RHS में जाने पर अंश में चला जायेगा।
अतः x=7×8
उदाहरण 7
निम्नलिखित समीकरणों को हल कीजिए:
(a) 2y+52=372
(b) 5t+28=10
(c) a5+3=2
(d)q4+7=5
(a) 2y+52=372
दिया हैं,
2y+52=372
हम जानते हैं की जब किसी चर या अचर को एक पक्ष से दूसरे पक्ष में ले जाया जाता है तो चिन्ह बदल जाता है।
अतः 52 को दायीं ओर ले जाने पर इसका चिन्ह ऋणात्मक हो जायेगा, अर्थात यह −52 हो जायेगा।
अतः 2y=372−52
⇒2y=37−52
⇒2y=322
चूँकि 32=2×16
implies 2y = (cancel (2) xx 16)/ cancel (2)
⇒2y=16
हम जानते हैं की जब कोई चर या अचर राशि एक पक्ष गुणक के रूप में हो तो उसे दूसरे पक्ष में ले जाने पर वह भाग के रूप में बदल जाता है।
अत: यहाँ 2 जो y के साथ गुणक के रूप में बायीं ओर है, दायीं ओर ले जाने पर यह 12 हो जायेगा।
⇒y=16×12
⇒y=162
चूँकि 16=2×2
implies y = (cancel (2) xx 8)/ cancel (2)
⇒y=8
अत: y=8 उत्तर
(b) 5t+28=10
दिया हैं,
5t+28=10
अत: 28 को बायें पक्ष से दायें पक्ष में ले जाने पर इसका चिन्ह ऋणात्मक हो जायेगा अर्थात यह –28 हो जायेगा।
⇒5t=10−28
⇒5t=–18
हम जानते हैं की जब कोई चर या अचर राशि एक पक्ष गुणक के रूप में हो तो उसे दूसरे पक्ष में ले जाने पर वह भाग के रूप में बदल जाता है।
अत: यहाँ 5 जो t के साथ गुणक के रूप में बायीं ओर है, दायीं ओर ले जाने पर यह 15 हो जायेगा।
⇒t=–18×15
अत: t=–185 उत्तर
(c) a5+3=2
दिया हैं,
a5+3=2
अत: 3 को बायें पक्ष से दायें पक्ष में ले जाने पर इसका चिन्ह ऋणात्मक हो जायेगा अर्थात यह –3 हो जायेगा।
⇒a5=2−3
⇒a5=−1
चूँकि 5 बायें पक्ष में हर में है अत: दायें पक्ष में ले जाने पर यह गुणक के रूप में अर्थात अंश में चला जायेगा।
⇒a=−1×5
⇒a=−5
अत: a=–5 उत्तर
(d) q4+7=5
दिया हैं,
q4+7=5
अत: 7 को बायें पक्ष से दायें पक्ष में ले जाने पर इसका चिन्ह ऋणात्मक हो जायेगा अर्थात यह –7 हो जायेगा।
⇒q4=5−7
⇒q4=−2
4 बायें पक्ष में हर में है अत: दायें पक्ष में ले जाने पर यह गुणक के रूप में अर्थात अंश में चला जायेगा।
⇒q=−2×4
अत: q=−8
हल से समीकरण
अभी तक हम समीकरण का हल निकालते थे लेकिन अब हम हल से समीकरण बनाना सीखेंगे।
जैसे - x=6 के लिए समीकरण बनाइए ?
हल:
दिया है, x=6
दोनों पक्षों को 2 से गुणा करने पर,
⇒x×2=6×2
⇒2x=12
दोनों पक्षों में 10 को जोड़ने पर,
⇒2x+10=12+10
⇒2x+10=22
अतः x=6 के लिए बनाया गया समीकरण 2x+10=22 हैं।
उदाहरण 8
(a) x=2 से प्रारंभ करते हुए, 3 समीकरण बनाइये।
(b) x=−2 से प्रारंभ करते हुए, 3 समीकरण बनाइये।
(a) x=2 से प्रारंभ करते हुए, 3 समीकरण बनाइये।
दिया हैं,
(i) x=2
दोनों पक्षों (दायाँ एवं बायाँ पक्ष ) में 3 जोड़ने पर,
⇒x+3=2+3
⇒x+3=5 समीकरण (i)
(ii) x=2
दोनों पक्षों (दायाँ एवं बायाँ पक्ष ) में 10 का गुणा करने पर,
⇒10×x=10×2
⇒10x=20
बायाँ पक्ष मे अचर पद लाने के लिए दोनों पक्षों में 2 जोड़ने पर,
⇒10x+2=20+2
⇒10x+2=22 समीकरण (ii)
(iii) x=2
दोनों पक्षों (दायाँ एवं बायाँ पक्ष ) में 5 से भाग करने पर,
x5=25 समीकरण (iii)
(b) x=−2 से प्रारंभ करते हुए, 3 समीकरण बनाइये।
दिया हैं,
(i) x=−2
दोनों पक्षों (दायाँ एवं बायाँ पक्ष ) में 5 जोड़ने पर,
⇒x+5=−2+5
⇒x+5=3 समीकरण (i)
(ii) x=−2
दोनों पक्षों (दायाँ एवं बायाँ पक्ष ) में 10 का गुणा करने पर,
⇒10×x=10×(−2)
⇒10x=−20
बायाँ पक्ष मे अचर पद लाने के लिए दोनों पक्षों मे 4 जोड़ने पर,
⇒10x+4=−20+4
⇒10x+4=−16 समीकरण (ii)
(iii) x=2
दोनों पक्षों (दायाँ एवं बायाँ पक्ष ) में 4 से भाग करने पर,
⇒x4=−24
impliesx/4 = (-cancel (2))/(cancel (2)xx 2 )
⇒x4=−12 समीकरण (iii)
सरल समीकरणों के अनुप्रयोग
हमने ऐसे बहुत से उदाहरण देखे हैं, जिनमें हमने दैनिक जीवन की भाषा से कथनों को लेकर उन्हें सरल समीकरणों के रूप में बदला था। हम यह भी सीख चुके हैं कि सरल समीकरणों को किस प्रकार हल किया जाता है।
जैसे - राम एक संख्या सोचता है। वह इसमें 19 जोड़कर योग को 5 से भाग देता हैं, उसे 8 प्राप्त होता हैं।
हल:
मान लिया कि राम द्वारा सोची गयी संख्या =m
अत: प्रश्न के अनुसार,
⇒m+195=8
अतः समीकरण m+195=8 होगा।
उदाहरण 9
निम्नलिखित स्थितियों के लिए समीकरण बनाइए और फिर उन्हें हल करके अज्ञात संख्याएँ ज्ञात कीजिए:
(a) एक संख्या के आठ गुने में 4 जोड़िये, आपको 60 प्राप्त होगा।
(b) एक संख्या का 15 घटा 4, संख्या 3 देता हैं।
(c) यदि मैं किसी संख्या का तीन - चौथाई लेकर इसमें 3 जोड़ दूँ, तो मुझे 21 प्राप्त होते हैं।
(d) जब मैंने किसी संख्या के दुगने में से 11 घटाया, तो परिणाम 15 प्राप्त हुआ।
(a) एक संख्या के आठ गुने में 4 जोड़िये, आपको 60 प्राप्त होगा।
दिया है,
एक संख्या के आठ गुने में 4 जोड़ने पर, 60 प्राप्त होता है।
माना की वह संख्या x हैं।
अत: संख्या (x) का आठ गुणा =8x
प्रश्न के अनुसार,
संख्या (x) का आठ गुणा +4=60
⇒8x+4=60
प्राप्त समीकरण के बायें पक्ष से 4 को दायें पक्ष में ले जाने पर यह −4 होगा।
⇒8x=60−4
⇒8x=56
अत: यहाँ 8 जो बायें पक्ष में x के साथ गुणा के रूप में है दायें पक्ष में ले जाने पर 18 हो जायेगा।
⇒x=56×18
⇒x=568
चूँकि 56=7×8
implies x = (7xxcancel ( 8 ))/cancel ( 8 )
⇒x=7 उत्तर
(b) एक संख्या का 15 घटा 4, संख्या 3 देता हैं।
दिया है,
संख्या का 15 में 4 घटाने पर 3 प्राप्त होता हैं।
माना की वह संख्या x हैं ।
अतः संख्या (x) का 15 गुना =x×15
अत: प्रश्न के अनुसार,
x×(15)−4=3
प्राप्त समीकरण के बायें पक्ष से −4 को दायें पक्ष में ले जाने पर यह 4 होगा।
⇒x5=3+4
⇒x5=7
यहाँ, चूँकि 5 बायें पक्ष में हर में है अत: दायें पक्ष में ले जाने पर यह गुणा के रूप में अंश में चला जायेगा।
⇒x=7×5
⇒x=35 उत्तर
(c) यदि मैं किसी संख्या का तीन - चौथाई लेकर इसमें 3 जोड़ दूँ, तो मुझे 21 प्राप्त होते हैं।
दिया है,
किसी संख्या के तीन चौथाई में 3 जोड़ने पर 21 प्राप्त होता हैं।
माना की वह संख्या x हैं।
संख्या (x) का तीन चौथाई =x×34
प्रश्न के अनुसार,
संख्या (x) का तीन चौथाई +3=21
⇒x×34+3=21
प्राप्त समीकरण के बायें पक्ष से 3 को दायें पक्ष में ले जाने पर यह −3 होगा।
⇒x×34=21−3
⇒x×34=18
यहाँ 4 बायें पक्ष में हर में है अत: दायें पक्ष में ले जाने पर यह गुणा के रूप में अंश में चला जायेगा।
⇒x×3=18×4
⇒x×3=72
⇒3x=72
अत: यहाँ 3 जो बायें पक्ष में x के साथ गुणा के रूप में है दायें पक्ष में ले जाने पर 13 हो जायेगा।
⇒x=72×13
⇒x=723
चूँकि 72=3×24
implies x = (cancel (3) xx 24 )/ cancel (3)
⇒x=24 उत्तर
(d) जब मैंने किसी संख्या के दुगने में से 11 घटाया, तो परिमाण 15 प्राप्त हुआ।
दिया है,
किसी संख्या के दुगने 2 में से 11 घटाने पर 15 प्राप्त होता हैं।
माना की वह संख्या x हैं।
अतः संख्या (x) का दोगुना =2×x
प्रश्न के अनुसार,
संख्या (x) का दोगुना −11=15
⇒2×x−11=15
⇒2x−11=15
प्राप्त समीकरण के बायें पक्ष से 11 को दायें पक्ष में ले जाने पर यह −11 होगा ।
⇒2x=15+11
⇒2x=26
यहाँ 2 जो बायें पक्ष में x के साथ गुणा के रूप में है दायें पक्ष में ले जाने पर 12 हो जायेगा।
⇒x=26×12
⇒x=262
चूँकि 26=2×13
impliesx = (cancel (2) xx 13)/cancel (2)
⇒x=13 उत्तर
सारांश
(i) दोनों पक्षों में एक ही संख्या जोड़ें या (ii) दोनों पक्षों में से एक ही संख्या घटाएँ या (iii) दोनों पक्षों को एक ही संख्या से गुणा करें या (iv) दोनों पक्षों को एक ही संख्या से भाग दें तो संतुलन में कोई परिवर्तन नहीं होता है अर्थात् LHS और RHS के मान समान रहते हैं।
उदाहरण, समीकरण x+3=8 में +3 का स्थानापन्न LHS से RHS करने पर x=8−3=5 प्राप्त होता है। हम व्यंजकों का भी स्थानापन्न उसी विधि से करते हैं जैसे एक संख्या का स्थानापन्न करते हैं।