ठोस आकारों का चित्रण कक्षा 7 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय में हम ठोस आकारों के चित्रण का अध्ययन करेंगे। समतल आकारों की लंबाई और चौड़ाई जैसी दो मापे होती हैं, इसलिए इन्हें द्विविमीय (two dimensional) आकार कहते हैं, जबकि ठोस आकारों की लंबाई, चौड़ाई और ऊंचाई या गहराई जैसी तीन मापे होती हैं, इसलिए इन आकारों को त्रिविमीय (three dimensional) आकार कहते हैं। इस अध्याय में हम त्रिविमीय (3-D) आकारों, 3-D आकार बनाने के लिए जाल तथा त्रिविमीय आकृतियों में फलकों, किनारों और शीर्षों का अध्ययन करेंगे। साथ ही सपाट पृष्ठ पर ठोसो को खींचना और किसी ठोस के विभिन्न भागों को विभिन्न दशाओं मे देखना सीखेंगे।
आइये जानते है, ठोस आकारों को और करीब से...
कक्षा 6 में हमने ठोस आकारों के बारे में पढ़ा है कि ठोस आकारों को त्रिविमीय आकार कहते हैं क्योंकि इसमें लंबाई एवं चौड़ाई के अतिरिक्त ऊंचाई अथवा गहराई भी होती है। घन, घनाभ, बेलन, शंकु एवं गोला त्रिविमीय आकृतियाँ है जबकि वर्ग, आयत, वृत्त आदि द्विविमीय आकृतियाँ है।
हमने यह पढ़ा है कि त्रिविमीय आकारों के फलक, किनारे एवं शीर्ष होते हैं कुछ आकारों के पृष्ठ समतल, कुछ के वक्राकार एवं कुछ आकारों में दोनों प्रकार के पृष्ठ होते हैं। इस अध्याय में हम ठोस आकारों का समतल पर चित्रण करना सीखेंगे।
तल आकृतियाँ और ठोस आकार
ऐसी आकृति जिन्हें हम अपनी अभ्यास पुस्तिका (Note Book) पर खींच सकते हैं, समतल आकृति (Plane Figure) कहलाती हैं तथा समतल आकृति में दो विमा, लंबाई और चौड़ाई होती हैं, इसलिए इन्हे द्विविमीय (two dimensional) (2D)आकृति भी कहते हैं।
जैसे -

ठोस आकृति: हमें दैनिक जीवन में अनेक ठोस, जैसे ईंट, बक्सा, माचिस की डिबिया, कमरा, प्लेट, जग, डस्टर आदि देखने को मिलते हैं। इन आकृतियों में लंबाई, चौड़ाई तथा ऊंचाई होती हैं, इसलिए इन्हें त्रिविमीय (three dimension) (3D) आकृति कहते हैं। तीन विमाओं वाली आकृति को घनाकृति या ठोस (solid) भी कहते हैं।
जैसे -
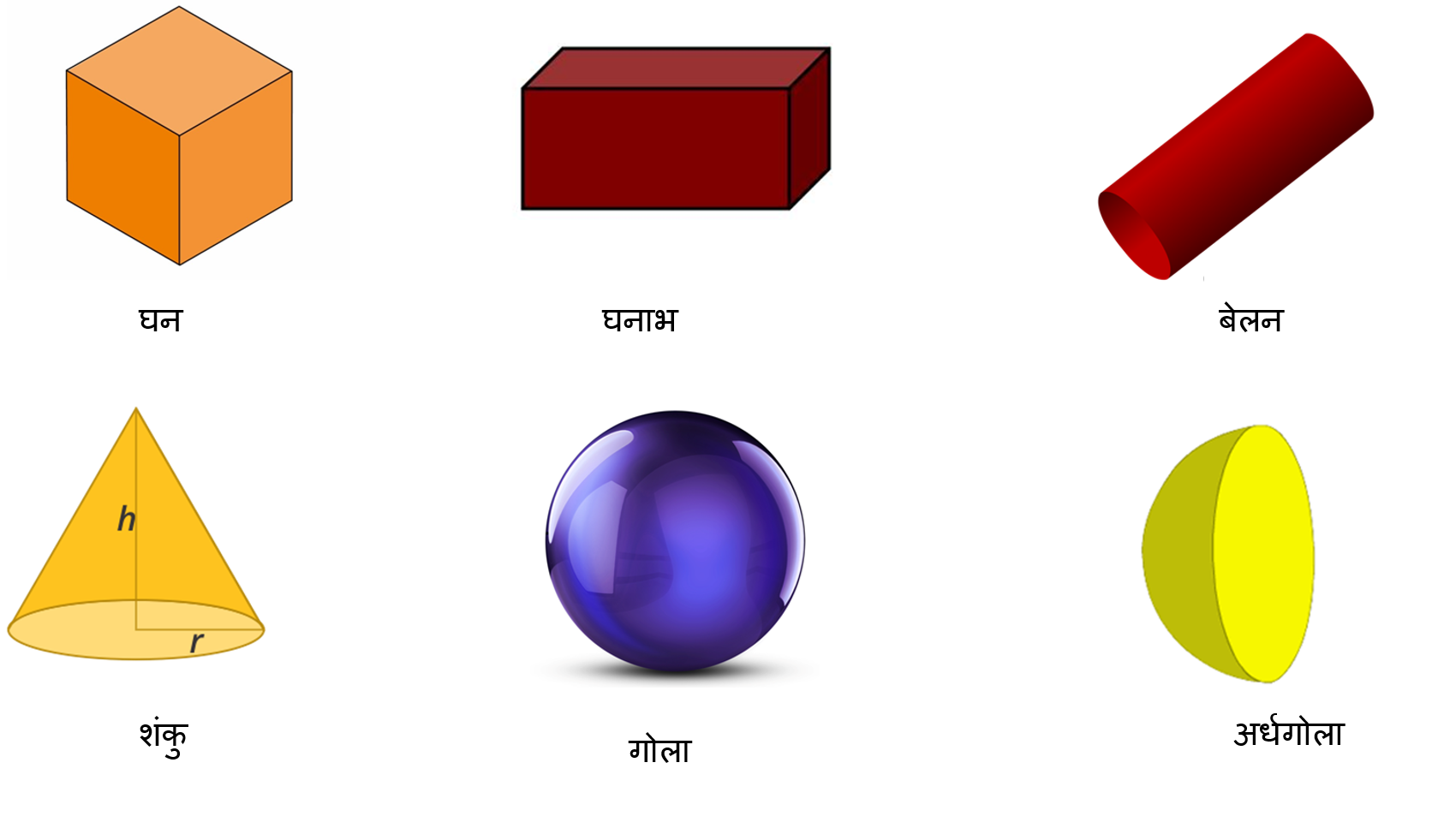
Note:- एक ठोस वस्तु कुछ स्थान घेरती है।
उदाहरण 1
निम्नलिखित ठोस आकृति को दैनिक जीवन से संबंधित एक उदाहरण से समझाइए।
घनाभ
हम जानते है कि घनाभ की आकृति निम्न प्रकार की होती है :-
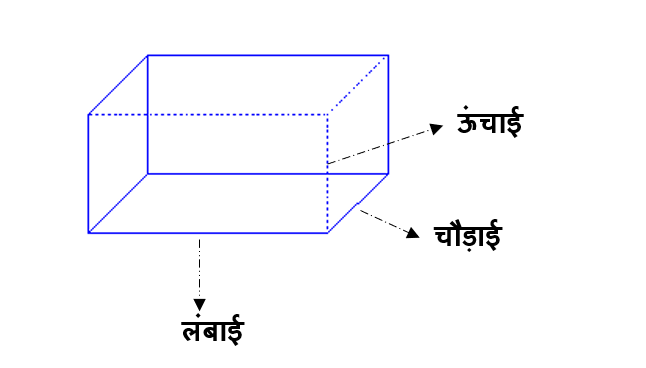
अतः हम देख सकते है कि घनाभ की लंबाई, चौड़ाई और ऊंचाई तीन मापे होती है।
अब हम एक किताब को देखे तो उसमे ये तीनों मापे होती है।

अब हम एक खाली कमरे को देखे तो उसमे भी ये तीनों मापे होती है।
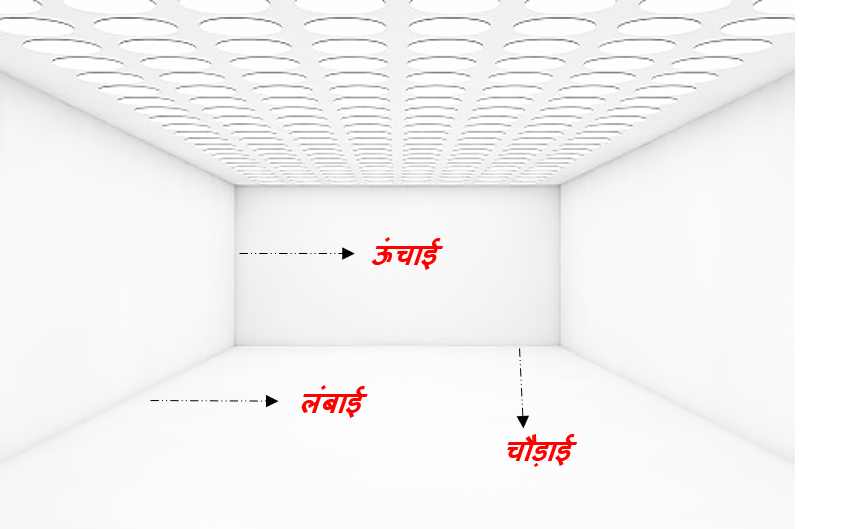
उदाहरण 2
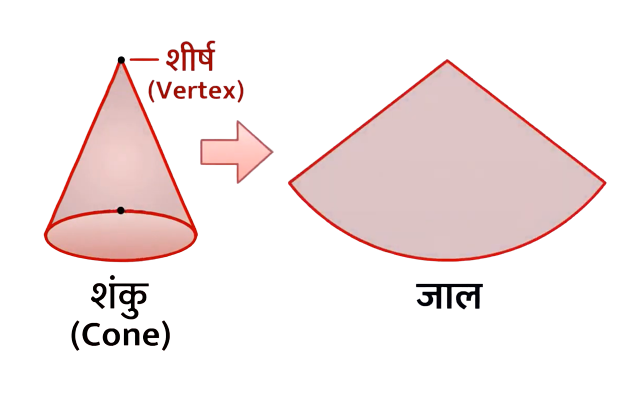
एक ऐसी आकृति का नाम लिखिए जिसका आधार वृत्ताकार हो एवं उसमे एक शीर्ष बिन्दु हो।
प्रश्नानुसार एक आकृति बनाते है :-
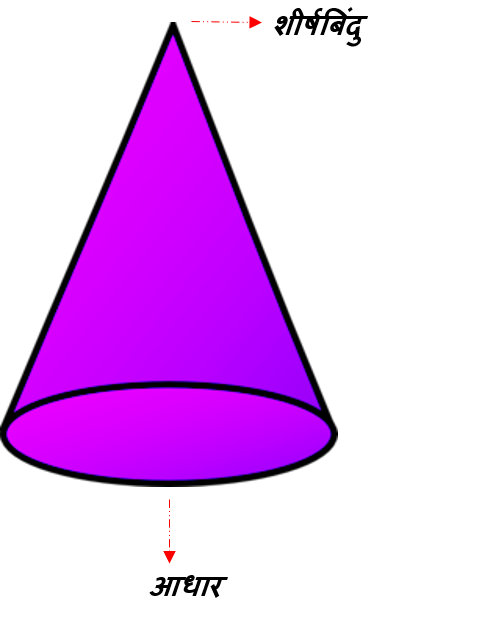
आकृति मे हम देख सकते है इसका आधार वृत्ताकार है तथा एक शीर्ष बिन्दु है। अतः इस प्रकार की आकृति एक शंकु की होती है।
उदाहरण 3
निम्नलिखित ठोस आकृति को दैनिक जीवन से संबंधित एक उदाहरण से समझाइए।
घन
हम जानते है कि घन की आकृति निम्न प्रकार की होती है :-
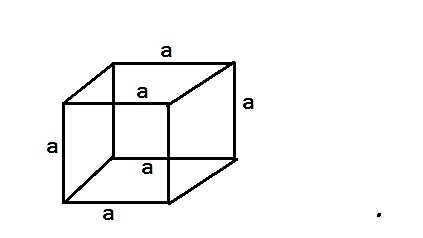
अतः हम देख सकते है कि घन की लंबाई, चौड़ाई और ऊंचाई तीनों माप समान होती है।
अब हम एक पासे को देखे तो उसमे ये तीनों मापे समान होती है।

अब हम एक उपहार बॉक्स (Gift Box) को देखे तो उसमे भी ये तीनों मापे समान ही प्रतीत होती है।

फलक, किनारे और शीर्ष
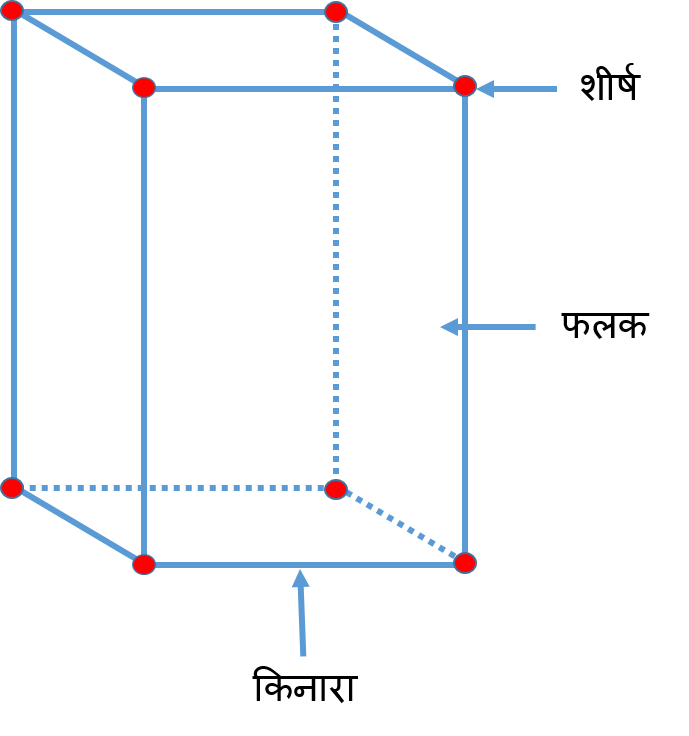
फलक: त्रिविमीय आकृतियों की सभी सतहें फलक कहलाते हैं।
किनारा: वे रेखाखंड जो ठोस आकृतियों की संरचना बनाते हैं, किनारे कहलाते हैं। दो फलक 3D आकृतियों के किनारों पर मिलते हैं।
शीर्ष: ठोस आकृतियों के कोने को शीर्ष कहते हैं, दो किनारे शीर्ष पर मिलते हैं।
ऑयलर सूत्र: ऑयलर सूत्र एक बहुफलक के किनारों, फलकों और शीर्षों के बीच संबंध को दर्शाता है।
प्रत्येक बहुफलक के लिए,
F+V=E+2
या F+V−E=2 सत्य होता है।
जहाँ,
F= फलकों की संख्या
V= शीषों की संख्या
E= किनारों की संख्या
यही ऑयलर सूत्र कहलाता है।
उदाहरण: ऑयलर सूत्र का प्रयोग करते हुए, यदि शीर्षों की संख्या 6 है और किनारों की संख्या 12 है, तो फलकों की संख्या ज्ञात कीजिए।
दिया हैं,
शीर्षों की संख्या (V)=6
किनारों की संख्या (E)=12
फलकों की संख्या (F)=?
ऑयलर सूत्र से हम जानते हैं कि,
F+V=E+2
⇒F+6=12+2
⇒F=12+2−6
⇒F=8
अतः, फलकों की संख्या 8 होंगी।
उदाहरण 4
समकोण प्रिज्म के फलकों की संख्या ज्ञात कीजिए जिसके 16 शीर्ष और 24 किनारे हो।
दिया हैं :-
फलक (F)=?
शीर्ष (V)=16
किनारे (E)=24
अब, ऑयलर सूत्र से,
F+V=E+2
⇒F+16=24+2
⇒F+16=26
⇒F=26−16
⇒F=10
अतः, समकोण प्रिज्म के फलकों की संख्या 10 होगी।
उदाहरण 5
ऑयलर सूत्र का प्रयोग करते हुए, अज्ञात संख्याओं को ज्ञात कीजिए:
| फलक | ? | 5 | 20 |
| शीर्ष | 6 | ? | 12 |
| किनारे | 12 | 9 | ? |
दिया हैं,
पहले कॉलम के लिए,
फलक (F)=?, शीर्ष (V)=6, किनारे (E)=12
अब, ऑयलर सूत्र से,
F+V=E+2
⇒F+6=12+2
⇒F+6=14
⇒F=14−6
⇒F=8
अतः, यहाँ 8 फलक हैं।
दूसरे कॉलम के लिए,
फलक (F)=5, शीर्ष (V)=?, किनारे (E)=9
अब, ऑयलर सूत्र से,
F+V=E+2
⇒5+V=9+2
⇒V=11−5
⇒V=6
अतः, यहाँ 6 शीर्ष हैं।
तीसरे कॉलम के लिए,
फलक (F)=20, शीर्ष (V)=12, किनारे (E)=?
अब, ऑयलर सूत्र से,
F+V=E+2
⇒20+12=E+2
⇒32=E+2
⇒E=30
अतः, यहाँ 30 किनारे हैं।
अतः
| फलक | 8 | 5 | 20 |
| शीर्ष | 6 | 6 | 12 |
| किनारे | 12 | 9 | 30 |
उदाहरण 6
क्या किसी बहुफलक के 10 फलक, 20 किनारे और 15 शीर्ष हो सकते हैं?
यहाँ दिया हैं:
फलकों की संख्या (F)=10
शीर्षों की संख्या (V)=15
किनारों की संख्या (E)=20
तब, ऑयलर सूत्र से,
F+V=E+2
LHS से,
LHS=F+V
=10+15
=25
RHS से,
RHS=E+2
=20+2
=22
LHS≠RHS
अतः यहाँ ऑयलर सूत्र सत्यापित नहीं है, इसलिए किसी बहुफलक के 10 फलक, 20 किनारे और 15 शीर्ष नहीं हो सकते।
`3`-`D` आकार बनाने के लिए जाल
ठोस का एक जाल दो विमाओं में एक ऐसा ढाँचा (या रूप रेखा) है, जिसे मोड़ने पर परिणामस्वरूप 3D (त्रिविमीय) आकार प्राप्त हो जाता है। एक ही ठोस के अनेक प्रकार के जाल हो सकते हैं।
आइए समझते हैं:

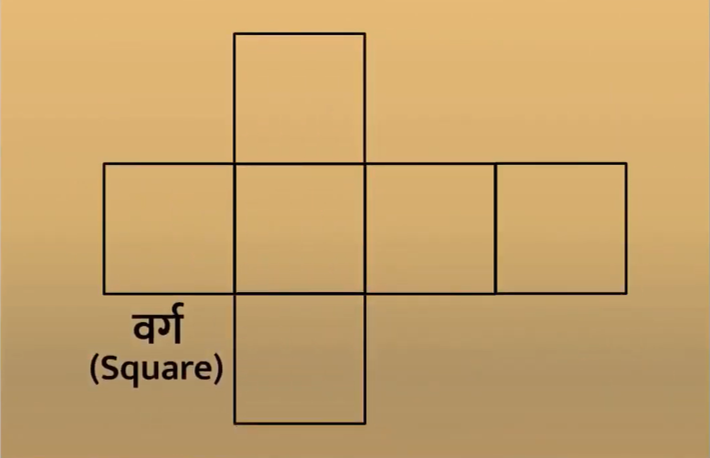
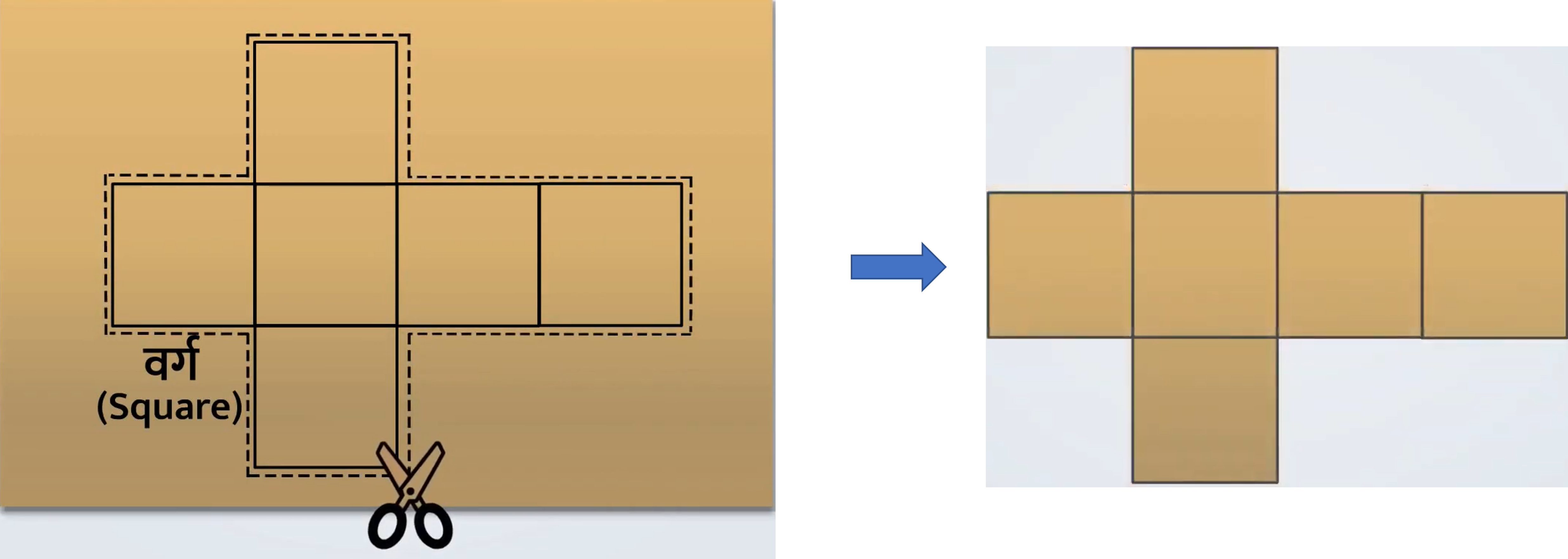

इस प्रकार, 2D में बनाए गए ढांचे से त्रिविमीय आकृति प्राप्त की जा सकती हैं।
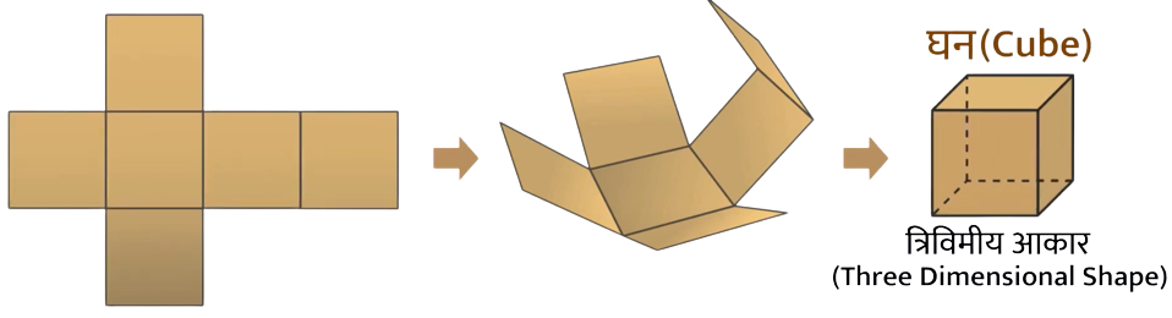
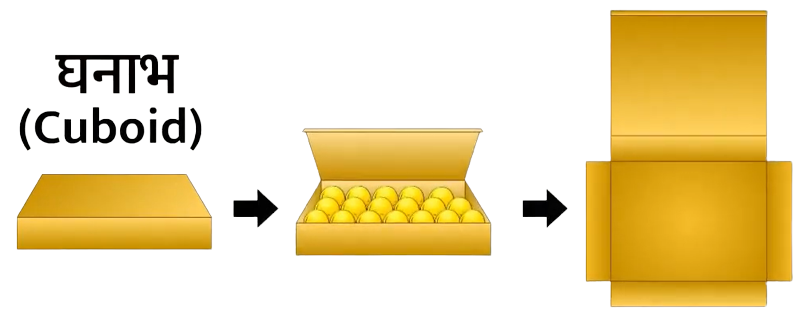
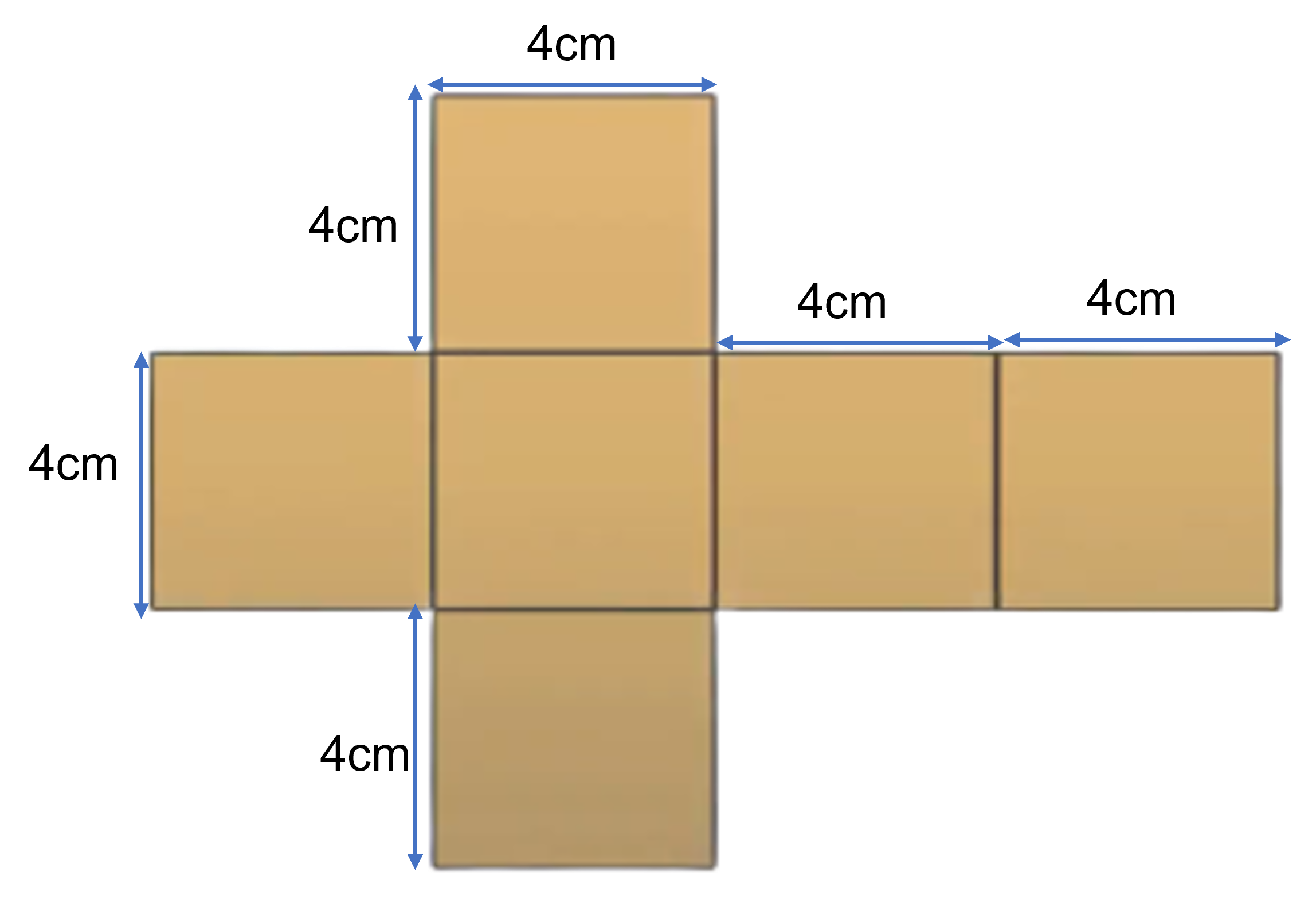
यह घनाभ का जाल (नेट) है।
OMR (One Minute Revision)
उदाहरण 7
उदाहरण 8
जालों को उपयुक्त ठोसों से मिलान कीजिए:
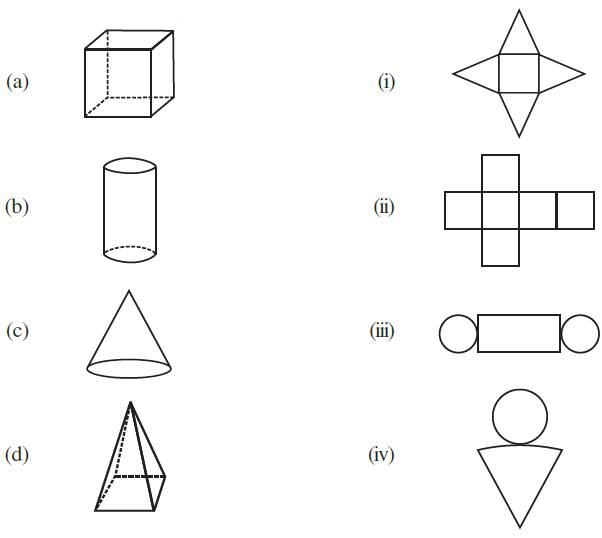
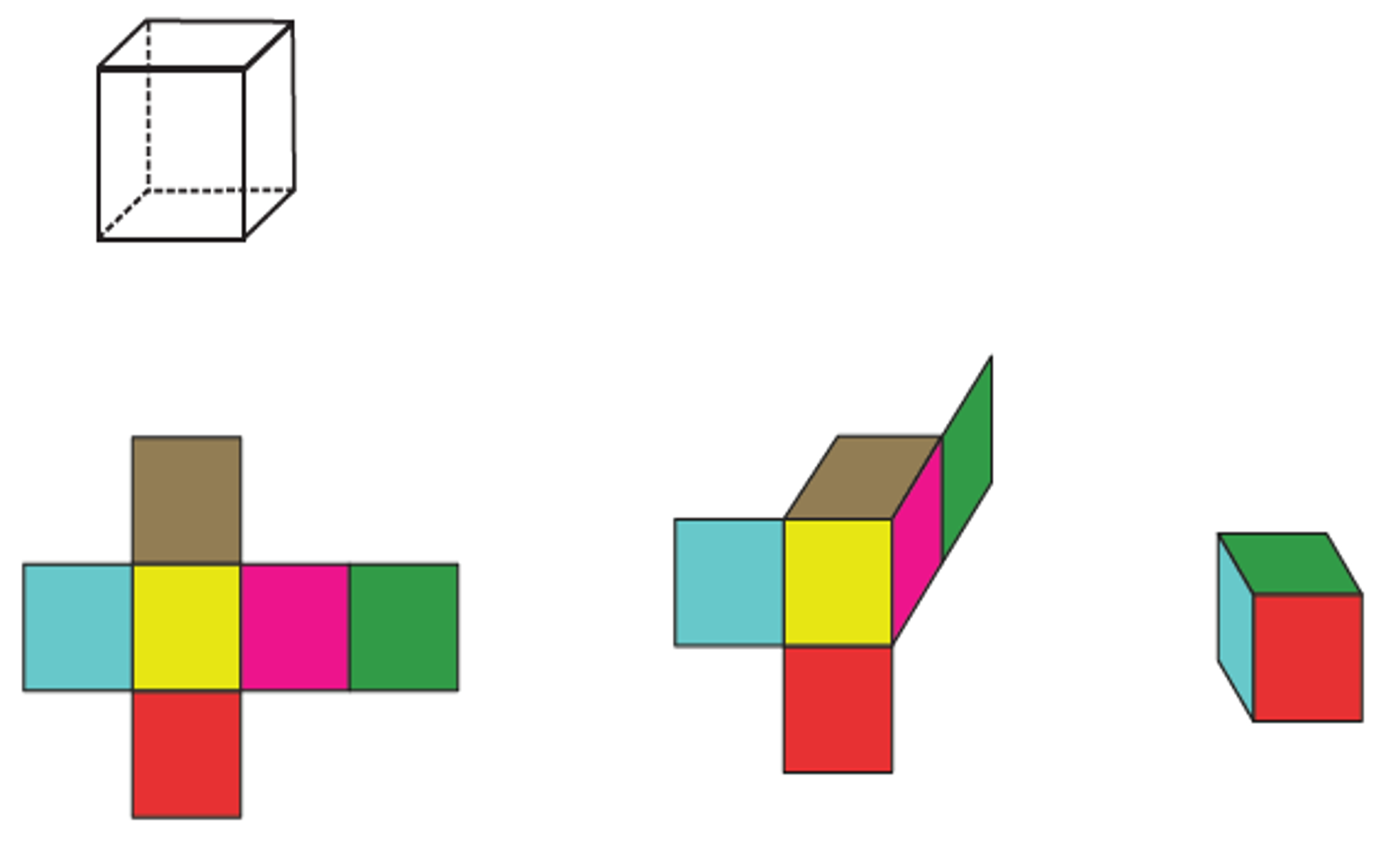
(a)→(ii)
क्योंकि जाल (ii) को वर्गाकार मोड़ा जा सकता है।
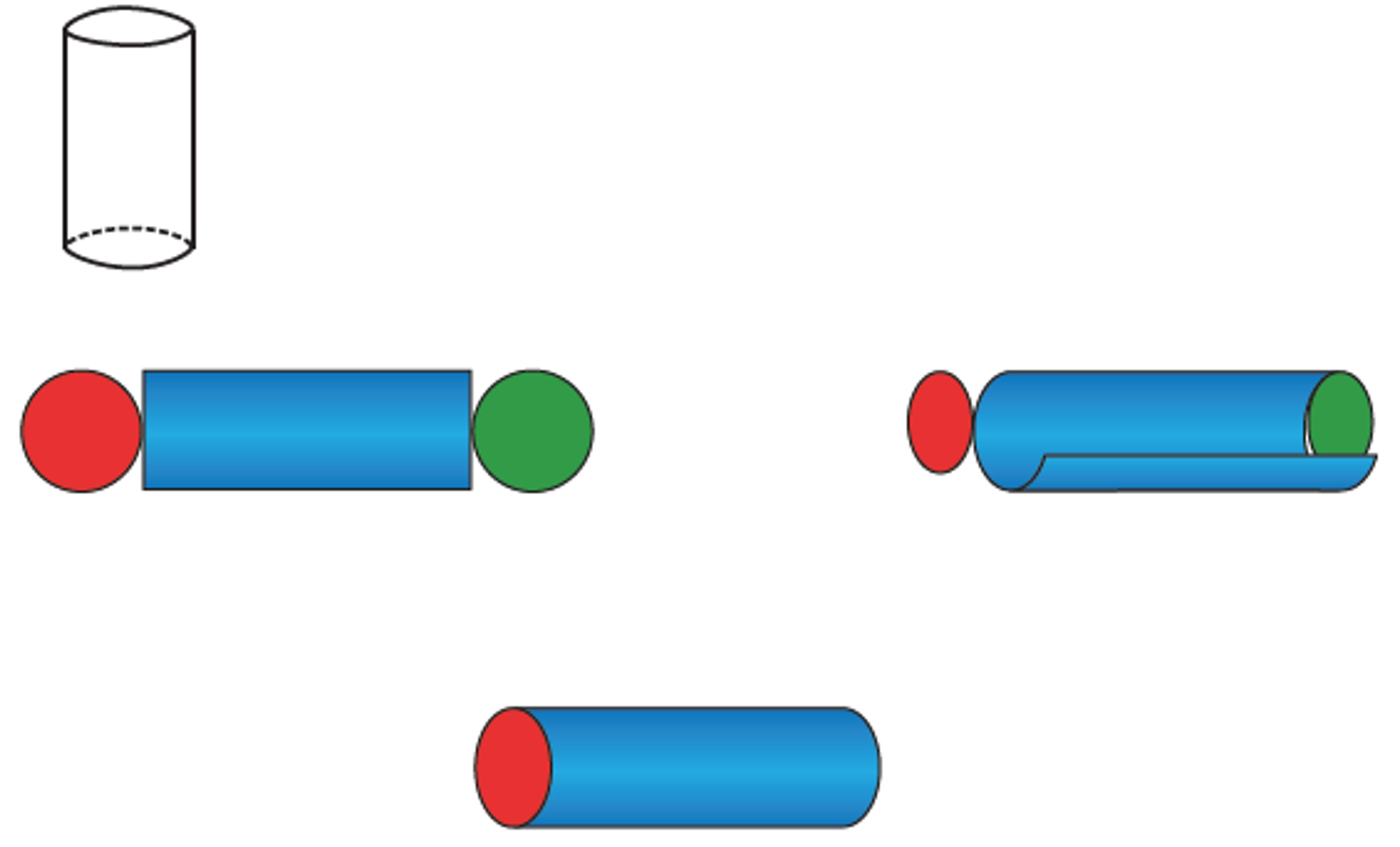
(b)→(iii)
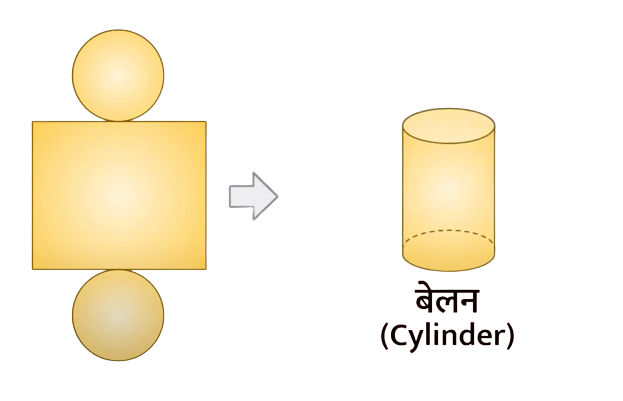
क्योंकि जाल (iii) को बेलन की तरह मोड़ा जा सकता है।
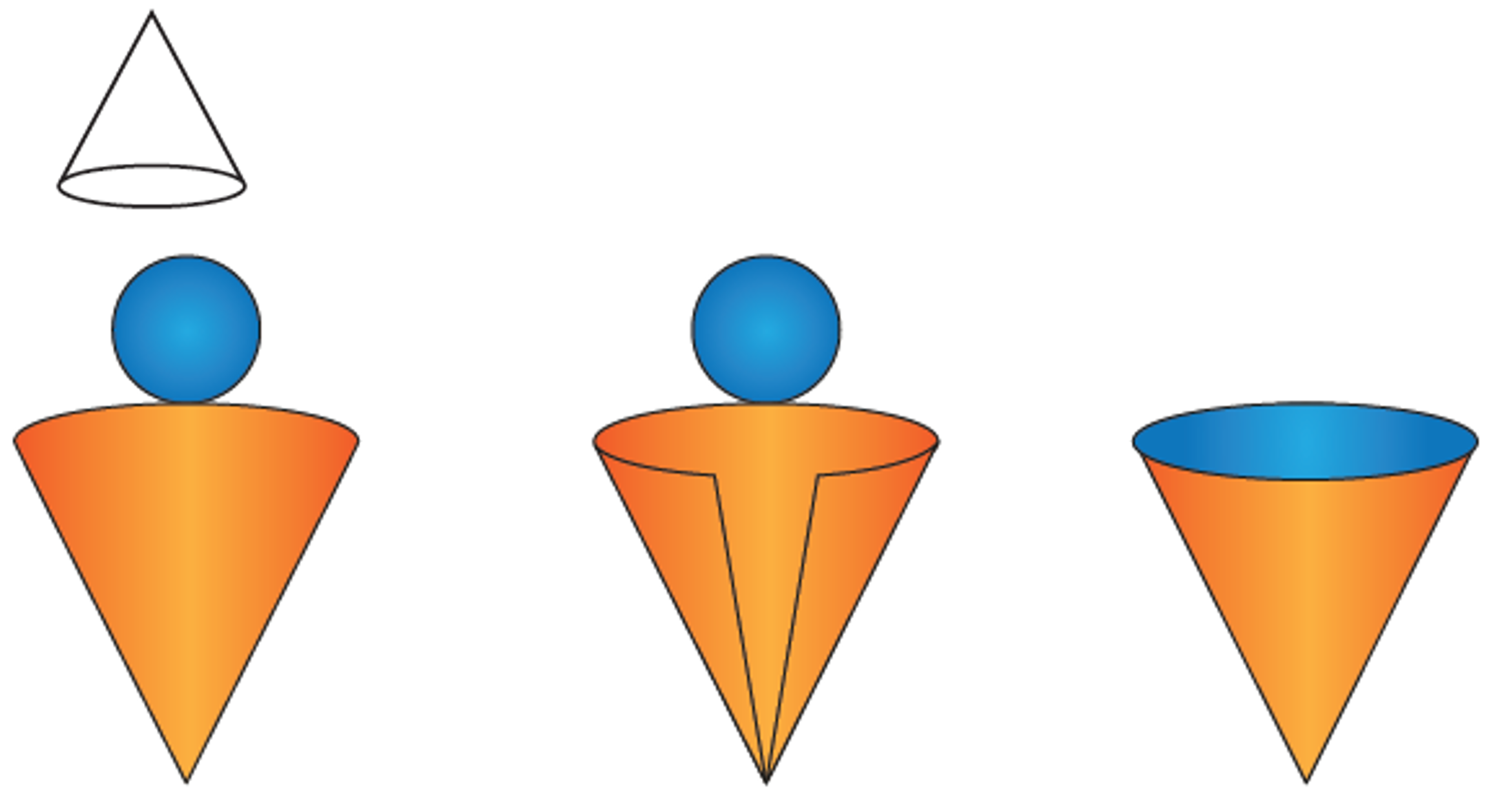
(c)→(iv)
क्योंकि जाल (iv) को एक शंकु के रूप में मोड़ा जा सकता है।
(d)→(i)
क्योंकि जाल (i) को पिरामिड की तरह मोड़ा जा सकता है।
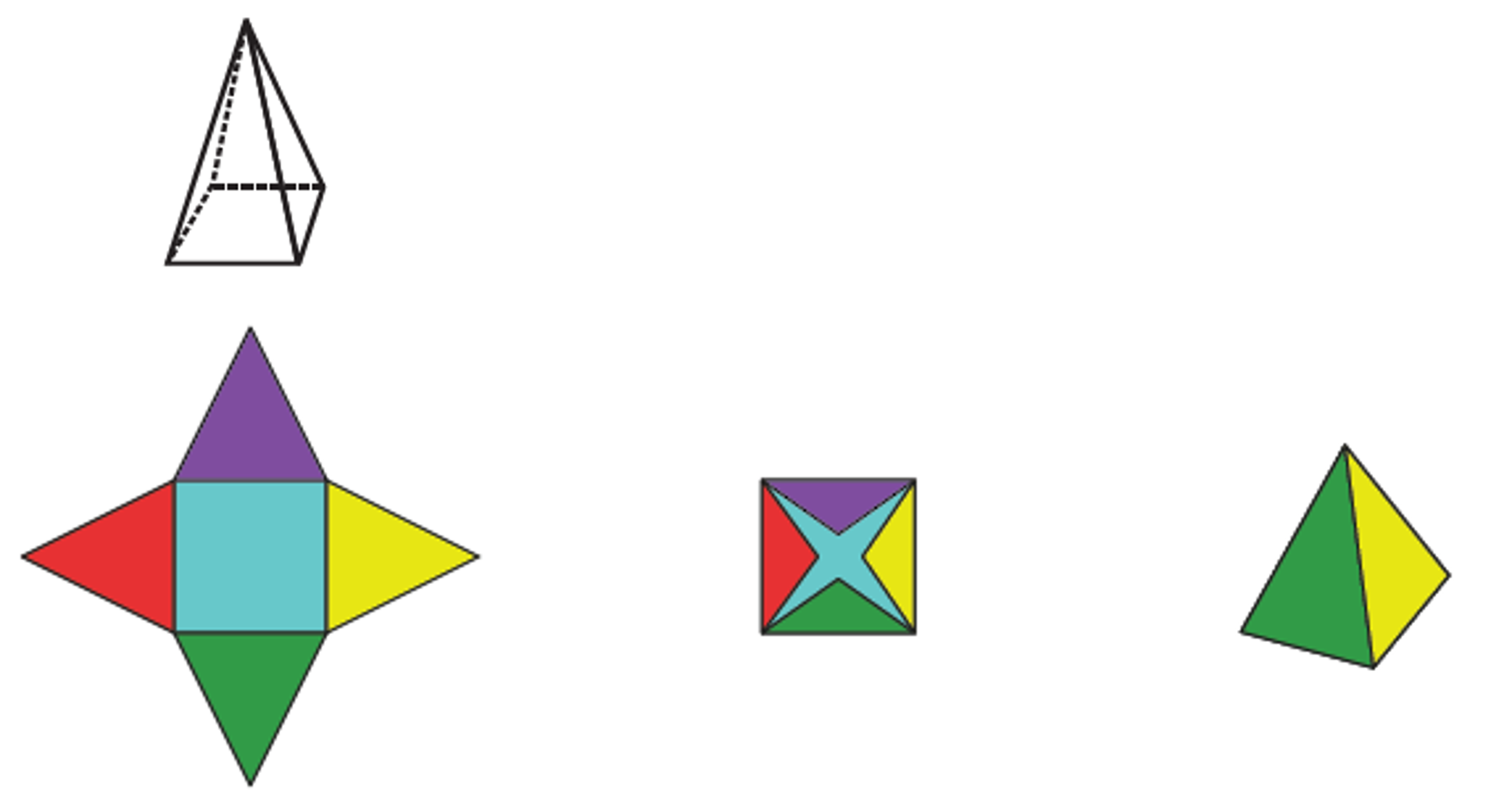
सपाट पृष्ठ पर ठोसो को खींचना
हम जानते है कि 3 - D आकार ऐसी आकृतियाँ होती है जो कुछ स्थान घेरती है। अतः हम कुछ विशेष तकनीकों के द्वारा समतल सतह पर भी 3 - D आकृतियों को प्रदर्शित कर सकते है। यह एक दृश्य भ्रम कहलाता है।
तिर्यक चित्र :-
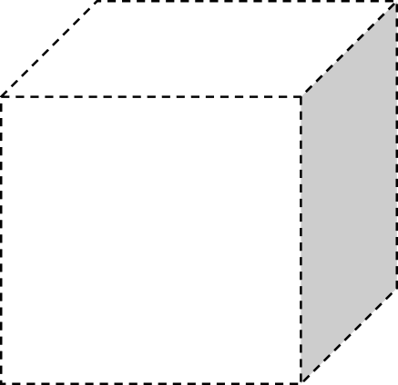
उपर्युक्त चित्र एक घन का चित्र है। इस चित्र मे भुजाओं की माप समान नहीं है जबकि घन मे यह आवश्यक होता है कि सभी भुजायें समान हो। इस भिन्नता के बाद भी हम इस आकृति को पहचान सकते है। अतः किसी ठोस का इस प्रकार चित्रण एक तिर्यक अथवा अनियमित चित्रण कहलाता है।
आइए इसके निर्माण की प्रक्रिया को चरणबद्ध तरीके से समझते है :-
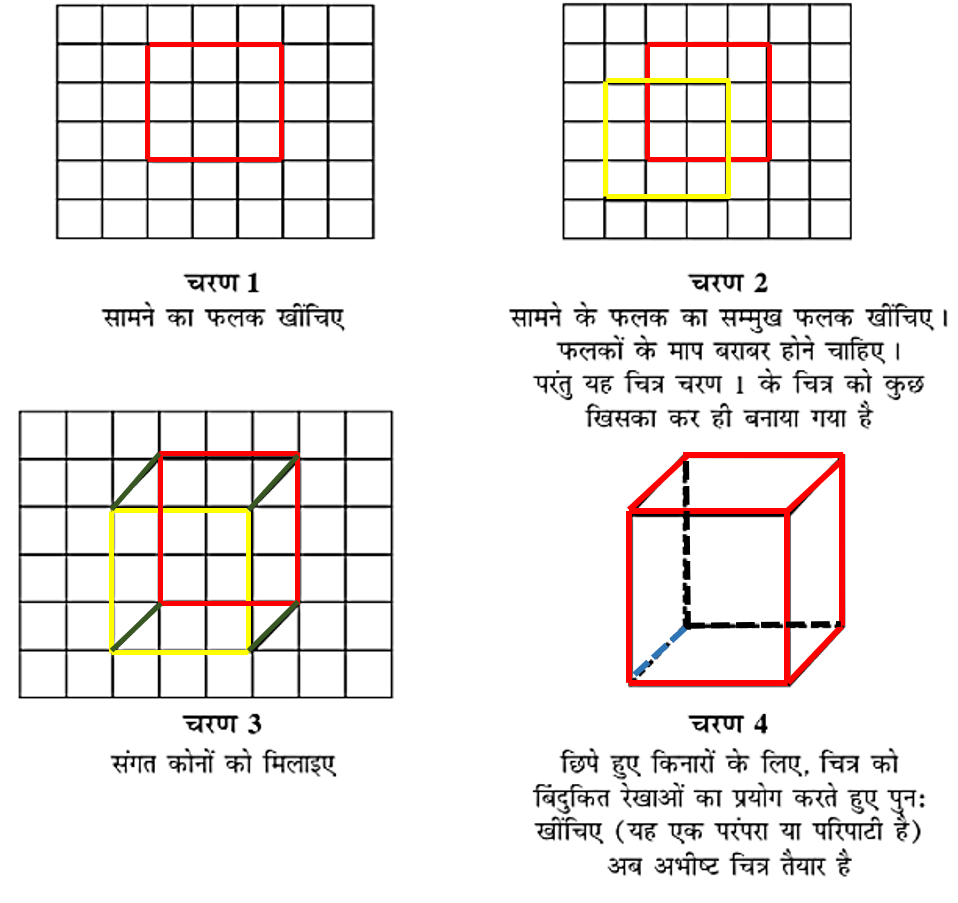
उपर्युक्त प्रक्रिया मे हम देख सकते है कि सामने के फलक और उसके सम्मुख फलक समान है तथा घन के किनारे जो समान है, चित्र मे भी समान प्रतीत हो रहे है जबकि इनको बराबर नहीं लिया गया हैं।
समदूरीक चित्र :-
समदूरीक शीट बिंदुओं से बनी शीट होती है जिसमे अनेक बिन्दु समान दूरी पर स्थित होते है। जब हम मूल आकृति के समानुपाती माप के साथ समदूरीक शीट पर आकृति बनाते है तो इसे समदूरीक चित्र कहते है।
आइए एक समदूरीक शीट पर 4×3×3 का एक घनाभ (जिसमे इसकी लंबाई, चौड़ाई तथा ऊंचाई क्रमश: 4,3,3 इकाइयों की है। ) बनाते है।
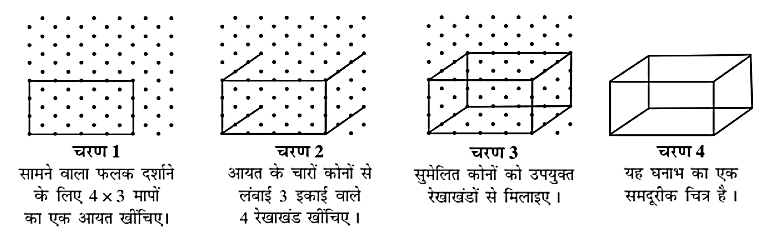
नोट :- समदूरीक चित्र मे मापन ठोस आकृति की दी गई यथार्थ मापों के समान होता है जबकि तिर्यक चित्र की स्थिति मे ऐसा नहीं होता है।
उदाहरण 9
एक तिर्यक चित्र खींचिए जिसमे घन की विमाएँ निम्न प्रकार हैं:
3 सेमी ×3 सेमी ×3 सेमी
यहाँ हम एक वर्गांकित कागज का प्रयोग करेंगे।
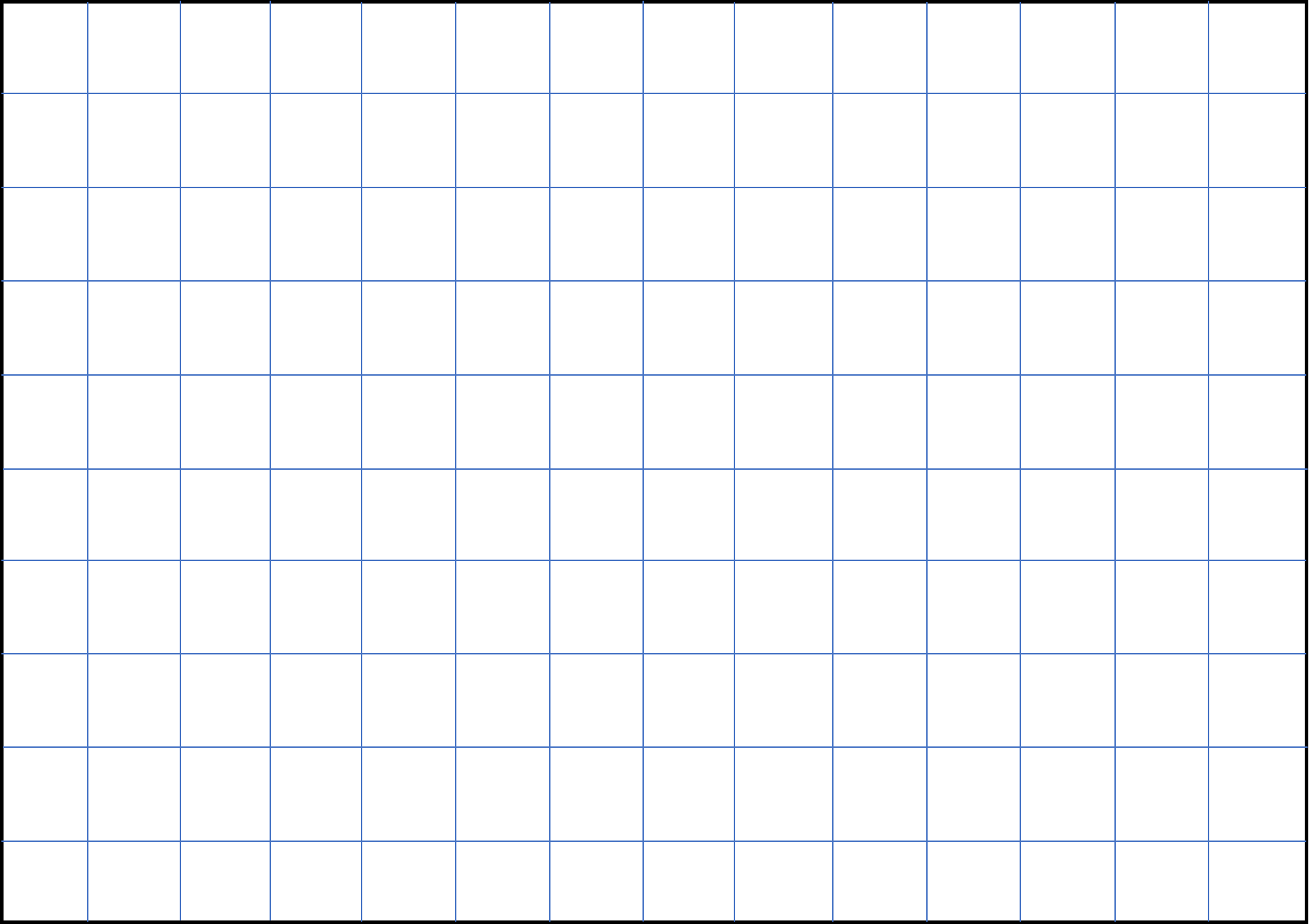
चरण 1: वर्गांकित कागज पर 3 सेमी किनारों वाला सामने का वर्गाकार फलक खींचिए।
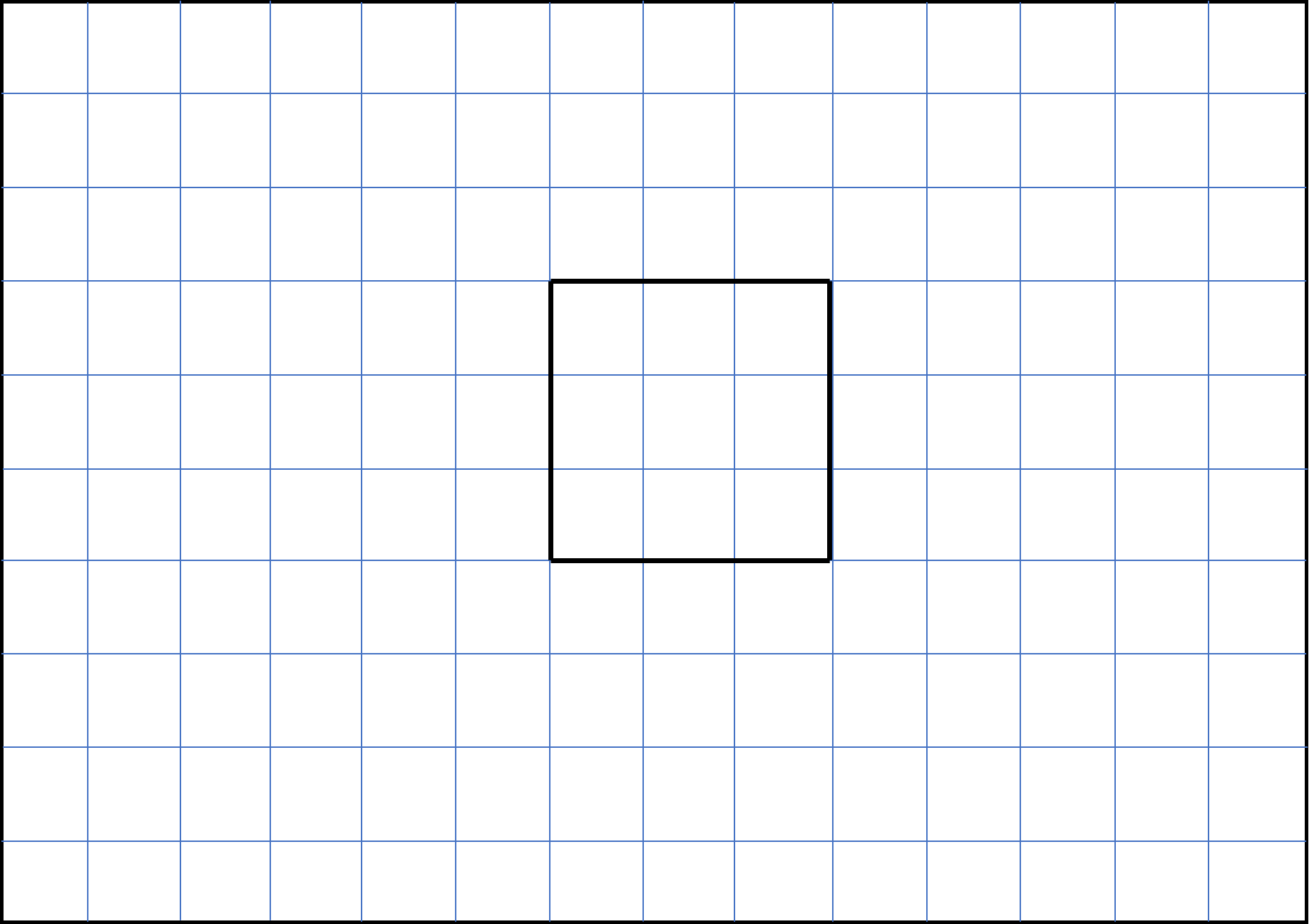
चरण 2: सामने के फलक का सम्मुख फलक खींचिए। फलकों के माप बराबर होने चाहिए। परंतु यह चित्र चरण 1 के चित्र को कुछ खिसका कर ही बनाया गया है।
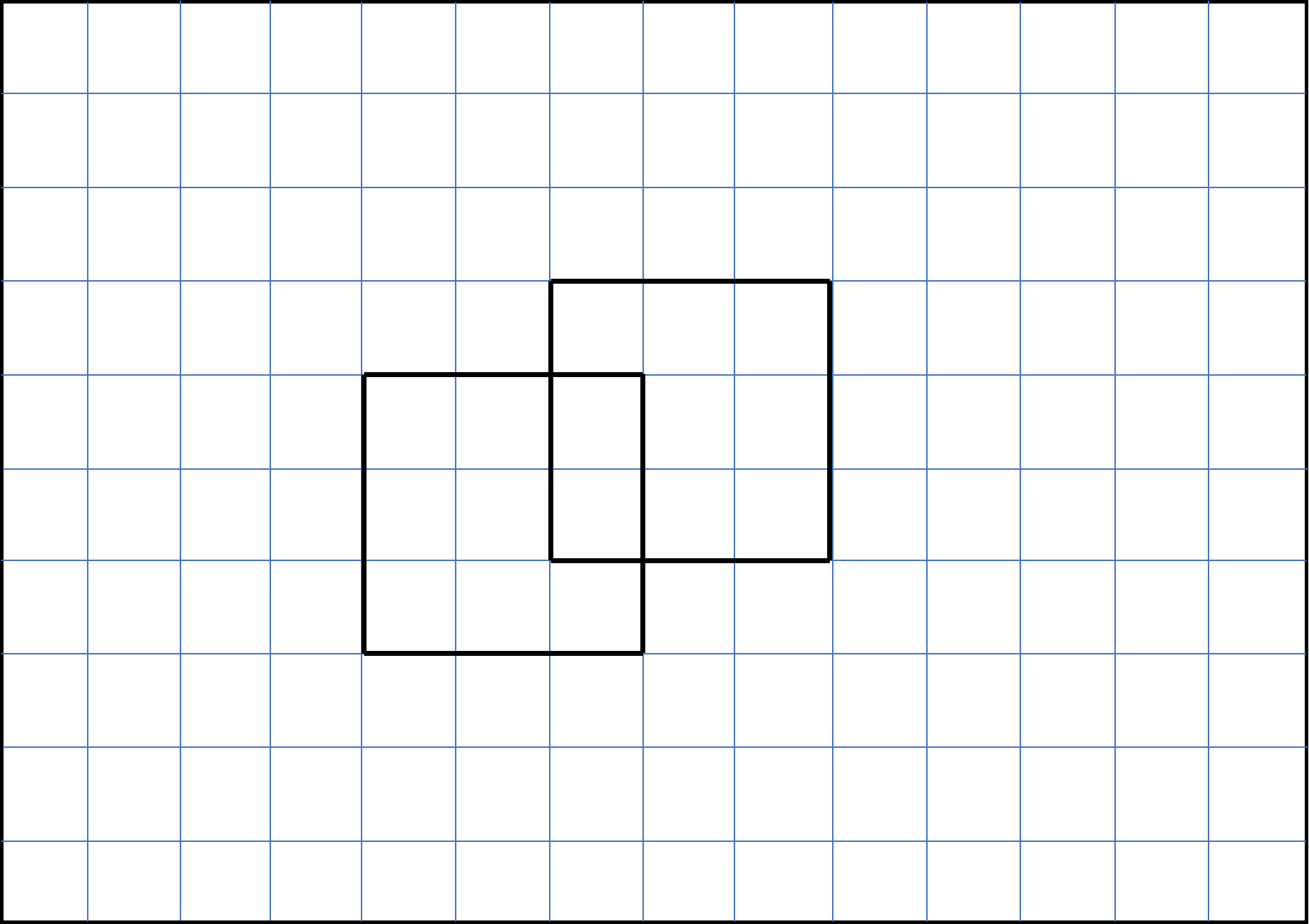
चरण 3: दोनों फलकों के संगत कोनों को जोड़ें।
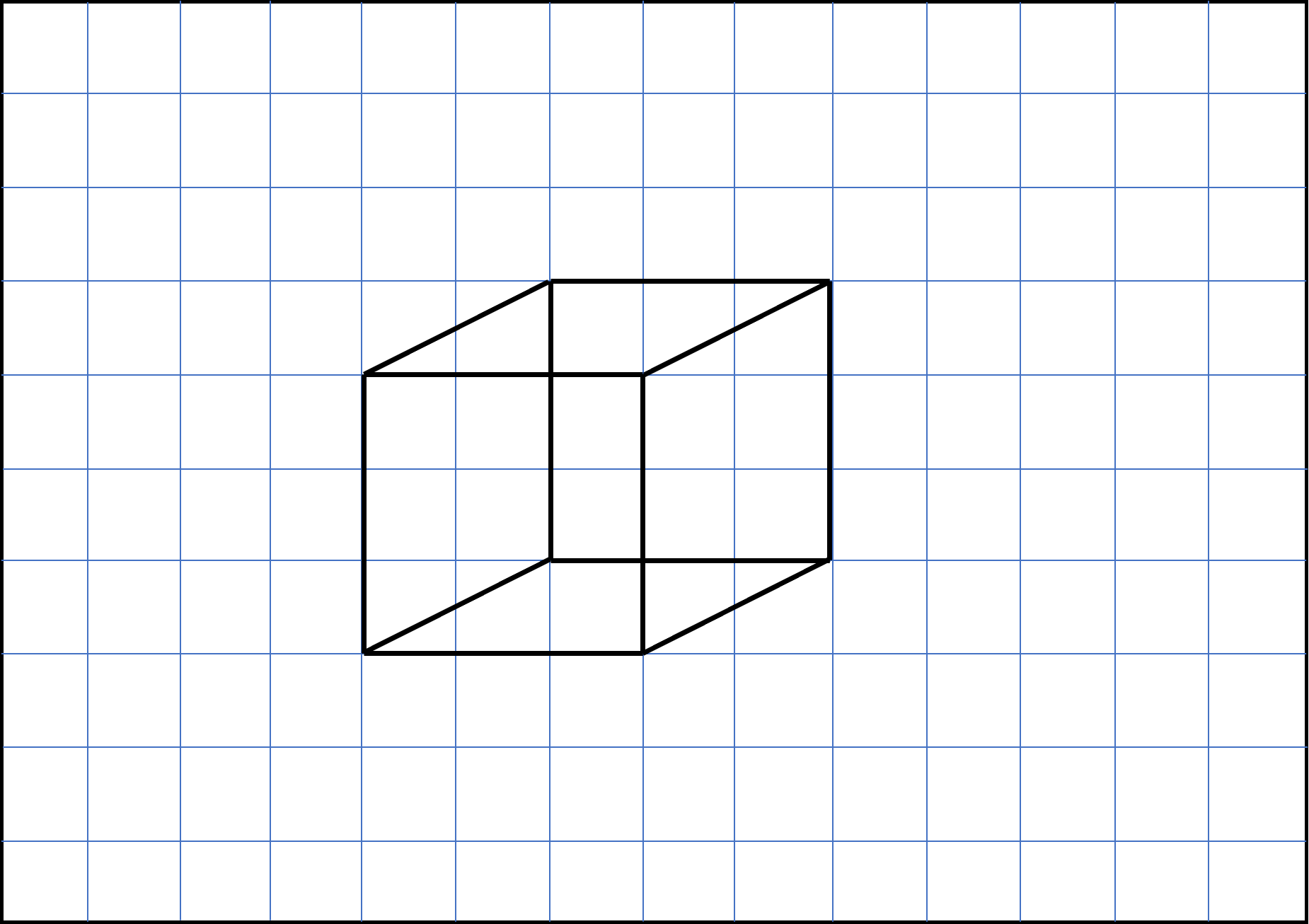
चरण 4: छिपे हुए किनारों को बिंदुकित रेखा से दर्शाएं।
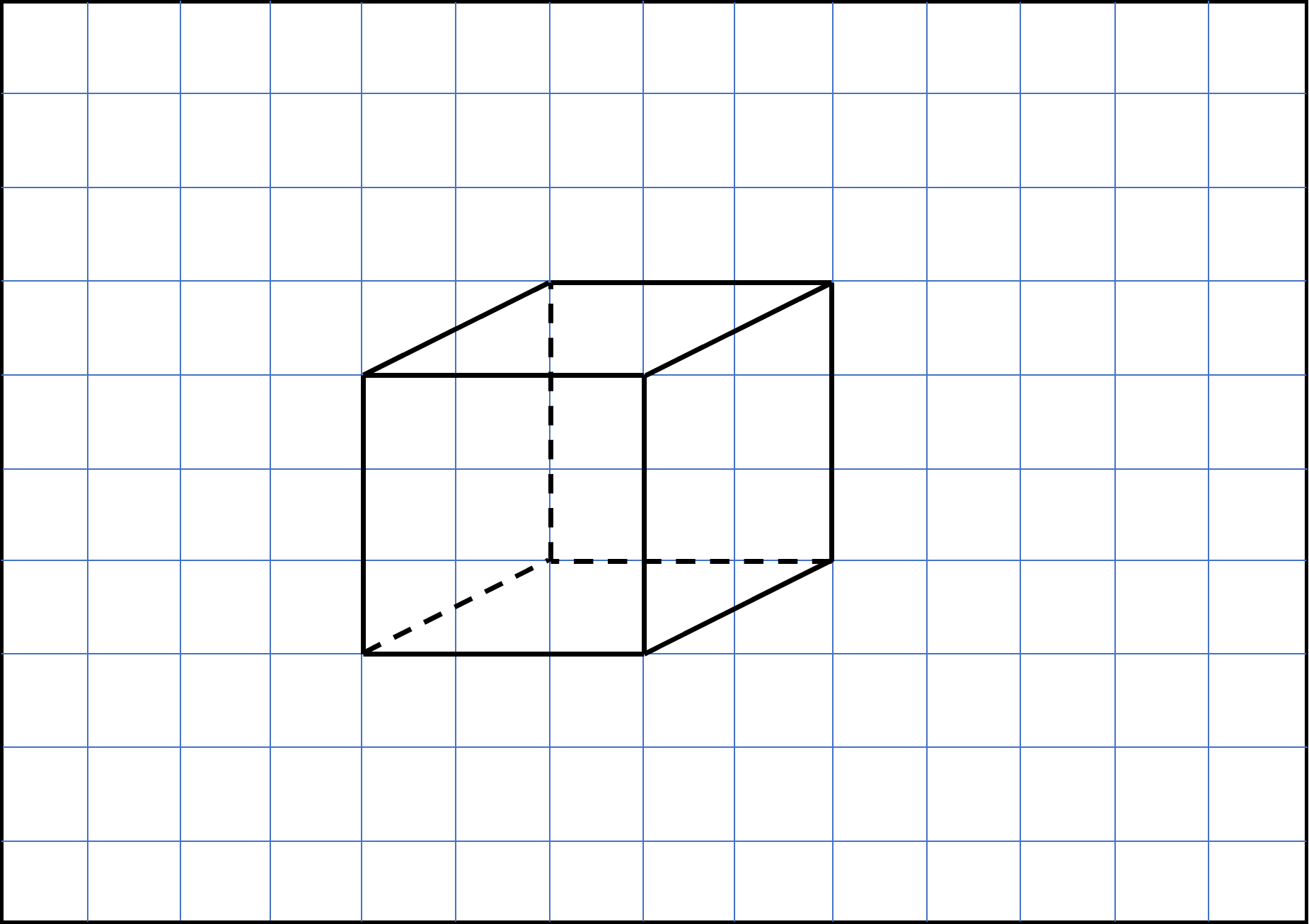
उदाहरण 10
किसी ठोस के विभिन्न भागों को देखना
हम जानते हैं, कि त्रिविमीय वस्तुएँ विभिन्न स्थानों से भिन्न-भिन्न रूप में दिखाई दे सकती हैं, इसलिए इनको विभिन्न परिपेक्षों (दृष्टियों) से खींचा जा सकता है। उदाहरणार्थ, एक दी हुई झोंपड़ी के निम्नलिखित दृश्य हो सकते हैं:
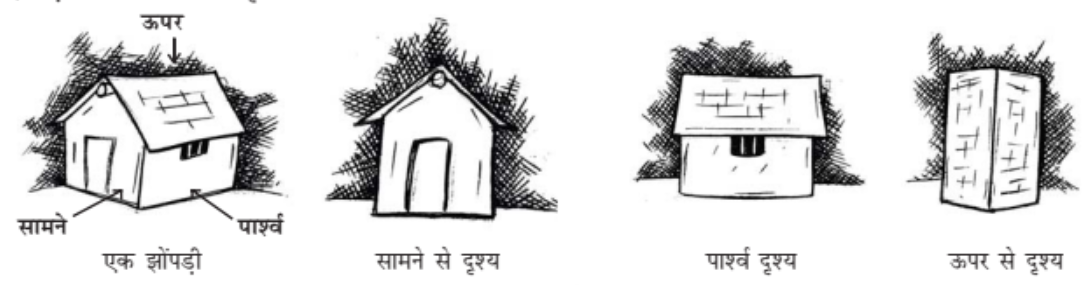
इसी प्रकार, नीचे आकृति मे घनों को जोड़कर बनाई गई आकृतियों के विभिन्न दृश्य प्राप्त कर सकते हैं:
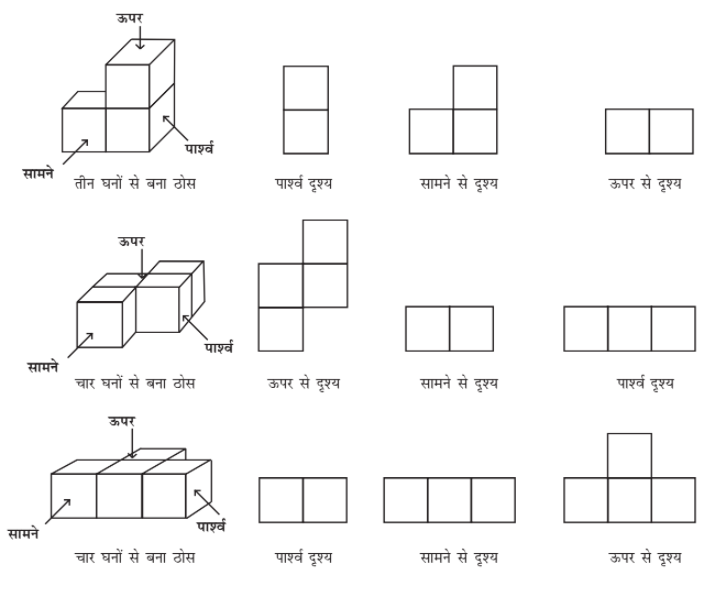
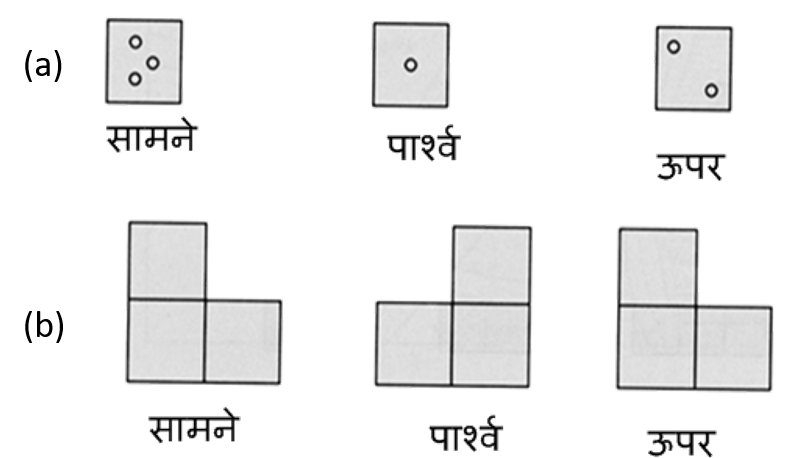
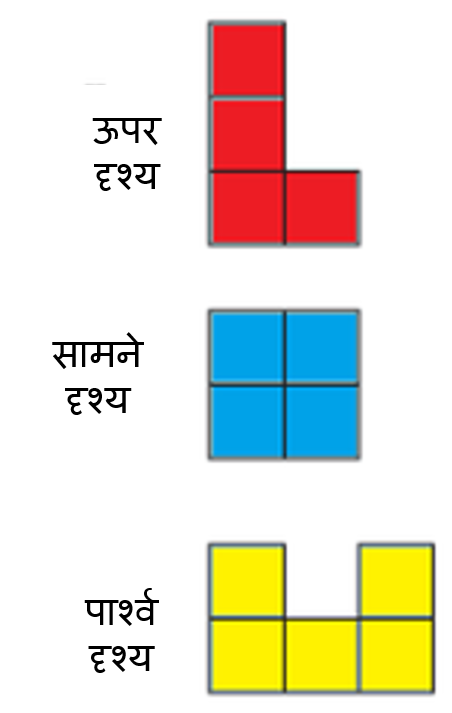
उदाहरण: दी गई आकृति का सामने का दृश्य, पार्श्व दृश्य और ऊपर का दृश्य बनाइए।
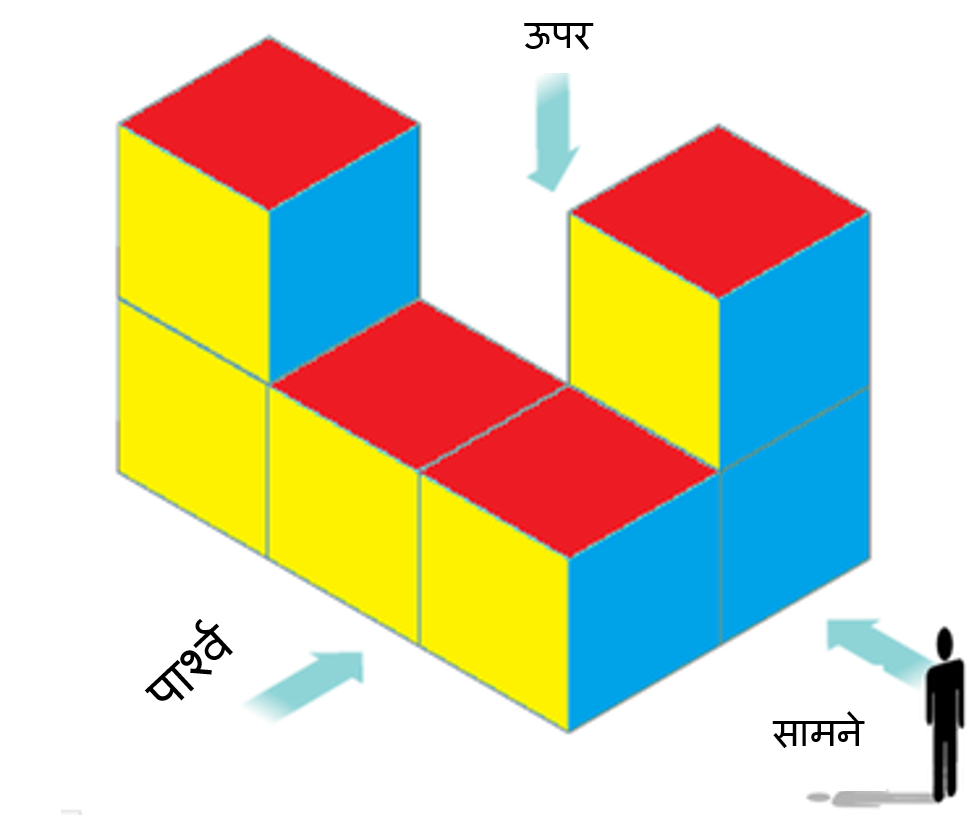
हल: दी गई आकृति को ऊपर से देखने पर हमे लाल रंग वाले घन, सामने से देखने पर नीले रंग वाले घन तथा पार्श्व से देखने पर पीले रंग वाले घन दिखाई देंगे -
OMR (One Minute Revision)
उदाहरण 11
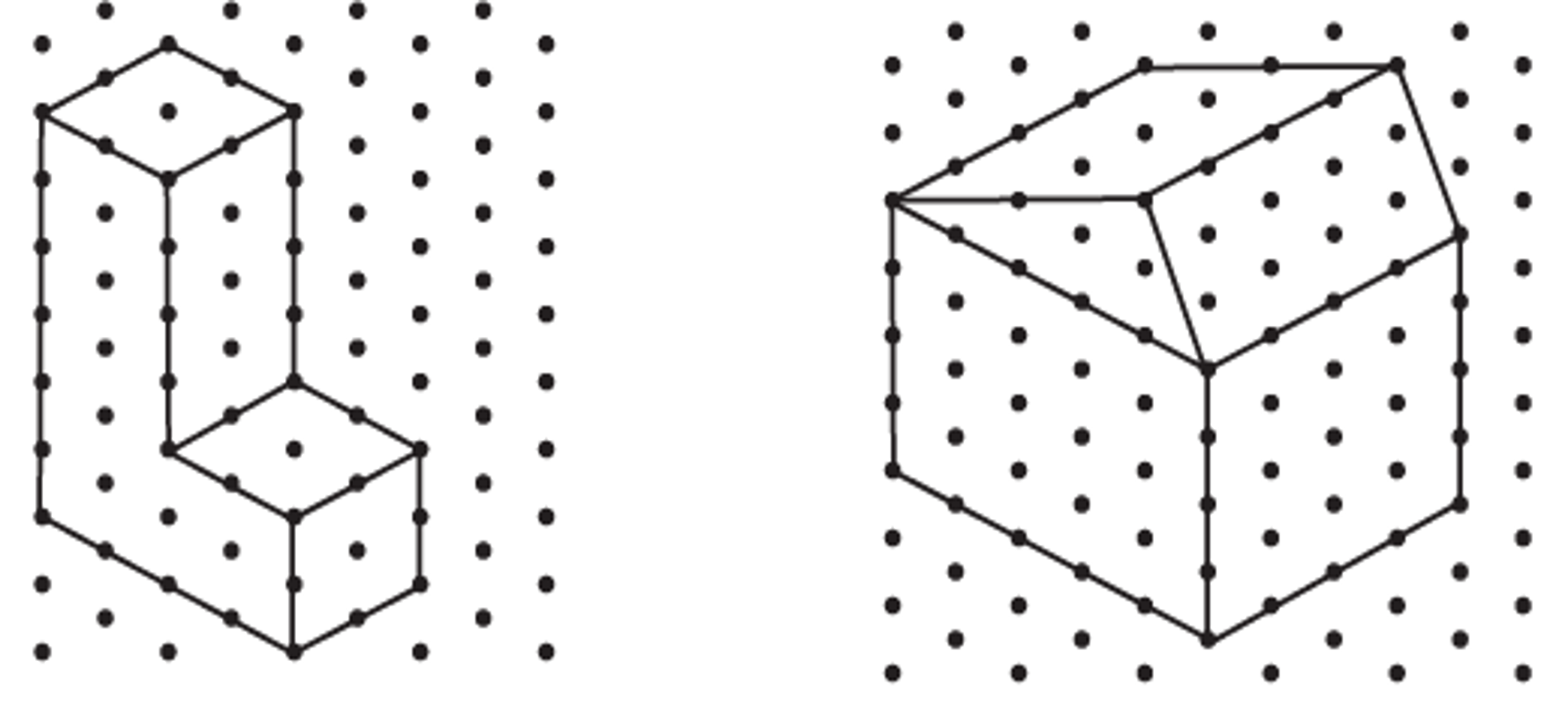
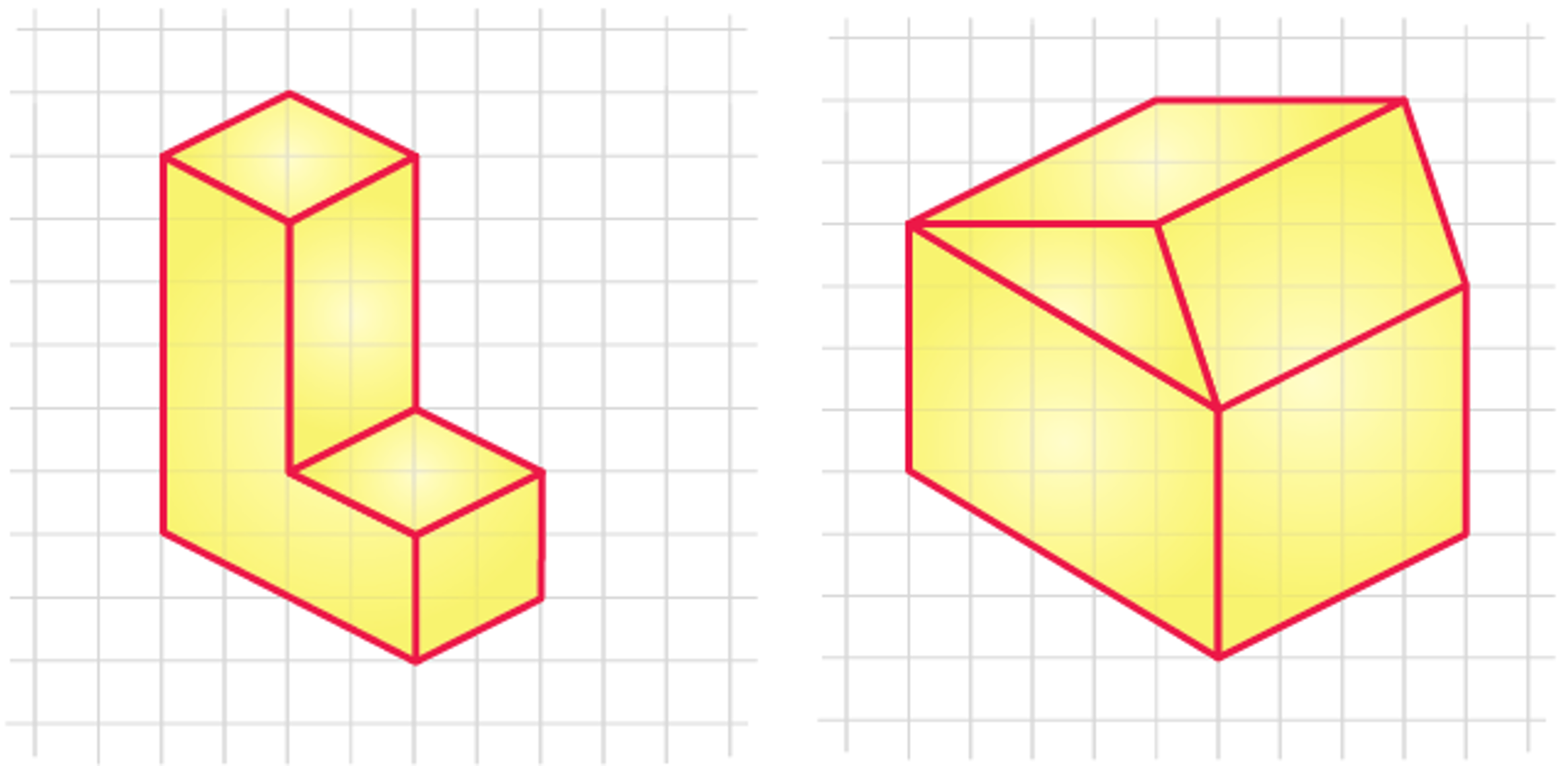
दिए गए एक षट्भुजाकार ब्लॉक के, सामने से दृश्य, पार्श्व से दृश्य और ऊपर से दृश्य खींचिए:
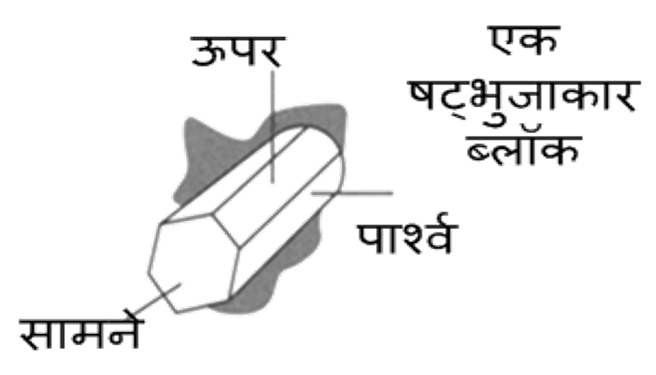
दिए गए षट्भुजाकार ब्लॉक को सामने से, पार्श्व से और ऊपर से देखने पर इस प्रकार दिखाई देगा -
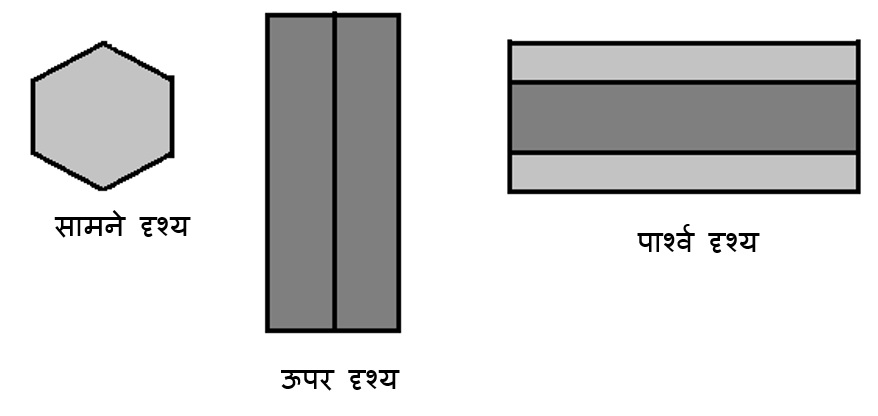
उदाहरण 12
सारांश
- वृत्त, वर्ग, आयत, चतुर्भज और त्रिभुज समतल आकृतियों के उदाहरण हैं तथा घन, घनाभ, गोला, बेलन, शंकु और पिरामिड ठोस आकारों के उदाहरण हैं।
- समतल आकृतियों की दो विमाएँ (संक्षिप्त में 2-D) होती हैं तथा ठोस आकारों की तीन विमाएँ (संक्षिप्त में 3-D) होती हैं।
- ठोस आकार के कोने उसके शीर्ष, उसके ढाँचें के रेखाखंड उसके किनारे (या कोर) तथा उसके सपाट पृष्ठ उसके फलक कहलाते हैं।
- ठोस का एक जाल दो विमाओं में एक ऐसा ढाँचा (या रूप रेखा) है, जिसे मोड़कर वह ठोस प्राप्त हो जाता है। एक ही ठोस के अनेक प्रकार के जाल हो सकते हैं।
- वास्तविक रूप से, ठोस आकारों को सपाट पृष्ठों (जैसे कागज) पर खींचा जा सकता है। हम इसे 3-D ठोस का 2-D निरूपण कहते हैं।
- एक ठोस के दो प्रकार के चित्र बनाना संभव है।
(a) एक तिर्यक चित्र, जिसमें लंबाइयाँ समानुपाती नहीं होती हैं। फिर भी यह ठोस के रूप के बारे में सभी महत्वपूर्ण जानकारी प्रदान कर देता है।
(b) एक समदूरीक चित्र को एक समदूरीक बिंदुकित कागज़ पर खींचा जाता है, जिसका एक प्रतिदर्श इस पुस्तक के अंत में दिया गया है। किसी ठोस के एक समदूरीक चित्र में लंबाइयों को समानुपाती रखा जाता है।
- यदि हम ठोस आकारों को विभिन्न कोणों से देखे तो हमे ठोस आकारों के सामने के दृश्यों, पार्श्व दृश्यों और ऊपर के दृश्यों से उन आकारों के अध्ययन में सहायता प्राप्त होती है।