FRACTIONS AND DECIMALS for Class 7 MATHS
INTRODUCTION
Hello baccho, kaise hai aap sab? Baccho, aapne apni previous classes m fractions and decimals k baare m pdha tha. Aap sabne fractions, mixed fractions, comparison of fractions, comparison of decimal numbers and representing decimals and fractions on number line jaise topics pdhe hue hai.
Iss chapter m hum seekhenge ki fractions and decimals ko multiply aur divide kaise krte hai. Hum apni day to day lives m fractions ko use krte hai.
Jaise ki, jab aap apne dosto k saath pizza khaa rhe hote hai aur uss pizza k 4 parts m se aapko one piece milta hai, to vo 14 of the pizza kehlaata hai. Similarly, aapne kabhi apni mummy se bola hoga ki vo aapko aadhi roti dede, to vo 12 of chapati kehlata hai. Ab hum fractions and decimals k concepts ko detail m pdhenge.
FRACTIONS
Baccho, fractions ka simple meaning hota hai ki they are a part of a whole. Whole ka mtlb hota hai "complete" and fractions ka mtlb bnjata hai "part of that complete term" yaani ki part of a whole. Fraction word ek latin word "fractio" se aaya tha jiska mtlb hota hai "to break".
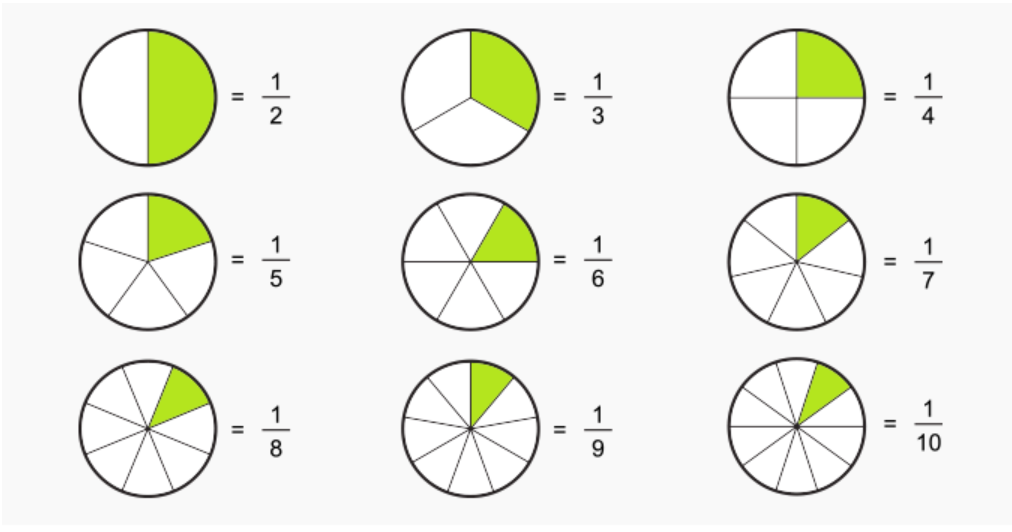
Proper Fractions
Proper fraction is the type of fraction where, the numerator is smaller than the denominator. For example, 314, 27, 49. In these examples, 3<14, 2<7 and 4<9. Hence, these are proper fractions.
Baccho, suppose you have a chocolate and aapne usko 5 parts m divide kia. Aapne unn 5 parts m se 3 parts apne dost ko dedie aur 2 parts khud rakhlie. To iss case m, aapka portion 25 hua and aapke dost ka portion 35. Both of these terms are proper fractions.
Improper Fractions
Improper fraction is a type of fraction in which numerator is greater than the denominator. For example, 52, 83, 95. In these examples, 5>2, 8>3, 9>5.
Baccho, suppose ki aapne apne lie ek pizza order kia jisme 6 slices thi, but vo saari 6 slices aapke dost n khaali. Fir aapne ek aur piza order kia jisme se aapne ek slice khaai bas. To total number of pizza slices eaten by you and your friend will be 7. To iss situation ko hum 76 k form m present krenge which is an improper fraction because 7>6.
Mixed Fractions
Mixed fraction is a type of fraction which is represented as a whole number and a proper fraction.
For example, in the above case, jaha p number of pizza slices eaten was represented as 76, to baccho 76 ka mtlb hua 66 (whole) + 16(proper fraction), which can be written as 116.
Group Of Fractions
A group of fractions is classified as :
(i) Like fractions
(ii) Unlike Fractions
(iii) Equivalent fractions
These groups are used to compare two or more fractions.
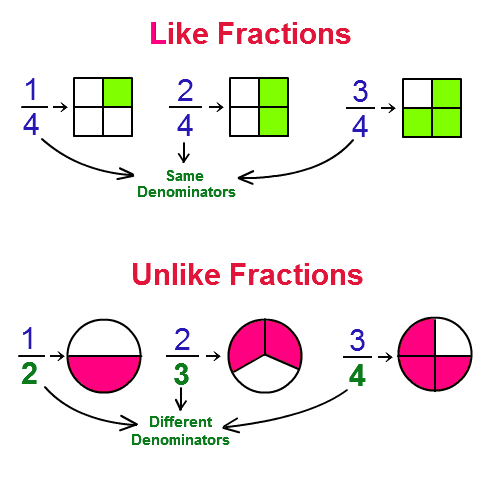
Like Fractions are those fractions which have the same denominator. For example, 16,26,36,46 are like fractions.
Unlike fractions are those fractions which do not have the same denominator. For example, 17,38,49 are unlike fractions.
Equivalent Fractions are those fractions which have different numerator and different denominators, but they have the same simplest form. For example, 39 and 618 have different numerators and denominators but 39=13 and 618=13, hence, they are equivalent fractions.
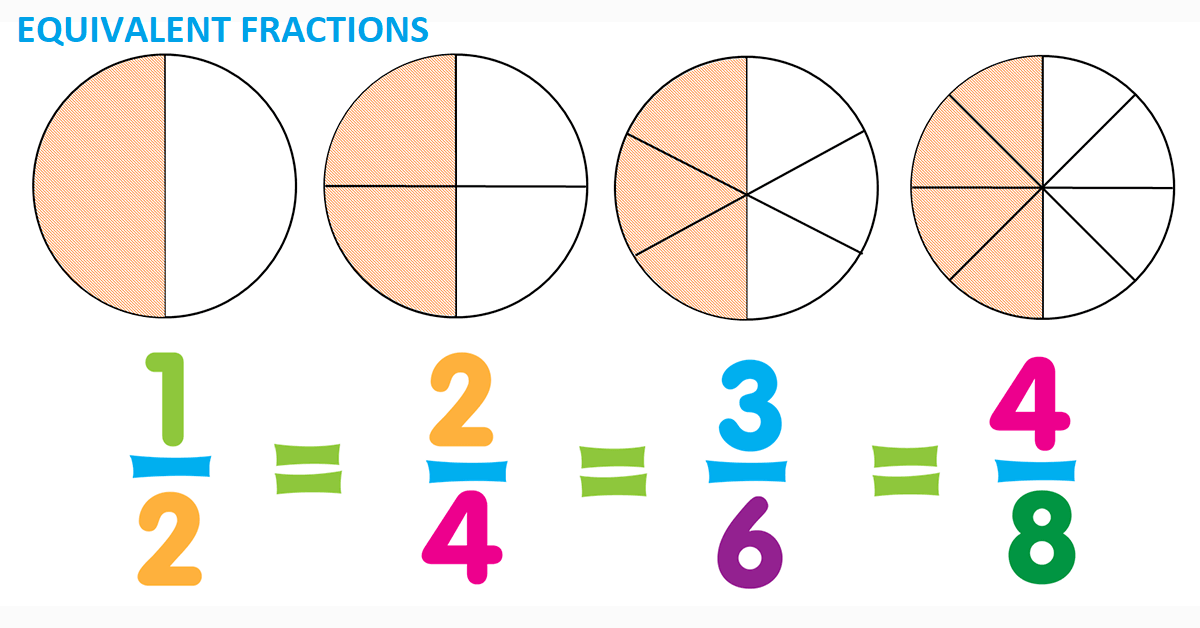
Example 1
Write five equivalent fractions of 35.
One of the equivalent fractions of 35 is
35 = 3×25×2=610
The other four can be calculated in the same manner by multiplying the numerator and the denominator by the same whole number.
Example 2
Ramesh solved 27 part of an exercise while Seema solved 45 of it. Who solved lesser part?
Part of the exercise solved by Ramesh =27=1035
Part of the exercise solved by Seema=45=2835
As, 1035<2835,
Ramesh solved lesser part.
Example 3
Sameera purchased 312 kg apples and 434 kg oranges. What is the total weight of fruits purchased by her?
Weight of apples purchased by Sameera =312 kg =72 kg
Weight of oranges purchased by Sameera =434 kg =194 kg
∴ Total weight of fruits purchased by Sameera =72+194=334 kg =814 kg
Example 4
Suman studies for 523 hours daily. She devotes 245hours of her time for Science and Mathematics. How much time does she devote for other subjects?
Total time of Suman’s study = 253 h = 173 h
Time devoted by her for Science and Mathematics = 425 h = 145 h
Thus, time devoted by her for other subjects = (173−145) h
= (17×515 − 14×315) h
= (85−4215) h
= 4315 h = 21315 h
MULTIPLICATION OF FRACTIONS
Baccho, jaise humne apne previous chapters m and previous classes m seekha ki numbers ko kaise multiply kia jaata hai, usi tarah ab hum fractions ko multiply krna seekhenge. For example baccho, suppose aapke paas 10 toffees hai, and aapko usme se half (12) apne dost ko deni hai. To ye calculate krne k lie ki kitni toffees aap apne dost ko denge, you will have to multiply the fraction 12 by the total number of toffees (10), so the answer will 12×10 = 5 toffees.
Fraction as an operator "of"
Baccho, in mathematics, the word "of" represents multiplication . Jab hum bolte hai 12 of 10, it means 12×10. Hum ek example se ise smjhte hai.
Farida has 20 marbles. Reshma has 15th of the number of marbles what
Farida has. How many marbles Reshma has?
As, ‘of ’ indicates multiplication,
so, Reshma has 15×20
=4 marbles.
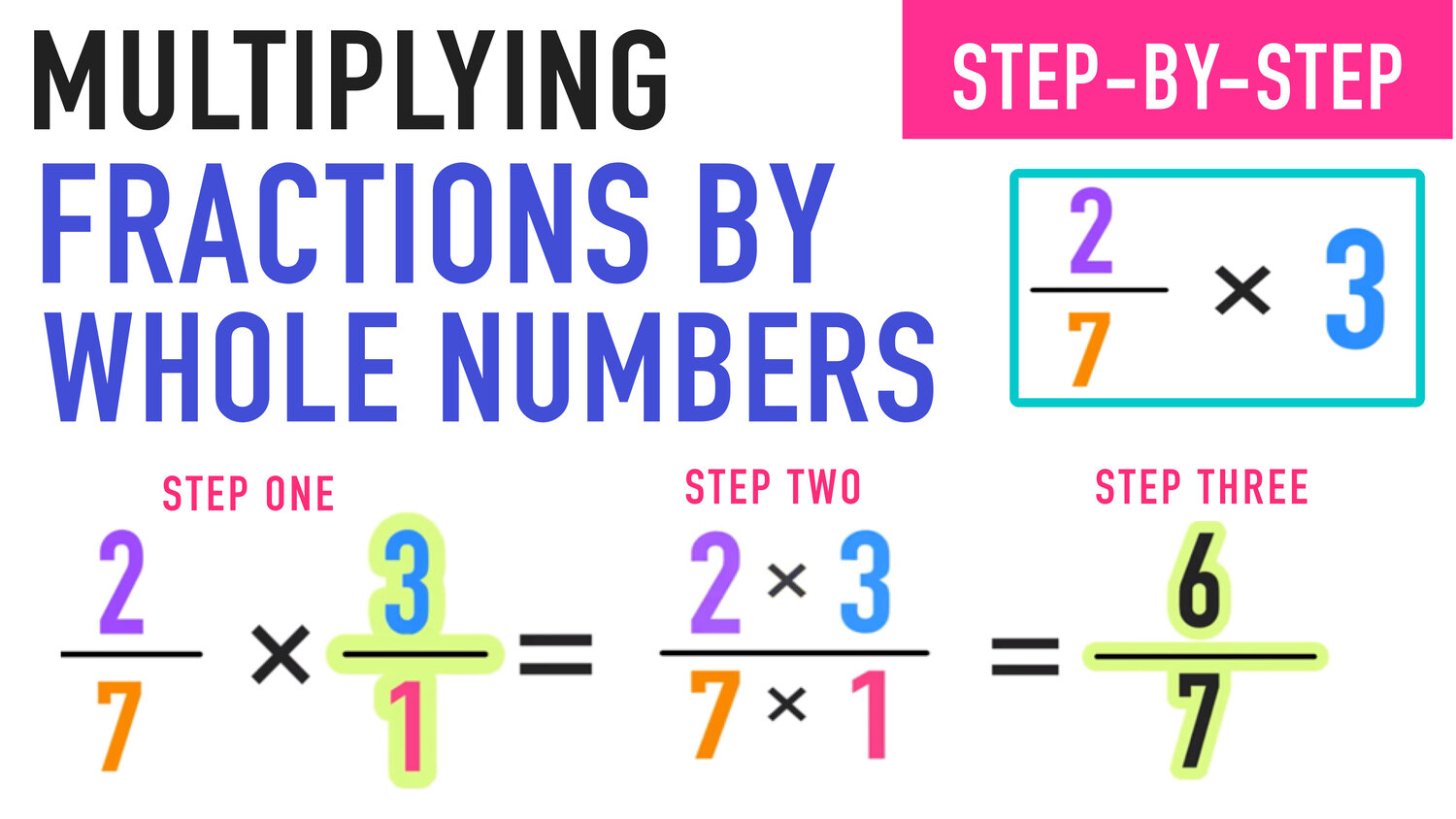
Multiplication of a fraction by a whole number
Multiplication of fractions by a whole number is an easy concept. We start by multiplying the numerator with the whole number and then make sure that the obtained fraction is in its simplest form. Let's look at the following example. When we multiplied the numerator 3 with the whole number 4, we got the numerator as 12 and since 12 and 5 do not have a common factor, therefore, the fraction is already in its simplest form.
∴35×4=125
The method remains the same for improper fractions too. To multiply a whole number with a proper or an improper fraction, we multiply the whole number with the numerator of the fraction, keeping the
denominator same.
To multiply a mixed fraction with a whole number, we first convert the mixed fraction to an improper fraction and then multiply the numerator with the denominator.
For example, 312×10
= (3×2+12)×10
= (6+12)×10
= 72×10
= 7×5
= 35
Example 5
In a class of 40 students 15of the total number of studetns like to study English, 25of the total number like to study mathematics and the remaining students like to study Science.
Total number of students =40
Total number of students who like to study English =15∗40=8
Total number of students who like to study Maths=25∗40=16
Fraction of total number of students who like to study Science=1−(15+25)=1−35=25
Multiplication of a fraction by another fraction
In order to find a fraction of another fraction, we multiply the two fractions, to get the answer. To multiply the two fractions, first make sure that they both are reduced to their simplest form to make the calculation easier. Next, multiply the numerator of the first fraction with the numerator of the second fraction. Do the same for the denominators.
For example, 34×56 = 3×54×6 = 1524
If the obtained fraction is improper, then convert it into mixed fractions. Let us look at another example, 74×95
= 7×94×5
= 6320
= 3320

Example 6
Sushant reads 13 part of a book in 1 hour. How much part of the book will he read in 2(15) hours?
Part of the book read by Sushant in 1 hour =13
Part of the book read by Sushant in 215 hours =13∗215=13∗115=1115
Value of the products
When we multiply two numbers, we observe that the product obtained is greater than those two numbers. For example, 4×5=20, where, 20>4,5.
But, does the same thing applies to fractions? Let's find out.
Multiplication of two proper fractions
23×45 = 815
On comparing, we find out that, 815<23and815<45
This is because, when we multiply two proper fractions, the result we get is a part of the fraction, hence, it cannot be greater.
Multiplication of two improper fractions
65×98=5440=2720
On comparing, we find out that, 2720>65and2720>98
This is because, multiplication of two improper fractions means multiplying with a number greater than the whole.
Multiplication of an improper and a proper fraction
35×98 = 2740
On comparing, we can conclude that, 2740<98and2740>35
As we can see, when we multiply an improper fraction with a proper fraction, the product is greater than the proper fraction but is lesser than the improper fraction.
RECIPROCAL OF A FRACTION
Reciprocal of a fraction is obtained by interchanging the numerator and the denominator. For example, reciprocal of 34 is 43.Similarly, reciprocal of 5 is 15
When we multiply a fraction with its reciprocal, the product obtained is 1. For example, 54×45=1

Example 7
Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers. (i) 37 (ii) 58 (iii) 97 (iv) 65 (v) 127 (vi) 18 (vii) 111
(i) Reciprocal of 37 is 73 which is an improper fraction.
(ii) Reciprocal of 58 is 85 which is an improper fraction.
(iii) Reciprocal of 97 is 79 which is a proper fraction.
(iv) Reciprocal of 65 is 56 which is a proper fraction.
(v) Reciprocal of 127 is 712 which is a proper fraction.
(vi) Reciprocal of 18 is 8 which is a whole number.
(vii) Reciprocal of 111 is 11 which is a whole number.
DIVISION OF FRACTIONS
Baccho, ab hum seekhenge ki fractions ko divide kaise kia jata hai. Hume pta hai ki division ka mtlb hota hai ek number ko equal parts m divide krne. The method used for division of fractions is related to the concept of multiplication of fractions. Let us see how.
Division of a whole number by a fraction
In order to divide a whole number with a fraction, we multiply the whole number with the reciprocal of the fraction . Let's look at an example,
6÷34
= 6×43
= 243
= 8

Division of a fraction by a whole number
When we divide a fraction by a whole number, we multiply the given fraction with the reciprocal of the whole number. For example, 78÷3
= 78×13
= 724
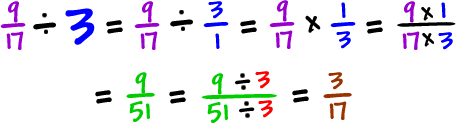
Divsion of a fraction by another fraction
In order to divide two fractions, we multiply the first fraction with the reciprocal of the second fraction. For example,
34÷56
= 34×65
= 1820
= 910
The same method is followed for improper fractions too.
For example, 74÷95
= 74×59
= 3536

DECIMALS
Baccho, aapne apni previous classes m decimals k baare m pdha hai ki decimal system ek aisa numeral system hota hai jisse integers and non-integer numbers ko denote kia jaata hai. Aapne apni day to day lives m decimals ko use hote hue dekha hoga. For example, Suresh scored 9.8 out of 10 in his maths exam. Or, a packet of chips contains 10.05 grams of fat.
MULTIPLICATION OF DECIMALS
We often come across situations where we need to multiply two decimal numbers to solve a problem. Baccho suppose, aap apni mummy k saath vegetables lene gye, waha p vegetable vendor n 1 kg potatoes ka rate Rs 8.50 btaya. Aapko 2.5 kgs potato lene hai, to aap final cost kaise nikaalenge?
In this case, we'll multiply 2.5×8.5 to get the final amount of money that you'll need to pay = Rs. 21.25 Let us see how to carry out such multiplications.
Multiplication of decimal numbers with whole numbers
Multiplication of decimal numbers with whole numbers is a very simple concept. We multiply them as whole numbers and then put the decimal while writing the product.
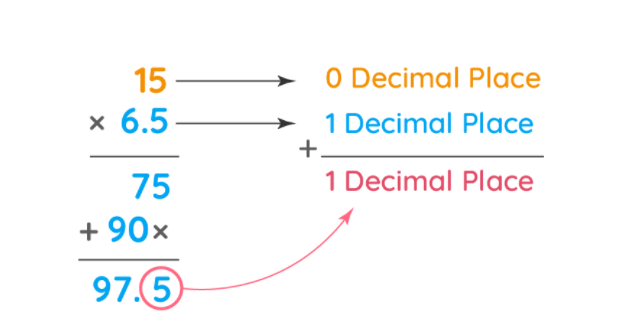
For example, Let's find the value of 8.78×4
To baccho, iss question m hum 878 and 4 ko multiply krenge (ignoring the decimal point), to humara answer aajaega 3512. Ye product nikaalne k baad we'll see ki question m decimal point right se kitne digits chord k laga tha. In this case, 8.78 m decimal point 2 digits chord k laga tha islie hum apne product m bhi decimal point 2 digits chord k laga denge jisse humara final answer bnjaaega 35.12
∴ 8.78×4=35.12
Example 8
The side of an equilateral triangle is 3.5 cm. Find its perimeter
Perimeter of an equilateral triangle = 3×side
∴Perimeter = 3×3.5=10.5cm.
Multiplication of decimal numbers with 10,100,1000
When a decimal number is multiplied with a power of 10(like10,100,1000,10000...), the decimal shifts to the right by the number of zeroes in its power.
For example, 54673.849×10=546738.49
As you can see, since 10 has only one 0, therefore, the decimal shifted one place to its right.
If the number of zeroes exceeds the number of digits in the decimal place, we start adding more zeroes at the end of the number.
For example, 4.65×10000=46500
In the above case, we had 4 zeroes in which 2 zeroes were used to shift the decimal two places to the right and the other two zeroes were put in the product.
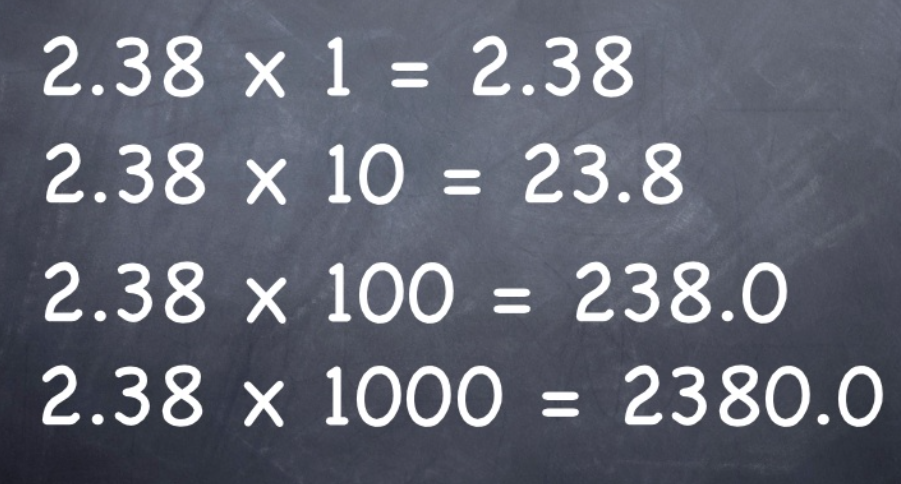
Multiplication of decimals with decimals
When multiplying two decimal numbers, we find the product of the numbers as whole numbers, then we combine the decimal places of the two numbers and put the decimal point in the final product.
For example, let's calculate 7.83×2.4.
First, we find the product of these two numbers (ignoring the decimal points), so we'll get 783×24=18,792
Iske baad baccho, hum dekhenge ki humare dono decimal numbers m point kitne places chord k laga hai. So, 7.83 m decimal point 2 places chord k laga hai and 2.4 m decimal point 1 place chord k laga hai. Inko combine krne k baad hum humare final product m decimal point 3 (2+1) places chord k laga denge jisse humara final product bnjaega 18.792
∴7.83×2.4=18.792

Example 9
The length of a rectangle is 7.1 cm and its breadth is 2.5 cm. What is the area of the rectangle?
Length of the rectangle =7.1cm
Breadth of the rectangle = 2.5cm
Therefore, area of the rectangle =7.1×2.5cm2
=17.75cm2
Representing decimals as fraction
Baccho, let's see ki hum decimals ko fractions m kaise convert kr skte hai. It's a very easy concept.
We first check that after how many digits the decimal has been put and then we put as many zeroes in the denominator after 1.
For example, let's convert 45.678 into a fraction.
as we can see that decimal point has been put after 3 digits from right, so we'll rewrite the number without the decimal and put 1000 (3 zeroes after 1) in the denominator
⇒ 456781000
Let's see another example,
674.22
=67422100
Since, the decimal was put after two digits in 674.22, therefore, we put 100 (2 zeroes after 1) in the denominator.

DIVISION OF DECIMALS
Baccho, ab hum seekhenge ki decimals ko divide kaise kia jaata hai. Jis tarah se hum multiplication of decimals m point ko ignore krke whole numbers ko multiply krte the, usi tarah hum yaha bhi decimal point ko ignore krke numbers ko as a whole divide krenge. Let us see a day to day life example of division of decimals.
Baccho, suppose ki aapke paas ek 40.5cm ki rope hai lekin aapko 4.5 cm k pieces chahie. Aisi situation m we'll divide 40.54.5 to get the number of pieces of the rope. So let us now learn how to divide such decimal numbers.
Division of a decimal number with a whole number
To divide a decimal number with a whole numbers, we divide them as whole numbers and then put the decimal while writing the quotient.
For example, Let's find the value of 8.484
To baccho, iss question m hum 848 and 4 ko divide krenge (ignoring the decimal point), to humara answer aajaega 212. Ye answer nikaalne k baad we'll see ki question m decimal point right se kitne digits chord k laga tha. In this case, 8.48 m decimal point 2 digits chord k laga tha islie hum apne quotient m bhi decimal point 2 digits chord k laga denge jisse humara final answer bnjaaega 2.12
∴ 8.484=2.12
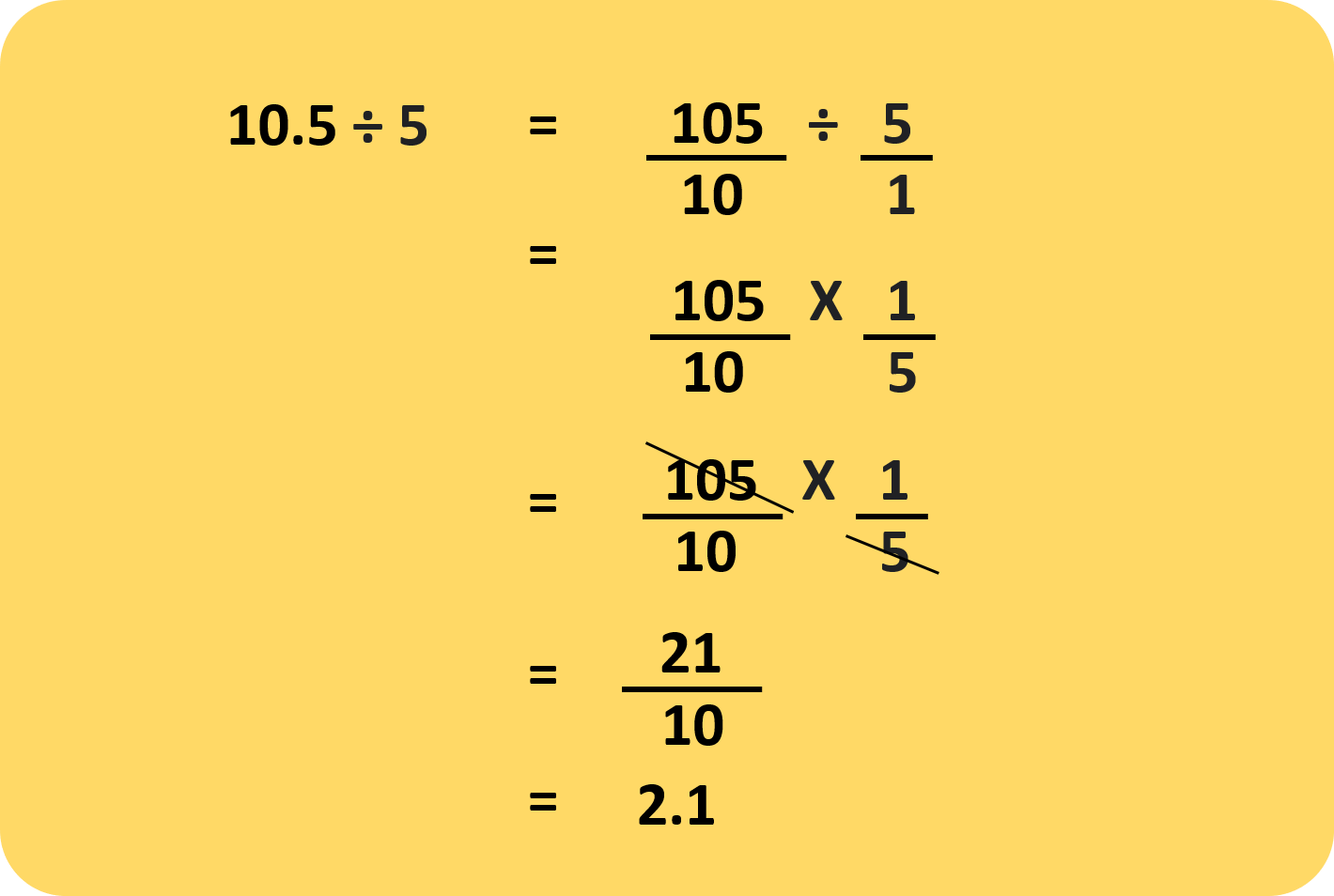
Example 10
Find the average of 4.2, 3.8 and 7.6.
The average of 4.2,3.8 and 7.6 is 4.2+3.8+7.63
=15.6
=5.2
Division of a decimal number by 10,100,1000
When a decimal number is divided by a power of 10(like10,100,1000,10000...), the decimal shifts to the left by the number of zeroes in its power.
For example, 54673.84910=5467.3849
As you can see, since 10 has only one 0, therefore, the decimal shifted one place to its left.
If the number of zeroes exceeds the number of digits in the decimal place, we start adding more zeroes at the beginning of the number.
For example, 4.6510000=0.000465
In the above case, we had 4 zeroes in the denominator of which 1 zero was used to shift the decimal one place to the left and the other three zeroes were put in the beginning of the number (before 4).

Division of a decimal number with another decimal number
When dividing two decimal numbers, we first convert both the decimal numbers in fractional form and then divide them as fractions and finally convert them into decimals.
For example, let's find 84.842.1
To baccho, aise question m hum phle 84.84 ko fractions m convert krenge, to we'll get 8484100 and 2.1 will become 2110
Next step m hum first fraction ko second fraction k reciprocal se multiply krdenge.
Reciprocal of 2110 is 1021
So now, we'll multiply, 8484100×1021
= 848402100
= 4040100 (dividing 84840 by 21)
= 40.4
To baccho, iss tarah se hum do decimal numbers ko divide krte hai.
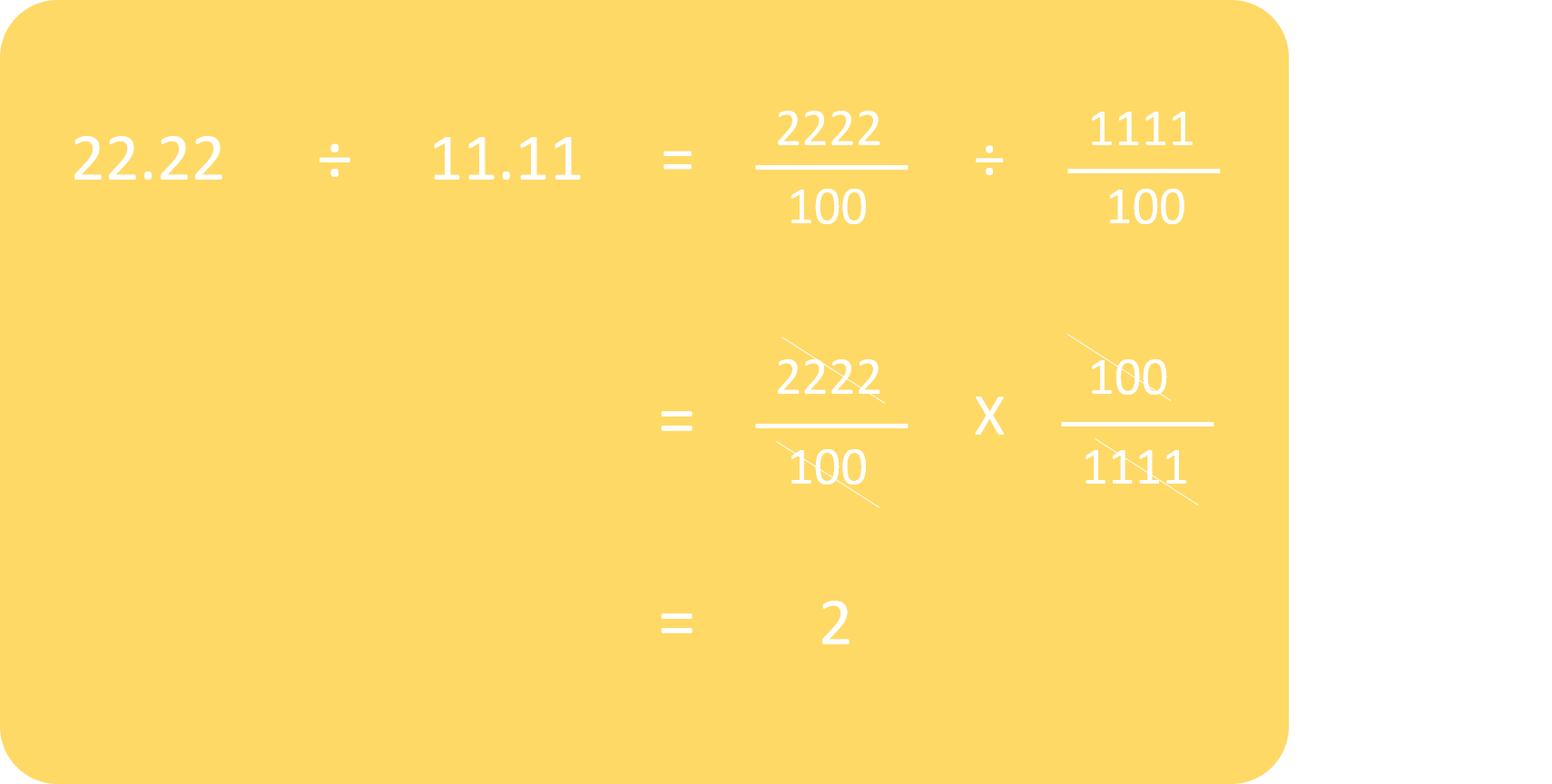
Example 11
Each side of a regular polygon is 2.5 cm in length. The perimeter of thepolygon is 12.5cm. How many sides does the polygon have?
The perimeter of a regular polygon is the sum of the lengths of all its equal sides =12.5cm.
Length of each side =2.5cm
Thus, the number of sides =12.52.5
=12525
=5
The polygon has 5 sides.
Example 12
A car covers a distance of 89.1 km in 2.2 hours. What is the averagedistance covered by it in 1 hour?
Distance covered by the car in 2.2 hours =89.1 km
∴ Distance covered by the car in 1 hour =89.12.2=812=40.5 km
Let's Summarize!
1. We have learnt about fractions and decimals alongwith the operations of addition and
subtraction on them, in the earlier class.
2. We now study the operations of multiplication and division on fractions as well as on
decimals.
3. We have learnt how to multiply fractions. Two fractions are multiplied by multiplying
their numerators and denominators separately and writing the product as
product of numerators ÷
product of denominators
For example, 23×57=2×53×7=1021
4. A fraction acts as an operator ‘of ’. For example,12 of 2 is 12×2=1.
5. (a) The product of two proper fractions is less than each of the fractions that are
multiplied.
(b) The product of a proper and an improper fraction is less than the improper
fraction and greater than the proper fraction.
(c) The product of two improper fractions is greater than the two fractions.
6. A reciprocal of a fraction is obtained by inverting it upside down.
7. We have seen how to divide two fractions.
(a) While dividing a whole number by a fraction, we multiply the whole number
with the reciprocal of that fraction.
For example, 2÷35=2×53=103
(b) While dividing a fraction by a whole number we multiply the fraction by the
reciprocal of the whole number.
For example, 23÷7=23×17=221
(c) While dividing one fraction by another fraction, we multuiply the first fraction by
the reciprocal of the other.
So, 23÷57=23×75=1415
8. We also learnt how to multiply two decimal numbers. While multiplying two decimal
numbers, first multiply them as whole numbers. Count the number of digits to the right
of the decimal point in both the decimal numbers. Add the number of digits counted.
Put the decimal point in the product by counting the digits from its rightmost place.
The count should be the sum obtained earlier.
For example, 0.5×0.7=0.35
9. To multiply a decimal number by 10,100 or 1000, we move the decimal point in the
number to the right by as many places as there are zeros over 1.
Thus, 0.53×10=5.3
0.53×100=53
0.53×1000=530
10. We have seen how to divide decimal numbers.
(a) To divide a decimal number by a whole number, we first divide them as whole
numbers. Then place the decimal point in the quotient as in the decimal number.
For example, 8.4÷4=2.1
Note that here we consider only those divisions in which the remainder is zero.
(b) To divide a decimal number by 10,100 or 1000, shift the digits in the decimal
number to the left by as many places as there are zeros over 1, to get the
quotient.
So, 23.9÷10=2.39
23.9÷100=0.239
23.9÷1000=0.0239
(c) While dividing two decimal numbers, first shift the decimal point to the right by
equal number of places in both, to convert the divisor to a whole number. Then
divide.
Thus, 2.4÷0.2=24÷2=12.
Let's Revise
1) Baccho, humne iss chapter m multiplication and division of fractions and decimals seekha. We know that fractions are basically a part of a whole and decimals are those numbers where the whole and fractional part is separated with a decimal point.
2) We revised about the three types of fractions : Proper Fractions, Improper fractions and Mixed Fractions.
Proper fractions have a numerator < denominator
Improper fractions have numerator > denominator
Mixed fractions are those fractions where the whole number and fractional part are written separately.
3) The group of fractions contain : Like fractions, Unlike fractions, and Equivalent fractions
Like fractions have the same denominator, for example, 35 and 15 are like fractions
Unlike fractions have different denominators, for example, 58 and 49 are two unlike fractions
Equivalent fractions have different numerators and denominators, but their values are same, which means, they have the same simplest form. For example, 816 and 48 have different numerators and denominators, but 816=12 and 48=12. Therefore, they are equivalent fractions.
4) A fractions acts as an operator 'of', which means, 34 of 8 = 34×8=3×2=6. Of means multiplication in maths.
5) Baccho, ek fraction ko ek whole number se multiply krne k lie, hum fraction k numerator ko whole number se multiply krte hai, and denominator ko as it is likhte hai. Lastly, we make sure ki the resulting fraction is in its simplest form. For example, 34×5=3×54=154
6) Ek fraction ko dusre fraction se multiply krne k lie, hum first fraction k numerator ko second fraction k numerator se multiply krte hai and first fraction k denominator ko second fraction k denominator se multiply krte hai. For example, 23×56=2×53×6=1018=59.
7) Jab hum do proper fractions ko multiply krte hai, the product is always less than the proper fractions.
Jab hum do improper fractions ko multiply krte hai, the product is always greater than those improper fractions.
Jab hum ek proper fraction ko ek improper fraction se multiply krte hai, the product is greater than the proper fraction but is less than the improper fraction.
8) Reciprocal of a fractions means interchanging the numerator and the denominator. For example, reciprocal of 56 is 65.
9) Ek whole number ko fraction se divide krne k lie, hum uss whole number ko fraction k reciprocal se multiply krte hai. For example, 5÷43=5×34=154
10) Ek fraction ko ek whole number se divide krne k lie hum uss fraction ko uss whole number k reciprocal se multiply krte hai. For example, 56÷3=56×13=518
11)Ek fraction ko dusre fraction se divide krne k lie hum first fraction ko dusre fraction k reciprocal se multiply krte hai. For example, 34÷79=34×97=2728
12) Ek decimal ko ek whole number se multiply krne k lie, hum unn dono numbers ko as a whole multiply krte hai (ignoring the decimal point) and final product m decimal point utne digits chord k lagate hai jitne digits question m chord k lage hue the. For example, to solve 5.6×2 , we'll calculate 56×2 , which is, 112, and kyunki 5.6 m ek digit chord k decimal laga tha islie hum product m bhi ek digit chord k decimal lgadenge, so our answer will be 11.2
13) Ek decimal ko dusre decimal se multiply krne k lie, hum phle points ko ignore krke unke whole values ko multiply krenge and last m jitne digits chord k question m points lage the, utne digits chord k hum answer m points laga denge.
For example, let's find out the value of 23.456×2.3. Iss case m we'll multiply 23456×23 (ignoring the decimal points) jisse hume product milega 539488 and finally kyunki 23.456 m 3 digits chord k decimal laga tha and 2.3 m 1 place chord k decimal laga tha, islie hum humare final product m 3+1=4 digits chord k decimal lagadenge, so our answer become 53.9488
14) Jab hum decimals ko power of 10 (10,100,1000...) se multiply krte hai, to answer same number hota hai bas decimal point utne places right side shift hojata hai jitne zeroes hote hai. For example, 4.567×10=45.67
15) Ek decimal ko ek whole number se divide krne k loe, hum uss decimal ko fractional form m likhte hai, and then we divide those numbers as fractions and convert them into decimals at the end.
16) Ek decimal number ko dusre decimal number se divide krne k lie, hum unn dono decimals ko fractional form m likhte hai and we divide them as fractions and convert the quotient into a decimal form.
17) Jab hum decimals ko power of 10 (10,100,1000..) se divide krte hai, to decimal point shifts to the left as many places as the zeroes. For example, 4.5100=0.045