PERIMETER AND AREA for Class 7 MATHS

Hello Bachcho, aaj hum iss chapter mai area and perimeter ke bare mai padhenge jaisa ki aap apni class $VI$ mai already perimeters of plane figures and areas of squares and rectangles padh chuke hai to aap in topic se familiar ho. So, abh hum iss class mai kuch new topics padhenge jaise ki perimeters and areas of a few more plane figures. So iss chapter ko padhne mai bahot maza aayega jaisa ki aap iss chapter ko already thoda thoda jante ho.

Perimeter defines the distance of the boundary of the shape whereas area explains the region occupied by it.

So bachcho, aap iss chapter ko already jante ho to aap iss chapter ko ache se samjh paoge aur iss chapter ke question aasani se kar paoge. So start karte hai iss chapter ko.

Jaisa ki aap log class $VI$ mai square and rectangle ke bare mai padh chuke ho to bas ab yaha usi cheej ko aur deep way mai padhenge. Agar koi do bacche hai $A$ and $B$ aur unme se ek $A$ ne rectangle sheet par painting banayi aur $B$ ne square sheet par ab wo dono un painting ko frame karana chhahte hai to hum inn dono shapes ka perimeter and area nikal kar bta sakte hai ki konse bacche ko zyada pay karna padega frame karane ke liye.Perimeter of a rectangle $=2\times (l+b)$ and Perimeter of a square = $4$ × side
Area of a rectangle = $l\times b,$ Area of a square = side × side
Triangles as Parts of Rectangles
Take a rectangle of sides $8$ cm and $5$ cm. Cut the rectangle along its diagonal to get two triangles.
Suppose one triangle on other
Are they exactly the same in size?
Can you say that both the triangles are equal in area?
Are the triangles congruent also?
What is the area of each of these triangles?
You will find that sum of the areas of the two triangles is the same as the area of the rectangle. Both the triangles are equal in area.
The area of each triangle $=\frac{1}{2}$ (Area of the rectangle)
$=\frac{1}{2}$ $\times$ (l $\times$ b)
$=\frac{1}{2}\times (8\times 5)$
$=20c{m}^2$

The perimeter of a rectangular sheet is $100$ cm. If the length is $35$ cm, find its breadth. Also find the area.

Perimeter of a rectangle, $P=2(l+b)=100cm$
Here. $l=$ length$=35cm$
$b=$ breadth
So, $100=2(35+b)\Rightarrow b+35=50$
$b=50-35=15cm$
So, Area of rectangle, $A=l\ast b=35\ast 15=525c{m}^2$

A wire is in the shape of a rectangle. Its length is $40$ cm and breadth is $22$ cm. If the same wire is regent in the shape of a square, what will be the measure of each side? Also find which shape encloses more area?

Length of rectangle $=40cm$
Breadth of rectangle $=22cm$
Perimeter of rectangle, $P=2(40+22)=124$
Let side of square is $a$ cm. Then,
Perimeter of square $=4a$ cm
As same wire is rebent into a square, their perimeters will be equal.
$4a=124\Rightarrow a=\frac{124}{4}=31cm$
So, side of square is $31$ cm. Area of rectangle $=40\ast 22=880c{m}^2$
Area of square $=31\ast 31=961c{m}^2$
So, square will encloses more area.

We come across many shapes other than squares and rectangles.
How will you find the area of a land which is a parallelogram in shape?
Is the area of the parallelogram equal to the area of the rectangle formed?
Yes, area of the parallelogram = area of the rectangle formed
rectangle length = parallelogram base
rectangle breadth = parallelogram height
Area of parallelogram = Area of rectangle
= length × breadth = $l\times b$
Thus, the area of parallelogram = base × height =$b\times h.$

A path 5 m wide runs along inside a square park of side $100m.$ Find the area of the path. Also find the cost of cementing it at the rate of $Rs250$ per $10m^2.$

$AB=PQ-5-5=90m$
$BC=90m$
Area of path $=(100\cdot 100)-(90\cdot 90)$
$=10000-8100$
=1900$m^2$
Cemetery cost $=1900\cdot 25=47500Rs$.

$DL\text{and}BM$ are the height on sides $AB\text{and}AD$ respectively of parallelogram $ABCD$ (Fig $11.24$). If the area of the parallelogram is $1470c{m}^2,AB=35cm\text{and}AD=49cm$ find the $BM\text{and}DL.$

Area = $b\times h$
$1470=49\times BM$
BM$=\frac{1470}{49}$
$=30cm$
Area = AB $\times$ DL
$1470=35\times$DL
DL$=\frac{1470}{35}=\frac{210}{5}$
$=42cm$
Answer

A gardener wants to know the cost of covering the whole of a triangular garden with grass.
In this case we need to know the area of the triangular region.
To hum isme ek method use karenge hum do traingle sheet lenge aur unhe jod denge wo ek parallelogram ki shape le lengi to hamare paas formula banke aayega ki
Area of each triangle $\frac{1}{2}$ (Area of parallelogram)
$=\frac{1}{2}$ (base × height) (Since area of a parallelogram = base × height)
$=\frac{1}{2}$ (b x h) (or $\frac{1}{2}$ bh, in short)
We conclude that all the congruent triangles are equal in area but the triangles equal in area need not be congruent.

$\Delta ABC$ is isosceles with $AB=AC=7.5cm\text{and}BC=13cm\text{and}AC=12cm.$ The height $AD$ from $A$ to $BC$ is $6cm.$ Find the area of $\Delta ABC.$ What will be the height from $C$ to $AB,CE$

Area of triangle=$\frac{1}{2}\cdot b\cdot h$
$=\frac{1}{2}\cdot 9\cdot 6$
$=27c{m}^2$
Area of triangle=$\frac{AB\cdot EC}{2}$
$27=\frac{7.5\cdot EC}{2}$ $EC=7.2cm$

A gardener wants to fence a circular garden of diameter $21m.$ Find the length of the rope he needs to purchase, if he makes $2$ rounds of fence. Also find the costs of the rope, if it cost Rs $4$ per meter. (take $\pi =\frac{22}{7}$)

$c=2\pi r$
$=21\times \pi$
$=21\times \frac{22}{7}$
$=66m$
length of the rope =$2\times 66=132m$
total cost of rope = length $x$ cost of $1m$ rope
$=132\times 4=528rs$
answer

A circle is the set of all points in a plane that are equidistant from a given point called the center of the circle.
Circumference of a Circle
The circumference of a circle is the perimeter of the circle. It is the total length of the boundary of the circle.
$C=2\pi r$
$C$ = circumference
$\pi$ = the constant pi
$r$ = radius of circle
Area of circle
The area of a circle is the space occupied by the circle in a two-dimensional plane.
The area of a circle is pi times the radius squared (A = π r²).

Diameter of a circular garden is $9.8$ m. Find its area.

Area of the circular garden , $A=\pi r^2$
Here, Diameter, $d=9.8$ m
So, radius, $r=\frac{d}{2}=\frac{9.8}{2}=4.9$ m
So, Area, $A=\frac{22}{7}\ast 4.9\ast 4.9=75.46m^2$

The adjoining figure shows two circles with the same centre. The radius of the larger circle is $10$ cm and the radius of the smaller circle is $4$ cm.

Here, radius of larger circle, $R=10$ cm
Radius of smaller circle, $r=4$ cm
(a) $\therefore$ Area of larger circle, $A=\pi R^2=3.14\ast 10\ast 10=314c{m}^2$
(b)Area of smaller circle $a=\pi r^2=3.14\ast 4\ast 4=50.24c{m}^2$
(c) Area of shaded region $=A-a=314-50.24=263.76c{m}^2$

We know that $1cm=10mm$ Can you tell $1c{m}^2$ is equal to how many $m{m}^2$ ?
Draw a square of side $1cm$
You find that this square of side $1cm$ will be divided into $100$ squares, each of side $1mm.$
Area of a square of side $1cm$= Area of $100$ squares, of each side $1mm.$
Therefore, $1c{m}^2=100\times 1m{m}^2$
or $1c{m}^2=100m{m}^2$
$1m^2=1m\times 1m$
$=100cm\times 100cm(As$1$m=100cm)$
$=10000c{m}^2$

To jaisa ki aap log jab park mai jate ho to aap log dekhte honge ki park ke side mai thodi si space bachi hui hoti h jaise ki park ka border park ke charo taraf ka area. To jab hum park ka area calculate karte hai to hume ye bache hue space ka area bhi calculate karna padta hai.

A path $5$ m wide runs along inside a square park of side $100$ m. Find the area of the path. Also find the cost of cementing it at the rate of $250$ per $10m^2$ .

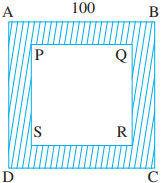Let $ABCD$ be the square park of side $100$ m. The shaded region represents the path $5$ m wide.
$PQ=100–(5+5)=90m$
Area of square $ABCD$ = ${(side)}^2$ = ${\left(100\right)}^2$ $m^2$ = $10000m^2$
Area of square $PQRS$ = ${(side)}^2$ $={\left(90\right)}^2$ $m^2$ $=8100m^2$
Therefore, area of the path = $(10000-8100)$ $m^2$ $=1900m^2$
Cost of cementing $10m^2=250$
Therefore, cost of cementing $1m^2$ = $Rs.\frac{250}{10}$
So, cost of cementing $1900m^2$ = Rs. $\frac{1250}{10}\times 1900=Rs.47,500$

In this chapter, you have studied the following points:

1. Perimeter is the distance around a closed figure whereas area is the part of plane occupied by the closed figure.
2. We have learnt how to find perimeter and area of a square and rectangle in the earlier class. They are:
   $\left(a\right)$ Perimeter of a square $=4\times$ side
   $\left(b\right)$ Perimeter of a rectangle $=2\times$ (length $+$ breadth)
   $\left(c\right)$ Area of a square $=$ side $\times$ side
   (d) Area of a rectangle = length × breadth
3. Area of a parallelogram $=$ base $\times$ height
4. Area of a triangle $=\frac{1}{2}$ (area of the parallelogram generated from it)
   $=\frac{1}{2}$ × base × height
5. The distance around a circular region is known as its circumference.
   Circumference of a circle $=\pi d$, where $d$ is the diameter of a circle and $\pi =\frac{22}{7}$ or $3.14$
6. Area of a circle $=\pi r^2$, where $r$ is the radius of the circle.
7. Based on the conversion of units for lengths, studied earlier, the units of areas can also be converted:
   $1c{m}^2=100m{m}^2$ , $1m^2=10000c{m}^2$ , $1hectare=10000m^2$