COMPARING QUANTITIES for Class 7 MATHS
INTRODUCTION
Baccho hum apni day to day life m aisi bohot si situations face krte hai jinme hume do quantities ko compare krna hota hai. For example, look at the following examples of number, weight and height.



Comparison ka mtlb hota hai do ya do se zyada cheezon ko alag alag qualitative ya quantitative basis p judge krna jaise ki based on length, breadth, weight, amount, price, profit, percentage, etc. Look at the following situation to understand how we represent comparison using simple ratios.
If Heena’s height was 150 cm and Amir’s was 100 cm, then the ratio of their heights would be,
Heena’s height : Amir’s height =150:100=150100=32=or3:2.
Baccho ye ek bohot simple example tha, hum isi tarah se alag alag quantities ko compare krte hai. We also use percentages to compare. In this chapter we will look at the different arithmetical tools to compare quantities. So let's begin!
EQUIVALENT RATIOS
Baccho ratio basically ek relation hota hai do numbers k beech m jisse ek comparison establish hota hai. Hume ratios se pta chlta h ki ek number dusre number k comparison m kitna badha ya chota hai. Hum do quantities ko ratio k through compare krne k lie division ko use krte hai. Here the dividend is called the 'antecedent' and the divisor is called the 'consequent'.
Equivalent ratios vo ratios hote hai jinka proportion same hota hai jab hum unhe unke simplest form m convert kre. To find if two ratios are equivalent or not, we first write them in the form of fractions and convert them to like fractions to compare. Let us look at an example to understand this better:
EXAMPLE: Are the ratios 1:2 and 2:3 equivalent?
SOLUTION:To check this, we need to know whether 12=23.
We have, 12=1×32×3=36;23=2×23×2=46
We find that, 36<46, which means that 12<23
Therefore, the ratio 1:2 is not equivalent to the ratio 2:3.
PROPORTION
If two ratios are equal, then they are said to be in proportion.
Symbol “::” or “=” is used to equate the two ratios.
Examples:
(i) Ratios 2:3 and 6:9 are equal. They can be represented as 2:3::6:9 or 2:3=6:9.
(ii) Ratios 1:2 and x:4 are in proportion. Find x.
⇒12=x4
⇒1×4=x×2
⇒2x=4
⇒x=2
Proportion shows the equality between two ratios. If two ratios are in proportion then these must be equal.

Example 1
Find the ratio of 3 km to 300 m.
First convert both the distances to the same unit.
So, 3 km=3×1000m=3000m.
Thus, the required ratio, 3km:300m is 3000:300=10:1.
Example 2
A map is given with a scale of 2cm=1000km. What is the actual distance between the two places in kms, if the distance in the map is 2.5cm?
2cm means 1000km
So, 1cm=10002km
Hence, 2.5cm means 10002×2.5km
=1250km
Example 3
6 bowls cost Rs. 90. What would be the cost of 10 such bowls?
Cost of 6 bowls is Rs. 90
Therefore, cost of 1 bowl = Rs.906
Hence, cost of 10 bowls = Rs. 906×10=Rs. 150
Example 4
The car that I own can go 150 km with 25 litres of petrol. How far can it go with 30 litres of petrol?
25 liter petrol=150km
1 liter petrol=15025=6km
30 liter petrol= 30×6=180km
PERCENTAGE
The term "percentage" was adapted from the Latin word "per centum", which means "by the hundred". Percentages are fractions with 100 as the denominator. In other words, it is the relation between part and whole where the value of whole is always taken as 100.
For example, if Sam scored 30% marks in his math test, it means that he scored 30 marks out of 100. It is written as 30100 in the fraction form and 30:100 in terms of ratio.
How do we calculate Percentage of an item if the total number of items do not add up to 100? In such cases, we need to convert the fraction to an equivalent fraction with denominator 100. Consider the following example: You have a necklace with twenty beads in two colours.
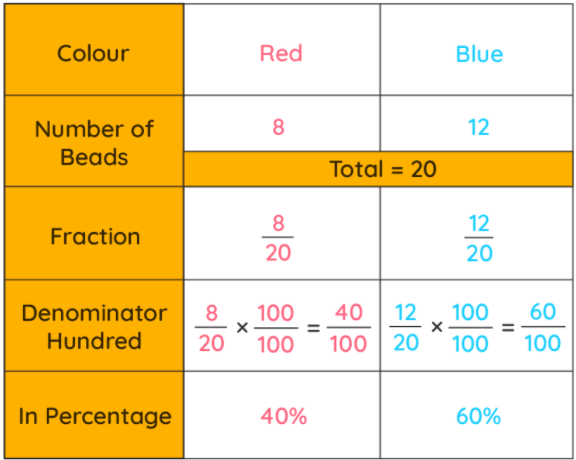
Another ways can also be used to solve such a problem, another one of them is as follows:
Out of 20 beads, the number of red beads is 8.
Hence, out of 100, the number of red beads is 820×100=40(out of hundred)=40%
CONVERSION OF PERCENTAGES
Converting Fractional Numbers to Percentage
Converting a fraction to percent means to convert the whole part into 100 and find how many are considered out of 100. Say, for example, Fraction =35 which means 3 parts are shaded out of 5.
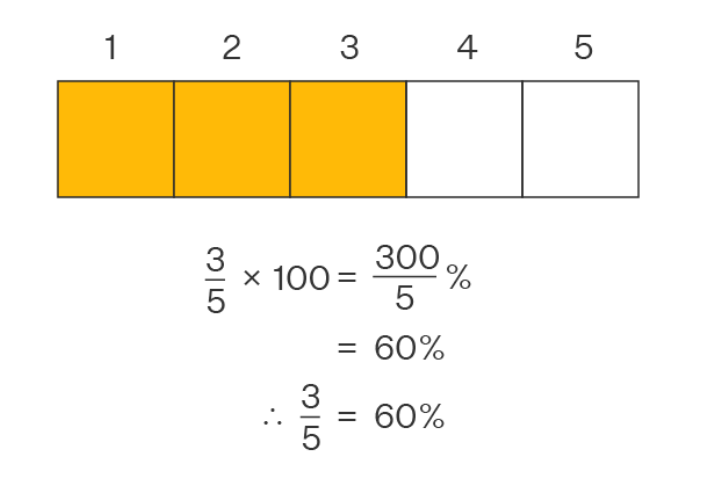
To find the percentage for this fraction, we have to find the number of parts that would be shaded out of 100. To convert a fraction to percent, we multiply it by 100.
Fraction to Percentage Formula
Percentage=(Value)(Total Value)×100
OR
Percentage=Fraction×100
Converting Decimals to Percentage
Decimal to percent conversion is important to learn and is helpful in calculations of commercial math and banking calculations. A decimal value can be converted into a percentage value by multiplying it with 100 and placing a percentage (%) symbol after it. Multiplying a decimal shifts the decimal point by two places towards the right. For example, 0.01 is 1%.
Let us look at the following two quick steps to convert decimals to percentages.
Step 1: Multiply the number by 100 by shifting the decimal point to the right by 2 places.
Step 2: Add the percent symbol (%) to it. Example: 0.43=0.43×100%=43%.

So, we have 0.43=0.43×100%=43%. Thus we have seen the conversion of decimal to a percent. We can even convert percent to a decimal by converting it into a fraction form and then rewriting it into a decimal form. Example:45%=45100=0.45.
Converting Percentages to Fractions or Decimals
Let us learn the method to convert percent to decimal step-wise. To convert a percentage to decimal, follow the steps given below:
Step 1: Remove the percentage sign (%).
Step 2: Put a decimal point by taking two jumps from the right side towards the left.
For example, let us convert 30% to a decimal. 30% can be written as 30 without the percent sign. Now, it is a whole number so consider the decimal point at the right end. 30 is the same as 30.0. Now, by shifting the decimal point two places towards the left, we get 0.3. Therefore, 30%=0.3.
In the case of a decimal percent also, for example, 2.5%, we have to shift the decimal point two places towards the left. So, 2.5%=0.025.

To convert percent to fraction we first convert it to decimals and then we convert it into fractions. Baccho aapne apni previous classes m seekha hua hi ki deciamls ko fractions m kaise convert kiya jaata hai. Look at the following example to understand better.

Example 5
Example 6
Out of 25 children in a class, 15 are girls. What is the percentage of girls?
Out of 25 children, there are 15 girls.
Therefore, percentage of girls =1525×100=60. There are 60% girls in the class.
Example 7
Convert the given fractional numbers to per cents.
(a)18
(b)54
(c)340
(d)27
(a) 18=18∗100%=252%=12.5%
(b)54=54∗100%=125%
(c)340=340∗100=152=7.5%
(d) 27=27∗100=2007=28.57%
Example 8
Convert the given decimals to per cents:
(a)0.75
(b)0.09
(c)0.2
(a)0.75=0.75×100%
=75100×100%=75%
(b)0.09=9100=9%
(c)0.2=210×100%=20%
ESTIMATING PERCENTAGES
Baccho, hum percentages visually bhi calculate kr skte a=hai by observing a figure. Ye concept hume aptitude aur logical thinking m help krta hai. Let's look at the following example:
Example: What percentage of the given circle is shaded?
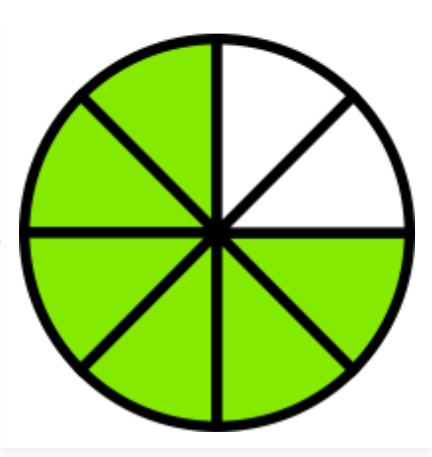
Estimation using percentages
Solution: The given triangle consists of 8 regions, out of which 6 regions are shaded.
So, the percentage of shaded regions will be 6/8 xx 100 = 3/4 xx 100 = 75 %
Example 9
What per cent of the adjoining figure is shaded?

We first find the fraction of the figure that is shaded. From this fraction, the percentage of the shaded part can be found.
You will find that half of the figure is shaded. And,
12=12×100%=50%
Thus, 50% of the figure is shaded.
USE OF PERCENTAGES
Interpreting percentage into usable data
Baccho, abhi tk humne seekha ki hum percentage ko kaise calculate aur convert krte hai. Ab hum dekhenge ki hum percentages ko kaise interpret krke apni daily life scenarios m use krte hai.
Let us look at the following example:
Baccho, iska mtlb hai ki 100 m se 40 clothes are not washed. Such interpretation helps us to visualize better.
Baccho iska mtlb hai ki agar ek class m 100 students hai to unme se 30 students ko fever hai.
Converting percentage to the form 'how many'
Baccho, iss section m hum dekhenge ki hum percentages ko numbers m kaise covert krenge because mostly when we use percentages, we also deal with whole numbers which give us definite values.
Let us understand with an example:
EXAMPLE: 200 chocolates were distributed among two children: Joe and Tom. Joe got 60% and Tom got 40% of the chocolates. How many chocolates will each get?
Solution: Total number of chocolates =200
Joe got 60% of the chocolates =60100×200=120
Tom got 40% of the chocolates =40100×200=80
∴ Joe and Tom will get 120 and 80 chocolates, respectively.
Converting Ratios to percentages
Baccho kabhi kabhi hume information ratios k form m di hoti hai aur hume use percentage m convert krna hota hai. Let's see how we can do that by studying the following example:
200 chocolates were distributed among two children: James and Jacob. James got 35 and Jacob got 25 of the chocolates. What is the percentage of chocolate that each got?
Solution: Total number of chocolates =200
James got 35 of the chocolates =35×100=60% of the total chocolates.
Jacob got 25 of the chocolates =25×100=40% of the total chocolates.
Increase or Decrease as Per Cent
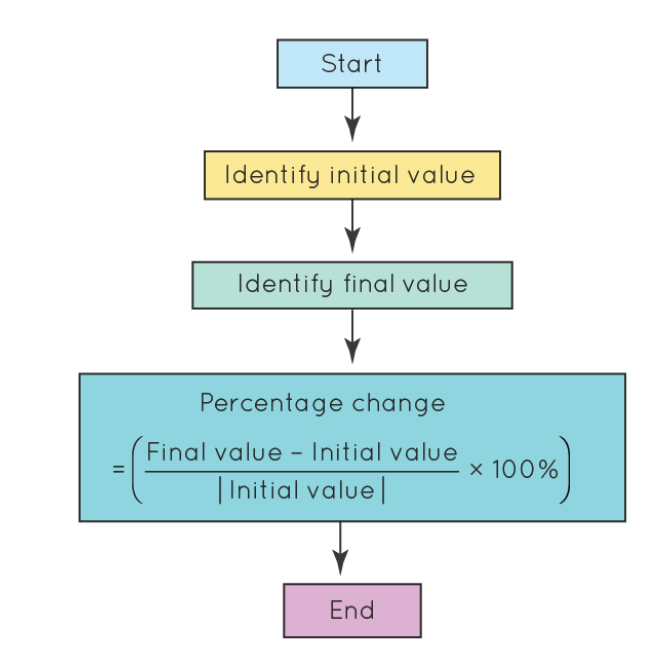
Percentage Change is the difference coming after subtracting the old value from the new value and then divide by the old value and the final answer will be multiplied by 100 to show it as a percentage.

For example, If 64 is increased to 120, find the percent change. To perform these methods, we need to identify the initial and final values.
Method
a)Subtract the initial value from the final value.
Final Value − Initial Value =120−64=56
b) Divide this by the absolute value of the initial value.
(Final Value - Initial Value)Initial Value=5664=0.875
c) Multiply the result by 100
(Final Value - Initial Value)Initial Value×100
=0.875×100=87.5%
Since the answer is positive, it is a percent increase.
Percent Increase =87.5%
Example 10
A school team won 6 games this year against 4 games won last year. What is the per cent increase?
The increase in the number of wins (or amount of change) =6–4=2.
Percentage increase =amount of changeoriginal amount or base×100
=increase in the number of winsoriginal number of wins×100=24×100=50
Example 11
The number of illiterate persons in a country decreased from 150 lakhs to 100 lakhs in 10 years. What is the percentage of decrease?
Original amount = the number of illiterate persons initially =150lakhs.
Amount of change = decrease in the number of illiterate persons =150–100=50lakhs
Therefore, the percentage of decrease
= amount of changeoriginal amount×100=50150×100=3313%
PRICES
Quantities are vastly compared in matters dealing with prices, profit and loss. We also use percentages to find profit, loss and even discounts. In this section, we will first get familiar with the terms related. These are:
Profit or Loss as a Percentage
The profit percentage (%) or loss percentage (%) is calculated with the help of the following formulas, which show that the profit or loss in a transaction is always calculated on its Cost Price:

Example: If the CP of a commodity =Rs. 800 and SP =Rs. 900, then let's find the profit (%).
Profit=SP−CP
=900−800=Rs. 100
Profit(%)=(ProfitCP)×100
=(100800)×100
=12.5%
Example 12
The cost of a flower vase is Rs 120. If the shopkeeper sells it at a loss of 10%, find the price at which it is sold.
Here, Cost price =Rs.120
Loss =10%
So, loss in rupees =120×10100=Rs.12
∴ Selling price =120−12=Rs.108
Example 13
Selling price of a toy car is Rs. 540. If the profit made by shop keeper is 20%, what is the cost price of this toy?
Cost Price= Selling price - Profit
=540−20100⋅540=540−108=Rs. 432.
SIMPLE INTEREST
Baccho aapne apne parents se suna hoga ya jaana hoga ki jab bhi hum koi loan lete hai bank se to uss amount p kuch percent ka interest lgta hai jo ki hume pay krna hota hai. This interest is basically revenue/income for banks. Jo amount hum borrow krte hai use Principal ya Sum Borrowed kaha jaata hai.
This money would be used by the borrower for some time before it is returned. Iss amount ko apne paas rakhne k lie borrower ko kuch paise bank ko pay krne hote hai. This is known as Interest.
You can find the amount you have to pay at the end of the year by adding the sum borrowed and the interest.
That is, Amount = Principal + Interest.
In order to find the simple interest, we can use one formula which can give us interest for one year and for multiple years as well. Let's see how:
Simple interest is calculated with the following formula: S.I. = P × R × T, where P = Principal, R = Rate of Interest in % per annum, and T = Time, usually calculated as the number of years. The rate of interest is in percentage r% and is to be written as r100.

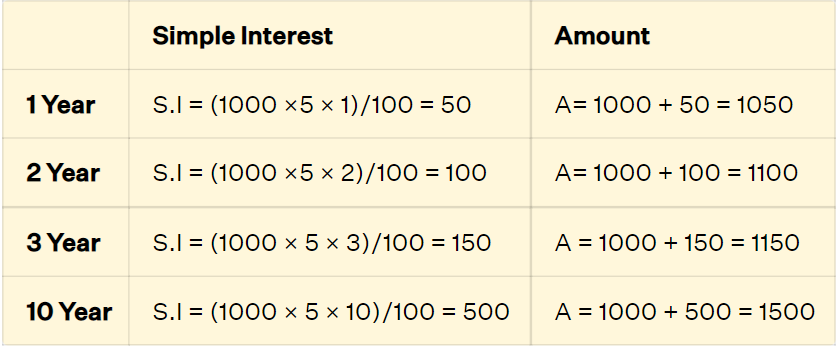
Example: Michael's father had borrowed Rs. 1,000 from the bank and the rate of interest was 5%. What would the simple interest be if the amount is borrowed for 1 year? Similarly, calculate the simple interest if the amount is borrowed for 2 years, 3 years, and 10 years?
Solution:Principal Amount =Rs. 1,000,
Rate of Interest =5%=5100.
Example 14
Anita takes a loan of Rs.5,000 at 15% per year as rate of interest. Find the interest she has to pay at end of one year.
Interest = 15%of the loan
=5000×15100
=50×15
=Rs. 750
Example 15
If Manohar pays an interest of Rs.750 for 2 years on a sum of Rs. 4,500, find the rate of interest.
Let rate of interest be x%
I=P×R×T100
750=4500⋅R⋅2100
R=750⋅1004500⋅2=75090
=759=253
interest of 2 yrs =750rs
interest of 1 year =7502=375rs
interest = x%of principal amount
=4500×x100=45x
45x=375
x=37545
x=253
Rate of interest = 253%
Let's Summarize
1. We are often required to compare two quantities in our daily life. They may be heights, weights, salaries, marks etc.
2. While comparing heights of two persons with heights 150cm and 75cm, we write it as the ratio150:75or2:1.
3. Two ratios can be compared by converting them to like fractions. If the two fractions are equal, we say the two given ratios are equivalent.
4. If two ratios are equivalent then the four quantities are said to be in proportion.
For example, the ratios 8:2 and 16:4 are equivalent therefore 8,2,16 and 4 are in
proportion.
5. A way of comparing quantities is percentage. Percentages are numerators of fractions
with denominator 100. Per cent means per hundred.
For example 82% marks means 82 marks out of hundred.
6. Fractions can be converted to percentages and vice-versa.
For example, 14=14×100% whereas, 75%=75100=34
7. Decimals too can be converted to percentages and vice-versa.
For example, 0.25=0.25×100%=25%
8. Percentages are widely used in our daily life,
(a) We have learnt to find exact number when a certain per cent of the total quantity is given.
(b) When parts of a quantity are given to us as ratios, we have seen how to convert them to percentages.
(c) The increase or decrease in a certain quantity can also be expressed as percentage.
(d) The profit or loss incurred in a certain transaction can be expressed in terms of
percentages.
(e) While computing interest on an amount borrowed, the rate of interest is given in
terms of per cents.
For example, 800 borrowed for 3 years at 12% per annum.
