RATIONAL NUMBERS for Class 7 MATHS
INTRODUCTION
Baccho, aapne apni previous chapters m numbers k baare pdha hai aur aap jaante hai ki numbers mathematics ka ek bohot important part hota hai. We use numbers to count and perform various mathematical operations in our daily life. Aapne number system k alag alag components k baare m bhi pdha hai like fractions, natural numbers, integers, whole numbers, etc. Iss chapter m hum number system k ek aur extended part k baare m pdhenge which is known as rational numbers. We'll cover several topics like equivalent rational numbers, positive and negative rational numbers, rational numbers on a number line, rational numbers in standard form, comparison of rational numbers, etc. So let's get started!
RATIONAL NUMBERS
Baccho aap sab integers ko kaise hum opposite situations ko depict krne m use krte hai. For example, if the distance of 3 km to the right of a place was denoted by 3, then
the distance of 5 km to the left of the same place could be denoted by –5. If a profit of 150 was represented by 150 then a loss of Rs. 100 could be written as –100. Aisi aur bhi situations hoti hai which involve fractions. You can represent a distance of 750m above sea level as 34 km. But what if you want to represent 34 km below sea level? Iss situation ko represent krne k lie hum likhenge −34 km but this is neither an integer nor a fraction. To include such numbers we extend our number system to get another seat of numbers known as rational numbers.
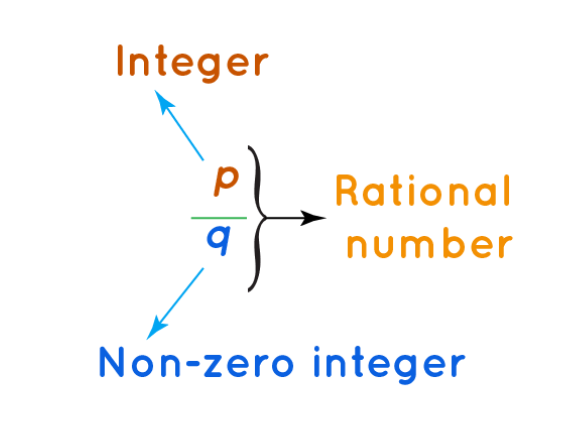
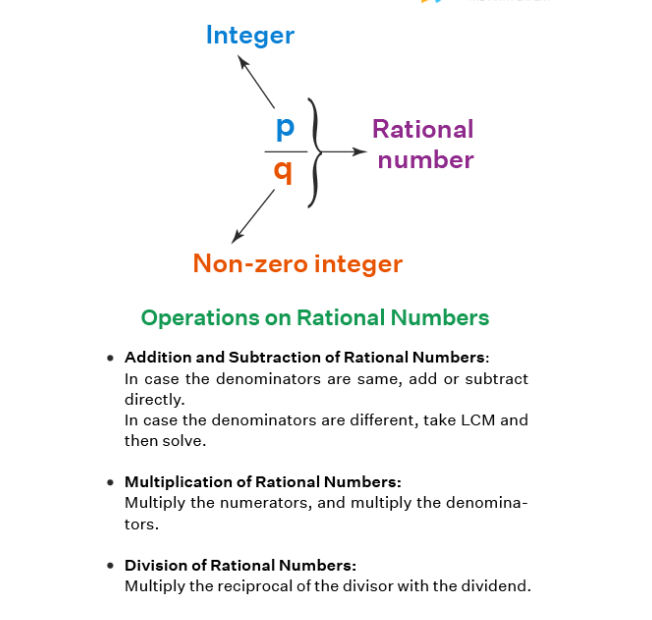
Rational numbers vo numbers hote hai jinhe hum pq k form m likh skte hai in which p and q are intergers and q≠0
Thus, 45 is a rational number. Here, p=4 and q=5. Also, −45 is also a rational number because both −4 and 5 are integers are 5≠0
You have seen many fractions like 384, 81, 23, etc. All fractions are rational numbers
Numerator and Denominator
In pq, the integer p is the numerator, and the integer q(≠0) is the denominator. Thus, in −37, the numerator is −3 and the denominator is 7.
Baccho saare integers can be represented as rational numbers because all integers have numerator 1. For example, the integer 26 can be written as 261 in pq form where p and q are integers are q≠0.
Thus, rational numbers include integers and fractions.
Equivalent rational numbers
Equivalent rational numbers are rational numbers that have the same value but can be represented in different forms. A rational number is a number of the form pq, where p and q are integers and q is not equal to 0.
Equivalent Rational Numbers by multiplication
For a rational number ab, consider a non zero integer m, then a×mb×m is a rational number equivalent to ab. Let's find the equivalent rational numbers of 25.
Therefore, the equivalent rational numbers of 25 are 410,615,820, and so on.
For a rational number ab, consider a common divisor m, of a and b, then a÷mb÷m is a rational number equivalent to ab. Let's find the equivalent rational numbers of 3672.
Therefore, the equivalent rational numbers of 3672 are 1836, 1224, 918, and so on.
Example 1
Give four rational numbers equivalent to: (i) −27 (ii) 5−3 (iii) 49
(i) Four numbers equivalent to −27 are
−27∗22=−414
−27∗33=−621
−27∗44=−828
−27∗55=−1035
(ii)Four numbers equivalent to −53 are
−53∗22=−106
−53∗33=−159
−53∗44=−2012
−53∗55=−2515
(iii)Four numbers equivalent to49 are
49∗22=818
49∗33=1227
49∗44=1636
49∗55=2045
POSITIVE AND NEGATIVE RATIONAL NUMBERS
Positive Rational Numbers
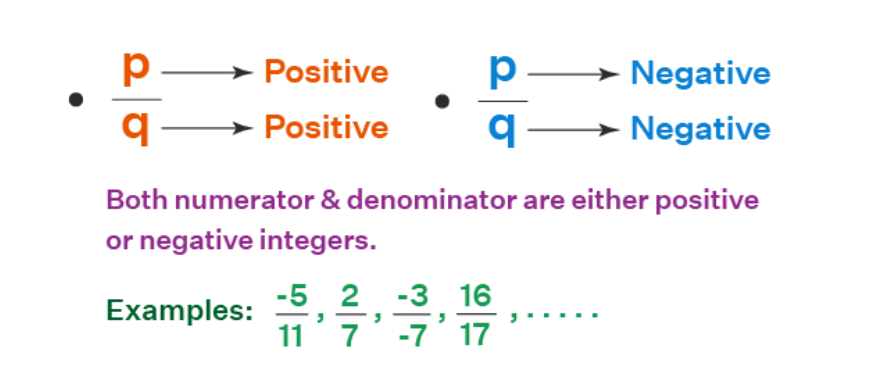
Positive rational numbers are the numbers for which both the numerator and the denominator are either positive integers or negative integers. In other words, a rational number is positive if both numerator and denominator have the same sign.
Examples of positive rational numbers are 38,910,−34−40, etc.
Negative Rational Numbers
The rational numbers that have a 'minus' sign are known as negative rational numbers. Given a rational number pq, if either of 'p' or 'q' is negative, then we get −pq which is a negative rational number. Therefore, when a 'minus' sign is included with a rational number, it gives us a negative rational number.
For example: −45,−76, etc.
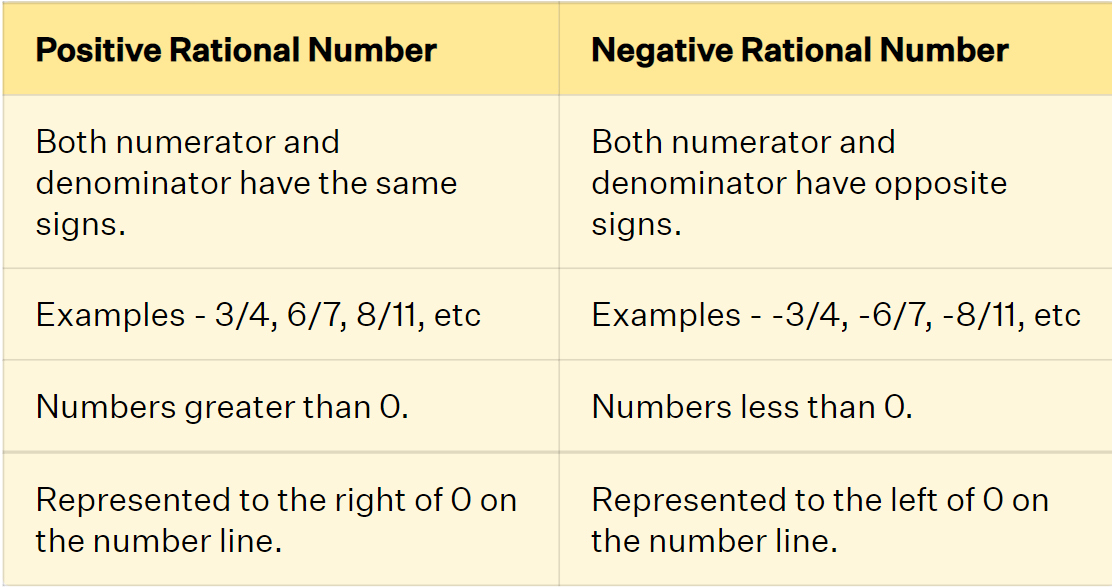
Given below are the points of differences between a positive and a negative rational number:
RATIONAL NUMBERS ON A NUMBER LINE
Baccho aapne apni previous classes m alag alag type k numbers ko number line p represent krna seekha hai jaise integers and fractions. Ab hum dekhenge ki hum rational numbers ko kaise number line p represent kr skte hai.
Representation of rational numbers on a number line is very similar to the representation of negative integers or negative fractions on a number line. On a number line, keeping '0' as the reference, the left-hand side of '0' represents the negative region, and the right-hand side of '0' represents the positive region. Let us look into the steps to represent rational numbers on a number line as shown below.
Example: We will plot 45 on the number line.
Step I: Draw a number line by marking 0 as the reference.
Step II: Identify the integers between which the rational number lies and mark them. 45 lies between 0 and 1.
Step III: Mark the number of divisions between the integers marked in step II equivalent to the denominator of the given rational number. Here, 45 has 5 as the denominator. Thus, we will make 5 divisions.
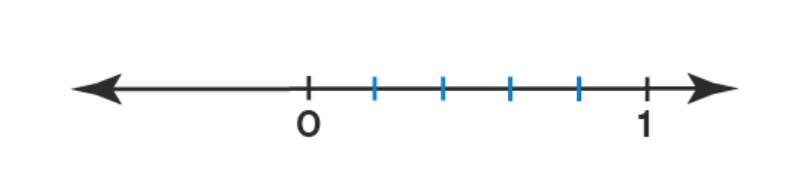
Step IV: Starting from 0, move towards the right by the number of steps equivalent to the numerator of the given rational number. For 45 we will be moving 4 units towards the right starting from 0.
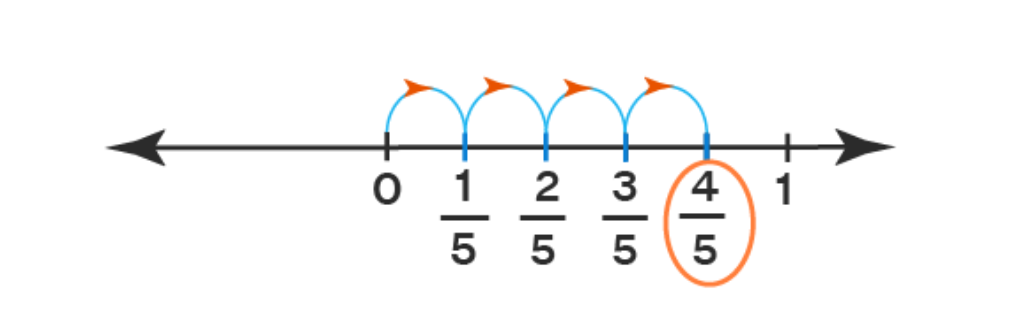
Thus, we have represented 45 on the number line as encircled above.
Negative Rational Numbers on Number Line
Representing negative rational numbers on the number line is similar to the representation of positive rational numbers except for the fact that the direction of movement is towards the left-hand side of the origin. All the steps described above remain the same performed on the left region of the number line. Let us take an example to understand the representation of negative rational numbers on a number line.
Example: Represent −34 on a number line.
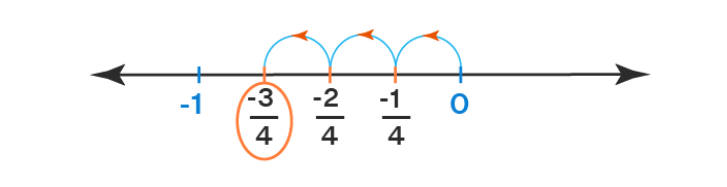
To represent −34 on a number line we will mark the integers 0 and −1 since −34 lies between them. We will then be making 4 divisions as the denominator of −34 is 4. Since the rational number is negative, therefore we will be moving towards the left-hand side starting from 0 by 3 units to plot −34 as shown above.
RATIONAL NUMBERS IN STANDARD FORM
Baccho aapne fractions ko standard form m represent krna seekha hai. Rational numbers ko standard form m represent krne k lie hum same concepts use krte hai. Ek rational number standard form m tab hota hai jab uska denominator ek positive integer ho aur numerator aur denominator m 1 k alawa koi common factor na ho.
Observe the rational numbers 35,−58,−711.
The denominators of these rational numbers are positive integers and 1 is the only common factor between the numerators and denominators. Further, the negative sign occurs only in the numerator.
Such rational numbers are said to be in standard form.
Example 2
Reduce −4530 to the standard form.
We have, −4530=−45÷330÷3=−1510=−15÷510÷5=−32
We had to divide twice. First time by 3 and then by 5. This could also be done as:
−4530=−45÷1530÷15=−32
In this example, note that 15 is the HCF of 45 and 30.
COMPARISON OF RATIONAL NUMBERS
Baccho aap sabne apne previous classes m fractions aur integers ko compare krna seekha hai. Hum bohot si aisi situations face krte hai jinme hume rational numbers ko compare krna hota hai. Iss section m hum seekhenge ki do rational numbers ko kaise compare kia jaata hai.
Example
Compare 45 and 38 and tell which one is greater.
Solution
To make their denominator same, we need to take the LCMof the denominator of both the numbers.
LCM of 5 and 8 is 40.
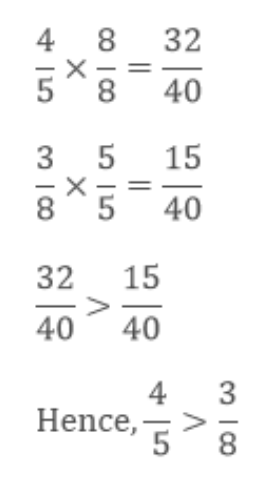
Compare −25 and −37 and tell which one is greater.
Solution
To compare, we need to compare them as normal numbers.
LCM of 5 and 7 is 35.
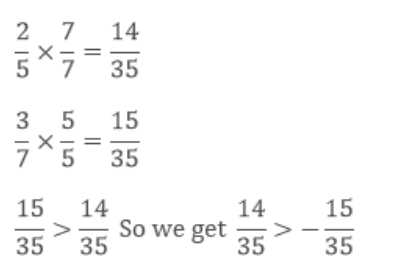
By reversing the order of the numbers. Hence, −25>−37
ExampleCompare 25 and −25 and tell which one is greater.
Solution
It is simply that 25>−25
Example 3
Do 4−9and16−36 represent the same rational number ?
4−9 can be written as 4−9∗44=16−36
∴ 4−9and16−36 represent the same rational number.
Example 4
Which is greater in each of the following: (i) 23,52 (ii) −56,−43 (iii) −34,2−3 (iv) −14,14 (v) (−3)27,(−3)45
(i)23=2∗23∗2=46
52=5∗32∗3=156
Clearly, 156>46. So, 52>23.
(ii)−56
−43=−4∗23∗2=−86
Clearly, −56>−86. So, −56>−43.
(iii)−34=−3∗34∗3=−912
2−3=2∗4−3∗4=8−12
Clearly, 8−12>−912. So, 2−3>−34.
(iv)Clearly, 14>−14.
(v)−327=−23∗57∗5=−11535
−345=−19∗75∗7=−13335
Clearly, −11535>−13335. So, −327>−345.
RATIONAL NUMBERS BETWEEN TWO RATIONAL NUMBERS
There are “n” numbers of rational numbers between two rational numbers. The different types of rational numbers include integers like −2,0,3 etc., fractions whose numerators and denominators are integers like 37,−65, etc. The rational numbers between any two rational numbers can be found using simple methods. Let us have a look at the two different methods.

Rational Numbers Between two Rational Numbers With the Same Denominator Value
In order to determine the rational numbers between two rational numbers, the very first step is to look for their denominators.
Step 1: Check the value of the denominators.
Step 2: If the denominator values are the same, check the value of the numerators.
Step 3: Decide as per the values of numerators. The rational numbers between the two given rational numbers are the ones written in increments of one for the numerator, the denominator being the same.
For example, the rational numbers between 117 and 917 are 217,317,417,517,617,717,817,817.
Rational Numbers Between two Rational Numbers with Different Values of Denominators
The rational numbers between two rational numbers with different denominators, denominators should be equated either by finding their LCM or by multiplying the denominators of one to both the numerator and denominator of the other. For example, the rational numbers between 38 and 56 can be calculated by taking the lcm of 6 and 8. Then, the equivalent rational numbers are 924 and 2024. Now, the rational numbers between 38 and 56 are all rational numbers between 924 and 2024, including 924 and 2024.
Example 5
List three rational numbers between –2 and –1.
There are infinite rational numbers between two rational numbers.
if a and b are the two rational numbers then rational numbers between them can be a+b2,a+a+b22,b+a+b22.
here a=2andb=1
the three rational numbers are - 32,1.25,1.75
Example 6
Write four more numbers in the following pattern −13,−26,−39,−412
Here, we can see that ,
−13∗22=−26
−13∗33=−39
−13∗44=−412
So, in similar pattern, next four numbers will be
−13∗55=−515
−13∗66=−618
−13∗77=−721
−13∗88=−824
OPERATIONS ON RATIONAL NUMBERS
Baccho aap sab jaante hai ki integers aur fractions m alag alag arithmetical operations kaise apply krte hai like multiplication, addition, subtraction, etc. Let us
now study these basic operations on rational numbers.
Addition
Adding rational numbers can be done in the same way as adding fractions. There are two cases related to the addition of rational numbers.
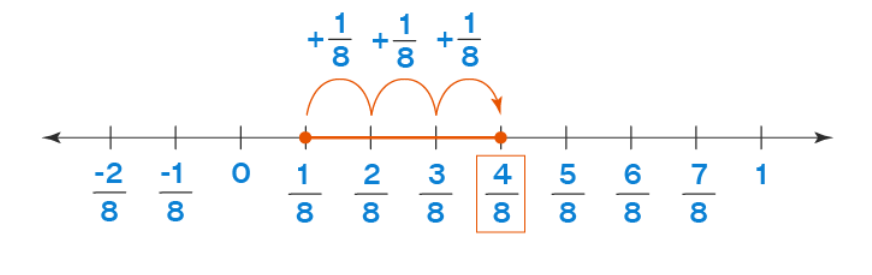
To add two or more rational numbers with like denominators, we simply add all the numerators and write the common denominator. For example, add 18 and 38. Let us understand this with the help of a number line.
When rational numbers have different denominators, the first step is to make their denominators equivalent using the LCM of the denominators. Let's consider an example. Let us add the numbers −13 and 35
Step 1: The denominators are different in the given numbers. Let's find the LCM of 3 and 5 to find the common denominator. LCM of 3 and 5=15
Step 2: Find the equivalent rational number with the common denominator. To do this, multiply −13 with 5 and 35 with 3. −13×55 and −515=35×33=915.
Step 3: Now the denominators are the same; simply add the numerators and then copy the common denominator. Always reduce your final answer to its lowest term. −13+35=(−13×55)+(35×33)=−55+915=415
Additive Inverse
Additive inverse is the number you add to a given number to make the sum zero. For example, if we take the number 3 and add −3 to it, the result is zero. Hence, the additive inverse of 3 is −3. Observe the following:
34+(−34)=0
−45+45=0
Hence, (−34) and 45 are additive inverse of 34 and −45 respectively.
Subtraction
The process of subtraction of rational numbers is the same as that of addition. While subtracting two rational numbers on a number line, we move toward the left. Let us understand this method using an example. Subtract 12−13
Step 1: Find the LCM of the denominators. LCM(2,3)=6.
Step 2: Convert the numbers into their equivalents with 6 as the common denominator. 12×33=36=13×22=26
Step 3: Subtract the numbers you obtained in step 2.
NOTE:While subtracting two rational numbers, we add the additive inverse of
the rational number that is being subtracted, to the other rational number.
Multiplication
Multiplication of rational numbers is similar to how we multiply fractions. To multiply any two rational numbers, we have to follow three simple steps. Let's multiply the following rational numbers: −23×(−45).
The steps to find the solution are:
Step 1: Multiply the numerators. (−2)×(−4)=8
Step 2: Multiply the denominators. (3)×(5)=15
Step 3: Reduce the resulting number to its lowest term. Since it's already in its lowest term, we can leave it as is. (−23)×(−45)=−2×−43×5=815
Division
We have learned in the whole number division that the dividend is divided by the divisor.
Dividend ÷ Divisor=Dividend/Divisor.
While dividing any two numbers, we have to see how many parts of the divisor are there in the dividend. This is the same for the division of rational numbers as well. Let us take an example to understand it in a better way. The steps to be followed to divide two rational numbers are given below:
Step 1: Take the reciprocal of the divisor (the second rational number). 29=92
Step 2: Multiply it to the dividend. −43×92
Step 3: The product of these two numbers will be the solution. −4×93×2=−6
Quick Revision
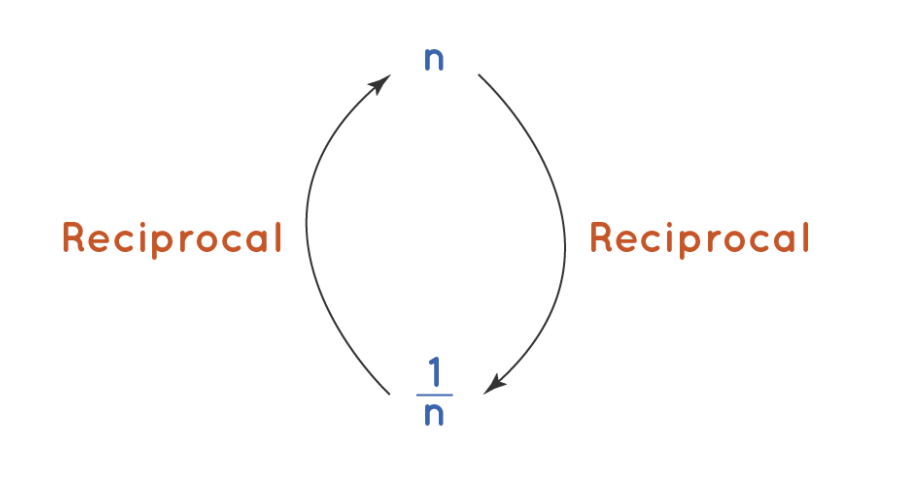
Baccho aap sabne apni previous classes m fractions k reciprocals k baare m pdha hai. Rational numbers k reciprocals m bhi same concept use hota hai. The reciprocal of −27 will be 7−2 i.e., −72; that of −35 would be −53.
SUMMARY
1. A number that can be expressed in the form pq, where p and q are integers and q≠0, is called a rational number. The numbers 27,38,3, etc. are rational numbers.
2. All integers and fractions are rational numbers.
3. If the numerator and denominator of a rational number are multiplied or divided by a non-zero integer, we get a rational number which is said to be equivalent to the given rational number. For example −37=−3×27×2=−614. So, we say 614 is the equivalent form of −37. Also note that −614=−6÷214÷2=−37
4. Rational numbers are classified as Positive and Negative rational numbers. When the numerator and denominator, both, are positive integers, it is a positive rational number.When either the numerator or the denominator is a negative integer, it is a negative rational number. For example, 38 is a positive rational number whereas −89 is a negative rational number.
5. The number 0 is neither a positive nor a negative rational number.
6. A rational number is said to be in the standard form if its denominator is a positive
integer and the numerator and denominator have no common factor other than 1.
The numbers −13,27 etc. are in standard form.
7. There are unlimited number of rational numbers between two rational numbers.
8. Two rational numbers with the same denominator can be added by adding their
numerators, keeping the denominator same. Two rational numbers with different denominators are added by first taking the LCM of the two denominators and
then converting both the rational numbers to their equivalent forms having the LCM as the denominator. For example, −23+38=−1624+924=−16+924=−724
Here, LCM of 3 and 8 is 24.
9. While subtracting two rational numbers, we add the additive inverse of the rational number to be subtracted to the other rational number.
Thus, 78−23=78+ additive inverse of 23=78+−23=21+(−16)24=524
10. To multiply two rational numbers, we multiply their numerators and denominators
separately, and write the product as product of numeratorsproduct of denominators.
11. To divide one rational number by the other non-zero rational number, we multiply the
rational number by the reciprocal of the other.
Thus, −72÷43=−72×reciprocal of43)=−72×34=−218
Let's Revise
1. baccho iss chapter m humne rational numbers k baare m pdha. Rational numbers vo numbers hote hai jo ki pq form m represent ho skte hai in which p and q are integers and q≠0. Rational numbers basically number system ka ek extension hota hai.
2. Saare integers aur fractions rational numbers hote hai but saare rational numbers integers are fractions nahi hote.
3. Equivalent rational numbers vo hote hai jo ki apne simplest form m equal hote hai. For example, 23 and 46 are equivalent rational numbers since they both can be reduced to 23.
4. Jab ek rational number k dono numerator aur denominator negative ya positive ho to vo positive rational numbers kehlaate hai. Lekin agar sirf numerator ya denominator negative ho to vo negative rational numbers kehlaate hai.
5. Ek rational number apne standard form m tab hota hai jab uske numerator aur denominator ka common factor sirf 1 hota hai aur denominator m minus ka sign nahi hota hai.
6. Do rational numbers k beech m infinite rational numbers hote hai.
7. Baccho lastly humne seekha ki hum rational numbers m arithmetical operations kaise apply kr skte hai.