SIMPLE EQUATIONS for Class 7 MATHS
INTRODUCTION
Baccho, aapne apni previous classes m algebra k baare m pdha hai. Hum algebra ko sub-conciously apni daily lives m use krte to figure out different problems. Chaliye ek game khelte hai to understand how algebra works. Follow the following steps:
Baccho, aapka answer aaya hai 2!
Surprised? This is an algebra trick. Basically agar aap observe krenge to hum isme chosen number ko x maan lete hai and usi around we multiply, divide and subtract iss tarah se taaki humara original number subtract hojaye and answer humesha 2 aaye.
Iss chapter m hum seekhenge ki equations kaise form ki jaati hai, unko solve kaise kia jaata hai using different operations like addition, subtraction, multiplication and division. Then we'll learn ki hum ek solution se equation kaise bnaa skte hai and lastly, we'll see the application of simple equations in our day-to-day lives. So let's begin!
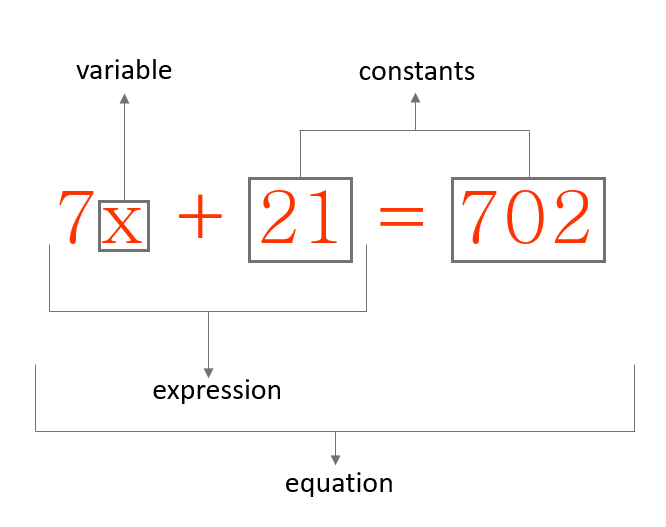
VARIABLES, CONSTANTS, EXPRESSIONS AND EQUATIONS
Baccho, sabse phle hum ye jaan lete hai ki variables, constants, equations and expressions ka kya mtlb hota hai. Aap in sabhi terms ko inke meanings se smjh skte hai.
FORMING EQUATIONS
Baccho ab hum dekhte hai ki sentences se equations kaise form krte hai. Look at the following statements:
1. The sum of four times of x and 12 is equal to 35.
Let's break down this sentence to understand better. "Four times of x" means 4×x which is equal to 4x. Also, the statement says that the sum of 4x and 12 is equal to 35, which gives us:
4x+12=35
2. Half of a number is 3 more than 8.
Baccho, in this sentence, let's take the number to be x which means "half a number" equals to 12x. Also, "3 more than 8" means that half of the number exceeds 8 by 3. Therefore, we get,
12x−8=3
To baccho, is tarah se hum sentences ko break down krke equations form krte hai.
Baccho, similarly hum equations se sentences form kr skte hai. For example, Add 1 to three times of x gives 8
This would give us the equation : 3x+1=8

Example 1
Write the following statements in the form of equations:
(i) The sum of three times x and 11 is 32.
(ii) If you subtract 5 from 6 times a number, you get 7.
(iii) One fourth of m is 3 more than 7.
(iv) One third of a number plus 5 is 8.
(i) The sum of three times x and 11 is 32. →3x+11=32
(ii) If you subtract 5 from 6 times a number, you get 7. →6x−5=7
(iii) One fourth of m is 3 more than 7.→14m−7=3
(iv) One third of a number plus 5 is 8.→13x+5=8
Example 2
Convert the following equations in statement form:
(i)x−5=9
(ii)5p=20
(iii)3n+7=1
(iv)m5−2=6
(i) Taking away 5 from x gives 9.
(ii) Five times a number p is 20.
(iii) Add 7 to three times n to get 1.
(iv) You get 6, when you subtract 2 from one-fifth of a number m.
Example 3
Raju’s father’s age is 5 years more than three times Raju’s age. Raju’s father is 44 years old. Set up an equation to find Raju’s age.
Let Raju's age is x years.
Then, his father age will be 3x+5 years.
We are given Raju's father age is 44 years.
So, required equation is,
3x+5=44
Using this equation, we can find Raju's age, that is 13 years.
Example 4
A shopkeeper sells mangoes in two types of boxes, one small and onelarge. A large box contains as many as 8 small boxes plus 4 loose mangoes.Set up an equation which gives the number of mangoes in each smallbox. The number of mangoes in a large box is given to be 100.
Let the number of mangoes in small box =x
Then, the number of mangoes in large box =8x+4
We are given, the number of mangoes in large box is 100.
So, the required equation is,
8x+4=100
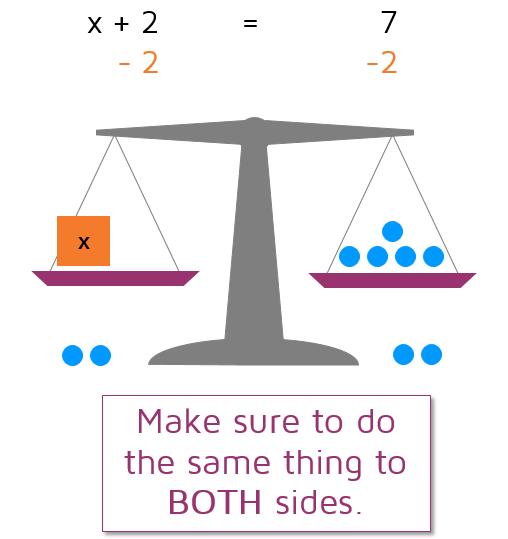
BALANCED EQUATION
When the LHS=RHS of an equation, then it is said to be a balanced equation. Let's see how an equation stays balanced
1. If we add the same number to both the sides.
We can add the same number on both the sides of a balanced equation, the equation will remain the same.
12–8=3+1
If we add 3 to both the sides,
12–8+3=7
3+1+3=7
LHS=RHS
2. If we subtract the same number from both sides.
We can subtract the same number from both the sides of a balanced equation, the equation will remain the same.
12−8=3+1
If we subtract 3 from both the sides,
12−8−3=1
3+1−3=1
LHS=RHS
3. If we multiply the same number to both the sides.
We can multiply the same number on both the sides of a balanced equation, the equation will remain the same.
12−8=3+1
If we multiply 3 to both the sides,
(12−8)×3=36−24=12
(3+1)×3=9+3=12
LHS=RHS
4. If we divide the same number from both sides.
We can divide the same number from both the sides of a balanced equation, the equation will remain the same.
12–8=3+1
If we divide both the sides by 2,
(12–8)÷2=4÷2=2
(3+1)÷2=4÷2=2
LHS=RHS
SOLVING AN EQUATION
Baccho ab hum seekhenge ki equations ko solve kaise kia jaata hai. Iss chapter m equations ko solve krne k lie hum do methods seekhenge:
1. By adding or subtracting the same number to both the sides of the equation as we have above seen that the equation will remain the same.
Baccho humne abhi pdha tha ki equations ko balanced rakhne k lie we apply the same operation on both the expressions on either side of the equal to sign (=). Iss method m basically hum alag alag operations ko iss tarah se apply krte hai taaki humari ek side m sirf variable ho aur dusri side m ek constant value ho. Let's look at the following example.
Example:
x+11=35
Solution:
Subtract 11 from both the sides.
x+11–11=35–11
x=24
Here, x=24 is the solution of the given equation.
Baccho observe kijiye ki
Example:
25y=125
Solution:
Divide both the sides by 25.
25y25=12525
y=5
Baccho, yaha second example m humne dono sides ko 25 se divide kia taaki humara variable ek side hojaye and constant dusri side hojaye. Ab hum equations ko solve krne k lie ek dusra method dekhenge.
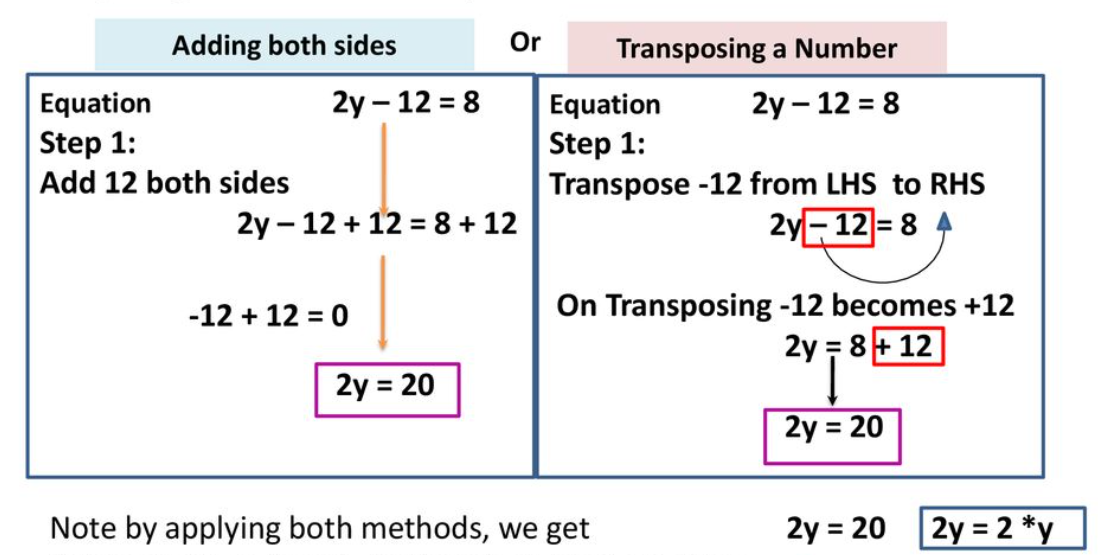
2.Transposing Method
In this method, we transpose the numbers from one side of the equation to the other side so that all the terms with variable come on one side and all the constants come on another side.
While transposing the numbers the sign of the terms will get changed. i.e. Negative will become positive and positive will become negative.
Baccho, iss method m hum variable ko ek side rakh k baaki saare constants ko dusri side le jaate hai. When we take a constant on the other side to uska sign change hojata hai, yaani ki agar koi number LHS (Left Hand Side) m add ho rha hai to vo RHS (Right Hand Side) m jaake subtract hojaega. Let's take a look at the following examples:
Example
:
x+11=35
Solution:
Now we will transfer 11 from LHS to RHS and its sign will get reversed.
x=35–11
x=24
To baccho ye do methods use hote equations solve krne k lie. Now we'll learn about ki hum solutions ko use krke equations kaise form kr skte hai.
Example 5
Solve : (a) 3n+7=25 (b) 2p−1=23
(a) We go stepwise to separate the variable n on the LHS of the equation. The LHS is
3n+7. We shall first subtract 7 from it so that we get 3n. From this, in the next step
we shall divide by 3 to get n. Remember we must do the same operation on both
sides of the equation. Therefore, subtracting 7 from both sides,
3n+7–7=25–7
3n=18
Now divide both sides by 3,
3n7=183
n=6
(b) What should we do here? First we shall add 1 to both the sides:
2p–1+1=23+1
2p=24
Now divide both sides by 2, we get 2p2=242
p=12
Example 6
Solve : 12p−5=25
Adding 5 on both sides of the equation,
12p−5+5=25+5
12p=30
Dividing both sides by 12,
12p12=3012
p=52
Example 7
Solve (a) 4(m+3)=18
(b) −2(x+3)=5
(a) 4(m+3)=18
Let us divide both the sides by 4. This will remove the brackets in the LHS We get,
m+3=184
m+3=92
m=92−3 (transposing 3 to RHS)
m=32 (required solution)
(b)−2(x+3)=8
We divide both sides by (–2), so as to remove the brackets in the LHS, we get,
x+3=−82
x+3=−4
x=−4−3
x=−7
FORMING EQUATIONS FROM SOLUTIONS
Baccho, solutions se equations form krna ek reverse process hota hai. Isme we need to make sure ki humari equation balanced rahe. Humne abhi pdha tha ki ek equation ko balanced rakhne k lie kya kya rules hote hai, jaise ki adding and subtracting the same numbers on both the sides. Isi concept ko use krke hum ek solution se ek equation derive kr skte hai. Let's take a look at an example and understand better:
Start here → x=4
Multiply both sides by 2 → 2x=8
Add 6 on both the side → 2x+6=8+6
Equation → 2x+6=14
Baccho, har equation ka ek single solution hota hai but jaisa ki aap dekh skte hai ki ek solution se infinite equations ban skti hai. Aap dono sides ko same numbers se multiply, divide, add, subtract krenge and everytime you'll get a new equation. Isn't this fun!
APPLICATION OF SIMPLE EQUATIONS TO PRACTICAL SITUATIONS
Baccho abhi tk humne jo concepts pdhe ab hum unhe apni daily life se connect krke dekhenge ki where do we use these learnings in practical situations. To solve such questions hum sabse phle required answer ko ek variable maanlete hai like x,y,z,a,b,etc. uske baad baccho hum usi variable k around different operations apply krte hai depending upon the given statement. Baccho humne abhi pdha tha ki equations ko kaise form kiya jaata hai. Fir humne equations ko solve krne k lie do methods seekhe. In this topic we will apply both of these concepts to solve it. Let's learn by observing the following situations:
Example 8
The sum of three times a number and 11 is 32. Find the number.
If the unknown number is taken to be x, then three times the number is 3x and the sum
of 3x and 11 is 32. That is, 3x+11=32
To solve this equation, we transpose 11 to RHS, so that
3x=32−11 or 3x=21
Now, divide both sides by 3
x=213=7
The required number is 7.
Example 9
Raju’s father’s age is 5 years more than three times Raju’s age. Find Raju’s age, if his father is 44 years old.
Let the age of Raju is x years. Then,
His father age =3x+5 years
So, 3x+5=44
3x=39⇒x=13
So, Age of Raju is 13 years.
Let's summarize
1. An equation is a condition on a variable such that two expressions in the variable should have equal value.
2. The value of the variable for which the equation is satisfied is called the solution of the
equation.
3. An equation remains the same if the LHS and the RHS are interchanged.
4. In case of the balanced equation, if we
(i) add the same number to both the sides, or
(ii) subtract the same number from
both the sides, or
(iii) multiply both sides by the same number, or
(iv) divide both
sides by the same number, the balance remains undisturbed, i.e., the value of the
LHS remains equal to the value of the RHS
5. The above property gives a systematic method of solving an equation. We carry out
a series of identical mathematical operations on the two sides of the equation in such
a way that on one of the sides we get just the variable. The last step is the solution of
the equation.
6. Transposing means moving to the other side. Transposition of a number has the same
effect as adding same number to (or subtracting the same number from) both sides of
the equation. When you transpose a number from one side of the equation to the
other side, you change its sign. For example, transposing +3 from the LHS to the
RHS in equation x+3=8 gives x=8−3(=5). We can carry out the transposition
of an expression in the same way as the transposition of a number.
7. We have learnt how to construct simple algebraic expressions corresponding to
practical situations.
8. We also learnt how, using the technique of doing the same mathematical operation
(for example adding the same number) on both sides, we could build an equation
starting from its solution. Further, we also learnt that we could relate a given equation
to some appropriate practical situation and build a practical word problem/puzzle
from the equation.
Let's Revise!
For example, x+2,2y−7,3z2+5,etc.
⇒2x+3−3=17−3
⇒2x=14
⇒2x2=142
⇒x=7
Putting x=7 in 2x+3=17
LHS⇒2×(7)+3
=14+3
=17
Also, LHS=17
∴ x=7 is the correct answer.