बीजीय व्यंजक एवं सर्वसमिकाएँ कक्षा 8 गणित

Table Of Contents

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय में हम बीजीय व्यंजक एवं सर्वसमिकाओं का अध्ययन करेंगे। कोई भी गणितीय व्यंजक जिसमे संख्याएँ, चर और संक्रियाओं का उपयोग किया गया हो, बीजीय व्यंजक कहलाते है।
इस अध्याय मे हम बीजीय व्यंजकों से संबंधित परिभाषाओं, बीजीय व्यंजकों के योग, व्यवकलन एवं गुणन तथा सर्वसमिकाओं का विस्तार से अध्ययन करेंगे।

आइये जानते है, बीजीय व्यंजक एवं सर्वसमिकाएँ को और करीब से...

एक बीजीय व्यंजक संख्याओं, चरों तथा मूलभूत संक्रियाओं का संयोजन होता है। एक बीजीय व्यंजक, जिसके हर में चर न हो तथा चरों के घातांक पूर्ण संख्याओं में हों तथा विभिन्न पदों के संख्यात्मक गुणांक वास्तविक संख्याएँ हों, बहुपद कहलाता है।

बीजीय सर्वसमिकाएँ वह समीकरण हैं जो समीकरण के बाएँ पक्ष का मान समान रूप से समीकरण के दाएँ पक्ष के मान के बराबर होता है। बीजीय सर्वसमिका गणितीय गणना के लिए सर्वाधिक महत्वपूर्ण इसलिए है क्योंकि इसका प्रयोग लगभग प्रत्येक बीजीय प्रश्न को हल करने के लिए होता है।

इस अध्याय मे हम बीजीय व्यंजकों तथा सर्वसमिकाओं का विस्तार से अध्ययन करेंगे।

व्यंजक का परिचय

पिछली कक्षाओं में हम बीजीय व्यंजकों (अथवा केवल व्यंजकों) के बारे में जानकारी प्राप्त कर चुके हैं। आइए इन पर कुछ और अध्ययन करते है :-
$x + 3,$ $2 y - 5,$ $3 x + 2,$ $4 x y + 7$ इत्यादि व्यंजकों के उदाहरण हैं।

हम जानते हैं व्यंजकों का निर्माण चरों एवं अचरों की सहायता से होता है। व्यंजक $2 x - 5$ को चर $x$ एवं अचरों $2$ तथा $5$ से बनाया गया है। इसी प्रकार व्यंजक $4 x y + 7$ को चरों $x$ तथा $y$ एवं अचरों $4$ तथा $7$ से बनाया गया है।

हम जानते हैं कि व्यंजक $2 y - 5$ में $y$ का मान कुछ भी हो सकता है। यह $2, 5, 3, 0, \frac{5}{7}, - 2, - 3$ इत्यादि हो सकता है अर्थात $y$ के असंख्य मान हो सकते हैं। व्यंजक के चर का मान बदलने पर व्यंजक का मान बदल जाता है। अतः इस प्रकार $y$ को विभिन्न मान देने पर $2 y - 5$ का मान बदलता रहता है।
जब $y = 2$ पर

$= 2 y - 5$

$= 2 (2) - 5$

$= - 1$

जब $y = 0$ पर

$= 2 y - 5$

$= 2 (0) - 5$

$= - 5$

इस प्रकार $y$ के प्रत्येक विभिन्न मान के लिए व्यंजक का मान बदलता रहेगा।

व्यंजकों से संबंधित परिभाषाएँ

एक व्यंजक के विभिन्न भाग होते है $:$ -

(i) पद :- प्रत्येक व्यंजक को जितने गणितीय चिह्नों $($ जोड़, व्यवकलन, गुणा आदि $)$ द्वारा अलग किया जाता है, वह व्यंजक उतने ही पद का होता है।
आइए एक उदाहरण से समझते है :-
उदाहरण : $4 x + 3$
उपर्युक्त व्यंजक $4 x$ और $3$ के योग से मिलकर बना है। अतः इसमे दो पद है।

(ii) गुणनखंड :- किसी पद का व्यापक लिखित रूप ही उस पद के गुणनखंड कहलाते है।
उपर्युक्त उदाहरण $4 x + 3$ मे $\Rightarrow$ $4 x$ के गुणनखंड $4 \times$ $x$ तथा $3$ का गुणनखंड $1$ और $3$ स्वयं है।

(iii) गुणांक :- किसी पद का संख्यात्मक गुणनखंड उसका संख्यात्मक गुणांक अथवा गुणांक कहलाता है।
उदाहरण : (i) पद $7 x y$ का गुणांक $7$ है। (ii) पद $- 5 x$ का गुणांक $- 5$ है।

(iv) एकपदी :- जिस व्यंजक मे केवल एक पद होता है, एकपदी व्यंजक कहलाता है।
उदाहरण : $4 x y,$ $9 x^{2},$ $87 m n p,$ $5 x y^{2}$ आदि।

(v) द्विपदी :- जिस व्यंजक मे दो पद होते है, द्विपदी व्यंजक कहलाते है।
उदाहरण : $4 x y + 4 r v,$ $9 x^{2} - 6 y^{3},$ $87 m n p - 12 x y,$ $5 x y^{2} + 8 x y$

(vi) त्रिपदी :- जिस व्यंजक मे तीन पद होते है, त्रिपदी व्यंजक कहलाता है।
उदाहरण : $a + b + c +,$ $2 x + 7 y - 8 z$ आदि।

(vii) बहुपदी :- व्यापकतः एक अथवा अधिक पदों वाला ऐसा व्यंजक जिसके चरों की घात केवल धनात्मक पूर्ण संख्या हो, बहुपद कहलाता है। बहुपद मे पदों की संख्या एक या एक से अधिक कुछ भी हो सकती है।
उदाहरण : $a + b + c + d,$ $3 x y,$ $7 x y z - 10,$ $2 x + 3 y + 7 z$ आदि।

उदाहरण 1

व्यंजक $x^{2} y^{2} - 10 x^{2} y + 5 x y^{2} - 20$ में प्रत्येक पद के गुणांक पहचानिए।

गुणांक :- किसी पद का संख्यात्मक गुणनखंड उसका संख्यात्मक गुणांक अथवा गुणांक कहलाता है।


पद	गुणांक
$x^{2} y^{2}$	$1$
$- 10 x^{2} y$	$- 10$
$5 x y^{2}$	$5$
$- 20$	$- 20$

Learn more

उदाहरण 2

निम्नलिखित बहुपदों को एकपद, द्विपद एवं त्रिपद के रूप में वर्गीकृत कीजिए
$- z + 5, x + y + z, x + y + z + 100, a b - a c$

चूंकि जिस व्यंजक मे एक पद होता है उसे एकपदी, जिसमे दो पद होते है उसे द्विपदी, जिसमे तीन पद होते है उसे त्रिपदी तथा तीन या तीन से अधिक पद वाले व्यंजक को बहुपदी कहते है।

एकपद : एक भी व्यंजक एकपदी नहीं है।

द्विपद : $- z + 5,$ $a b - a c$

त्रिपद : $x + y + z$

बहुपद : $x + y + z + 100$

Learn more

उदाहरण 3

निम्नलिखित व्यंजक में प्रत्येक के पदों एवं गुणांकों को पहचानिए :
$4 x^{2} y^{2} - 4 x^{2} y^{2} z^{2} + z^{2}$

व्यंजक $:$ $4 x^{2} y^{2} - 4 x^{2} y^{2} z^{2} + z^{2}$

पद $:$
$(i)$ $4 x^{2} y^{2}$
$(i i)$ $- 4 x^{2} y^{2} z^{2}$
$(i i i)$ $z^{2}$

$(i)$ $4 x^{2} y^{2}$ का गुणांक $:$ $4$

$(i i)$ $- 4 x^{2} y^{2} z^{2}$ का गुणांक $:$ $- 4$

$(i i i)$ $z^{2}$ का गुणांक $:$ $1$

Learn more

समान एवं असमान पद

समान पद :- समान चर वाले पद समान पद कहलाते है।
उदाहरण $: 2 x$ और $- 9 x$ $\Rightarrow$ चूंकि यहाँ दोनों पदों मे चर समान है अतः ये पद समान पद होंगे।

असमान पद :- भिन्न - भिन्न चर वाले पद असमान पद कहलाते है।
उदाहरण $: 2 x$ और $- 9 y$ $\Rightarrow$ चूंकि यहाँ दोनों पदों मे चर असमान है अतः ये पद असमान पद होंगे।

OMR (One Minute Revision)

व्यंजकों का निर्माण चरों एवं अचरों की सहायता से होता है।

किसी पद का व्यापक लिखित रूप ही उस पद के गुणनखंड कहलाते है।

किसी पद का संख्यात्मक गुणनखंड उसका संख्यात्मक गुणांक अथवा गुणांक कहलाता है।

जिस व्यंजक मे केवल एक पद होता है, एकपदी व्यंजक कहलाता है।

जिस व्यंजक मे दो पद होते है, द्विपदी व्यंजक कहलाते है।

जिस व्यंजक मे तीन पद होते है, त्रिपदी व्यंजक कहलाता है।

समान चर वाले पद समान पद कहलाते है।

भिन्न - भिन्न चर वाले पद असमान पद कहलाते है।

उदाहरण 4

निम्नलिखित के दो समान पद लिखिए :
$7 x y$

समान पद :- समान चर वाले पद समान पद कहलाते है।

$7 x y$ चूंकि यह एक गुणात्मक बीजीय व्यंजक है। अतः हमे ऐसे पद ज्ञात करने है जो गुणात्मक रूप मे हो।

अतः $7 x y$ के लिए समान पद $:$ $9 x y,$ $15 y x$

चूंकि गुणन क्रमविनिमेय होता है इसलिए चर का स्थान बदलने पर मान पर कोई प्रभाव नहीं पड़ता है।

Learn more

बीजीय व्यंजकों का योग एवं व्यवकलन

बीजीय व्यंजकों को जोड़ने या घटाने के लिए निम्नलिखित प्रक्रिया का प्रयोग करना चाहिए :-

$\Rightarrow$ सबसे पहले हमें बीजीय व्यंजकों को अलग - अलग पंक्तियों में इस प्रकार लिखना चाहिए कि समान पद के नीचे समान पद आए।

$\Rightarrow$ यदि समान चर का कोई पद किसी अन्य व्यंजक में नहीं है तो उसके स्थान पर रिक्त अथवा शून्य का प्रयोग करते है तथा योगफल मे उसको फिर से लिख देते है।

$\Rightarrow$ अंत मे इन्हे सामान्य जोड़ अथवा व्यवकलन की तरह हल करते है।

आइए उदाहरणों की सहायता से समझते है :-
उदाहरण : $7 x^{2} - 4 x + 5$ और $9 x - 10$ को जोड़िए।
हल :

उदाहरण : $7 x y + 5 y z - 3 z x, 4 y z + 9 z x - 4 y, - 3 x z + 5 x - 2 x y$ का योग कीजिए।
हल :
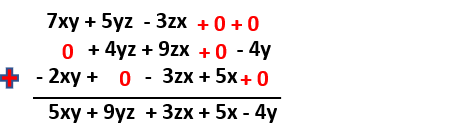
ocr_image

नोट : किसी संख्या का घटाना उसके योज्य प्रतिलोम को जोड़ने के समान होता है। इस प्रकार

- 3

को घटाना

+ 3

को जोड़ने के समान है, इसी प्रकार

6 y

को घटाना

- 6 y

को जोड़ने के समान है।
अतः दूसरी पंक्ति के प्रत्येक पद के नीचे तीसरी पंक्ति मे लिखे चिह्न से हमे व्यवकलन करने मे सहायता मिलती है।

उदाहरण : $7 x^{2} - 4 x y + 8 y^{2} + 5 x - 3 y$ मे से $5 x^{2} - 4 y^{2} + 6 y - 3$ को घटाइए।
हल :
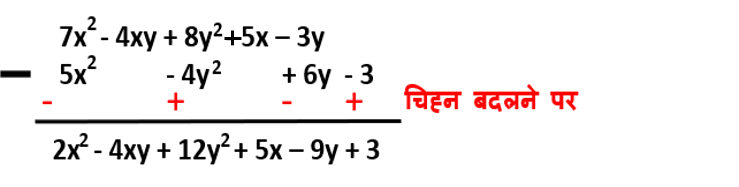
ocr_image

इस प्रकार हम उपर्युक्त विधि से बीजीय व्यंजकों का योग और व्यवकलन आसानी से कर सकते है।

उदाहरण 5

निम्नलिखित का योग ज्ञात कीजिए :
$2 p^{2} q^{2} - 3 p q + 4, 5 + 7 p q - 3 p^{2} q^{2}$

बीजीय व्यंजकों को जोड़ने के लिए उन्हे अलग - अलग पंक्तियों मे समान पद के नीचे समान पद के रूप मे व्यवस्थित करते है फिर उन्हे जोड़ते है।

Learn more

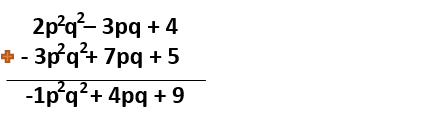
उदाहरण 6

निम्नलिखित का योग ज्ञात कीजिए :
$l^{2} + m^{2}, m^{2} + n^{2}, n^{2} + l^{2}, 2 l m + 2 m n + 2 n l$

चूंकि हम जानते है कि जोड़ या व्यवकलन करते समय कोई पंक्ति का पद नहीं दिया गया हो तो हम उस स्थान पर रिक्त स्थान अथवा शून्य का प्रयोग कर सकते है।

Learn more

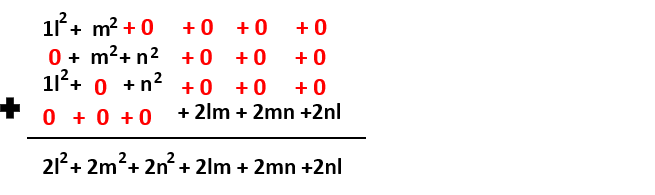
उदाहरण 7

$12 a - 9 a b + 5 b - 3$ में से $4 a - 7 a b + 3 b + 12$ को घटाइए।

घटाने के लिए भी हम व्यंजकों को अलग - अलग पंक्तियों मे व्यवस्थित कर नीचे वाली पंक्ति के चिह्न बदलकर फिर उसे हल करते है।

Learn more

उदाहरण 8

$5 x y - 2 y z - 2 z x + 10 x y z$ में से $3 x y + 5 y z - 7 z x$ को घटाइए।

Learn more

बीजीय व्यंजकों का गुणन

बीजीय व्यंजकों का गुणन करते समय ध्यान रखने योग्य बिंदु-

1. दो एकपदियों का गुणन -

इसमें अचर पदों का गुणा, अचर पदों से होता हैं तथा चर पदों का गुणा, चर पद से होता हैं।

उदाहरण के लिए :- दो बीजीय व्यंजक $4 x$ व $3 x$ हैं तो इन दोनों बीजीय व्यंजको के गुणन में अचर पद $4$ तथा $3$ का आपस में गुणा होगा तथा चर पद $x$ व $x$ का गुणा आपस में होगा अर्थात $x \times x = x^{2}$ ( $∵$ आधार समान होने पर घाते जुड़ जाती हैं अर्थात $a^{m} \times a^{n} = a^{m + n}$ ) अतः
$= (4 x) \times (3 x)$
$= (4 \times 3) (x \times x)$
$= 12 x^{2}$

2. तीन या तीन से अधिक एकपदियों का गुणन -

इसमें अचर पदों का गुणा अचर पदों से होता हैं तथा विभिन्न चर पदों का गुणा निम्न होता हैं -

चर अलग-अलग होने पर वे सब आपस में गुणा हो जायेंगे।

यदि कुछ चर समान हैं तो उनकी घाते आपस में जुड़ जाएगी।

उदाहरण के लिए :- तीन बीजीय व्यंजक

3 x

5 y

व

4 x y z

हैं तो इन बीजीय व्यंजको के गुणन में अचर पद

3

5

तथा

4

का अलग से आपस में गुणा होगा तथा चर पद का अलग से आपस मे गुणा होगा अर्थात

= (3 x) \times (5 y) \times (4 x y z)

= (3 \times 5 \times 4) (

x

\times y \times

x y z)

= (60) \times (x^{2} y^{2} z)

= 60

x^{2} y^{2} z

3. एकपद का बहुपद से गुणन -

इसमे एकपद को त्रिपद के प्रत्येक पद से अलग - अलग गुणा करके हल किया जाता है।

उदाहरण के लिए :-

3 p \times (4 p^{2} + 5 p + 7)

को हल कीजिए।

= (3 p \times 4 p^{2}) + (3 p \times 5 p) + (3 p \times 7)

= 12 p^{3} + 15 p^{2} + 21 p

इस प्रकार हम वितरण नियम का प्रयोग कर आसानी से इन व्यंजकों का गुणन कर सकते है।

4. द्विपद का बहुपद से गुणन -

इसमे द्विपद के प्रत्येक पद को बहुपद के प्रत्येक पद से अलग - अलग गुणा करके अर्थात वितरण नियम का प्रयोग करके हल किया जाता है।

उदाहरण के लिए :-

(a + 7) \times (a^{2} + 3 a + 5)

को हल कीजिए।

वितरण नियम का प्रयोग करने पर

= a \times (a^{2} + 3 a + 5) + 7 \times (a^{2} + 3 a + 5)

= (a^{3} + 3 a^{2} + 5 a) + (7 a^{2} + 21 a + 35)

(∵

a^{m} \times a^{n} = a^{m + n})

= a^{3} + (3 a^{2} + 7 a^{2}) + (5 a + 21 a) + 35

= a^{3} + 10 a^{2} + 26 a + 35

इस प्रकार हम सभी प्रकार के बीजीय व्यंजकों का गुणन आसानी से कर सकते है।

उदाहरण 9

निम्नलिखित एकपदी युग्म का गुणनफल ज्ञात कीजिए :
$- 4 p,$ $7 p q$

चूंकि हम जानते है कि बीजीय व्यंजकों के गुणन के लिए बीजीय व्यंजकों के गुणांकों तथा चरों का अलग - अलग गुणा करते है अतः

$=$ $- 4 p \times$ $7 p q$

$=$ $(- 4 \times 7) \times (p \times p q)$

$=$ $(- 28) \times (p^{2} q)$ $(∵ a^{m} \times a^{n} = a^{m + n})$

$=$ $- 28 p^{2} q$

Learn more

उदाहरण 10

निम्नलिखित का गुणनफल ज्ञात कीजिए :
$2, 4 y,$ $8 y^{2}, 16 y^{3}$

$= 2 \times 4 y \times 8 y^{2} \times 16 y^{3}$

$= (2 \times 4 \times 8 \times 16) \times (y \times y^{2} \times y^{3})$

$= (64 \times 16) \times (y^{1 + 2 + 3})$ $(∵ a^{m} \times a^{n} = a^{m + n})$

$= (1024) \times (y^{6})$

$= 1024$ $y^{6}$

Learn more

सर्वसमिकाएँ

परिभाषा : ऐसी समिका जो चर के प्रत्येक मान के लिए सत्य होती है सर्वसमिका कहलाती है।

आइए इन्हे विस्तार से समझते है :-
चूंकि हमे नीचे एक समिका दी गई है।
समिका $(a + 1) (a + 2) = a^{2} + 3 a + 2$

इस समिका मे $a$ के निम्नलिखित मानों के लिए हम इसके दोनों पक्षों का मान ज्ञात करते है।
$a = 10$ के लिए
बायाँ पक्ष LHS $= (a + 1) (a + 2) = (10 + 1) (10 + 2) = 11 \times 12 = 132$

दायाँ पक्ष RHS $= a^{2} + 3 a + 2 = 10^{2} + 3 \times 10 + 2 = 100 + 30 + 2 = 132$

अतः $a = 10$ के लिए समिका के दोनों पक्षों के मान समान हैं।

$a = - 5$ के लिए
बायाँ पक्ष LHS $= (a + 1) (a + 2) = (- 5 + 1) (- 5 + 2) - (- 4) \times (- 3) = 12$

दायाँ पक्ष RHS $= a^{2} + 3 a + 2 = (- 5^{2}) + 3 (- 5) + 2$ $= 25 - 15 + 2 = 10 + 2 = 12$

अतः $a = - 5$ के लिए भी समिका के दोनों पक्षों के मान समान हैं।

अतः $a$ के किसी भी मान के लिए इस समिका का दायाँ और बायाँ पक्ष बराबर है।
अतः यह समिका एक सर्वसमिका है।

कुछ मानक सर्वसमिकाएँ

(i)

{(a + b)}^{2} = (a + b) (a + b)

= a (a + b) + b (a + b)

= a^{2} + a b + b a + b^{2}

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ सर्वसमिका $... ... .$ $(i)$

(i i)

{(a - b)}^{2} = (a - b) (a - b)

= a (a - b) - b (a - b)

= a^{2} - a b - b a + b^{2}

${(a + b)}^{2} = a^{2} - 2 a b + b^{2}$ सर्वसमिका $... ... .$ $(i i)$

(i i)

a^{2} - b^{2} = (a + b) (a - b)

= a (a - b) + b (a - b)

" "=a^2-cancel(ab)+cancel(ba)-b^2

$a^{2} - b^{2} = (a + b) (a - b)$ सर्वसमिका $... ... .$ $(i i i)$

(i v)

(x + a) (x + b) =

= x (x + b) + a (x + b)

= x^{2} + x b + a x + a b

= x^{2} + x (a + b) + a b

$(x + a) (x + b) = x^{2} + x (a + b) + a b$ सर्वसमिका $... ... .$ $(i v)$

सर्वसमिकाओं का उपयोग

उपर्युक्त सर्वसमिकाओं के उपयोग से हम द्विपद व्यंजकों के गुणन एवं संख्याओं के गुणन को आसानी से हल कर सकते है।

आइए कुछ उदाहरणों की सहायता से समझते है:-
उदाहरण : सर्वसमिका की सहायता से निम्नलिखित व्यंजक को हल कीजिए ।
${(2 x + 3 y)}^{2}$

हल :

चूंकि यह व्यंजक

{(a + b)}^{2}

सर्वसमिका का अनुशरण करता है अतः

a = 2 x

b = 3 y

{(a + b)}^{2} = a^{2} + 2 a b + b^{2}

{(2 x + 3 y)}^{2} = {(2 x)}^{2} + 2 (2 x) (3 y) + {(3 y)}^{2}

{(2 x + 3 y)}^{2} = 4 x^{2} + 12 x y + 9 y^{2}

अतः इस प्रकार हम सर्वसमिका के प्रयोग से सरलता से समिकाओं को हल कर सकते है।

OMR (One Minute Revision)

दो एकपदियों के गुणन में अचर पदों का गुणा अचर पदों से होता हैं तथा चर पदों का गुणा चर पद से होता हैं।

यदि कोई चर समान हैं तो उनकी घाते आपस में जुड़ जाती है।

द्विपद का बहुपद से गुणन मे द्विपद के प्रत्येक पद को बहुपद के प्रत्येक पद से अलग - अलग गुणा करके हल किया जाता है।

ऐसी समिका जो चर के प्रत्येक मान के लिए सत्य होती है सर्वसमिका कहलाती है।

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ सर्वसमिका $... ... .$ $(i)$

${(a + b)}^{2} = a^{2} - 2 a b + b^{2}$ सर्वसमिका $... ... .$ $(i i)$

$a^{2} - b^{2} = (a + b) (a - b)$ सर्वसमिका $... ... .$ $(i i i)$

$(x + a) (x + b) = x^{2} + x (a + b) + a b$ सर्वसमिका $... ... .$ $(i v)$

उदाहरण 11

$a = 2, b = 3, x = 5$ के लिए सर्वसमिका $a + b = x$ का सत्यापन कीजिए।

चूंकि दिया गया है :-

$a = 2$
$b = 3$
$x = 5$

सत्यापन $:$
$a + b = x$

मान रखने पर :-

$2 + 3 = 5$

$5 = 5$

$L H S = R H S$

अतः दी गई सर्वसमिका $a + b = x$ $;$ $a = 2, b = 3, x = 5$ के लिए संतुष्ट है।

Learn more

उदाहरण 12

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ का सत्यापन कीजिए।
$a = 3, b = 2$ के लिए

दिया गया है :-

$a = 3$
$b = 2$

सत्यापन $:$

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

मान रखने पर :-

${(3 + 2)}^{2} = 3^{2} + 2 \times 3 \times 2 + 2^{2}$

${(5)}^{2} = 9 + 12 + 4$

$25 = 25$

$L H S = R H S$

अतः दी गई सर्वसमिका ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ $;$ $a = 3, b = 2$ के लिए संतुष्ट है।

Learn more

उदाहरण 13

निम्नलिखित गुणनफल को प्राप्त करने के लिए उचित सर्वसमिका का उपयोग कीजिए :
$(- a + c) (- a + c)$

चूंकि हम जानते है कि योग क्रमविनिमेय होता है अतः

$\Rightarrow (c - a) (c - a)$ $= {(c - a)}^{2}$

अतः सर्वसमिका ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ का उपयोग करने पर :-

${(c - a)}^{2} = c^{2} - 2 c a + a^{2}$

अथवा

${(c - a)}^{2} = a^{2} - 2 a c + c^{2}$

Learn more

उदाहरण 14

$(a + b) (a - b) =$ $a^{2} - b^{2}$ , का उपयोग करते हुए, निम्नलिखित मान ज्ञात कीजिए :
${(51)}^{2} - {(49)}^{2}$

माना $:$
$a = 51$
$b = 49$

सर्वसमिका का उपयोग करने पर $\Rightarrow$

$a^{2} - b^{2}$ $= (a + b) (a - b)$

मान रखने पर $\Rightarrow$

${(51)}^{2} - {(49)}^{2}$ $= (51 + 49) (51 - 49)$

${(51)}^{2} - {(49)}^{2}$ $= (100) (2)$

${(51)}^{2} - {(49)}^{2}$ $= 200$

Learn more

सारांश

चरों एवं अचरों की सहायता से व्यंजक बनते हैं।

व्यंजक बनाने के लिए पदों को जोड़ा जाता है। स्वयं पदों का निर्माण गुणनखंडों के गुणनफल के रूप में होता हैं।

व्यंजक जिनमें एक, दो तथा तीन पद होते हैं क्रमश: एकपदी, द्विपदी और त्रिपदी कहलाते हैं। सामान्यतः एक अथवा अधिक पदों वाला व्यंजक जिसमें पदों के गुणांक शून्येतर हैं और चरों की घात ऋणेतर है, बहुपद कहलाता है।

समान चरों से समान पद बनते हैं, और इन चरों की घात भी समान होती है। समान पदों के गुणांक समान होने आवश्यक नहीं है।

बहुपदों को जोड़ने (अथवा घटाने) के लिए सबसे पहले समान पदों को ढूंढ़िए और उन्हें जोड़ (अथवा घटा) दीजिए, उसके पश्चात् असमान पदों को उपयोग में लीजिए।

बहुत सी परिस्थितियों में हमें बीजीय व्यंजकों को गुणा करने की आवश्यकता होती है। उदाहरणार्थ आयत का क्षेत्रफल ज्ञात करने के लिए, जिसकी भुजाएँ बीजीय व्यंजकों के रूप में दी हुई हैं।

एकपदी को एकपदी से गुणा करने पर हमेशा एकपदी प्राप्त होता है।

बहुपद को एकपदी से गुणा करने के लिए बहुपद का प्रत्येक पद को एकपदी से गुणा किया जाता है।

सर्वसमिका एक ऐसी समिका है जो चर के सभी मानों के लिए सत्य होती है, जबकि समीकरण चरों के कुछ निश्चित मानों के लिए सत्य होता है। समीकरण सर्वसमिका नहीं है।

निम्नलिखित मानक सर्वसमिकाएँ हैं :

{(a + b)}^{2} = a^{2} + 2 a b + b^{2}

{(a - b)}^{2} = a^{2} - 2 a b + b^{2}

(a + b) (a - b) = a^{2} - b^{2}

(x + a) (x + b) = x^{2} + (a + b) \cdot x + a b

एक अन्य उपयोगी सर्वसमिका है।

उपर्युक्त चार सर्वसमिकाएँ बीजीय व्यंजकों का गुणनफल ज्ञात करने में एवं वर्ग करने में सहायक हैं। ये सर्वसमिकाएँ हमें संख्याओं का गुणनफल ज्ञात करने के लिए सरल वैकल्पिक विधियाँ प्रदान करती हैं।

Home
Ask Doubt
Profile