आँकड़ों का प्रबंधन कक्षा 8 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय में हम आँकड़ों के प्रबंधन का अध्ययन करेंगे। आँकड़ों के प्रबंधन का अर्थ है - आँकड़ों को एकत्र करना और उन्हे समायोजित ढंग से प्रस्तुत करना। आँकड़ों के प्रबंधन से हमे इनके अध्ययन में सहायता मिलती है।
संख्याओं, शब्दों, मापों, प्रतीकों या किसी अन्य रूप में एकत्र की गई कोई भी जानकारी आंकड़े (Data) कहलाते है। आंकड़े, मिलान चिह्न का प्रयोग कर सारणी रूप में भी व्यवस्थित किए जा सकते हैं।
इस अध्याय मे हम आँकड़ों के आलेखीय निरूपण [ चित्र आलेख, दंड आलेख, वृत्त आलेख (पाई चार्ट) ] तथा इनके संगठन और वर्गीकरण का अध्ययन करेंगे। एवं संयोग और प्रायिकता को भी समझेंगे।
आइये जानते है, आँकड़ों के प्रबंधन को और करीब से...
हम टेलीविजन, पत्रिकाओं, समाचार-पत्रों और अन्य साधनों से विभिन्न प्रकार के आँकड़ों को देख चुके हैं। ये सभी आंकड़े हमें किसी न किसी प्रकार की सूचना अवश्य देते हैं। अतः आँकड़ों के प्रबंधन से तात्पर्य हैं कि आँकड़ों को कुछ इस तरह लिखना या व्यवस्थित करना जिससे हमे कुछ जानकारी मिल सके।
आइए एक उदाहरण से समझते हैं :-
एक कक्षा मे 10 अंकों का गणित का टेस्ट पेपर लिया गया जिसमे 15 बच्चे उपस्थित हुए और टेस्ट मे बच्चों को 6,9,8,5,6,7,8,9,5,8,5,5,8,10,7 अंक प्राप्त हुए ।
अब हम इन आँकड़ों को देखकर आसानी से निष्कर्ष नहीं निकाल सकते है क्योंकि इन आँकड़ों मे कौन से बच्चे ने कितना अच्छा प्रदर्शन किया है, इसका पता नहीं चल पा रहा हैं। अतः अब इसे हम सारणी मे लिखते हैं।
| प्राप्त अंक | बच्चों की संख्या |
|---|---|
| 10 | 1 |
| 9 | 2 |
| 8 | 4 |
| 7 | 2 |
| 6 | 2 |
| 5 | 4 |
अतः प्राप्त अंकों को सारणी मे लिखने से हम आसानी से बता सकते है कि कितने बच्चों ने कितने अंक प्राप्त किये।
जैसे :-
(i) 2 बच्चों ने 9 अंक प्राप्त किये।
(ii) 1 बच्चे ने 10 अंक प्राप्त किये।
(iii) 4 बच्चों ने 5 अंक प्राप्त किये आदि ।
इसी प्रकार आँकड़ों के प्रबंधन से और भी चीजों का पता लगाया जा सकता हैं जिसका अध्ययन हम इस अध्याय मे करेंगे।
आंकड़े
संख्याओं, शब्दों, मापों, प्रतीकों या किसी अन्य रूप में एकत्र की गई कोई भी सूचना या जानकारी आंकड़े (Data) कहलाते है।
जैसे :-
(i) पिछले 10 टेस्ट मैचों में एक बल्लेबाज द्वारा बनाए गए कुल रन।
(ii) पिछले 10 एक दिवसीय अंतर्राष्ट्रीय मैचों (ODI) में एक गेंदबाज द्वारा लिए गए कुल विकेट।
(iii) आपकी कक्षा के विद्यार्थियों द्वारा गणित के यूनिट टेस्ट में प्राप्त किए गए अंक।
(iv) आपके मित्रों में से प्रत्येक द्वारा पढ़ी गई पुस्तकों की संख्या, इत्यादि।
इन सभी स्थितियों में एकत्रित की गई सूचनाएँ आंकड़े (Data) कहलाते हैं।
आंकड़े प्रायः एक ऐसी स्थिति के संदर्भ में एकत्रित किए जाते हैं जिसका हम अध्ययन करना चाहते हैं।
उदाहरणार्थ :-
एक अध्यापिका की अपनी कक्षा के विद्यार्थियों की औसत ऊँचाई जानने में रुचि हो सकती है। इसे ज्ञात करने के लिए, वह अपनी कक्षा के सभी विद्यार्थियों की ऊँचाइयाँ लिखेगी तथा इन आँकड़ों को एक क्रमबद्ध रूप से संगठित करेगी और तदनुसार उनकी व्याख्या करेगी।
उदाहरण 1
ऐसे कोई 5 आँकड़ों के उदाहरण लिखिए जिन्हे आप दैनिक जीवन मे एकत्रित कर सकते है।
5 उदाहरण निम्न प्रकार है :-
(i) अपनी कक्षा के विद्यार्थियों की संख्याओं के आंकड़े।
(ii) अपने स्कूल मे पंखों की संख्याओं के आंकड़े।
(iii) समाचार पत्रों मे प्राप्त चुनावों के परिणामों के आंकड़े।
(iv) शैक्षिक सर्वेक्षणों मे प्राप्त साक्षरता के आंकड़े।
(v) पिछले 2 वर्षों मे घर की बिजली के बिल के आंकड़े।
आँकड़ों का आलेखीय निरूपण
कभी-कभी आँकड़ों को यह सुस्पष्ट करने के लिए कि वे क्या निरूपित करते हैं, आलेखीय रूप से (Graphically) निरूपित किया जाता है। इससे हम आँकड़ों का सरलता से निष्कर्ष निकाल सकते है।
आँकड़ों का आलेखीय निरूपण 3 प्रकार से होता है :-
(i) चित्र आलेख [ Picto Graph ]
(ii) एक - दंड आलेख [ bar Graph ]
(iii) द्वि - दंड आलेख [ Double Bar Graph ]
(i) चित्र आलेख [ Picto Graph ] : जब हम चित्रों या प्रतीकों के माध्यम से आँकड़ों का निरूपण करते है, तो इसे चित्र आलेख कहते है।
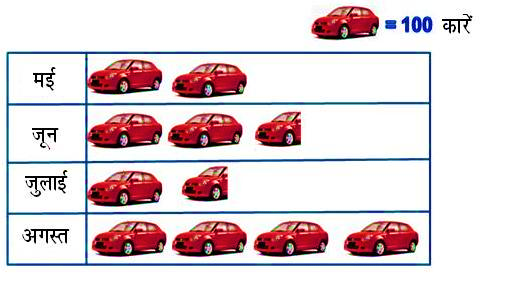
यहाँ चित्र मे 1 कार = 100 कारों को निरूपित करती है।
इसमे एक तरफ महीने लिख रखे है तथा दूसरी तरफ उस महीने मे कारों का उत्पादन लिखा हुआ है।
चित्र की सहायता से हम सरलता से बता सकते है की किस महीने मे कितना उत्पादन हुआ है। जैसे :-
(i) सबसे अधिक उत्पादन अगस्त माह मे हुआ है। [ 400 कार ]
(ii) जून माह मे 250 कारों का उत्पादन हुआ है ।
इस प्रकार हम इस चित्र से संबंधित सभी सवालों का उत्तर सरलता से दे सकते है।
(ii) एक - दंड आलेख [ bar Graph ] : एक समान चौड़ाई के दंडों का प्रयोग करते हुए, सूचना का प्रदर्शन करना एक - दंड आलेख कहलाता है।
जिसमें दंडों की लंबाइयाँ (ऊँचाइयाँ) क्रमशः उनके मानों के समानुपातिक होती हैं।
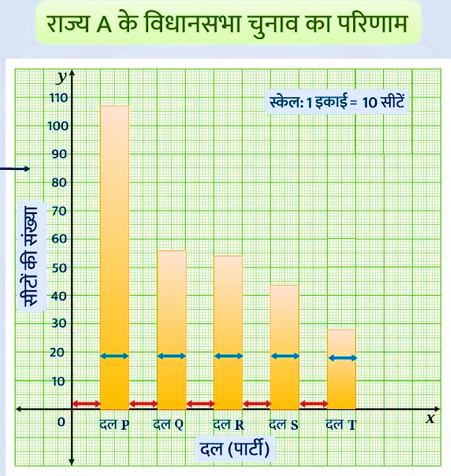
- दंड की लंबाई प्रत्येक दल की प्राप्त सीटों को दर्शाती है।
- दंड समान चौड़ाई के हैं और दो क्रमागत दंडों के बीच में भी समान दूरी रखी गई है।
इस दंड आलेख की सहायता से हम निम्न प्रश्नों का उत्तर सरलता से दे सकते है :-
प्रश्न : किस दल ने सर्वाधिक सीटें प्राप्त की ?
उत्तर : P दल मे सर्वाधिक सीटें (107) प्राप्त की ।
प्रश्न : दल Q ने कितनी सीटें प्राप्त की ?
उत्तर : 55 सीटें प्राप्त की।
प्रश्न : दल R और दल S मे से किसने अधिक सीटें प्राप्त की ?
उत्तर : दल R ने अधिक सीटें प्राप्त की ।
इस प्रकार आंकड़ो के आलेखीय निरूपण का यह तरीका भी काफी सरल होता है।
(iii) द्वि - दंड आलेख [ Double Bar Graph ] : आँकड़ों के दो समूहों को एक साथ दर्शाने वाला दंड आलेख द्वि - दंड आलेख कहलाता है।
हम आँकड़ों की तुलना करने के लिए द्वि - दंड आलेख का उपयोग कर सकते है क्योंकि यह एक साथ दो मात्राओं ( सूचनाओं ) की जानकारी देता है।
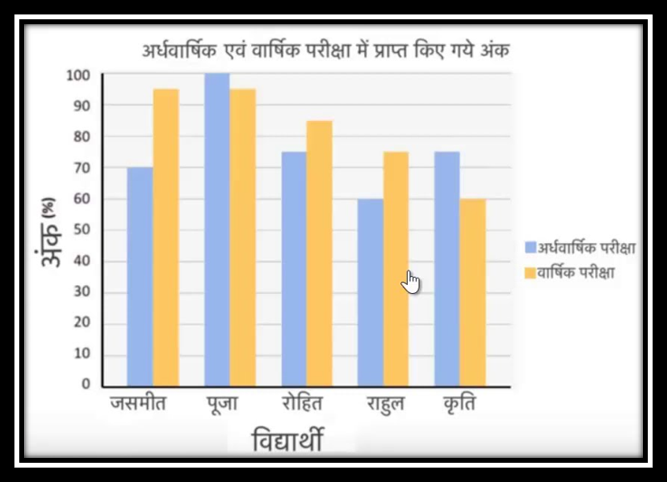
उपर्युक्त आलेख मे दो दंड दर्शाये गए है जिसमे नीला दंड अर्द्धवार्षिक परीक्षा को तथा पीला दंड वार्षिक परीक्षा को निरूपित करता है।
इस द्वि - दंड आलेख की सहायता से हम निम्न प्रश्नों का उत्तर सरलता से दे सकते है :-
प्रश्न : रोहित मे अर्द्धवार्षिक परीक्षा से वार्षिक परीक्षा मे कितने प्रतिशत अंकों का सुधार किया ?
उत्तर : रोहित मे अर्द्धवार्षिक परीक्षा से वार्षिक परीक्षा मे 10% अंकों का सुधार किया।
प्रश्न : कितने बच्चों ने अर्द्धवार्षिक परीक्षा से वार्षिक परीक्षा मे अपने अंकों मे सुधार किया ?
उत्तर : 3 बच्चों ( जसमीत, रोहित और राहुल ) ने सुधार किया।
अतः इस द्वि - दंड आलेख की सहायता से हम दो आँकड़ों की तुलना बड़ी सरलता से कर सकते है।
उदाहरण 2
दिए गए दंड आलेख की सहायता से निम्नलिखित प्रश्नों का उत्तर दीजिए।
(i) कौन-सा पालतू पशु अधिक लोकप्रिय है ?
(ii) कितने विद्यार्थियों का पालतू पशु कुत्ता है ?
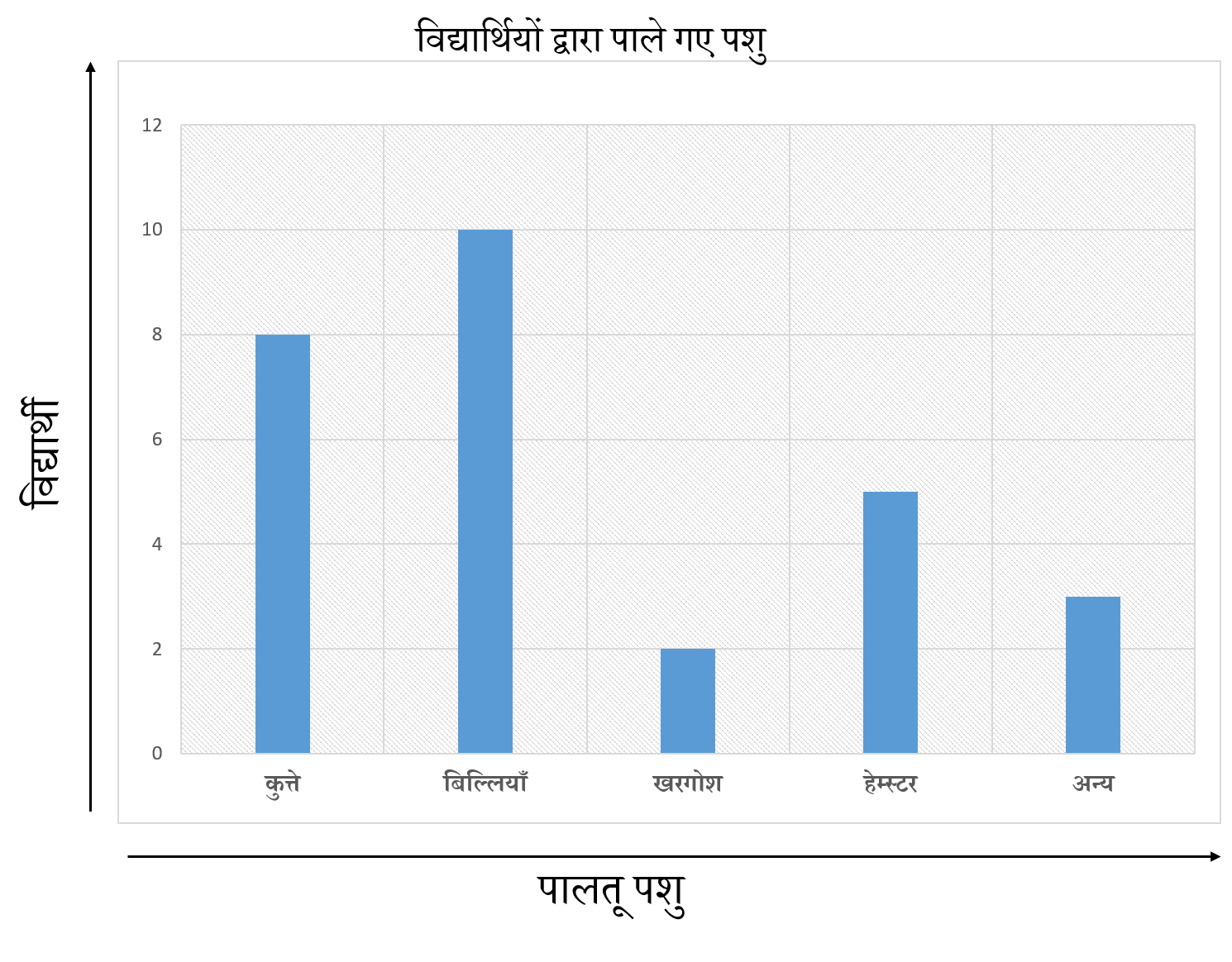
(i) स्पष्ट हैं की बिल्लियों का दंड आलेख सबसे बड़ा हैं जो की 10 विद्यार्थियों के पास हैं। अतः बिल्ली सबसे ज्यादा लोकप्रिय पशु हैं।
(ii) दंड आलेख में देख सकते हैं की कुल 8 विद्यार्थी हैं जिनका पालतू पशु कुत्ता हैं।
उदाहरण 3
एक विद्यार्थी के प्रथम सत्र और द्वितीय सत्र का प्रदर्शन दिया हुआ है । एक उपयुक्त स्केल चुनकर एक दोहरा दंड आलेख खीचिए और दिए गए प्रश्नों के उत्तर दीजिए :-
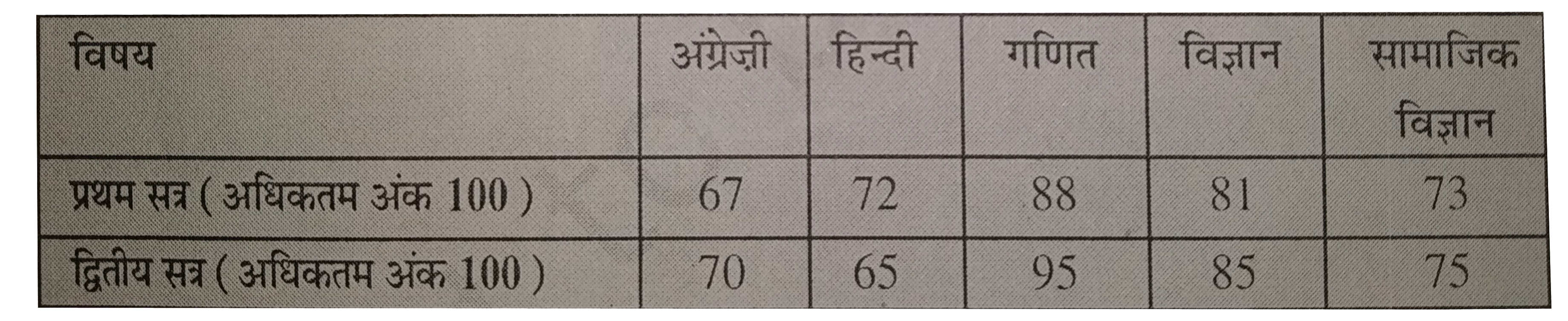
(i) किस विषय में विद्यार्थी ने अपने प्रदर्शन में सबसे अधिक सुधार किया है ?
(ii) किस विषय में सुधार सबसे कम है ?
(iii) क्या किसी विषय में प्रदर्शन नीचे गिरा है ?
दिए गए आँकड़ों को दंड आलेख मे व्यक्त करते हैं,
सर्वप्रथम दो अक्ष बना लेते हैं X अक्ष (क्षैतिज रेखा) और Y अक्ष (ऊर्ध्वाधर रेखा ), X अक्ष में विषय को और Y अक्ष में अंक को दर्शाते हैं।
Y अक्ष मे एक स्केल लेते हैं, 1 cm =10 अंक और 0 से 100 तक के अंक को Y अक्ष मे दर्शाते हैं।
प्रथम सत्र के लिए नीले रंग का दंड आलेख का तथा द्वितीय सत्र के लिए नारंगी रंग का दंड आलेख बनाते हैं।
जैसे; प्रथम सत्र में अंग्रेजी का प्रदर्शन 67 अंक और द्वितीय सत्र में 70 अंक हैं, अतः अंग्रेजी विषय पर 6.7 cm का प्रथम सत्र के लिए नीले रंग का दंड आलेख तथा 7.0 cm का द्वितीय सत्र के लिए नारंगी रंग का दंड आलेख बनाते हैं।
इसी प्रकार, हिन्दी, गणित, विज्ञान और सामाजिक विज्ञान सभी विषयों पर दंड आलेख बनाते हैं जिसे आकृति में देख सकते हैं।
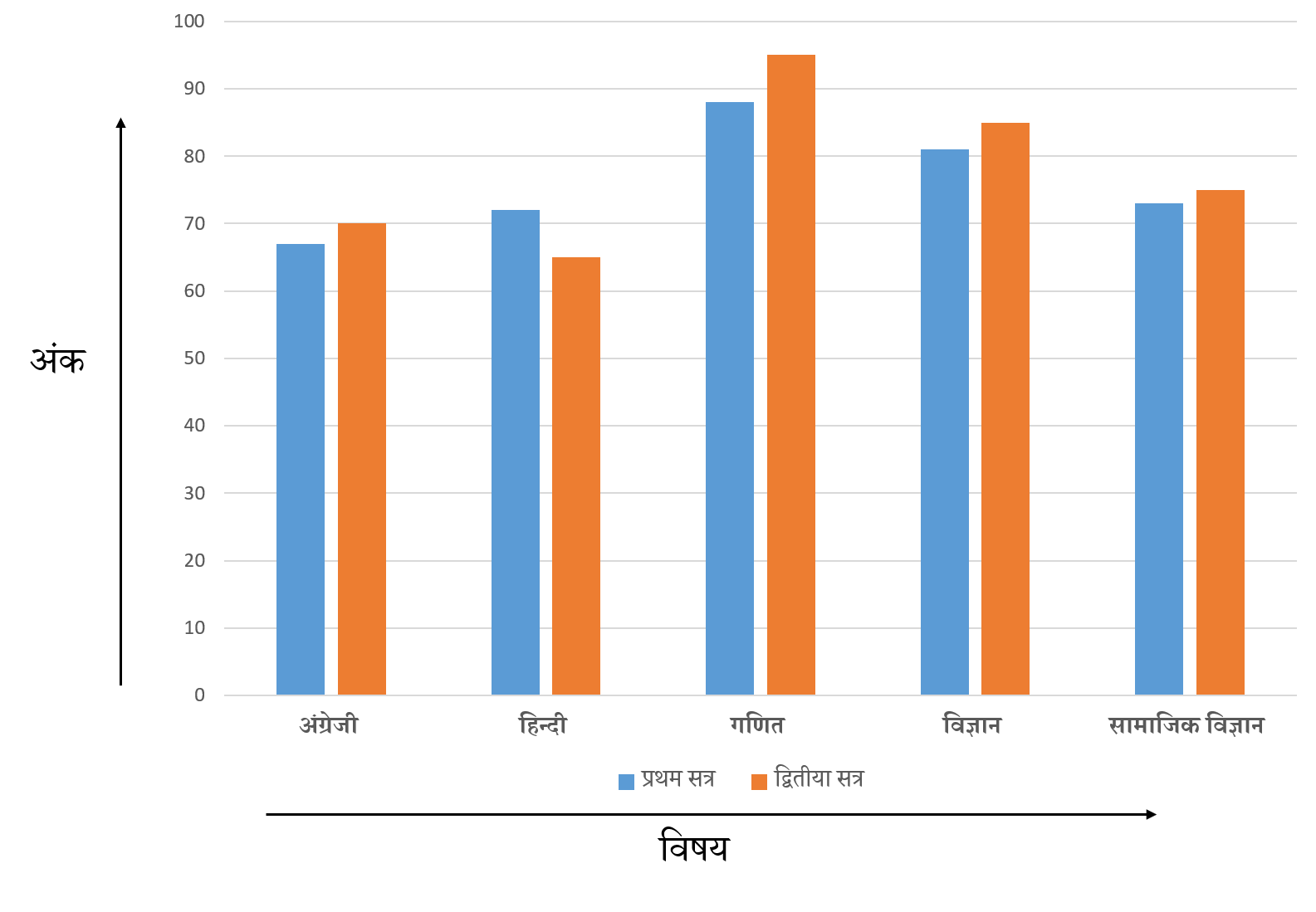
अतः स्पष्ट है की
अंग्रेजी, गणित, विज्ञान और सामाजिक विज्ञान मे सुधार हुआ है क्योंकि इनके द्वितीय सत्र का दंड आलेख प्रथम सत्र के दंड आलेख से बडा हैं। इसके विपरीत हिन्दी मे प्रथम सत्र का दंड आलेख द्वितीय सत्र के दंड आलेख से बडा हैं अतः हिन्दी मे प्रदर्शन नीचे गिरा हैं अतः
अंग्रेजी मे सुधार ⇒ द्वितीय सत्र मे प्राप्त अंक − प्रथम सत्र मे प्राप्त अंक =70−67=3
गणित मे सुधार ⇒ द्वितीय सत्र मे प्राप्त अंक − प्रथम सत्र मे प्राप्त अंक =95−88=7
विज्ञान मे सुधार ⇒ द्वितीय सत्र मे प्राप्त अंक − प्रथम सत्र मे प्राप्त अंक =85−81=4
सामाजिक विज्ञान मे सुधार ⇒ द्वितीय सत्र मे प्राप्त अंक − प्रथम सत्र मे प्राप्त अंक =75−73=2
(i) अतः सबसे अधिक सुधार गणित मे 7 अंकों का हुआ हैं।
(ii) सबसे कम सुधार सामाजिक विज्ञान मे 2 अंकों का हुआ हैं।
(iii) हाँ, हिन्दी मे प्रदर्शन 7 अंकों से नीचे गिरा है।
आँकड़ों का संगठन
असंगठित रूप में प्राप्त आंकड़े यथाप्राप्त आंकड़े (Raw Data) कहलाते है। इन आँकड़ों से हम अर्थपूर्ण निष्कर्ष प्राप्त नहीं कर सकते है।
अतः अर्थपूर्ण निष्कर्ष निकालने के लिए, हमें इन आँकड़ों को एक क्रमबद्ध रूप में संगठित करने की आवश्यकता होती है।
उदाहरणार्थ :- विद्यार्थियों के एक समूह से उनके मनपसंद विषयों के बारे में पूछा गया।
इसके परिणामों की सूची निम्न प्रकार है :-
कला, गणित, विज्ञान, अंग्रेजी, गणित, कला, अंग्रेजी, गणित, अंग्रेजी, कला, विज्ञान, कला, विज्ञान, विज्ञान, गणित, कला, अंग्रेजी, कला, विज्ञान, गणित, विज्ञान, कला।
प्रश्न : कौन - सा विषय सबसे अधिक पसंद किया गया और कौन - सा विषय सबसे कम पसंद किया गया ?
उपर्युक्त परिणामों से हम इस प्रश्न का उत्तर सरलता से नहीं दे सकते है।
अतः सरलता से प्रश्नों का उत्तर देने के लिए हम बारंबारता ( मिलान चिह्न ) का प्रयोग करते है।
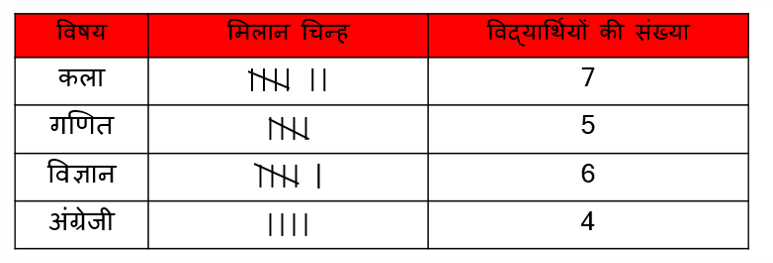
अतः अब हम सारणी की मदद से देख सकते हैं कि कौनसा विषय अधिक पसंद किया गया है और कौनसा सबसे कम ।
प्रत्येक विषय के सम्मुख लिखी मिलान चिह्नों की संख्या से हम विशिष्ट विषय को पसंद करने वाले विद्यार्थियों की संख्या प्राप्त कर सकते हैं।
यह संख्या उस विषय की बारंबारता (frequency) कहलाती है अर्थात मिलान चिह्नों को ही बारंबारता कहते है।
जैसे :-
अंग्रेज़ी को पसंद करने वाले विद्यार्थियों की बारंबारता 4 है।
गणित को पसंद करने वाले विद्यार्थियों की बारंबारता 5 है।
उपरोक्त रूप से बनाई गई सारणी एक बारंबारता बंटन सारणी (frequency distribution table) कहलाती है, क्योंकि इससे पता चलता है कि एक प्रविष्टि कितनी बार दोहराई गई है।
अतः आँकड़ों के इस तरह संगठन से हम सरलता से बता सकते है की कला विषय सबसे अधिक ( 7 विद्यार्थियों ने ) पसंद किया गया और अंग्रेजी विषय सबसे कम ( 4 विद्यार्थियों ने ) पसंद किया गया।
OMR (One Minute Revision)
उदाहरण 4
किसी विभागीय स्टोर पर खरीददारी करने के लिए आए व्यक्तियों को इस प्रकार अंकित किया जाता है - पुरुष (M), महिला (W), लड़का (B) या लड़की (G)
निम्नलिखित सूची उन खरीददारों को दर्शाती है, जो प्रातःकाल पहले घण्टे में आए हैं-
W,W,W,G,B,W,W,M,G,G,M,M,W,W,W,W,G,B,M,W,B,G,G,M,W,W,M,M,W,W,W,M,W,B,W,G,M
मिलान चिह्नों का प्रयोग करते हुए एक बारम्बारता बंटन सारणी बनाइए तथा निम्न प्रश्नों का उत्तर दीजिए :-
(i) स्टोर पर प्रातःकाल सबसे अधिक खरीददारी किसने की ?
(ii) स्टोर पर प्रातःकाल आने वाले लड़के व लड़कियों की संख्या मे से किसकी संख्या अधिक है तथा इनका अंतर भी ज्ञात कीजिए ।
हम जानते है कि दिए गए आंकड़े यथाप्राप्त आंकड़े है। इनके माध्यम से हम किसी भी प्रश्न का सटीक उत्तर नहीं दे सकते है। अतः इन्हे बारंबारता बंटन सारणी मे निरूपित करते है।
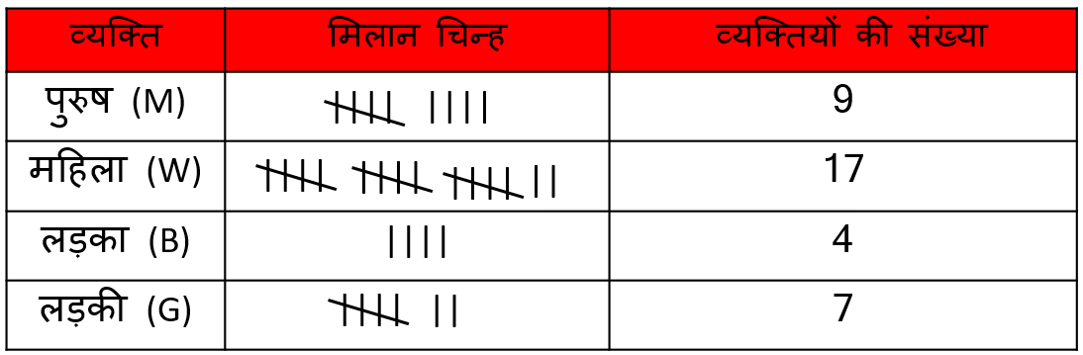
(i) स्टोर पर प्रातःकाल सबसे अधिक खरीददारी महिलाओं (Women) ने की जिनकी संख्या 17 है।
(ii) लड़के और लड़कियों की संख्या मे से लड़कियों की संख्या ज्यादा है क्योंकि प्रातःकाल स्टोर पर लड़के केवल 4 ही आए थे जबकि लड़कियाँ 7 आई थी।
इनका अंतर 7−4=3 है।
आँकड़ों का वर्गीकरण
जब हमारे पास बड़ी संख्या में मात्राएँ होती है तो इस स्थिति मे हमें प्रेक्षणों को समूहीकृत करके तालिका बनाने की आवश्यकता होती है। ऐसी तालिका को समूहीकृत बारंबारता वितरण तालिका कहा जाता है।
इस वितरण तालिका को ही वर्गीकृत आंकड़े कहते है।
उदाहरणार्थ :-
कक्षा VIII के 60 विद्यार्थियों द्वारा गणित में प्राप्त किए गए ( 50 में से ) निम्नलिखित अंकों पर विचार कीजिए :-
21,10,30,22,33,5,37,12,25,42,15,39,26,32,18,27,28,19,29,35,31,24,36,18,20,38,22,44,16,24,10,27,39,28,49,29,32,23,31,21,34,22,23,36,24,36,33,47,48,50,39,20,7,16,36,45,47,30,22,17
इस स्थिति मे हम यदि प्रत्येक प्रेक्षण के लिए एक बारंबारता बंटन सारणी बनाऐगे, तो वह बहुत लंबी हो जायेंगी। इसलिए हम सुविधा के लिए इन प्रेक्षणों के कुछ समूह या वर्ग बनाते हैं, ( जैसे :- 0−10,10−20 इत्यादि ) फिर प्रत्येक समूह या वर्ग में आने वाले प्रेक्षणों की संख्या के आधार पर एक बारंबारता बंटन (Frequency Distribution) प्राप्त करते हैं।
आइये इन प्रेक्षणों के लिए एक बारंबारता बंटन सारणी बनाते है :-
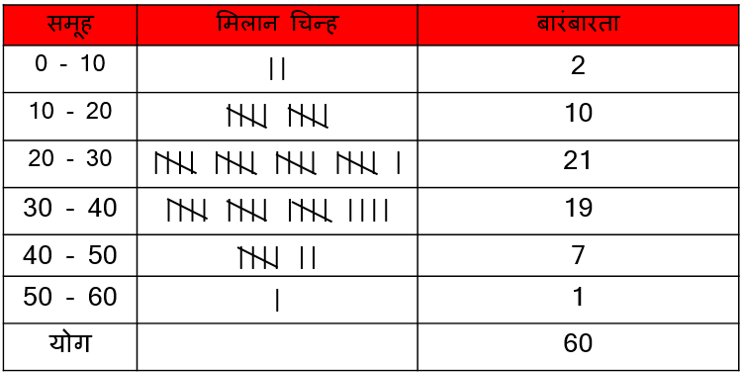
उपर्युक्त प्रकार से व्यवस्थित आँकड़े वर्गीकृत आँकड़े (Grouped Data) कहलाते हैं तथा प्राप्त बंटन वर्गीकृत बारंबारता बंटन कहलाता है।
इससे हम आसानी से अर्थपूर्ण निष्कर्ष निकाल सकते है, जैसे :-
(i) अधिकांश विद्यार्थियों ने 20 और 40 के बीच अंक प्राप्त किए हैं।
(ii) 8 विद्यार्थियों ने 50 में से 40 से अधिक अंक प्राप्त किए हैं।
वर्गीकृत बारंबारता बंटन से संबंधित कुछ महत्वपूर्ण तथ्य :-
(i) वर्ग - अंतराल या वर्ग : जब सभी अवलोकनों को उनके आकार के अनुसार कई समूहों में वर्गीकृत किया जाता है तो ये समूह वर्ग - अंतराल ( वर्ग ) कहलाते है। जैसे :-
⇒(0−10) या (10−20) या (20−30) इत्यादि ये सभी वर्ग अंतराल है।
(ii) निम्न - वर्ग सीमा : प्रत्येक वर्ग अंतराल में सबसे कम मान वाली संख्या, निम्न-वर्ग सीमा कहलाती है। जैसे :-
⇒ वर्ग अंतराल (10−20) में 10 निम्न - वर्ग सीमा ( Lower Class Limit ) कहलाती है।
(iii) उच्च - वर्ग सीमा : प्रत्येक वर्ग अंतराल में सबसे अधिक मान वाली संख्या उच्च - वर्ग सीमा कहलाती है। जैसे :-
⇒ वर्ग अंतराल (10−20) में 20 उच्च - वर्ग सीमा ( Upper Class Limit ) कहलाती है।
(iv) वर्ग अंतराल की चौड़ाई : उच्च वर्ग सीमा और निम्न वर्ग सीमा के बीच के अंतर को वर्ग अंतराल की चौड़ाई या माप (Size) कहते है। जैसे :-
⇒(0−10) या (10−20) या (20−30) इत्यादि सभी वर्ग अंतरालों मे उच्च वर्ग सीमा और निम्न वर्ग सीमा का अंतर बराबर है अर्थात 10 है अतः इस वर्ग अंतराल की चौड़ाई 10 होगी।
Note :-
प्रेक्षण 10 दोनों वर्गों (0−10) और (10−20) में सम्मिलित है। इसी प्रकार 20 भी दोनों वर्गों (10−20) और (20−30) में सम्मिलित है।
परंतु एक प्रेक्षण (10 या 20) दो वर्गों में एक साथ सम्मिलित नहीं हो सकता है अतः इस स्थिति से बचने के लिए, हम एक परिपाटी अपनाते हैं जिसमे उभयनिष्ठ प्रेक्षण को हमेशा उच्चतर वर्ग में सम्मिलित किया जाता है अर्थात प्रेक्षण 10 केवल वर्ग अंतराल (10−20) में सम्मिलित होगा (0−10) में नहीं। अतः इसी प्रकार अन्य सभी अंतराल मे करेंगे ।
आयतचित्र
समान चौड़ाई वाले दंड जिनके बीच में कोई रिक्तता नहीं होती है, आयतचित्र (Histogram) कहलाता है।इसमे दंड की लंबाई एक विशिष्ट समूह या वर्ग में आने वाले प्रेक्षणों की संख्या दर्शाती है और यही उस वर्ग की बारंबारता होती है।
आइये इसे निम्न आलेख से समझते है :-
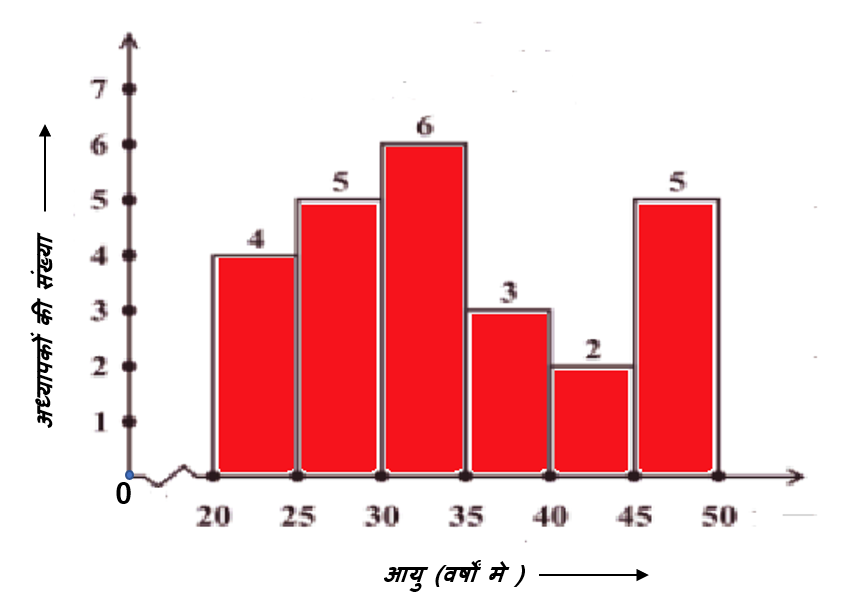
इस दंड आलेख मे दंड एक स्कूल के 25 अध्यापकों की आयु को प्रदर्शित कर रहे है।
इस आलेख मे प्रारंभ मे वह टेढ़ी - मेढ़ी रेखा क्षैतिज अक्ष के अनुदिश यह दर्शाने के लिए प्रयोग की गई है कि हम 0 से 20 तक की संख्याएँ प्रदर्शित नहीं कर रहे हैं।
इस आयतचित्र के दंडों से हम निम्नलिखित प्रश्नों के उत्तर सरलता से दे सकते हैं :
(i) कितने अध्यापकों की आयु 45 वर्ष या उससे अधिक है परंतु 50 वर्ष से कम है ?
उत्तर : कुल 5 अध्यापक है, क्योंकि इसमे केवल 45 से 50 वर्ष की आयु वाले अध्यापक आएगे।
(ii) 35 वर्ष से कम आयु वाले अध्यापकों की संख्या कितनी है ?
उत्तर : कुल 15 अध्यापक है, क्योंकि इसमे 20 से 35 वर्ष तक आयु वाले सभी अध्यापक आएगे।
उदाहरण 5
निम्नलिखित बारंबारता बंटन सारणी का अध्ययन कीजिए और उसके नीचे दिए हुए प्रश्नो के उत्तर दीजिये :-
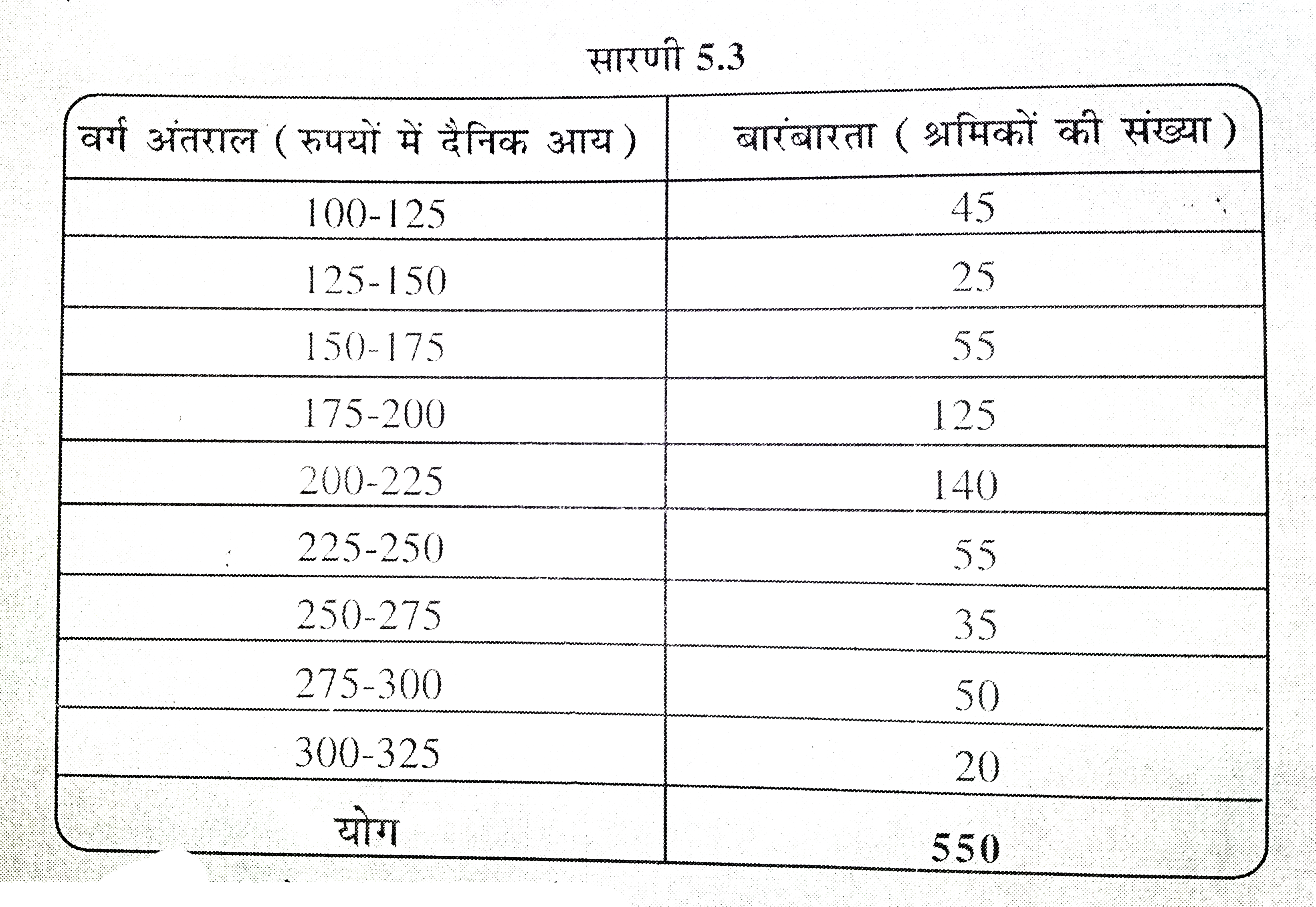
(i) वर्ग अंतरालों की माप क्या है ?
(ii) किस वर्ग के सबसे अधिक बारंबारता है ?
(iii) किस वर्ग के सबसे कम बारंबारता है ?
(iv) वर्ग अंतराल (250−275) की उच्च सीमा क्या है ?
(v) किन दो वर्गों की बारंबारता एक ही है ?
(i) वर्ग अंतरालों की माप = उच्च वर्ग सीमा और निम्न वर्ग सीमा के बीच के अंतर को वर्ग अंतराल की चौड़ाई या माप (Size) कहलाती है।
चूंकि (100 - 125) या (125 - 150) या (150 -175) इत्यादि सभी वर्ग अंतरालों मे उच्च वर्ग सीमा और निम्न वर्ग सीमा का अंतर बराबर है अर्थात 25 है।
अतः इस वर्ग अंतराल की माप 25 होगी।
(ii) सर्वाधिक बारंबारता = वर्ग अंतराल (200 - 225) की बारंबारता सर्वाधिक , 140 है।
(iii) सबसे कम बारंबारता = वर्ग अंतराल (300 - 225) की बारंबारता सबसे कम, 20 है।
(iv) वर्ग अंतराल (250 - 275) की उच्च सीमा = 275
(v) वर्ग अंतराल (150 - 175) और (225 - 250) की बारंबारता एक ही है अर्थात 55 है।
उदाहरण 6
नीचे एक आयत-चित्र द्वारा किसी कक्षा के छात्रों के प्राप्तांक दर्शाये गये हैं

किस प्राप्तांक-वर्ग वाले छात्रों की संख्या अधिकतम हैं और किस प्राप्तांक-वर्ग वाले छात्रों की संख्या निम्नतम हैं ?
अधिकतम छात्रों की संख्या वाला प्राप्तांक वर्ग =60−70
निम्नतम छात्रों की संख्या वाला प्राप्तांक वर्ग =20−30
वृत्त आलेख (पाई चार्ट)
बच्चों! अब तक हमने आँकड़ों का केवल दंड आलेखों के रूप मे अध्ययन किया है। अब हम आँकड़ों का वृत्त के रूप मे अध्ययन करेंगे।
जब हम आँकड़ों को वृत्त के रूप में निरूपित करते हैं तो इसे वृत्त आलेख ( Circle Graph ) कहा जाता है।
यह ग्राफ पूरे वृत्त और उसके हिस्सों के बीच के संबंधों को दर्शाता है। इसके लिए हम वृत्त को त्रिज्यखंडों में विभाजित करते है। प्रत्येक त्रिज्यखंड अपनी संबंधित गतिविधि के समानुपाती होता है।
इसका प्रयोग उस स्थिति मे करते है जब हमे प्रतिशत या भिन्न की जानकारी प्राप्त होती है।
आइये एक उदाहरण से समझते है :-
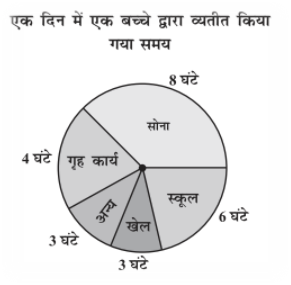
उपर्युक्त वृत्त मे एक बच्चे द्वारा एक दिन मे व्यतीत किए गए समय का विवरण दिया गया है।
इस आलेख में सोने की क्रिया में 8 घंटे व्यतीत किए है। हम इसका पूरे वृत्त से आनुपातिक भाग निम्न प्रकार ज्ञात कर सकते है :-
आनुपातिक भाग =
=
=13 (भाग )
इसीलिए, इस त्रिज्यखंड को ( सोने वाले घंटों को ) वृत्त के 13 भाग के रूप में खींचा गया है। इसी प्रकार अन्य त्रिज्यखंडों की माप भी ज्ञात कर सकते हैं।
पाई चार्ट बनाना
वृत्त आलेख पाई चार्ट ( Pie Chart ) भी कहलाता है।
आइये एक उदाहरण से समझते है :-
आइसक्रीमों की महक या स्वाद को पसंद करने वाले किसी स्कूल के विद्यार्थियों का विवरण ( प्रतिशतों में ) निम्न सारणी मे दिया गया है :-
| महक | महकों को पसंद करने वाले विद्यार्थियों का प्रतिशत |
|---|---|
| चॉकलेट | 50% |
| वनीला | 25% |
| अन्य प्रकार | 25% |
अब इन आँकड़ों को एक पाई चार्ट के रूप में व्यवस्थित करते है।
चूंकि हम जानते है की वृत्त के केंद्र पर पूरा कोण 360° का होता है। अतः इन त्रिज्यखंडो के केंद्रीय कोण (Central Angles) 360° के भाग होंगे।
अतः अब इन त्रिज्यखंडों के केन्द्रीय कोणों को ज्ञात करने के लिए एक सारणी बनाते है :-
| महक | महक को पसंद करने वाले विद्यार्थियों का प्रतिशत | सम्पूर्ण भाग | केन्द्रीय कोण |
|---|---|---|---|
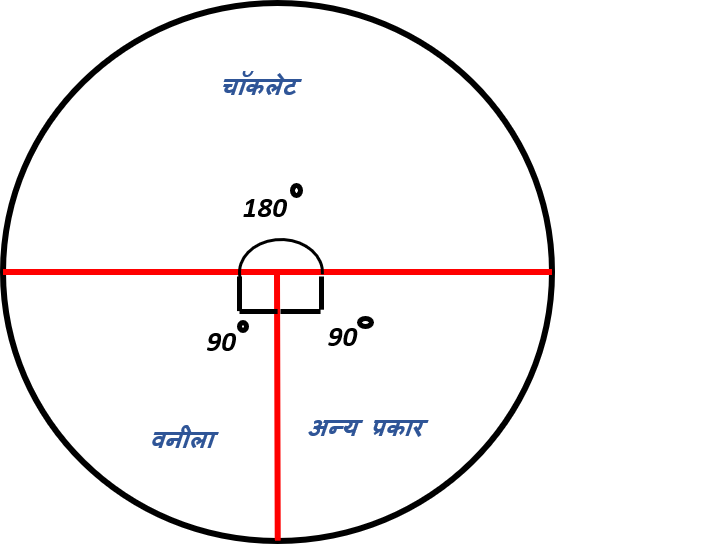
| चॉकलेट | 50% | 50100=12 | 360∘ का 12=180∘ |
| वनीला | 25% | 25100=14 | 360∘ का 14=90∘ |
| अन्य प्रकार | 25% | 25100=14 | 360∘ का 14=90∘ |
उपर्युक्त सारणी से हम सरलता से बता सकते है की :-
विद्यार्थी सबसे अधिक चॉकलेट की महक पसंद करते है क्योंकि चॉकलेट का केन्द्रीय कोण का मान सबसे अधिक है।
चूंकि जिसका केन्द्रीय कोण का मान सबसे अधिक होता है उसकी मात्रा भी सबसे अधिक होती है।
हम उपर्युक्त सारणी को वृत्त के माध्यम से भी दर्शा सकते है।
आइये कुछ और उदाहरणों से समझते है -
उदाहरण 7
1080 छात्रों द्वारा स्कूल जाने के विभिन्न साधनों का आँकड़ा निम्नलिखित है -

इन आँकड़ों को एक पाई चार्ट के द्वारा निरूपित कीजिए।
चूंकि हम जानते है की पाई चार्ट को वृत्त आलेख भी कहते है अतः दिए गए आँकड़ों को पाई चार्ट मे प्रदर्शित करने के लिए आँकड़ों का वृत्त के अंदर अंशीय कोण ज्ञात करना होगा।
वृत्त का पूर्ण कोण 360∘ का होता है। अतः छात्रों की संख्या को वृत्त मे प्रदर्शित करने के लिए पहले एक छात्र द्वारा घेरा गया अंशीय कोण ज्ञात करते है। हमे सभी छात्रों को वृत्त (पाई चार्ट) मे प्रदर्शित करना है। अतः
चूंकि कुल छात्र =1080
वृत्त का पूर्ण कोण =360∘
कुल छात्र = वृत्त का पूर्ण कोण
1080 छात्र =360∘
1 छात्र =360∘1080
1 छात्र =(13)∘
अतः एक छात्र द्वारा वृत्त का (13)∘ भाग घेरा जाता है। अब हम भिन्न - भिन्न साधनों से जाने वाले सभी बच्चों का अंशीय कोण ज्ञात करेंगे ।
(i) बस द्वारा जाने वाले बच्चों का अंशीय कोण =
= बस द्वारा जाने वाले कुल छात्र × 1 छात्र द्वारा घेरा गया कोण
= 360×(13)∘
=120∘
(ii) साइकिल द्वारा जाने वाले बच्चों का अंशीय कोण =
=180×(13)∘
=60∘
(iii) ट्रेन द्वारा जाने वाले बच्चों का अंशीय कोण =
=315×(13)∘
=105∘
(iv) गाड़ी द्वारा जाने वाले बच्चों का अंशीय कोण =
=90×(13)∘
=30∘
(v) पैदल जाने वाले बच्चों का अंशीय कोण =
=135×(13)∘
=45∘
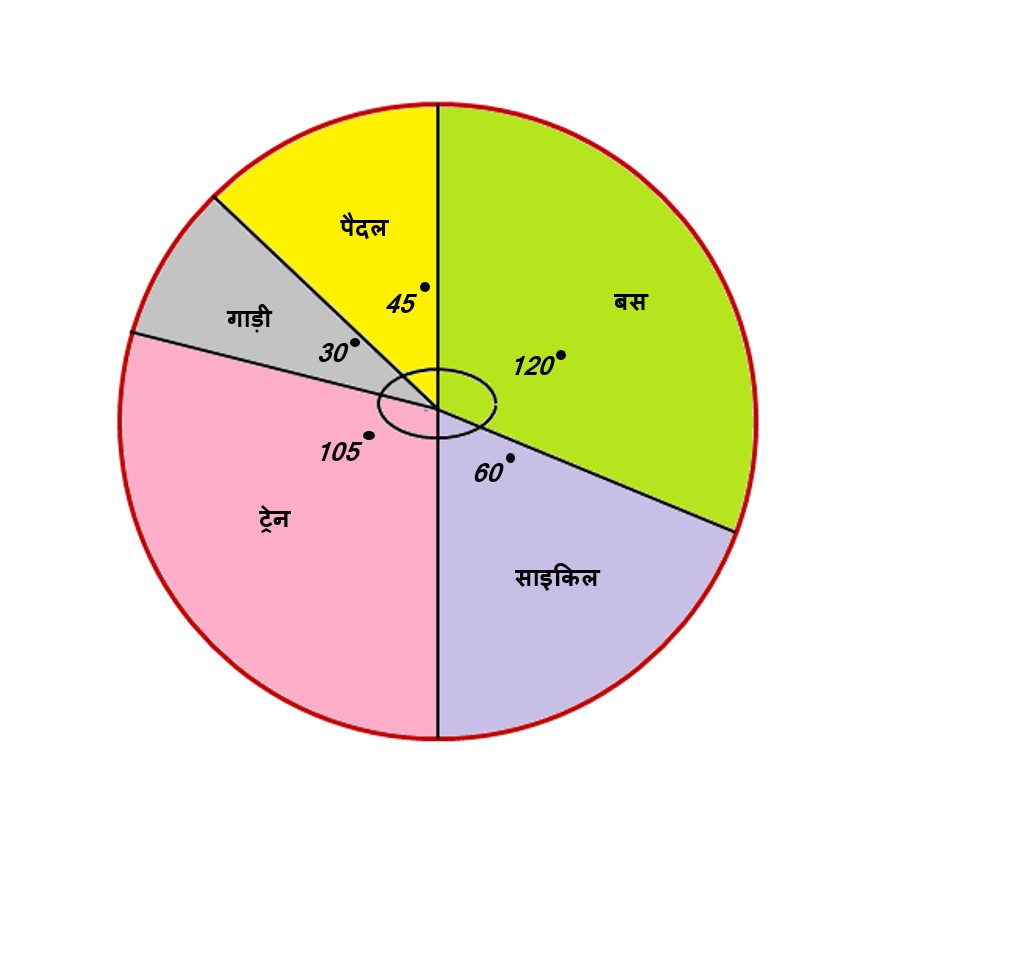
सभी अंशीय कोणों का योग =120∘+60∘+105∘+30∘+45∘=360∘
अतः अब हम इन्हे सरलता से वृत्तीय कोण अर्थात पाई चार्ट मे दर्शा सकते है।
संयोग और प्रायिकता
संयोग और प्रायिकता मे अंतर
इसे हम निम्न उदाहरण से समझ सकते हैं -जैसे :- आपने परीक्षा के लिए 5 मे से 4 अध्याय का अध्ययन किया लेकिन परीक्षा मे उस अध्याय मे से प्रश्न आता हैं जिसका आपने अध्ययन नहीं किया है तो उस अध्याय मे से प्रश्न का आना एक संयोग मात्र हैं।
अन्य उदाहरण :-

आकृति से पता चलता है कि,
अर्थात चित (Head) और पट (Tail) दोनों के आने के बराबर मौके है।
वे प्रयोग जिनका परिणाम ज्ञात नहीं होता है तो वे प्रयोग यादृच्छिक प्रयोग कहलाते है।
जब हम कोई प्रयोग करते हैं तो उसके अलग-अलग परिणाम हो सकते हैं, इन यादृच्छिक प्रयोग की कुल संभावनाओं को उस प्रयोग की प्रायिकता कहते हैं।
प्रायिकता गणित की वह शाखा हैं जिसमे गणितीय संक्रियाओं के द्वारा किसी घटना के होने या ना होने की कितनी संभावना (chance) हैं, निकाल सकते हैं।
जब हम किसी सिक्के को उछालते हैं, तो हम जानते है कि इसके दो संभव परिणाम चित या पट है। साथ ही एक पासे को फेंकने पर 6 संभव परिणाम है। साथ ही हम यह भी जानते हैं कि एक सिक्के के लिए, चित या पट का प्राप्त करना एक समान रूप से संभावित घटना है अर्थात
चित आने की प्रायिकता (probability) 12 है तथा पट आने की प्रायिकता भी 12 है।
समान रूप से संभावित परिणाम
यदि प्रत्येक परिणाम के होने की संभावना समान होती है तो इन परिणामों को समान रूप से संभावित परिणाम कहा जाता है।उदाहरण :-
यदि हम एक पासा फेंकते हैं तो प्रत्येक संख्या के बराबर होने की संभावना होती है।
अर्थात एक पासे की 1,2,3,4,5 और 6 प्राप्त करने की समान संभावना है।
संयोग को प्रायिकता से जोड़ना
हम जानते हैं की,प्रायिकता p (E) =
उदाहरण :- एक डिब्बे में 6 कंचे हैं, जिन पर 1 से 6 संख्याएँ अंकित हैं।
(i) संख्या 2 वाले कंचे को इसमें से निकालने की प्रायिकता क्या है?
(ii) संख्या 5 वाले कंचे को इसमें से निकालने की प्रायिकता क्या है?
उत्तर:-

प्रायिकता p(E)=
(i) संख्या 2 वाले कंचे को निकालने प्रायिकता
p(2)=16
(ii) संख्या 5 वाले कंचे को निकालने प्रायिकता
p(5)=16
OMR (One Minute Revision)
उदाहरण 8
निम्नलिखित प्रश्नों का उत्तर दीजिए।
निम्नलिखित में से किसका होना निश्चित है, किसका होना असंभव है तथा कौन हो भी सकता है, परन्तु निश्चित रूप से नही।
अपने उत्तर की पुष्टि भी कीजिए ।
(i) आज आप कल से अधिक आयु के हैं।
(ii) एक सिक्के को उछालने पर चित आएगा।
(iii) एक पासे को फेंकने पर 8 आएगा।
(iv) अगली ट्रैफिक लाइट हरी दिखेगी।
(v) कल बादल घिरे होंगे।
(i) निश्चित हैं।
पुष्टि : क्योंकि अगर आज आप की आयु 20 साल 1 दिन है तो कल आपकी आयु निश्चित रूप से 20 साल 2 दिन हो जाएगी।
(ii) चित आ तो सकता हैं परंतु निश्चित नहीं हैं।
पुष्टि : क्योंकि 1 सिक्के को उछालने पर चित या पट दोनों आने की समान संभावना होती है।
(iii) असंभव हैं।
पुष्टि : क्योंकि पासे मे केवल 6 फलक होती हैं, अतः एक पासे को फेकने पर अधिकतम 6 अंक आ सकता हैं।
(iv) हो सकता हैं परंतु निश्चित नहीं हैं।
पुष्टि : हम जानते हैं की ट्रैफिक लाइट मे 3 रंग की लाइट होती हैं। ( लाल, हरा, पीला ) अतः जब आप ट्रैफिक लाइट के पास पहुचेंगे तो रंग लाल, हरा, पीला, कोई भी हो सकता हैं परंतु एक समय जरूर आएगा जब रंग हरा होगा।
(v) हो सकता हैं परंतु निश्चित नहीं हैं।
पुष्टि : क्योंकि यह केवल पूर्वानुमान है। कल के मौसम के बारे मे हम सिर्फ अंदाजा लगा सकते है। इसलिए कल बादल घिरे हो भी सकते है और नहीं भी।
उदाहरण 9
जब एक पासे को फेंका जाता है, तो निम्न परिणाम प्राप्त होते हैं, इन घटनाओं की प्रायिकता ज्ञात करें।
(a) एक अभाज्य संख्या
(b) एक अभाज्य संख्या नहीं
(c) 5 से बड़ी एक संख्या
(d) 5 से बड़ी संख्या नहीं
एक पासे को उछालने पर प्राप्त कुल परिणाम= {1,2,3,4,5,6}=6
(a) एक अभाज्य संख्या -
पासे पर अभाज्य संख्या ={2,3,5}
अतः अनुकूल परिणाम =3
प्रायिकता =
=36
=12
(b) एक अभाज्य संख्या नहीं -
=1− अभाज्य संख्या आने की प्रायिकता
=1−12
=12
(c) 5 से बड़ी एक संख्या -
अनुकूल परिणाम ={6} अर्थात 1
प्रायिकता =
=16
(d) 5 से बड़ी संख्या नहीं -
अनुकूल परिणाम ={1,2,3,4,5} अर्थात 5
प्रायिकता =
=56
सारांश
एक वृत्त आलेख एक संपूर्ण और उसके भागों में संबंध को दर्शाता है।