घातांक और घात कक्षा 8 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय में हम घातांक और घात का अध्ययन करेंगे। बहुत बड़ी संख्याओं या छोटी संख्याओं को पढ़ना, समझना और इनकी तुलना करना कठिन होता है। इन संख्याओं को सरलता से पढ़ने, समझने और इनकी तुलना करने के लिए हम घातांकों (exponents) का प्रयोग करते हैं। पिछली कक्षा 7 में हमने घातांक और घात का अध्ययन किया है, जिसमे घातांक के नियम व इसके प्रयोग तथा किसी बहुत बड़ी संख्या को मानक रूप में व्यक्त करना सीख चुके हैं। घातांक का सामान्य अर्थ है, जिस संख्या के ऊपर जो संख्या (घात) है, उस संख्या को उतनी बार गुणा करना, जितनी उसके ऊपर संख्या (घात) है।
इस अध्याय में हम ऋणात्मक घातांकों की घात, घातांक के नियम, छोटी संख्याओं को घातांकों का प्रयोग कर मानक रूप में व्यक्त करने का अध्ययन करेंगे।
आइये जानते है, घातांक और घात को और करीब से...
घातांक वह संख्या प्रदर्शित करता है कि दी गई संख्या खुद से ही कितनी बार गुणा की जाएगी।
माना कोई संख्या a है जिसको n बार गुणा किया जाता है।
∴a×a×a×a×....×a (n बार)=an
जहाँ, a वास्तविक संख्या है जिसको आधार (Base) तथा n को घातांक (Indices) कहते हैं।
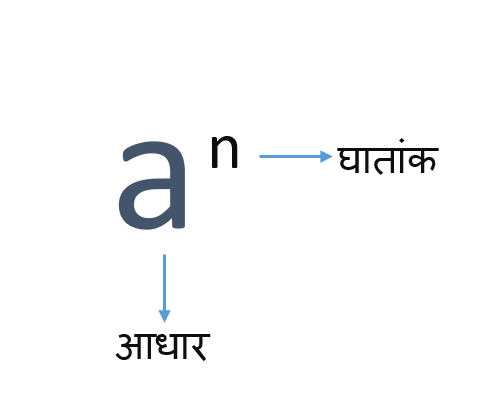
इसे पढ़ा जाता है, a की घात n
उदाहरण: 105
यहाँ, 10 की घात 5 हैं, अतः 10 को 10 से 5 बार गुणा करेंगे।

∴105=10×10×10×10×10
ऋणात्मक घातांकों की घात
घातांक ऋणात्मक भी हो सकते हैं और हम उन्हें धनात्मक में परिवर्तित कर सकते हैं।
जैसे:
3−2=132
3−3=133
3−4=134
3−5=135
इसी प्रकार,
5−2=152
5−5=155
10−5=1105
साधारणतया हम कह सकते हैं कि किसी शून्येतर परिमेय संख्या a के लिए
a−m=1am
जहाँ, m धनात्मक पूर्णांक है और am, a−m का गुणात्मक प्रतिलोम है।
उदाहरण 1
उदाहरण 2
उदाहरण 3
(−4)−2 का मान ज्ञात कीजिए।
हम जानते हैं कि
a−m=1am
∴(−4)−2=1(−4)2
=1−4×1−4
=116
अतः, (−4)−2=116
उदाहरण 4
मान ज्ञात कीजिए :
(12)−2+(13)−2+(14)−2
दिया हैं;
(12)−2+(13)−2+(14)−2
=(21)2+(31)2+(41)2 [∵a−m=1am]
=(2)2+(3)2+(4)2
=(2×2)+(3×3)+(4×4)
=4+9+16
=29
अतः, (12)−2+(13)−2+(14)−2=29
घातांक के नियम
घातांकीय रूप में संख्याएँ कुछ नियमों का पालन करती हैं, जो इस प्रकार हैं:
यहाँ आधार के रूप में a और b तथा घातांक के रूप में m और n होंगे:
नियम 1: यदि गुणनफल की क्रिया में आधार समान हो, तो सभी घातों का योगफल ज्ञात करके उसे आधार की घात में लिखते हैं।
am×an=am+n
उदाहरण 1:
3−2×3−4
=3(−2)+(−4)
=3(−2−4)
=3−6 [∵a−m=1am]
=136
उदाहरण 2:
(−5)−2×(−5)7
=(−5)(−2+7)
=(−5)5
नियम 2: यदि भाग की क्रिया में आधार समान हो, तो भाज्य वाली घात में से भाजक वाली घात को घटाकर प्राप्त संख्या को आधार की घात में लिखते हैं।
aman=am−n
उदाहरण:
5−25−4
=5(−2)−(−4)
=5(−2+4)
=52
=5×5=25
नियम 3: यदि घात की भी घात बनती जा रही हो, तो सभी घातों का आपस में गुणा कर देते हैं और इस प्रकार प्राप्त गुणनफल को आधार की घात में लिखते हैं।
(am)n=(a)m×n
उदाहरण:
[5(−4)](−2)
=5(−4)×(−2)
=58
नियम 4: यदि गुणनफल की क्रिया में घात समान तथा आधार भिन्न-भिन्न हो तो,
am×bm=(a×b)m
उदाहरण:
4−2×(−2)−2
=[4×(−2)]−2
=(−8)−2
=1(−8)2 [∵a−m=1am]
=1−8×1−8=164
नियम 5: यदि भागफल की क्रिया में घात समान तथा आधार भिन्न-भिन्न हो तो,
ambm=(ab)m
उदाहरण:
4−22−2
=(42)−2
=2−2
=122 [∵a−m=1am]
=14
नियम 6: किसी भी शून्येतर (अशून्य) संख्या की घात शून्य हो, तो उस पूरी राशि का मान एक (1) होता है।
a0=1
जैसे: 90=1, (−9)0=1, 150=1
OMR (One Minute Revision)
a−m=1am
जहाँ m धनात्मक पूर्णांक है और am, a−m का गुणात्मक प्रतिलोम है।
(i) am×an=am+n
(ii) aman=am−n
(iii) (am)n=(a)m×n
(iv) am×bm=(a×b)m
(v) ambm=(ab)m
(vi) a0=1; (a≠0)
उदाहरण 5
घातांक रूप को सरल कीजिए :
(−2)−3×(−2)−4
दिया हैं:
(−2)−3×(−2)−4
हम जानते हैं कि,
am×an=am+n
∴ (−2)−3×(−2)−4
=(−2)(−3)+(−4)
=(−2)(−3−4)
=(−2)−7
=−127 (∵a−m=1am)
अतः, (−2)−3×(−2)−4=−127
उदाहरण 6
घातांक रूप को सरल कीजिए :
32×3−5×36
दिया हैं:
32×3−5×36
∵am×an×al=am+n+l
∴32×3−5×36=3[2+(−5)+6]
=32−5+6
=33
=3×3×3
=27
अतः, 32×3−5×36=27
उदाहरण 7
मान ज्ञात कीजिए :
{(−23)−2}2
दिया हैं:
{(−23)−2}2
=(−23)(−2)×2 [∵(am)n=(a)m×n]
=(−23)−4
=(−32)4 [∵a−m=1am]
=(−3)424
=(−3)×(−3)×(−3)×(−3)2×2×2×2
=8116
अतः, {(−23)−2}2=8116
उदाहरण 8
सरल कीजिए और उत्तर घातांक के रूप में लिखिए :
(25÷28)5×2−5
दिया हैं:
(25÷28)5×2−5
=(2528)5×2−5
=(25−8)5×2−5 [∵aman=am−n]
=(2−3)5×2−5
=2(−3)×5×2−5 [∵(am)n=(a)m×n]
=2−15×2−5
=2(−15)+(−5) [∵am×an=am+n]
=2−15−5
=2−20
=1220 [∵a−m=1am]
अतः, (25÷28)5×2−5=1220
उदाहरण 9
निम्नलिखित को हल करे :
(35)4×(35)7=(35)2x−1
दिया हैं;
(35)4×(35)7=(35)2x−1
⇒(35)4+7=(35)2x−1 [∵am×an=am+n]
⇒4+7=2x−1
⇒11=2x−1
पक्षांतर करने पर,
⇒2x=11+1
⇒2x=12
दोनों पक्षों में 2 का भाग देने पर,
2x2=122
⇒x=6
छोटी संख्याओं को घातांकों का प्रयोग कर मानक रूप में व्यक्त करना
बहुत बड़ी या बहुत छोटी संख्याओं को घातांकों की सहायता से मानक रूप में निरूपित किया जा सकता है। कोई भी संख्या यदि m×10n के रूप में लिखी हो तो यह संख्या का मानक रूप कहलाता है।
जहाँ, m एक दशमलव संख्या हैं साथ ही 1≤m<10
तथा n धनात्मक या ऋणात्मक पूर्णांक होता हैं।
हम पिछली कक्षा में बहुत बड़ी संख्याओं को मानक रूप मे परिवर्तित करना सीख चुके हैं जिसमे हमने पढ़ा हैं, यदि बहुत बड़ी संख्या है, तो हमें दशमलव को बाईं ओर ले जाने की आवश्यकता होती है, और जब हम ऐसा करते हैं, तो घातांक धनात्मक होते हैं।
जैसे: 150,000,000,000=1.5×1011 (∵ मानक रूप मे बदलने के लिए दशमलव को बाईं और 11 स्थान आगे बढ़ाया गया हैं इसलिए घातांक धनात्मक होंगे।)
इसी तरह,
120000=1.2×106 (मानक रूप मे लिखने के लिए दशमलव को बाईं ओर 6 स्थान आगे बढ़ाया गया हैं।)
आइए अब समझते हैं बहुत छोटी संख्याओं को घातांकों की सहायता से मानक रूप में निरूपित करना
यदि बहुत छोटी संख्या है, तो हमें दशमलव स्थान को उसके मानक रूप में दर्शाने के लिए क्रम में दाईं ओर आगे ले जाने की आवश्यकता होती हैं दशमलव का दाईं ओर स्थानांतरित होने पर, आधार संख्या 10 का घातांक ऋणात्मक होगा।
उदाहरण से समझते हैं:
0.0000007 को मानक रूप मे परिवर्तित कीजिए।
इस स्थिति में, दी गई संख्या को मानक रूप मे लिखने के लिए दशमलव स्थान को 6 स्थान दाईं ओर आगे ले जाने की आवश्यकता हैं, अतः दशमलव स्थान को 6 स्थान दाईं ओर आगे ले जाने पर आधार संख्या 10 का घात −6 होगा।
0.0000007=7×10−6
इसी तरह
0.002=2×10−3 (मानक रूप मे लिखने के लिए दशमलव को दाईं ओर 3 स्थान आगे बढ़ाया गया हैं, अतः आधार संख्या 10 का घात −3 होगा )
0.004=4×10−3
0.0016=1.6×10−3
0.0000123=1.23×10−5
0.0998=9.98×10−2
नोट: किसी भी छोटी संख्या को मानक रूप मे लिखने के लिए दशमलव को जितना स्थान दाईं ओर आगे बढ़ाया गया होता हैं उतना ही ऋणात्मक आधार संख्या 10 का घातांक होता हैं।
बहुत बड़ी संख्याओं और बहुत छोटी संख्याओं की तुलना:
उदाहरण से समझते हैं:
सूर्य का व्यास =1.4×109m
पृथ्वी का व्यास =1.2756×107m
इनके व्यासों की तुलना करनी है।
अतः,
⇒1.4×1091.2756×107
⇒1.4×109−71.2756 (∵aman=am−n)
⇒1.4×1021.2756 (∵1.2756≈1.4)
⇒1.4×1021.4
⇒100
अतः सूर्य का व्यास, पृथ्वी के व्यास का लगभग 100 गुना है।
एक और उदाहरण से समझते हैं:
लाल रक्त कोशिकाएँ जो कि 0.000007m माप की है और पौधों की कोशिकाएँ जो कि 0.00001275m माप की है इनके मापों की तुलना कीजिए।
लाल रक्त कोशिकाओं का आकार =0.000007m=7×10−6m (मानक रूप मे लिखने के लिए दशमलव को दाईं ओर 6 स्थान आगे बढ़ाया गया हैं, अतः आधार संख्या 10 का घात −6 होगा। )
पौधों की कोशिकाओं का आकार =0.00001275m=1.275×10−5m (मानक रूप मे लिखने के लिए दशमलव को दाईं ओर 5 स्थान आगे बढ़ाया गया हैं, अतः आधार संख्या 10 का घात −5 होगा।)
तुलना करते हैं:
⇒7×10−61.275×10−5
⇒7×10(−6)−(−5)1.275 (∵aman=am−n)
⇒7×10(−6+5)1.275
⇒7×10−11.275 (∵7×10−1=0.7,1.275≈1.4)
⇒0.71.4
⇒12
अतः, लाल रक्त कोशिकाएँ आकार में, पौधों की कोशिकाओं की लगभग आधी हैं।
OMR (One Minute Revision)
जहाँ, m एक दशमलव संख्या हैं साथ ही 1≤m<10
तथा n धनात्मक या ऋणात्मक पूर्णांक होता हैं।
जैसे: 0.002=2×10−3
0.0002=2×10−4
0.00002=2×10−5
0.000002=2×10−6
0.0000021=2.1×10−6
0.00000213=2.13×10−6
उदाहरण 10
0.000000564 को मानक रूप में लिखिए।
हम जानते हैं कि, कोई भी संख्या यदि m×10n के रूप में लिखी हो तो यह संख्या का मानक रूप कहलाता है।
जहाँ, m एक दशमलव संख्या हैं साथ ही 1≤m<10
तथा n एक धनात्मक या ऋणात्मक पूर्णांक हैं।
अतः, इस स्थिति में, दी गई संख्या को मानक रूप मे लिखने के लिए दशमलव स्थान को 7 स्थान दाईं ओर आगे ले जाने की आवश्यकता हैं, अतः दशमलव स्थान को 7 स्थान दाईं ओर आगे ले जाने पर आधार संख्या 10 का घात −7 होगा।
∴0.000000564=5.64×10−7
उदाहरण 11
0.0000000000085 को मानक रूप में लिखिए।
हम जानते हैं कि, कोई भी संख्या यदि m×10n के रूप में लिखी हो तो यह संख्या का मानक रूप कहलाता है।
जहाँ, m एक दशमलव संख्या हैं साथ ही 1≤m<10
तथा n एक धनात्मक या ऋणात्मक पूर्णांक हैं।
अतः, इस स्थिति में, दी गई संख्या को मानक रूप मे लिखने के लिए दशमलव स्थान को 12 स्थान दाईं ओर आगे ले जाने की आवश्यकता हैं, अतः दशमलव स्थान को 12 स्थान दाईं ओर आगे ले जाने पर आधार संख्या 10 का घात −12 होगा।
∴0.0000000000085=8.5×10−12
उदाहरण 12
3×10−8 को सामान्य रूप में व्यक्त कीजिए।
दी गई संख्या को हम लिख सकते हैं,
3.0×10−8
चूंकि दी गई संख्या मे आधार 10 की घात −8 हैं, अतः सामान्य रूप मे लिखने के लिए दशमलव स्थान को 8 स्थान तक बाईं ओर रखना होगा।
∴3.0×10−8=0.00000003
सारांश
a−m=1am
जहाँ m धनात्मक पूर्णांक है और am, a−m का गुणात्मक प्रतिलोम है।
(i) am×an=am+n
(ii) aman=am−n
(iii) (am)n=(a)m×n
(iv) am×bm=(a×b)m
(v) ambm=(ab)m
(vi) a0=1; (a≠0)