एक चर वाले रैखिक समीकरण कक्षा 8 गणित

अध्याय के शीर्षक के अनुसार इस अध्याय मे हम एक चर वाले रैखिक समीकरण का अध्ययन करेंगे। जैसा की आपने पिछली कक्षाओ मे चर राशियों के बारे मे जाना था, साथ ही हमने अनेक बीजीय व्यंजकों और समीकरणों के बारे में अध्ययन किया हैं। ऐसे व्यंजक जो हमने देखे हैं, उनके कुछ उदाहरण हैं -

$5x,2x-3,3x+y,2xy+5,5xyz+x+y+z,x^2+1,y+y^2$

इन व्यंजकों में कुछ में एक से अधिक चर प्रयोग हुए हैं। उदाहरण के लिए, $2xy+5$ में दो चर हैं, अब यदि इन व्यंजकों मे केवल एक चर का प्रयोग हो तो वह व्यंजक एक चर वाला हो जाएगा। अब हम इस अध्याय मे समीकरण बनाने के लिए केवल एक चर वाले व्यंजक का प्रयोग करेंगे और जो व्यंजक समीकरण बनाने में लिखे जाएँगे साथ ही वे समीकरण रैखिक होंगे अर्थात व्यंजकों में प्रयोग होने वाले चर की घात एक होगी। एक चर वाले रैखिक समीकरणों के कुछ उदाहरण निम्न है:

$5x=25,2x-3=9,2y+\frac{5}{2}=37$

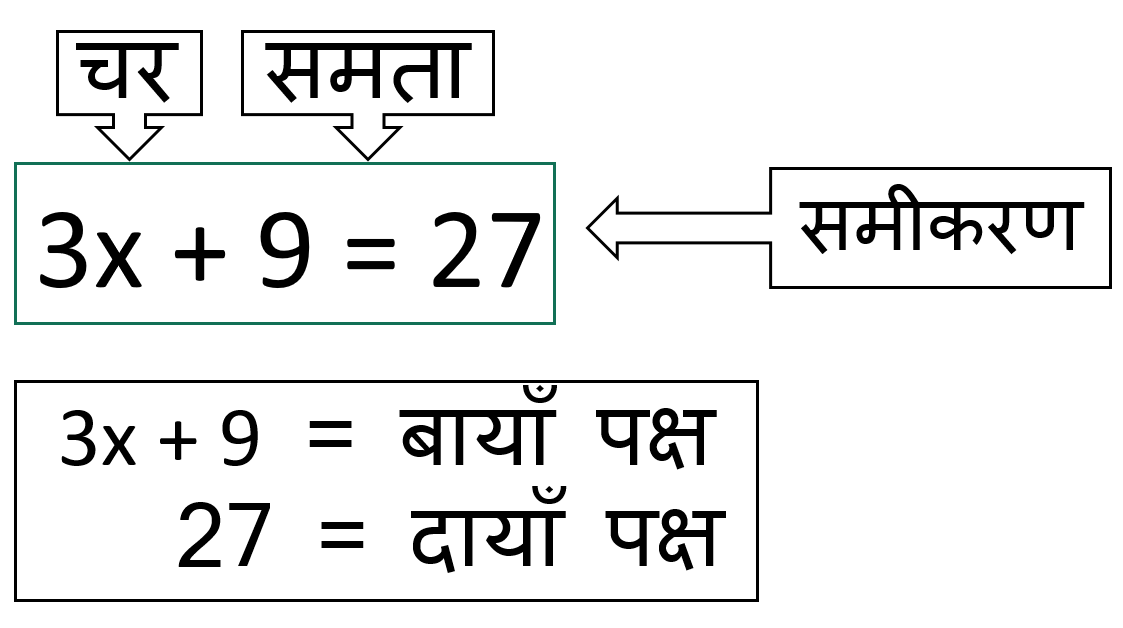
बीजगणितीय रैखिक समीकरण जिसमें रैखिक व्यंजकों में केवल एक ही चर हों तथा उस चर की अधिकतम घात एक हो, एक चर वाले रैखिक समीकरण कहलाते हैं।

उदाहरण:

(1) $3x+9=27$

(2) $6x–3=39$

(3) $2x+7x=108$

हल ज्ञात कीजिए -
$2x-3=7$

$2x-3=7$

पक्षान्तर करने पर

$2x=7+3$

$2x=10$

$x=\frac{10}{2}$

$x=5$

हल कीजिए $\frac{15}{4}-7x=9$

$\frac{15}{4}-7x=9$

$\frac{15}{4}-9=7x$

$\frac{15-36}{4}=7x$

$-\frac{21}{4}=7x$
$x=-\frac{21}{4\times 7}$

$x=-\frac{3}{4}$

एक परिमेय संख्या को $\frac{5}{2}$ से गुणा कर $\frac{2}{3}$ जोड़ने पर $-\frac{7}{12}$ प्राप्त होता है | वह संख्या क्या है ?

माना परिमेय संख्या $=x$

तब प्रश्न से,

$\frac{5}{2}x+\frac{2}{3}$$=-\frac{7}{12}$

$\frac{5}{2}x$$=-\frac{7}{12}-\frac{2}{3}$ ($12$ व $3$ का ल.स. $=12$)

$\Rightarrow \frac{5x}{2}=\frac{-7\times 1-2\times 4}{12}$

$\Rightarrow \frac{5x}{2}=\frac{-7-8}{12}$

$\frac{5x}{2}=-\frac{15}{12}$

$x=\frac{-15\times 2}{12\times 5}$

$x=-\frac{3}{6}$

$x=-\frac{1}{2}$

परिमेय संख्या $=x=-\frac{1}{2}$

हमारे सामने ऐसी बहुत सारी परिस्थितियाँ आती हैं जहाँ व्यंजक उपयोग होते हैं

जैसे -

एक आयताकार तरण-ताल $\left(\text{swimming pool}\right)$ की लंबाई उसकी चौड़ाई के दुगुने से 2 मीटर अधिक है यदि इसका परिमाप 154 मीटर है तो इसकी लंबाई व चौड़ाई ज्ञात कीजिए।

माना, तरन -ताल की चौड़ाई $=b$

तब उसकी लम्बाई $l=2b+2$

चूंकि, दिया हैं :

परिमाप$=154$

$2(l+b)=154$

$l+b=\frac{154}{2}$

$2b+2+b=\frac{154}{2}$ (चूंकि $l=2b+2$)

$3b+2=77$

$3b=77-2$

$b=\frac{75}{3}$

$b=25$

चौड़ाई $=b=25$

तब उसकी लम्बाई $l$

$=2b+2$

$=2\times 25+2$

$=50+2$

$=52$

किसी कक्षा में बालक और बालिकाओं की संख्याओं में अनुपात 7:5 है | यदि बालकों की संख्या बालिकाओं की संख्या से 8 अधिक है तो कक्षा में कुल कितने विद्यार्थी हैं?

दिया है,

दो संख्याएँ $7:5$ के अनुपात में हैं, अतः हम एक संख्या $7x$ और दूसरी $5x$ मान सकते हैं।
(ध्यान दीजिए $7x:5x$ में $7:5$ का अनुपात है।)

चूंकि,
बालको की संख्या $\left(7x\right)$, बालिकाओ की संख्या $\left(5x\right)$ से, $8$ अधिक हैं अतः

$7x=5x+8$

$7x-5x=8$

$2x=8$

$x=\frac{8}{2}$

$x=4$

क्योंकि संख्याएँ $7x$ तथा $5x$ हैं
अत: संख्याएँ $7\times 4$ तथा $5\times 4$ अर्थात् $28$ तथा $20$ है

अतः कुल विद्यार्थी $=28+20=48$

$8$ के तीन लगातार गुणजों का योग $888$ है, गुणजों को ज्ञात कीजिए।

माना,
$8$ पहला गुणज $=x$

दूसरा गुणज $=x+8$

तीसरा गुणज $=x+16$

गुणजो का योग$=888$

$x+(x+8)+(x+16)=888$

$3x+24=888$

$3x=888-24$

$3x=864$

$x=\frac{864}{3}=288$

अतः

पहला गुणज $=x=288$

दूसरा गुणज $=x+8$

$=288+8$

$=296$

तीसरा गुणज $=288+16=304$

मेरे पास 300 रूपये मूल्य के 1 रूपये, 2 रूपये और 5 रूपये वाले सिक्के हैं। 2 रूपये वाले सिक्कों की संख्या 5 रूपये वाले सिक्कों की संख्या की तिगुनी है और सिक्कों की कुल संख्या 160 है। मेरे पास प्रत्येक प्रकार के कितने-कितने सिक्के है?

माना,

5 रुपये के सिक्को की संख्या $=x$

2 रुपये के सिक्को की संख्या $=3x$

1 रुपये के सिक्को की संख्या $=160-3x-x=160-4x$

$1(160-4x)$$+2\left(3x\right)$$+5x$$=300$

$160-4x$$+6x$$+5x$$=300$

$7x$$=300-160$

$7x=140$

$x=\frac{140}{7}$$=20$

5 रुपये के सिक्को की संख्या $=x=20$

2 रुपये के सिक्को की संख्या $=3x=3\times 20=60$

1 रुपये के सिक्को की संख्या

$=160-4x$

$=160-4\cdot 20$

$=160-80$

$=80$

अब हम जानते हैं कि एक समीकरण मे दो बीजीय व्यंजकों के मानों में समता होती है। समीकरण $2x-3=7$ में एक व्यंजक $2x-3$ हैं तथा दूसरा व्यंजक 7 है ।

अभी तक लिए गए लगभग सभी उदाहरणों में बायाँ पक्ष में ही चर राशि थी । लेकिन ऐसा होना सदैव आवश्यक नहीं है। चर राशि दोनों पक्षों में भी हो सकती है।

उदाहरण के लिए, समीकरण $2x-3=x+2$ में, दोनों ही पक्षों में चर वाले व्यंजक हैं।

बायाँ पक्ष में व्यंजक है$(2x-3)$।
दायाँ पक्ष में व्यंजक हैं $(x+2)$।

आइए इस समीकरण $2x-3=x+2$ को हल करते हैं।

हल :

दिया हैं:

$2x-3=x+2$

दोनों पक्षों मे 3 जोड़ने पर

$2x-3+3=x+2+3$

$\Rightarrow 2x=x+5$

दोनों पक्षों मे $x$ घटाने पर,

$2x-x=x+5-x$

$\Rightarrow x=5$ उत्तर

हमने यहाँ समीकरण के दोनों पक्षों से, एक संख्या ही नहीं, बल्कि चर वाला पद भी घटाया हैं। हम ऐसा कर सकते हैं क्योंकि चर का मान भी कोई संख्या ही है। ध्यान दीजिए कि $x$ दोनों पक्षों से घटाने से तात्पर्य है $x$ को बाएँ पक्ष में पक्षांतरण करना अर्थात एक पक्ष से $x$ को विलुप्त करना है।

दो संख्याओं में अनुपात 5:3 है। यदि उनमे अंतर $18$ है तो संख्याएँ ज्ञात कीजिए।

माना,
पहली संख्या $=x$

तब प्रश्न से

पहली संख्या $-$ दूसरी संख्या $=18$

दूसरी संख्या $=$ पहली संख्या $-18$

दूसरी संख्या $=x-18$

प्रश्न से,
$\frac{x}{x-18}=\frac{5}{3}$

तिर्यक गुणा

$3x=5(x-18)$

$3x=5x-18\times 5$

$3x=5x-90$

$90=5x-3x$

$90=2x$ (पक्षांतर)

$x=45$

अतः पहली संख्या $=x=45$

दूसरी संख्या $=$ पहली संख्या $-18$

$=45-18$

$=27$

बच्चों! यदि हमें कोई जटिल समीकरण दिया गया है तब दी गई संक्रियाओ को हल करके हम उसे सरल रूप मे प्राप्त कर सकते है। इस अध्याय में हम रैखिक समीकरणों पर ही चर्चा करेंगे अर्थात जटिल रूप मे प्राप्त समीकरण को सरल रैखिक समीकरण रूप मे लाने का प्रयास करेंगे। आइए इसे कुछ उदाहरणों द्वारा समझने का प्रयास करते है -

$3(5z-7)-2(9z-11)$$=4(8z-13)-17$

$3(5z-7)-2(9z-11)$ $=4(8z-13)-17$

$\Rightarrow 3\times 5z-3\times 7$$-2\times 9z-2\times (-11)$

$=4\times 8z$$-4\times 13-17$

$\Rightarrow 15z-21$$-18z+22$

$=32z-52-17$

$\Rightarrow -3z+1$$=32z-69$

$\Rightarrow 69+1=32z+3z$

$\Rightarrow 70=35z$

$\Rightarrow \frac{70}{35}=z$

$\Rightarrow z=2$

$\frac{3t-2}{4}$$-\frac{2t+3}{3}$$=\frac{2}{3}-t$

$\frac{3t-2}{4}-\frac{2t+3}{3}$$=\frac{2}{3}-t$

पक्षांतर करने पर

$\frac{3t-2}{4}$$-\frac{2t+3}{3}+\frac{t}{1}$$=\frac{2}{3}$

$\frac{(3t-2)3-(2t+3)4+12t}{12}$$=\frac{2}{3}$

$\frac{9t-6-(8t+12)+12t}{12}$$=\frac{2}{3}$

$\frac{9t-6-8t-12+12t}{12}$$=\frac{2}{3}$

$\frac{t+12t-18}{12}$$=\frac{2}{3}$

$\frac{13t-18}{12}$$=\frac{2}{3}$

तिर्यक गुणा

$(13t-18)\times 3$$=2\times 12$

$\Rightarrow 39t-54$$=24$

$\Rightarrow 39t$$=54+24$

$\Rightarrow t=\frac{78}{39}$

$\Rightarrow t=2$

ऐसे कुछ समीकरण होते है जो रैखिक समीकरण तो नहीं होते हैं लेकिन उन्हे रैखिक समीकरण के रूप मे गणितीय संक्रियाओं के द्वारा बदला जा सकता हैं।

जैसे - $\frac{x+1}{2x+3}=\frac{3}{8}$

स्पष्ट हैं कि यह समीकरण रैखिक नहीं है क्योंकि इसके बाएँ पक्ष में व्यंजक रैखिक नहीं है परन्तु इसे हम एक रैखिक समीकरण के रूप में बदल सकते हैं।

अतः हम समीकरण के दोनों पक्षों को $(2x+3)$ से गुणा करते हैं,

$\Rightarrow \frac{x+1}{2x+3}\times (2x+3)$

$=\frac{3}{8}\times (2x+3)$

implies (x+1)/cancel(2x+3)xx cancel(2x+3)

$=\frac{3}{8}\times (2x+3)$

$\Rightarrow x+1$ $=\frac{3}{8}\times (2x+3)$

$\Rightarrow 8\times (x+1)$ $=3\times (2x+3)$

$\Rightarrow 8x+8$ $=6x+9$

$\Rightarrow 8x+8-6x-9$ $=0$

$\Rightarrow 2x-1$ $=0$

अतः अब हमें एक रैखिक समीकरण मिला जिसे हम हल करना जानते हैं।

दो अंकों वाली दी गई एक संख्या में एक अंक दूसरे का तीन गुना है। इसके अंकों के स्थान बदलकर प्राप्त संख्या को दी गई संख्या में जोड़ने पर $88$ प्राप्त होता है। दी गई संख्या ज्ञात कीजिए।

माना कि,

संख्या का इकाई अंक $=x$

तब प्रश्न से दहाई अंक $=3x$

$(3x\cdot 10+x)$$+(x\cdot 10+3x)$$=88$

$\Rightarrow 30x+x$$+10x+3x=88$

$\Rightarrow 44x=88$

$\Rightarrow x=\frac{88}{44}$

$\Rightarrow x=2$

संख्या का इकाई अंक $=x=2$

दहाई अंक $=3x=6$

अतः दी गई संख्या $=62$

अनु तथा राज की वर्तमान आयु का अनुपात $4:5$ है। $8$ वर्ष बाद उनकी आयु का अनुपात $5:6$ होगा। उनकी वर्तमान आयु ज्ञात कीजिए।

माना कि,

अनु तथा राज की वर्तमान आयु क्रमश: $4x$ तथा $5x$ हैं।

$8$ वर्ष बाद अनु की आयु $=(4x+8)$ वर्ष

$8$ वर्ष बाद राज की आयु $=(5x+8)$ वर्ष

उनकी आयु का अनुपात $=\frac{4x+8}{5x+8}$

दिया है,

आयु का अनुपात $5:6$ है अतः

$(4x+8):(5x+8)$$=5:6$

$\frac{4x+8}{5x+8}$$=\frac{5}{6}$

$6(4x+8)$$=5(5x+8)$

$24x+48$$=25x+40$

$24x+48-40=25x$

$24x+8=25x$

$8=25x-24x$

$8=x$

$x=8$

अतः अनु की वर्तमान आयु

$4x=4\times 8=32$ वर्ष

तथा राज की वर्तमान आयु

$5x=5\times 8=40$ वर्ष