क्षेत्रमिति कक्षा 8 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय में हम क्षेत्रमिति का अध्ययन करेंगे। पिछली कक्षाओं में भी हमने क्षेत्रमिति का अध्ययन किया हैं। किसी बंद समतल आकृति की सीमा के चारों ओर की दूरी उसका परिमाप कहलाता है और उस आकृति द्वारा घिरे हुए क्षेत्र को उसका क्षेत्रफल कहते हैं। हम त्रिभुज, आयत, वृत्त इत्यादि विभिन्न समतल आकृतियों का परिमाप और क्षेत्रफल ज्ञात करना सीख चुके हैं।
अब, इस अध्याय में हम चतुर्भुज जैसी दूसरी बंद आकृतियों के क्षेत्रफल एवं परिमाप तथा घन, घनाभ और बेलन जैसे ठोसों के पृष्ठीय क्षेत्रफल एवं आयतन का अध्ययन करेंगे।
आइये जानते है, ठोस आकारों को और करीब से...
क्षेत्रमिति के अंतर्गत हम किसी द्विविमीय और त्रिविमीय आकृतियों के क्षेत्रफल, परिमाप, आयतन आदि का अध्ययन करते हैं।
द्विविमीय (2D) आकृति: ऐसी आकृति जिनमे दो विमाएँ लंबाई और चौड़ाई होती हैं, द्विविमीय आकृति कहलाती हैं।
जैसे: आयत, वर्ग, समकोण त्रिभुज, समद्विबाहु त्रिभुज, समबाहु त्रिभुज, विषमबाहु त्रिभुज आदि।
त्रिविमीय (3D) आकृति: ऐसी आकृति जिनमे तीन विमाएँ लंबाई, चौड़ाई और ऊंचाई या गहराई होती हैं, त्रिविमीय आकृति कहलाती हैं।
जैसे: घन, घनाभ, बेलन, शंकु, गोला, आदि।
क्षेत्रफल (Area): किसी आकृति के उसके सभी भुजाओं से घिरे हुए तल को उस आकृति का क्षेत्रफल कहते हैं।
क्षेत्रफल की इकाई (Unit) वर्ग मीटर, वर्ग सेंटीमीटर, वर्ग किलोमीटर आदि होती हैं।
परिमाप (Perimeter): किसी आकृति की सभी भुजाओं की लंबाइयों का योग उस आकृति का परिमाप या परिमिति कहलाता हैं।
परिमाप की इकाई (unit) मीटर, सेंटीमीटर, किलोमीटर आदि होती हैं।
कुछ द्विविमीय (2D) आकृतियों का क्षेत्रफल और परिमाप
| आलेख | आकार | क्षेत्रफल | परिमाप |
|---|---|---|---|
 | वर्ग | a×a | 4×a |
 | आयत | l×b | 2(l+b) |
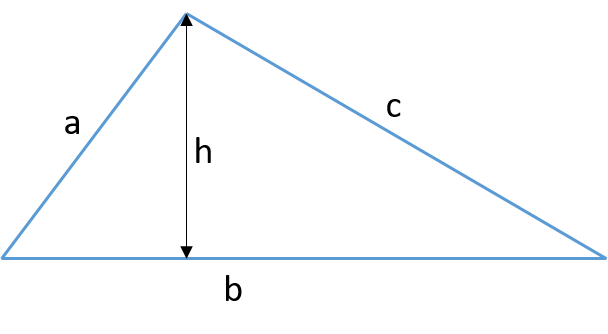 | त्रिभुज | 12×b×h | a+b+c |
 | समांतर चतुर्भुज | b×h | 2(b+h) |
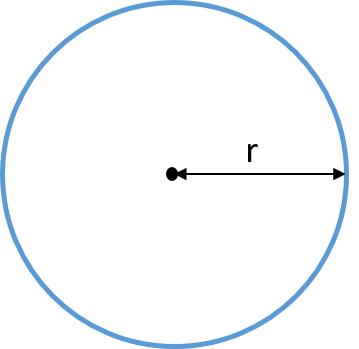 | वृत्त | πr2 | 2πr |
आयतन (Volume): किसी त्रिविमीय या ठोस वस्तु द्वारा घिरी हुई जगह उसका आयतन कहलाता है।
जैसे: गेंद, डस्टर, पुस्तक ये सभी चीजे अपना एक स्थान घेरती हैं और ये जितना स्थान घेरती हैं उसको आयतन कहते हैं।
आयतन की इकाई (Unit) घन मीटर, घन सेंटीमीटर, घन किलोमीटर आदि होती हैं।
उदाहरण 1
दिए गए चित्र में एक वर्गाकार और एक आयताकार खेत के माप दिए हुए हैं। यदि इनके परिमाप समान है, तो किस खेत का क्षेत्रफल अधिक होगा?

दिया है:
वर्गाकार खेत की भुजा =60m
आयताकार खेत की भुजा =80m
हम जानते हैं कि,
आयत का परिमाप =2(l+b) (l=80= लंबाई, b= चौड़ाई )
वर्ग का परिमाप =4×भुजा
प्रश्नानुसार,
आयताकार खेत का परिमाप = वर्गाकार खेत का परिमाप
2(l+b)=4×भुजा
⇒2(80+b)=4×60
⇒2(80+b)=240
⇒80+b=120
⇒b=120−80
⇒b=40m
∵आयताकार खेत का क्षेत्रफल = लंबाई × चौड़ाई
=l×b
=80m×40m
=3200m2
∵वर्गाकार खेत का क्षेत्रफल = (भुजा)2
=602m2
=3600m2
अतः, वर्गाकार खेत का क्षेत्रफल आयताकार खेत के क्षेत्रफल से अधिक होगा।
उदाहरण 2
एक मैदान आयत के आकार का है जिसके एक छोर पर अर्द्धवृत्त का आकार है, जैसा चित्र में दिखाया गया है। मैदान का क्षेत्रफल ज्ञात करे।

चूंकि मैदान आयताकार है। इसलिए,
मैदान की लंबाई AB=60m
मैदान की चौड़ाई AD=28m
यहाँ, मैदान का एक छोर पर अर्द्धवृत्त का आकार का है।
अतः, मैदान का कुल क्षेत्रफल = आयत का क्षेत्रफल + अर्द्धवृत्त का क्षेत्रफल
आयत ABCD का क्षेत्रफल = लंबाई × चौड़ाई
=AB×AD
=60m×28m=1680m2
हम जानते हैं कि ,
अर्द्धवृत्त का क्षेत्रफल =πr22
चूंकि, त्रिज्या r=d2
जहाँ, d व्यास हैं।
∴ त्रिज्या r=282=14m
अतः, अर्द्धवृत्त का क्षेत्रफल =π×1422
=227×14×142
=308m2
अतः, मैदान का कुल क्षेत्रफल =1680m2+308m2=1988m2
समलंब का क्षेत्रफल
चार भुजाओं से घिरी वह आकृति, जिसकी केवल दो भुजाएँ समांतर हों, और अन्य दो भुजाएँ समांतर ना हो, तो वह चतुर्भुज समलंब चतुर्भुज कहलाता हैं।
जैसा कि, आकृति में देख सकते हैं, ABCD एक समलंब चतुर्भुज हैं, जिसमें सिर्फ AB तथा DC समांतर भुजाएँ हैं।
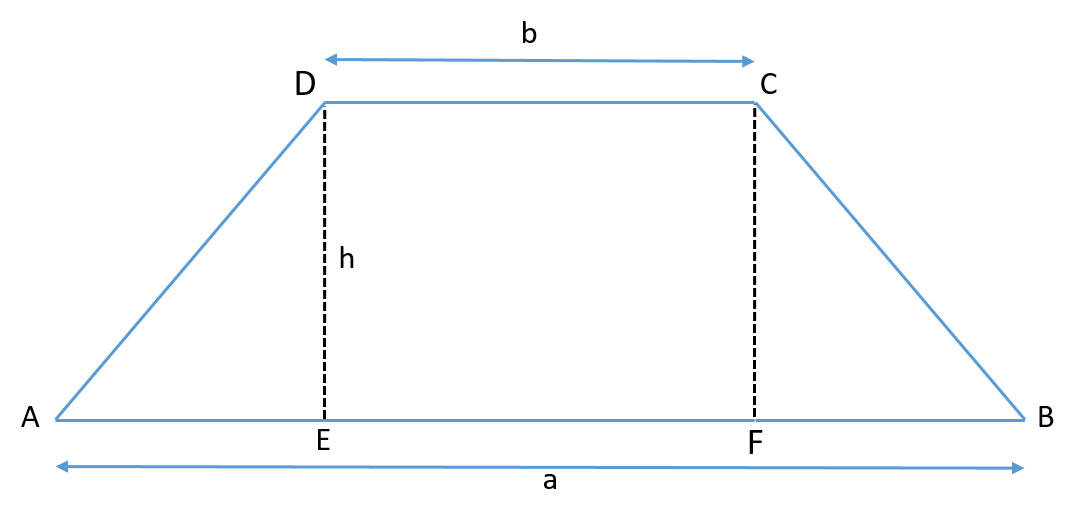
समलंब चतुर्भुज का क्षेत्रफल =12× ऊंचाई × समांतर भुजाओं का योग
यहाँ समलंब की ऊंचाई DE=CF=h
समांतर भुजाओं का योग =AB+CD=a+b
समलंब चतुर्भुज का क्षेत्रफल =12×h(a+b)
Note: यहाँ, समलंब चतुर्भुज ABCD तीन भागों में विभाजित हुआ है, एक आयत और दो त्रिभुज।
अतः, समलंब चतुर्भुज का क्षेत्रफल, आयत का क्षेत्रफल और दोनों त्रिभुजों के क्षेत्रफल का योग करके भी प्राप्त किया जा सकता हैं।
अतः, समलंब चतुर्भुज का क्षेत्रफल = त्रिभुज ADE का क्षेत्रफल + चतुर्भुज CDEF का क्षेत्रफल + त्रिभुज BFC का क्षेत्रफल
उदाहरण: एक समलंब चतुर्भुज की दो समांतर भुजाओं की लंबाई क्रमशः 16 मीटर और 20 मीटर है। यदि ऊंचाई 10 मीटर हैं, तो वर्ग मीटर में उसका क्षेत्रफल ज्ञात कीजिए?
हल:
माना कि, समलंब की दो समांतर भुजाओं में से,
एक की लंबाई DC=a=16 मीटर
दूसरी की लंबाई AB=b=20 मीटर
ऊंचाई DE=CF=h=10 मीटर
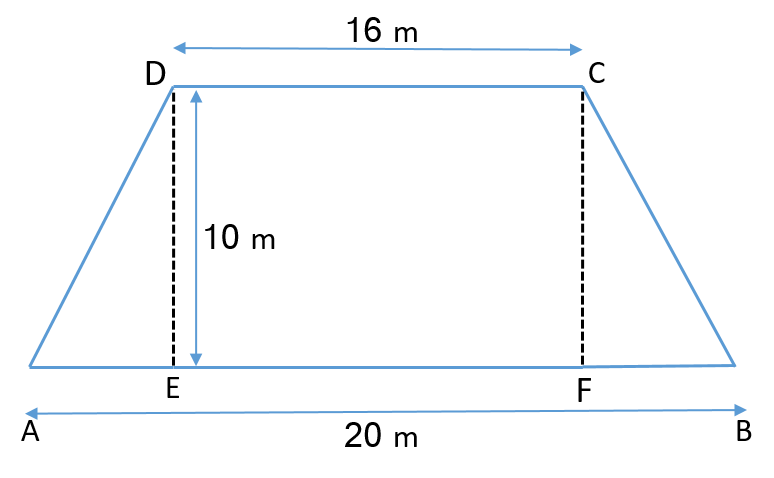
हम जानते हैं कि,
समलंब चतुर्भुज का क्षेत्रफल =12×h(a+b)
=12×10(16+20) वर्ग मीटर
=5×36 वर्ग मीटर
=180 वर्ग मीटर
उदाहरण 3
एक समलम्बाकार की समांतर भुजाएँ 3 सेमी और 4 सेमी है। इनके बीच की दूरी 3 सेमी है। समलम्बाकार क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
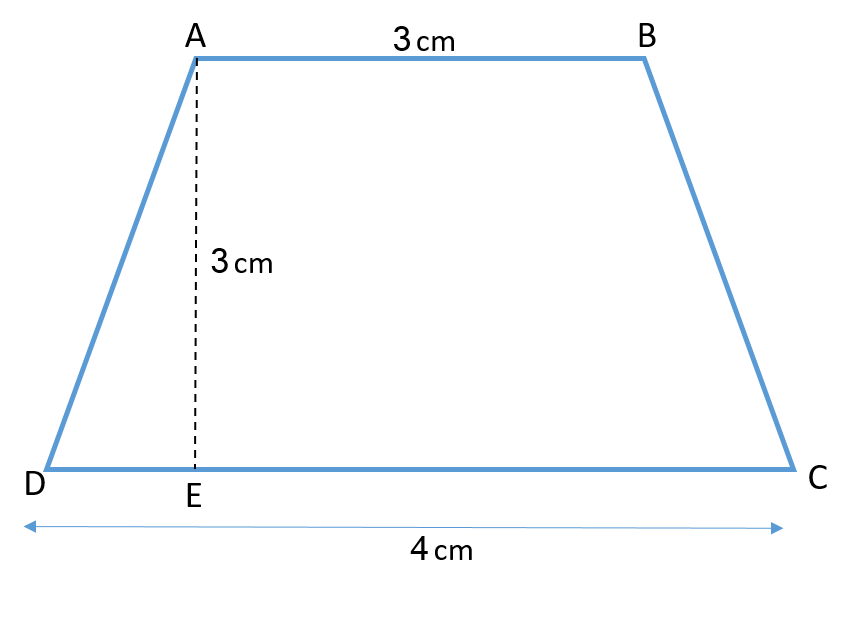
माना कि,
पहली समांतर भुजा की लंबाई =AB=3cm
दूसरी समांतर भुजा की लंबाई =DC=4cm
ऊंचाई =3cm
समलंब चतुर्भुज का क्षेत्रफल =12×समांतर भुजाओं का योग × ऊंचाई
=12×(AB+DC)×h
=12×(3+4)×3
=212
=10.5cm2
उदाहरण 4
3 सेमी ऊंचाई के समलम्बाकार क्षेत्र का क्षेत्रफल 36 वर्ग सेमी है। इसकी समांतर भुजाओं में से एक भुजा की लंबाई 9 सेमी है। दूसरी समांतर भुजा की लंबाई ज्ञात कीजिए।
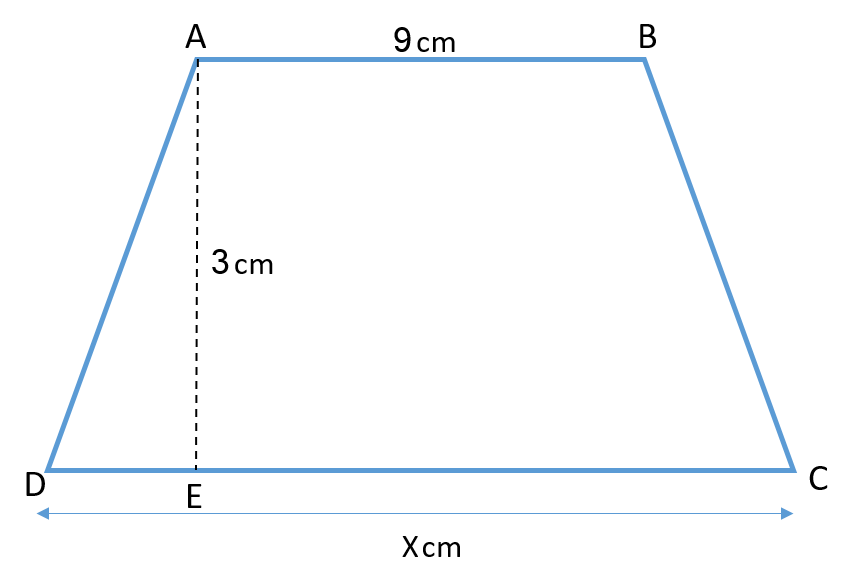
पहली भुजा की लंबाई AB=9cm
ऊंचाई AE=3cm
माना कि दूसरी भुजा की लंबाई =xcm मीटर
समलंब चतुर्भुज का क्षेत्रफल =12×समांतर भुजाओं का योग × ऊंचाई
36=12×(AB+DC)×AE
36=12(9+x)×3
24=9+x
x=15cm
अतः, दूसरी समांतर भुजा की लंबाई 15cm होगी।
उदाहरण 5
एक समलम्बाकार क्षेत्र का क्षेत्रफल 270 वर्ग मीटर है और उसकी ऊंचाई 15 मीटर है। यदि समांतर भुजाओं में से एक, दूसरी की दोगुनी हो, तो दोनों समांतर भुजाओं की लंबाई ज्ञात कीजिए।
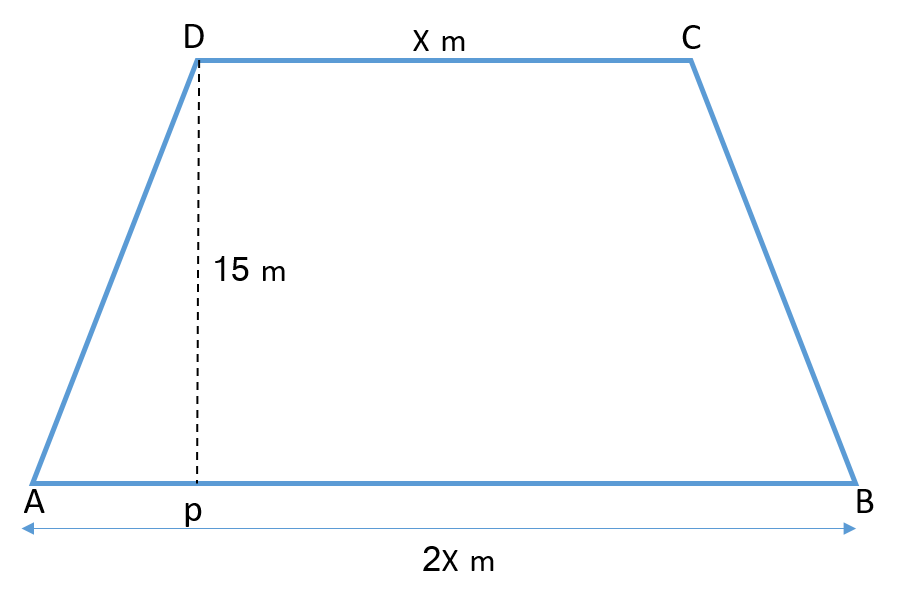
चूंकि हम जानते है कि समलंब चतुर्भुज की संगत भुजाओं का एक युग्म समांतर होता है। अतः
AB∣∣CD
ऊंचाई (DP)=15 मीटर
क्षेत्रफल =270 वर्ग मीटर
माना एक समांतर भुजा CD=x मीटर
दूसरी समांतर भुजा AB=2x मीटर
समलंब चतुर्भुज का क्षेत्रफल =12× ऊंचाई × समांतर भुजाओं का योग
270=12(AB+CD)×DP
⇒270=12(2x+x)×15
⇒270×215=3x
⇒270×215×3=x
⇒x=12 मीटर
अतः, पहली समांतर भुजा CD=x=12 मीटर
दूसरी समांतर भुजा AB=2x=2×12=24 मीटर
सामान्य चतुर्भुज का क्षेत्रफल
किसी भी चतुर्भुज का क्षेत्रफल ज्ञात करने के लिए एक विकर्ण खींचकर उसे दो त्रिभुजों में विभक्त किया जा सकता है और फिर दोनों त्रिभुजों के क्षेत्रफल की अलग-अलग गणना करके क्षेत्रफल की गणना आसानी से की जा सकती है।
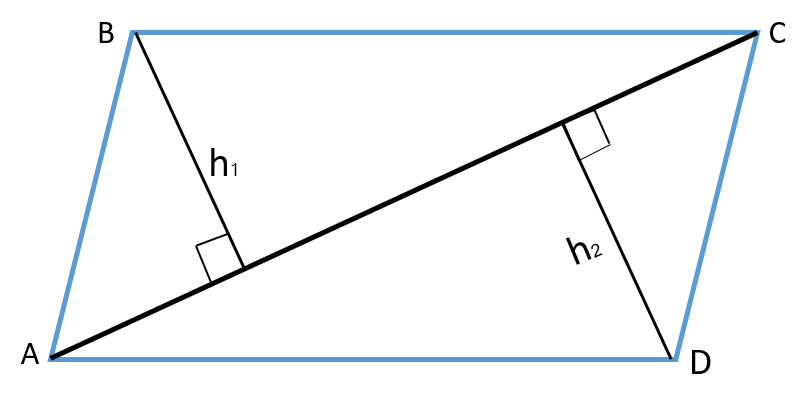
अतः, दी गई आकृति में,
ABCD एक चतुर्भुज हैं, AC विकर्ण खींचकर उसे दो त्रिभुजों में विभक्त किया गया हैं।
अतः, चतुर्भुज ABCD का क्षेत्रफल =ΔABC का क्षेत्रफल + ΔADC का क्षेत्रफल
=12×AC×h1+12×AC×h2
=12AC(h1+h2)
=12d(h1+h2)
यहाँ, h1 और h2 दोनों त्रिभुजों, ΔABC व ΔADC की ऊंचाई हैं और d उभयनिष्ठ विकर्ण अर्थात् AC की लंबाई है।
अतः, हम कह सकते हैं कि,
दो त्रिभुजों में विभक्त चतुर्भुज का क्षेत्रफल = 12× विकर्ण × चतुर्भुज के अन्य शीर्षों से खींचे गये लम्बों का योग
उदाहरण: चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
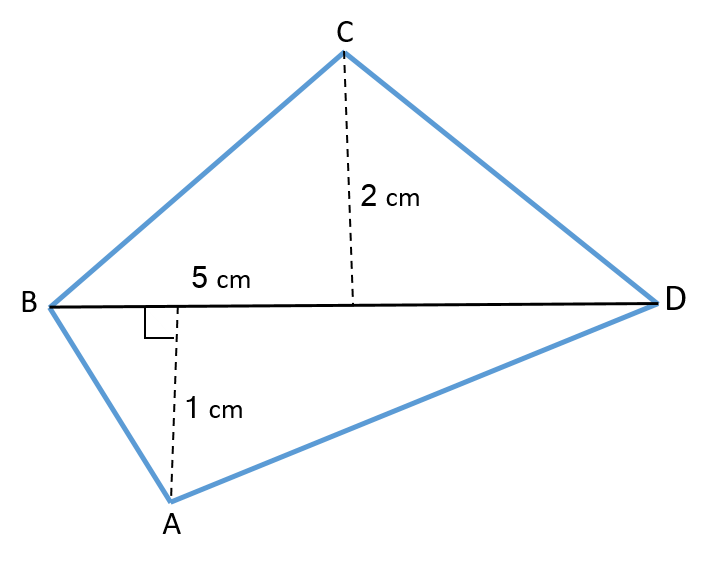
दिए गए चतुर्भुज ABCD में,
BD उभयनिष्ठ विकर्ण है इसलिए d=5 सेमी
दोनों त्रिभुजों की ऊंचाई h1=2 सेमी और h2=1 सेमी है।
चतुर्भुज ABCD का क्षेत्रफल =12d(h1+h2)
=12×5(2+1) वर्ग सेमी
=12×5×3 वर्ग सेमी
=7.5 वर्ग सेमी
विशेष चतुर्भुजों का क्षेत्रफल:
त्रिभुजों में विभक्त करने वाली इस विधि को हम समचतुर्भुज के क्षेत्रफल का सूत्र ज्ञात करने में उपयोग कर सकते हैं।
एक समचतुर्भुज एक चतुर्भुज होता है जिसकी सभी भुजाएँ समान और समांतर होती हैं लेकिन समकोण नहीं, इसके दो विकर्ण परस्पर लंब समद्विभाजक होते हैं।
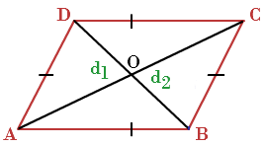
समचतुर्भुज ABCD का क्षेत्रफल = ΔACD का क्षेत्रफल + ΔABC का क्षेत्रफल
=12×AC×OD+12×AC×OB
=12AC(OD+OB) (यहाँ, OD+OB=BD=d2 और AC=d1)
=12AC×BD
=12d1×d2
अतः, समचतुर्भुज ABCD का क्षेत्रफल =12d1×d2
जहाँ, d1 और d2 विकर्ण हैं।
अतः हम कह सकते है, कि समचतुर्भुज का क्षेत्रफल विकर्णों के गुणनफल का आधा होता हैं।
OMR (One Minute Revision)

जहाँ, a और b समांतर भुजाएँ तथा h ऊंचाई हैं।
चतुर्भुज का क्षेत्रफल =12d(h1+h2)

जहाँ, h1 और h2 दोनों त्रिभुजों की ऊंचाई हैं और d उभयनिष्ठ विकर्ण है।

समचतुर्भुज का क्षेत्रफल =12d1×d2
जहाँ, d1 और d2 विकर्ण हैं।
उदाहरण 6
एक चतुर्भुज आकार के खेत का विकर्ण 24m है और सम्मुख शीर्षो से इस विकर्ण पर खींचे गए लंब 8m एवं 13m है खेत का क्षेत्रफल ज्ञात कीजिये।
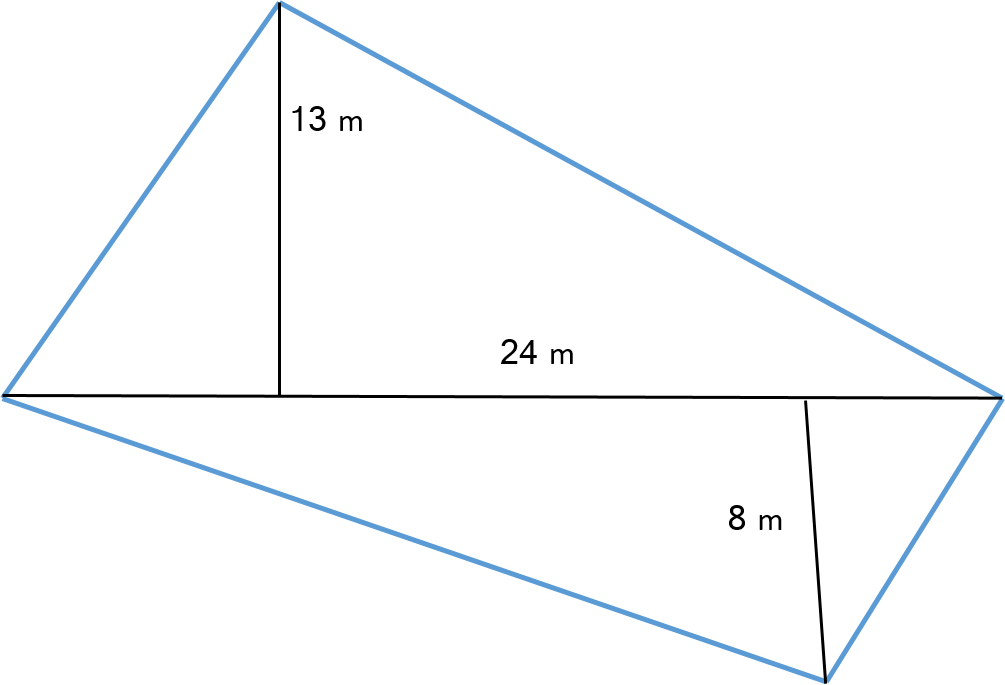
हम जानते हैं कि,
दो त्रिभुजों में विभक्त चतुर्भुज का क्षेत्रफल = 12 (विकर्ण × चतुर्भुज के अन्य शीर्षों से खींचे गये लम्बों का योग)
अर्थात, दो त्रिभुजों में विभक्त चतुर्भुज का क्षेत्रफल =12×d(h1+h2)
यहाँ, विकर्ण d=24m
तथा एक लंब की लंबाई h1=13m
तथा दूसरे लंब की ऊंचाई h2=8m
अत:, दिये गये चतुर्भुज का क्षेत्रफल =12×24(13+8)
=12×21=252m2
अतः, खेत का क्षेत्रफल 252m2 हैं।
Note: उपर्युक्त प्रश्न में दोनों त्रिभुजों का क्षेत्रफल ज्ञात करके योग करने से भी खेत का क्षेत्रफल प्राप्त किया जा सकता हैं।
उदाहरण 7
एक समचतुर्भुज का क्षेत्रफल 20cm2 है तथा इसके एक विकर्ण की लंबाई 4cm है, तो दूसरे विकर्ण की लंबाई क्या होंगी।
मान लीजिए,
एक विकर्ण की लंबाई d1=4cm
दूसरे विकर्ण की लंबाई =d2
समचतुर्भुज का क्षेत्रफल =20cm2
हम जानते हैं कि,
समचतुर्भुज का क्षेत्रफल =12d1×d2
अतः, 20=12×4×d2
⇒20=2×d2
⇒d2=202cm
⇒d2=10cm
अतः, दूसरे विकर्ण की लंबाई 10cm होंगी।
बहुभुज का क्षेत्रफल
बहुभुज के क्षेत्रफल के लिए कोई विशेष सूत्र नहीं है, इसलिए हमें इसे त्रिभुज, आयत, समलंब आदि में विभाजित करने की आवश्यकता होती है। सभी विभाजित आकृतियों के क्षेत्रफल को जोड़ने पर हमें बहुभुज का क्षेत्रफल प्राप्त हो जाता है।
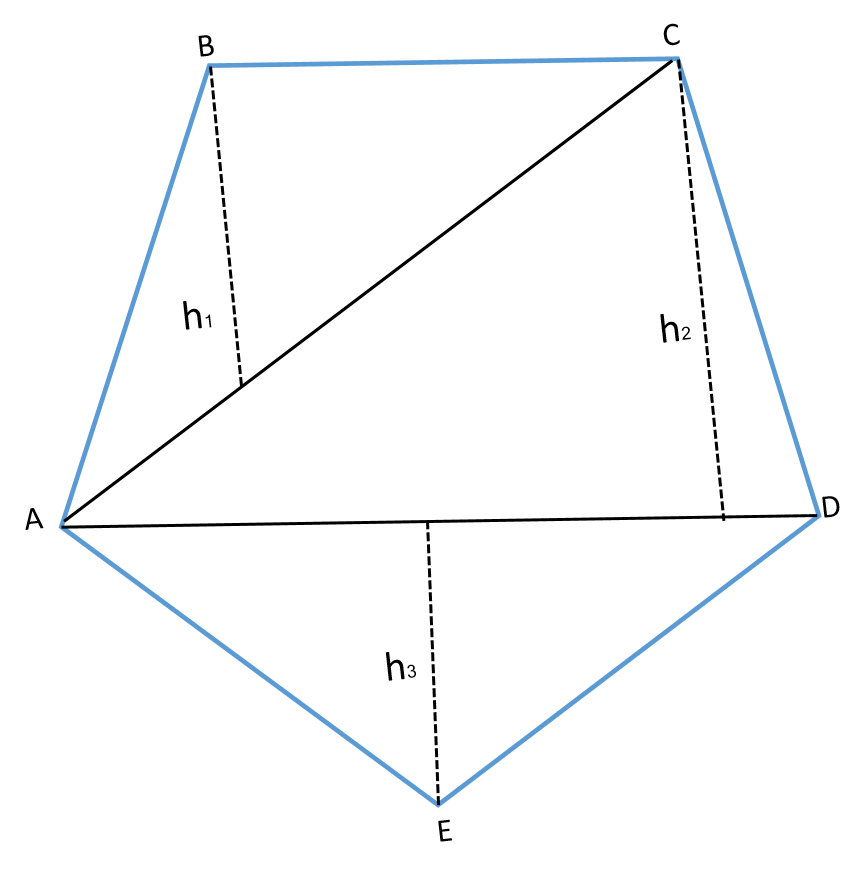
आकृति मे देख सकते है कि, विकर्ण AC तथा AD की रचना करते हुए पंचभुज ABCDE को तीन भागों में बाँटा गया है, इसलिए,
ABCDE का क्षेत्रफल = ΔABC का क्षेत्रफल + ΔADC का क्षेत्रफल + ΔAED का क्षेत्रफल
उदाहरण 8
एक ऊपर उठे हुए चबूतरे का ऊपरी पृष्ठ अष्टभुज के आकार का हैं, जैसा कि आकृति में दर्शाया गया हैं। अष्टभुजी पृष्ठ का क्षेत्रफल ज्ञात कीजिए।
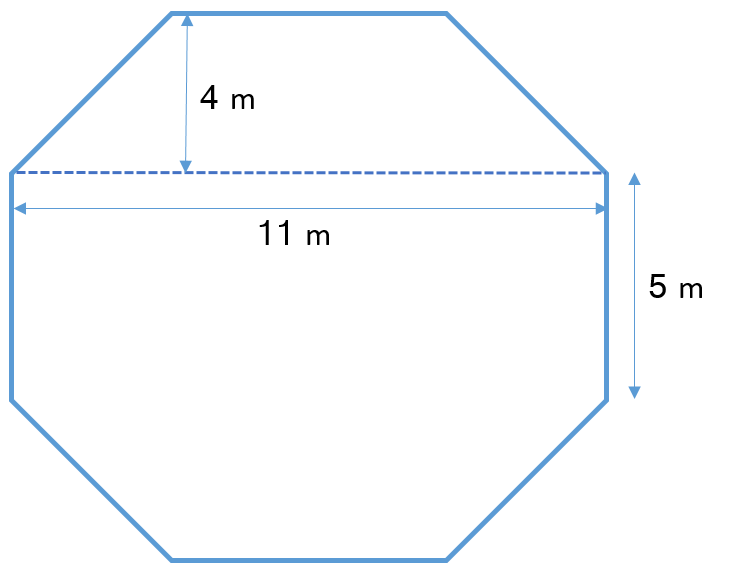
चूंकि, अष्टभुज की प्रत्येक भुजा की लंबाई =5m
अष्टभुज को तीन भागों में विभाजित किया जा सकता हैं, दो समलंब जिसकी समांतर भुजाएँ क्रमशः 11m और 5m है तथा लंबवत् दूरी 4m है और एक आयत, जिसकी लंबाई और चौड़ाई क्रमशः 11m और 5m है।
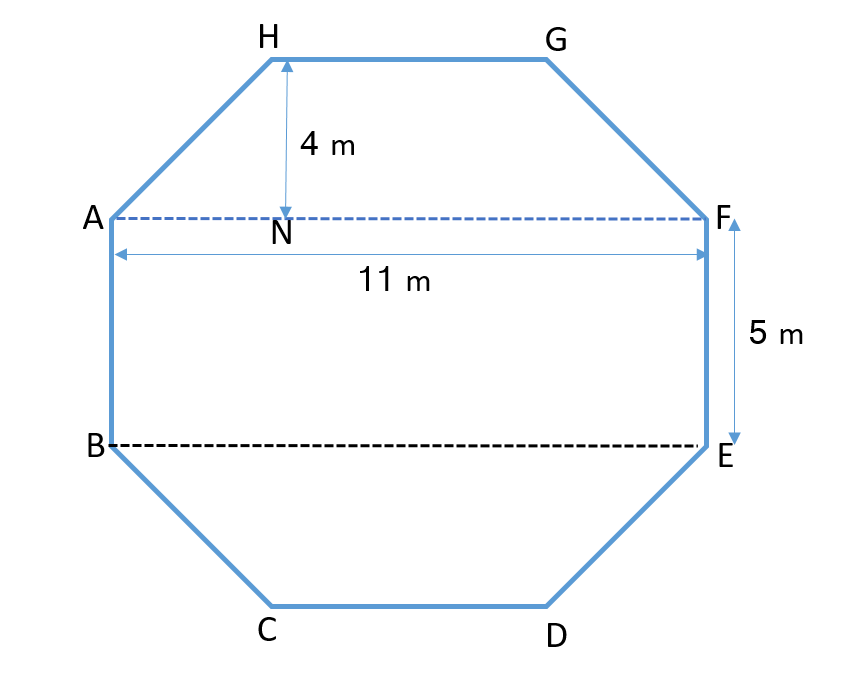
अतः, अष्टभुज आकार के चबूतरे का क्षेत्रफल = समलंब AFGH का क्षेत्रफल + आयत ABEF का क्षेत्रफल + समलंब BCDE का क्षेत्रफल
हम जानते हैं कि,
समलंब चतुर्भुज का क्षेत्रफल =12×समांतर भुजाओं का योग × ऊंचाई
माना, समांतर भुजा a=AF=11m
तथा समांतर भुजा b=HG=5m
तथा ऊंचाई h=HN=4m
∴ समलंब AFGH का क्षेत्रफल =12×(a+b)×h
=12×(11+5)×4
=12×16×4
=8×4=32m2
यहाँ, समलंब AFGH का क्षेत्रफल = समलंब BCDE का क्षेत्रफल =32m2
आयत ABEF का क्षेत्रफल = लंबाई × चौड़ाई
=AF×EF
=11×5=55m2
अष्टभुज आकार के चबूतरे का क्षेत्रफल =32m2+55m2+32m2=119m2
अत:, अष्टभुज आकार के चबूतरे का क्षेत्रफल 119m2 हैं।
ठोस आकार
हमें दैनिक जीवन में अनेक ठोस, जैसे ईंट, बक्सा, माचिस की डिबिया, प्लेट, जग, डस्टर आदि देखने को मिलते हैं। इन आकृतियों में लंबाई, चौड़ाई तथा ऊंचाई होती हैं, इसलिए इन्हें त्रिविमीय (three dimension) (3D) आकृति कहते हैं। तीन विमाओं वाली आकृति को घनाकृति या ठोस (solid) भी कहते हैं।
जैसे -
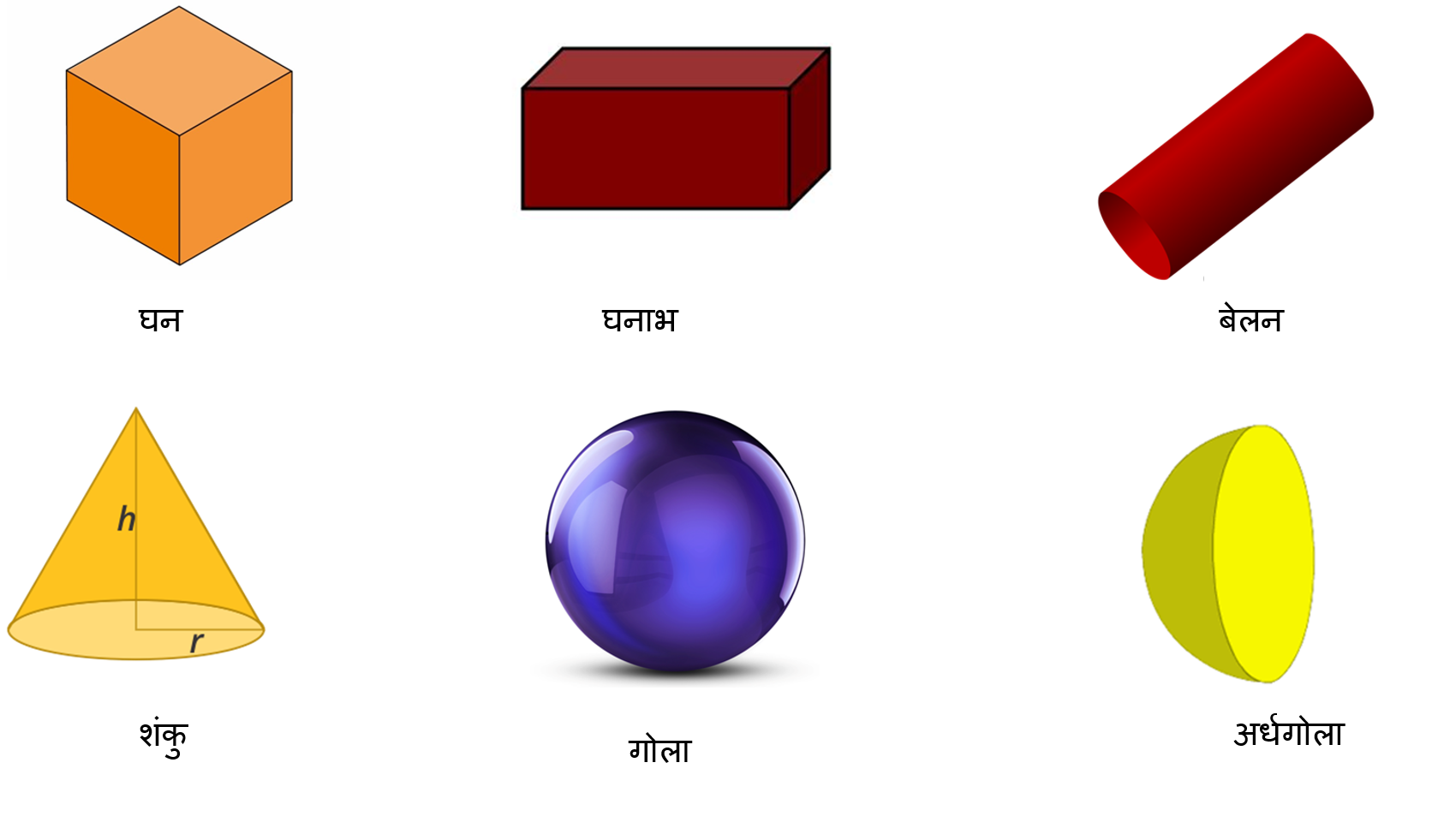
घन, घनाभ और बेलन का पृष्ठीय क्षेत्रफल
किसी त्रिविमीय या ठोस वस्तु की सतह का कुल क्षेत्रफल उसका पृष्ठीय क्षेत्रफल कहलाता है।
घनाभ (Cuboid): छः आयताकार पृष्ठों से घिरी आकृति को घनाभ कहते हैं।
जैसै - दियासलाई की डिबिया, ईंट, बक्सा आदि।
घनाभ के आमने-सामने के पृष्ठ (फलक) बराबर तथा समांतर होते हैं। घनाभ में 12 किनारे (कोर), 8 कोने (शीर्ष) और 6 फलक होते हैं। विपरीत शीर्षों (opposite vertices) को मिलाने वाली रेखा घनाभ का विकर्ण कहलाता है। घनाभ में कुल चार विकर्ण होते हैं जिनकी लंबाई बराबर होती हैं।
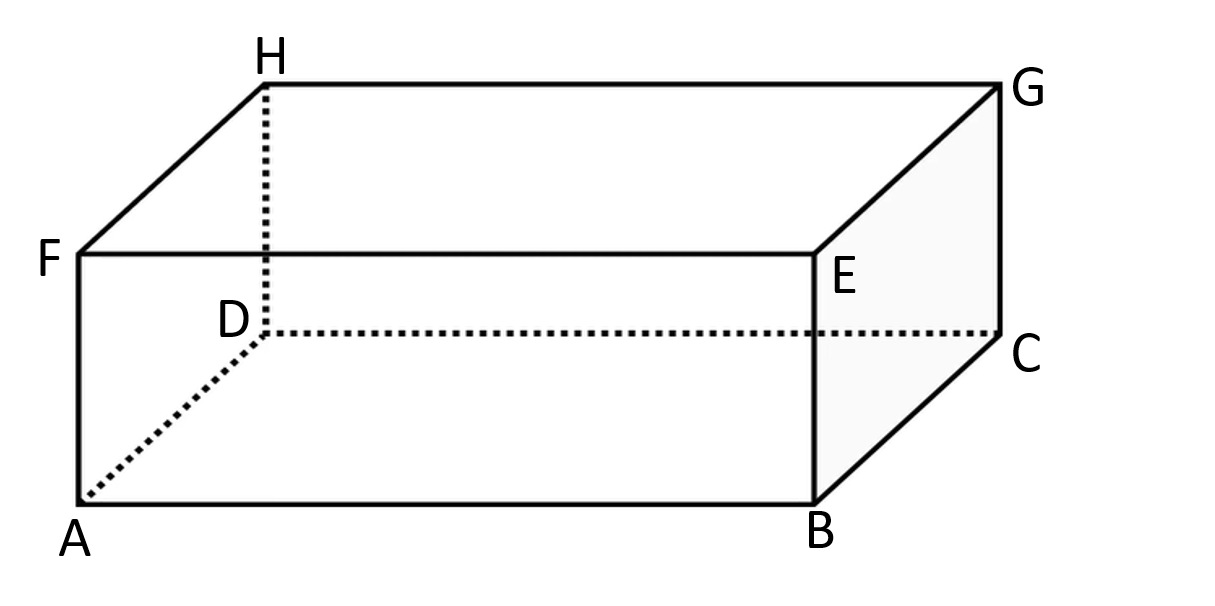
अतः चित्र में देख सकते हैं की, एक घनाभ है जिसमें AB लंबाई, BC चौड़ाई तथा EB ऊंचाई है। आमने-सामने के पृष्ठ ABCD, FEGH बराबर तथा समांतर हैं। इसी प्रकार AFHD, BEGC बराबर और समांतर है एवं पृष्ठ ABEF तथा DCGH भी बराबर और समांतर हैं। BH, AG, CF तथा DE घनाभ के विकर्ण हैं।
घनाभ का पृष्ठीय क्षेत्रफल
माना कि, घनाभ की लंबाई =l, चौड़ाई =b तथा ऊंचाई =h हैं।
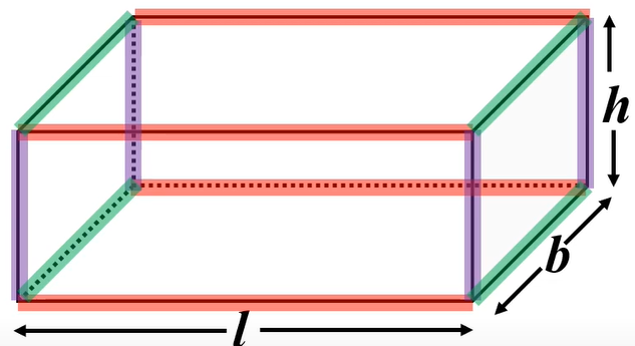
चूंकि घनाभ के फलक आयताकार होते हैं।

घनाभ का कुल क्षेत्रफल, छः आयताकार फलकों के क्षेत्रफल का योग होगा।
फलक I का क्षेत्रफल =l×b
फलक II का क्षेत्रफल =l×b
फलक III का क्षेत्रफल =l×h
फलक IV का क्षेत्रफल =l×h
फलक IV का क्षेत्रफल =b×h
फलक V का क्षेत्रफल =b×h
घनाभ का कुल क्षेत्रफल = फलक I का क्षेत्रफल + फलक II का क्षेत्रफल + फलक III का क्षेत्रफल+ फलक IV का क्षेत्रफल + फलक V का क्षेत्रफल + फलक VI का क्षेत्रफल
=l×b+l×b+l×h+l×h+b×h+b×h
=2(l×b)+2(l×h)+2(b×h)
अतः घनाभ का कुल पृष्ठीय क्षेत्रफल =2(l×b+l×h+b×h)
घन (Cube): घन एक ऐसी त्रिविमीय आकृति को कहा जाता है जिसकी लंबाई, चौड़ाई एवं ऊंचाई सामान होती हैं। एक घन में 6 फलक, 12 किनारे एवं 8 कोने होते हैं।
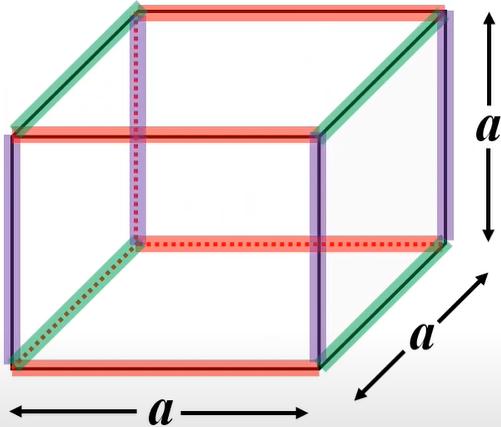
जैसे - पासा, रुबिक्स क्यूब (rubik's cube)।

घन के सभी फलक वर्गाकार होते हैं क्योंकि इसके सभी भुजाओं (किनारों) की लंबाई समान होती है। वास्तव में घनाभ जिसकी लंबाई, चौड़ाई और ऊंचाई बराबर हों एक घन (cube) कहलाता है।
लंबाई = चौड़ाई = ऊंचाई
l=b=h=a
घन का पृष्ठीय क्षेत्रफल
हम जानते हैं कि,
घनाभ का कुल पृष्ठीय क्षेत्रफल =2(l×b+l×h+b×h)
∴घन का कुल पृष्ठीय क्षेत्रफल =2(a×a+a×a+a×a)
=2(a2+a2+a2)
=2(3a2)
अतः घन का कुल पृष्ठीय क्षेत्रफल =6a2
पार्श्व पृष्ठीय क्षेत्रफल (Lateral surface area)
मान लीजिए हम घनाभ और घन के छः फलकों (faces) में से केवल चार फलकों के क्षेत्रफल, निचले और ऊपरी फलकों को छोड़कर (फलक I और II को छोड़कर) ज्ञात करें। ऐसी स्थिति में, इन चारों फलकों का क्षेत्रफल पार्श्व पृष्ठीय क्षेत्रफल कहलाता है।
जैसे की अगर हम एक कमरे को देखे, तो अगर फर्श को और छत को छोड़कर बाकी के चारों दीवारों आगे, पीछे, दाएं और बाएं का क्षेत्रफल मिलाकर पार्श्व पृष्ठीय क्षेत्रफल हैं।
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल = फलक III का क्षेत्रफल + फलक IV का क्षेत्रफल + फलक V का क्षेत्रफल + फलक VI का क्षेत्रफल
=l×h+l×h+b×h+b×h
=2(l×h+b×h)
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल =2h(l+b)
इसी प्रकार, घन का पार्श्व पृष्ठीय क्षेत्रफल
चूंकि घन में, लंबाई = चौड़ाई = ऊंचाई
अतः घन का पार्श्व पृष्ठीय क्षेत्रफल =2a(a+a)
=2a(2a)
घन का पार्श्व पृष्ठीय क्षेत्रफल =4a2
बेलन: यदि आयत की एक भुजा स्थिर हो और आयत इस स्थिर भुजा के चारों ओर घूमे तो घूमने से जो पिण्ड बनता है उसे लंब वृत्तीय बेलन (right circular cylinder) कहते हैं या जब कोई रेखा किसी वृत्त की परिधि पर इस प्रकार घूमे कि वह वृत्त के तल पर हमेशा लंब रहे तो घूमने से जो पिण्ड बनता है उसे लंब वृत्तीय बेलन कहते हैं।
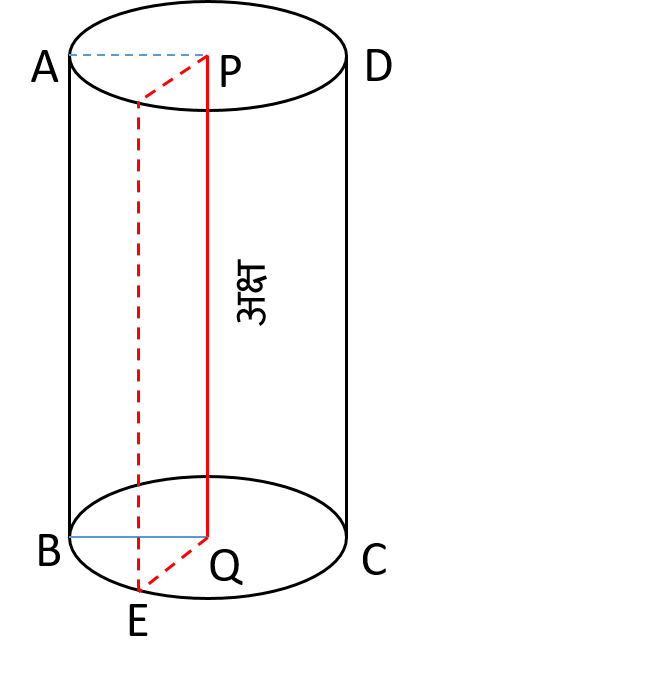
चित्र में रेखा AB के वृत्त BEC की परिधि पर घूमने से लम्ब वृत्तीय बेलन बनता है। घूमने वाली रेखा AB जनक रेखा (generating line) तथा केन्द्रों को मिलाने वाली रेखा PQ बेलन का अक्ष है। वृत्त BEC बेलन का आधार है।
यदि कागज के बहुत सारे वृत्ताकार शीटों को एक के ऊपर एक आधार के लम्बवत् h ऊंचाई तक रखा जाय तो, इस तरह से प्राप्त ठोस (पिण्ड) एक लंब वृत्तीय बेलन होगा। वृत्त की त्रिज्या बेलन की त्रिज्या कहलाती है तथा यदि वृत्ताकार शीटों को h ऊंचाई तक रखा गया है तो बेलन की ऊंचाई h होगा।
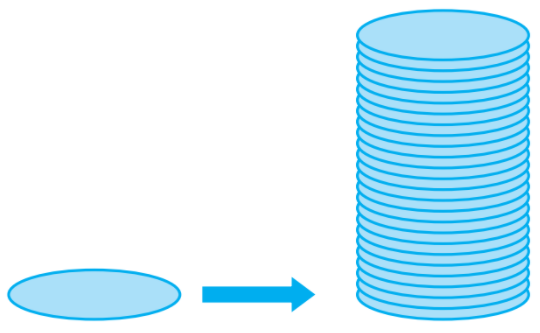
लंब वृत्तीय बेलन का आधार तथा ऊपरी सतह वृत्ताकार होता है। यदि इस वृत्त की त्रिज्या r हो तो दोनों वृत्ताकार सतहों का क्षेत्रफल (πr2+πr2) 2πr2 होगा।
बेलन का वक्र पृष्ठीय क्षेत्रफल
बेलन का वक्र पृष्ठ जानने के लिए एक खोखला बेलन लेते हैं और अक्ष के समांतर इसे काटकर जमीन पर फैला दिया तो पूरा पृष्ठ एक आयत के रूप में बदल गया जिसकी लंबाई बेलन के आधार की परिधि होगी तथा चौड़ाई बेलन की ऊंचाई होगी।
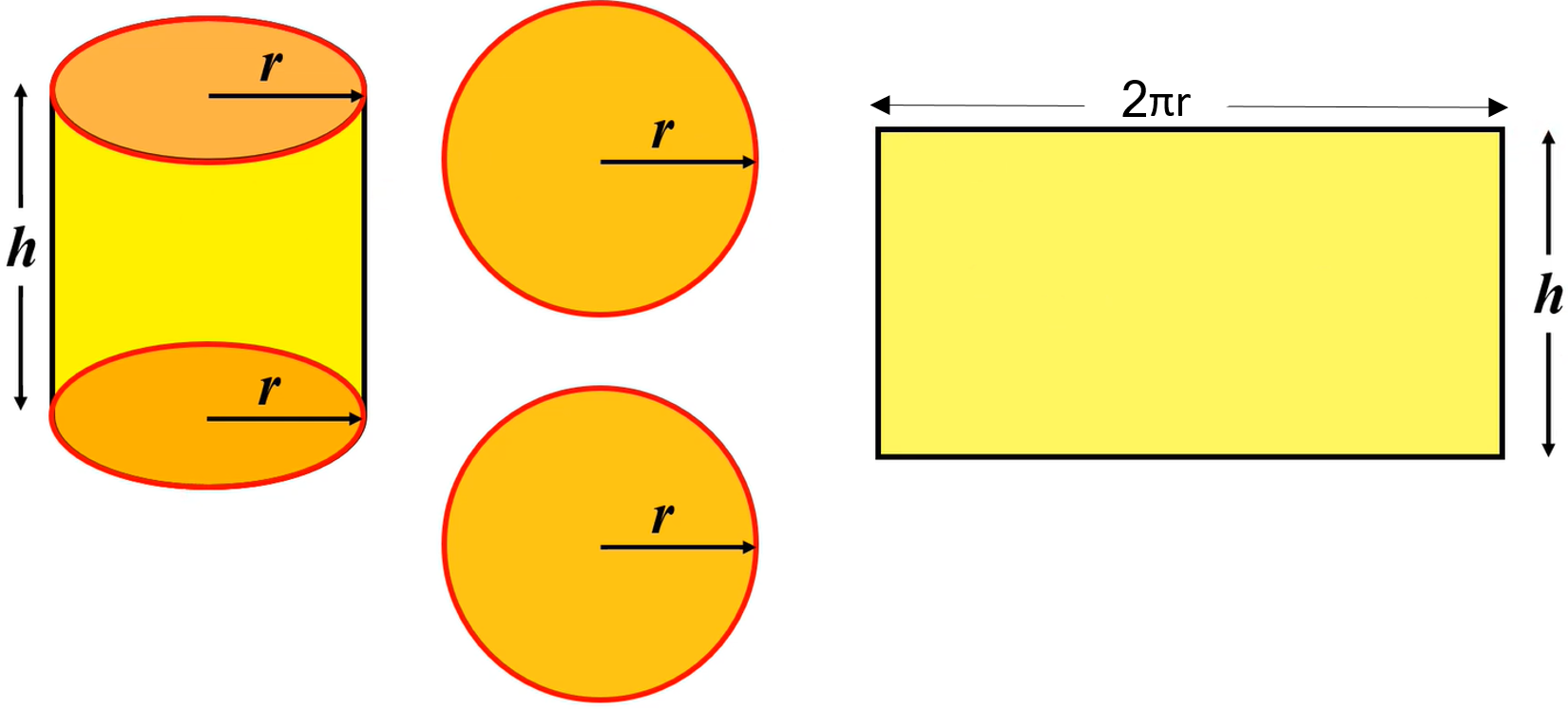
बेलन का वक्र पृष्ठीय क्षेत्रफल = आधार की परिमाप × ऊंचाई
चूंकि यहाँ आधार वृत्ताकार हैं और हम जानते हैं की वृत्त का परिमाप 2πr होता हैं।
∴ बेलन का वक्र पृष्ठीय क्षेत्रफल =2πr×h
अतः बेलन का वक्र पृष्ठीय क्षेत्रफल =2πrh
जहाँ r बेलन की त्रिज्या और h ऊंचाई है।
बेलन का कुल पृष्ठीय क्षेत्रफल
हम कागज का एक आयताकार शीट लेते हैं जिसकी लंबाई l तथा ऊंचाई h है यदि हम इस कागज को l की दिशा में गोल - गोल मोड़े तो हमे h ऊंचाई का एक बेलन प्राप्त होता हैं।
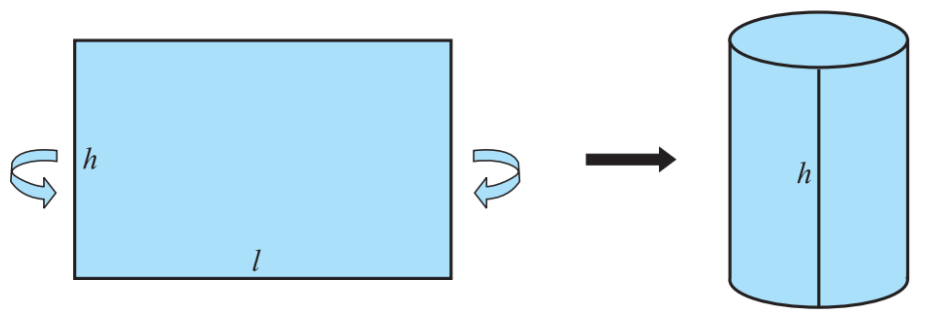
यदि बेलन के ऊपरी और निचले सिरों को भी कागज से ढकना हो, तो 2 वृत्तों ( वृत्ताकार क्षेत्रों ) की आवश्यकता होगी, जिनमे से प्रत्येक की त्रिज्या r और क्षेत्रफल πr2 होगा।
अतः बेलन का कुल पृष्ठीय क्षेत्रफल
= बेलन के दोनों आधारों का क्षेत्रफल + बेलन का वक्रपृष्ठ का क्षेत्रफल
=(πr2+πr2)+2πr×h
=2πr2+2πrh
=2πr(r+h)
अतः बेलन का कुल पृष्ठीय क्षेत्रफल =2πr(r+h)
OMR (One Minute Revision)
| आकार | सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) | पार्श्व / वक्र पृष्ठीय क्षेत्रफल (वर्ग इकाई) | |
|---|---|---|---|
| घनाभ | 2(l×b+l×h+b×h) | 2h(l+b) | l= लंबाई b= चौड़ाई h= ऊंचाई | घन | 6a2 | 4a2 | a= घन का किनारा | बेलन | 2πr(r+h) | 2πrh | r= बेलन की त्रिज्या h= ऊंचाई |
उदाहरण 9
एक घनाभ की लंबाई, चौड़ाई तथा ऊंचाई क्रमश: 75 सेमी, 40 सेमी और 30 सेमी है। इस घनाभ को रंगीन कागज से ढकने के लिए कितने क्षेत्रफल के कागज की आवश्यकता होगी?
माना कि,
घनाभ की लंबाई l=75 सेमी
घनाभ की चौड़ाई b=40 सेमी
घनाभ की ऊंचाई h=30 सेमी
घनाभ का सम्पूर्ण पृष्ठ का क्षेत्रफल =?
हम जानते हैं कि,
घनाभ का सम्पूर्ण पृष्ठ का क्षेत्रफल
=2(l×b+l×h+b×h)
=2(75×40+75×30+40×30)
=12900 सेमी 2
अतः, घनाभ को रंगीन कागज से ढकने के लिए 12900 सेमी 2 क्षेत्रफल के कागज की आवश्यकता होगी।
उदाहरण 10
एक घन की भुजा ज्ञात कीजिये जिसका पृष्ठीय क्षेत्रफल 3174 सेमी2 है।
दिया हैं,
घन का कुल पृष्ठीय क्षेत्रफल =3174 सेमी 2
हम जानते हैं कि,
घन का कुल पृष्ठीय क्षेत्रफल =6a2
जहाँ, a घन की भुजा हैं।
∴6a2=3174
⇒a2=31746
⇒a2=529
⇒a=23 सेमी
उदाहरण 11
निम्नलिखित बेलन का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
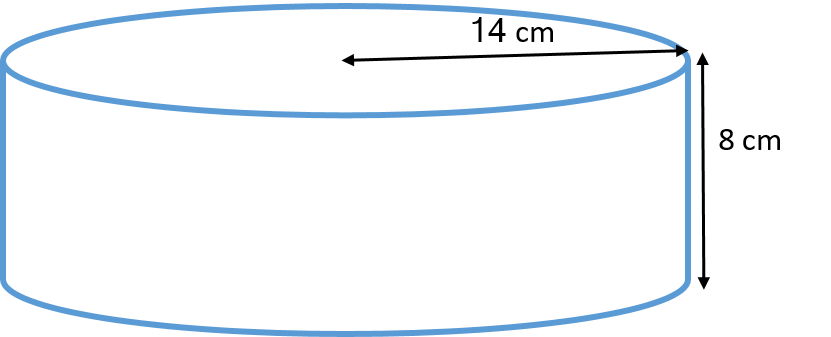
माना दिए गए बेलन मे,
बेलन की त्रिज्या r=14cm
बेलन की ऊंचाई h=8cm
हम जानते हैं कि,
बेलन का कुल पृष्ठीय क्षेत्रफल =2πr(r+h)
=2π×14(14+8)
=2×227×14(14+8)
=1936 सेमी 2
अतः, बेलन का कुल पृष्ठीय क्षेत्रफल =1936 सेमी 2
घन, घनाभ और बेलन का आयतन
किसी त्रिविमीय या ठोस वस्तु द्वारा घिरी हुई जगह उसका आयतन कहलाता है।
जैसे, गेंद, डस्टर, पुस्तक ये सभी चीजे अपना एक स्थान घेरती हैं और ये जितना स्थान घेरती हैं आयतन कहलाता हैं।
जैसे, किसी बाल्टी में जीतना पानी आ सकता हैं, वही उस बाल्टी का आयतन होगा।
घनाभ का आयतन: यदि किसी घनाभ की लंबाई, चौड़ाई तथा ऊंचाई क्रमशः l,b,h हैं, तब
घनाभ का आयतन = लंबाई × चौड़ाई × ऊंचाई
∴ घनाभ का आयतन =l×b×h
चूंकि हम जानते हैं कि घन की लंबाई, चौड़ाई तथा ऊंचाई तीनों समान होती हैं।
∴l=b=h=a (माना )
अतः घन का आयतन =a×a×a=a3
बेलन का आयतन
माना कि लंब वृत्तीय बेलन की ऊंचाई h, आधार की त्रिज्या r तथा आयतन V है।
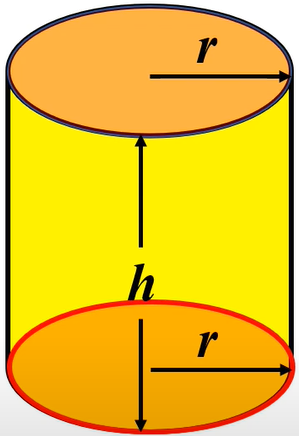
बेलन का आयतन = आधार का क्षेत्रफल × ऊंचाई
V=πr2×h
अतः बेलन का आयतन V=πr2h
Note: आयतन का मात्रक (unit) घन लंबाई का मात्रक होता है। जैसे - घन मिमी, घन सेमी, घन मीटर आदि।
OMR (One Minute Revision)
| आकार | आयतन (घन इकाई) | |
|---|---|---|
| घनाभ | l×b×h | l= लंबाई b= चौड़ाई h= ऊंचाई |
| घन | a3 | a= घन का किनारा | बेलन | πr2h | r= बेलन के आधार की त्रिज्या h= ऊंचाई |
उदाहरण 12
यदि किसी घनाभ के आधार का क्षेत्रफल 25cm2 है तथा उसकी ऊंचाई 10cm है तब उसका आयतन होगा।
दिया हैं,
घनाभ के आधार का क्षेत्रफल =25cm2
तथा ऊंचाई h=10cm
आयतन =?
चूंकि घनाभ के आधार का क्षेत्रफल = लंबाई × चौड़ाई =25cm2
हम जानते हैं कि,
घनाभ का आयतन = लंबाई × चौड़ाई × ऊंचाई
=25cm2×10cm=250cm3
उदाहरण 13
यदि एक घन का आयतन 512 सेमी3 है, तो इस घन के सभी पृष्ठों का कुल क्षेत्रफल ज्ञात कीजिये।
दिया हैं,
घन का आयतन =512 सेमी 3
घन का कुल पृष्ठीय क्षेत्रफल =?
हम जानते हैं कि,
घन का आयतन =a3
जहाँ, a घन की भुजा हैं।
∴a3=512
⇒a=3√512
⇒a=3√8×8×8
⇒a=8 सेमी
चूंकि, घन का कुल पृष्ठीय क्षेत्रफल =6×a2
=6×82
=6×64=384 सेमी 2
अतः, घन के सभी पृष्ठों का कुल क्षेत्रफल =384 सेमी 2
उदाहरण 14
एक बेलन के वृत्ताकार पृष्ठ की परिधि 44 सेमी है और इसकी ऊंचाई 60 सेमी है। बेलन का आयतन ज्ञात कीजिये।
दिया है,
बेलन की ऊंचाई (h)=60 सेमी
बेलन के वृत्ताकार पृष्ठ की परिधि (2πr) =44 सेमी
2πr=44
2×227×r=44
r=7 सेमी
हम जानते हैं कि,
बेलन का आयतन =πr2h
=227×7×7×60
=22×7×60
=154×60
=9240 सेमी 3
अतः, बेलन का आयतन =9240 सेमी 3
आयतन और धारिता
आयतन किसी भी वस्तु द्वारा घेरे जाने वाले कुल स्थान को कहते हैैं अर्थात यदि किसी वस्तु को जल में डुबोया जाय तो वह जल की जितनी मात्रा को विस्थापित करता है वह उसका आयतन कहलाता है। आयतन को घन मिमी, घन सेमी, घन मीटर से मापा जाता है।
धारिता का अर्थ होता है धारण करने की क्षमता अर्थात किसी पात्र या बर्तन में हवा, जल या कोई अन्य द्रव आदि अधिकतम कितनी मात्रा में भरे जा सकते हैं वह उसकी धारिता कहलाता है। धारिता को लीटर या मिलीलीटर में मापा जाता है।
नोट: यदि किसी पानी रखे जाने वाले टिन के बर्तन में 100cm3 पानी भरा जा सकता है तो उस टिन के बर्तन की धारिता 100cm3 है।
लीटर और cm3 में निम्नलिखित संबंध है:
1L=1000mL
1mL=1cm3
1L=1000cm3
1m3=1000000cm3=1000L
उदाहरण 15
एक कुंड के अंदर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन 108m3 है, तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?

चूंकि दिया गया है,
कुंड का आयतन =108m3
∵ 1m3=1000 l
∴108m3=108000 l
चूंकि 60 l भरने मे 1 मिनट लगती है।
अतः 108000 l भरने मे लगा कुल समय =
=10800060
=54003
=1800 मिनट
180060=30 घंटे (चूंकि 1 घंटे मे 60 मिनट होती है।)
सारांश
- समलंब का क्षेत्रफल
(i) समलंब का क्षेत्रफल = समांतर भुजाओं की लंबाइयों के योग का आधा × उनके बीच की लंबवत् दूरी
(ii) समचतुर्भुज का क्षेत्रफल = विकर्णो के गुणनफल का आधा
- एक ठोस का पृष्ठीय क्षेत्रफल इसके फलकों के क्षेत्रफलों के योग के समान होता है।
आकार सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) पार्श्व / वक्र पृष्ठीय क्षेत्रफल (वर्ग इकाई) घनाभ 2(l×b+l×h+b×h) 2h(l+b) l= लंबाई
b= चौड़ाई
h= ऊंचाईघन 6a2 4a2 a= घन का किनारा बेलन 2πr(r+h) 2πrh r= बेलन की त्रिज्या
h= ऊंचाई
- किसी ठोस द्वारा घिरी हुई जगह की मात्रा उसका आयतन कहलाती है।
आकार आयतन (घन इकाई) घनाभ l×b×h l= लंबाई
b= चौड़ाई
h= ऊंचाईघन a3 a= घन का किनारा बेलन πr2h r= बेलन के आधार की त्रिज्या
h= ऊंचाई
- (i) 1cm3=1mL
(ii) 1L=1000cm3
(in) 1m3=1000000cm3=1000L
