संख्याओं के साथ खेलना कक्षा 8 गणित
भूमिका
बच्चों! हमने विभिन्न प्रकार की संख्याओं जैसे प्राकृत संख्याओं, पूर्ण संख्याओं, पूर्णांकों और परिमेय संख्याओं के बारे में बारे में पढ़ा है। इनके अनेक रोचक गुणों का भी अध्ययन किया हैं। इस अध्याय में, हम संख्याओं के बारे में और अधिक विस्तृत जानकारी प्राप्त करेंगे तथा विभाज्यता के नियमों की जाँच (tests of divisibility) का भी अध्ययन करेंगे।
आइये जानते है, संख्याओं को और करीब से...
बच्चों! हम जानते हैं कि, प्राकृत संख्या, पूर्ण संख्या, पूर्णांक और परिमेय संख्या ये सभी संख्याओं के प्रकार हैं।
प्राकृतिक या प्राकृत संख्याएँ (Natural Numbers): एक से लेकर अनंत तक की संख्याएँ, प्राकृतिक संख्याएँ कहलाती हैं।
जैसे - 1,2,3,4,5.......∞
पूर्ण संख्याएँ (Whole Numbers): शून्य से लेकर अनंत तक की संख्याएँ, पूर्ण संख्याएँ कहलाती हैं।
जैसे - 0,1,2,3,4.......∞
पूर्णांक (Integers): ऋणात्मक अनंत से शून्य तक एवं शून्य से अनंत तक की संख्याएँ, पूर्णांक कहलाती हैं।
जैसे - −∞.......–4,–3,–2,–1,0,1,2,3,4,.......∞
परिमेय संख्याएँ (Rational Numbers): वे सभी संख्याएँ जिन्हें PQ (जहाँ Q≠0) रूप में लिखा जा सकता है, परिमेय संख्याएँ कहलाती है। यहाँ P तथा Q धानात्मक पूर्णांक या पूर्ण संख्याएँ हैं।
जैसे - 51,74,95
व्यापक रूप में संख्याएँ
किसी संख्या को व्यापक रूप मे लिखना संख्या को विस्तारित रूप मे लिखने के जैसा ही हैं।
हमने पिछली कक्षाओं में संख्याओं के स्थानीय मान के बारे में पढ़ा हैं।
किसी दी हुई संख्या का स्थानीय मान निकालने के लिए सर्वप्रथम यह देखते हैं कि वह संख्या इकाई, दहाई, सैकड़ा, हज़ार, दस हज़ार, लाख, दस लाख करोड़, दस करोड़, अरब दस अरब, आदि में किस स्थान पर स्थित है, इसके बाद किसी अंक का स्थानीय मान निकालने के लिए उस स्थान से दाएं ओर तक के पूरे मान से उस अंक को गुणा करके प्राप्त करते हैं।
किसी संख्या का व्यापक रूप अंकों के गुणनफल को उनके स्थानीय मान के साथ जोड़कर प्राप्त किया जाता है।
आइए समझते हैं:
दो अंकों की संख्या के लिए:
व्यापक रूप में, अंकों a,b से बनी किसी दो अंकों की संख्या ab को इस रूप में लिखा जा सकता है:
ab=10×a+1×b
⇒ab=10a+b
यहाँ दो अंको की संख्या में a (दहाई अंक) का मान 1 से 9 तक के अंक तथा b (इकाई अंक ) का मान 0 से लेकर 9 तक के अंक हो सकते हैं।
जैसे: 56=10×5+1×6=50+6
25=10×2+5×1=20+5
85=10×8+5×1=80+5
नोट: संख्याओं में ab=a×b नहीं होता है। जैसे 56 को 5×6 नहीं लिखा जा सकता है
तीन अंकों की संख्या के लिए:
व्यापक रूप में, अंकों a,b और c से बनी किसी तीन अंकों की संख्या abc को इस रूप में लिखा जा सकता है:
abc=100×a+10×b+1×c
⇒abc=100a+10b+c
यहाँ a,b,c बीजीय अंक है तथा a शून्येतर अंक और b तथा c शून्य से लेकर 9 तक का कोई अंक हैं। (शून्येतर →0 को छोड़कर, 1 से 9 तक का कोई भी अंक)
यदि a शून्य हो जाए तो व्यापक संख्या 10b+c हो जाती है।
जैसे: 579=100×5+10×7+1×9=500+70+9
125=100×1+10×2+1×5=100+20+5
875=100×8+10×7+1×5=800+70+5
इसी प्रकार, तीन से अधिक अंकों वाली संख्याओं को भी व्यापक रूप में लिखा जा सकता हैं।
OMR (One Minute Revision)
व्यापक रूप में दो अंकों की संख्या
ab=10a+b
व्यापक रूप में तीन अंकों की संख्या
abc=100a+10b+c
जहाँ, a,b,c⇒0 से 9 तक के अंक तथा a≠0
उदाहरण 1
73 को व्यापक रूप में लिखिए।
∵ab को व्यापक रूप में लिखा जा सकता हैं:
ab=10×a+1×b=10a+b
∴73 का व्यापक रूप
73=10×7+1×3 =70+3
उदाहरण 2
302 को व्यापक रूप में लिखिए।
∵abc को व्यापक रूप में लिखा जा सकता हैं:
abc=100×a+10×b+1×c=100a+10b+c
∴302 का व्यापक रूप
302=100×3+10×0+1×2 =300+2
उदाहरण 3
उदाहरण 4
संख्याओं के साथ खेल
अंकों का पलटना - दो अंकों की संख्या:
चरण 1: आइए हम कोई दो अंकों की संख्या ab लेते हैं, जिसे (10a+b) के रूप में लिखा जा सकता है।
चरण 2: ab की विपरीत संख्या ba होगी, जिसे (10b+a) के रूप में लिखा जा सकता है।
चरण 3: दोनों संख्याओं का योग ab+ba है, हम इसे (10a+b)+(10b+a)=11a+11b=11(a+b) के रूप में भी लिख सकते हैं।
चरण 4: संख्या को 11 से विभाजित करने पर हमें 11(a+b)11=(a+b) प्राप्त होता है।
स्पष्टतः यहाँ शेषफल शून्य तथा भागफल a+b है, जो दी गई संख्या ab के अंकों का योग है।
जैसे: 68
दी गई संख्या =68
68 की विपरीत संख्या =86
दोनो संख्याओं का योग =68+86=154
15411=14 ; शेषफल =0
चरण 1: आइए हम कोई दो अंकों की संख्या ab लेते हैं, जिसे (10a+b) के रूप में लिखा जा सकता है।
चरण 2: ab की विपरीत संख्या ba होगी, जिसे (10b+a) के रूप में लिखा जा सकता है।
चरण 3: अब दोनो संख्याओं में बड़ी संख्या में से छोटी संख्या को घटाते हैं।
यदि दहाई का अंक इकाई के अंक से बड़ा है (अर्थात् a>b है), तो वह इस प्रकार घटता है :
ab−ba
=(10a+b)−(10b+a)
=10a+b−10b−a
=9a−9b
=9(a−b)
यदि दहाई का अंक इकाई के अंक से बड़ा है (अर्थात् a<b है), तो वह इस प्रकार घटता है :
ba−ab
=(10b+a)−(10a+b)
=10b+a−10a−b
=9b−9a
=9(b−a)
चरण 4: संख्या को 9 से विभाजित करने पर हमें 9(a−b)9=(a−b) या 9(b−a)9=(b−a) प्राप्त होता है।
स्पष्टतः यहाँ शेषफल शून्य तथा भागफल a−b या b−a है, जो दी गई संख्या ab के अंकों का व्यवकलन है।
जैसे: 68
दी गई संख्या =68
68 की विपरीत संख्या =86
दोनो संख्याओं का व्यवकलन =86−68=18
189=2; शेषफल =0
अंकों का पलटना - तीन अंकों की संख्या:
चरण 1: आइए कोई तीन अंकों की संख्या abc लेते हैं जिसे (100a+10b+c) के रूप में लिखा जा सकता है।
चरण 2: abc की विपरीत संख्या cba होगी, जिसे (100c+10b+a) के रूप में लिखा जा सकता है।
चरण 3: अब दोनो संख्याओं में बड़ी संख्या में से छोटी संख्या को घटाते हैं।
यदि a>c हो, तो संख्याओं का अंतर:
abc−cba
=(100a+10b+c)−(100c+10b+a)
=100a+10b+c−100c−10b−a
=99a−99c
=99(a−c)
यदि a<c हो, तो संख्याओं का अंतर:
cba−abc
=(100c+10b+a)−(100a+10b+c)
=100c+10b+a−100a−10b−c
=99c−99a
=99(c−a)
चरण 4: संख्या को 99 से विभाजित करने पर हमें 99(a−c)99=(a−c) या 99(c−a)99=(c−a) प्राप्त होता है।
स्पष्टतः यहाँ शेषफल शून्य तथा भागफल a−c या c−a है, जो दी गई संख्या ac के अंकों का व्यवकलन है।
जैसे: 784
दी गई संख्या =784
784 की विपरीत संख्या =487
दोनो संख्याओं का व्यवकलन =784−487=297
29799=3 ; शेषफल =0
दिए हुए तीन अंकों से तीन अंकों की संख्याएँ बनाना:
यदि हम कोई तीन अंकों की संख्या (abc) को इस तरह पुनर्व्यवस्थित करते हैं कि सभी तीन संख्याएँ (abc,bca,cab) अलग हो और हम उन सभी को जोड़ते हैं और फिर इसे 37 से विभाजित करते हैं, तो शेषफल शून्य प्राप्त होता हैं अर्थात प्राप्त संख्या 37 के गुणज होती हैं।
चरण 1: आइए तीन अंकों की कोई भी संख्या abc लेते हैं, जिसे (100a+10b+c) के रूप में लिखा जा सकता है।
चरण 2: संख्या को इस तरह से पुनर्व्यवस्थित करते हैं कि यह दो अलग-अलग संख्याएँ और बनाती है। एक संख्या bca हो सकता है जिसे (100b+10c+a) लिखा जा सकता है और दूसरा cab हो सकता है जिसे (100c+10a+b) लिखा जा सकता है।
चरण 3: तीनों संख्याओं अर्थात abc+bca+cab को जोड़ने पर हमें (100a+10b+c)+(100b+10c+a)+(100c+10a+b)=111(a+b+c) प्राप्त होता है।
चरण 4: अब, संख्या को 37 से विभाजित करने पर हमें शेषफल शून्य प्राप्त होगा।
जैसे: 389
दी गई संख्या =389
पुनर्व्यवस्थित करने पर हमारे पास दो अन्य संख्याएँ अर्थात् 893 और 938 होंगी।
तीनों संख्याओं जोड़ने पर,
=389+893+938
=2220
=222037
=60; शेषफल =0
उदाहरण 5
बिना वास्तविक योगफल निकाले ज्ञात कीजिए कि 78 और 87 के योगफल को 11 से भाग देने पर भागफल क्या होगा?
∵78,87 का विपरीत अंक हैं क्योंकि दहाई और इकाई के अंक परस्पर बदले गए है।
78+8711
हम जानते हैं कि, ab+ba को 11 से विभाजित किया जाता है तो भागफल a+b आता है।
अतः, भागफल =a+b=7+8=15
दूसरी विधि:
78+8711
⇒(77+1)+(88−1)11
⇒77+1+88−111
⇒77+8811
⇒7711+8811
⇒7+8=15
अतः, भागफल =15
उदाहरण 6
बिना घटाए ज्ञात कीजिए कि 95−59 को 9 से भाग देने पर भागफल क्या होगा?
∵95, 59 का विपरीत अंक हैं क्योंकि दहाई और इकाई के अंक परस्पर बदले गए है।
95−599
हम जानते हैं कि, ab−ba को 9 से विभाजित किया जाता है तो भागफल a−b आता है।
अतः, भागफल =a−b=9−5=4
दूसरी विधि:
95−599
⇒(90+5)−(54+5)9
⇒90+5−54−59
⇒90−549
⇒909−549
⇒10−6=4
अतः, भागफल =4
अंकों के लिए अक्षर
यहाँ कुछ पहेलियाँ हैं जहाँ एक अंकगणितीय प्रश्न में अंकों के स्थानों पर अक्षर होते हैं तथा समस्या यह ज्ञात करने की है कि कौन-सा अक्षर किस अंक को निरूपित करता है। अत: यह एक प्रकार से कोड को हल करने जैसी बात है। ऐसी पहेलियों को हल करते समय अपनाए जाने वाले दो नियम हैं:
1. पहेली में, प्रत्येक अक्षर केवल एक ही अंक को प्रदर्शित करना चाहिए। एक अंक केवल एक ही अक्षर से प्रदर्शित किया जाना चाहिए।
2. एक संख्या का पहला अंक शून्य नहीं हो सकता। जैसे संख्या छप्पन को 056 या 0056 न लिखकर केवल 56 लिखते हैं।
नोट: एक पहेली का केवल एक ही उत्तर होना चाहिए।
उदाहरण: निम्नलिखित योग में P ज्ञात कीजिए।
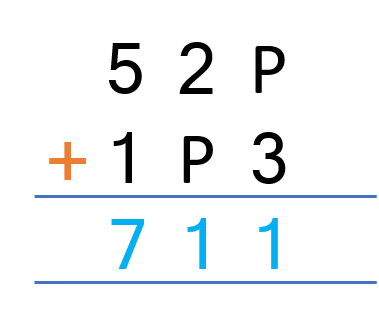
यहाँ केवल एक अक्षर P है जिसका हमें मान ज्ञात करना है। इकाई के स्तंभ में, P+3 से हमें 1 प्राप्त होता है अर्थात 3 में वह संख्या जोड़ें जिससे इकाई का अंक 1 प्राप्त हो।
ऐसा होने के लिए P का मान अंक 8 होना चाहिए क्योंकि 8 में 3 जोड़ने पर इकाई का स्थान 1 होता है।
अतः, P=8
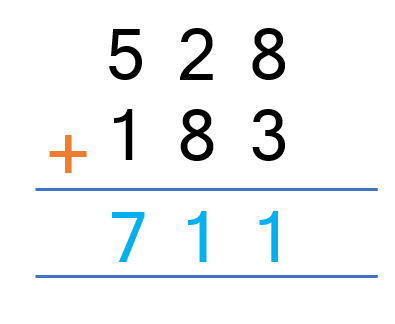
उदाहरण: P और Q का मान ज्ञात कीजिए।
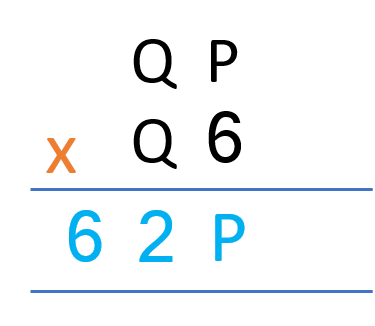
यहाँ भी दो अक्षर P और Q हैं जिनके मान ज्ञात किए जाने हैं क्योंकि 6×P इकाई का अंक P है।
अतः, P=4
अब Q=1 रखे तो 14×16=224 जो कि कम है।
यदि Q=3 रखे तो 34×36=1224 जो कि अधिक है।
अतः Q=2 रखने पर 24×26=624 जो कि सही है।
∴Q=2,p=4
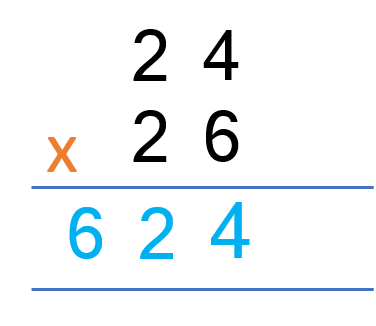
OMR (One Minute Revision)
उदाहरण 7
निम्नलिखित संक्रिया मे A और B का मान ज्ञात कीजिए।
3 A+2 5¯¯¯¯¯¯¯¯¯¯¯ B 2
चूंकि हम जानते है कि ऐसी संक्रियाओं को हल करने के लिए हम दिए गए अक्षरों के संभावित मानों का प्रयोग करते है। अतः
A के संभावित मान =1,2,3,4,5,6,7,8,9,0
B के संभावित मान =1,2,3,4,5,6,7,8,9,0
अब इन मानों का प्रयोग हम दी गई संक्रिया मे करते है :-
3 A+2 5¯¯¯¯¯¯¯¯¯¯¯¯ B 2
उपर्युक्त मानों मे से हमे A के लिए ऐसे मान का चयन करना है जिससे कि उत्तर मे इकाई का अंक 2 प्राप्त हो।
A के संभावित मानों मे से 7 का प्रयोग A के स्थान पर करते है :-
3 7+2 5¯¯¯¯¯¯¯¯¯¯¯¯ B 2
चूंकि 7+5=12 प्राप्त हुआ जिससे इसका इकाई का अंक 2 प्राप्त हुआ है।
अब संक्रिया को आगे हल करने पर हमे 3+2+1=6 प्राप्त होता है जो कि B का मान है। अतः
3 7+2 5¯¯¯¯¯¯¯¯¯¯¯ 6 2
अतः A=7,B=6
उदाहरण 8
निम्नलिखित संक्रिया मे A और B का मान कारण सहित ज्ञात कीजिए।
3 7+A B¯¯¯¯¯¯¯¯¯¯¯ 9 A
चूंकि हम जानते है कि ऐसी संक्रियाओं को हल करने के लिए हम दिए गए अक्षरों के संभावित मानों का प्रयोग करते है। अतः
A के संभावित मान =1,2,3,4,5,6,7,8,9,0
B के संभावित मान =1,2,3,4,5,6,7,8,9,0
अब इन मानों का प्रयोग हम दी गई संक्रिया मे करते है :-
3 7+A B¯¯¯¯¯¯¯¯¯¯¯ 9 A
इस संक्रिया मे B का मान A पर निर्भर कर रहा है, अतः हमे B का मान ज्ञात करने से पहले A का मान ज्ञात करना होगा।
A का ऐसा मान हो जिससे कि दहाई तरफ के अंकों का योग 9 प्राप्त हो।
अतः B=8 रखने पर :-
3 7+A 8¯¯¯¯¯¯¯¯¯¯¯ 9 A
अतः 7+8=15
अतः 15 मे इकाई का 5 प्राप्त हुआ है। इसे A के स्थान पर रखते है :-
3 7+A 8¯¯¯¯¯¯¯¯¯¯ 9 5
अब 3+A+1=3+5+1=9 (यहाँ 1 हासिल को जोड़ा गया है।)
3 7+5 8¯¯¯¯¯¯¯¯¯¯ 9 5
अतः A=5,B=8
उदाहरण 9
निम्नलिखित संक्रिया मे A,B और C का मान कारण सहित ज्ञात कीजिए।
AB×3¯¯¯¯¯¯¯¯¯¯¯CAB
चूंकि हम जानते है कि ऐसी संक्रियाओं को हल करने के लिए हम दिए गए अक्षरों के संभावित मानों का प्रयोग करते है। अतः
A के संभावित मान =0,1,2,3,4,5,6,7,8,9
B के संभावित मान =0,1,2,3,4,5,6,7,8,9
C के संभावित मान =0,1,2,3,4,5,6,7,8,9
संक्रिया :-
AB×3¯¯¯¯¯¯¯¯¯¯¯CAB
चूंकि यहाँ AB दो अंकों की संख्या है तथा हम देख सकते है कि गुणनफल मे B इकाई अंक के रूप मे, A दहाई अंक के रूप मे तथा C सैकड़े अंक के रूप मे आएगा।
यदि हम दी गई संक्रिया मे B=0 रखे तो हमे निम्न उत्तर प्राप्त होगा :-
0×3=0
A 0×3¯¯¯¯¯¯¯¯¯¯CA0
अब हमे A के स्थान पर ऐसा मान रखना होगा जिससे की हमे दो अंकों की संख्या प्राप्त हो तथा इसका इकाई का अंक A ही प्राप्त हो :-
अतः यदि हम A=5 रखे तो :-
5×3=15 अतः प्राप्त संख्या 15 मे इकाई का अंक 5 ही है जो कि A का मान है।
5 0×3¯¯¯¯¯¯¯¯¯150
विभाज्यता की जाँच
भाजकता का नियम यह निर्धारित करने की एक विधि है कि क्या दी गयी संख्या एक निश्चित भाजक (divisor) द्वारा विभाज्य (divisible) है या नहीं।
हमारे पास 2,3,4,5,6,7,8,9,10 और 11 के लिए विभाज्यता नियम हैं।
आइए समझते है :-
2 से विभाज्यता : यदि किसी संख्या के इकाई का अंक 0,2,4,6 या 8 है, तो वह संख्या 2 से विभाज्य होती है।
उदाहरण: 12,34,56 और 78 आदि।
3 से विभाज्यता: एक संख्या 3 से विभाज्य होती है, यदि उसके अंकों का योग 3 से विभाज्य हो।
उदाहरण: 27
क्योकि 2+7=9 जो की 3 से विभाज्य हैं।
अत: 27, 3 से विभाज्य है।
4 से विभाज्यता : कोई संख्या 4 से विभाज्य होती है यदि उसके अंतिम दो अंकों (अर्थात इकाई और दहाई) से बनी संख्या 4 से विभाज्य हो।
उदाहरण: 1396, 4 से विभाज्य है क्योंकि इसके अंतिम दो अंक यानी 96, 4 से विभाज्य है।
5 से विभाज्यता :
यदि किसी संख्या का इकाई का अंक 5 या 0 है, तो वह संख्या 5 से विभाज्य होती है।
उदाहरण: 75,90,100 और 125 आदि।
8 से विभाज्यता : कोई संख्या 8 से विभाज्य होती है, यदि उसके अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य हो।
उदाहरण: 73512, 8 से विभाज्य है क्योंकि इसके अंतिम तीन अंक यानी 512, 8 से विभाज्य हैं।
9 से विभाज्यता : एक संख्या 9 से विभाज्य होती है यदि उसके अंकों का योग 9 के द्वारा विभाज्य हो।
उदाहरण: 126
इसके अंकों का योग =1+2+6=9, जो 9 से विभाज्य है।
अत: 126, 9 से विभाज्य है।
10 से विभाज्यता : यदि किसी संख्या का इकाई का अंक 0 है, तो वह 10 से विभाज्य है।
उदाहरण: 90,100 आदि।
11 से विभाज्यता : किसी संख्या के विषम स्थानों (दाईं ओर से) के अंकों के योग और सम स्थानों (दाईं ओर से) के अंकों के योग के बीच अंतर ज्ञात कीजिए यदि अंतर या तो 0 है या 11 से विभाज्य है, तो वह संख्या 11 से विभाज्य है।
उदाहरण: 1234321, 11 से विभाज्य है,
क्योंकि
(1+3+3+1)−(2+4+2)
=8−8
=0
जो 11 से विभाज्य है।
उदाहरण 10
21436587 की 9 से विभाज्यता की जांच कीजिए।
हम जानते हैं, कि संख्या 9 से विभाजित होती है यदि उसके अंकों का योग 9 से विभाजित हो।
दी गई संख्या 21436587
अंकों का योग =2+1+4+3+6+5+8+7
=36
=369=4
अतः, दी गई संख्या 9 से विभाजित होगी।
उदाहरण 11
यदि 63x,3 का गुणज है, जहाँ x एक अंक है, तो x का मान ज्ञात कीजिए।
हम जानते हैं, कि संख्या 3 से विभाजित होती है यदि उसके अंकों का योग 3 से विभाजित हो।
दी गई संख्या 63x, 3 का गुणज है
अंकों का योग =6+3+x
=9+x
x=0,3,6,9 रखने पर संख्या 3 से विभाज्य होगी।
x=0
9+0⇒93=3
x=3
9+3⇒123=4
x=6
9+6⇒153=5
x=9
9+9⇒183=6
अतः, x=0,3,6,9
उदाहरण 12
यदि 75y5, 9 का एक गुणज है, जहाँ y एक अंक है, तो y का मान होगा।
हम जानते हैं, कि संख्या 9 से विभाजित होती है यदि उसके अंकों का योग 9 से विभाजित हो।
दी गई संख्या 75y5, 9 का गुणज है
अंकों का योग =7+5+y+5
=17+y
y=1 रखने पर संख्या 9 से विभाज्य होंगी।
17+1=189=2
अतः, y=1
उदाहरण 13
यदि संख्या 8242a,4 से विभाज्य हो, जहाँ a कोई अंक हैं, तो a का मान ज्ञात कीजिए।
दी गई संख्या 8242a
4 के विभाज्यता के नियमानुसार,
2a4
यहाँ, a=0,4,8 रखने पर संख्या 4 से पूर्णतः विभाज्य होंगी।
a=0⇒204=5
a=4⇒244=6
a=8⇒284=7
अतः, a=0,4,8
उदाहरण 14
57248 में एक अंक की कौन-सी संख्या जोड़ी जाए कि यह 5 से विभाज्य हो जाए।
दी गई संख्या 57248
हम जानते हैं, कि संख्या 5 से विभाजित होती है यदि संख्या के इकाई का अंक 0 या 5 हो।
यदि संख्या में 2,7 जोड़ा जाए तो इकाई अंक क्रमशः 0,5 प्राप्त होगा।
57248+2⇒57250 (5 से विभाज्य हैं।)
57248+7⇒57255 (5 से विभाज्य हैं।)
अतः संख्या 57248 मे 2 या 7 जोड़ने पर यह 5 से विभाज्य होगा।