प्रायोगिक ज्यामिति कक्षा 8 गणित

Table Of Contents

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय में हम प्रायोगिक ज्यामिति का अध्ययन करेंगे अर्थात ज्यामिति की रचना के संबंध में अध्ययन करेंगे। पिछली कक्षाओ में हम ज्यामिति की आधारभूत अवधारणाओं का अध्ययन कर चुके हैं तथा कक्षा 7 में हम त्रिभुज (Triangle) की रचना करना सीख चुके है, जिसमें हमें एक अद्वितीय त्रिभुज की रचना के लिए तीन मापों ( भुजाओं और कोणों ) की आवश्यकता थी।
इस अध्याय में हम आगे चतुर्भुज की रचना करना सीखेंगे।

आइये जानते है, प्रायोगिक ज्यामिति को और करीब से...

प्रायोगिक ज्यामिति में ज्यामिति की निश्चित मापे होती है। इस अध्याय में हम चतुर्भुज की विभिन्न स्थितियों में रचना करना सीखेंगे। जिसके लिए आवश्यक उपकरण जैसे रूल, पेंसिल, रूलर (स्केल), परकार, चाँदा आदि की आवश्यकता होगी। इसमें हम सीखेंगे की एक अद्वितीय चतुर्भुज की रचना करने के लिए कितनी मापों की आवश्यकता होती है।

SSS निर्माण

त्रिभुज की रचना करना हम पिछली कक्षा में पढ़ चुके है। आइए इस पर कुछ अध्ययन करते हैं -

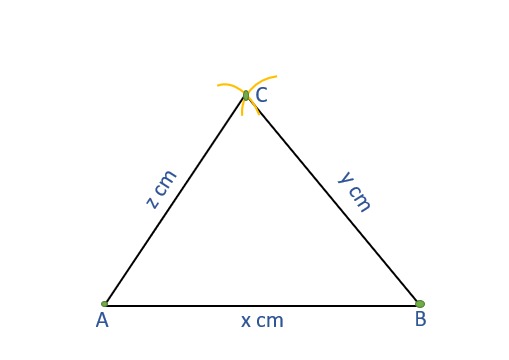
$△$ ABC की रचना, जिसकी भुजाओं की लंबाई AB = $x$ cm, BC = y cm और AC = z cm है, हम निम्न प्रकार कर सकते हैं :

• सर्वप्रथम एक रेखाखंड AB खींचते है, जिसकी लंबाई $x$ cm है।

• A को केंद्र मानकर z cm त्रिज्या का एक चाप ऊपर की तरफ खींचते है।

• B को केंद्र मानकर, उसी तरफ y cm त्रिज्या का एक चाप खींचते है।

• वह बिंदु जहाँ दोनों चाप प्रतिच्छेद करते हैं, बिंदु C अंकित करते हैं तथा बिन्दु C को बिन्दु A और B से मिला देते है।

• इस प्रकार एक अभीष्ट त्रिभुज ABC प्राप्त होता है।

क्रियाकलाप

जिस प्रकार पिछली कक्षा में एक अद्वितीय त्रिभुज की रचना के लिए उसकी तीन मापों ( भुजाओं और कोणों ) की आवश्यकता थी, उसी प्रकार इस अध्याय में हम देखेंगें की एक अद्वितीय चतुर्भुज की रचना के लिए कितनी मापों की आवश्यकता होगी।

आइये एक क्रियाकलाप की सहायता से समझते हैं -

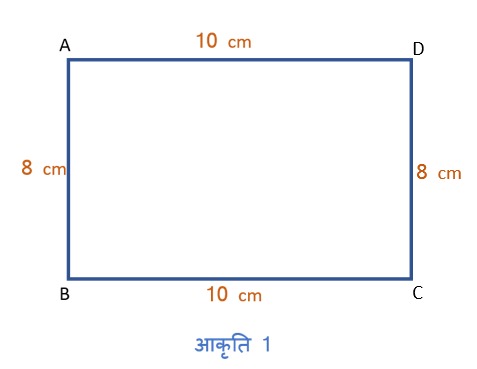
चरण 1 : हम समान लंबाई ( माना 10 cm) वाली तीलियों ( Sticks) का एक युग्म लेते है। अब एक दूसरा समान लंबाई ( माना 8 cm) वाली तीलियों का युग्म और लेते है। अब इन्हें आपस में इस प्रकार जोड़ते हैं जिससे 10cm लंबाई तथा 8cm चौड़ाई वाला एक आयत प्राप्त होता है। इस आयत का निर्माण 4 मापों के उपयोग से किया गया है। (आकृति 1)

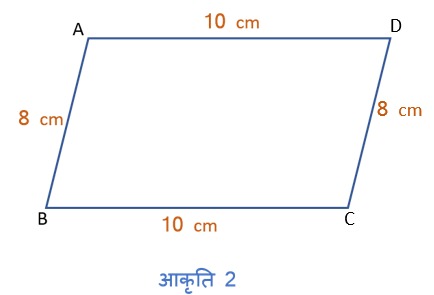
चरण 2 : अब आयत की चौड़ाई के अनुदिश दबाव डालते हैं तो हमें एक नई आकृति प्राप्त होती है, जो एक समांतर चतुर्भुज की होती है।
परंतु हमने यहाँ तीलियों की लंबाइयों को नहीं बदला है। (आकृति 2 )

ocr_image

चरण 3 : अब नयी प्राप्त आकृति पर दूसरी दिशा में दबाव डालते हैं तो हमें पुनः एक समांतर चतुर्भुज प्राप्त होता हैं जो की पहले वाली आकृति से पूर्णतः भिन्न तो हैं परंतु अद्वितीय नहीं हैं क्योंकि इसकी भुजाओं की माप समान है। (आकृति 3)

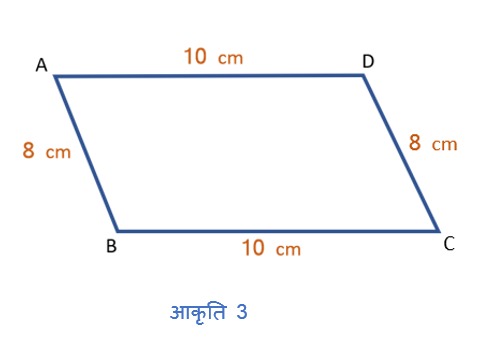
ocr_image

अतः यह क्रियाकलाप दर्शाता हैं कि एक चतुर्भुज की चार मापों से एक अद्वितीय चतुर्भुज प्राप्त नहीं किया जा सकता है।

चरण 4 : अब इस क्रियाकलाप पर पुनः विचार करते है। हम प्रत्येक 10cm लंबाई की दो तीलियों एवं प्रत्येक 8cm लंबाई की दो तीलियों की सहायता से एक आयत की रचना कर चुके हैं। अब BD के बराबर लंबाई वाली एक दूसरी तीली को BD के अनुदिश बांधते है। (आकृति 4)

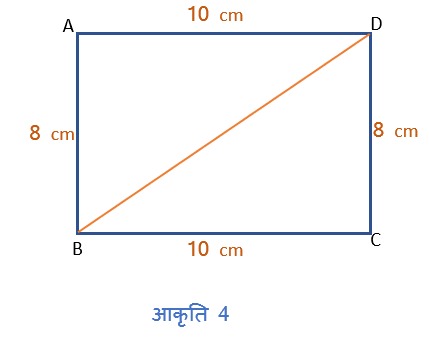
ocr_image

चरण 5 : अब हम चौड़ाई के अनुदिश दबाव डालते हैं तो हमें नई आकृति प्राप्त नहीं होती है, अर्थात पाँचवीं तीली के प्रवेश ने आयत को अद्वितीय रूप से स्थिर कर दिया है।

अतः पाँच मापों से एक अद्वितीय चतुर्भुज की रचना की जा सकती है।

वे पाँच मापे निम्न प्रकार हो सकती हैं -

एक चतुर्भुज की रचना जब चारो भुजाओं और एक विकर्ण की लंबाई दी गई हों -

हम इस रचना को एक उदाहरण की सहायता से समझ सकते है-

उदाहरण : एक चतुर्भुज PQRS की रचना करते हैं जिसमें
PQ = 4 cm. QR = 6 cm, RS = 5 cm, PS = 5.5cm और PR = 7 cm हो।

हल: एक कच्ची ( $R o u g h$ ) आकृति इस रचना को समझने में हमारी सहायता करेगी।
सर्वप्रथम हम एक कच्ची आकृति खींचते हैं और मापों को चिह्नित करते हैं।

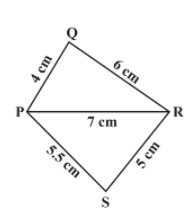
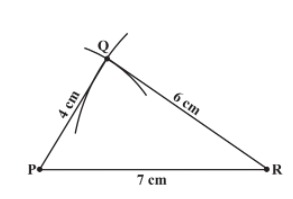
चरण 1 : कच्ची आकृति से हम देख सकते हैं की बड़ी आसानी से SSS रचना कसौटी से

△

PQR की रचना की जा सकती है।
अतः

△

PQR की रचना करते हैं और इसको नामांकित करते है।

ocr_image

चरण 2 : अब हमें चौथे बिंदु

S

का पता लगाना है। यह बिंदु S, PR के संदर्भ में, बिंदु Q की विपरीत दिशा में होगा।
बिन्दु P से, बिन्दु S, 5.5 cm की दूरी पर स्थित है। अतः P को केंद्र मानकर 5.5 cm त्रिज्या का एक चाप बिन्दु Q की विपरीत दिशा में खींचते है।

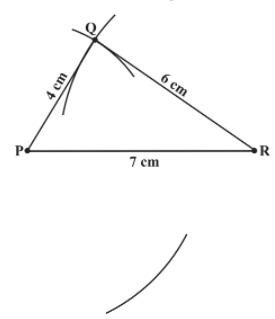
ocr_image

चरण 3 : R से बिन्दु S की दूरी 5 cm है। अतः R को केंद्र मानकर 5 cm त्रिज्या का एक चाप बिन्दु Q की विपरीत दिशा में खींचते है।

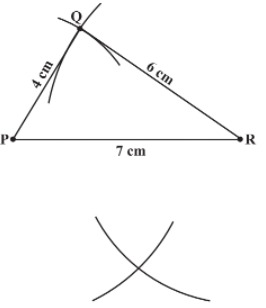
ocr_image

चरण 4 : बिन्दु S खींचे गए दोनों चापों के कटान बिन्दु पर स्थित होगा। अतः वहाँ S अंकित करते हैं तथा बिन्दु P और R को बिन्दु S से मिला देते हैं और चतुर्भुज PQRS को पूरा करते है।

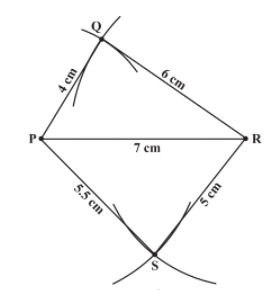
ocr_image

चरण 5 : इस प्रकार हमें अभीष्ट चतुर्भुज PQRS प्राप्त होता है।

आइए कुछ और उदाहरणों की सहायता से समझते है-

उदाहरण 1

निम्नलिखित चतुर्भुज की रचना कीजिए :
चतुर्भुज $A B C D$ जिसमे
$A B = 4.5$ $c m$
$B C = 5.5$ $c m$
$C D = 4$ $c m$
$A D = 6$ $c m$
$A C = 7$ $c m$ है।

दिया है,

चतुर्भुज $A B C D$ जिसमे
$A B = 4.5$ $c m$
$B C = 5.5$ $c m$
$C D = 4$ $c m$
$A D = 6$ $c m$
$A C = 7$ $c m$

चतुर्भुज $A B C D$ में $A B$ , $B C$ , $C D$ , $A D$ चारों भुजाएँ हैं क्योंकि ये संलग्न हैं तथा $A C$ संलग्न नहीं हैं अर्थात $A C$ विकर्ण है।
दिये गये चतुर्भुज की रचना को समझने के लिए सबसे पहले चतुर्भुज की एक कच्ची आकृति खींचकर उसकी मापों को चिन्हित करते है।

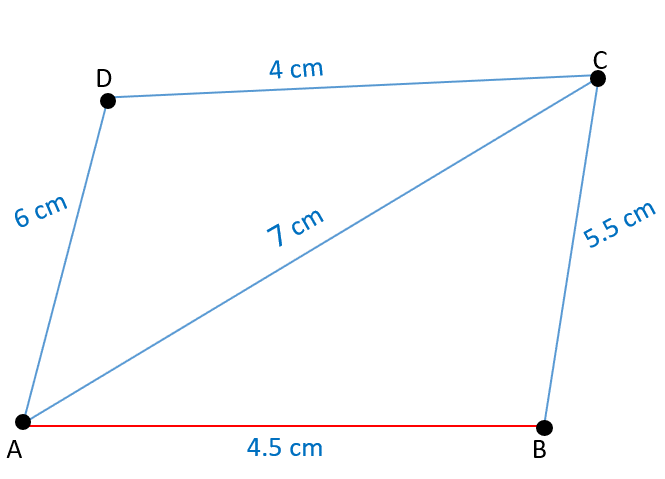
चरण 1: सर्वप्रथम

A B = 4.5

c m

का एक रेखाखंड खींचते हैं।

ocr_image

चरण 2: बिन्दु

B

को केन्द्र मानते हुए ऊपर की तरफ 5.5

c m

त्रिज्या का चाप बनाया जिसे C से चिन्हित करते हैं।

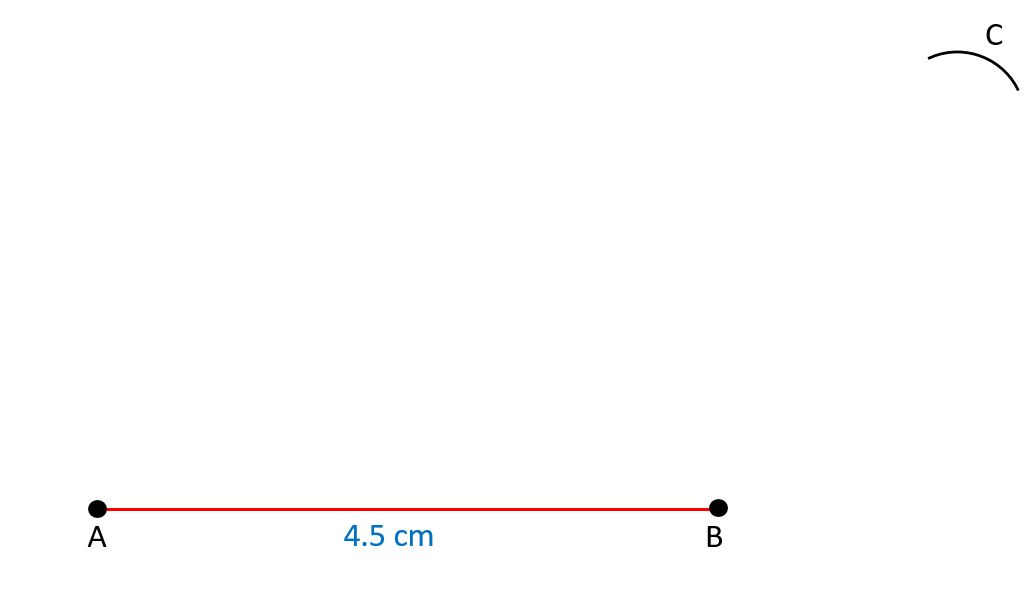
ocr_image

चरण 3: बिन्दु

A

को केन्द्र मानते हुए 7

c m

त्रिज्या का चाप बनाया, जो पहले चाप को बिन्दु C पर काटता हैं।

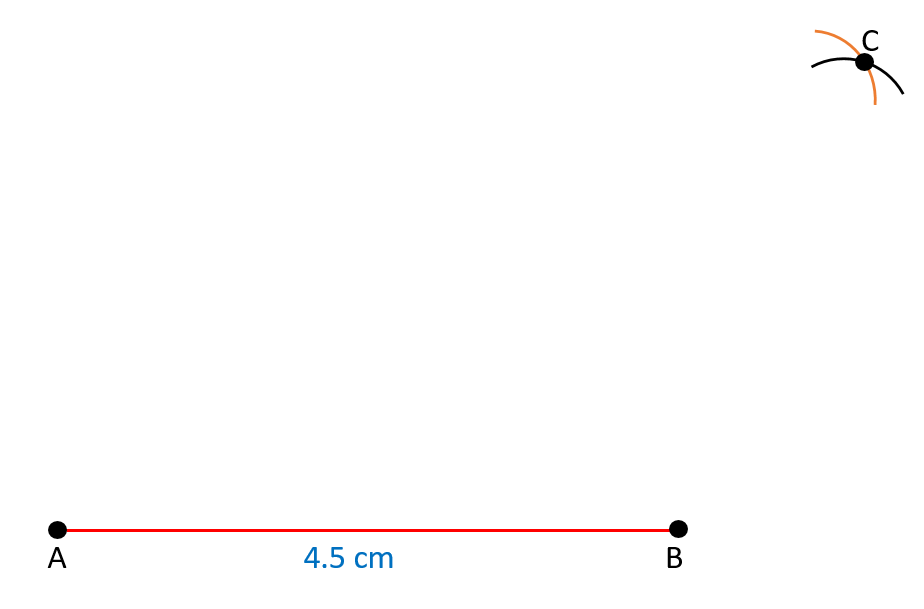
ocr_image

चरण 4:अब बिन्दु

C

को बिन्दु

A

और

B

से मिलाते हैं।

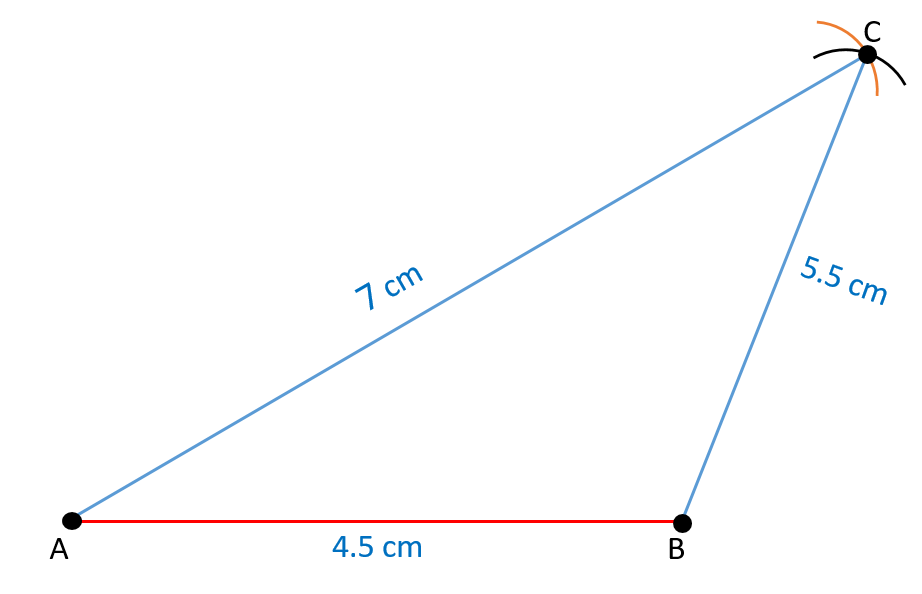
ocr_image

चरण 5: बिन्दु A को केन्द्र मानते हुए 6

c m

त्रिज्या का चाप बनाया।

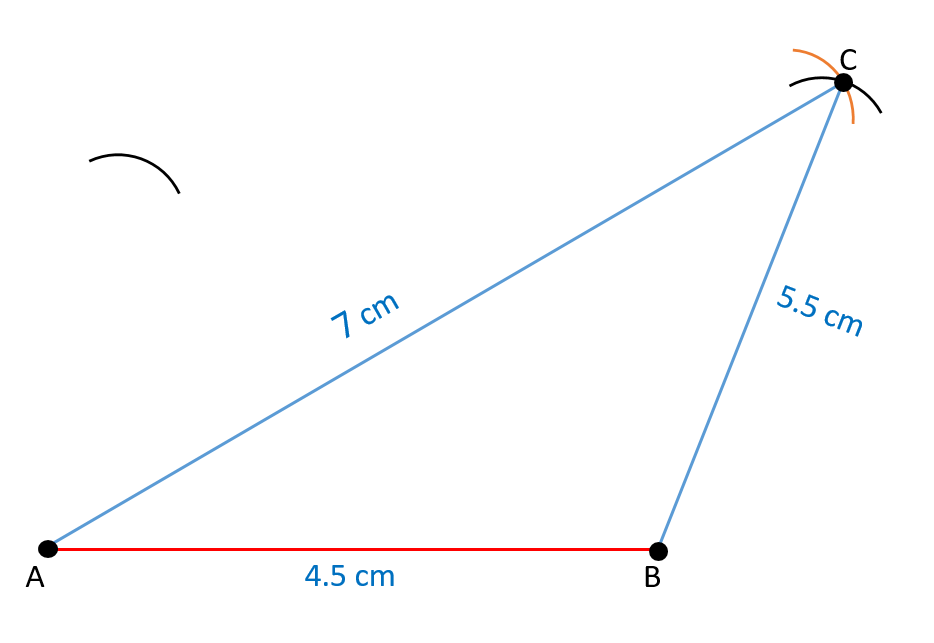
ocr_image

चरण 6: बिन्दु C को केंद्र मानते हुए 4

c m

त्रिज्या का चाप बनाया, जो पहले चाप को बिन्दु

D

पर काटता हैं।

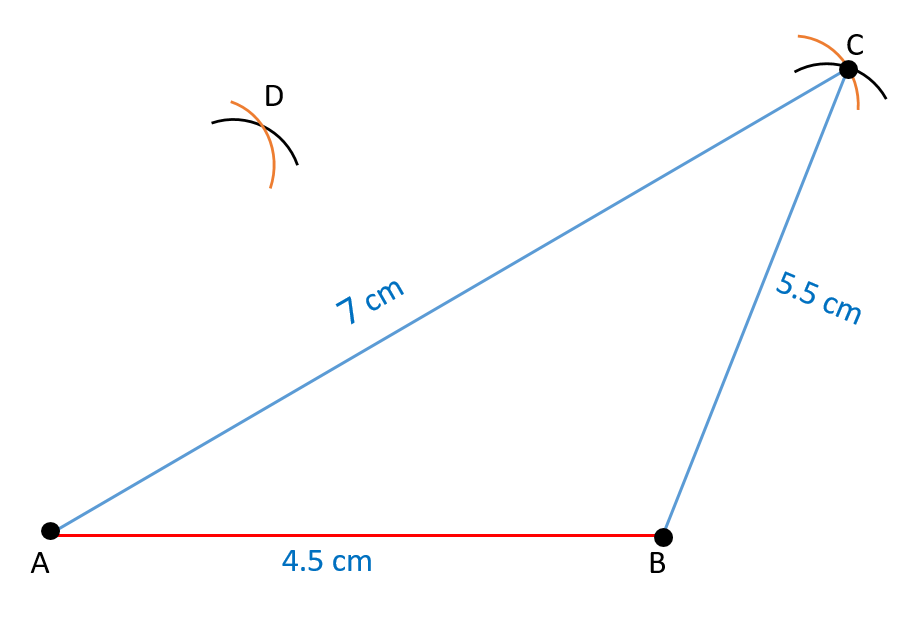
ocr_image

चरण 7: बिन्दु

D

को बिन्दु

A

और

C

से मिलाते हैं तथा माप अंकित करते है।

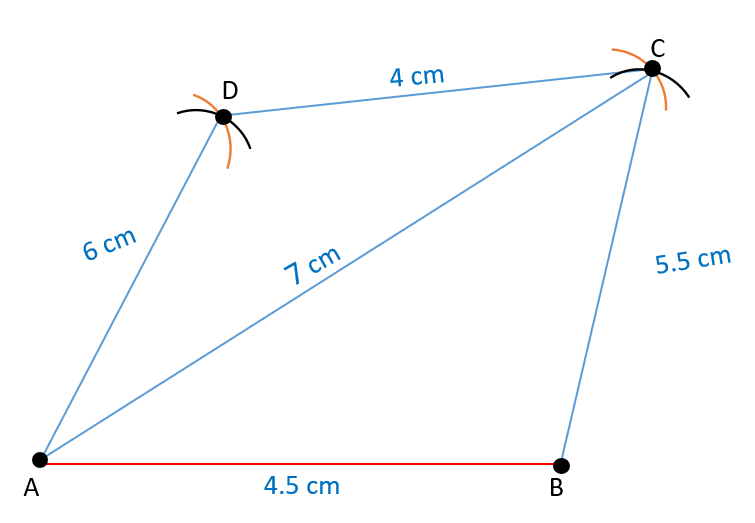
ocr_image

अतः एक अभीष्ट चतुर्भुज

A B C D

की रचना हुई।

Learn more

उदाहरण 2

निम्नलिखित चतुर्भुज की रचना कीजिए :
चतुर्भुज $J U M P$ जिसमे
$J U = 3.5$ $c m$
$U M = 4$ $c m$
$M P = 5$ $c m$
$P J = 4.5$ $c m$
$P U = 6.5$ $c m$ है।

दिया है,

चतुर्भुज $J U M P$ जिसमे
$J U = 3.5$ $c m$
$U M = 4$ $c m$
$M P = 5$ $c m$
$P J = 4.5$ $c m$
$P U = 6.5$ $c m$ है।

चतुर्भुज $J U M P$ में $J U$ , $U M$ , $M P$ , $P J$ चारों भुजाएँ हैं क्योंकि ये संलग्न हैं तथा $P U$ संलग्न नहीं हैं अर्थात $P U$ विकर्ण है।
दिए गये चतुर्भुज की रचना को समझने के लिए सबसे पहले चतुर्भुज की एक कच्ची आकृति खींचकर उसकी मापों को चिन्हित करते है।

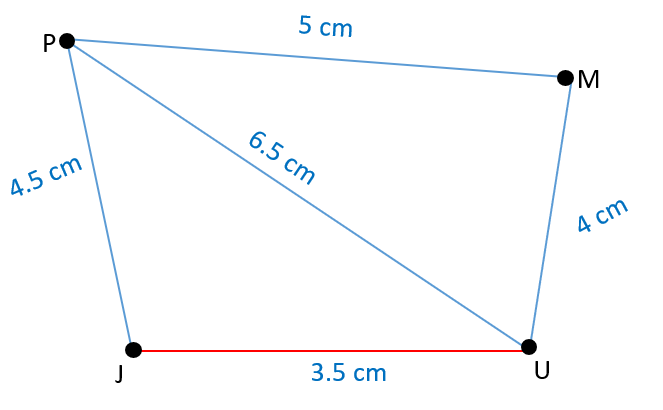
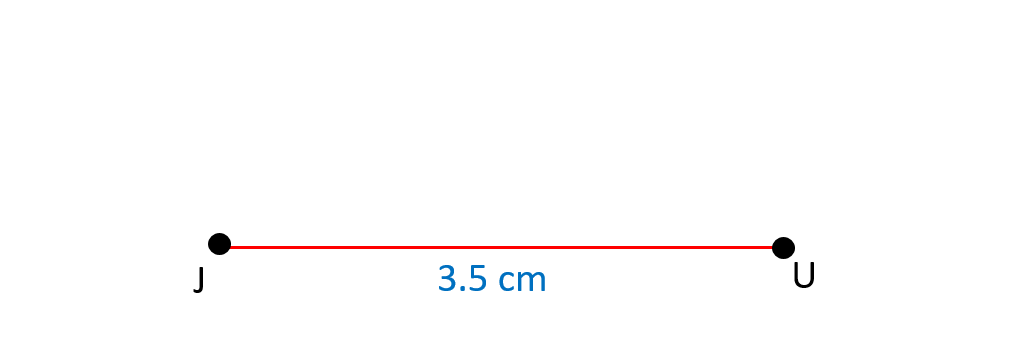
चरण 1: सर्वप्रथम

J U = 3.5

c m

का एक रेखाखंड खींचते हैं।

ocr_image

चरण 2: बिन्दु

U

को केन्द्र मानते हुए ऊपर की तरफ 6.5

c m

त्रिज्या का चाप बनाया जिसे

P

से चिन्हित करते हैं।

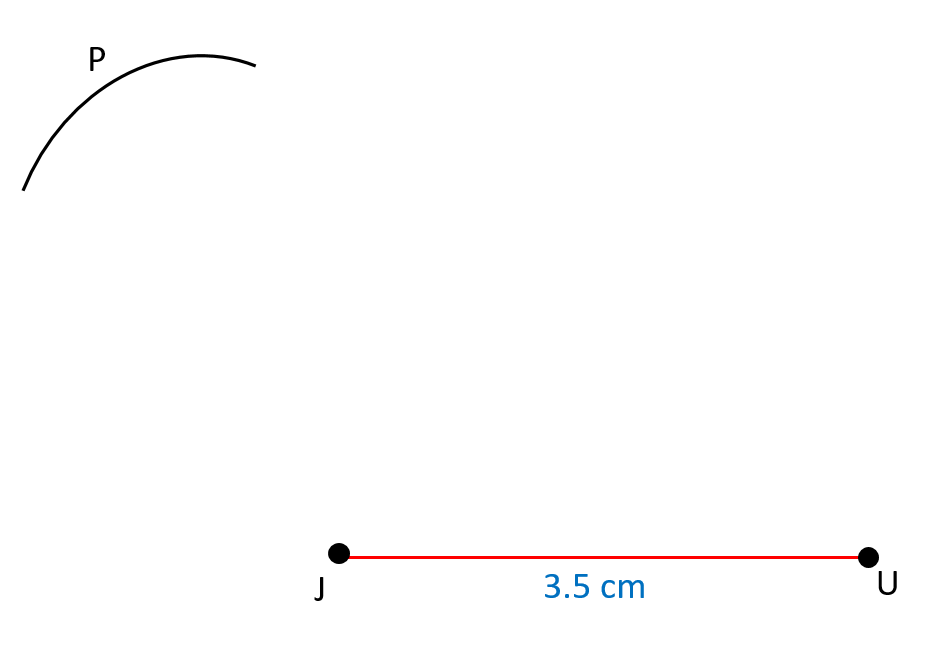
ocr_image

चरण 3: बिन्दु

J

को केन्द्र मानते हुए 4.5

c m

त्रिज्या का चाप बनाया, जो पहले चाप को बिन्दु

P

पर काटता हैं।

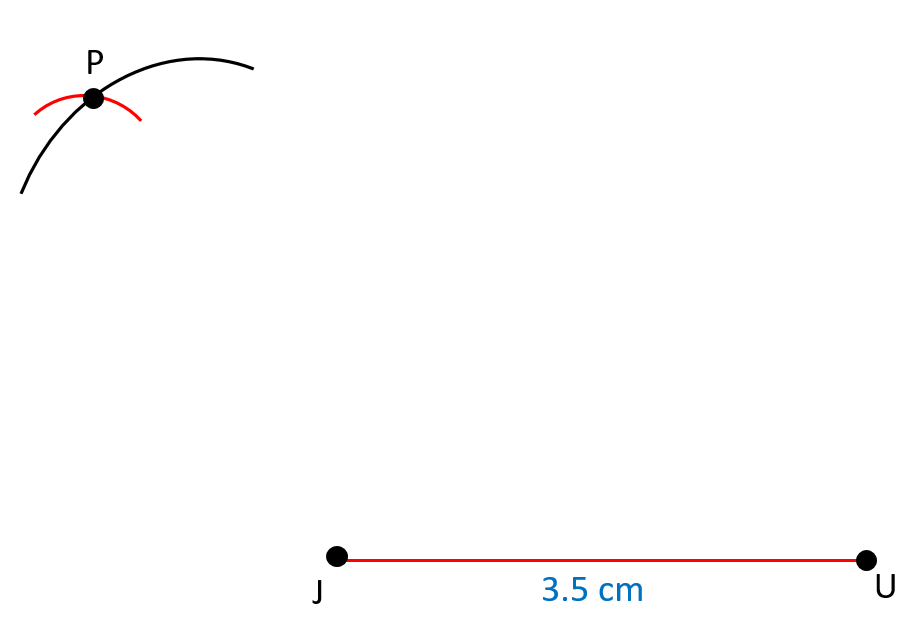
ocr_image

चरण 4: अब बिन्दु

P

को बिन्दु

J

और बिन्दु

U

से मिलाते हैं तथा माप अंकित करते है।

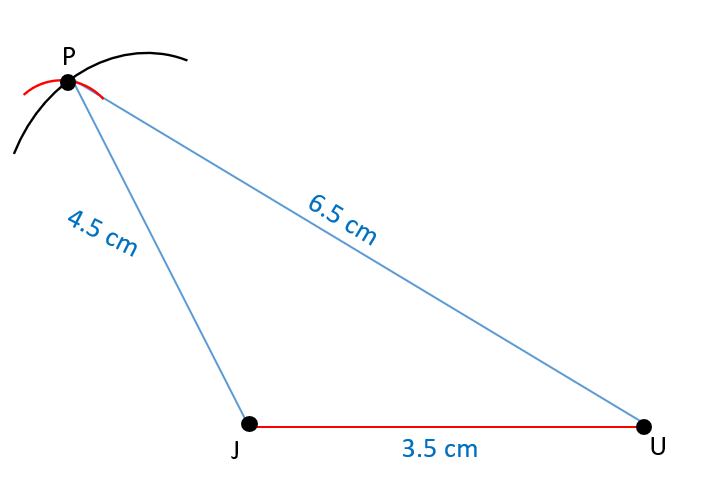
ocr_image

चरण 5: बिन्दु

U

को केन्द्र मानते हुए ऊपर की तरफ 4

c m

त्रिज्या का चाप बनाया जिसे M से चिन्हित करते हैं।

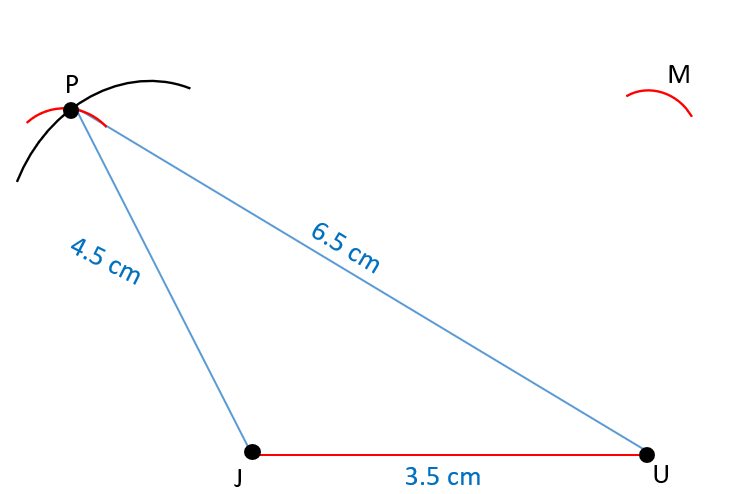
ocr_image

चरण 6: बिन्दु

P

को केंद्र मानते हुए 5

c m

त्रिज्या का चाप बनाया, जो पहले चाप को बिन्दु M पर काटता हैं।

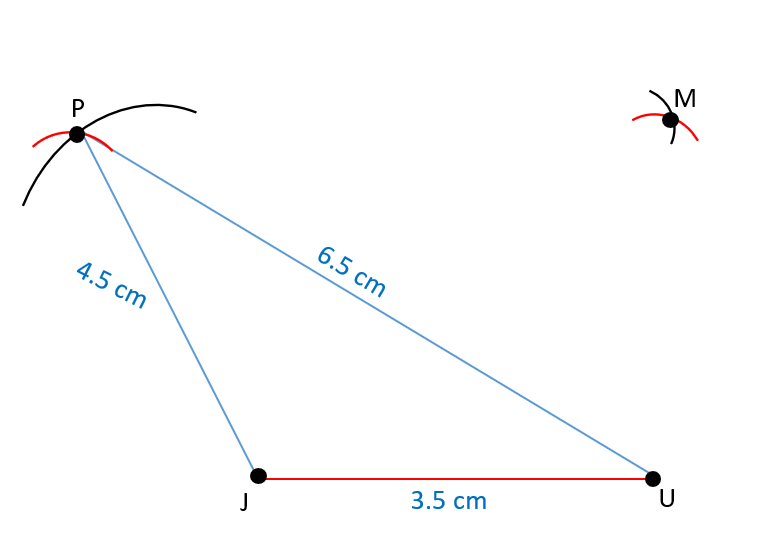
ocr_image

चरण 7: अब बिन्दु

M

को बिन्दु

P

और बिन्दु

U

से मिला देते है तथा माप अंकित करते है।

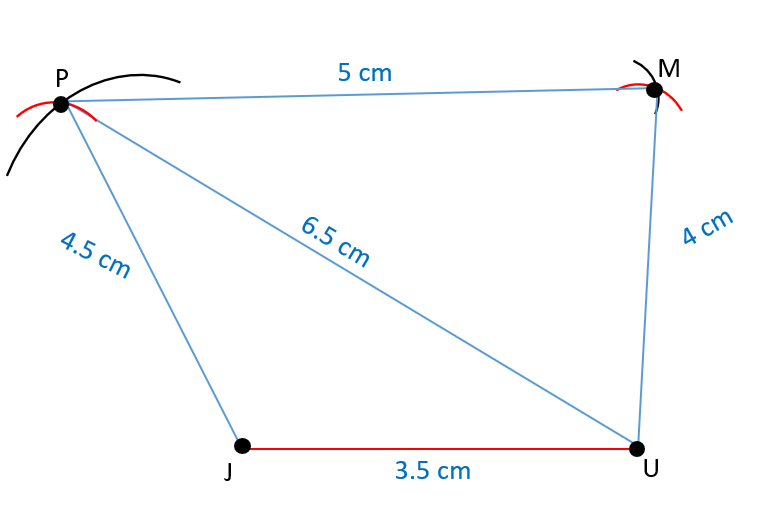
ocr_image

अतः एक अभीष्ट चतुर्भुज

J U M P

की रचना हुई।

Learn more

एक चतुर्भुज की रचना जब तीन भुजाओं और दोनों विकर्णों की लंबाई दी गई हों -

हम इस रचना को भी एक उदाहरण की सहायता से समझ सकते है-

उदाहरण : एक चतुर्भुज ABCD की रचना करते हैं जिसमें
BC = 4.5 cm, AD = 5.5 cm, CD = 5 cm
विकर्ण AC = 5.5 cm और विकर्ण BD = 7 cm है।

हल :एक कच्ची ( $R o u g h$ ) आकृति इस रचना को समझने में हमारी सहायता करेगी।
सर्वप्रथम हम एक कच्ची आकृति खींचते हैं और मापों को चिह्नित करते हैं।

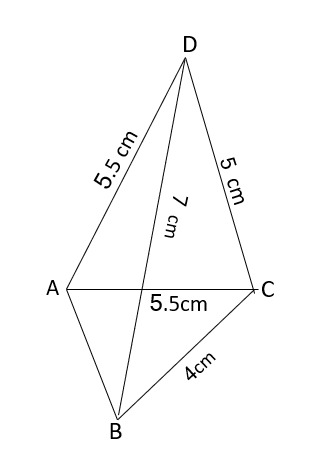
चरण 1 : SSS रचना कसौटी के उपयोग से

△

ACD की रचना करते है।

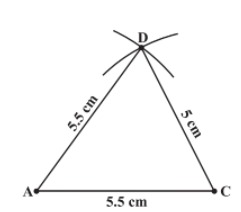
ocr_image

चरण 2 : अब D को केंद्र मानकर 7 cm त्रिज्या का चाप नीचे की तरफ काटते है।

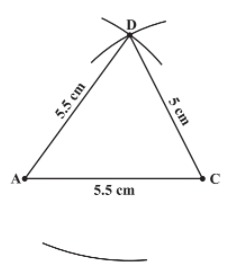
ocr_image

चरण 3 : अब C को केंद्र मानकर 4.5 cm त्रिज्या का चाप पहले वाले चाप के ऊपर काटते हैं जिससे दोनों चाप एक - दूसरे को प्रतिच्छेद करे।

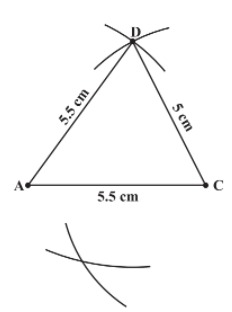
ocr_image

चरण 4 : जहाँ दोनों चाप एक-दूसरे को प्रतिच्छेद करते हैं वहाँ बिन्दु B अंकित करते हैं तथा बिन्दु D, A और C को बिन्दु B से मिला देते हैं और चतुर्भुज ABCD को पूरा करते है।

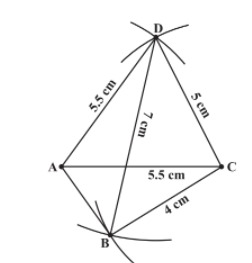
ocr_image

चरण 5 : इस प्रकार हमें अभीष्ट चतुर्भुज ABCD प्राप्त होता है।

आइए कुछ और उदाहरणों की सहायता से समझते है-

उदाहरण 3

निम्नलिखित चतुर्भुज की रचना कीजिए :
चतुर्भुज $L I F T$ जिसमे
$L I = 4$ $c m$
$I F = 3$ $c m$
$T L = 2.5$ $c m$
$L F = 4.5$ $c m$
$I T = 4$ $c m$ है।

दिया हैं,

चतुर्भुज $L I F T$ जिसमे
$L I = 4$ $c m$
$I F = 3$ $c m$
$T L = 2.5$ $c m$
$L F = 4.5$ $c m$
$I T = 4$ $c m$

चतुर्भुज $L I F T$ में $L I$ , $I F$ , $T L$ तीनों भुजाएँ हैं क्योंकि ये तीनों संलग्न हैं तथा $L F$ और $I T$ दोनों संलग्न नहीं हैं अर्थात दोनों विकर्ण है।

दिए गये चतुर्भुज की रचना को समझने के लिए सबसे पहले चतुर्भुज की एक कच्ची आकृति खींचकर उसकी मापों को चिन्हित करते है।

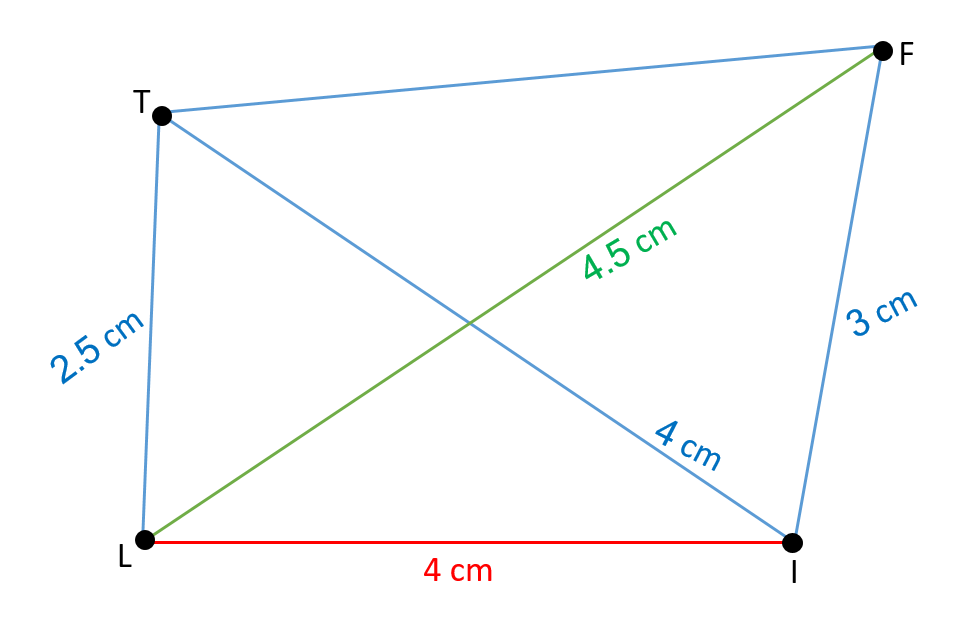
चरण 1: सर्वप्रथम

L I = 4

c m

का एक रेखाखंड खींचते हैं।

ocr_image

चरण 2: बिन्दु

I

को केन्द्र मानते हुए ऊपर की तरफ 3

c m

त्रिज्या का चाप बनाया जिसे

F

से चिन्हित करते है।

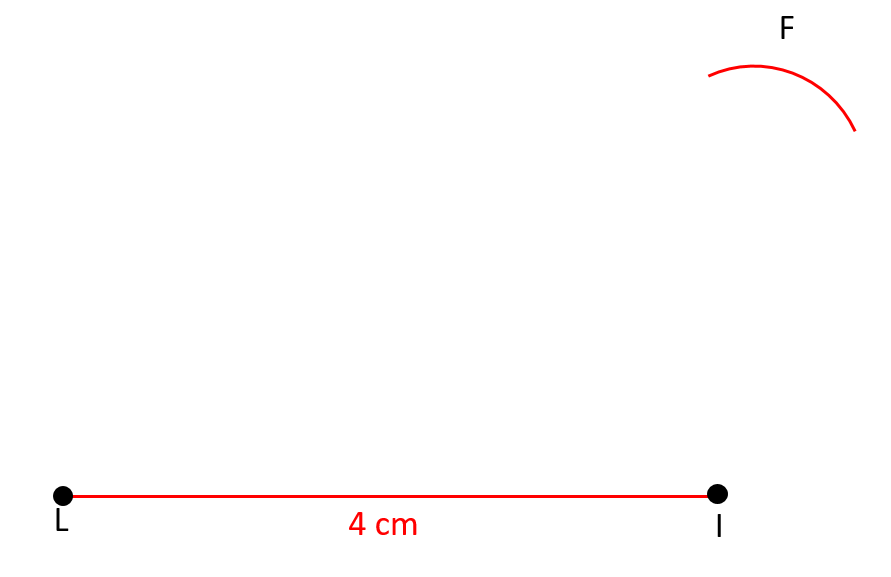
ocr_image

चरण 3: बिन्दु

L

को केन्द्र मानते हुए 4.5

c m

त्रिज्या का चाप बनाया, जो पहले चाप को बिन्दु

F

पर काटता हैं।

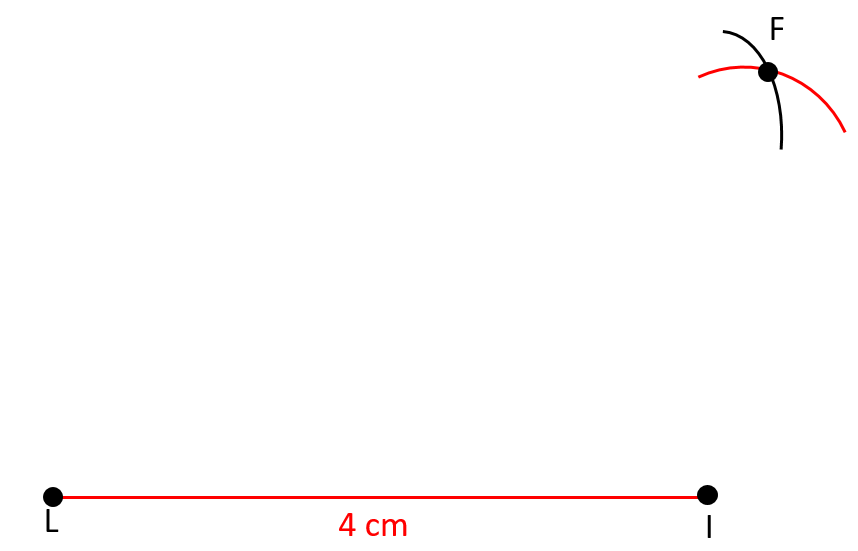
ocr_image

चरण 4:अब बिन्दु

F

को बिन्दु

L

एवं बिन्दु

I

से मिलाते हैं तथा माप अंकित करते है।

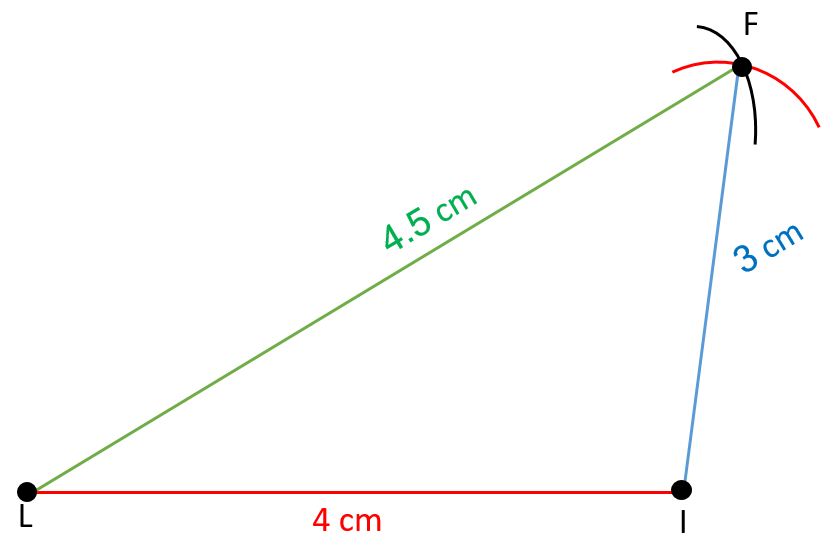
ocr_image

चरण 5:अब बिन्दु

L

को केन्द्र मानते हुए 2.5

c m

त्रिज्या का चाप बनाया, जिसे T से चिन्हित करते है।

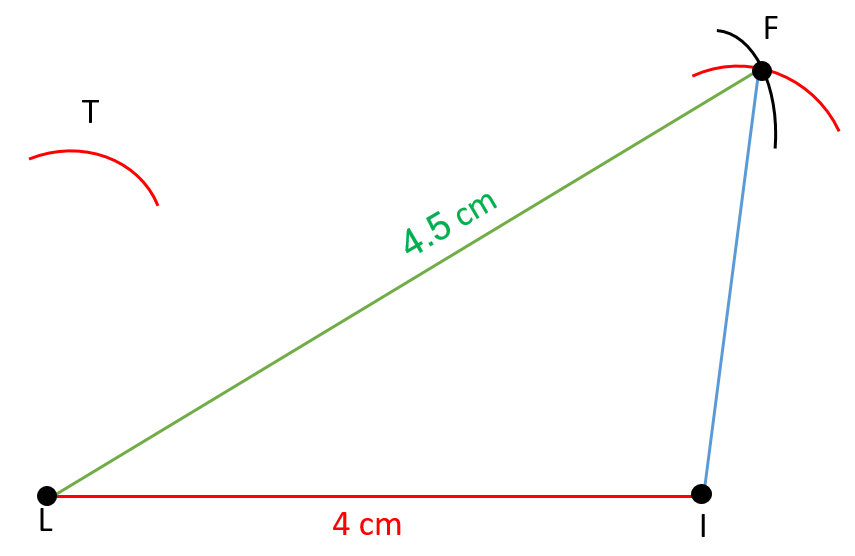
ocr_image

चरण 6: बिन्दु

I

को केंद्र मानते हुए 4

c m

त्रिज्या का चाप बनाया, जो पहले चाप को बिन्दु T पर काटता हैं।

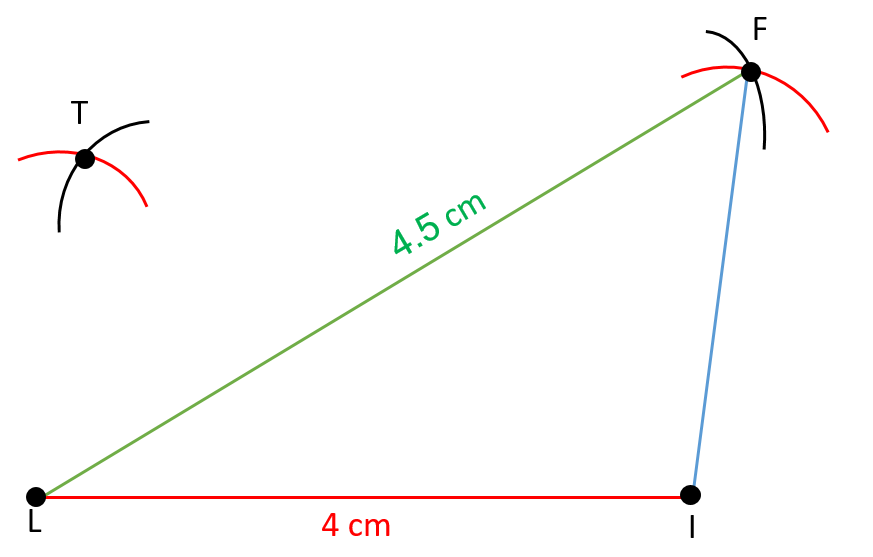
ocr_image

चरण 7: अब बिन्दु

T

को बिन्दु

L

एवं बिन्दु

I

से मिलाते हैं तथा चतुर्भुज को पूरा करके मापे अंकित करते है।

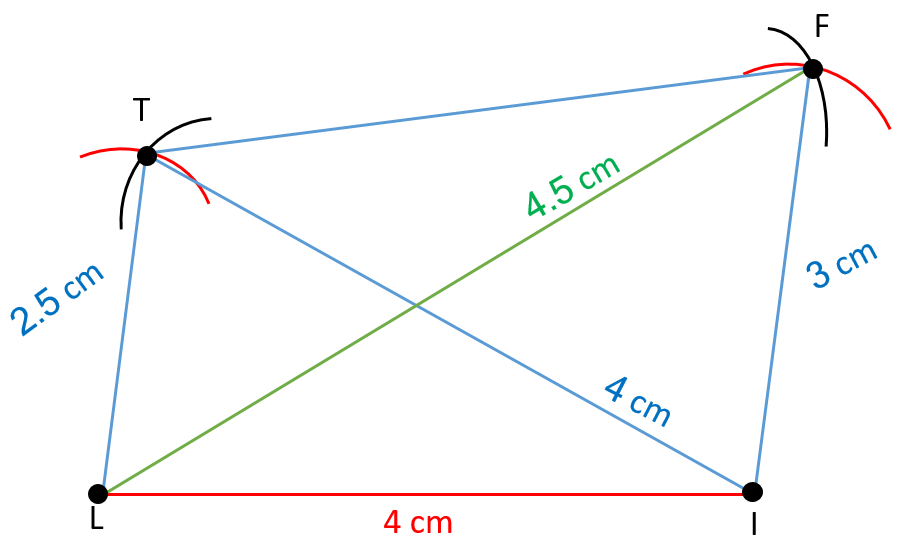
ocr_image

अतः एक अभीष्ट चतुर्भुज

L I F T

की रचना हुई।

Learn more

एक चतुर्भुज की रचना जब दो आसन्न भुजाओं और तीन कोणों की माप दी गई हों -

हम इस रचना को भी एक उदाहरण की सहायता से समझ सकते है-

उदाहरण : एक चतुर्भुज MIST की रचना करते है, जिसमे
MI = 3.5 cm, IS = 6.5 cm
$∠ M = 75 °$ , $∠ I = 105^{\circ}$ और $∠ S = 120 °$ है।

हल : एक कच्ची ( $R o u g h$ ) आकृति इस रचना को समझने में हमारी सहायता करेगी।
सर्वप्रथम हम एक कच्ची आकृति खींचते हैं और मापों को चिह्नित करते हैं।

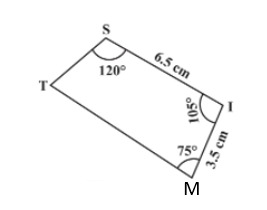
चरण 1 : इस चतुर्भुज की रचना के लिए हम सबसे पहले एक 3.5 cm का रेखाखण्ड MI खींचते है।
अब बिन्दु I पर परकार व पेंसिल की सहायता से

105^{\circ}

का कोण बनाते हैं और उस रेखा पर 6.5 cm की दूरी पर बिन्दु S अंकित करते है।

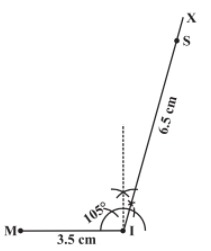
ocr_image

चरण 2 : उसी प्रकार अब बिन्दु S पर

∠ I S Y = 120^{\circ}

बनाते है।
यहाँ बिन्दु Y केवल रेखा के अंतिम छोर को प्रदर्शित करता है।

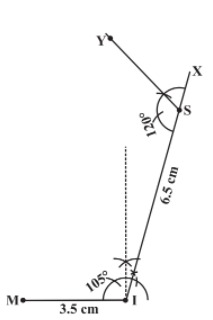
ocr_image

चरण 3 : अब बिन्दु M पर

∠ I M Z = 75^{\circ}

परकार व पेंसिल की सहायता से बनाते हैं तथा कोण वाली रेखा को आगे बढ़ा देते है।
यहाँ बिन्दु Z केवल रेखा के अंतिम छोर को प्रदर्शित करता है।
SY और MZ एक - दूसरे को जिस बिन्दु पर प्रतिच्छेद करते हैं वहाँ बिन्दु T अंकित करते हैं तथा चतुर्भुज MIST को पूरा करते है।

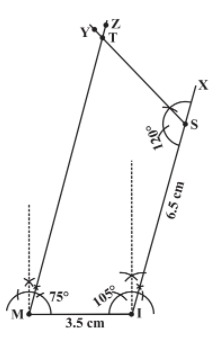
ocr_image

चरण 4 : इस प्रकार हमें अभीष्ट चतुर्भुज MIST प्राप्त होता है।

आइए कुछ और उदाहरणों की सहायता से समझते है-

उदाहरण 4

निम्नलिखित चतुर्भुज की रचना कीजिए :
चतुर्भुज $M O R E$ जिसमें
$M O = 6$ $c m$
$O R = 4.5$ $c m$
$∠ M = 60^{\circ}$
$∠ O = 105^{\circ}$
$∠ R = 105^{\circ}$ है।

दिया है,

चतुर्भुज $M O R E$ जिसमें
$M O = 6$ $c m$
$O R = 4.5$ $c m$
$∠ M = 60^{\circ}$
$∠ O = 105^{\circ}$
$∠ R = 105^{\circ}$

चतुर्भुज $M O R E$ में दो भुजाओं और तीन कोणों की माप दी गई है।
दिए गये चतुर्भुज की रचना को समझने के लिए सबसे पहले चतुर्भुज की एक कच्ची आकृति खींचकर उसके मापों को चिन्हित करते है।

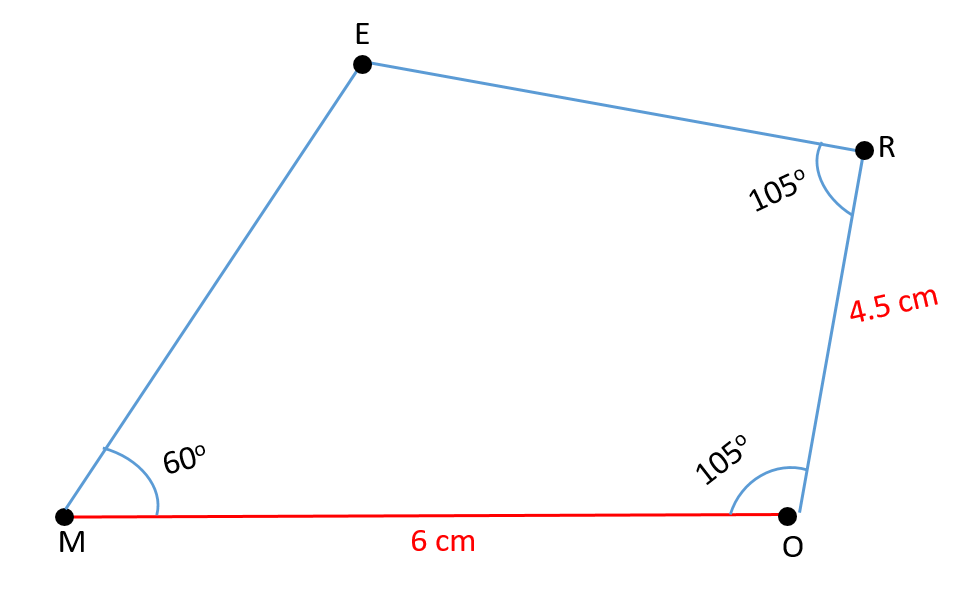
चरण 1: सर्वप्रथम

M O = 6

c m

का एक रेखाखंड खींचते हैं।

ocr_image

चरण 2:

M

को केन्द्र मानते हुए

60^{\circ}

का कोण तथा

O

को केंद्र मानते हुए

105^{\circ}

का कोण परकार व पेंसिल की सहायता से बनाते हैं।

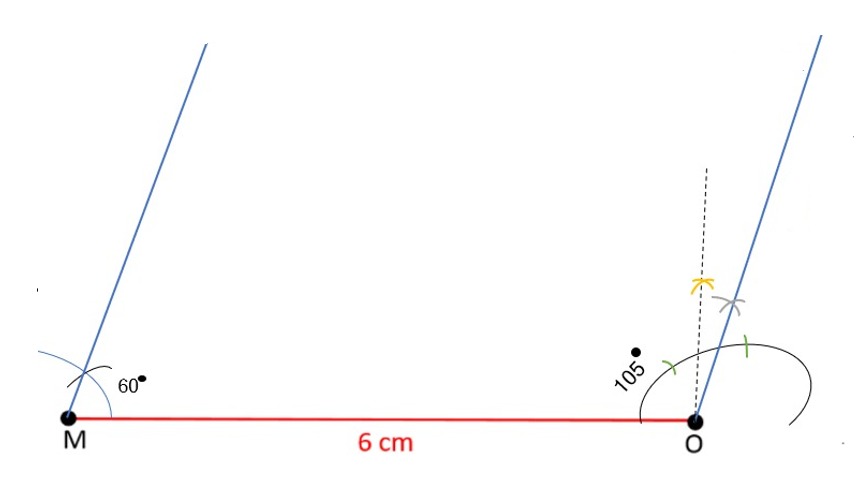
ocr_image

चरण 3: अब परकार में 4.5

C M

त्रिज्या का चाप भरकर कोण

O

वाली रेखा पर ऊपर की तरफ काटते हैं तथा वहाँ बिन्दु

R

अंकित करते है।

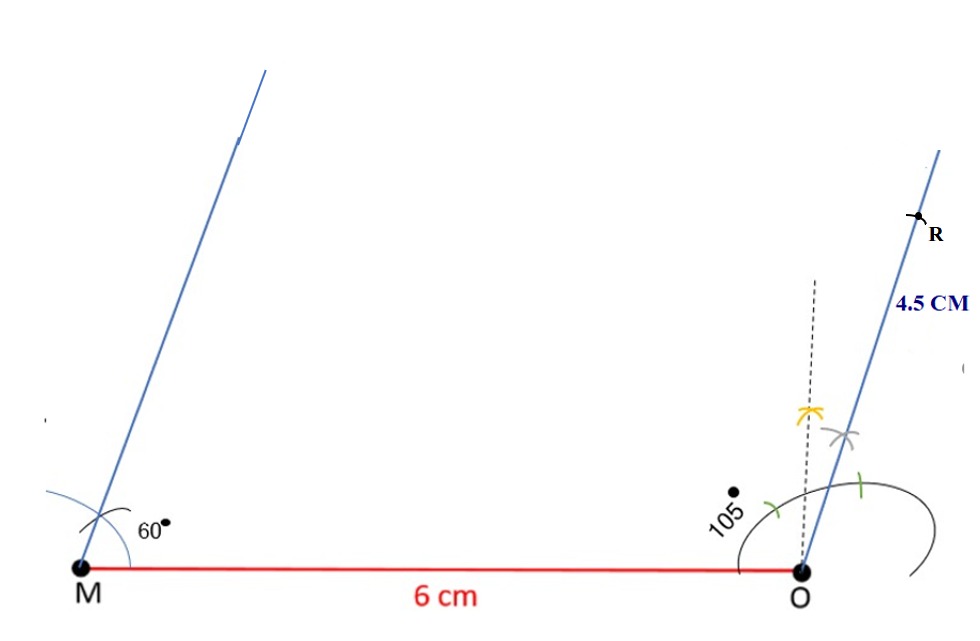
ocr_image

चरण 4: बिन्दु

R

को केन्द्र मानते हुए

105^{\circ}

का कोण परकार व पेंसिल की सहायता से बनाते हैं तथा कोण वाली रेखा को आगे खींचते है।

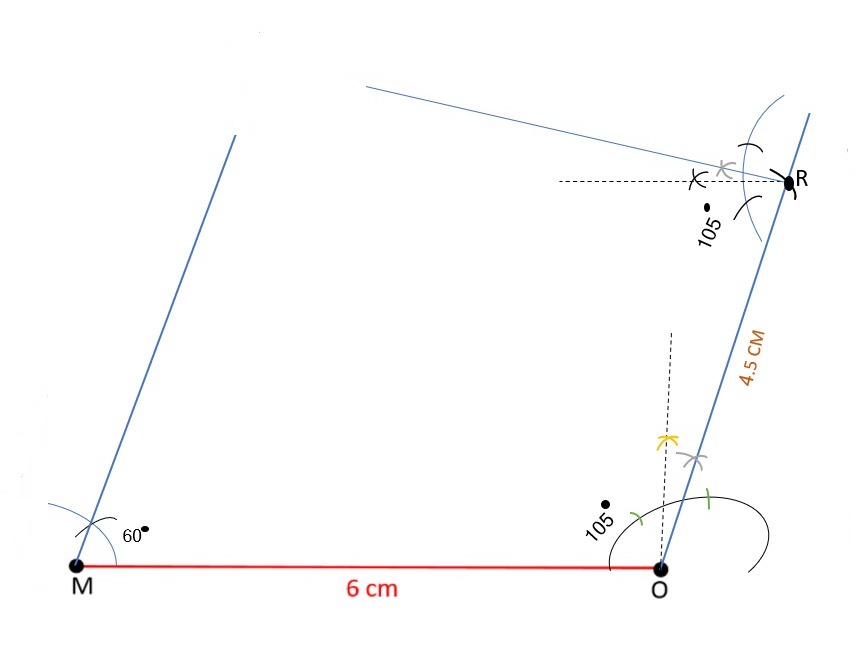
ocr_image

चरण 5:

∠ M

और

∠ R

की रेखाओ को आगे बढ़ाते हैं तथा जहाँ ये रेखाएँ एक - दूसरे को काटती हैं वहाँ बिन्दु

E

अंकित कर देते हैं और चतुर्भुज को पूरा करते है।

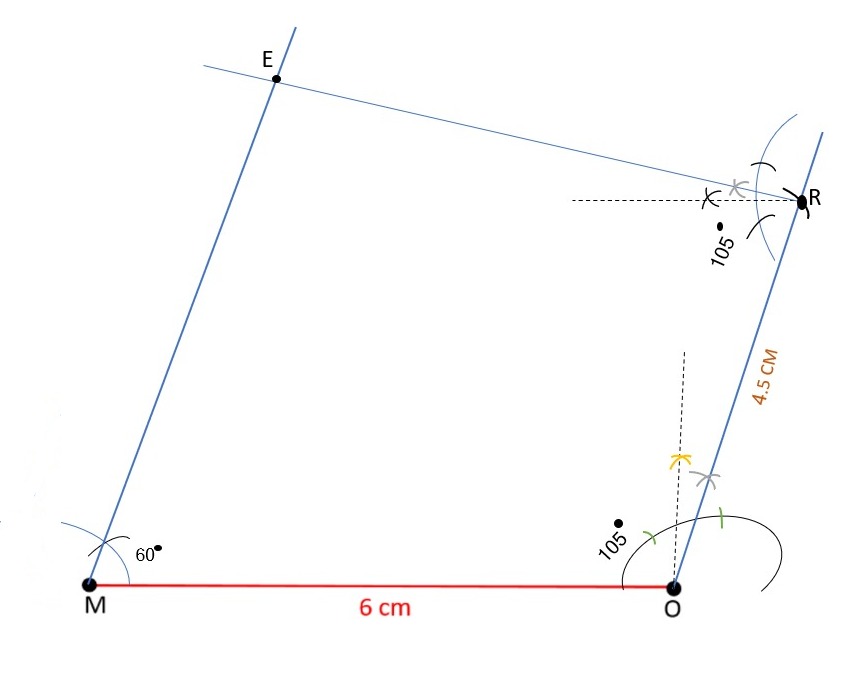
ocr_image

अतः एक अभीष्ट चतुर्भुज

M O R E

की रचना हुई।

Learn more

उदाहरण 5

निम्नलिखित चतुर्भुज की रचना कीजिए :
चतुर्भुज $P L A N$ जिसमें
$P L = 4$ $c m$
$L A = 6.5$ $c m$
$∠ P = 90^{\circ}$
$∠ A = 110^{\circ}$
$∠ N = 85^{\circ}$ हैं।

दिया है,

चतुर्भुज $P L A N$ जिसमें
$P L = 4$ $c m$
$L A = 6.5$ $c m$
$∠ P = 90^{\circ}$
$∠ A = 110^{\circ}$
$∠ N = 85^{\circ}$ है।

चतुर्भुज $P L A N$ में दो भुजाओं और तीन कोणों की माप दी गई है।
दिए गये चतुर्भुज की रचना को समझने के लिए, सबसे पहले चतुर्भुज की एक कच्ची आकृति खींचकर उसके मापों को चिन्हित करते है।

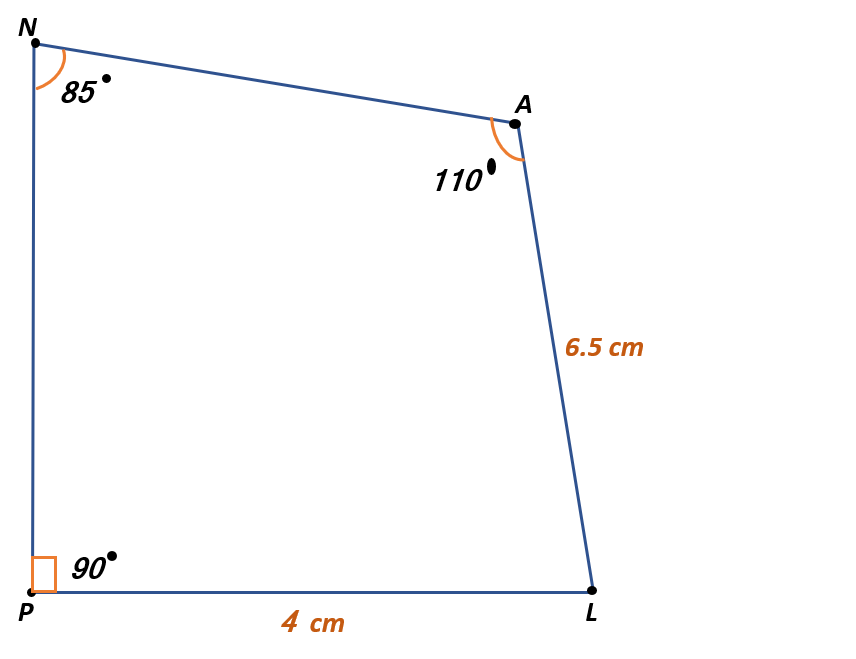
यहाँ चूँकि

∠ L

नहीं दिया गया है,

∠ L

दिये गये दोनों भुजाओं के बीच का कोण है, अत: इन आसन्न भुजाओं के बीच के कोण को ज्ञात किये बिना दिये गये चतुर्भुज की रचना सम्भव नहीं है।

हम जानते हैं की चतुर्भुज के चारों कोणों का योग

= 360^{\circ}

∠ P + ∠ A + ∠ N + ∠ L = 360^{\circ}

\Rightarrow 90^{\circ} + 110^{\circ} + 85^{\circ} + ∠ L = 360^{\circ}

\Rightarrow ∠ L + 285^{\circ} = 360^{\circ}

\Rightarrow ∠ L = 360^{\circ} - 285^{\circ}

\Rightarrow ∠ L = 75^{\circ}

चरण 1: सर्वप्रथम

P L = 4

c m

का एक रेखाखंड खींचते हैं।

ocr_image

चरण 2: बिन्दु

P

को केन्द्र मानते हुए

90^{\circ}

का कोण तथा बिन्दु

L

को केन्द्र मानते हुए

75^{\circ}

का कोण परकार व पेंसिल की सहायता से बनाते है।

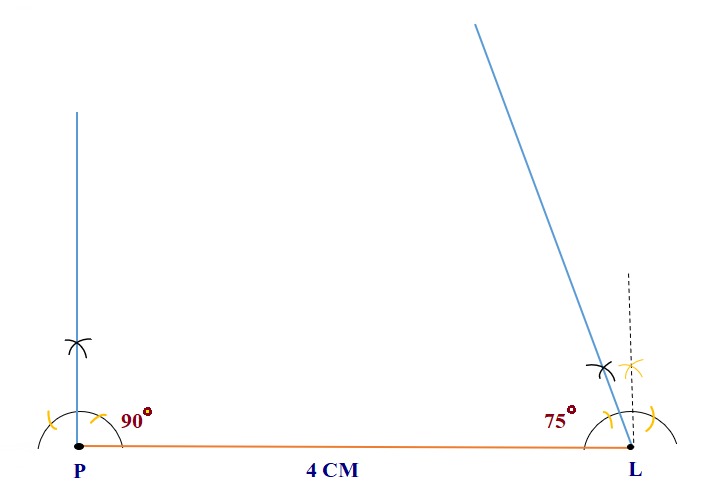
ocr_image

चरण 3: अब

75^{\circ}

कोण वाली रेखा पर 6.5

c m

त्रिज्या का एक चाप काटते हैं जिसे बिन्दु

A

से चिन्हित करते है।

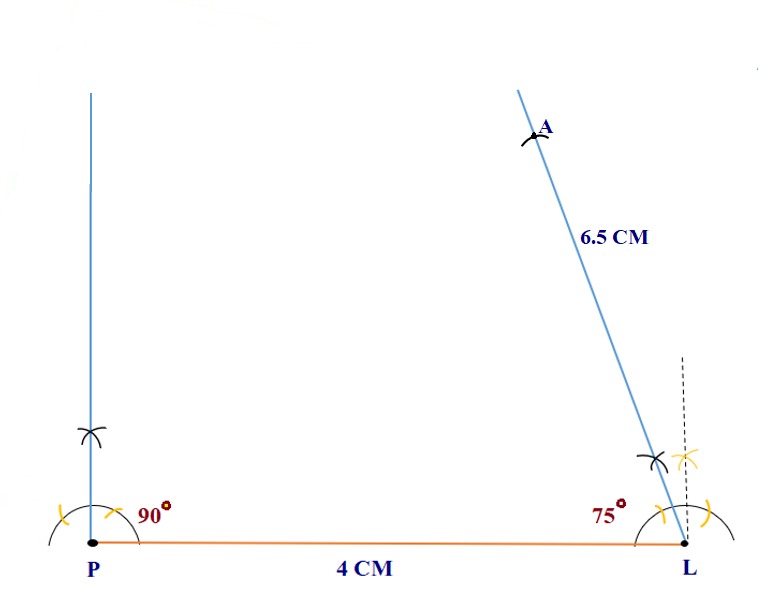
ocr_image

चरण 4:अब बिन्दु

A

को केंद्र मानते हुए

110^{\circ}

का कोण चांदे की सहायता से बनाते हैं तथा कोण वाली रेखा को आगे बढ़ाते है।

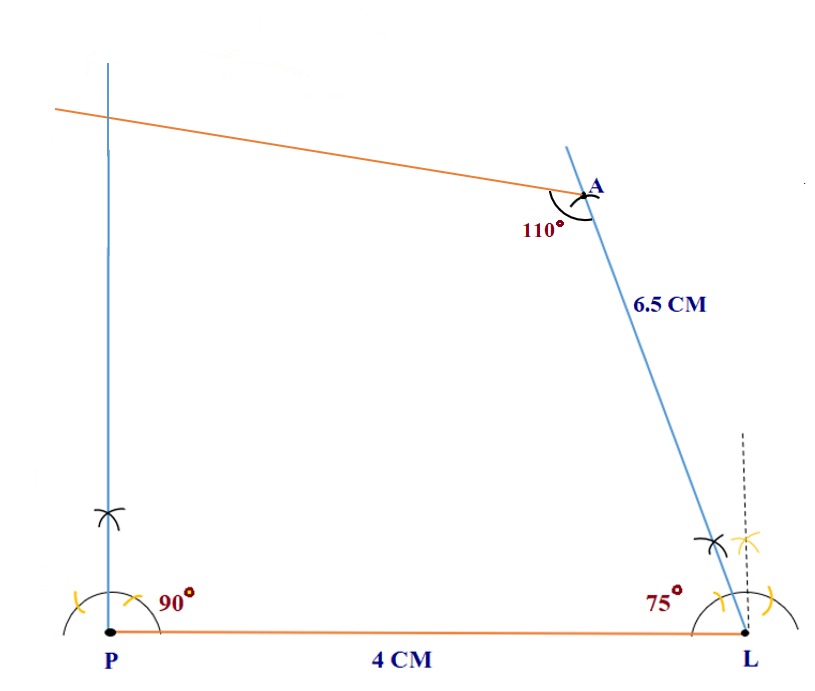
ocr_image

चरण 5: अब

∠ P

और

∠ A

की रेखाएँ एक - दूसरे को जहाँ काटती हैं वहाँ बिन्दु

N

अंकित करते है। इस बिन्दु पर

85^{\circ}

का कोण बनता हैं जिसकी जांच हम चांदे की सहायता से करेंगे।

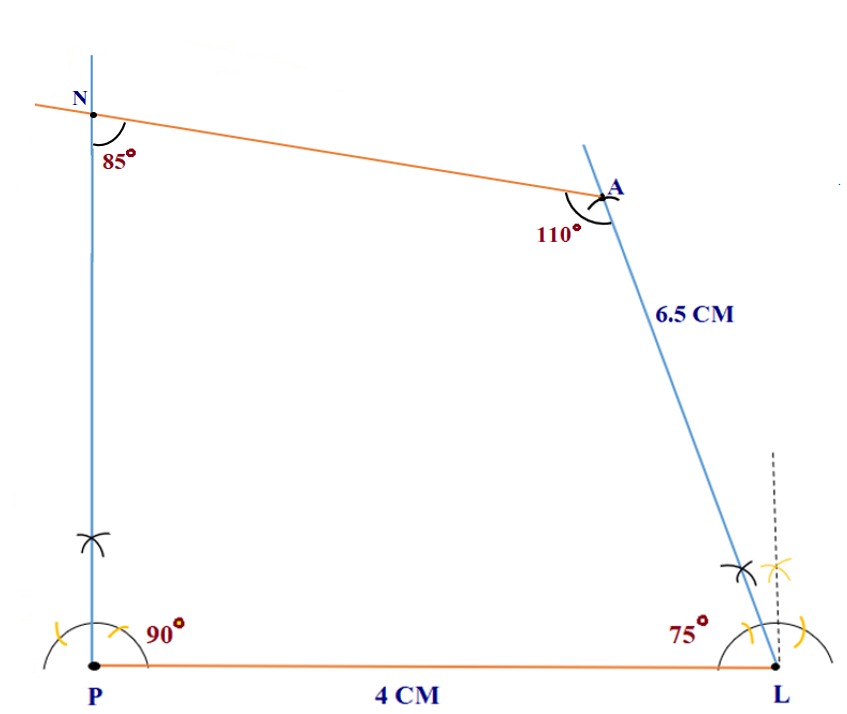
ocr_image

अतः एक अभीष्ट चतुर्भुज

P L A N

की रचना हुई।

Learn more

एक चतुर्भुज की रचना जब तीन भुजाओं और उनके बीच के दो कोणों की माप दी गई हों -

अब हम एक ऐसे चतुर्भुज की रचना करना सीखेंगे जिसमें उसकी तीन भुजाएँ तथा उनके मध्य के दो कोणों की माप दी गई हो।

हम इस रचना को भी एक उदाहरण की सहायता से समझ सकते है-

उदाहरण : एक चतुर्भुज ABCD की रचना करते है, जिसमे
$A B = 4 c m, B C = 5 c m, C D = 6.5 c m$
$∠ B = 105 °$ , $∠ C = 80^{\circ}$ है।

हल : एक कच्ची ( $R o u g h$ ) आकृति इस रचना को समझने में हमारी सहायता करेगी।
सर्वप्रथम हम एक कच्ची आकृति खींचते हैं और मापों को चिह्नित करते हैं।

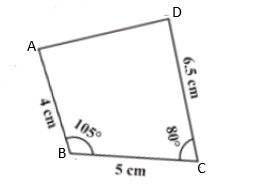
चरण 1 : अब एक रेखाखण्ड BC = 5 cm खींचतें है। अब हमें बिन्दु B पर

105^{\circ}

का कोण बनाना है। जिसके लिए हमें पहले

90^{\circ}

का कोण बनाना पड़ेगा उसके बाद

105^{\circ}

का बनायेगें। कोण बनाने के बाद कोण वाली रेखा को आगे खींचते हैं तथा अंतिम छोर पर X अंकित करते है।
अब बिन्दु B से 4 cm की दूरी पर रेखा BX पर, बिन्दु A अंकित करते है।
इस तरह हम इस चतुर्भुज के तीन बिन्दु प्राप्त हो चुके है।

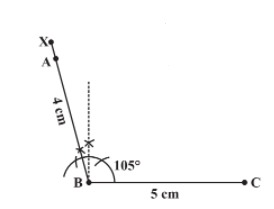
ocr_image

चरण 2 :अब हमें चतुर्थ बिन्दु D प्राप्त करना हैं जिसके लिए हमें बिन्दु C पर

80^{\circ}

का कोण बनाना पड़ेगा। अतः बिन्दु C पर

80^{\circ}

का कोण चांदे की सहायता से बनाते है।
अब इस कोण वाली रेखा को आगे खींचते हैं तथा वहांँ बिन्दु Y अंकित करते हैं जो केवल अंतिम छोर पर स्थित मात्र एक बिन्दु है।

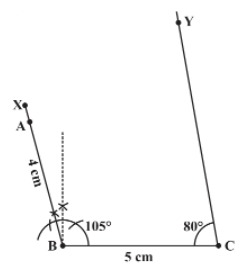
ocr_image

चरण 3 : बिन्दु D रेखा CY पर कही स्थित है। इसका पता लगाने के लिए हम परकार में 6.5 cm का चाप भरकर बिन्दु C से, रेखा CY पर खींचते है।
यह चाप CY को जहां काटता हैं वहाँ बिन्दु D अंकित कर देते हैं अथवा इस बिन्दु को हम सीधा स्केल से नाप कर भी अंकित कर सकते है।

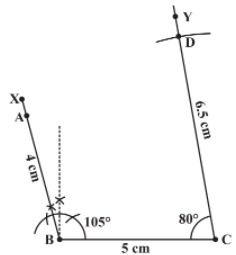
ocr_image

चरण 4 : अब बिन्दु A और D को मिलाते हैं तथा चतुर्भुज ABCD को पूरा करते है।

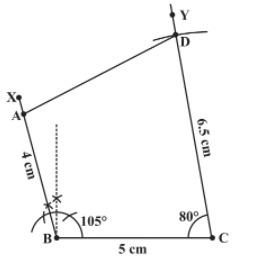
ocr_image

उदाहरण 6

निम्नलिखित चतुर्भुज की रचना कीजिए :
चतुर्भुज $D E A R$ जिसमें
$D E = 4$ $c m$
$E A = 5$ $c m$
$A R = 4.5$ $c m$
$∠ E = 60^{\circ}$
$∠ A = 90^{\circ}$ हैं।

दिया है,

$D E = 4$ $c m$
$E A = 5$ $c m$
$A R = 4.5$ $c m$
$∠ E = 60^{\circ}$
$∠ A = 90^{\circ}$

चतुर्भुज $D E A R$ में 3 भुजाएँ और 2 कोणों की माप दी गई है।
दिए गये चतुर्भुज की रचना को समझने के लिए सबसे पहले चतुर्भुज की एक कच्ची आकृति खींचकर उसकी मापों को चिन्हित करते है।

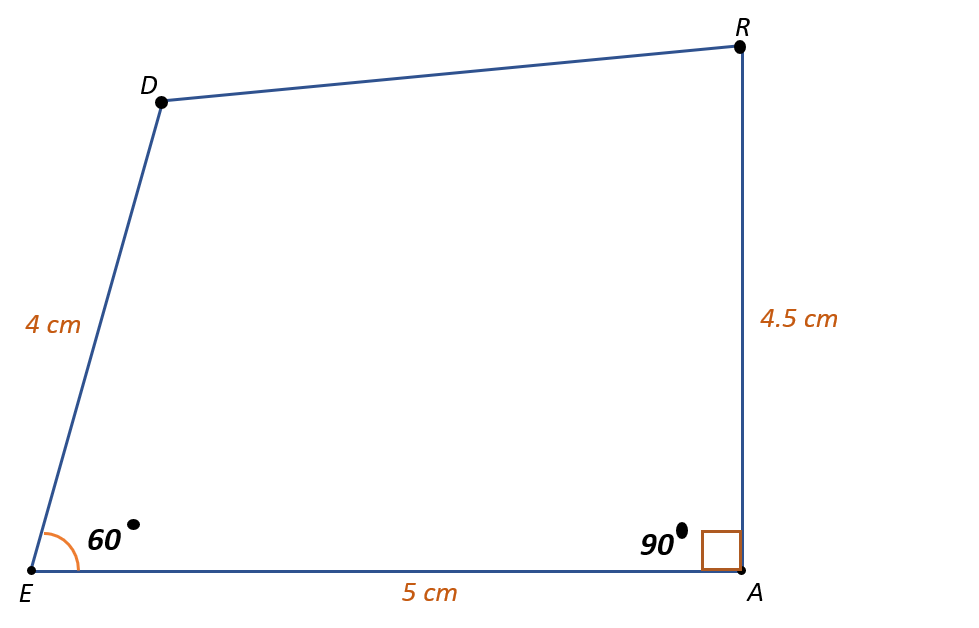
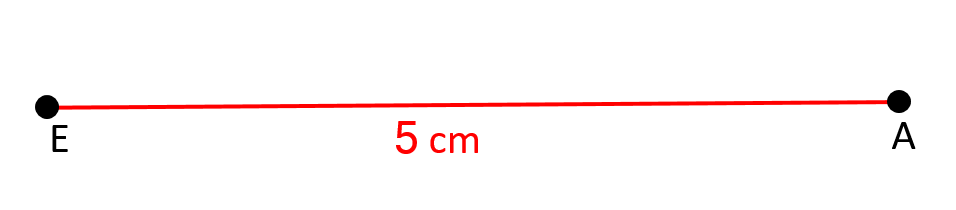
चरण 1: सर्वप्रथम

E A = 5

c m

का एक रेखाखंड खींचते हैं।

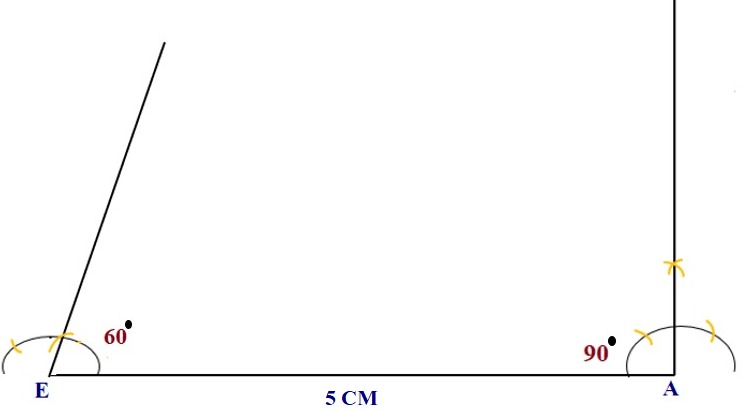
ocr_image

चरण 2: अब बिन्दु

E

को केन्द्र मानते हुए

60^{\circ}

का कोण तथा बिन्दु

A

को केन्द्र मानते हुए

90^{\circ}

का कोण परकार व पेंसिल की सहायता से बनाते है।

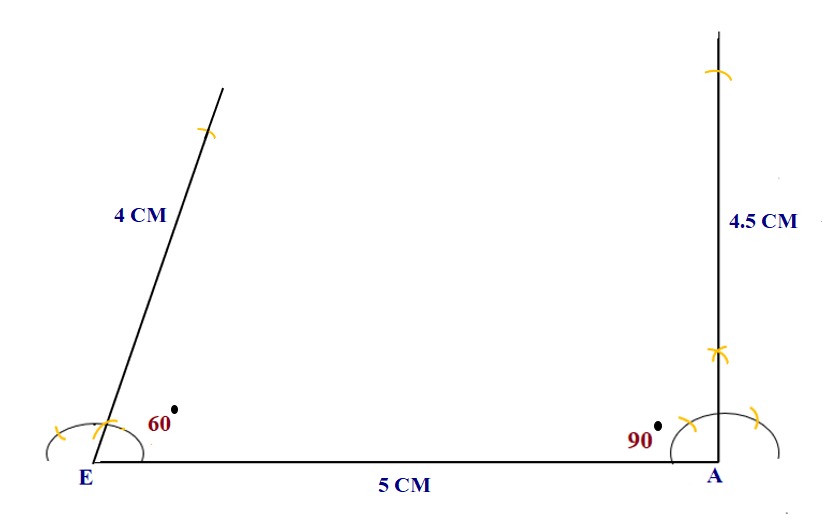
ocr_image

चरण 3: अब परकार में 4

C M

त्रिज्या का चाप भरकर

∠ E

वाली रेखा पर तथा 4.5

C M

त्रिज्या का चाप भरकर

∠ A

वाली रेखा पर ऊपर की तरफ काटते हैं।

ocr_image

चरण 4:

∠ E

वाली रेखा पर जहाँ चाप कटा, वहाँ बिन्दु

D

अंकित करते हैं तथा

∠ A

वाली रेखा पर जहाँ चाप कटा, वहाँ बिन्दु

R

अंकित करते है।
अब बिन्दु

D

और

R

को मिला देते हैं तथा चतुर्भुज को पूरा करते है।

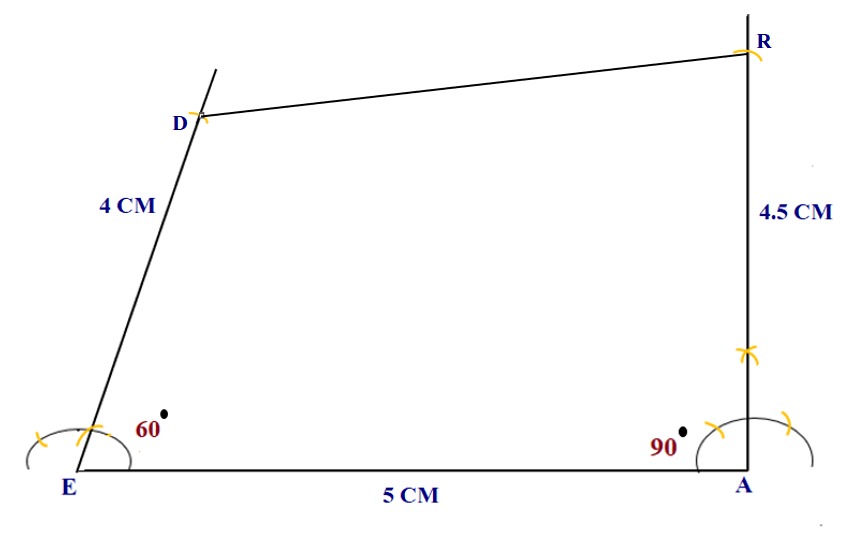
ocr_image

अतः एक अभीष्ट चतुर्भुज

D E A R

की रचना हुई।

Learn more

विशिष्ट स्थितियाँ -

बच्चों! अब तक हमने ऐसे चतुर्भुजो की रचना करना सीखा हैं जिसमें कम से कम हमें पाँच मापे दी हुई थी, परंतु क्या किसी ऐसे चतुर्भुज की रचना करना संभव हैं जिसकी पाँच मापे नहीं दी गई हो।
आइए अब एक ऐसे चतुर्भुज की रचना करना सीखतें हैं, जिसकी पाँच मापे नहीं दी गई हो।

ऐसे चतुर्भुजों की कुछ विशेषताएँ होती है। वे विशिष्ट प्रकार के चतुर्भुज होते हैं जैसे - वर्ग, समचतुर्भुज आदि।
बच्चों ऐसे चतुर्भुजो की रचना को हम निम्न उदाहरण की सहायता से समझ सकते हैं -

उदाहरण: एक समचतुर्भुज की रचना कीजिए जहाँ AC = 6 cm और BD = 7 cm हो।
हल: चूंकि हमें पता हैं की यह चतुर्भुज एक समचतुर्भुज हैं जिसकी हमें दो मापे दी गई हैं जो इसके विकर्णों की लंबाई है।
इसकी रचना के लिए हमें इसके गुणों के बारे में ज्ञात होना चाहिए। जैसे -

- समचतुर्भुज की सभी भुजाएँ आपस में बराबर होती हैं।
- समचतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं तथा एक दूसरे पर लम्ब होते हैं आदि।

एक कच्ची ( $R o u g h$ ) आकृति इस रचना को समझने में हमारी सहायता करेगी।
हम एक कच्ची आकृति खींचते हैं और मापों को चिह्नित करते हैं।

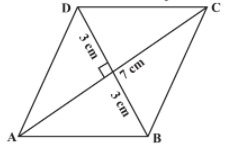
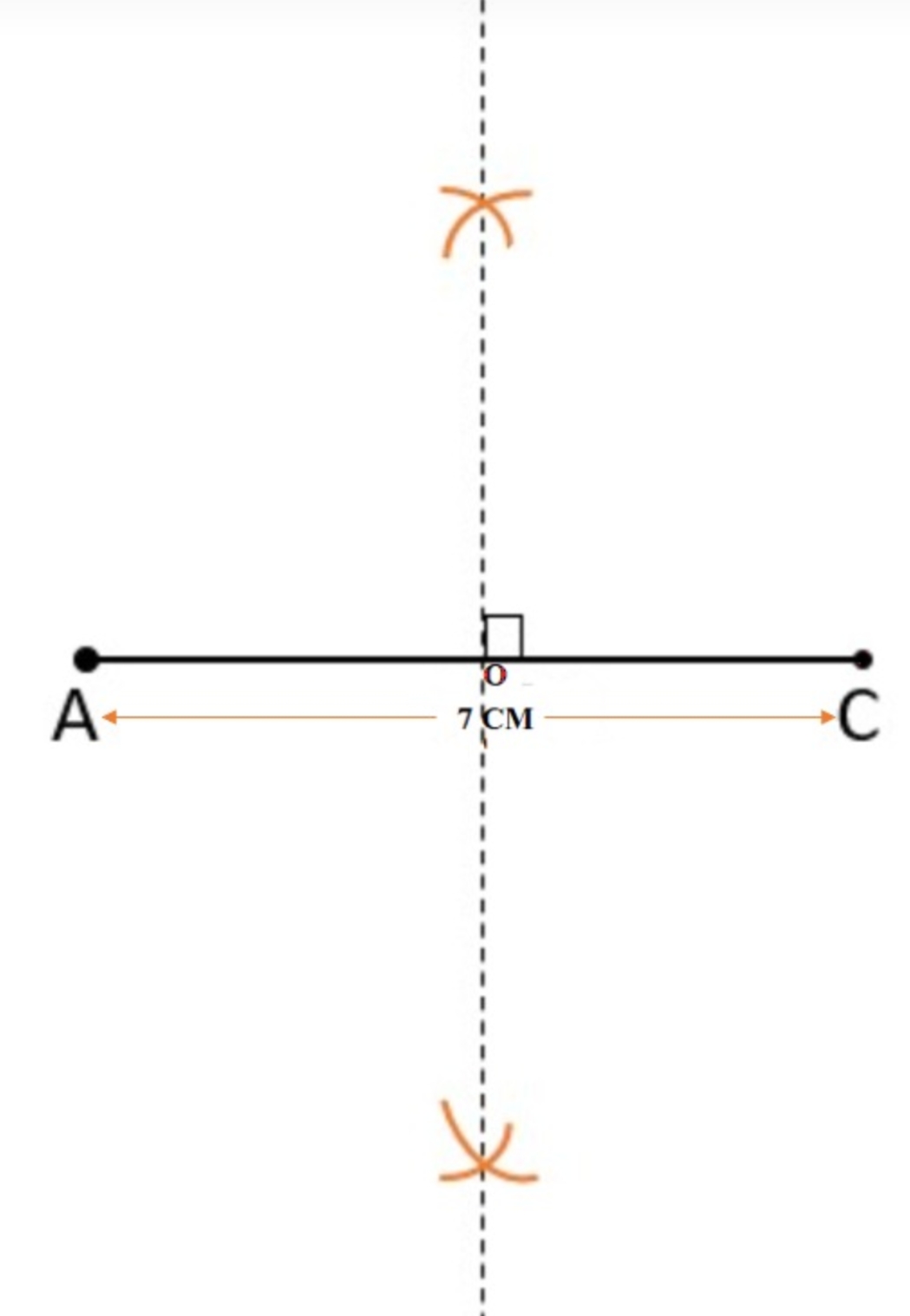
चरण 1 : सर्वप्रथम हम एक रेखाखण्ड AC = 7 cm खींचते है। अब इसका लंब समद्विभाजन करेंगे।
लंब समद्विभाजन करने के लिए परकार में रेखाखण्ड AC की आधी से ज्यादा माप भरकर बिन्दु A से, एक चाप ऊपर की तरफ और एक चाप नीचे की तरफ काटते है।
उसी माप से बिन्दु C पर परकार की नोक रखकर एक चाप ऊपर की तरफ पहले वाले चाप पर तथा एक चाप नीचे की तरफ काटते है, जो पहले वाले चाप को प्रतिच्छेद करता है।
अब दोनों प्रतिच्छेदित चापो को एक सीधी रेखा से मिला देते हैं तथा AC के मध्य में बिन्दु O अंकित करते है, जो AC को समान दो भागों में बांटता है।

ocr_image

चरण 2 : चूंकि हम जानते हैं की समचतुर्भुज के विकर्ण एक - दूसरे को लंब पर समद्विभाजित करते है, अतः

AO = OC = $\frac{7}{2}$ = 3.5 cm

BO = OD = $\frac{6}{2}$ = 3 cm

अब हम परकार में 3 cm का चाप भरकर बिन्दु O से लंब समद्विभाजक वाली रेखा पर एक - एक चाप ऊपर और नीचे की तरफ काटते है।
ऊपर की तरफ जहाँ चाप कटा, वहाँ बिन्दु B और नीचे की तरफ जहाँ चाप कटा, वहाँ बिन्दु D अंकित करते है।

चरण 3 : अब चारों बिन्दुओ को मिलाकर चतुर्भुज को पूरा करते है।

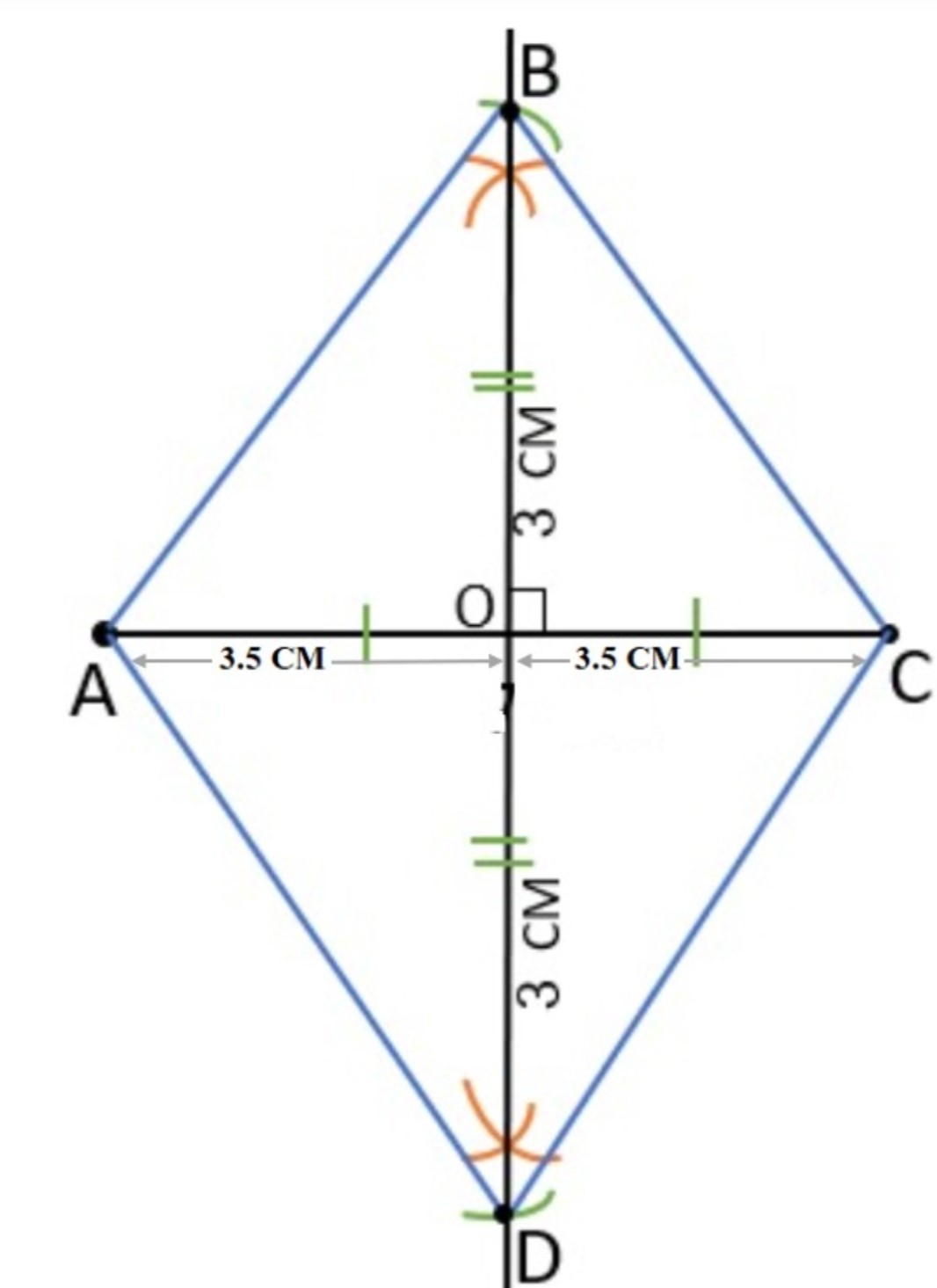
ocr_image

चरण 4 : इस प्रकार हमें अभीष्ट समचतुर्भुज ABCD प्राप्त होता है।

आइए कुछ और उदाहरणों की सहायता से समझते है-

उदाहरण 7

एक वर्ग की रचना कीजिए, जिसकी प्रत्येक भुजा 6.4 $c m$ हैं।

दिया है,

वर्ग जिसकी प्रत्येक भुजा 6.4 $c m$ हैं हम जानते हैं कि
एक वर्ग के सभी कोण समकोण अर्थात $90^{\circ}$ के होते हैं और सभी भुजाएँ आपस में बराबर होती हैं।

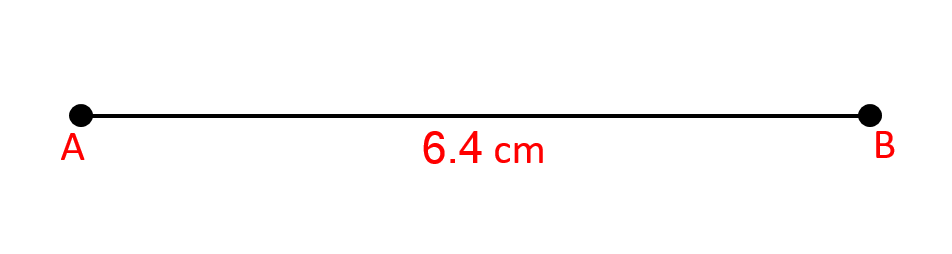
चरण 1: सर्वप्रथम 6.4 $c m$ का एक रेखाखंड खींचते हैं और एक सिरे को $A$ तथा दूसरे सिरे को $B$ से चिन्हित करते हैं।

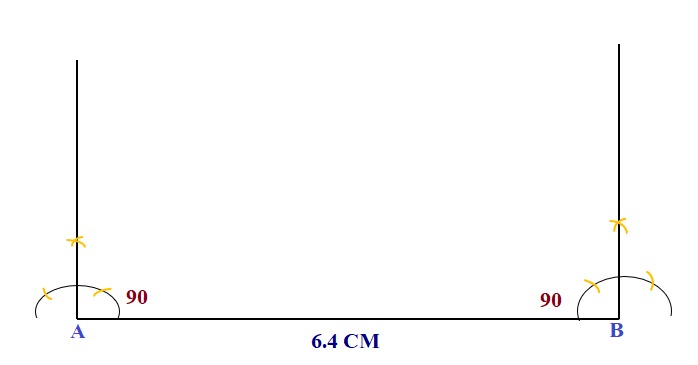
चरण 2: अब बिन्दु

A

को केन्द्र मानते हुए

90^{\circ}

का कोण और

B

को केन्द्र मानते हुए

90^{\circ}

का कोण परकार व पेंसिल की सहायता से बनाते हैं।

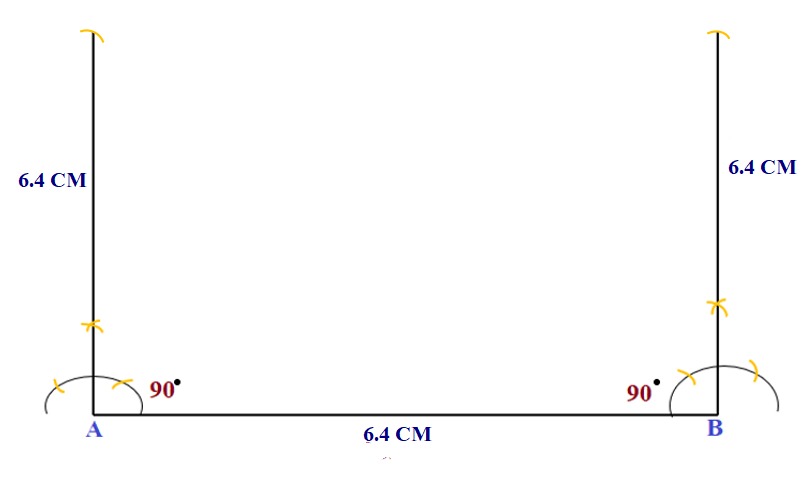
ocr_image

चरण 3: बिन्दु

A

को केन्द्र मानते हुए 6.4

c m

त्रिज्या का चाप कोण वाली रेखा पर काटते हैं, उसी प्रकार

B

को केन्द्र मानते हुए 6.4

c m

त्रिज्या का चाप कोण वाली रेखा पर काटते हैं तथा माप अंकित करते है।

ocr_image

चरण 4: बिन्दु

A

पर जहाँ चाप कटा वहाँ

D

तथा बिन्दु

B

पर जहाँ चाप कटा वहाँ

C

अंकित करते हैं और दोनों बिंदुओं को एक सरल रेखा से मिला देते है।
बिन्दु

C

व

D

पर इस सरल रेखा से

90^{\circ}

के कोण स्वतः ही बन जाएगे। अतः उन्हे भी चिन्हित करते है। इन कोणों की जांच हम चांदे की सहायता से कर सकते है।

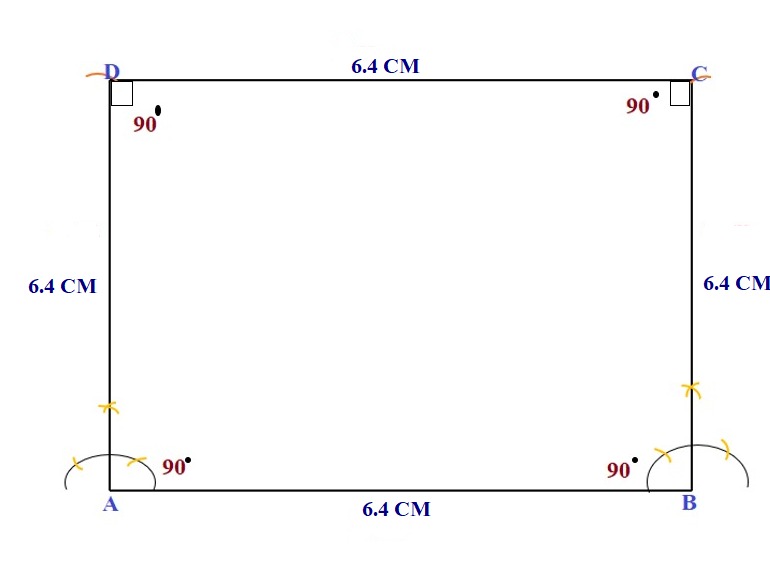
ocr_image

अतः यह एक वर्ग की रचना हैं जिसकी प्रत्येक भुजा 6.4

c m

हैं।

Learn more

उदाहरण 8

निम्नलिखित की रचना कीजिए :
एक आयत जिसकी आसन्न भुजाओ की लंबाइयाँ 5 $c m$ और 4 $c m$ है।

दिया है,

आयत जिसकी आसन्न भुजाओं की लंबाई 5 $c m$ और 4 $c m$ हैं।

हम जानते हैं कि एक आयत का प्रत्येक कोण समकोण अर्थात $90^{\circ}$ का होता हैं और सम्मुख भुजाएँ अर्थात आमने सामने की भुजाएँ बराबर होती हैं।

चरण 1: सर्वप्रथम 5 $c m$ का एक रेखा खींचते हैं और एक सिरे को $A$ तथा दूसरे सिरे को $B$ से चिन्हित करते हैं।

चरण 2: अब बिन्दु

A

को केन्द्र मानते हुए

90^{\circ}

का कोण और बिन्दु

B

को केन्द्र मानते हुए

90^{\circ}

का कोण परकार व पेंसिल की सहायता से बनाते हैं।

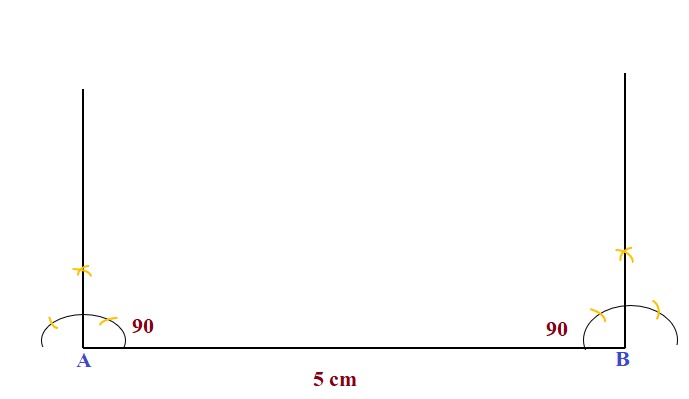
ocr_image

चरण 3: बिन्दु

A

और

B

को केन्द्र मानते हुए 4 - 4

c m

त्रिज्या के चाप

90^{\circ}

कोण वाली दोनों रेखाओं पर काटते हैं और मापे अंकित करते है।

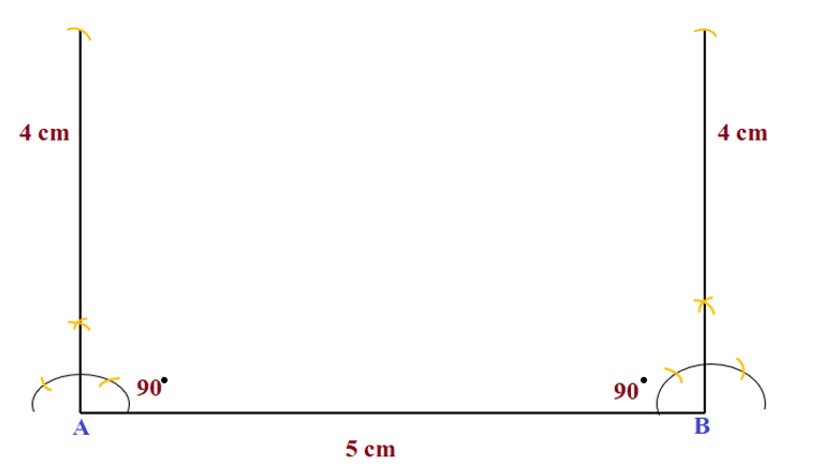
ocr_image

चरण 4: बिन्दु

A

पर जहाँ चाप कटा वहाँ

D

तथा बिन्दु

B

पर जहाँ चाप कटा वहाँ

C

अंकित करते हैं और दोनों बिंदुओं को एक सरल रेखा से मिला देते हैं तथा माप अंकित करते है।
बिन्दु

C

व

D

पर इस सरल रेखा से

90^{\circ}

के कोण स्वतः ही बन जाएगे जिसकी जांच हम चांदे की सहायता से करते है। अतः उन्हे भी चिन्हित करते है।

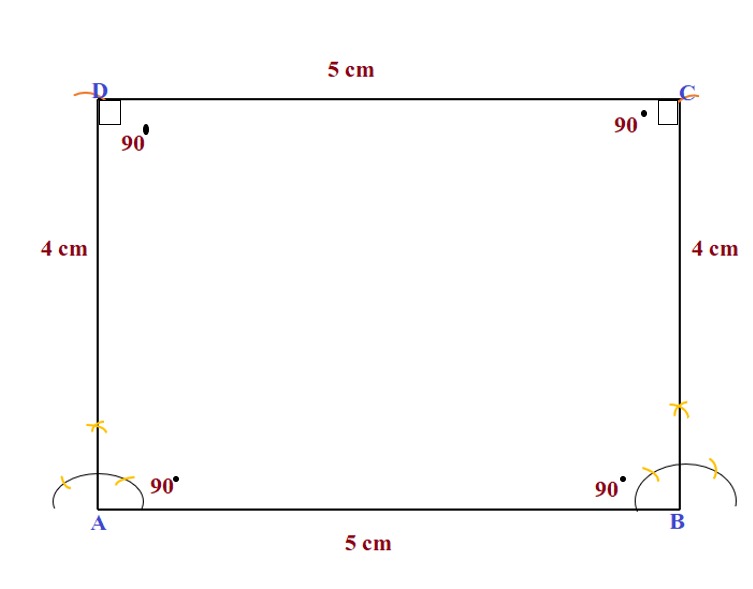
ocr_image

अतः यह एक आयत

A B C D

की रचना हैं जिसकी आसन्न भुजाओं की लंबाइयाँ 5

c m

और 4

c m

है।

Learn more

सारांश

SSS रचना कसौटी के प्रयोग से एक त्रिभुज की रचना आसानी से कर सकते है।

पाँच मापों से एक अद्वितीय चतुर्भुज प्राप्त हो सकता है।

एक अद्वितीय चतुर्भुज की रचना की जा सकती हैं यदि उसकी चार भुजाओं और एक विकर्ण की लंबाई दी गई हो।

एक अद्वितीय चतुर्भुज की रचना की जा सकती हैं यदि उसकी तीन भुजाओं और दो विकर्णों की लंबाई दी गई हो।

एक अद्वितीय चतुर्भुज की रचना की जा सकती हैं यदि उसकी दो आसन्न भुजाओं और तीन कोणों की माप दी गई हो।

एक अद्वितीय चतुर्भुज की रचना की जा सकती हैं यदि उसकी तीन भुजाओं और दो बीच के कोणों की माप दी गई हो।

Home
Ask Doubt
Profile