परिमेय संख्याएँ कक्षा 8 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम परिमेय संख्याओं का अध्ययन करेंगे। जैसे कि हमने कक्षा 7 में पढ़ा था, दो पूर्णांकों p और q (q≠0) के अनुपात p:q को pq लिखा जा सकता है। यही वह रूप है जिसमें परिमेय संख्याएँ व्यक्त की जाती हैं । इस अध्याय में हम परिमेय-अपरिमेय संख्याओं के गुणों का अध्ययन करेंगे।
आइये जानते है, परिमेय संख्या को और करीब से ...
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम परिमेय संख्याओं का अध्ययन करेंगे, हम पिछली कक्षाओं में कुछ संख्याओं का अध्ययन कर चुके हैं, आइए उन्हे पुनः उन्हें देख लेते है −
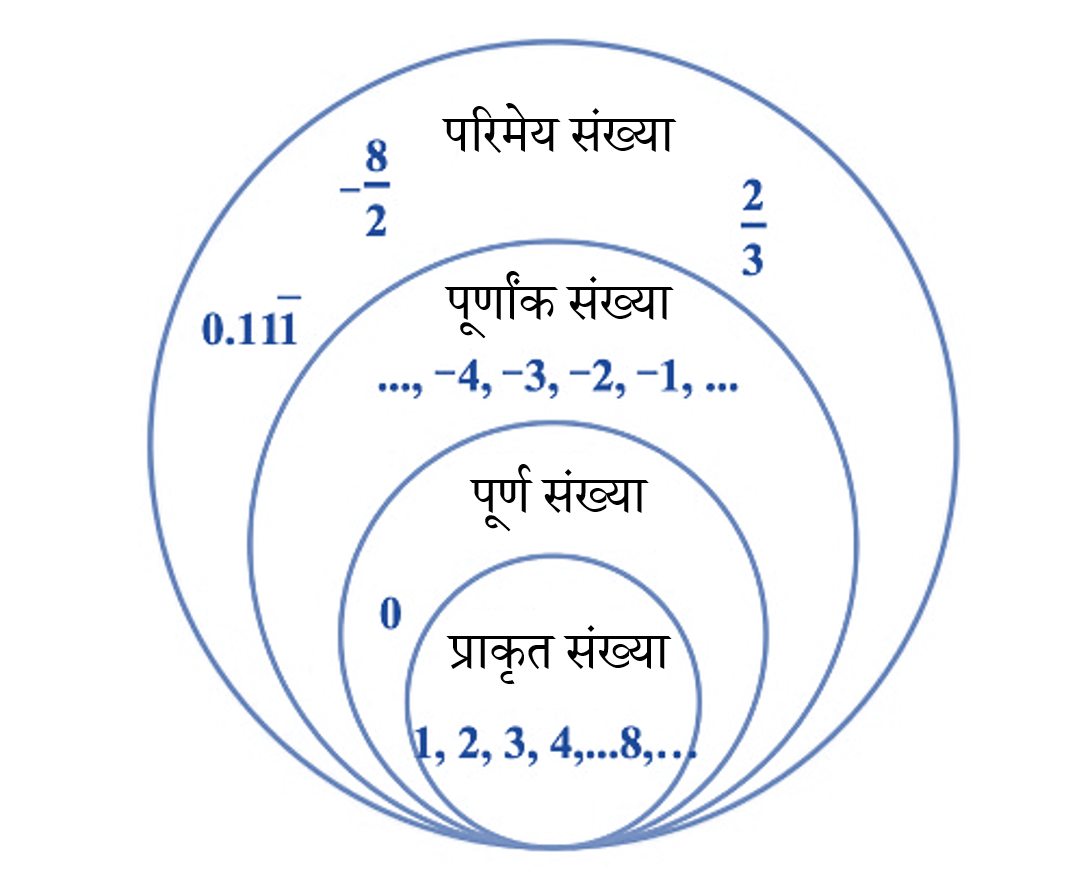
(1) प्राकृतिक संख्या = 1,2,3,......,∞, सभी धनात्मक पूर्णांक
2) पूर्ण संख्या=शून्य सहित सभी प्राकृत संख्याएँ पूर्ण संख्याएँ कहलाती हैं।
(3) पूर्णांक संख्या = शून्य सहित सभी ऋणात्मक और धनात्मक संख्याएँ पूर्णांक कहलाती हैं। (जिसमे भिन्न सम्मिलित नहीं होगा।)
परिमेय संख्या
जहाँ p और q पूर्णांक हैं (q≠0)
परिमेय संख्याओं के गुणधर्म
1. संवृत
यदि दो परिमेय संख्याओं की संक्रिया ( योग, व्यवकलन, गुणा या भाग ) से हमें परिमेय संख्या ही प्राप्त हो तो परिमेय संख्या उस संक्रिया के अंतर्गत संवृत होगा।
| संक्रिया | संवृत गुण की जांच | टिप्पणी |
|---|---|---|
| योग | दो परिमेय संख्या 14 एवं 56 को जोड़ते हैं - 14+56=6+2024 =2624=1312 1312 एक परिमेय संख्या है | संवृत है |
| व्यवकलन | दो परिमेय संख्या 14 एवं 34 को घटाते हैं - 14−34=−24 =−12 −12 एक परिमेय संख्या है | संवृत है |
| गुणा | दो परिमेय संख्या 16 एवं 34 का गुणा करते हैं - 16⋅34=1⋅36⋅4 =324 324 एक परिमेय संख्या है | संवृत है |
| भाग | परिमेय संख्या 56 को परिमेय संख्या 13 से भाग देते हैं - (56)÷(13) =(56)⋅(31)=52 52 एक परिमेय संख्या है किन्तु यदि यहाँ भाजक 13 की जगह अन्य परिमेय संख्या 0 लेते हैं तो यह भाग अपरिभाषित होगा क्यूंकि हर में शून्य होने पर संख्या अपरिभाषित होती है अथवा हमें परिमेय संख्या प्राप्त नहीं होगी। अतः सभी परिमेय संख्याओं के लिए भाग करने पर परिमेय संख्या प्राप्त नहीं होगी। | संवृत नहीं है |
2. क्रम विनिमेयता
यदि दो परिमेय संख्याओं के मध्य संक्रिया करने पर प्राप्त परिणाम संख्याओं के क्रम पर निर्भर नहीं करता है (क्रम बदलने पर भी परिणाम नहीं बदलता) तब वह संक्रिया परिमेय संख्या पर क्रम विनिमेय होगी।
| संक्रिया | क्रम विनिमेयता की जांच | टिप्पणी |
|---|---|---|
| योग | दो परिमेय संख्या 14 एवं 56के लिए 14+56=6+2024 =2624=1312 क्रम बदलने पर - 56+14=20+624 =2624=1312 दोनों स्थितियों में परिणाम समान है | क्रम विनिमेय है |
| व्यवकलन | दो परिमेय संख्या 14 एवं 34 को घटाते हैं - 14−34=−24 =−12 क्रम बदलने पर - 34−14=24 =12 दोनों स्थितियों में परिणाम समान नहीं है | क्रम विनिमेय नहीं है |
| गुणा | दो परिमेय संख्या 16 एवं 34 का गुणा करते हैं - 16⋅34=1⋅36⋅4 =324 क्रम बदलने पर - 34⋅16=3⋅14⋅6 =324 दोनों स्थितियों में परिणाम समान है | क्रम विनिमेय है |
| भाग | परिमेय संख्या 56 को परिमेय संख्या 13 से भाग देते हैं - (56)÷(13) =(56)⋅(31)=52 क्रम बदलने पर - (13)÷(56) =(13)⋅(65)=25 दोनों स्थितियों में परिणाम समान नहीं है | क्रम विनिमेय नहीं है |
3. साहचर्यता
यदि ⋆ एक संक्रिया (योग, व्यवकलन, गुणा अथवा भाग ) हो तब साहचर्यता से -
a⋆(b⋆c)=(a⋆b)⋆c
| संक्रिया | साहचर्यता की जांच | टिप्पणी |
|---|---|---|
| योग | तीन परिमेय संख्या 14, 38 एवं 56 के लिए 14+(38+56)=14+{9+2024} 14+2924=6+2924 =3524 अब - (14+38)+56={2+38}+56 =58+56=15+2024 =3524 दोनों स्थितियों में परिणाम समान है | साहचर्य है |
| व्यवकलन | तीन परिमेय संख्या 14, 12 एवं 34 के लिए - 14−(12−34)=14−{2−34} =14−(−14) =14+14=24=12 अब - (14−12)−34={1−24}−34 =−14−34 =−44=−1 दोनों स्थितियों में परिणाम समान नहीं है | साहचर्य नहीं है |
| गुणा | तीन परिमेय संख्या 16, 25 एवं 34 का गुणा करते हैं - 16⋅(25⋅34)=16⋅{2⋅35⋅4} =16⋅620 =120 अब - (16⋅25)⋅34={1⋅26⋅5}⋅34 =230⋅34=2⋅330⋅4 =120 दोनों स्थितियों में परिणाम समान है | साहचर्य है |
| भाग | तीन परिमेय संख्या 56, 16एवं 13 का भाग देते हैं - (56)÷{(16)÷(13)} =56÷{(16)⋅(31)}=56÷12 =53 अब - {(56)÷(16)}÷(13) ={56⋅61}÷13)}=51÷13 =51⋅31=15 दोनों स्थितियों में परिणाम समान नहीं है | साहचर्य नहीं है |
OMR (One Minute Revision)
(i) क्रमविनिमेय हैं।
(ii) साहचर्य हैं।
उदाहरण 1
ज्ञात कीजिए 37+(−611)+(−821)+(522)
37+(−611)+(−821)+(522)
=198462+(−252462)+(−176462)+(105462)
(नोट कीजिए कि 7, 11, 21 तथा 22 का ल.स.प. 462 है। )
=198−252−176+105462
=−125462
METHOD-2
हम इसे निम्नलिखित प्रकार से भी हल कर सकते हैं :
37+(−611)+(−821)+522
=[37+(−821)]+[−611+522]
(क्रम विनिमेयता और साहचर्यता के उपयोग से)
=[9+(−8)21]+[−12+522]
(7 और 21 का ल.स.प. 21 है। 11 और 22 का ल.स.प. 22 है।)
=121+(−722)
=22−147462
=−125462
उदाहरण 2
ज्ञात कीजिए - 45×37×1516×(−149)
−45×37×1516×(−149)
=−4×35×7×15×(−14)16×9
=−1235×(−3524)
=−12×(−35)35×24
=1/2
METHOD-2
हम इसे निम्नलिखित प्रकार से भी हल कर सकते हैं : -
45×37×1516×(−149)
=(−45×1516)×[37×(−149)]
(क्रमविनिमेयता और साहचर्यता के उपयोग से)
=−34×(−23)
=12
तत्समक तथा प्रतिलोम
1.योज्य तत्समक
परिमेय संख्याओं के योग के लिए शून्य योज्य तत्समक हैं अतः जब परिमेय संख्याओं मे शून्य जोड़ा जाता हैं | तो योग फिर से वही परिमेय संख्या देता हैं |
जैसे 12+0=12
माना कि a परिमेय संख्या हैं -
अतः a + 0 = a
2. गुणात्मक तत्समक
परिमेय संख्याओं के गुणन के लिए 1 गुणात्मक तत्समक हैं अतः जब परिमेय संख्याओं मे 1 का गुणा किया जाता हैं | तो गुणन फिर से वही परिमेय संख्या देता हैं |
जैसे 12×1=12
माना कि a परिमेय संख्या हैं -
अतःa×1=a
3.योज्य प्रतिलोम
किसी भी परिमेय संख्याओं के लिए उस परिमेय संख्या की ऋणात्मकता उसका योज्य प्रतिलोम होता हैं तथा परिमेय संख्या और उसका योज्य प्रतिलोम योग हमेशा शून्य होता हैं | अतः परिमेय संख्या abके लिए ab+(−ab)=(−ab)+ab=0 प्राप्त है |
हम कह सकते है कि, abका योज्य प्रतिलोम −abहोगा और −abका योज्य प्रतिलोम abहोगा |
इसी प्रकार 12का योज्य प्रतिलोम −12होगा और −12का योज्य प्रतिलोम 12होगा |
4. व्युत्क्रम या गुणात्मक प्रतिलोम
व्युत्क्रम या गुणात्मक प्रतिलोम एक परिमेय संख्या ab दूसरी परिमेय संख्या cdका व्युत्क्रम या गुणात्मक प्रतिलोम होगा, यदि ab×cd=1आप 821को किस परिमेय संख्या से गुणा करेंगे ताकि गुणनफल । हो जाए? स्पष्ट रूप से 218 से क्योंकि 821×218=1
इसी प्रकार, −57 को 7−5 से गुणा करना चाहिए ताकि गुणनफल । प्राप्त हो सके।
हम कहते हैं कि821का व्युत्क्रम 218 है और −57 का व्युत्क्रम7−5 है।
Note -कोई ऐसी परिमेय संख्या नही है जिसे शून्य से गुणा करने पर 1 प्राप्त हो जाए। अतः शून्य का कोई व्युत्क्रम नहीं है।
5.वितरण
वितरण गुण एक ब्रैकेट के भीतर किसी अन्य गणितीय ऑपरेशन पर संचालन की वितरण क्षमता की व्याख्या करता है। यह या तो जोड़ पर गुणन का वितरण गुण हो सकता है या घटाव पर गुणन का वितरण गुण हो सकता है। यहां, पूर्णांकों को पहले जोड़ा या घटाया जाता है और फिर कोष्ठक के भीतर प्रत्येक संख्या के साथ गुणा किया जाता है और फिर जोड़ा या घटाया जाता है। इसे किसी भी परिमेय संख्या a , b और c के लिए इस प्रकार दर्शाया जा सकता है,अतः
a×(b+c)=a×b+a×c
एवं
a×(b−c)=a×b−a×c
OMR (One Minute Revision)
परिमेय संख्याएँ a, b और c के लिए
a(b+c)=ab+ac और
a(b−c)=ab−ac
उदाहरण 3
निम्नलिखित के गुणात्मक प्रतिलोम ज्ञात कीजिए:
(i) -13
(ii) −1319
(iii) 15
(iv) −58×(−37)
(v) −1×(−25)
(vi) −1
एक परिमेय संख्या ab दूसरी परिमेय संख्या cd का व्युत्क्रम या गुणात्मक प्रतिलोम होगा | यदि ab×cd=1
⇒cd=ba
परिमेय संख्या ab का व्युत्क्रम या गुणात्मक प्रतिलोम =ba
अतः
(i) −113
(ii) −1913
(iii) 5
(iv) (−85)×(−73)
=5615
(v) −1×(−52)
=52
(vi) −1
उदाहरण 4
निम्नलिखित प्रत्येक में गुणन के अंतगर्त उपयोग किये गए गुणधर्म का नाम लिखिए:
(i) −45×1=1×(−45)=−45
(ii) −1317×(−27)=−27×−1317
(iii) −1929×29−19=1
(i) −45×1=1×(−45)=−45
1 गुणात्मक तत्समक है!
क्रमविनिमयता नियम
(ii) −1317×(−27)=−27×−1317
क्रमविनिमयता नियम
(iii) −1929×29−19=1
गुणात्मक प्रतिलोम
परिमेय संख्याओं का संख्या रेखा पर निरूपण
परिमेय संख्याओं का संख्या रेखा पर निरूपण निम्न प्रकार से किया जाता हैं
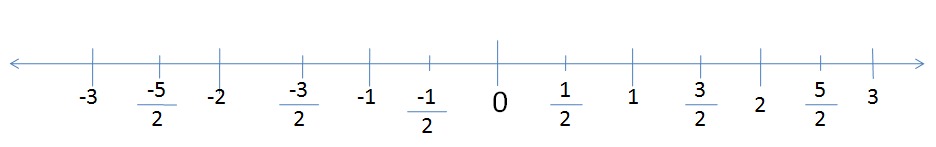
यह रेखा संख्या रेखा कहलाती है।
जबकि ऋणात्मक परिमेय संख्याओं को O के बाईं ओर संख्या रेखा पर बिंदुओं द्वारा दर्शाया जाता है
परिमेय संख्या का हर बराबर भागों की संख्या को इंगित करता है।
हम किन्हीं दो परिमेय संख्याओं के बीच अपरिमित रूप से अनेक परिमेय संख्याएँ ज्ञात कर सकते हैं।
उदाहरण 5
दो परिमेय संख्याओं के बीच परिमेय संख्या
दो परिमेय संख्याओं के बीच अनंत परिमेय संख्याएँ होती हैं|
आइए समझते हैं -
310 और 710 के बीच मे कितनी परिमेय संख्या हैं ? शायद आप सोच रहे हॉँ की वे संख्याएँ 410,510,610 होंगी इन परिमेय संख्याओं की संख्या तीन हैं|
परंतु आप 310को 30100 और 710 को 70100 लिख सकते हैं|
अब संख्याएँ 3110,3210,3310.....6810,6910 सभी310 और 710 के बीच में हैं। इन परिमेय संख्याओं की संख्या 39 है।
इसके अतिरिक्त 310 को 300010000और 710को 700010000 इसके के रूप में लिखा जा सकता है।
अब हम पाते हैं कि परिमेय संख्याएँ 3000110000,3000210000......699810000,699910000 में हैं सभी 310 और710 ये कुल 3999 संख्याएँ हैं।
इस प्रकार हम 310 और 710 के बीच में अधिक से अधिक संख्याओं का समावेश कर सकते है। यह संख्याएँ 39999,399999999........अनंत तक हो सकती हैं |
एक और उदाहरण पर विचार करते हैं-
−110 और 310 के बीच मे कितनी परिमेय संख्याएँ हैं ? स्पष्ट रूप से दी हुई संख्याओं के बीच मे 010,110,210 परिमेय संख्याएँ हैं।
यदि हम −110को −10000100000 तथा 310 को 30000100000के रूप मे लिखते हैं तो हम−110 और310 के बीच मे −9999100000,9998100000......29998100000,2999910000 परिमेय संख्याएँ प्राप्त होंगे|
OMR (One Minute Revision)
उदाहरण 6
−56 और 58 के बीच में दस परिमेय संख्यां ज्ञात कीजिए!
सर्वप्रथम हम −56 और 58 को समान हर वाली परिमेय संख्याओं के रूप में परिवर्तित करते हैं।
−5×46×4=−2024
−2024
5×38×3
=1524
के मध्य निम्नलिखित परिमेय संख्याएँ प्राप्त करते हैं।
−1924,−1824,−1724,...1424
इसी प्रकार हम इनमें से कोई भी दस संख्याएँ ले सकते हैं।
उदाहरण 7
14 और 12 के मध्य तीन परिमेय संख्यां ज्ञात कीजिए!
हम दी हुई संख्याओं का माध्य ज्ञात करते हैं।
इन संख्याओं का माध्य 38 हैं और
14<38<12
14,38 के बीच में एक और परिमेय संख्या ज्ञात करते हैं। इसके लिए हम पुनः इनका माध्य ज्ञात करते हैं।
अर्थात्
14+382=58×12=516
14<516<38<12
38,12 के बीच में एक और परिमेय संख्या ज्ञात करते हैं। इसके लिए हम पुनः इनका माध्य ज्ञात करते हैं।
अर्थात्
38+122=78×12=716
14<516<38<716<12
सारांश
- परिमेय संख्याएँ योग व्यवकलन और गुणन की संक्रियाओं के अंतर्गत संवृत हैं।
- परिमेय संख्याओं के लिए योग और गुणन की सक्रियाएँ
(i) क्रमविनिमेय हैं।
(ii) साहचर्य हैं। - परिमेय संख्याओं के लिए परिमेय संख्या शून्य योज्य तत्समक है।
- परिमेय संख्याओं के लिए परिमेय संख्या 1 गुणनात्मक तत्समक है।
- परिमेय संख्या ab का योज्य प्रतिलोम −abहै, और विलोमतः भी सत्य है।
- यदि ab×cd=1 तो परिमेय संख्या ab का व्युत्क्रम अथवा गुणनात्मक प्रतिलोम cd है।
- परिमेय संख्याओं की वितरकता :
परिमेय संख्याएँ a, b और c के लिए
a(b+c)=ab+ac और
a(b−c)=ab−ac - परिमेय संख्याओं को संख्या रेखा पर निरूपित किया जा सकता है।
- दी हुई दो परिमेय संख्याओं के मध्य अपरिमित परिमेय संख्याएँ होती हैं। दो परिमेय संख्याओं के मध्य परिमेय संख्याएँ ज्ञात करने में माध्य की अवधारणा सहायक है।