वर्ग और वर्गमूल कक्षा 8 गणित

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय में हम वर्ग और वर्गमूल का अध्ययन करेंगे। जब हम किसी संख्या को उसी संख्या से गुणा करते हैं, तो प्राप्त संख्या उस संख्या का वर्ग कहलाती हैं तथा वर्गमूल ज्ञात करना किसी संख्या का वर्ग ज्ञात करने की प्रतिलोम संक्रिया है। इस अध्याय मे हम वर्ग संख्याओं के गुणधर्म, वर्ग संख्याओं का प्रतिरूप, संख्याओं का वर्ग ज्ञात करना तथा वर्गमूल एवं वर्गमूल ज्ञात करने की विधियों का अध्ययन विस्तार से करेंगे।

आइये जानते है, वर्ग और वर्गमूल को और करीब से...

पिछली कक्षाओं में हमने प्राकृत संख्याओं का अध्ययन किया हैं, यहाँ हम प्राकृत संख्याओं का स्वयं से गुणा करने पर हम देखते हैं:
$1 \times 1 = 1^{2} = 1$
$2 \times 2 = 2^{2} = 4$
$3 \times 3 = 3^{2} = 9$
$4 \times 4 = 4^{2} = 16$
$5 \times 5 = 5^{2} = 25$

हम जानते हैं कि, जिस प्रकार $2 + 2 + 2$ को संक्षेप में $2 \times 3$ लिखते हैं, उसी प्रकार $2 \times 2$ को $2^{2}$ लिखते हैं तथा इसे 2 की घात 2 या 2 का वर्ग पढ़ते हैं।

इसी प्रकार $3 \times 3 = 3^{2}$ को 3 की घात 2 या 3 का वर्ग पढ़ते हैं अर्थात् जब किसी संख्या का घातांक 2 होता है, तो प्राप्त होने वाली संख्या वर्ग (Square) कहलाती है।

उदाहरण : 4 को $2 \times 2 = 2^{2}$ या 2 का वर्ग कहते हैं, अतः 4 एक वर्ग संख्या हैं। इसी प्रकार 9, 3 का वर्ग हैं, 16, 4 का वर्ग है।

Note:- यदि एक प्राकृत संख्या $m$ को $n^{2}$ से व्यक्त किया जाता है, जहाँ $n$ भी एक प्राकृत संख्या है, तब $m$ एक वर्ग संख्या है।

1 से 20 तक की प्राकृत संख्याओं के वर्ग


संख्या	वर्ग	संख्या	वर्ग
$1$	$1$ $(1 \times 1 = 1^{2})$	$11$	$121$ $(11 \times 11 = 11^{2})$
$2$	$4$ $(2 \times 2 = 2^{2})$	$12$	$144$ $(12 \times 12 = 12^{2})$
$3$	$9$ $(3 \times 3 = 3^{2})$	$13$	$169$ $(13 \times 13 = 13^{2})$
$4$	$16$ $(4 \times 4 = 4^{2})$	$14$	$196$ $(14 \times 14 = 14^{2})$
$5$	$25$ $(5 \times 5 = 5^{2})$	$15$	$225$ $(15 \times 15 = 15^{2})$
$6$	$36$ $(6 \times 6 = 6^{2})$	$16$	$256$ $(16 \times 16 = 16^{2})$
$7$	$49$ $(7 \times 7 = 7^{2})$	$17$	$289$ $(17 \times 17 = 17^{2})$
$8$	$64$ $(8 \times 8 = 8^{2})$	18	$324$ $(18 \times 18 = 18^{2})$
$9$	$81$ $(9 \times 9 = 9^{2})$	$19$	$361$ $(19 \times 19 = 19^{2})$
$10$	$100$ $(10 \times 10 = 10^{2})$ $\frac{<}{t} d > < t d >$ 20 $\frac{<}{t} d > < t d >$ 400(20xx20=20^2)

सारणी में संख्याएँ 1, 4, 9, 16, 25, 36,..............., 361, 400 आदि पूर्ण वर्ग संख्याएँ (Perfect Square) कहलाती हैं

तथा वर्गमूल ज्ञात करना किसी संख्या का वर्ग ज्ञात करने की प्रतिलोम संक्रिया है।

जैसे:-
1 का वर्गमूल 1 होता है।
4 का वर्गमूल 2 है।
9 का वर्गमूल 3 होता है।

वर्ग संख्याओं के गुणधर्म

निचे सारणी मे देख सकते हैं, की प्रथम 10 प्राकृत संख्याओं के वर्गों के इकाई के स्थान पर अंक 0, 1, 4, 5, 6 व 9 ही आते हैं। अतः इनके अलावा जिन संख्याओं के इकाई के अंक 2, 3, 7 या 8 हैं वे संख्याएँ पूर्ण वर्ग नहीं होती हैं।


संख्या	वर्ग	संख्या	वर्ग
$1$	$1$	$11$	$121$
$2$	$4$	$12$	$144$
$3$	$9$	$13$	$169$
$4$	$16$	$14$	$196$
$5$	$25$	$15$	$225$
$6$	$36$	$16$	$256$
$7$	$49$	$17$	$289$
$8$	$64$	18	$324$
$9$	$81$	$19$	$361$
$10$	$100$	$20$	$400$

जब कोई वर्ग संख्या 1 पर समाप्त होती है तो वह जिस संख्या का वर्ग है, उसका इकाई अंक या तो 1 या 9 होगा।

जैसे:-


वर्ग	अंक
$1$	$1$
$81$	$9$
$121$	$11$
$361$	$19$
$441$	$21$

जब कोई वर्ग संख्या 4 पर समाप्त होती है तो वह जिस संख्या का वर्ग है, उसका इकाई अंक या तो 2 या 8 होगा।

जैसे:-


वर्ग	अंक
$4$	$2$
$64$	$8$
$144$	$12$
$324$	$18$
$484$	$22$

जब कोई वर्ग संख्या 5 पर समाप्त होती है तो वह जिस संख्या का वर्ग है, उसका इकाई अंक 5 ही होगा।

जैसे:-


वर्ग	अंक
$25$	$5$
$225$	$15$
$625$	$25$
$1225$	$35$
$2025$	$45$

जब कोई वर्ग संख्या 6 पर समाप्त होती है तो वह जिस संख्या का वर्ग है, उसका इकाई अंक या तो 4 या 6 होगा।

जैसे:-


वर्ग	अंक
$16$	$4$
$36$	$6$
$196$	$14$
$256$	$16$
$576$	$24$

जब कोई वर्ग संख्या 9 पर समाप्त होती है तो वह जिस संख्या का वर्ग है, उसका इकाई अंक या तो 3 या 7 होगा।

जैसे:-


वर्ग	अंक
$9$	$3$
$49$	$7$
$169$	$13$
$289$	$17$
$529$	$23$

वर्ग संख्याओं के अंत में शून्यों की संख्या केवल सम होती है अर्थात यदि कोई संख्या शून्यों की सम संख्या के साथ समाप्त होती है, तो इसका एक वर्गमूल हो सकता है।
जैसे:- 100 का वर्गमूल 10 हैं, 900 का वर्गमूल 30 हैं।

Note:- यदि एक संख्या के अंत मे एक शून्य हैं तो उसके वर्ग मे दो शून्य होंगे।

जैसे:-

20^{2} = 400

30^{2} = 900

40^{2} = 1600

50^{2} = 2500

यदि एक संख्या के अंत मे 2 शून्य हैं तो उसके वर्ग मे 4 शून्य होंगे।

जैसे:-

200^{2} = 40000

300^{2} = 90000

400^{2} = 160000

500^{2} = 250000

इसी प्रकार यदि 3 शून्य है तो 6 शून्य, 4 शून्य है तो 8 शून्य आदि होंगे।

सम संख्याओं के वर्ग सदैव सम होते हैं तथा विषम संख्याओं के वर्ग सदैव विषम होते हैं।

जैसे :-
सम संख्याएँ :-

2^{2} = 4

4^{2} = 16

6^{2} = 36

8^{2} = 64

विषम संख्याएँ :-

3^{2} = 9

5^{2} = 25

9^{2} = 81

11^{2} = 121

उदाहरण 1

संख्या $89722$ स्पष्ट रूप से पूर्ण वर्ग संख्या नहीं हैं, इसका कारण दीजिए।

हम जानते हैं कि, पूर्ण वर्ग संख्याओं के इकाई के अंक 0, 1, 4, 5, 6 और 9 होते हैं। यहाँ, 89722 का इकाई का अंक 2 है, अतः स्पष्ट हैं की संख्या $89722$ पूर्ण वर्ग संख्या नहीं है।

Learn more

उदाहरण 2

संख्या $34393$ के वर्ग का इकाई के अंक ज्ञात कीजिए।

$34393$ में इकाई के स्थान पर 3 है और 3 का वर्ग 9 होता हैं $\Rightarrow 3^{2} = 3 \times 3 = 9$
अतः, 34393 के वर्ग में इकाई का अंक 9 होगा।

Learn more

वर्ग संख्याओं के प्रतिरूप

त्रिकोणीय संख्याओं के जोड़ : यदि संख्याओं को बिंदुओं के प्रतिरूप में त्रिभुजाकार रूप में व्यवस्थित किया जा सकें तो ये संख्याएँ त्रिभुजीय संख्याएँ कहलाती हैं।

तथा दो क्रमागत त्रिभुजाकार संख्याओं को जोड़ने पर वर्ग संख्या प्राप्त होती है। जैसे :-

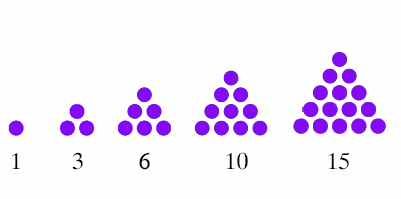
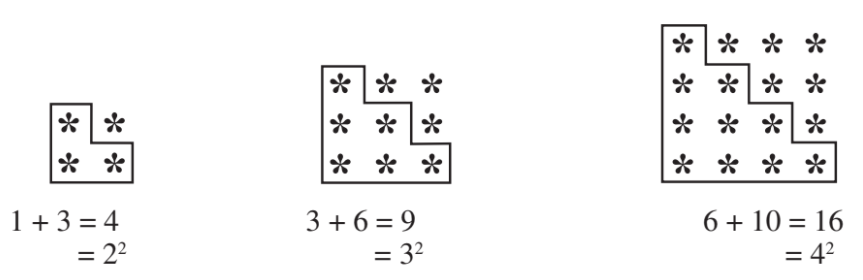
ocr_image

वर्ग संख्याओं के बीच की संख्याएँ : किन्ही दो क्रमागत प्राकृत संख्याओ

n

तथा

n + 1

के वर्गों के बीच

2 n

संख्याएँ होती है जो पूर्ण वर्ग नही होती है।
दूसरे शब्दों में कहा जाए तो

n

तथा

n + 1

के वर्गों के अंतर से 1 कम, अपूर्ण वर्ग संख्याएँ प्राप्त होती है।

उदाहरण :- दो क्रमागत संख्या 2 व 3 को लेते हैं।
2 का वर्ग

= 4

, 3 का वर्ग

= 9

2 व 3 के वर्गों का अंतर

= 9 - 4 = 5

प्राप्त संख्या वर्गों के अंतर से एक कम होती है
अत:

5 - 1 = 4

अत: 2 व 3 के वर्गों के मध्य प्राप्त चार संख्याएँ 5, 6, 7, 8 हैं।

सूत्र से :- दो क्रमागत संख्या 2 व 3 हैं
अतः

(n

व

n + 1) = (2

व

2 + 1)

दिया है

n = 2

तब 2 व 3 के वर्गों के मध्य प्राप्त संख्याओ की संख्या:-

2 n = 2 (2) = 4

अत: 2 व 3 के वर्गों के मध्य प्राप्त चार संख्याएँ 5, 6, 7, 8 हैं।

विषम संख्याओं का जोड़ : प्रथम

n

विषम प्राकृत संख्याओं का योग

n^{2}

होता है।
जैसे :-
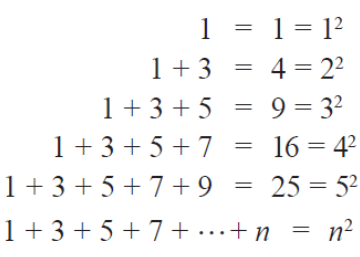
ocr_image

Note:- कोई भी वर्ग संख्या 1 से शुरू होने वाली क्रमागत विषम संख्याओं का योग होनी चाहिए।
यदि कोई प्राकृत संख्या जो 1 से शुरू होने वाली क्रमागत विषम प्राकृत संख्याओं का योग नहीं है, तो वह पूर्ण वर्ग नहीं होगी।

क्रमागत प्राकृत संख्याओं का योग : एक विषम संख्या n के वर्ग को दो क्रमागत धनात्मक पूर्णांकों के योग के रूप में व्यक्त किया जा सकता है अतः प्रत्येक विषम वर्ग संख्या दो क्रमागत धनात्मक प्राकृत संख्याओं का योग होता है।

प्रथम संख्या

= \frac{n^{2} - 1}{2}

दूसरी संख्या

= \frac{n^{2} + 1}{2}

जैसे :-

5^{2} = 25

प्रथम संख्या

= \frac{n^{2} - 1}{2} = \frac{5^{2} - 1}{2} = \frac{24}{2} = 12

दूसरी संख्या

= \frac{n^{2} + 1}{2} = \frac{5^{2} + 1}{2} = \frac{26}{2} = 13

अतः

12 + 13 = 25 = 5^{2}

स्पष्ट हैं की 25 एक विषम वर्ग संख्या हैं जो की दो क्रमागत धनात्मक प्राकृत संख्याओं का योग हैं।

इसी प्रकार,

7^{2} = 49 = 24 + 25

9^{2} = 81 = 40 + 41

11^{2} = 121 = 60 + 61

दो क्रमागत सम या विषम प्राकृत संख्याओं का गुणनफल : यदि हमारे पास दो क्रमागत विषम या सम संख्याएँ

(a + 1)

और

(a - 1)

हैं, तो उनका गुणनफल

(a^{2} - 1)

होगा।
जहाँ

a

एक प्राकृतिक संख्या हैं।

अतः दो क्रमागत विषम संख्याएँ 11 और 13 लेते हैं।

11 \times 13 = (12 - 1) \times (12 + 1) = 12^{2} - 1

इसी प्रकार,

13 \times 15 = (14 - 1) \times (14 + 1) = 14^{2} - 1

44 \times 46 = (45 - 1) \times (45 + 1) = 45^{2} - 1

वर्ग संख्याओं के कुछ और प्रतिरूप :

ocr_image

उदाहरण 3

योग संक्रिया किए बिना योगफल ज्ञात कीजिए:
$1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19$

हम जानते हैं कि, प्रथम $n$ विषम प्राकृत संख्याओं का योग $n^{2}$ होता है।

दिया हैं; $1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19$
यहाँ 10 क्रमागत विषम संख्याओं का योग दिया है
चूंकि 10 का वर्ग $(10^{2}) = 100$
$∴ 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19$
$= 10^{2} = 100$

Learn more

उदाहरण 4

निम्नलिखित संख्याओं के वर्ग के बीच में कितनी संख्याएँ हैं?
$99$ और $100$

हम जानते हैं कि $n^{2}$ और ${(n + 1)}^{2}$ के बीच में संख्याएँ $= 2 n$
यहाँ, $n = 99$
इसलिए, 99 और 100 के वर्ग बीच में संख्याएँ,
$2 n = 2 \times 99 = 198$
अतः $99$ और $100$ के वर्ग के बीच में $198$ संख्याएँ होंगी।

Learn more

संख्याओं का वर्ग ज्ञात करना

हम जानते हैं कि, यदि $n$ एक संख्या है, तो इसका वर्ग $n \times n = n^{2}$ होगा।

जैसे:- 5 का वर्ग $5^{2} = 25$ , 9 का वर्ग $9^{2} = 81$

इस तरह से छोटी संख्याएँ जैसे 3, 4, 5, 6, 7, ... इत्यादि का वर्ग आसानी से ज्ञात किया जा सकता है लेकिन बड़ी संख्याओं का नहीं।

किसी भी संख्या का वर्ग ज्ञात करने के लिए हमें उस संख्या को दो भागों में विभाजित करने की आवश्यकता होती है तो हम इसे आसानी से हल कर सकते हैं।

उदाहरण से समझते हैं:

42 का वर्ग ज्ञात कीजिए।

42 का वर्ग ज्ञात करने के लिए सबसे पहले इसे दो भागों मे विभाजित कर लेते हैं:

अतः $42 = (40 + 2)$

अब, ${(42)}^{2} = {(40 + 2)}^{2}$

चूंकि हम जानते हैं की, ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

इसलिए, ${(40 + 2)}^{2} = {(40)}^{2} + 2 \times 40 \times 2 + {(2)}^{2}$

$\Rightarrow (40 \times 40) + 160 + (2 \times 2)$

$\Rightarrow 1600 + 160 + 4$

$\Rightarrow 1764$

अतः $42$ का वर्ग $1764$ होगा।

वर्ग के अन्य प्रतिरूप

यदि किसी संख्या के इकाई स्थान मे 5 आता हैं, जैसे 15, 25, 35, 45,....इत्यादि, इस तरह के संख्याओं का एक प्रतिरूप बनाया जा सकता हैं।

जैसे :- $15^{2} = (1 \times 2)$ 100 $+ 25 = 225$

[यहाँ दी गई संख्या में 5 के अतिरिक्त अंक को उससे एक अधिक से गुणा कर लिखते है जैसे 15 में 5 के अतिरिक्त अंक 1 हैं इसलिए 1 का गुणा $(1 \times 2)$ उसके बाद वाली संख्या 2 से किया गया हैं।]

इसी प्रकार,
$25^{2} = (2 \times 3)$ 100 $+ 25 = 625$
$35^{2} = (3 \times 4)$ 100 $+ 25 = 1225$
$45^{2} = (4 \times 5)$ 100 $+ 25 = 2025$
$55^{2} = (5 \times 6)$ 100 $+ 25 = 3025$
$65^{2} = (6 \times 7)$ 100 $+ 25 = 4225$
$75^{2} = (7 \times 8)$ 100 $+ 25 = 5625$
$85^{2} = (8 \times 9)$ 100 $+ 25 = 7225$
$95^{2} = (9 \times 10)$ 100 $+ 25 = 9025$
$105^{2} = (10 \times 11)$ 100 $+ 25 = 11025$
$115^{2} = (11 \times 12)$ 100 $+ 25 = 13225$
$125^{2} = (12 \times 13)$ 100 $+ 25 = 15625$
इस तरह के संख्याओं का वर्ग निचे दिए गए सूत्र से भी ज्ञात किया जा सकता हैं:
माना की $a$ एक प्राकृत संख्या हैं तथा इसके इकाई के स्थान पर 5 हैं अर्थात $a 5$ ।
${(a 5)}^{2} = a (a + 1)$ 100 $+ 25$
जैसे:- $15^{2} = 1 (1 + 1) 100 + 25 = 1 (2)$ 100 $+ 25 = 225$

इसी प्रकार,
$25^{2} = 2 (2 + 1)$ 100 $+ 25 = 2 (3)$ 100 $+ 25 = 625$
$95^{2} = 9 (9 + 1)$ 100 $+ 25 = 9 (10)$ 100 $+ 25 = 9025$

पाइथागोरस त्रिक

किसी प्राकृत संख्या $m > 1$ के लिए, पाइथागोरस त्रिक निम्न रूप मे होती है :-
$\Rightarrow {(2 m)}^{2} + {(m^{2} - 1)}^{2} = {(m^{2} + 1)}^{2}$
अर्थात पाइथागोरस त्रिक $2 m, m^{2} - 1$ और $m^{2} + 1$ के रूप मे होती है।
पाइथागोरस त्रिक ऐसी तीन संख्याओ का समूह होता है जिसमे किन्ही दो संख्याओ के वर्गों का योग तीसरी संख्या के वर्ग के बराबर होता है।

उदाहरण :
$\Rightarrow 3^{2} + 4^{2} = 5^{2}$
$\Rightarrow 9 + 16 = 25$
$\Rightarrow 25 = 25$
यहाँ $3$ और $4$ के वर्गों का योग $5$ के वर्ग के बराबर है अतः यह समूह पाइथागोरस त्रिक है।

आइए एक और उदाहरण से समझते है :-
एक पाइथागोरस त्रिक लिखे जिसकी सबसे छोटी संख्या $8$ हो।
हल : चूंकि हम जानते है की पाइथागोरस त्रिक $2 m, m^{2} - 1$ और $m^{2} + 1$ के रूप मे होती है।
अतः $2 m = 8 \Rightarrow m = 4$

$m^{2} - 1 = 4 \times 4 - 1 = 16 - 1 = 15$
$m^{2} + 1 = 4 \times 4 + 1 = 16 + 1 = 17$

अतः $8, 15$ और $17$ एक ऐसा पाइथागोरस त्रिक है जहां $8$ सबसे छोटी संख्या है।

OMR (One Minute Revision)

एक प्राकृत संख्या एक पूर्ण वर्ग कहलाती है यदि वह किसी प्राकृत संख्या का वर्ग है अर्थात यदि

m = n^{2}

हो, तो

m

एक पूर्ण वर्ग है, जहाँ m और n प्राकृत संख्याएँ हैं।

जब किसी संख्या को स्वयं उसी से गुणा किया जाए तो उससे प्राप्त संख्या उस संख्या का वर्ग कहलाती हैं।

सम संख्याओं के वर्ग सम संख्याएँ होती हैं।

विषम संख्याओं के वर्ग विषम संख्याएँ होती हैं।

एक पूर्ण वर्ग की इकाई का अंक केवल 0, 1, 4, 5, 6 या 9 हो सकता हैं।

संख्या

n

और

n + 1

के वर्गों के बीच में

2 n

प्राकृत संख्याएँ है।

प्रथम

n

विषम प्राकृत संख्याओ का योग

n^{2}

से प्राप्त होता है।

वह संख्या जिसके अंत में शून्यों की संख्या विषम हो, एक पूर्ण वर्ग नही होती है।

प्रत्येक प्राकृत संख्या

m > 1

के लिए

2 m

m^{2} - 1

और

m^{2} + 1

से एक पाइथागोरस त्रिक बनती है।

उदाहरण 5

$86$ का वर्ग ज्ञात कीजिए।

यहाँ $86^{2} = ?$
86 को 2 भागों मे विभाजित किया जा सकता हैं:

$80 + 6 = 86 \Rightarrow {(86)}^{2} = {(80 + 6)}^{2}$

हम जानते हैं की, ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

$∴ {(86)}^{2} = {(80 + 6)}^{2} = {(80)}^{2} + 2 \times 80 \times 6 + {(6)}^{2}$
$\Rightarrow {(86)}^{2} = {(80 + 6)}^{2} = 6400 + 960 + 36$
$\Rightarrow {(86)}^{2} = 7396$

अतः $86$ का वर्ग $7396$ हैं।

Learn more

उदाहरण 6

पाइथागोरस त्रिक लिखिए जिसका एक सदस्य $18$ है।

हम जानते हैं की,
पाइथागोरस त्रिक की तीन संख्याएँ $2 m$ , $m^{2} - 1$ और $m + 1$ हैं।

यहाँ $2 m = 18 \Rightarrow m = \frac{18}{2} = 9$
इसलिए,
दूसरी संख्या $(m^{2} - 1) = (9^{2} - 1) = 81 - 1 = 80$
तीसरी संख्या $(m^{2} + 1) = (9^{2} + 1) = 81 + 1 = 82$
अतः, पाइथागोरस त्रिक जिसका एक सदस्य 18 हैं: $(18, 80, 82)$

Learn more

वर्गमूल

अब हम जानते हैं कि 4, 25, 36...... पूर्ण वर्ग है। अतः $2^{2} = 4$ अर्थात $2$ का वर्ग $4$ है, इसके विपरीत हम यह भी कह सकते हैं कि संख्या $2$ , $4$ का वर्गमूल है। इसी प्रकार चूंकि $5^{2} = 25$ , इसलिए $25$ का वर्गमूल $5$ है।

अतः किसी संख्या $a$ का वर्गमूल वह संख्या होती है, जिसे इसी संख्या से गुणा करने पर संख्या $a$ प्राप्त होती है।

यदि $n = y \times y$ तो हम कहते हैं कि संख्या $y$ , संख्या $n$ का एक वर्गमूल है।

दूसरे शब्दों में दी गई संख्या $n$ का वर्गमूल वह संख्या है जिसका उसी के साथ गुणा करने पर गुणनफल $n$ प्राप्त हो।
वर्गमूल का संकेत $\sqrt{}$ होता है।

उदाहरण : $25$ के वर्गमूल को हम $\sqrt{25}$ लिखते हैं।
अतः $\sqrt{25} = \sqrt{5 \times 5} = 5$ या $5 = \sqrt{25}$

इसी प्रकार,
$\sqrt{9} = \sqrt{3 \times 3} = 3$ , $\sqrt{64} = \sqrt{8 \times 8} = 8$ तथा $\sqrt{100} = \sqrt{10 \times 10} = 10$


कथन	निष्कर्ष
$1^{2} = 1$	$\sqrt{1} = 1$
$2^{2} = 4$	$\sqrt{4} = 2$
$3^{2} = 9$	$\sqrt{9} = 3$
$4^{2} = 16$	$\sqrt{16} = 4$
$5^{2} = 25$	$\sqrt{25} = 5$
$6^{2} = 36$	$\sqrt{36} = 6$
$7^{2} = 49$	$\sqrt{49} = 7$
$8^{2} = 64$	$\sqrt{64} = 8$
$9^{2} = 81$	$\sqrt{81} = 9$
$10^{2} = 100$	$\sqrt{100} = 10$

Note:- सम पूर्ण संख्या का वर्गमूल सम तथा विषम पूर्ण संख्या का वर्गमूल विषम होता हैं।

घटाने की संक्रिया के द्वारा वर्गमूल ज्ञात करना

प्रथम

n

विषम प्राकृत संख्याओं का योग

n^{2}

होता हैं अतः प्रत्येक वर्ग संख्या को 1 से प्रारंभ कर क्रमागत प्राकृत संख्याओं के योग के रूप में व्यक्त किया जा सकता है।

अतः इस विधि मे किसी भी पूर्ण संख्या का वर्गमूल निकालने के लिए उस संख्या को बार-बार 1 से प्रारंभ होने वाली विषम प्राकृत संख्याओं (1, 3, 5, 7, 9, 11, 13, 15...) से घटाना होता हैं जब तक की वह शून्य न हो जाए।

जैसे:

100

का वर्गमूल ज्ञात करते हैं।

100 - 1 = 99

99 - 3 = 96

96 - 5 = 91

91 - 7 = 84

84 - 9 = 75

75 - 11 = 64

64 - 13 = 51

51 - 15 = 36

36 - 17 = 19

19 - 19 = 0

अतः 100 को संख्या 1 से क्रमागत विषम संख्याओं से घटाने पर 10वाँ पद शून्य प्राप्त होता है अतः

\sqrt{100} = 10

होगा।

एक और उदाहरण से समझते हैं:

81

का वर्गमूल ज्ञात करते हैं।

81 - 1 = 80

80 - 3 = 77

77 - 5 = 72

72 - 7 = 65

65 - 9 = 56

56 - 11 = 45

45 - 13 = 32

32 - 15 = 17

17 - 17 = 0

अतः 81 को संख्या 1 से क्रमागत विषम संख्याओं से घटाने पर 9वाँ पद शून्य प्राप्त होता है अतः

\sqrt{81} = 9

होगा।

अभाज्य गुणनखंडन के द्वारा वर्गमूल ज्ञात करना

इस विधि से किसी दी गई संख्या का वर्गमूल निकालने के लिए सबसे पहले उस संख्या को अभाज्य गुणनखंड के रूप में तोड़ लेते हैं और फिर बराबर संख्या का जोड़ा बना लेते हैं। इसके बाद प्रत्येक जोड़े की एक - एक संख्या को लेकर गुणा करते हैं, तब दी गई संख्या का अभीष्ट वर्गमूल प्राप्त हो जाता है।

उदाहरण :-

4900

का वर्गमूल ज्ञात कीजिए।

चरण 1: दी गई संख्या का अभाज्य गुणनखंड ज्ञात करते हैं।
जैसे:-
ocr_image

अतः 4900 का अभाज्य गुणनखंड

= 2 \times 2 \times 5 \times 5 \times 7 \times 7

चरण 2: अभाज्य गुणनखंड के युग्म बनाते हैं अर्थात दो - दो समान अभाज्य गुणनखंडों की जोड़ी बनाते हैं।
जैसे:-

4900 = 2 \times 2 - ---- - \times 5 \times 5 - ---- - \times 7 \times 7 - ---- -

चरण 3: प्रत्येक जोड़े में से एक - एक गुणनखंड लेकर उनका आपस में गुणा करते हैं।
जैसे:-

\sqrt{4900} = \sqrt{2 \times 2 - ---- - \times 5 \times 5 - ---- - \times 7 \times 7 - ---- -} = 2 \times 5 \times 7 = 70

चरण 4: प्राप्त गुणनफल ही दी गई संख्या का अभीष्ट वर्गमूल होगा।
जैसे:-

\sqrt{4900} = 70

उदाहरण :

256

का वर्गमूल ज्ञात कीजिए।
ocr_image

अतः

256

का अभाज्य गुणनखंड

= 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2

∴ \sqrt{256} = \sqrt{2 \times 2 - ---- - \times 2 \times 2 - ---- - \times 2 \times 2 - ---- - \times 2 \times 2 - ---- -}

(अभाज्य गुणनखंड के युग्म बनाते हैं)

\Rightarrow \sqrt{256} = 2 \times 2 \times 2 \times 2

\Rightarrow \sqrt{256} = 16

अतः 256 का वर्गमूल 16 होगा।

उदाहरण: क्या संख्या

8820

पूर्ण वर्ग है? यदि नहीं, तो वह संख्या ज्ञात कीजिए जिससे

8820

को गुणा करने पर गुणनफल पूर्ण वर्ग बन जाए।
ocr_image

अतः

8820

का अभाज्य गुणनखंड

= 2 \times 2 \times 5 \times 3 \times 3 \times 7 \times 7

\Rightarrow 8820 = 2 \times 2 - ---- - \times 3 \times 3 - ---- - \times 7 \times 7 - ---- - \times 5

यहाँ हम देखते हैं कि अभाज्य संख्या 5 युग्म रूप में उपस्थित नहीं है। अतः

8820

पूर्ण वर्ग संख्या नहीं है।

संख्या

8820

को 5 से गुणा करने पर,

8820 \times 5 = 44100 = 2 \times 2 - ---- - \times 3 \times 3 - ---- - \times 7 \times 7 - ---- - \times 5 \times 5 - ---- -

अब प्रत्येक अभाज्य संख्या युग्म रूप में उपस्थित है इसलिए संख्या

8820 \times 5 = 44100

पूर्ण वर्ग संख्या है।
अतः वह अभीष्ट संख्या 5 है अर्थात् 8820 को 5 से गुणा करने पर गुणनफल पूर्ण वर्ग होगा।

Note:- (i) उपर्युक्त उदाहरण में गुणज 5 उपस्थित नहीं हैं। अतः 8820 को यदि 5 से भाग दें तो भी प्राप्त संख्या पूर्ण वर्ग संख्या होंगी।

अतः

\frac{8820}{5} = 1764 = 2 \times 2 - ---- - \times 3 \times 3 - ---- - \times 7 \times 7 - ---- -

Note:- (ii) यदि किसी संख्या के अभाज्य गुणनखंड में कोई संख्या एक बार आया हैं तो उसके वर्ग के अभाज्य गुणनखंड मे वह संख्या दो बार आएगा।


एक संख्या का अभाज्य गुणनखंड	इसके वर्ग का अभाज्य गुणनखंड
$6 = 2 \times 3$	$36 = 2 \times 2 \times 3 \times 3$
$8 = 2 \times 2 \times 2$	$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2$
$12 = 2 \times 2 \times 3$	$144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3$
$15 = 3 \times 5$	$225 = 3 \times 3 \times 5 \times 5$

जैसे:- 6 के अभाज्य गुणनखंड में 2 एक बार आया हैं इसलिए इसके वर्ग के अभाज्य गुणनखंड में 2, दो बार आया हैं।

भागफल विधि से वर्गमूल ज्ञात करना

जब संख्याएँ बड़ी हों तब अभाज्य गुणनखंड विधि से वर्गमूल ज्ञात करना लंबा और कठिन होता है। इस समस्या से निकलने के लिए हम भागफल विधि (दीर्घ विभाजन विधि) का प्रयोग करते हैं। इसके लिए हमें वर्गमूल में अंकों की संख्या को ज्ञात करने की आवश्यकता है।

1 से 9 तक की संख्या के वर्गों में अधिकतम 2 अंक होते हैं। जैसे : ( 1, 2, 3, 4,.......,9 के वर्ग क्रमश: 1, 4, 9, 16,.......,81) हैं।

चूंकि 10 का वर्ग 100 एवं 99 का वर्ग 9801 हैं अतः संख्या 10 से 99 तक की संख्याओं के वर्गों में 3 अंक या 4 अंक होंगे।

इसी प्रकार 100 से 999 तक की संख्याओं के वर्गों में 5 अंक या 6 अंक होंगे।


पूर्ण वर्ग संख्या में अंकों की संख्या	इस संख्या के वर्गमूल में अंकों की संख्या
1 या 2	1
3 या 4	2
5 या 6	3

उदाहरण से समझते हैं:

529 का वर्गमूल ज्ञात कीजिए।

चरण 1 इकाई स्थान से प्रारंभ करते हुए प्रत्येक युग्म पर बार लगाते हैं। यदि अंकों की संख्या विषम है तब बाएँ तरफ एक अंक पर बार लगाते हैं। जैसे:-

¯ 5

¯ ¯¯ ¯ 29

चरण 2 वह सबसे बड़ी संख्या ज्ञात करते हैं जिसका वर्ग सबसे बाईं तरफ के बार के नीचे लिखी संख्या से कम या बराबर हो

(2^{2} < 5 < 3^{2})

। सबसे बाईं बार के नीचे भाज्य (यहाँ 5) के साथ भाजक और भागफल के रूप में इस संख्या को लेकर भाग करते हैं और शेषफल ज्ञात करते हैं (इस स्थिति में 1 है।)
ocr_image

चरण 3 अगली बार के नीचे की संख्या (इस स्थिति में 29) को शेषफल के दाएँ ओर लिखते हैं, अतः अगली भाज्य 129 होगी।
ocr_image

चरण 4 भाजक को दुगुना करके, इसे इसके दाएँ में रिक्त स्थान के साथ लिखते हैं।
ocr_image

चरण 5 रिक्त स्थान को भरने के लिए सबसे बड़े संभावित अंक का अनुमान लगाते हैं जो कि भागफल में नया अंक होगा और नए भाजक को नए भागफल से गुणा करने पर गुणनफल भाज्य से कम या बराबर होगी।
इस स्थिति में

42 \times 2 = 84

43 \times 3 = 129

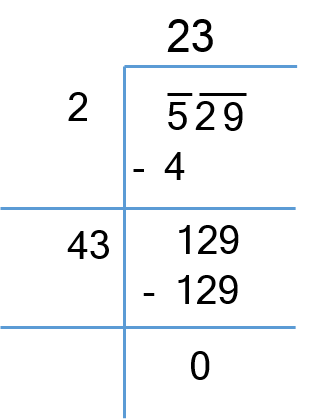
अतः भागफल में नया अंक 3 होगा।

चरण 6 क्योंकि शेषफल शून्य है और दी गई संख्या में कोई अंक शेष नहीं है।
अतः

\sqrt{529} = 23

एक और उदाहरण से समझते हैं:

4096 का वर्गमूल ज्ञात कीजिए

चरण 1 इकाई स्थान से प्रारंभ करते हुए प्रत्येक युग्म पर बार लगाते हैं। जैसे:-

¯ ¯¯ ¯ 40

¯ ¯¯ ¯ 96

(6^{2} < 40 < 7^{2})

। सबसे बाईं बार के नीचे भाज्य (यहाँ 40) के साथ भाजक और भागफल के रूप में इस संख्या को लेकर भाग करते हैं और शेषफल ज्ञात करते हैं (इस स्थिति में 4 है।)
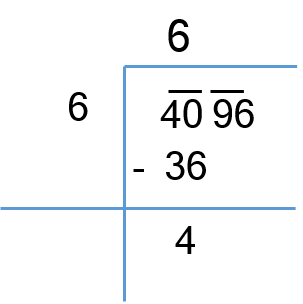
ocr_image

चरण 3 अगली बार के नीचे लिखी संख्या (अर्थात् 96) को शेषफल के दायीं तरफ लिखते हैं। अतः नया भाज्य 496 होगा।
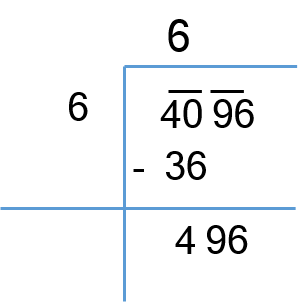
ocr_image

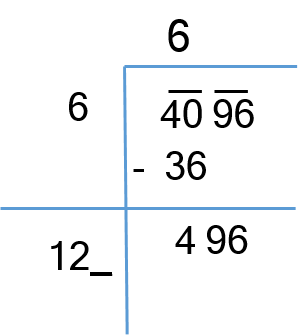
चरण 5 रिक्त स्थान को भरने के लिए सबसे बड़े संभावित अंक का अनुमान लगाते हैं जो अंक भागफल में नया होगा, इस प्रकार नया अंक को जब भागफल से गुणा करते है तब गुणनफल भाज्य से छोटा या बराबर होना चाहिए। इस स्थिति में हम देखते हैं कि

124 \times 4 = 496

अतः भागफल में नया अंक 4 है।
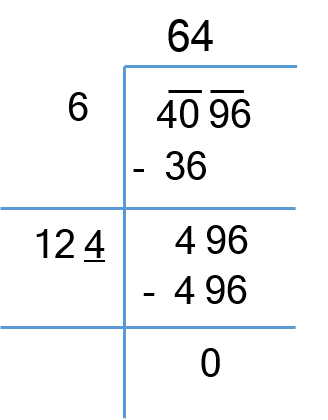
ocr_image

चरण 6 चूँकि शेषफल शून्य है और कोई बार नहीं है अत:

\sqrt{4096} = 64

होगा।

Note:- यदि किसी संख्या का वर्गमूल भागफल विधि से ज्ञात करने पर शेषफल प्राप्त होता हैं, तो दी गई संख्या में शेषफल को घटाने पर पूर्ण वर्ग संख्या प्राप्त होती हैं।

उदाहरण 7

अभाज्य गुणनखंड विधि से $400$ का वर्गमूल ज्ञात कीजिए।

अतः

400

का अभाज्य गुणनखंड

= (2 \times 2) \times (2 \times 2) \times (5 \times 5)

∴ \sqrt{400} = \sqrt{2 \times 2 - ---- - \times 2 \times 2 - ---- - \times 5 \times 5 - ---- -}

(अभाज्य गुणनखंड के युग्म बनाते हैं)

\Rightarrow \sqrt{400} = 2 \times 2 \times 5

\Rightarrow \sqrt{400} = 20

अतः 400 का वर्गमूल 20 होगा।

Learn more

उदाहरण 8

संख्या $1620$ में सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे इस संख्या को भाग देने पर वह एक पूर्ण वर्ग बन जाए। इस तरह प्राप्त की गई संख्या का वर्गमूल भी ज्ञात कीजिए।

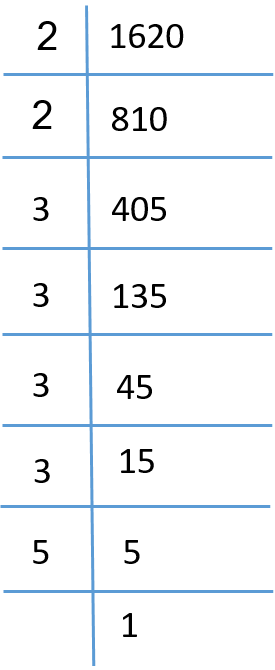
अतः

1620

का अभाज्य गुणनखंड

= 2 \times 2 \times 3 \times 3 \times 3 \times 3 \times 5

\Rightarrow 1620 = 2 \times 2 - ---- - \times 3 \times 3 - ---- - \times 3 \times 3 - ---- - \times 5

यहाँ हम देखते हैं कि अभाज्य संख्या 5 युग्म में उपस्थित नहीं है इसलिए

1620

पूर्ण वर्ग संख्या नहीं है।

अतः 1620 को 5 से भाग देने पर प्राप्त संख्या पूर्ण वर्ग संख्या होगा।

∴ \frac{1620}{5} = 324

जो की एक पूर्ण वर्ग संख्या हैं

और

\sqrt{324} = \sqrt{2 \times 2 - ---- - \times 3 \times 3 - ---- - \times 3 \times 3 - ---- -}

अतः

\sqrt{324} = 2 \times 3 \times 3 = 18

Learn more

उदाहरण 9

$1989$ में से न्यूनतम संख्या क्या घटाई जाए कि एक पूर्ण वर्ग संख्या प्राप्त हो जाए। इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए।

चूंकि यहाँ प्रश्न मे दिया गया है की $1989$ में से न्यूनतम संख्या क्या घटाई जाए कि एक पूर्ण वर्ग संख्या प्राप्त हो, इस तरह के प्रश्नों को भागफल विधि से हल करते हैं।

अतः $1989$ का वर्गमूल भागफल विधि से,

इकाई स्थान से प्रारंभ करते हुए 1989 के युग्म $(¯ ¯¯ ¯ 19$ $¯ ¯¯ ¯ 89)$ बनाते हैं।
जैसा की हम जानते हैं की एक ऐसी संख्या का वर्ग ज्ञात करना होगा जिसका वर्ग 19 के बराबर या छोटा हो अतः यहाँ $(4^{2} < 19 < 5^{2})$

$∴$

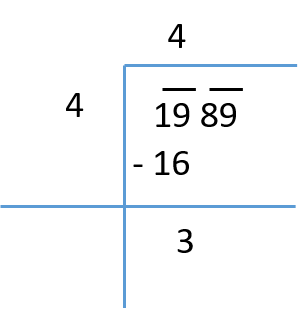
अब अगले युग्म 89 को 3 के साथ लिखते हैं अतः अब भाज्य 389 हैं।

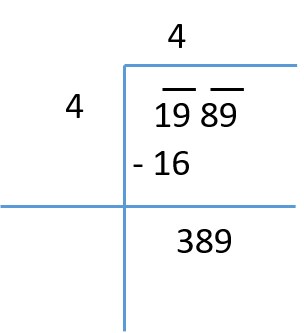
ocr_image

भाजक 4 को दुगुना करके दाएं तरफ रिक्त स्थान छोड़ते हैं।
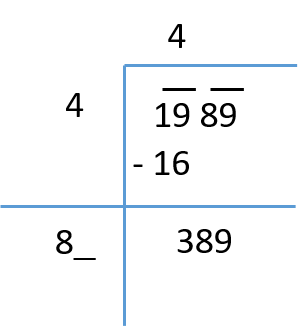
ocr_image

अब जैसा की हम जानते हैं रिक्त स्थान को भरने के लिए सबसे बड़े संभावित अंक का अनुमान लगाते जो अंक भागफल में नया होगा, इस प्रकार नया अंक को जब भागफल से गुणा करते है तब गुणनफल भाज्य से छोटा या बराबर होगा।

यहाँ

83 \times 3 = 249

84 \times 4 = 336

85 \times 5 = 425

चूंकि

336 < 389 < 425

अतः छोड़ा गया रिक्त स्थान मे 4 आएगा और हमे शेषफल 53 प्राप्त होता हैं।

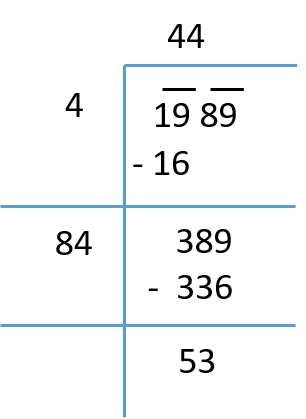
ocr_image

स्पष्ट हैं की भागफल विधि से वर्गमूल निकालने पर शेषफल 53 हैं। अतः 1989 में से 53 को घटाने पर प्राप्त संख्या पूर्ण वर्ग होंगी।

∴ 1989 - 53 = 1936

अब 1936 का वर्गमूल:
ocr_image

अतः 1936 एक पूर्ण वर्ग संख्या हैं जिसका वर्गमूल 44 हैं।

Learn more

दशमलव का वर्गमूल

उदाहरण से समझते हैं:-
संख्या 17.64 का वर्गमूल ज्ञात कीजिए।

चरण 1 दशमलव संख्या का वर्गमूल ज्ञात करने के लिए हम पूर्ण संख्या पर सामान्य रूप से बार लगाते हैं। दशमलव भाग पर भी पहले दशमलव स्थान से प्रारंभ करके बार लगाते हैं। जैसे:- $¯ ¯¯ ¯ 17 . ¯ ¯¯ ¯ 64$

चरण 2 अब एक ऐसी संख्या का वर्ग ज्ञात करना होता हैं जिसका वर्ग 17 के बराबर या छोटा हो यहाँ, $4^{2} < 17 < 5^{2}$ इस संख्या को भाजक के रूप में लेते हैं और सबसे बाई बार के नीचे की संख्या (अर्थात् 17) को भाज्य के रूप में लेकर भाग करते हैं और शेषफल ज्ञात करते हैं।

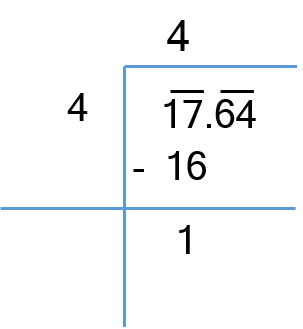
चरण 3 चूंकि यहाँ शेषफल 1 है अतः अगली बार के नीचे की संख्या अर्थात् 64 शेषफल के दाएँ ओर लिखते हैं, अतः नया भाज्य 164 होगा।

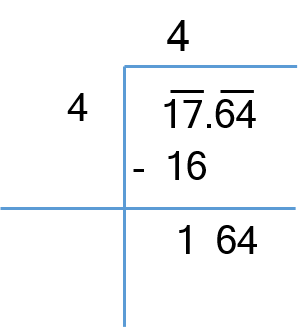
ocr_image

चरण 4 भाजक को दुगुना करके रिक्त स्थान के साथ दाई तरफ़ लिखते हैं। चूंकि 64 दशमलव भाग में था अतः भागफल भी दशमलव में होगा।

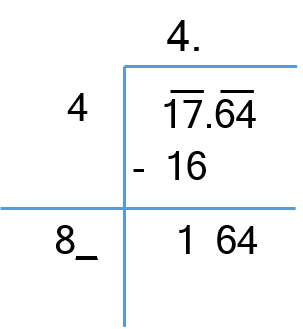
ocr_image

चरण 5 अब हम जानते हैं की,

82 \times 2 = 164

अतः भागफल में नया अंक 2 होगा, अब भाग देकर शेषफल ज्ञात करते हैं।

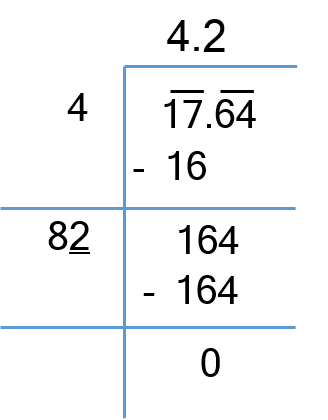
ocr_image

चरण 6 चूँकि शेषफल शून्य है और कोई बार नहीं है अत:

\sqrt{17.64} = 4.2

होगा।

उदाहरण 10

दशमलव संख्या $7.29$ के वर्गमूल ज्ञात कीजिए।

$7.29$ का वर्गमूल भागफल विधि से,

दशमलव संख्या का वर्गमूल ज्ञात करने के लिए हम पूर्ण संख्या पर सामान्य रूप से बार लगाते हैं तथा दशमलव भाग पर भी पहले दशमलव स्थान से प्रारंभ करके बार लगाते हैं, ( यहाँ

¯ 7

¯ ¯¯¯ ¯ .29

)

अब एक ऐसी संख्या का वर्ग ज्ञात करना होता हैं जिसका वर्ग 7 के बराबर या छोटा हो अतः यहाँ

2^{2} < 7 < 3^{2}

∴

चूंकि यहाँ शेषफल 3 है अतः अगली बार के नीचे की संख्या अर्थात् 29 को शेषफल 3 के दाएँ ओर लिखते हैं, अतः नया भाज्य 329 होगा।
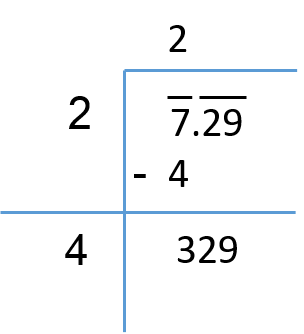
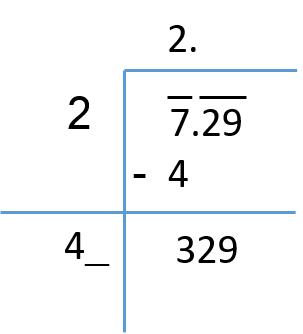
ocr_image

अब भाजक को दुगुना करके रिक्त स्थान के साथ दाई तरफ़ लिखते हैं। चूंकि 29 दशमलव भाग में था अतः भागफल भी दशमलव में होगा।
ocr_image

अब जैसा कि हम जानते हैं, कि

47 \times 7 = 329

अतः भागफल में नया अंक 7 होगा। अब भाग देकर शेषफल ज्ञात करते हैं।
ocr_image

स्पष्ट हैं कि शेषफल शून्य है और कोई युग्म नहीं है अत:

\sqrt{7.29} = 2.7

होगा।

Learn more

वर्गमूल का अनुमान लगाना

कभी - कभी हमें किसी संख्या के वर्गमूल का अनुमान लगाना पड़ता है क्योंकि दी गई संख्या का उचित वर्गमूल की गणना करना संभव नहीं होता है।

उदाहरण 300 के वर्गमूल का अनुमान लगाए।

हम जानते हैं कि 300, 100 और 400 के बीच आता है

अतः $100 < 400 < 300$

चूंकि $\sqrt{100} = 10$ तथा $\sqrt{400} = 40$

अतः हम कह सकते हैं की, $\sqrt{300}$ , 10 एवं 20 के बीच होगा।

$∴ 10 < \sqrt{300} < 20$

लेकिन फिर भी हम वर्ग संख्या के करीब नहीं हैं।

हम जानते हैं कि $17^{2} = 289$ और $18^{2} = 324$

अतः $17 < \sqrt{300} < 18$ और 289, 324 की तुलना में 300 के अधिक करीब है।

$∴ \sqrt{300} = 17$ (लगभग)

सारांश

m = n^{2}

हो, तो

m

एक पूर्ण वर्ग है, जहाँ m और n प्राकृत संख्याएँ हैं।

जब किसी संख्या को स्वयं उसी से गुणा किया जाता हैं, तो उससे प्राप्त संख्या उस संख्या का वर्ग कहलाती हैं।

सम संख्याओं के वर्ग सम संख्याएँ होती हैं।

विषम संख्याओं के वर्ग विषम संख्याएँ होती हैं।

एक पूर्ण वर्ग की इकाई का अंक केवल 0, 1, 4, 5, 6 या 9 हो सकता हैं।

संख्या

n

और

n + 1

के वर्गों के बीच में

2 n

प्राकृत संख्याएँ है।

प्रथम

n

विषम प्राकृत संख्याओ का योग

n^{2}

से प्राप्त होता है।

वह संख्या जिसके अंत में शून्यों की संख्या विषम हो, एक पूर्ण वर्ग नही होती है।

प्रत्येक प्राकृत संख्या

m > 1

के लिए

2 m

m^{2} - 1

और

m^{2} + 1

से एक पाइथागोरस त्रिक बनती है।

Home
Ask Doubt
Profile