ALGEBRAIC EXPRESSIONS AND IDENTITIES for Class 8 MATHS
INTRODUCTION
Baccho aapne apni previous classes m algebraic expressions k baare m pdha hai. Algebraic expressions basically vo expressions hote hai jo ki constants and variables ko use krke bnte hai. In an expressions, constants and variables are used along with mathematical operations like addition, subtraction, multiplication, etc. Hum complex problems ko easily solve krne k lie unhe algebraic expressions m convert krte hai. Before starting with the chapter, let's revise how we represent analgebaic expression on a number line.
Consider the expression x+5. Let us say the variable x has a position X on the number line. First, mark the distance x and then x+5 will be 5 unit to the right of x.
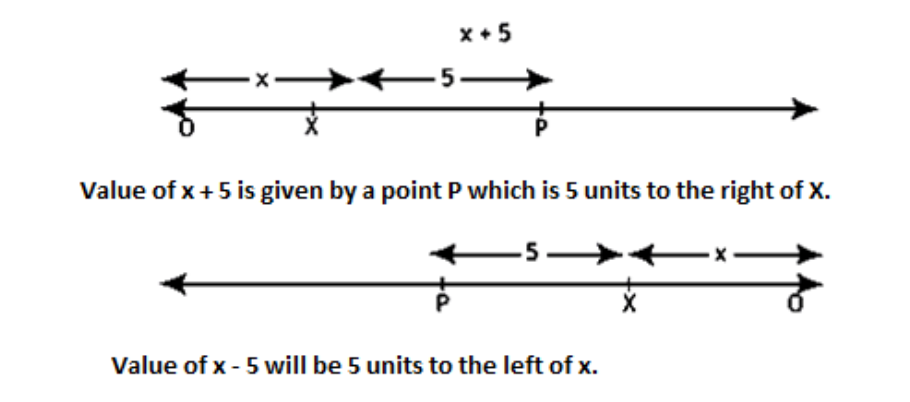
In the case of x–5 we will start from the right and move towards the negative side. x–5 will be 5 units to the left of x.
Iss chapter m hum seekhenge ki algebraic expressions ko kaise form kia jaata hai aur unse related identities konsi hoti hai. So let's begin!
Terms, Factors and Coefficients
Baccho, An algebraic expression (or) a variable expression is a combination of terms by the operations such as addition, subtraction, multiplication, division, etc. Ek algebraic expression k different components hote hai. These are known as Variables, Constants, Terms, and Coefficients of any algebraic expression. Inhe smjhne k lie hum ek expression ka example lenge.
Let us have a look at the expression 5x+7.
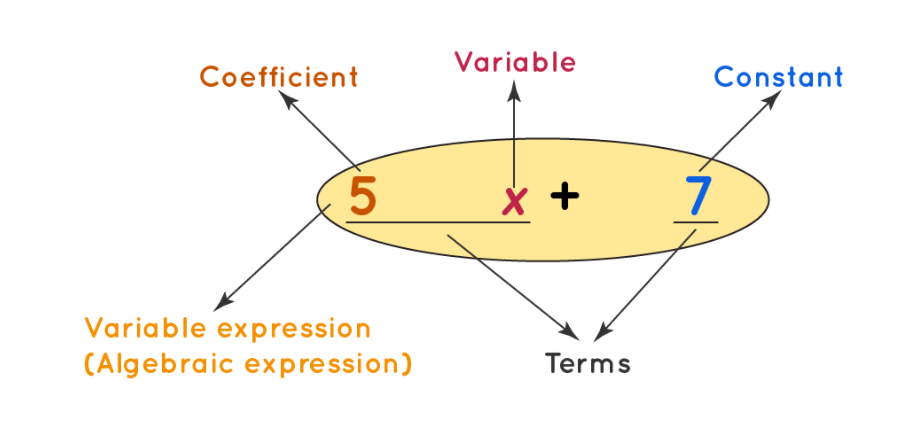
Baccho, variable ek aisa symbola hota hai jiski koi fixed value nahi hoti. For example, in the above example, x is a variable because we don't know what definite value it depicts.
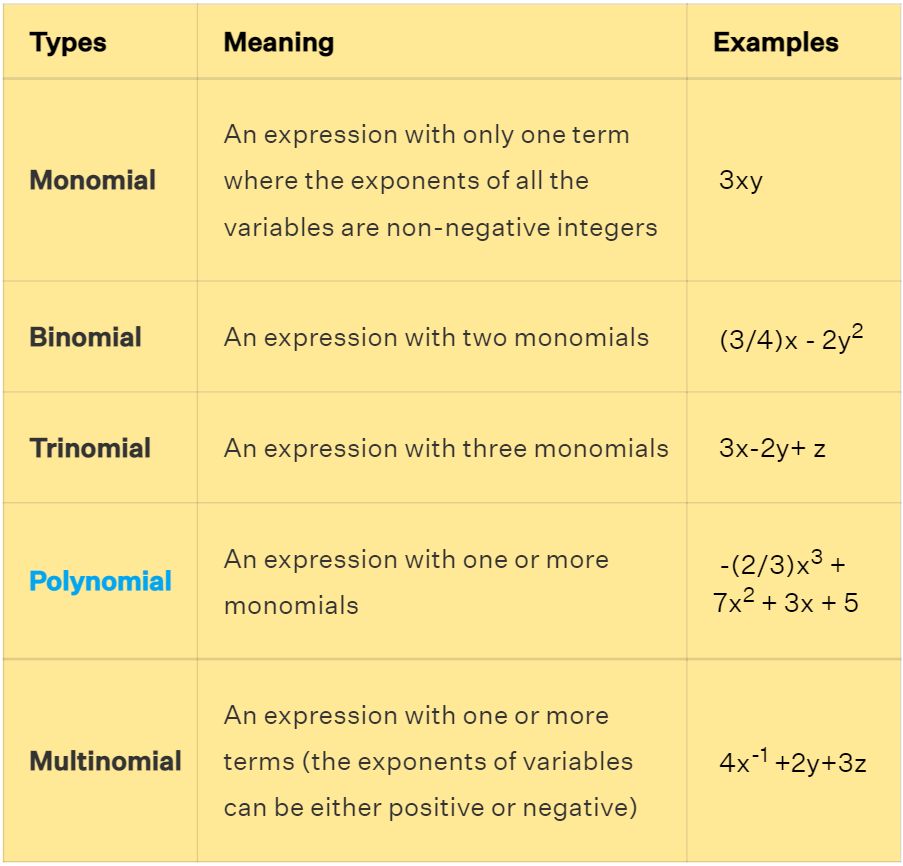
Monomials, Binomials and Polynomials
The types of algebraic expressions are based on the variables found in that particular expression, the number of the terms of that expression, and the values of the exponents of the variables in each expression. Given below is a table that divides the algebraic expressions into five different categories. Let us have a look at the table.
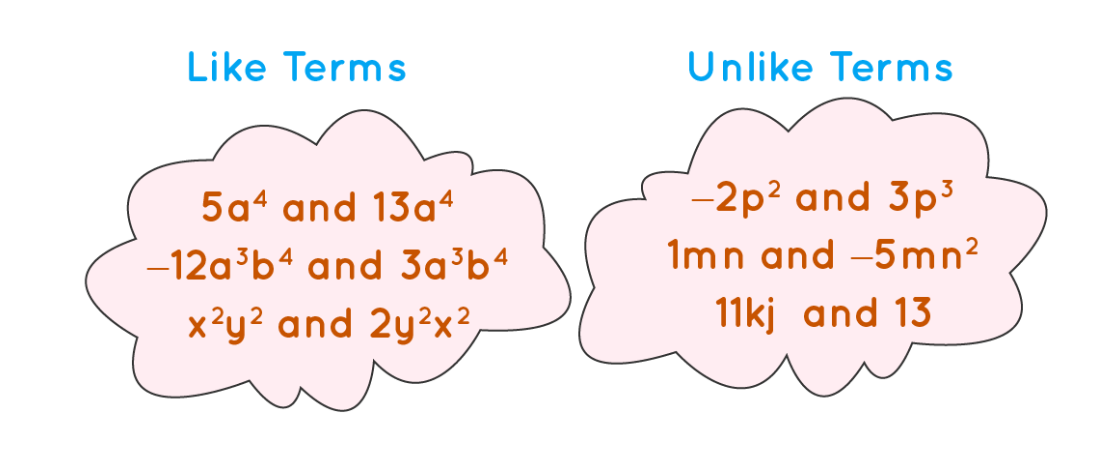
Like and Unlike Terms
Baccho, like terms vo hote hai jinke same variables hote hai aur vo same power p raised hote hai. Like terms k same algebraic factors hote hai. The numerical coefficient of like terms can be different.
For example, 3x2y and 5x2y are like terms.
Agar do terms k variables ya unki powers alag ho to vo unlike terms kehlaate hai. Let's see which of the following are like terms:
7x,14x,–13x,5x2,7y,7xy,–9y2,–9x2,–5yx
Addition and Subtraction of Algebraic Expressions
ADDITION OF ALGEBRAIC EXPRESSIONS
Addition of algebraic expressions is quite similar to the addition of numbers. However, the addition of algebraic expressions requires categorizing the terms in an algebraic expression into two types - like and unlike terms. Then, taking up the like terms and adding them.
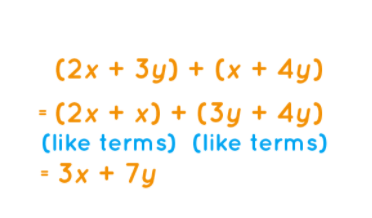
Steps to be followed to do the addition of algebraic expressions are written below:
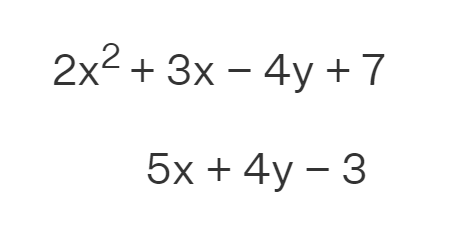
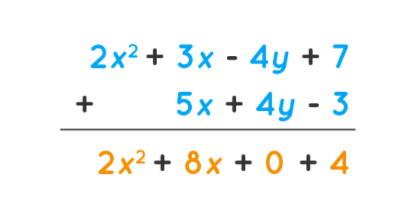
SUBTRACTION OF ALGEBRAIC EXPRESSIONS
For subtracting two or more algebraic expressions, it requires categorizing the terms in an algebraic expression into two types - like and unlike terms. Then, taking up the like terms and then subtracting them accordingly.
Steps to be followed to do subtraction of algebraic expressions are written below:
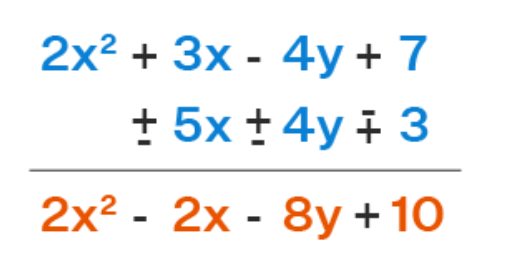
NOTE:
Baccho, subtraction of a number is the same as addition of its additive inverse.
Yaani ki −3 ko subtract krna aur +3 ko add krne p effect same hi aata hai. Similarly, subtracting 6y is the same as
adding –6y; subtracting –4y2 is the same as adding 4y2 and so on. Jab hum second row k baad signs change krte hai usse hume pata chlta hai ki konsa operation apply krna hai.
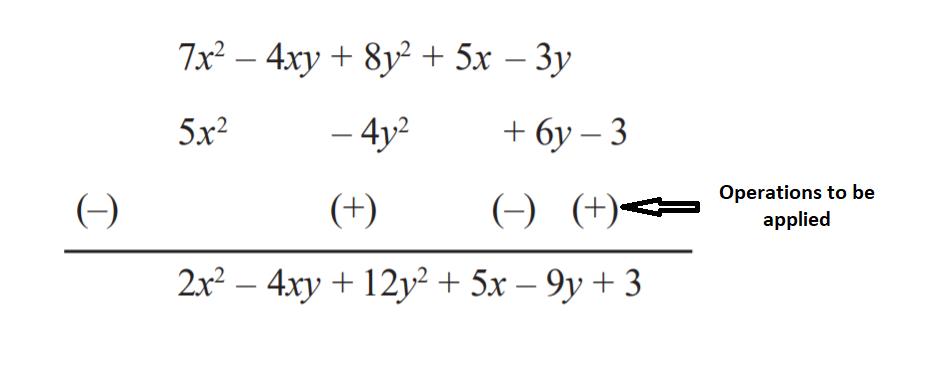
Multiplying a Monomial by a Monomial
Baccho, hum apni day to day life m aisi bohot si situations face krte hai jisme hume problems ko algebraic expressions k form m multiply krna hota hai. Ek bohot hi common example hai ki jab hum kisi 3d shape ka volume nikaal rahe hote hai. To find the volume of cube, we use the formula as a×a×a, in which a is a variable representing the side of the cube. Ek aur example lete hai. Suppose aap apni class m baithe hai aur aapko ye find out krna h ki aap total number os students sitting in class ko kaise represent kroge agar ek row m m students hai aur ek column m n students hai. For this we'll multiply m and n and will say that the number of students sitting in class are m×n Let us see how we multiply the different types of algebraic expressions.
Multiplying a Monomial by a Monomial
An algebraic expression is considered a monomial when it only contains one term like 5ab. Monomials usually include variables, numbers, or multiple numbers and/or variables that are multiplied together.
Product of two monomials = numerical coefficients xx variable parts
Example: Find the product of 6ab and −3a2b3
Solution
6ab×−3a2b3
=6×−3×ab×a2b3
=−18×a1+2×b1+3
=−18a3b4
Observe the following examples.
(i)2x×5y×7z=(2x×5y)×7z=10xy×7z=70xyz
(ii)4xy×5x2y2×6x3y3=(4xy×5x2y2)×6x3y3=20x3y3×6x3y3=120x3y3×x3y3
=120(x3×x3)×(y3×y3)=120x6×y6=120x6y6
Example 1
Complete the table for area of a rectangle with given length and breadth.
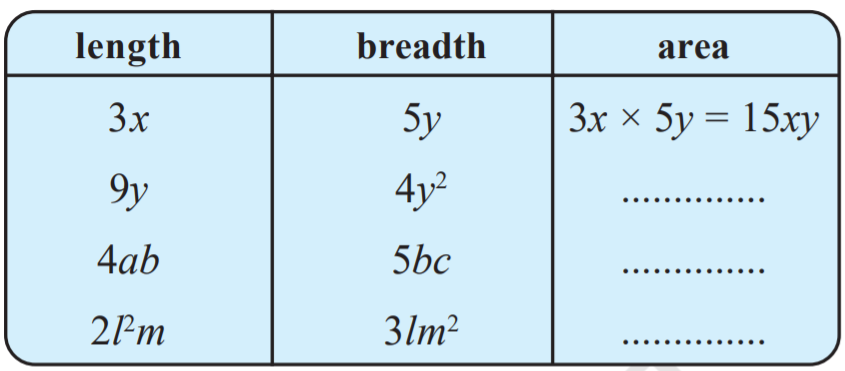
Area of rectangle = llength(l) * breadth(b)
(i)Here, length =3x, breadth=5y
So, Area =3x∗5y=15xy
(ii)Here, length=9y,breadth =4y2
So, Area =9y∗4y2=36y3
(iii)Here, length=4ab,breadth=5bc
So, Area =4ab∗5bc=20ab2c
(iv)Here, length=2l2m, breadth =3lm2
So, Area =2l2m∗3lm2=6l3m3
Multiplying a Monomial by a Polynomial
An algebraic expression is considered a polynomial when it contains variables, coefficients, that involve only the operations of subtraction, addition, multiplication, and non-negative integer exponentiation of variables.
Multiply each term of the polynomial by the monomial, using the distributive law: a×(b+c)=a×b+a×c
Example: Find following product: 5a2b2×(3a2−4ab+6b2)
Solution
5a2b2×(3a2−4ab+6b2)
=(5a2b2)×(3a2)+(5a2b2)×(−4ab)+(5a2b2)×(6b2)
=15a4b2−20a3b3+30a2b4
Multiplying a monomial by a trinomial
Consider 3p×(4p2+5p+7). As in the earlier case, we use distributive law;
3p×(4p2+5p+7)=(3p×4p2)+(3p×5p)+(3p×7)
=12p3+15p2+21p
Multiply each term of the trinomial by the monomial and add products.
Observe, by using the distributive law, we are able to carry out the multiplication term by term.
Example 2
Simplify the expressions and evaluate them as directed:
(i) x(x−3)+2 for x=1
(ii) 3y(2y−7)−3(y−4)−63 for y=2
(i) x(x−3)+2=x2−3x+2
At x=1,(1)2−3(1)+2=1−3+2=0
(ii)3y(2y−7)−3(y−4)−63=6y2−21y−3y+12−63
6y2−24y−51
At y=2,6(2)2−24(2)−51=24−48−51=−75
At y=−2,6(−2)2−24(−2)−51=24+48−51=21
Example 3
Subtract 3pq(p−q) from 2pq(p+q)
3pq(p−q)=3p2q−3pq2→(1)
2pq(p+q)=2p2q+2pq2→(2)
Subtracting ,(2)−(1),
2p2q+2pq2−(3p2q−3pq2)
=−p2q+5pq2
Multiplying a Polynomial by a Polynomial
Baccho, iss section m hum do types pdhenge polynomial-polynomial multiplication ki category k under. These are:
1. Multiplying a binomial by a binomial
baccho, ek algebraic expression binomial tab kehlaai jaati hai jab vo do terms k sum ya difference se bnti hai. Hum do binomials ko multiply krne k lie distributive law ko do baari use krte hai.
Let us find the product of two binomials (a+b) and (c+d).
(a+b)×(c+d)
=a×(c+d)+b×(c+d)
=a×c+a×d+b×c+b×d
=ac+ad+bc+bd
Example: Multiply (3a+5b) and (5a−7b).
Solution:
(3a+5b)×(5a−7b)
=3a×(5a−7b)+5b×(5a−7b)
=(3a×5a−3a×7b)+(5b×5a−5b×7b)
=(15a2−21ab)+(25ab−35b2)
=15a2−21ab+25ab−35b2
=15a2+4ab−35b2
ial by a trinomial
2. Multiplying a binomial by a trinomial
Baccho, hum iss type ko smjhne k lie bhi ek example lenge.
Example: Multiply (a+7) with (a2+3a+5)
Solution:
a×(a2+3a+5)+7×(a2+3a+5)
[Using the distributive law]
=a3+3a2+5a+7a2+21a+35
=a3+(3a2+7a2)+(5a+21a)+35
=a3+10a2+26a+35
Standard Identities
Algebraic identities are an important set of formulas in math. They form the foundation working principle of algebra and are helpful to perform computations in simple and easy steps. Certain algebraic problems require working across numerous mathematical step to obtain the answer. Here, with the use of algebraic identities, we are able to perform the calculations without any additional steps. Many of the algebraic identities have been obtained from the binomial expansion of terms.
An algebra identity means that the left-hand side of the equation is identically equal to the right-hand side, for all values of the variables. Baccho, to understand the concept of equality in identities, let's take an example:
Consider the equality (a+1)(a+2)=a2+3a+2
Baccho, ab hum iss equation ki dono sides (right and left side of "=") ko alag alag evaluate krenge for the value a=10.
LHS=(a+1)(a+2)=(10+1)(10+2)=11×12=132
RHS=a2+3a+2=102+3×10+2=100+30+2=132
jaisa ki aap dekh skte hai, dono sides ko solve krne p we get the same values, this means that the equality holds true.
An equation is true for only certain values of the variable in it. It is not true for
all values of the variable.
Baccho, ab hum dekhenge ki humari standard identities konsi hoti hai aur vo konse binomials k multiplication se derive hoti hai.
(a+b)2=(a+b)(a+b)
=a(a+b)+b(a+b)
=a2+ab+ba+b2
=a2+2ab+b2
Therefore, (a+b)2=a2+2ab+b2
=a2–ab–ba+b2=a2–2ab+b2
Therefore, (a–b)2=a2–2ab+b2
=a2–ab+ba–b2=a2–b2 (since ab=ba)
therefore, (a+b)(a–b)=a2–b2
Baccho, these are our three standard identities.
(x+a)(x+b)=x(x+b)+a(x+b)
=x2+bx+ax+ab
Therefore, (x+a)(x+b)=x2+(a+b)x+ab
Applying Identities
Now we'll see how we can use the standard identities to multiply different binomials and polynomials.
Example : Using identities, solve 297×303.
Solution: 297×303 can be written as (300−3)×(300+3)
And this is based on the algebraic identity (a+b)(a−b)=a2−b2
Here we have a=300, and b=3
Substituting the values in the above identity, we get:
(300−3)(300+3)=3002−32
=90000−9
=89991
Answer: Therefore 297×303=89991
Example : Simplify (7x+4y)2+(7x−4y)2
Solution: To solve this, we need to use the following algebraic identities:
(a+b)2=a2+2ab+b2
(a−b)2=a2−2ab+b2
Adding the above two formulas we have:
(a+b)2+(a−b)2=a2+2ab+b2+a2−2ab+b2
(a+b)2+(a−b)2=2a2+2b2
Here we have a= 7x and b=4y. Substituting this in the above expression we have:
(7x+4y)2+(7x−4y)2=2(7x)2+2(4y)2
=98x2+32y2
Answer: (7x + 4y)^2 + (7x - 4y)^2 = 98x^2 + 32y^2
Example 4
Using Identity find
(i) (4p−3q)2
(ii) (49)2
(i) (4p−3q)2
=16p2+9q2−24pq
(ii)(49)2
(50−1)2
502+1−100
2500−100+1
2401.
Example 5
Using identities, evaluate.
(i) 712
(ii) 992
(iii) 1022
(iv) 9982
(v) 5.22
(vi) 297×303
(vii) 78×82
(viii) 892
(ix) 105×95
(i) 712=(70+1)2
(70)2+2(70)(1)+(1)2
=4900+140+1=5041
(ii) 992=(100−1)2
=1002−2(100)(1)+1
=10000−200+1
=9801
(iii) 1022=(100+2)2
=1002+22+2⋅2⋅100=200+4+400=604
(iv) 9982=(100−2)2
=1002+22−2⋅2⋅100=−200+4=−196
(v) 5.22=(5+0.2)2
=52+0.22+2(0.2)(5)
=25+0.04+2=27.04
(vi) 297×303=(300−3)×(300+3)
=(300)2−32
=90000−9=89991
(vii)78×82=(80−2)(80+2)
(80)2−(2)2=6400−4=6396
(viii) 8.92=(9−0.1)2
=92+0.12−2(0.1)(9)
=81+0.01−1.8
=79.21
(ix) 1.05×9.5
105100×95100
=(100+5)(100−5)1000
=1002−521000
=10000−251000
=99751000=9.975
SUMMARY
1. Expressions are formed from variables and constants.
2. Terms are added to form expressions. Terms themselves are formed as product of factors.
3. Expressions that contain exactly one, two and three terms are called monomials, binomials and
trinomials respectively. In general, any expression containing one or more terms with non-zero
coefficients (and with variables having non- negative exponents) is called a polynomial.
4. Like terms are formed from the same variables and the powers of these variables are the same,
too. Coefficients of like terms need not be the same.
5. While adding (or subtracting) polynomials, first look for like terms and add (or subtract) them;
then handle the unlike terms.
6. There are number of situations in which we need to multiply algebraic expressions: for example, in finding area of a rectangle, the sides of which are given as expressions.
7. A monomial multiplied by a monomial always gives a monomial.
8. While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the
monomial.
9. In carrying out the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term, i.e., every term of the polynomial is multiplied by every term in the binomial (or trinomial).
Note that in such multiplication, we may get terms in the product which are like and have to be
combined.
10. An identity is an equality, which is true for all values of the variables in the equality.
On the other hand, an equation is true only for certain values of its variables. An equation is not an identity.
11. The following are the standard identities:
(a+b)2=a2+2ab+b2....(I)
(a–b)2=a2–2ab+b2....(II)
(a+b)(a–b)=a2–b2....(III)
12. Another useful identity is (x+a)(x+b)=x2+(a+b)x+ab....(IV)
13. The above four identities are useful in carrying out squares and products of algebraic expressions.
They also allow easy alternative methods to calculate products of numbers and so on.
Let's Revise
1. Baccho, iss chapter m humne algebraic expressions k baare m pdha. Humne alag alag type k expressions k baare m bhi seekha aur ye bhi jaana ki unse related identities konsi hoti hai. hai
2. Constant ek aisa symbol hota hai jiski ek fixed numerical value hoti hai. For example, 1,2,3,4,.....
3. Variable ek aisa symbol hota hai jiski koi fixed numerical value nahi hoti hai aur vo kisi bhi value ko represent krne k lie use ho skta hai. For example, a,b,c,...
4. A term is a variable alone (or) a constant alone (or) it can be a combination of variables and constants by the operation of multiplication or division. Some examples of terms are 3x2,−(2y3),√5x, etc.
5.Jin terms m same variables aur unki powers same raised hoti hai unhe like terms kaha jaata hai. Jin terms k different values ya degrees hote hai unhe unlike terms kaha jaata hai.
6.Monomials vo expressions hote hai jinme ek single term hota hai. Jin expressions m do terms hote hai unhe binomial kaha jaata hai aur jin expressions m teen terms hote hai unhe trinomial kaha jaata hai. In general, agar kisi expression m ek ya ek se zyada terms ho with non-zero coefficients, unhe polynomials kaha jaata hai.
7. Humne seekha ki hum kaise alag alag types of expressions ko add, subtract aur multiply krte hai.
8. Calculations ko asaan banane k lie hum kuch identities use kr skte hai jo ki binomials ko multiply krke derive hoti hai. Inhe standard identities kaha jaata hai.
9. The following are the standard identities:
(a+b)2=a2+2ab+b2....(I)
(a–b)2=a2–2ab+b2....(II)
(a+b)(a–b)=a2–b2....(III)
10 Another useful identity is (x+a)(x+b)=x2+(a+b)x+ab....(IV)