CUBES AND CUBE ROOTS for Class 8 MATHS

INTRODUCTION

Baccho, aapne apne previous chapter m square and square roots k baare m pdha tha. Humne seekha tha ki square unit basically kisi figure k area k lie use kia jaata hai. Jab ek number khud se multiply hota hai to vo uska square kehlaata hai. But what if agar hum ek number ko usi se teen baari multiply kre $(a \times a \times a)$ ? Baccho, ise cube kehte hai. Jis tarah squares area nikaalne m use aate hai vaise hi cubes volume nikaalne m kaam ate hai. Kisi ek $3 D$ figure m kitni space hoti hai use volume kehte hai. Suppose aapke paas ek cuboidal container hai jiski aapko height, length aur breadth given hai. Jab aap iss container ka volume nikaalenge to aapko answer unit cube $(u n i t^{3})$ m milega. Kyunki yaha p volume nikaalne k lie we multiply $3$ measurements, islie we call it as unit cube This is one example of application of cubes. In this chapter we will learn about cubes and cube roots and different methods to find them. We will also learn about quick vedic math tricks to help us build our concepts. So let's begin!

CUBE

Baccho jab hum ek number ko usi number se do aur baari multiply krte hai jisse humare paas teen numbers ka product aata hai, use hum uss number ka cube kehte hai. When we multiply a number two times by itself, we get the product of 3 numbers, all three numbers being the same. The resultant number(product) is known as the cube of the original number. We call it a cube because it is used to represent the volume of a cube. Hum ye bhi keh skte hai ki jab ek number ko $3$ ki power (exponent) p raise kiya jaata hai to resultant ko uss number ka cube kaha jaata hai. For example, the cube of $3$ is $27$ . That means $3 \times 3 \times 3 = 27$ , and it can be written as $3^{3}$ . Similarly, the cube of $4$ is $64$ , and the cube of $5$ is $125$ , and so on. Bachho, cube k concept se related ek interesting example hai Hardy-Ramanujan Number.
Hardy Ramanujan was a mathematical genius who pointed out that the number $1729$ is very unique because it is the smallest number that can be expressed as a sum of two cubes in two different ways:

1729 = 1728 + 1 = 12^{3} + 1^{3}

1729 = 1000 + 729 = 10^3 + 9^3

\frac{<}{l} i > < b r >

1729

h a s sin c e b e e n k n o w n a s t h e < b > H a r d y - R a m a ν j a n N u m b e r \frac{<}{b} > . B a h o a i s e a u r b h i ν m b e r s h o t e h a i j o d o a l a g ν m b e r s k c u b e k \sum m exp r e s s k i y e j a a s k t e h a i . S o m e o f t h e m a r e : < b r > < l i >

4104

(2^3+16^3 ; 9^3+15^3)

\frac{<}{l} i > < b r > < l i >

13832

(18^3+20^3 ; 2^3+24^3)

\frac{<}{l} i > < b r > T r y and exp l or e m or e s u c h ν m b e r s! < b r > < b > C u b e s R e l a t i o n w i t h C u b e N u m b e r s \frac{<}{b} > < b r > I n \geq o m e t r y, a c u b e i s a s o l i g u r e w h e r e a l l e d \geq s a r e e q u a l and a r e p e r p e n d i c a - - r \to e a c h o t h e r . < b r > F or e x a m p \leq, t a k e a c u b e o f u n i t s . I f w e a r r a n \geq t h e s e c u b e s \to f or m a b i g \geq r c u b e o f s

u n i t s, w e f \in d t ˆ t h e r e a r e a \to t a l o f

s u c h u n i t c u b e s t ˆ m a k e u p a c u b e o f

u n i t s . S i m i l a r l y, a c u b e o f

u n i t s w i l l h a v e

64 such unit cubes.
ocr_image

Look at the following list of numbers and their cubes. Memorizing cubes of these numbers will help you a lot in your further classes.
ocr_image

INTERESTING PATTERNS

Let's observe some patterns related numbers and their cubes.
$1.$ Adding Consecutive Odd Numbers

1 = 1 = 1^{3}

3 + 5 = 8 = 2^{3}

7 + 9 + 11 = 27 = 3^{3}

13 + 15 + 17 + 19 = 64 = 4^{3}

21 + 23 + 25 + 27 + 29 = 125 = 5^{3}

We can see from the above pattern, if we need to find the

n^{3}

n

consecutive odd numbers will be needed, such that their sum is equal to

n^{3}

.
This pattern holds true for all natural numbers.
Also, if we need to find

n^{3}

then we should add

n

consecutive natural numbers starting from odd natural number.
$2.$ Cubes and their prime factors
In this pattern we'll observe that in the prime factorization of any number, if each prime factor appears three times, then the number is a perfect cube.
Let's look at the steps to find the Perfect Cube
The perfect cube of a number can be checked by following the steps given below:
Step 1: Prime factorize the given number starting from the smallest prime number

(2)

.
Step 2: Once the prime factorization is done, club every three same factors together.
Step 3: Repeat the step for all the sets of the group of the same three factors. If there are any factors that are left behind and do not fit into a group of three same factors, then the given number is not a perfect cube. Otherwise, the given number is a perfect cube.
Let us understand this with an example.
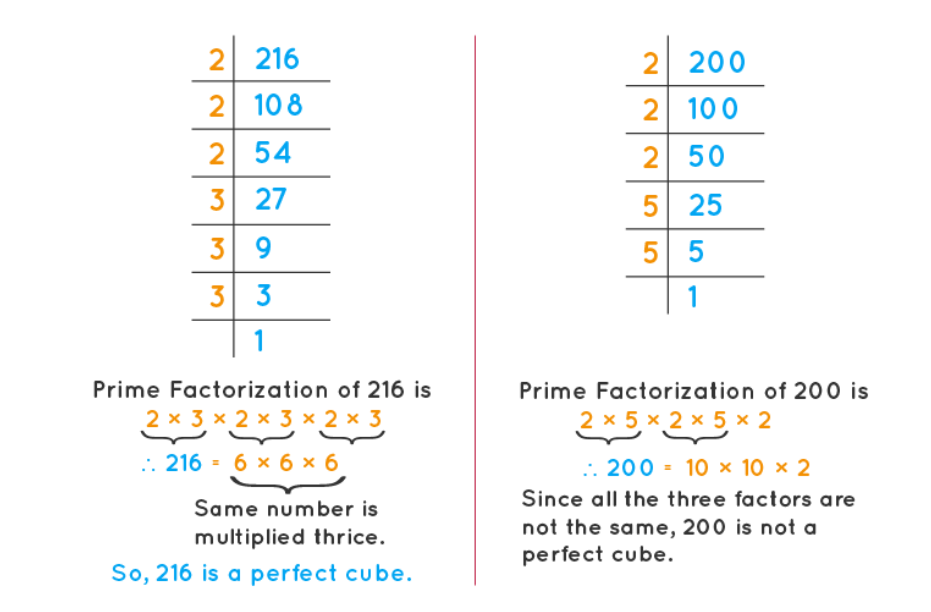
ocr_image

Here are a few more examples following the same pattern:

64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^{3} \times 2^{3} = 4^{3}

216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^{3} \times 3^{3} = 6^{3}

3375 = 3 \times 3 \times 3 \times 5 \times 5 \times 5 = 3^{3} \times 5^{3} = 15^{3}

1728 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^{3} \times 2^{3} \times 3^{3}

Example 1

Is $243$ a perfect cube?

Prime Factorization of $243$
$243 = 3 \times 3 \times 3 \times 3 \times 3$
Since, $3$ is not in a triplet
$∴ 243$ is not perfect cube.

Learn more

SMALLEST MULTIPLE THAT IS A PERFECT CUBE

Baccho, iss section m hum seekhenge ki hum smallest number kaise nikaal skte hai jisko kisi number se multiply/divide krke vo number perfect cube bnjaaye. It is related to the previous topic about prime factorization. As we have seen that the group of three prime factors makes a number perfect cube, so to make a number perfect cube we need to multiply it with the smallest multiple of that number. Let's understand this with a situational example.
Baccho suppose ki aapke paas ek clay ka cuboid hai jiski dimensions hai : $Length = 15 cm, Breadth = 30 cm, Height = 15 cm$
Aapko ye pta lgana hai ki aise aur kitne cuboids ko use krke aap ek perfect cube bna skte hai. Try to relate this with prime factorization pattern that we studied above. That pattern allows us to know that by multiplying what number we can get a triplet and a perfect cube.
Volume of cuboid is $15 \times 30 \times 15 = 3 \times 5 \times 2 \times 3 \times 5 \times 3 \times 5$
$= 2 \times 3 \times 3 \times 3 \times 5 \times 5 \times 5$
Since there is only one 2 in the prime factorization. So we need $2 \times 2, i.e., 4$ to make it a perfect cube. Therefore, we need $4$ such cuboids to make a cube.

Example 2

Is $392$ a perfect cube? If not, find the smallest natural number by which $392$ must be multiplied so that the product is a perfect cube.

Factorization of $392 = 2 \times 2 \times 2 \times 7 \times 7$
No, this is not a perfect cube.
After multiplying by $7$ we can make it perfect cube
New number $= 392 \times 7 = 2744$ .

Learn more

Example 3

Is $53240$ a perfect cube? If not, then by which smallest natural number should $53240$ be divided so that the quotient is a perfect cube?

$53240 = 2 \times 2 \times 2 \times 5 \times 11 \times 11 \times 11 = 2^{3} \times 11^{3} \times 5$
Thus, $53240$ is not a perfect cube.
If we divide it by $5$ it will a perfect cube.

Learn more

Example 4

Is $1188$ a perfect cube? If not, by which smallest natural number should $1188$ be divided so that the quotient is a perfect cube?

$1188 = 11 \times 3 \times 3 \times 3 \times 2 \times 2$
Thus, $1188$ is not a perfect cube.
If we divide it by $44 (11 \times 2 \times 2)$ it will be a perfect cube.

Learn more

Example 5

Is $68600$ a perfect cube? If not, find the smallest number by which $68600$ must be multiplied to get a perfect cube.

Factorization of $68600 = 2 \times 2 \times 2 \times 5 \times 5 \times 7 \times 7 \times 7$
No, it is not a perfect cube
After multiplying by $5$ this number can be a perfect cube.

Learn more

CUBE ROOT OF A CUBE

When we think about the words cube and root, the first picture that might come to our mind is a literal cube and the roots of a tree. Isn't it? Well, the idea is similar. Root means the primary source or origin. So, we just need to think "cube of which number should be taken to get the given number".
Baccho jaise humne previous chapter m squares k baare m pdha tha, humne ye bhi jaana tha ki har square ka inverse operation square root hota hai. Similarly, cube ka inverse operation cube root hota hai. Cube root vo number hota hai jise khud se do baari multiply krke hume ek cube number milta hai. In mathematics, the definition of cube root is written as, "Cube root is the number that needs to be multiplied three times to get the original number." Now, let us look at the cube root formula, where $y$ is the cube root of $x$ .
$\sqrt[3]{x} = y$
. The radical sign $\sqrt[3]{}$ is used as a cube root symbol for any number with a small $3$ written on the left of the sign. Another way to denote cube root is to write $\frac{1}{3}$ as the exponent of a number like $x^{\frac{1}{3}}$
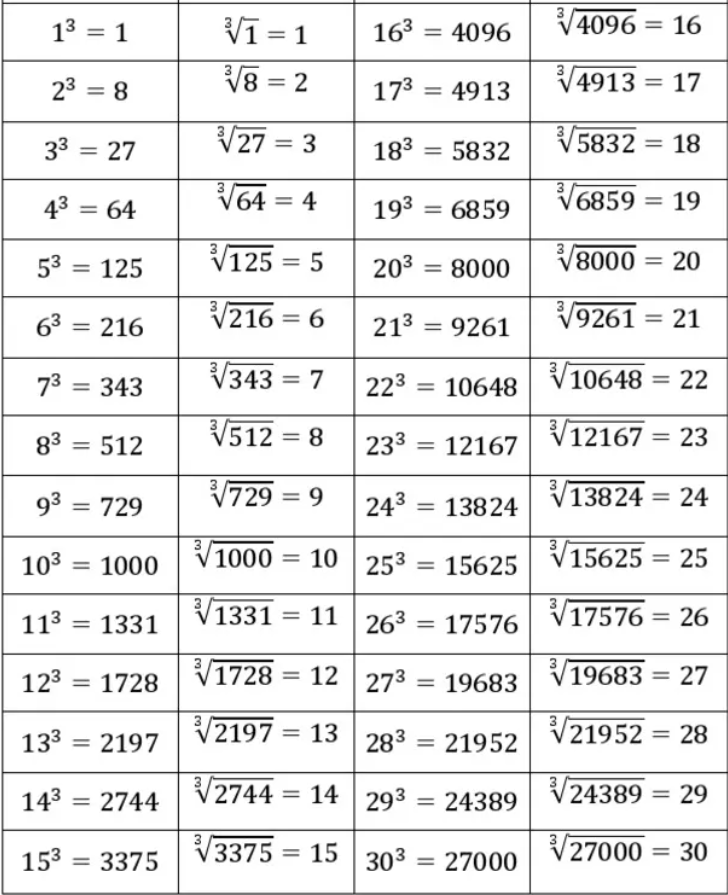
ocr_image
The following table represents perfect cubes from $1 - 30$ and their cube roots.

CUBE ROOTS THROUGH PRIME FACTORIZING

The cube root of a number can be determined by using the prime factorization method. In order to find the cube root of a number, start with the prime factorization of the given number. Then make triplets of the obtained factors. After that, count each triplet as one multiply the factors to get the answer. If there is any factor left that doesn't form a triplet, that means the given number is not a perfect cube.
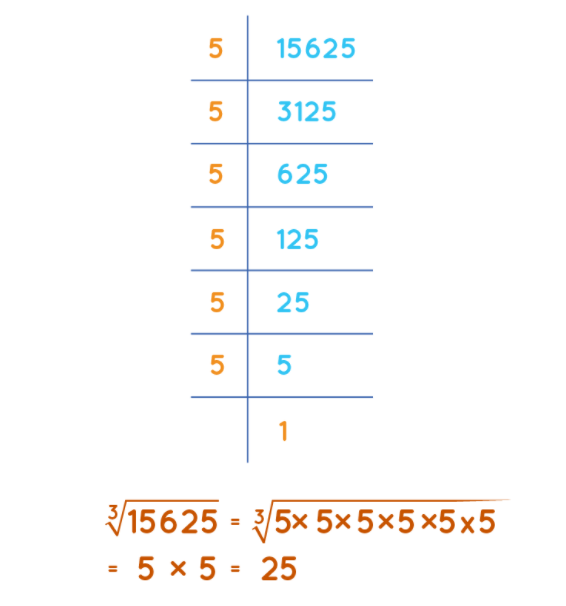
For example, let us see how we find the cube root of $15625$ .
ocr_image

Example 6

Find the cube root of $8000$ .

Prime factorisation of $8000$ is $2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 5$
So, $\sqrt[3]{8000} = 2 \times 2 \times 5 = 20$

Learn more

Example 7

Find the cube root of $13824$ by prime factorization method.

Prime Factorization of $13824 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^{3} \times 2^{3} \times 2^{3} \times 3^{3}$
Therefore, $\sqrt[3]{13824} = 2 \times 2 \times 2 \times 3 = 24$

Learn more

CUBE ROOT OF A CUBE NUMBER USING ESTIMATION

Baccho humne previous chapter m square roots estimate krna seekha tha. Now we'll see how we can estimate cube roots. Estimation means kisi cheez ko closely guess krna. If a cube number is given we can find out its cube root using the following steps:

Take any cube number say

117649

and start making groups of three starting from the rightmost digit of the number. So

117649

has two groups, and first group

(649)

and the second group

(117)

The unit’s digit of the first group

(649)

will decide the unit digit of the cube root. Since the number

649

ends with

9

, the cube roots unit’s digit is

9

Find the cube of numbers between which the second group lies. The other group is

117

. We know that

4^{3} = 64

and

5^{3} = 125

64 < 117 < 125

. Take the smaller number between

4

and

5

as the ten’s digit of the cube root. So,

49

is the cube root of

117649

Example 8

Find the cube root of $17576$ through estimation.

$17576$
$20^{3} < 17576 < 30^{3}$
Unit digit of $17576$ is $6$
$∴$ Unit digit of $\sqrt[3]{17576}$ will be $6$
$\Rightarrow \sqrt[3]{17576} = 26$

Learn more

TRICKS TO CALCULATE CUBE AND CUBE ROOTS

Baccho, cubes and cube roots calculate krne k lie hume repeated multiplication aur prime factorization jaise methods ko use krna pdhta hai jo ki lengthy hote hai especially for bigger numbers. Iss section m hum kuch quick tricks and methods seekhenge to calculate cubes and cube roots. So let's begin!
Let's learn to find cube roots of bigger numbers like $39304$ through a shortcut method involving four steps:
$STEP 1:$
To find the unit place of the cube root always remember the following points:

If the last digit of a cube root is

8

then the unit digit will be

2

If the last digit of a cube root is

2

then the unit digit will be

8

If the last digit of a cube root is

3

then the unit digit will be

7

If the last digit of a cube root is

7

then the unit digit will be

3

If the last digit of a cube root is other than

2, 3, 7

and

8

then put the same number as the unit digit.

Therefore, the unit digit will be

4

STEP 2:

Now, strike off the last

3

digits of the given number.

39304

STEP 3:

Now, find the nearest cube of the first

2

digit from the left, i.e.,

39

.
The nearest cube is

27

STEP 4:

Now,

3

is the cube root of

27

.
Therefore, the ten’s place digit will be

3

.
So, the answer will be

34

.
ANOTHER EXAMPLE
Let us now find the cube root of

238328

with the same method

The unit digit will be

2

Now, strike off the last

3

digits of the given number.

238328

Now, find the nearest cube of the first

3

digit from the left, i.e.,

238

The nearest cube is

216

Now,

6

is the cube root of

216

.Therefore, the ten’s place digit will be

6

So, the answer will be

62

Baccho, now let's learn to find cubes using vedic maths tricks:
Type $1$ : Numbers starting with $1$

{(16)}^{3}

1 .

We consider

1

1^{s t}

term and

6

2^{n d}

term, we will write the given term as it is i.e.
ocr_image

2 .

Square the

2^{n d}

term i.e.

6^{2} = 36

and also cube the

2^{n d}

term i.e.

= 6^{3} = 216

and write the values in

1^{s t}

row i.e.

3 .

2^{n d}

row double the

2

middle terms (. i.e. is

2^{n d}

term and

3^{r d}

term) & write just below

2^{n d}

3^{r d}

term.

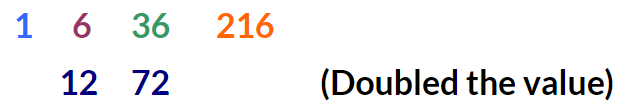
4 .

Add them vertically in column. carry forward the

10^{t h}

places digit to next column
ocr_image

∴ 16^{3} = 4096

Type 4: Numbers having different digit

{(32)}^{3}

1 .

We consider

3

1^{s t}

term and

2

2^{n d}

term, Cube the

1^{s t}

term and

2^{n d}

term i.e.

{(3)}^{3} = 27

and

{(2)}^{3} = 8

2 .

Square the

1^{s t}

term i.e.

3^{2} = 9

then multiply by

2^{n d}

term i.e.

9 \times 2 = 18

3 .

Square the

2^{n d}

term i.e.

2^{2} = 4

then multiply by

1^{s t}

term i.e.

4 \times 3 = 12

4 .

2^{n d}

row double the

2

middle terms (. i.e. is

2^{n d}

term and

3^{r d}

term) & write just below

2^{n d}

3^{r d}

term.

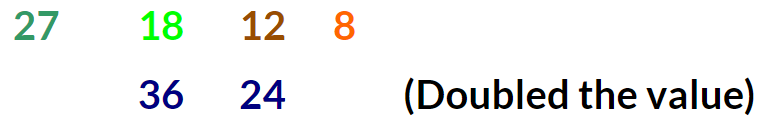
5 .

Add them vertically in column. carry forward the

10^{t h}

places digit to next column
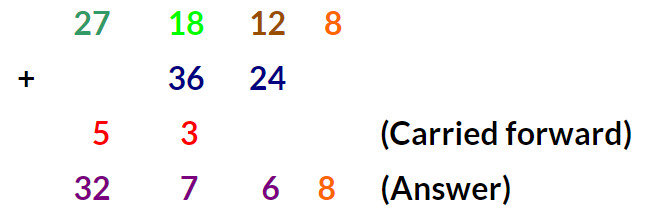
ocr_image

∴ {(32)}^{3} = 32, 768

Let's Summarize

$1 .$ Numbers like $1729, 4104, 13832,$ are known as Hardy – Ramanujan Numbers. They can be expressed as sum of two cubes in two different ways.
$2 .$ Numbers obtained when a number is multiplied by itself three times are known as cube numbers.
For example $1, 8, 27, ...$ etc.
$3 .$ If in the prime factorization of any number each factor appears three times, then the number is a perfect cube.
$4 .$ The symbol $3$ denotes cube root.
For example $\sqrt[3]{27} = 3 .$

Let's Revise

Baccho, iss chapter m humne cubes and cube roots k baare m seekha. Humne seekha ki cube and cube roots k kya meaning hote hai aur unhe calculate krne k different methods kya hote hai.

Cube vo number hota hai jo ki kisi number ko usse

2

times ultiply krne k baad aata hai jisse hume

3

numbers ka product milta hai. For example, cube of

3

3 \times 3 \times 3 = 9

There are different interesting patterns related with cube numbers. We can find cubes by adding consecutive odd numbers.
For example:

3 + 5 = 8 = 2^{3}

7 + 9 + 11 = 27 = 3^{3}

We can also find cubes by prime factorization method. Agar kisi number k prime factorization m har factor three times appear hota hai, then the number is a perfect cube.
Consider, the number

216

. By prime factorization,

216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^{3} \times 3^{3} = 6^{3}

Hence,

216

is a perfect cube.

Prime factorization k method ko use krke hum smallest number find kr skte hai jisko kisi aur number se multiply ya divide krne se hume perfect cube mil skta hai.

Cube root vo number hota hai jise khud se do baari multiply krne se hume ek cube milta hai. For example,

2^{3} = 8 = \sqrt[3]{2}

Cube roots ko calculate krne k lie bhi hum prime factorization ko use kr skte hai. If the prime factors of a cube number forms triplets of same numbers then its a perfect cube and its cube root can be found by multiplying the factors formed with triplets.
For example,

216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3

Since

2

and

3

forms triplets, therefore,

\sqrt[3]{216} = 2 \times 3 = 6

We also learnt we can estimate cube roots by finding the nearest cube to that number and by using out the unit digits of the cube

Lastly, humne different vedic techniques bhi seekhe jinki help se hum cubes and cube roots quickly calculate kr skte hai in easy steps.

Home
Ask Doubt
Profile