EXPONENTS AND POWERS for Class 8 MATHS

Baccho kya aap jaante hai ki Earth ka mass 5,970,000,000,000, 000, 000, 000, 000 kg hai!. Humne apni previous classes m pdha hua hai ki aise bdhe numbers ko kaise represent kre taaki vo better understandable ho using exponents like $5.97\times {10}^{24}kg$.
We read ${10}^{24}$ as $10$ raised to the power $24$.
We know , $25=2\times 2\times 2\times 2\times 2$
and $2^m=2\times 2\times 2\times 2\times ...\times 2\times 2...\left(\text{m times}\right)$
Baccho, iss chapter m hum negative exponents k baare m pdhenge. We will also learn about laws of exponents, use of exponents and comparison using exponents. So let's begin!

The exponent of a number shows how many times the number is multiplied by itself. For example, $2\times 2\times 2\times 2$ can be written as $2^4$, as $2$ is multiplied by itself $4$ times. Here, $2$ is called the "base" and $4$ is called the "exponent" or "power." In general, $x^n$ means that $x$ is multiplied by itself for $n$ times.

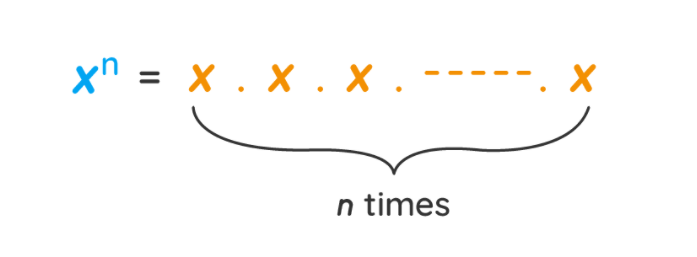
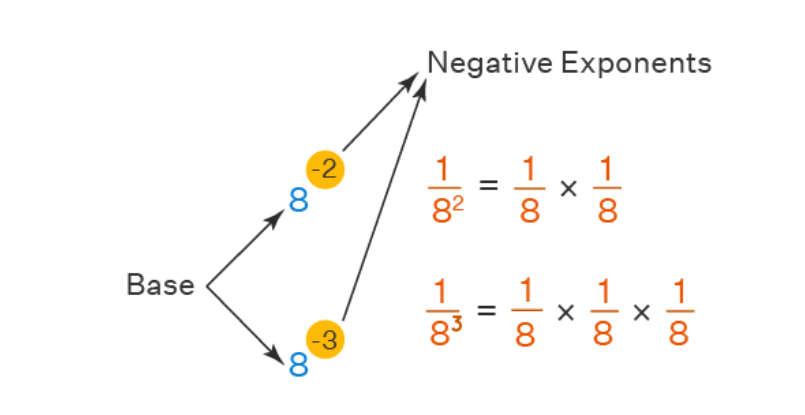
Negative exponents tell us that the power of a number is negative and it applies to the reciprocal of the number. We know that an exponent refers to the number of times a number is multiplied by itself. For example, $32=3\times 3$. In the case of positive exponents, we easily multiply the number (base) by itself, but what happens when we have negative numbers as exponents? A negative exponent is defined as the multiplicative inverse of the base, raised to the power which is opposite to the given power. In simple words, we write the reciprocal of the number and then solve it like positive exponents. Consider the $8^{-2}$, here, the base is $8$ and we have a negative exponent $(-2)$. $8^{-2}$ is expressed as $\frac{1}{8^2}=\frac{1}{8}\times \frac{1}{8}$.

Here are a few examples which express negative exponents with variables and numbers. Observe the table to see how the number is written in its reciprocal form and how the sign of the powers changes.

$\text{Negative Exponent Rules}$
We have a set of rules or laws for negative exponents which make the process of simplification easy. Given below are the basic rules for solving negative exponents.
Rule 1: The negative exponent rule states that for every number $\text{'}a\text{'}$ with the negative exponent $-n$, take the reciprocal of the base and multiply it according to the value of the exponent: $a^{-n}=\frac{1}{a^n}=\frac{1}{a}\times \frac{1}{a}\times ....n$ times
Rule 2: The rule for a negative exponent in the denominator suggests that for every number $\text{'}a\text{'}$ in the denominator and its negative exponent $-n$, the result can be written as $:\frac{1}{a^{-n}}=a^n=a\times a\times ....n$ times.

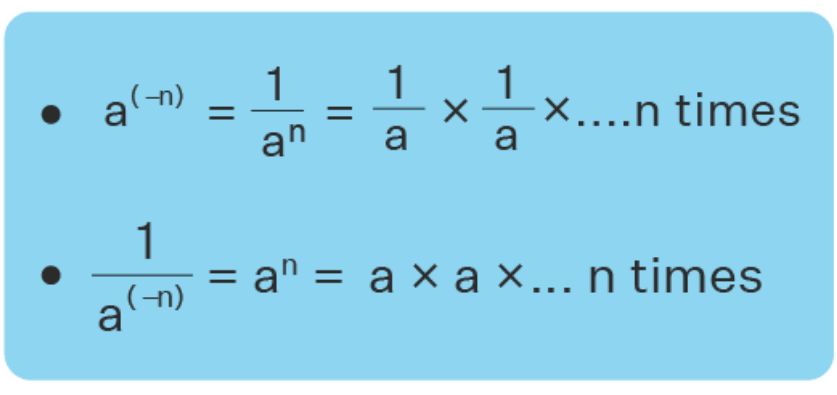
Let us apply these rules and see how they work with numbers.
Example :
Solve- $2^{-2}+3^{-2}$
Solution:
Use the negative exponent rule $a^{-n}=\frac{1}{a^n}$
$2^{-2}+3^{-2}=\frac{1}{2^2}+\frac{1}{3^2}=\frac{1}{4}+\frac{1}{9}$
Take the Least Common Multiple (LCM): $\frac{9+4}{36}=\frac{13}{36}$
Therefore, $2^{-2}+3^{-2}=\frac{13}{36}$
Example 2: Solve- $\frac{1}{4^{-2}}+\frac{1}{2^{-3}}$
Solution:
Use the second rule with a negative exponent in the denominator: $\frac{1}{a^{-n}}=a^n$
$\frac{1}{4^{-2}}+\frac{1}{2^{-3}}=4^2+2^3=16+8=24$
Therefore, $\frac{1}{4^{-2}}+\frac{1}{2^{-3}}=24$.

Express $4^{-3}$ as a power with the base $2$

${\left(4\right)}^{-3}$
$={(2\cdot 2)}^{-3}$
$={\left(2^2\right)}^{-3}$
$=2^{-6}$

The different 'rules and laws of exponents' are also known as the 'properties of exponents'. A few of them are listed as follows: the product rule of exponents, the quotient rule of exponents, the zero rule of exponents, and the negative rule of exponents. Let us learn each of these in detail now.
$1.$Product Law of Exponents
The product rule of exponents is used to multiply expressions with the same bases. This rule says, "To multiply two expressions with the same base, add the exponents while keeping the base the same."

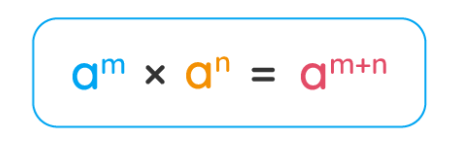
Observe the following example.

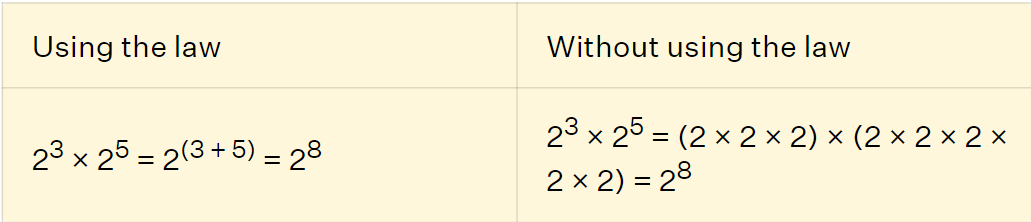
This shows that without using the law, the expression involves more calculation.
$2.$Quotient Law of Exponents
The quotient property of exponents is used to divide expressions with the same bases. This property says, "To divide two expressions with the same base, subtract the exponents while keeping the base same."

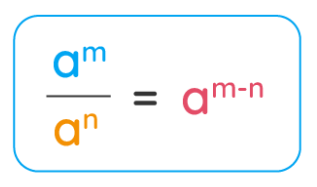
$3.$Zero Law of Exponents
The zero property of exponents is applied when the exponent of an expression is $0$. This property says, "Any number (other than $0$) raised to $0$ is $1$." Note that $0^0$ is not defined. The will help us understand that irrespective of the base the value for a zero exponent is always equal to $1$.

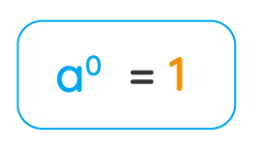
$4.$Negative Law of Exponents
The negative property of exponents is used when an exponent is a negative number. This property says, "To convert any negative exponent into positive exponent, the reciprocal should be taken." The expression is transferred from the numerator to the denominator with the change in sign of the exponent values.

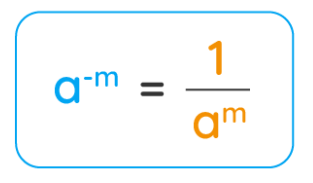
$5.$Power of a Power Law of Exponents
The 'power of a power property of exponents' is used to simplify expressions of the form ${\left(a^m\right)}^n$. This property says, "When we have a single base with two exponents, just multiply the exponents." The two exponents are available one over the other. These can be conveniently multiplied to make a single exponent.

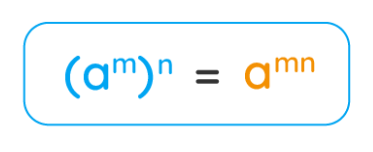
$6.$Power of Product Rule of Exponents
The 'power of a product property of exponents' is used to find the result of a product that is raised to an exponent. This property says, "Distribute the exponent to each multiplicand of the product."

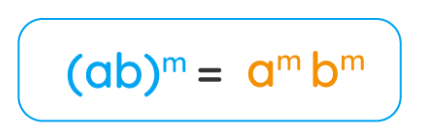
$7.$Power of a Quotient Rule of Exponents
The power of a quotient property of exponents is used to find the result of a quotient that is raised to an exponent. This property says, "Distribute the exponent to both the numerator and the denominator." Here, the bases are different and the exponents are the same for both the bases.

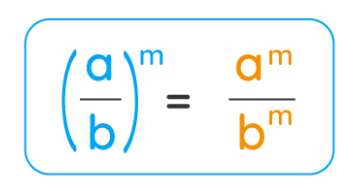
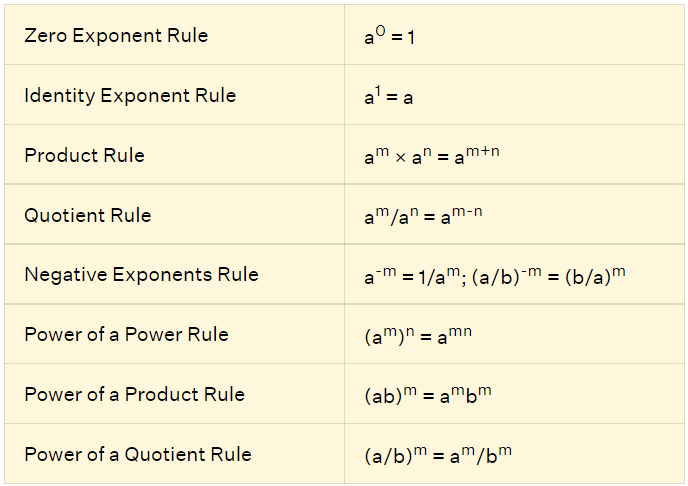
$\text{Exponent Rules Chart}$
The rules of exponents explained above can be summarized in a chart as shown below.

Baccho, inn laws ko smjhne k lie hum ab kuch examples dekhenge:

Simplify and express the result in power notation with positive exponent. (i) ${(-4)}^5÷{(-4)}^8$ (ii) ${\left(\frac{1}{2^3}\right)}^2$ (iii) ${(-3)}^4\times {\left(\frac{5}{3}\right)}^4$ (iv) $(3^{-7}÷3^{-10})\times 3^{-5}$ (v) $2^{-3}\times {(-7)}^{-3}$

(i) $(-4)÷{(-4)}^8$
${(-4)}^{5-8}$
${(-4)}^{-3}$
$=\frac{1}{{-4}^3}$
(ii) ${\left(\frac{1}{2^3}\right)}^2$
$={\left(2^{-3}\right)}^2=2^{-6}$
$=\frac{1}{2^6}$
(iii) ${(-3)}^4\times {\left(\frac{5}{3}\right)}^4$
$={(-1)}^4\cdot {\left(3\right)}^{4-4}\cdot 5^4$
$=5^4$
(iv) $(3^{-7}÷3^{-10})\times 3^{-5}$
$=3^{-7+10}\times 3^{-5}$
$=3^3\times 3^{-5}$
$=3^{-5+3}=3^{-2}$
$=\frac{1}{3^2}$
(v) $2^{-3}\times {(-7)}^{-3}$
${(2\times -7)}^{-3}=-{14}^{-3}$
$\frac{1}{{14}^3}$

Simplify and write the answer in the exponential form. (i) ${(2^5÷2^8)}^5\times 2^{-5}$ (ii) ${(-4)}^{-3}\times {\left(5\right)}^{-3}\times {(-5)}^{-3}$ (iii) $\frac{1}{8}\times {\left(3\right)}^{-3}$ (iv) $(-3)64\times {\left(\frac{5}{3}\right)}^4$

(i) ${\left(2^{5-8}\right)}^5\times 2^{-5}$
${\left(2^{-3}\right)}^5\times 2^{-5}$
$2^{-15}\times 2^{-5}$
$2^{-15-5}=2^{-20}$
(ii) ${(-4)}^{-3}\times {\left(5\right)}^{-3}\times {(-5)}^{-3}$
${(-4\times 5\times -5)}^{-3}$
$={\left(100\right)}^{-3}$
(iii) $\frac{1}{8}\times {\left(3\right)}^{-3}$
$=\frac{1}{2^3}\times {\left(3\right)}^{-3}$
= $2^{-3}\times 3^{-3}$
$={(2\times 3)}^{-3}$
$=6^{-3}$
(iv) ${(-3)}^4\times {\left(\frac{5}{3}\right)}^4$
${(-3\times \frac{5}{3})}^4$
$={(-5)}^4$

Baccho ab hum seekhenge ki hum exponents ko use krke kaise complex numbers ko standard form express kr skte hai.
Observe the following facts.
$1.$ The distance from the Earth to the Sun is $149,600,000,000m$.
$2.$ The speed of light is $300,000,000\text{m/sec}$.
$3.$ Thickness of Class VII Mathematics book is 20 mm.
$4.$ The average diameter of a Red Blood Cell is $0.000007mm$.
$5.$ The thickness of human hair is in the range of $0.005cm$ to $0.01cm$.
$6.$ The distance of moon from the Earth is $384,467,000m$ (approx).
$7.$ The size of a plant cell is $0.00001275m$.
$8.$ Average radius of the Sun is $695000km$.
$9.$ Mass of propellant in a space shuttle solid rocket booster is $503600kg$.
$10.$ Thickness of a piece of paper is $0.0016cm$.
$11.$ Diameter of a wire on a computer chip is $0.000003m$.
$12.$ The height of Mount Everest is $8848m$.
Observe that there are few numbers which we can read like $2cm,8848m,6,95,000km$. There are some large numbers like $150,000,000,000m$ and some very small numbers like $0.000007m$.
Let's understand the steps for writing numbers in standard form:
Step 1: Put a decimal point after the first digit of the number from the right. If there is only one digit in a number excluding zeros, then we don't need to put decimal.
Step 2: Multiply that number with a power of $10$ such that the power will be equal to the number of times we shift the decimal point.
By following these two simple steps we can write any number in standard form with exponents, for example, $560000=5.6\times {10}^5,0.00736567=7.36567\times {10}^{-3}.$
Another Example-
$2.5$ million is written as $2500000$
$25\times 100000$
Let's write $100000$ in powers of $10$
$25\times {10}^5$
or, $2.5\times 10\times {10}^5$
or, $2.5\times {10}^6$
$\therefore 25$ million can be written as $2.5\times {10}^6$

Express the following numbers in standard form.
$\left(i\right)0.0000000000085$
$\left(ii\right)0.00000000000942$
$\left(iii\right)6020000000000000$
$\left(iv\right)0.00000000837$
$\left(v\right)31860000000$

(i) $8.5\times {10}^{-2}$
(ii) $9.42\times {10}^{-2}$
(iii) $6.02\times {10}^{15}$
(iv) $6.37\times {10}^{-9}$
(v) $3.186\times {10}^{10}$

Baccho, suppose ki aapko compare krna hai ki Earth aur Sun m se kiska diamete zyada hai. The diameter of the Sun is $1.4\times {10}^9$ $m$ and the diameter of the Earth is $1.2756\times {10}^7$ $m$.
Aise case m you have to make sure that their exponents are the same. Let's make their exponents same:
Diameter of the Sun $=1.4\times {10}^{9}m$
$=14\times {10}^{8}m$
$=140\times {10}^{7}m$
Clearly, $140\times {10}^{7}m>1.2756\times {10}^{7}m$
Therefore, diameter of the Sun is greater than the diameter of the Earth.
When we have to add numbers in standard form, we convert them into numbers with the same exponents.Let's understand this with an example.
Mass of earth is 5.97 × 1024 kg and mass of moon is $7.35\times 1022kg$. What is the total mass?
Total mass $=5.97\times {10}^{24}kg+7.35\times {10}^{22}kg.$
$=5.97\times 100\times 1022+7.35\times 1022=597\times {10}^{22}+7.35\times {10}^{22}$
$=(597+7.35)\times {10}^{22}$
$=604.35\times {10}^{22}kg.$

$1.$ Numbers with negative exponents obey the following laws of exponents.
$\left(a\right)a^m\times a^n=a^{m+n}$
$\left(b\right)a^m÷a^n=a^{m–n}$
$\left(c\right){\left(a^m\right)}^n=a^{mn}$
$\left(d\right)a^m\times b^m={\left(ab\right)}^m$
$\left(e\right)a^0=1$
$\left(f\right)\frac{a^m}{b^m}={\left(\frac{a}{b}\right)}^m$
$2.$ Very small numbers can be expressed in standard form using negative exponents.

$1.$ Baccho iss chapter m humne pdha ki exponents m negative integers ko kaise use kia jaata hai.
$2.$ We learnt about various laws of exponents and powers and also saw various examples about using them.
$3.$ Hum laws of exponents ko use krke complex aur large numbers ko standard form m express kr skte hai.
$4.$ Lastly, humne seekha ki exponents ko compare ya add krne k lie hume phle unhe same exponential form m laana hota hai. Once they are in the same exponents, we can simply see which number is greater to compare.