VISUALISING SOLID SHAPES for Class 8 MATHS
INTRODUCTION
Baccho, aapne apne previous classes m solid shapes k baare m pdha hai aur seekha hai ki hum unhe visualize kaise kr skte hai. Plane shapes ya 2D shapes majorly 2 measurements m hote hai which are: length and breadth whereas, solid shapes ki teen measurements hote hai length, breadth and height or depth, hence they are called 3D shapes. These 3D shapes also occupy some spcae in their environment, which implies they have volume unlike like 2D shapes which only have area and no volume. Iss chapter m hum mapping k baare m pdhenge aur alag alag solids k faces, edges and vertices k baare m pdhenge. So let's begin!
Views of 3D-Shapes
Baccho, sabse phle hum 2D and 3D shapes se related apni understandng ko revise krenge.
A 2D shape is a flat shape that has only two dimensions – length and width, with no thickness or depth, that is the reason why it is called a two-dimensional shape. For example, a sheet of paper is two-dimensional in shape. It consists of a length and a width but does not have any depth or height. Some common 2D shapes are squares, rectangles, triangles, circles, and hexagons. In comparison to these, a 3D (three-dimensional) shape has three dimensions – length, width, and height. For example, a dice is three-dimensional because it consists of a length, a width, and a height. Some common 3D shapes are cuboids, cones, pyramids, and cylinders. The figures given below shows the 2D and 3D shapes that we commonly come across.


Baccho, humne pdha hua hai ki 3D shapes alag alag views se alag dikhte hai. There are 3 major views known as : Front, Top and Side view. Let's understand the different views of a shape.
Views of Solid Shapes
All solid shapes have a top view, a side view and a front view. Let us check out each one of them.
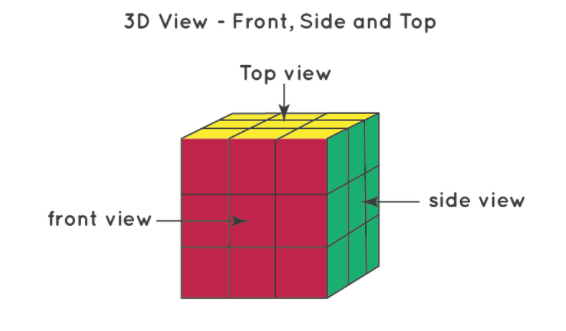
Top View: The top view of a solid shape is the shape of an object when we see it from the top.
Side View: The side view of a solid shape is the shape of an object when it is seen from one of its sides.
Front View: The front view of an object is the shape of an object when it is seen from the front side of the object.
Observe the cube given below which shows its top, side and front view.
Mapping Space Around Us
A map is different from a picture. A map depicts the location of a particular object/place in relation to other objects/places. Symbols are used to depict different objects/places. There is no reference or perspective on a map. However, perspective is very important for drawing a picture. Moreover, maps involve a scale which is fixed for a particular map. A map shows the location of a particular thing with respect to others.
Some important points related to map:

This is the map which shows the different routes from Nehru road.
Faces, Edges and Vertices
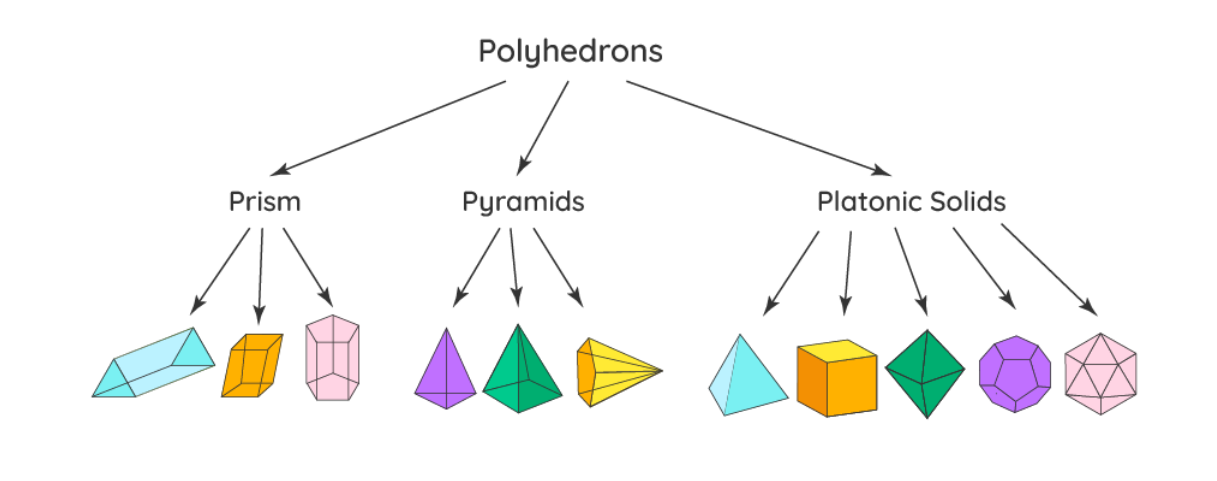
A polyhedron is a 3D shape that has flat faces, straight edges, and sharp vertices (corners). The word "polyhedron" is derived from a Greek word, where 'poly' means "many" and hedron means "surface".Thus, when many flat surfaces are joined together they form a polyhedron. These shapes have names according to their faces that are usually polygons. The most common names are cubes, hexahedrons, etc. Observe the following figure which shows the different kinds of polyhedrons.
All solid shapes are defined by a certain number of faces, vertices and edges. Let us understand each of these terms.
Faces:
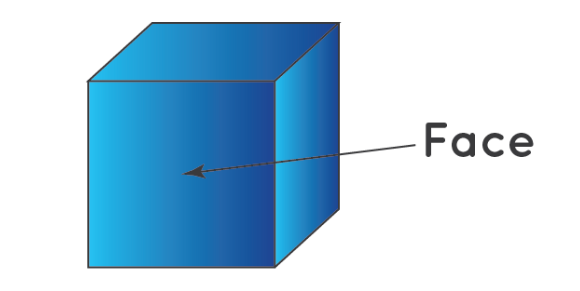
Every single surface of a solid shape is called a face. For example, a cube has 6 faces. Observe the figure shown below that shows a face of a cuboid.
Vertices:
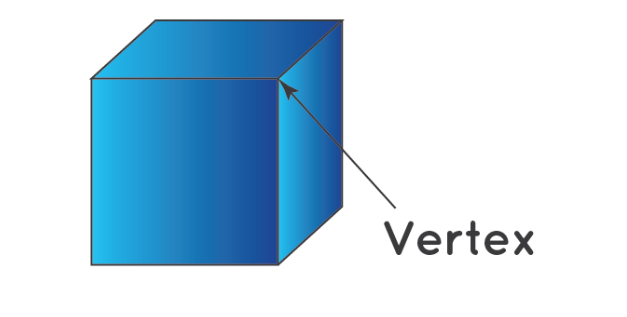
In a solid shape, a 'Vertex' is defined as a point where two or more lines meet. Vertices is the plural form of the word 'Vertex'. A sphere is an exceptional shape which does not have a vertex. Observe the following figure which shows the vertex of a cube
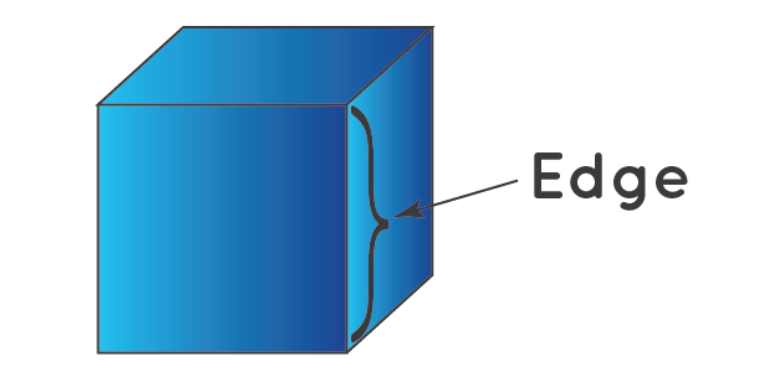
Edges:
In a solid shape, an 'Edge' is defined as a line segment joining two vertices or two corners. The following figure shows the edge of a cube.
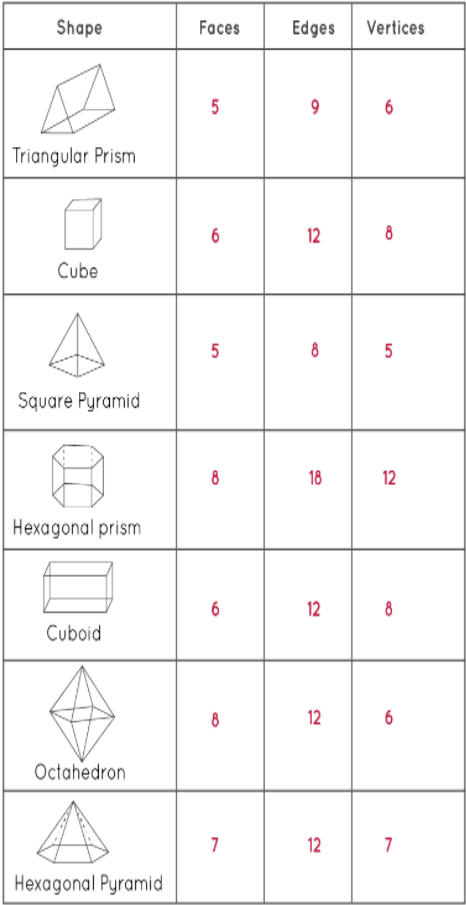
The table shown below lists some three-dimensional shapes with the details of their faces, edges and vertices.
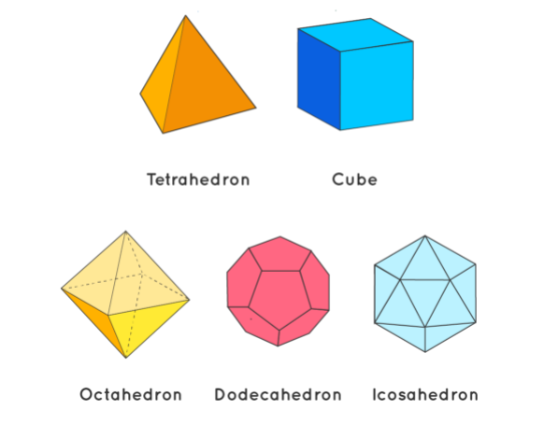
Types of Polyhedron
Polyhedra are mainly divided into two types – regular polyhedron and irregular polyhedron.
Regular Polyhedron:
A regular polyhedron is also called a platonic solid whose faces are regular polygons and are congruent to each other. In a regular polyhedron, all the polyhedral angles are equal. There are five regular polyhedrons. The following is the list of five regular polyhedrons.
Regular Dodecahedron: A regular dodecahedron has 12 faces, 30 edges, 20 vertices; and the shape of each face is a regular pentagon.
Observe the following figure which shows the various types of regular polyhedrons.
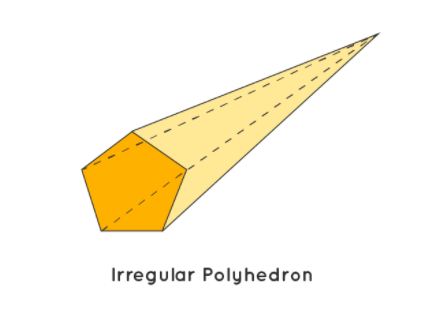
Irregular Polyhedron
A polyhedron with irregular polygonal faces that are not congruent to each other, and in which the polyhedral angles are not equal is called an irregular polyhedron.
Convex Polyhedron
A convex polyhedron is just like a convex polygon. If a line segment joining any two points on the surface of a polyhedron entirely lies inside the polyhedron, it is called a convex polyhedron.

EULER'S FORMULA
Baccho, ab hum pdhenge euler's formula k baare m. According to Euler’s formula, in any polyhedron, F+V−E=2, where ‘F’ stands for the number of faces, ‘V’ stands for the number of vertices and ‘E’ stands for the number of edges. We verify Euler's formula to study any three-dimensional space and not just polyhedra.
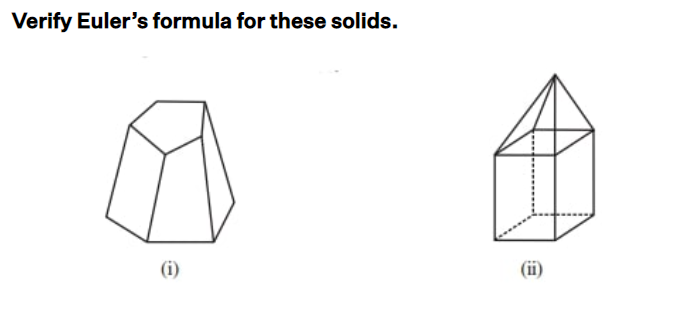
SOLUTION:
(i) In the figure we can see that top and bottom faces are pentagons.
Number of faces, F=7
Number of edges, E=15
Number of vertices, V=10
Let’s verify Euler’s formula,
F+V−E=7+10−15
=17−15=2
Thus, Euler's formula is verified.
(ii) In the figure we can see that its top is a square pyramid and the bottom is a square prism.
Number of faces, F=9
Number of edges, E=16
Number of vertices, V=9
Let’s verify Euler’s formula,
F+V−E=9+9−16
=18−16=2
Thus, Euler's formula is verified.
Example 1
Can a polyhedron have for its faces
(i)3 triangles
(ii)4triangles
(iii)a square and four triangles?
1) no, minimum 4 faces
2) Yes
3) Yes.
Example 2
Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
It is possible if number of face is greater than 3.
Example 3
(i)How are prisms and cylinders alike?
(ii)How are pyramids and cones alike?
1)prism with circular base is cylinder
2)Pyramids with circular base is cone.
Example 4
Can a polyhedron have 10 faces, 20 edges and 15 vertices? Check using Euler's formula.
Euler's formula
faces+vertices-edges should equal to 2
F+V-E=10+2-15=5
this polyhedral not satisfy Euler's formula.
SUMMARY
1. Recognising 2D and 3D objects.
2. Recognising different shapes in nested objects.
3.3D objects have different views from different positions.
4. A map is different from a picture.
5. A map depicts the location of a particular object/place in relation to other objects/places.
6. Symbols are used to depict the different objects/places.
7. There is no reference or perspective in a map.
8. Maps involve a scale which is fixed for a particular map.
9. For any polyhedron,
F+V–E=2
where ‘F’ stands for number of faces, V stands for number of vertices and E stands for number of edges. This relationship is called Euler’s formula.
Let's Revise
1. Baccho iss chapter m humne solid shapes k baare m pdha aur apni previous knowledge k uppr build kia.
2. Humne 2D and 3D shapes k baare m recapitulate kia aur jaana ki inme major differences kya hote hai.
3. Baccho, humne maps k baare m pdha aur seekha ki kaise ek map kisi ek particular location ko depict krti hai. A map has no refernce or perspective.
4. Humne polyhedra k baare m pdha aur unke major teen views k baare m jaana , which are, top, side and front view. These three views give us the maximum information about the form of a solid shape.
5. Lastly, humne Euler's formula k baare m pdha aur dekha ki kaise euler's formula ko use krke hum solid shapes k faces, vertices and edges verify kr skte hai.