निर्देशांक ज्यामिति कक्षा 9 गणित
MOTIVATION
हैलो बच्चों!
स्वागत है आप सभी का कक्षा -9 वीं के तीसरे अध्याय निर्देशांक ज्यामिति में।
मैं आशा करता हूँ कि इन notes को पढ़कर आपको मजा आएगा और साथ ही साथ आपके सभी Concept भी clear हो जायेंगे।
इन notes में उन सभी concept को आसान भाषा में समझाया गया है जिनका प्रयोग आपको परीक्षा में प्रश्नों को हल करने में करना होगा
साथ ही साथ इस अध्याय के concepts का प्रयोग आपको class-10 में भी करना होगा , इसलिए सभी बिंदुओं को आप बहुत ध्यान से पढ़ें और उनसे संबंधित प्रश्नों को हल करे।
भूमिका
दोस्तों यदि आप शब्द निर्देशांक पर ध्यान दे तो ये दो शब्दों निर्देश + अंक से मिलकर बना है अर्थात हम ऐसे अंको के विषय में जानेंगे जो किसी बिंदु की किसी समतल में स्थिति व् दिशा का निर्धारण करता हो।
चलिए एक उदाहरण से समझते हैं :
मान लो कोई अध्यापक किसी कक्षा में पढ़ा रहे हैं, अगर उन्हें किसी एक विद्यार्थी से कोई प्रश्न पूछना हो तो वह कितने विभिन्न प्रकारों से यह पूछ सकते हैं इसे हम समझते हैं:
(i) अपनी उंगली को उस छात्र की और निर्देशित कर जहां वह बैठा है
(ii)उस छात्र या छात्रा की सीट के पास जाकर
(iii) या फिर वह इस प्रकार से कहें कि तृतीय पंक्ति तथा पांचवें स्तंभ में जो छात्र बैठा है वह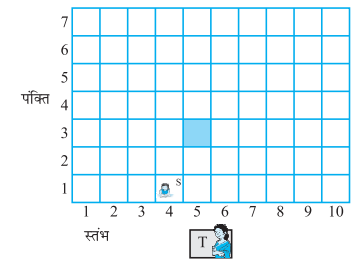
वैसे जो पहली विधि सामान्यतः प्रयोग होती है लेकिन यदि वह तीसरी विधि का प्रयोग करता है तो वह अप्रत्यक्ष रूप से निर्देशांक ज्यामितीय का पालन करेगा
किसी बिंदु को समतल में प्रदर्शित करने की व्याख्या सर्वप्रथम फ्रांसीसी गणितज्ञ रेने दकार्ते ने की थी।
निर्देशांक ज्यामिति बीजगणित को ज्यामितीय से जोड़ने की एक कड़ी है।
व्यावहारिक जीवन में निर्देशांक ज्यामिति के अनुप्रयोग
वास्तव में निर्देशांक ज्यामितीय किसी वस्तु या बिंदु की अक्षों के सापेक्ष स्थिति को दर्शाता है।
यदि व्यावहारिक जीवन में निर्देशांक ज्यामिति के प्रयोग को देखें तो वर्तमान में हम यदि किसी नए स्थान पर होते हैं और हमें वहां से किसी अन्य स्थान पर जाना होता है तो हम तुरंत अपने SMART PHONE में GOOGLE MAP खोलते हैं (आकृति देखिए ) :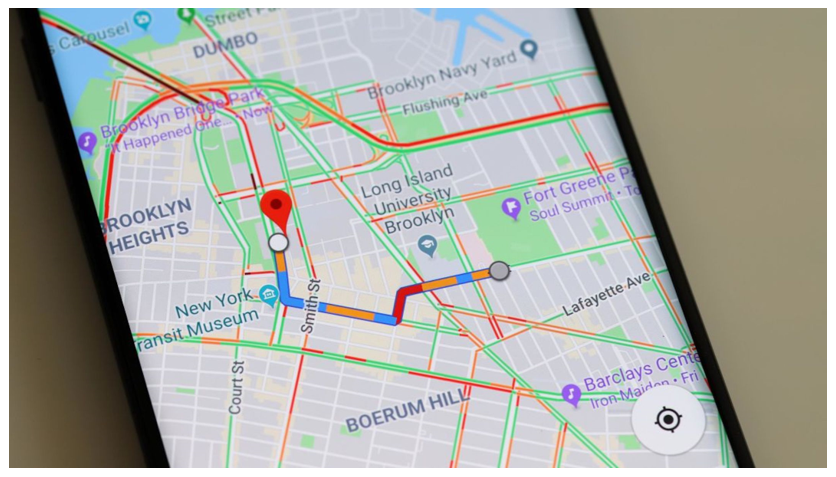
और देखते हैं कि वह स्थान आप की वर्तमान स्थिति से कितना दूर है या फिर वहां तक पहुंचने का सबसे सुलभ और छोटा मार्ग कौन सा है और यह सब हम चुटकियों में देख लेते हैं इस तकनीक में मुख्य रूप से प्रयोग होने वाले सिद्धांतों में एक निर्देशांक ज्यामिति भी है।
इसी प्रकार वायुयान के मार्ग तथा स्थिति के निर्धारण में भी निर्देशांक ज्यामिति का प्रयोग होता है।
इस प्रकार हम कह सकते हैं कि निर्देशांक ज्यामिति के हमारे व्यवहारिक जीवन में और विज्ञान तकनीकी में विस्तृत अनुप्रयोग है।
उदाहरण 1 :
(सड़क योजना) : एक नगर में दो मुख्य सड़कें हैं, जो नगर के केन्द्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व-पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समांतर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पाँच सड़कें हैं।
1 सेंटीमीटर = 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।
आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम की दिशा में। प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता है: यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पाँचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2, 5) कहेंगे। इसी परंपरा से यह ज्ञात कीजिए कि
(i) कितनी क्रॉस-स्ट्रीटों को (4, 3) माना जा सकता है।
(ii) कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
जब हम स्वयं से एक पेपर पर सड़क मानचित्र बनाएंगे तो कुछ इस प्रकार की योजना प्राप्त होगी :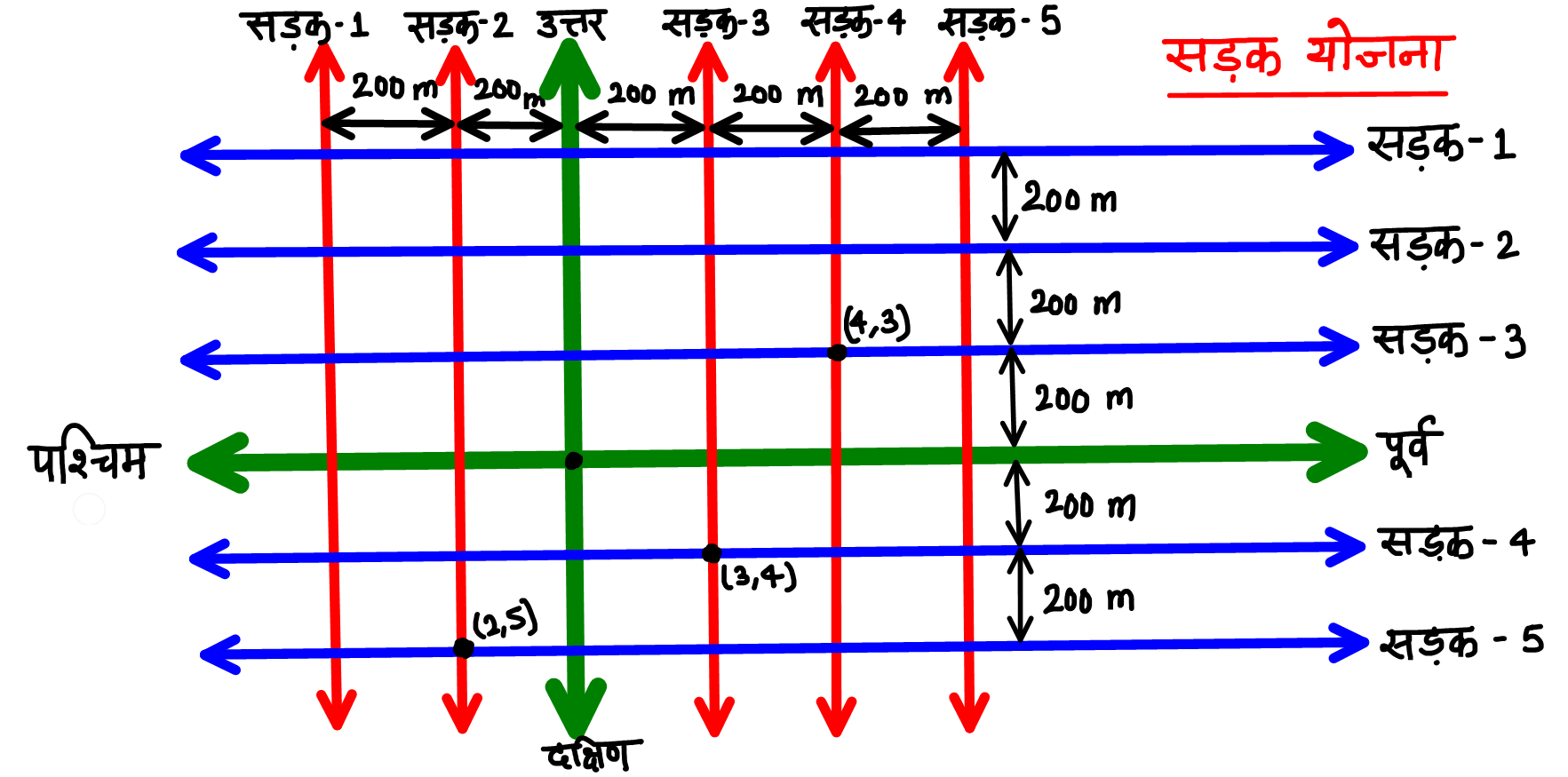
जैसा की हम उपर्युक्त सड़क योजना में देख सकते हैं केवल एक ही ऐसा बिन्दु है जो (4,3) को दर्शाता है और इसी प्रकार केवल एक ही बिन्दु है जो (3,4) की स्थिति को दिखा रहा है |
अतः हम कह सकते हैं कि :
(i) केवल 1 क्रॉस-स्ट्रीटों को (4,3) माना जा सकता है।
(ii) केवल 1 क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
निर्देशांक ज्यामिति से सम्बन्धित शब्दावली
∗ कार्तीय पद्धति : महान गणितज्ञ रेने दकार्ते ने किसी बिन्दु की स्थिति का पता लगाने की समस्या का हल निकाला जैसा कि आप आगे अध्याय में देखेंगे की उनकी विधि अक्षांश और देशान्तर की पुरानी विचारधारा की ही एक विकसित रूप थी | तल में स्थित किसी बिन्दु की स्थिति का निर्धारण करने में प्रयुक्त पद्धति को दकार्ते के सम्मान में कार्तीय पद्धति ( Cartesian System) कहा जाता है |
∗ मूल बिंदु (Origin) :बच्चों " संख्या पद्धति " के अध्याय में हम संख्या रेखा के बारे में पढ़ चुके हैं | संख्या रेखा पर एक नियत बिंदु से बराबर इकाई की दूरियों में बायीं और तथा दायीं ओर क्रमशः धनात्मक तथा ऋणात्मक दिशा में अंकित किया जाता है | यह नियत बिंदु ही मूल बिंदु कहलाता है क्योंकि यहीं से शुरुआत होती है | 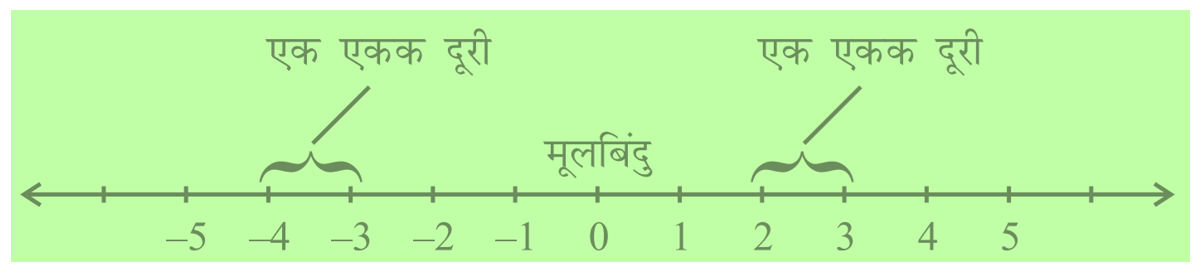
∗ एक एकक दूरी (One unit distance) : प्यारे बच्चों हम संख्याओं को संख्या रेखा पर दर्शाने के लिए , दो संख्याओं के बीच में जो दूरी लेते हैं उस नियत दूरी को एक एकक दूरी कहते हैं | ( उपर्युक्त आकृति देखिए )
∗ निर्देशांक अक्ष (Co-ordinate Axis) :किसी बिंदु का स्थान निर्धारण करना हो तो हमें दो संख्या रेखा की आवश्यकता होती है जो उस तल को दो लंबवत अक्षों में विभाजित करते हैं |
∗ वास्तविक संख्या रेखा :
∗ क्षैतिज संख्या रेखा या X− अक्ष : जो संख्या रेखा क्षैतिज रूप से आधार यानि जमीन के सहारे लेटी हुई होती है उसे X− अक्ष कहते हैं |(आकृति देखिए) :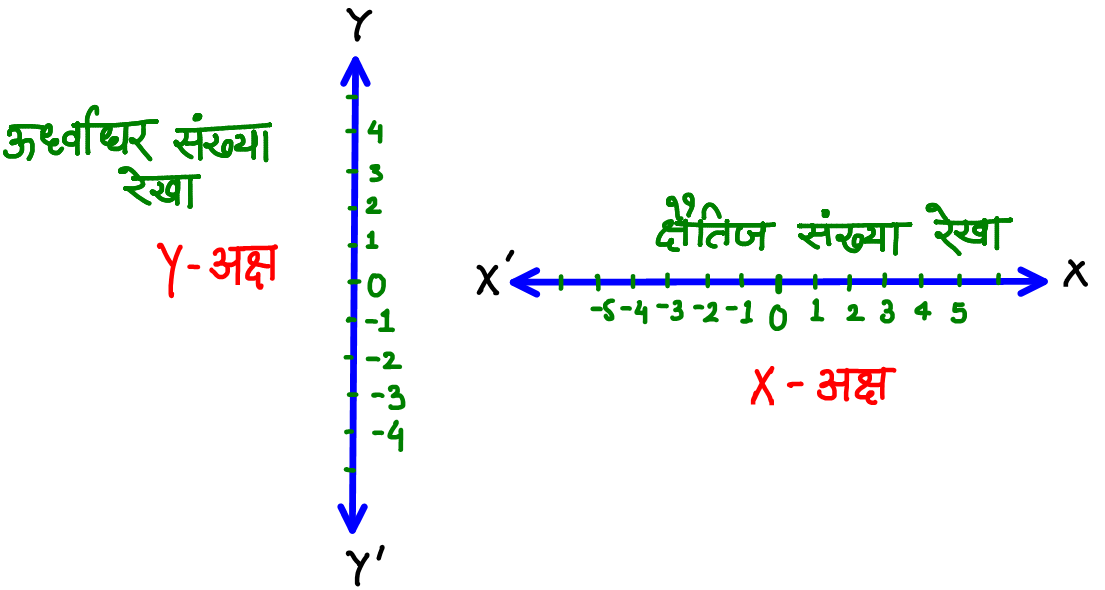
∗ ऊर्ध्वाधर संख्या रेखा या Y− अक्ष : जो संख्या रेखा बिल्कुल सीधी खड़ी होती है ठीक 90∘ के कोण पर उसे हम ऊर्ध्वाधर रेखा या Y− अक्ष कहते है।(उपर्युक्त आकृति देखिए)
X− अक्ष ,Y− अक्ष तथा मूलबिंदु सामूहिक रूप से निर्देश तंत्र कहलाते है।
∗ निर्देशांक तल या कार्तीय तल (Cartesian Plane) :वह समतल जिसमे X− अक्ष तथा Y− अक्ष स्थित होते है ,कार्तीय तल कहलाता है। (आकृति देखिए )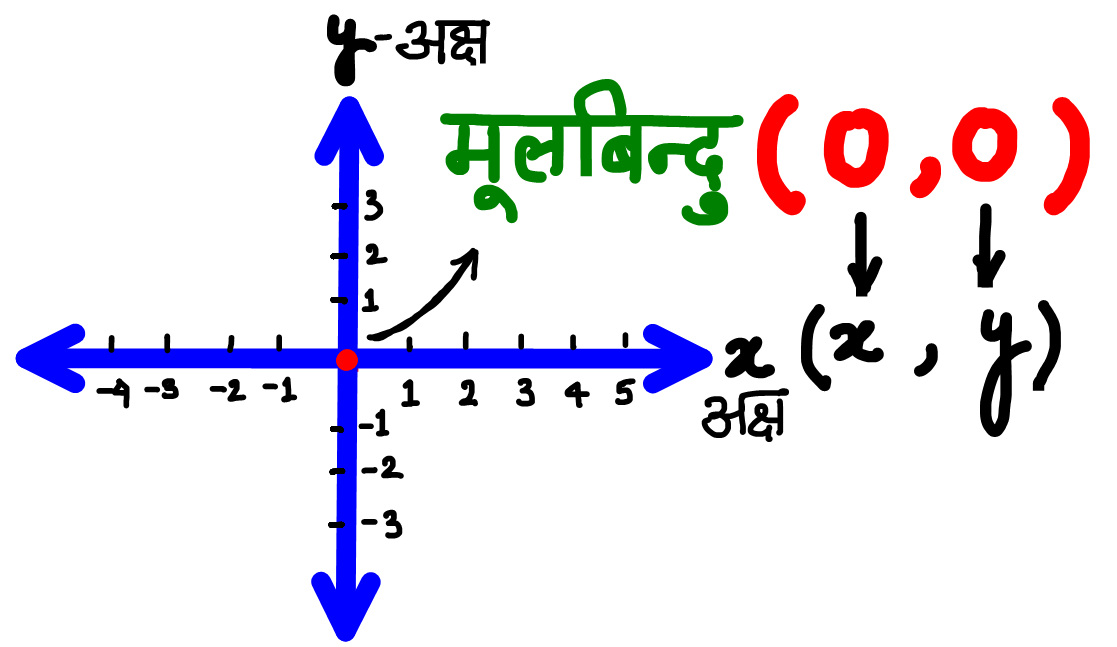
∗ चतुर्थांश (Quadrants) : दोनों अक्ष क्रमशः अक्ष XOX' तथा YOY' और मूलबिंदु Oतीनों मिलकर समतल को चार बराबर भागों में विभाजित करते है जिन्हे चतुर्थांश कहते है। अक्ष OX तथा OY से घिरा भाग प्रथम चतुर्थांश ,OX'तथा OYसे घिरा भाग द्वितीय चतुर्थांश ,OX'तथा OY'से घिरा भाग तृतीय चतुर्थांश और OX तथा OY' से घिरा भाग चतुर्थ चतुर्थांश कहलाता है।(उपर्युक्त आकृति देखिए )
किसी बिन्दु की अक्षों से दूरी
मान लीजिए आपको कार्तीय तल में कुछ बिंदु दिए जाते हैं तथा उनकी अक्षों से दूरियाँ ज्ञात करनी है
प्यारे बच्चों एक प्रश्न की सहायता से समझने की कोशिश करते हैंनिम्न आलेख में अक्षों से बिन्दु P और Q की दूरियाँ ज्ञात करें :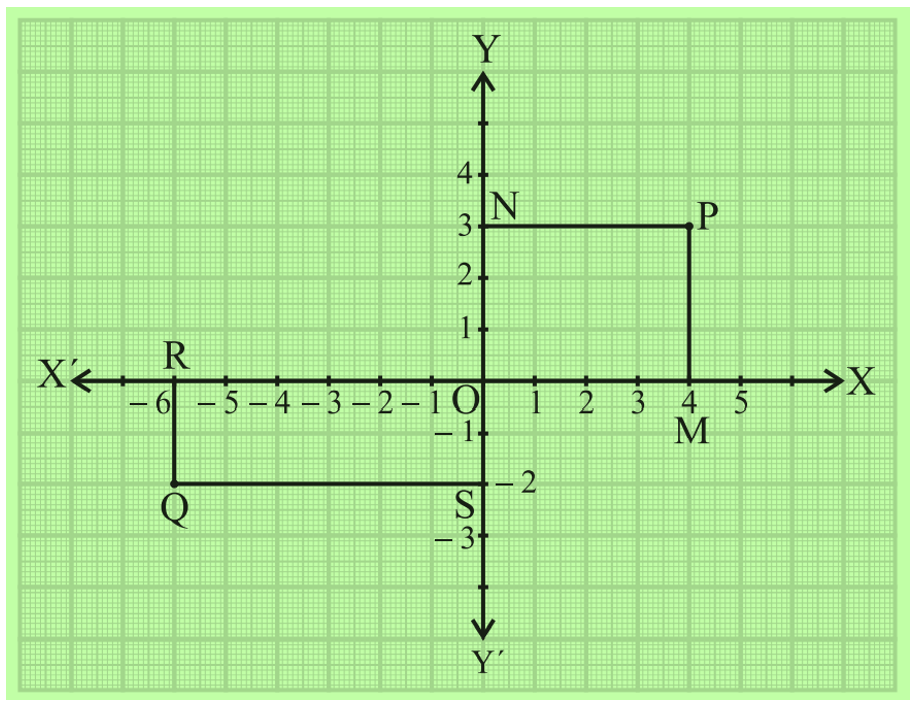
हल : इसके लिए हम बिन्दु P से x अक्ष तथा y अक्ष पर लंब क्रमशः PM तथा PN डाला | इसी प्रकार लंब QR तथा QS डाला |
(i) y-अक्ष से बिन्दु P की लांबिक दूरी, जिसे x-अक्ष की धनात्मक दिशा में मापा गया है, PN = OM = 4 एकक है।
(ii) x-अक्ष से बिन्दु P की लांबिक दूरी, जिसे y-अक्ष की धनात्मक दिशा में मापा गया है, PM = ON = 3 एकक है।
(iii) y-अक्ष से बिन्दु Q की लांबिक दूरी, जिसे x-अक्ष की ऋणात्मक दिशा में मापा गया है, OR = SQ = 6 एकक है।
(iv) x-अक्ष से बिन्दु Q की लांबिक दूरी, जिसे y-अक्ष की ऋणात्मक दिशा में मापा गया है, OS = RQ = 2 एकक है।
उदाहरण 2 :
नीचे दी गई आकृति को देखकर निम्नलिखित कथनों को पूरा कीजिए: 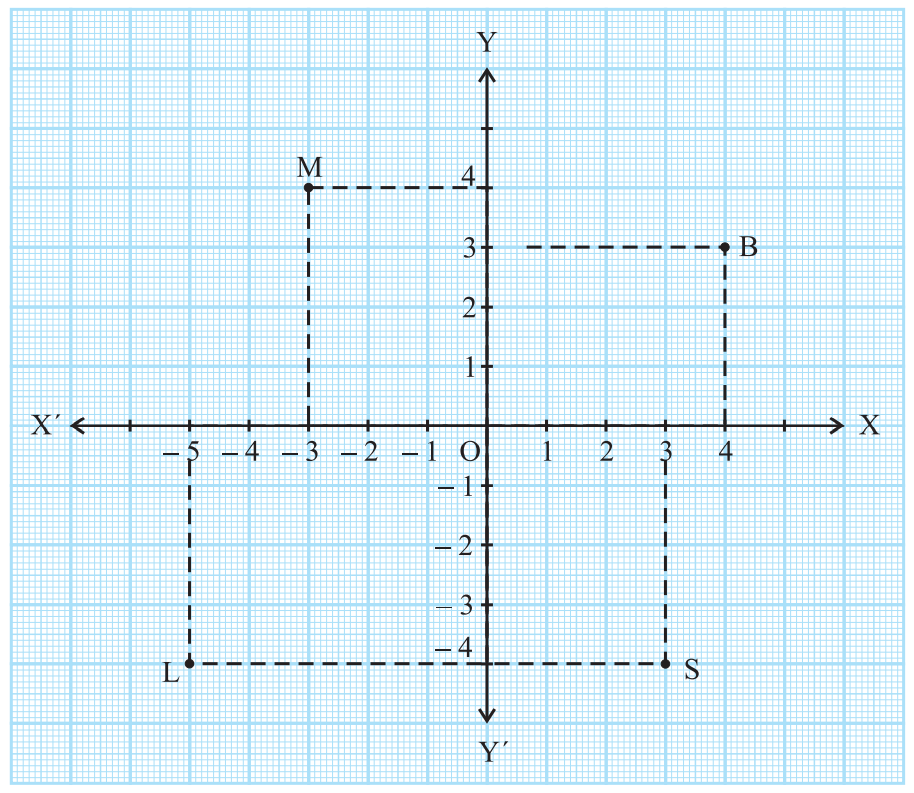
(i) बिन्दु B का भुज और कोटि क्रमशः ____ और____ हैं। अत: B के निर्देशांक (___, _ _ _) हैं।
(ii) बिन्दु M के -निर्देशांक और y-निर्देशांक क्रमशः ___और___ हैं। अत: M के निर्देशांक (_ _, _ _) हैं।
(iii) बिन्दु L के x-निर्देशांक और y-निर्देशांक क्रमशः _ _ _ और _ _ _ हैं। अतः L के निर्देशांक (_ _, _ _) हैं।
(iv) बिन्दु S के x-निर्देशांक और y-निर्देशांक क्रमशः _ _ _ और ___ हैं। अत: S के निर्देशांक (_ _, _ _) हैं।
(i) क्योंकि y-अक्ष से बिन्दु B की दूरी 4 एकक है, इसलिए बिन्दु B का x-निर्देशांक या भुज 4 होगा।
x-अक्ष से बिन्दु B की दूरी 3 एकक है, इसलिए बिन्दु B का y-निर्देशांक अर्थात् कोटि 3 होगी।
अतः बिन्दु B के निर्देशांक (4, 3) हैं।
ऊपर (i) की भांतिः (ii) बिन्दु M के x-निर्देशांक और y-निर्देशांक क्रमशः-3 और 4 हैं।
अतः बिन्दु M के निर्देशांक (-3, 4) हैं।
(iii) बिन्दु L के x-निर्देशांक और y- निर्देशांक क्रमशः -5 और – 4 हैं।
अतः बिन्दु L के निर्देशांक (-5, - 4) हैं।
(iv) बिन्दु S के x-निर्देशांक और y- निर्देशांक क्रमशः 3 और – 4 है।
अतः बिन्दु S के निर्देशांक (3, – 4) हैं।
उदाहरण 3 :
निम्नलिखित प्रश्नों में से प्रत्येक प्रश्न का उत्तर दीजिए
(i) कार्तीय तल में किसी बिन्दु की स्थिति निर्धारित करने वाली क्षैतिज और ऊर्ध्वाधर रेखाओं के क्या नाम हैं?
(ii) इन दो रेखाओं से बने तल के प्रत्येक भाग के नाम बताइए।
(iii) उस बिन्दु का नाम बताइए जहाँ ये दो रेखाएँ प्रतिच्छेदित होती हैं।:
(i) x अक्ष और y अक्ष
(ii) चतुर्थांश
(iii) मूलबिंदु
OMR (One Minute Revision)
∗ मूलबिंदु (Origin) : कार्तीय तल में जिस बिंदु पर X− अक्ष तथा Y− अक्ष एक दूसरे को प्रतिच्छेद करते है उसे मूलबिंदु कहते है।
मूलबिंदु के निर्देशांक (0,0) होते हैं |
किसी बिन्दु के निर्देशांक
निर्देशांक अक्षों का एक युग्म हमें एक तल पर किसी बिन्दु की स्थिति निर्धारित करने के योग्य बनाता है।
किसी बिन्दु की y–अक्ष से दूरी उस बिन्दु का x–निर्देशांक (x–coordinate) कहलाता है। 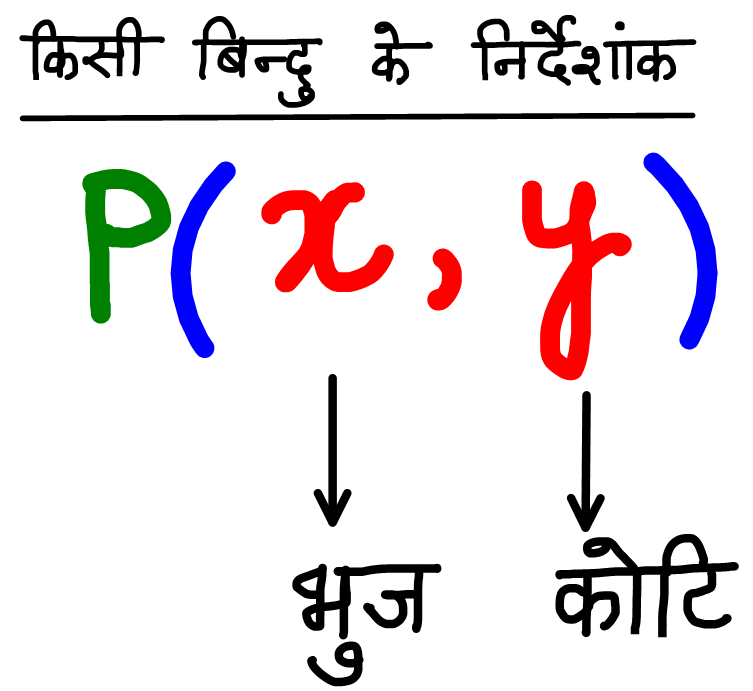
प्यारे बच्चों किसी बिन्दु की x–अक्ष से दूरी उस बिन्दु का y–निर्देशांक (y–coordinate) कहलाता है।
क्रमित युग्म प्यारे बच्चों क्रमित का अर्थ होता है क्रम से और युग्म का अर्थ होता है जोड़ा , इस प्रकार क्रमित युग्म का मतलब होता है कि x तथा y अक्ष के मान को हम क्रम से लिखते हैं तो वो एक युग्म (जोड़ा ) माना जाता है या हम यह भी कह सकते हैं कि x तथा y के संगत मान मिलकर क्रमित युग्म बनाते हैं | हम जानते हैं कि किसी भी बिन्दु के निर्देशांक में सबसे पहले उस बिन्दु का x निर्देशांक लिखा जाता है तथा इसके बाद " , " लगाकर फिर y निर्देशांक लिखा जाता है | माना कोई बिन्दु P है तब क्रमित युग्म होगा :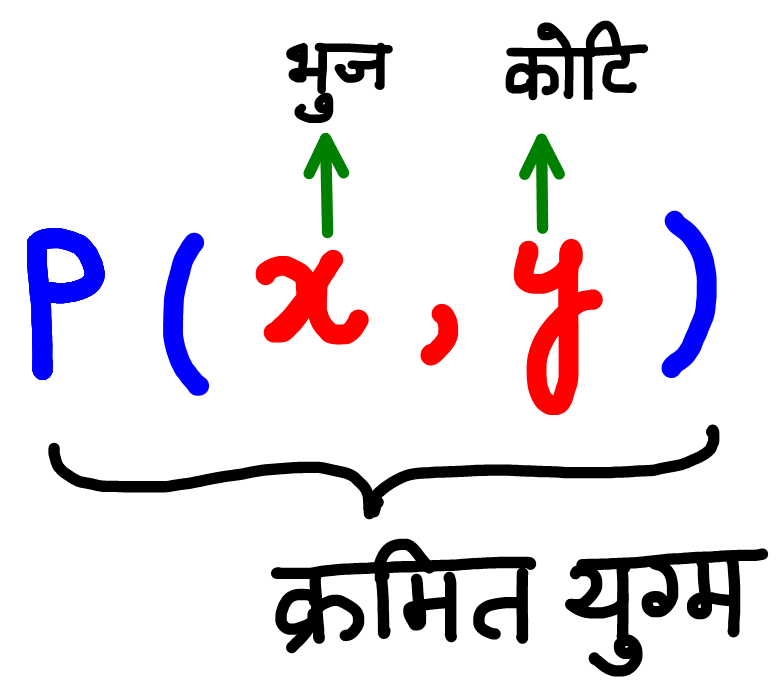
भुज तथा कोटि
भुज तथा कोटि : किसी बिन्दु के x− निर्देशांक को उस बिन्दु का भुज (abscissa) तथा y– निर्देशांक को उस बिन्दु की कोटि (ordinate) भी कहा जाता है। 
उदाहरण : बिन्दु (3,-5) में भुज तथा कोटि बताइए |
अब चूंकि यहाँ बिन्दु का x निर्देशांक 3 है तथा y निर्देशांक −5 है इसलिए
भुज = 3 , कोटि = -5
OMR (One Minute Revision)
∗ कार्तीय तल में (x,y) की स्थिति (y, x) की स्थिति से भिन्न होती है। अतः यदि हम निर्देशांकों x और y में अदला-बदली करें, तो (y, x) की स्थिति (x, y) की स्थिति से भिन्न हो जाएगी। इससे यह अर्थ निकलता है कि (x, y) में x और y के क्रम का काफी महत्व होता है। क्रमित युग्म (x, y) ≠ क्रमित युग्म (y, x), यदि x ≠ y है और (x, y) = (y, x), यदि x = y है |
चिन्ह परिपाटी
किसी बिन्दु के चिन्ह ( Signs of a point ) : माना किसी समतल में क्षैतिज अक्ष XOX' तथा ऊर्ध्वाधर अक्ष YOY'है। मूल बिंदु से दायीं ओर का क्षैतिज अक्ष धन OX−अक्ष कहलाता है तथा बायीं ओंर का क्षैतिज अक्ष ऋण OX'−अक्ष कहलाता है। इसी प्रकार मूल बिंदु से ऊर्ध्वाधर ऊपर की ओंर धन OY−अक्ष तथा नीचे की ओंर ऋण OY'−अक्ष होता है। प्रथम चतुर्थांश में वे क्रमित युग्म होते है जिनके भुज तथा कोटि दोनों धनात्मक हो (+,+) ,द्वितीय चतुर्थांश में वे युग्म होंगे जिनके भुज ऋणात्मक तथा कोटि धनात्मक हो (−,+),तृतीय चतुर्थांश में आने वाले क्रमित युग्मो के भुज तथा कोटि दोनों ऋणात्मक होंगे (−,−), इसी प्रकार चतुर्थ चतुर्थांश में जो क्रमित युग्म आएंगे उनके भुज धनात्मक तथा कोटि ऋणात्मक होंगे(+,−)(आकृति देखिए)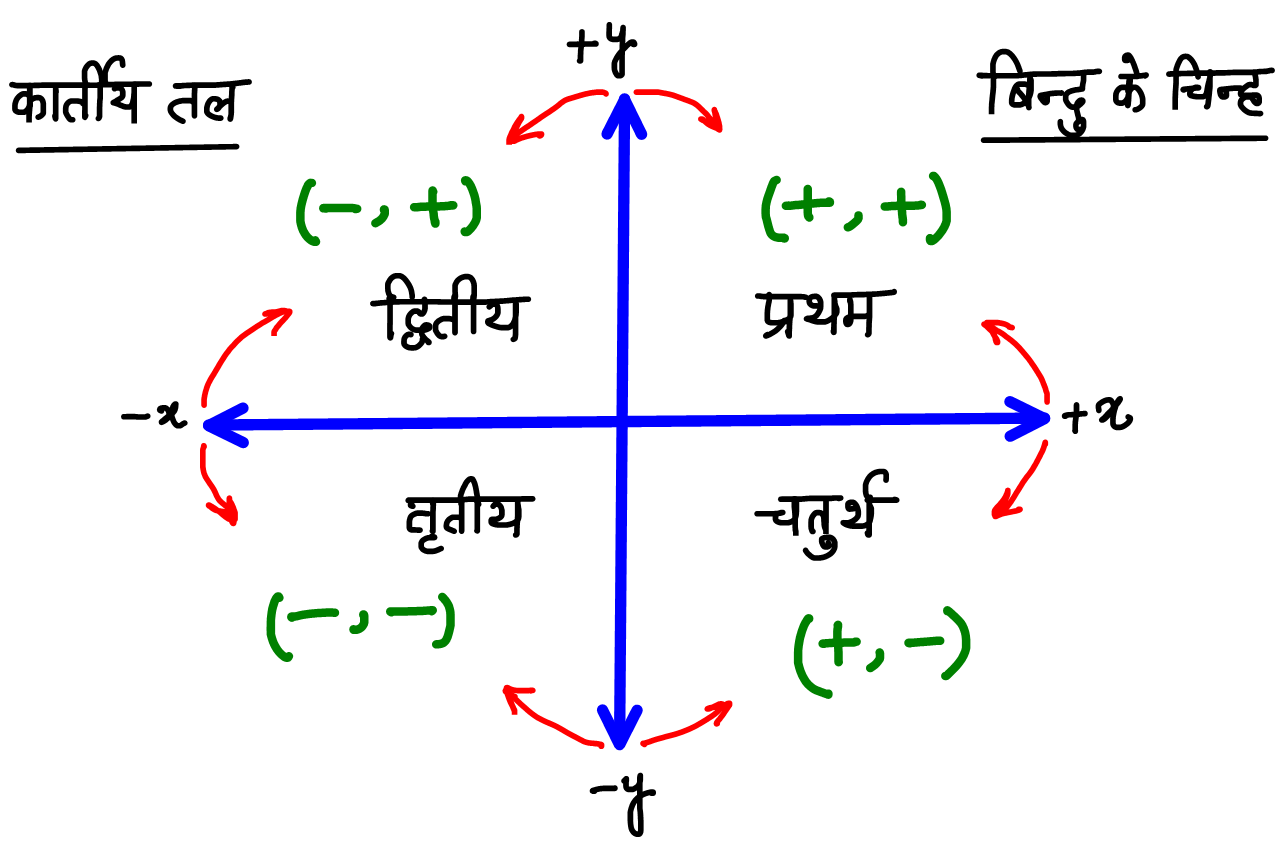
अक्षों पर स्थित किसी बिंदु के निर्देशांक -X−अक्ष में स्थित क्रमित युग्म की कोटि सदैव शून्य होती है अर्थात x अक्ष पर स्थित किसी भी बिन्दु के निर्देशांक (x,0) रूप के होंगें तथा इसी प्रकर Y−अक्ष में स्थित क्रमित युग्म का भुज सदैव शून्य होते है,अर्थात y अक्ष पर जितने भी बिन्दु स्थित होते हैं उन सबके निर्देशांक (0,y) के रूप के होते हैं |
OMR (One Minute Revision)
∗ एक तल में स्थित एक बिन्दु की व्याख्या करने के संबंध में ऊपर हमने जिस पद्धति के बारे में चर्चा की है, वह केवल एक परंपरा है जिसको पूरे विश्व में स्वीकार किया जाता है। उदाहरण के लिए, पद्धति में ऐसा भी हो सकता है कि पहले कोटि लिखी जाए और उसके बाद भुज लिखा जाए। फिर भी, जिस पद्धति का उल्लेख हमने किया है उसे पूरा विश्व बिना किसी भ्रम के स्वीकार करता है।
∗x अक्ष का समीकरण x अक्ष का समीकरण y=0 होता है क्योंकि पूरे x अक्ष पर स्थित किसी भी बिन्दु का y निर्देशांक = 0 होता है |
∗ y अक्ष का समीकरण इसी प्रकार y अक्ष का समीकरण x=0 होता है क्योंकि पूरे y अक्ष पर स्थित किसी भी बिन्दु का x निर्देशांक = 0 होता है |
तल में एक बिन्दु आलेखित करना जबकि इसके निर्देशांक दिए हुए हों
अभी तक हमने बिन्दु खींचे हैं और आपसे उनके निर्देशांक बताने के लिए कहा है। अब हम यह अध्ययन करेंगें कि तल में इन बिन्दुओं को किस प्रकार अंकित करते हैं जबकि इनके निर्देशांक हमें ज्ञात हों। इस प्रक्रम को हम “बिन्दु का आलेखन" (plotting the _point) कहते हैं।मान लीजिए एक बिन्दु के निर्देशांक (3, 5) हैं। हम इस बिन्दु को निर्देशांक तल में आलेखित करना चाहते हैं। हम निर्देशांक अक्ष खींचते हैं और अपने एककों का चयन इस प्रकार करते हैं कि दोनों अक्षों पर एक सेंटीमीटर एक एकक को निरूपित करता हो। बिन्दु (3, 5) के निर्देशांक से हमें यह पता चलता है कि धनात्मक x-अक्ष पर इस बिन्दु की y-अक्ष से दूरी 3 एकक है और धनात्मक y-अक्ष पर इस बिन्दु की x-अक्ष से दूरी 5 एकक है। 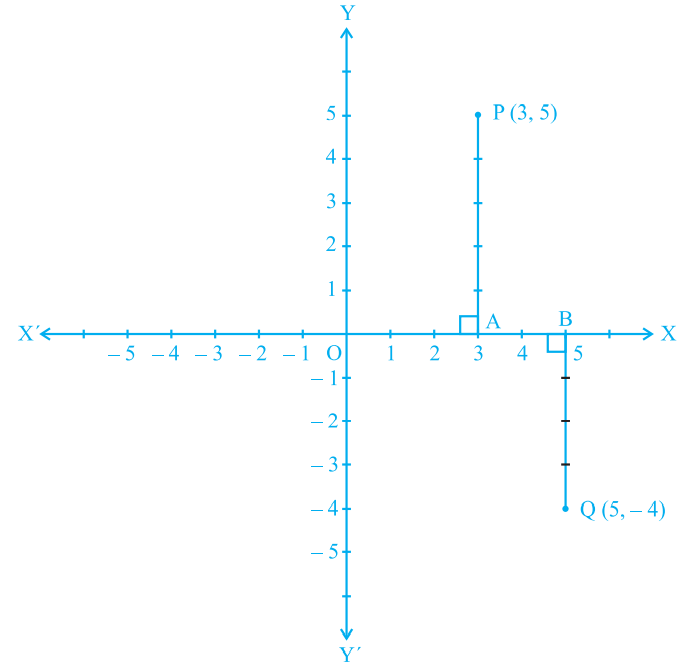
मूलबिन्दु O से प्रारंभ करके हम धनात्मक x-अक्ष पर 3 एकक की गिनती करते हैं और संगत बिन्दु को A के रूप में अंकित करते हैं। अब A से प्रारंभ करके हम y-अक्ष की धनात्मक दिशा में चलते हैं और 5 एकक की गिनती करते हैं तथा संगत बिन्दु को P के रूप में अंकित करते हैं (देखिए आकृति )। आप यहाँ यह देखते हैं कि y-अक्ष से P की दूरी 3 एकक है और x - अक्ष से 5 एकक है। अतः P विचाराधीन बिन्दु की स्थिति है। ध्यान दीजिए कि P पहले चतुर्थांश में स्थित है, क्योंकि P के दोनों निर्देशांक धनात्मक हैं।
उदाहरण 4 :
कार्तीय तल में बिन्दुओं (5, 0), (0, 5), (2, 5), (5, 2), (-3, 5), (-3, -5), (5, -3) और (6, 1) का स्थान निर्धारण कीजिए।
1cm = 1 एकक लेकर हम x-अक्ष और y-अक्ष खींचते हैं। बिन्दुओं की स्थितियों को आकृति में गहरे बिन्दुओं से दिखाया गया है 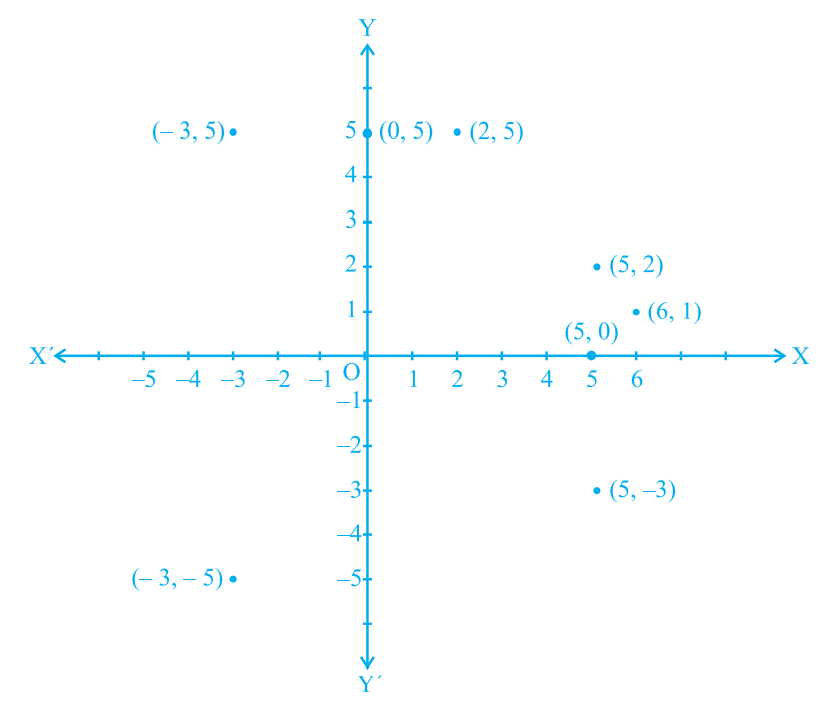
उदाहरण 5 :
निम्नलिखित संख्या-युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए। अक्षों पर पैमाना 1 सेंटीमीटर = 1 एकक लीजिए।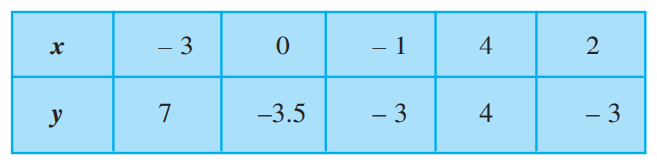
सारणी में दिए गए संख्या-युग्मों को बिन्दुओं (-3, 7), (0, -3.5), (- 1, - 3), (4, 4) और (2,-3) से निरूपित किया जा सकता है। बिन्दुओं के स्थानों को आकृति में गहरे बिन्दुओं से दिखाया गया है।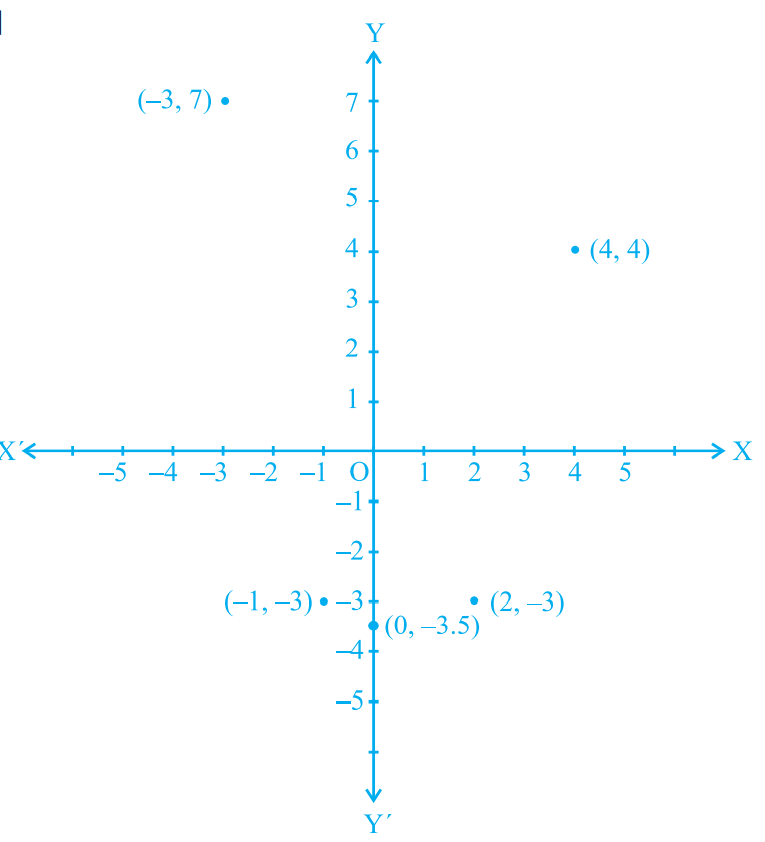
OMR (One Minute Revision)
∗ प्यारे बच्चों पूरे x अक्ष पर y निर्देशांक 0 शून्य होता है इसी प्रकार पूरे y अक्ष पर x निर्देशांक 0 (शून्य ) होता है |
∗ कार्तीय तल में बिन्दुओं के आलेखन की तुलना कुछ सीमा तक समय-दूरी ग्राफ, भुजा-परिमाप ग्राफ, आदि जिनका अध्ययन आप पिछली कक्षाओं में कर चुके हैं, जैसी विभिन्न स्थितियों से की जा सकती है। ऐसी स्थिति में, x-अक्ष और y-अक्ष के स्थान पर अक्षों को t-अक्ष, d-अक्ष, s-अक्ष या p-अक्ष आदि कह सकते हैं।
परीक्षा के लिए स्मरणीय बिन्दु
∗ निर्देशांक ज्यामितीय (Coordinate Geometry): वास्तव में निर्देशांक ज्यामितीय किसी वस्तु या बिंदु की अक्षों के सापेक्ष स्थिति को दर्शाता है।
∗ किसी बिंदु को समतल में प्रदर्शित करने की व्याख्या सर्वप्रथम फ्रांसीसी गणितज्ञ रेने दकार्ते ने की थी।
∗ कार्तीय पद्धति ( Cartesian System) : तल में स्थित किसी बिन्दु की स्थिति का निर्धारण करने में प्रयुक्त पद्धति को दकार्ते के सम्मान में कार्तीय पद्धति कहा जाता है
∗ संख्या रेखा (Number Line): किसी बिंदु का स्थान निर्धारण करना हो तो हमें दो संख्या रेखा की आवश्यकता होती है जो उस तल को दो लंबवत अक्षों में विभाजित करते हैं |
∗ X− अक्ष या क्षैतिज संख्या रेखा : जो संख्या रेखा क्षैतिज रूप से आधार यानि जमीन के सहारे लेटी हुई होती है उसे X− अक्ष कहते हैं |
∗ Y− अक्ष या क्षैतिज संख्या रेखा : जो संख्या रेखा बिल्कुल सीधी खड़ी होती है ठीक 90∘ के कोण पर उसे हम ऊर्ध्वाधर रेखा या Y− अक्ष कहते है।
∗ मूलबिंदु (Origin) : कार्तीय तल में जिस बिंदु पर X− अक्ष तथा Y− अक्ष एक दूसरे को प्रतिच्छेद करते है उसे मूलबिंदु कहते है।
मूलबिंदु के निर्देशांक (0,0) होते हैं |
∗ एकक दूरी (Unit Distance): प्यारे बच्चों हम संख्याओं को संख्या रेखा पर दर्शाने के लिए , दो संख्याओं के बीच में जो दूरी लेते हैं उस नियत दूरी को एक एकक दूरी कहते हैं |
∗ चतुर्थांश (Quadrants) : दोनों अक्ष क्रमशः अक्ष XOX' तथा YOY' और मूलबिंदु Oतीनों मिलकर समतल को चार बराबर भागों में विभाजित करते है जिन्हे चतुर्थांश कहते है।
∗ चार चतुर्थांश : हमारे पास चार चतुर्थांश होते हैं : प्रथम , द्वितीय , तृतीय तथा चतुर्थ
∗ चतुर्थांशों में स्थित किसी बिन्दु के चिन्ह :
(i) प्रथम चतुर्थांश ⇒(+,+)
(ii) द्वितीय चतुर्थांश ⇒(−,+)
(iii) तृतीय चतुर्थांश ⇒(−,−)
(iv) चतुर्थ चतुर्थांश ⇒(+,−)
∗ किसी बिन्दु के निर्देशांक : कार्तीय तल में स्थित किसी बिन्दु के निर्देशांक में सबसे पहले उसका x निर्देशांक फिर उसका y निर्देशांक लिखा जाता है , अर्थात P(x,y)
∗ भुज तथा कोटि (Abscissa & ordinate): किसी बिन्दु के x− निर्देशांक को उस बिन्दु का भुज तथा y– निर्देशांक को उस बिन्दु की कोटि भी कहा जाता है।
∗ क्रमित युग्म (Ordered Pair) : क्रमित युग्म का मतलब होता है कि x तथा y अक्ष के मान को हम क्रम से लिखते हैं तो वो एक युग्म (जोड़ा ) माना जाता है या हम यह भी कह सकते हैं कि x तथा y के संगत मान मिलकर क्रमित युग्म बनाते हैं |
∗ x−अक्ष पर एक बिन्दु के निर्देशांक (x,0) के रूप के होते हैं और y−अक्ष पर बिन्दु के निर्देशांक (0,y) के रूप के होते हैं।
∗ यदि x ≠ y हो, तो (x, y) ≠ (y, x) होगा और यदि x = y हो, तो (x, y) = (y, x) होगा।
∗ xतथा y अक्ष का समीकरण x का समीकरण y=0 होता है और y अक्ष का समीकरण x=0 होता है |
सारांश
इस अध्याय में, आपने निम्नलिखित बिन्दुओं का अध्ययन किया है:
1. एक तल में एक वस्तु या एक बिन्दु का स्थान निर्धारण करने के लिए दो लांबिक रेखाओं की आवश्यकता होती है जिसमें एक क्षैतिज होती है और दूसरी ऊर्ध्वाधर होती है।
2. तल को कार्तीय या निर्देशांक तल कहा जाता है और रेखाओं को निर्देशांक अक्ष कहा जाता
3. क्षैतिज रेखा को x -अक्ष और ऊर्ध्वाधर रेखा को y-अक्ष कहा जाता है।
4. निर्देशांक अक्ष तल को चार भागों में बाँट देते हैं, जिन्हें चतुर्थांश कहा जाता है।
5. अक्षों के प्रतिच्छेद बिन्दु को मूलबिन्दु कहा जाता है।
6. y - अक्ष से किसी बिन्दु की दूरी को उसका x-निर्देशांक या भुज कहा जाता है। साथ ही, x-अक्ष से बिन्दु की दूरी को y-निर्देशांक या कोटि कहा जाता है।
7. यदि एक बिन्दु का भुज x हो और कोटि । हो, तो (x, y) को बिन्दु के निर्देशांक कहा जाता है।
8. x-अक्ष पर एक बिन्दु के निर्देशांक (x, 0) के रूप के होते हैं और y-अक्ष पर बिन्दु के निर्देशांक (0, y) के रूप के होते हैं।
9. मूलबिन्दु के निर्देशांक (0, 0) होते हैं।
10. एक बिन्दु के निर्देशांक पहले चतुर्थांश में (+, +) के रूप के दूसरे चतुर्थांश में (-, +) के रूप के, तीसरे चतुर्थांश में (-,-) के रूप के और चौथे चतुर्थांश में (+, -) के रूप के होते हैं, जहाँ "+" एक धनात्मक वास्तविक संख्या को और "–" एक ऋणात्मक वास्तविक संख्या को प्रकट करते हैं।
11. यदि x ≠ y हो, तो (x, y) ≠ (y, x) होगा और यदि x = y हो, तो (x, y) = (y, x) होगा।